PSEB 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.4

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.4

जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) लीजिए।

प्रश्न 1.
निम्न त्रिज्या वाले गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए :
(i) 10.5 cm
(ii) 5.6 cm
(iii) 14 cm
हल :
गोले की त्रिज्या = 105 cm
∴ गोले का पृष्ठीय क्षेत्रफल = 4πR²
= 4 × \(\frac{22}{7}\) × 10.5 × 10.5 cm²
= 4 × \(\frac{22}{7} \times \frac{56}{10} \times \frac{56}{10}\) cm²
= 1386 cm²

(ii) गोले की त्रिज्या = 5.6 cm
गोले का पृष्ठीय क्षेत्रफल
= 4πR² = 4 × \(\frac{22}{7}\) × 5.6 × 5.6
= 4 × \(\frac{22}{7} \times \frac{56}{10} \times \frac{56}{10}\)
= 394.24 cm²

(iii) गोले की त्रिज्या = 14 cm
गोले का पृष्ठीय क्षेत्रफल
= 4πR² = 4 × \(\frac{22}{7}\) × 14 × 14 cm²
= 2464 cm²

प्रश्न 2.
निम्न व्यास वाले गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए :
(i) 14 cm
(ii) 21 cm
(iii) 3.5 m
हल :
(i) गोले का व्यास = 14 cm
गोले की त्रिज्या, R = \(\frac{14}{2}\) = 7 cm
गोले का पृष्ठीय = 4πR²
= 4 × \(\frac{22}{7}\) × 7 × 7 = 616 cm²

(ii) गोले का व्यास = 21 cm
गोले की त्रिज्या, R = \(\frac{21}{2}\) cm
गोले का पृष्ठीय क्षेत्रफल
= 4πR² = 4 × \(\frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}\)
= 1386 cm²

(iii) गोले का व्यास = 3.5 cm
गोले की त्रिज्या, R = \(\frac{3.5}{2}\) = 1.75 cm
गोले का पृष्ठीय क्षेत्रफल = 4πR²
= 4 × \(\frac{22}{7}\) × 1.75 × 1.75 cm²
= 4 × \(\frac{22}{7} \times \frac{175}{100} \times \frac{175}{100}\) cm²
= 4 × \(\frac{22}{7} \times \frac{7}{4} \times \frac{7}{4}\) m²
= 38.5 m²

प्रश्न 3.
10 cm त्रिज्या वाले एक अर्ध गोले का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए)
हल:
मान लीजिए अर्ध गोले की त्रिज्या = r cm
∴ r = 10 cm

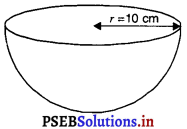
अर्ध गोले का कुल पृष्ठीय क्षेत्रफल = वक्र पृष्ठीय क्षेत्रफल + ऊपरी वृत्ताकार भाग का क्षेत्रफल
= 2πr + πr²
= 3πr²
= 3 × 3.14 × (10)² cm
= 3 × \(\frac{314}{100}\) × 100 cm²
= 3 × 314 cm²
= 942 cm²
अतः, अर्धगोले का कुल पृष्ठीय क्षेत्रफल 942 cm² है।

प्रश्न 4.
एक गोलाकार गुब्बारे में हवा भरने पर, उसकी त्रिज्या 7 cm से 14 cm हो जाती है। इन दोनों स्थितियों में, गुब्बारे के पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :
पहली स्थिति में
गुब्बारे की त्रिज्या ; r = 7 cm
∴ गुब्बारे का पृष्ठीय क्षेत्रफल = 4πr²
= 4π × 7 × 7 cm² (I)

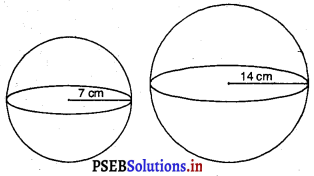
दूसरी स्थिति में
गुब्बारे की त्रिज्या ; R = 14 cm
∴ गुब्बारे का पृष्ठीय क्षेत्रफल = 4πr²
= 4π × 14 × 14 cm² (II)
अब, पृष्ठीय क्षेत्रफलों में अनुपात

अतः, वांछित अनुपात = 1 : 4

प्रश्न 5.
पीतल से बने एक अर्धगोलाकार कटोरे का आंतरिक व्यास 10.5 cm है। 16 रुपए प्रति 100 cm² की दर से इसके आंतरिक पृष्ठ पर कलई कराने का व्यय ज्ञात कीजिए।
हल :
कटोरे का आंतरिक व्यास = 10.5 cm
कटोरे की आंतरिक त्रिज्या
r = \(\frac{10.5}{2}\) = 5.25 cm

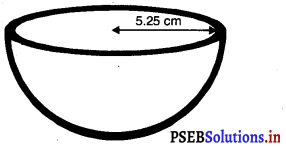
∵ कटोरा अर्धगोलाकार है
∴ कटोरे का आंतरिक पृष्ठीय क्षेत्रफल = 2πr²

100 cm² पृष्ठ पर कलई कराने का व्यय = 16 रु
1 cm² पृष्ठ पर कलई कराने का व्यय = \(\frac{16}{100}\) रु
\(\frac{693}{4}\) cm² पृष्ठ पर कलाई कराने का व्यय
= \(\frac{16}{100} \times \frac{693}{4}\) = 27.72 रु०

प्रश्न 6.
उसे गोले की त्रिज्या ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 154 cm² है।
हल :
गोले का पृष्ठीय क्षेत्रफल = 154 m²
मान लीजिए गोले की त्रिज्या = R
∴ 4πR² = 15
या 4 × \(\frac{22}{7}\) × R² = 154
या R² = 154 × \(\frac{7}{22} \times \frac{1}{4}=\frac{7 \times 7}{4}=\frac{49}{4}\)
या, R = \(\sqrt{\frac{49}{4}}\) = \(\frac{7}{2}\) = 3.5 cm

प्रश्न 7.
चन्द्रमा का व्यास पृथ्वी के व्यास का लगभग एक चौथाई है। इन दोनों के पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :
मान लीजिए पृथ्वी का व्यास = x

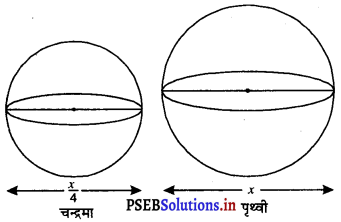
∴ पृथ्वी की त्रिज्या ; R = \(\frac{x}{2}\)
∵ क्योंकि पृथ्वी को गोलाकार माना गया है
∴ पृथ्वी का पृष्ठीय क्षेत्रफल = 4πR²
= 4π × \(\frac{x}{2} \times \frac{x}{2}\)
= π × x ……(i)
अब चंद्रमा का व्यास
= पृथ्वी के व्यास का \(\frac{1}{4}\) भाग
∴ चंद्रमा की त्रिज्या कह लीजिए,
= \(\frac{1}{4}\) × x = \(\frac{x}{4}\)
चंदरमा की त्रिज्या ; r = \(\frac{x}{4 \times 2}=\frac{x}{8}\)
∵ चंद्रमा भी गोलाकार है
∴ चंद्रमा का पृष्ठीय क्षेत्रफल
= 4πr² = 4 × π × \(\frac{x}{8} \times \frac{x}{8}\)
= \(\frac{\pi \times x^2}{16}\) ….(ii)

वांछित अनुपात = 1 : 16

प्रश्न 8.
एक अर्धगोलाकार कटोरा 0.25 cm मोटी स्टील से बना है। इस कटोरे की आंतरिक त्रिज्या 5 cm है। कटोरे का बाहरी वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :
कटोरे की आंतरिक त्रिज्या ; r = 5 cm
स्टील की मोटाई ; t = 0.25 cm
कटोरे की बाहरी त्रिज्या ; R = r + t
= 5 + 0.25 = 5.25 cm
कटोरे का बाहरी पृष्ठीय क्षेत्रफल = 2πR²

प्रश्न 9.
एक लंब वृत्तीय बेलन त्रिज्या वाले एक गोले को पूर्णतया घेरे हुए है (देखिए आकृति) ज्ञात कीजिए :
(i) गोले का पृष्ठीय क्षेत्रफल
(ii) बेलन का वक्र पृष्ठीय क्षेत्रफल
(iii) ऊपर (i) और (ii) में प्राप्त क्षेत्रफल का अनुपात

हल :
(i) गोले की त्रिज्या = r
∴ गोले का पृष्ठीय क्षेत्रफल = 4π²
(ii) ∵ गोला बेलन के अंतर्गत है।
∴ बेलन की ऊँचाई गोले के व्यास तथा बेलन की त्रिज्या गोले की त्रिज्या के बराबर होगी।
अब बेलन की त्रिज्या = r
बेलन की ऊँचाई h = 2r
∴ बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2πr × 2r [∵ h = 2r]
= 4πr²

∴ वांछित अनुपात = 1 : 1