PSEB 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.6

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.6 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.6

जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) लीजिए।

प्रश्न 1.
एक बेलनाकार बर्तन के आधार की परिधि 132 cm और उसकी ऊँचाई 25 cm है। इस बर्तन में कितने लीटर पानी आ सकता है ?(1000 cm³ = 1लीटर)
हल :
बर्तन के आधार की परिधि = 132 cm

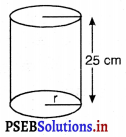
मान लीजिए आधार की त्रिज्या = r
∵ बेलन का आधार वृत्तीय है।
∴ πrh = 132
या 2 × \(\frac{22}{7}\) × r = 132
या r = 132 × \(\frac{1}{2}\) × \(\frac{7}{22}\) = 21 cm
बर्तन की ऊँचाई h = 25 cm
बर्तन का आयतन = बेलन का आयतन
= πr²h
= \(\frac{22}{7}\) × 21 × 21 × 35 = 34650 cm³
= \(\frac{34650}{1000}\) लीटर
[∵ 1000 cm³ = 1 लीटर]
= 34.65 लीटर

प्रश्न 2.
लकड़ी के एक बेलनाकार पाइप का आंतरिक व्यास 24 cm है और बाहरी व्यास 28 cm है। इस पाइप की लंबाई 35 cm है। इस पाइप का द्रव्यमान ज्ञात कीजिए, यदि 1 cm³ लकड़ी का द्रव्यमान 0.6 ग्राम है।
हल :
बेलनाकार पाइप का आंतरिक व्यास = 24 cm
∴ पाइप की आंतरिक त्रिज्या r = \(\frac{24}{2}\) = 12 cm

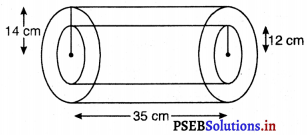
पाइप का बाह्य व्यास = 28 cm
∴ पाइप की बाह्य त्रिज्या R = \(\frac{28}{2}\) = 14 cm
पाइप की लंबाई = 35 cm
लकड़ी का आयतन = बेलन का बाह्य आयतन – बेलन का आंतरिक आयतन
= πR²h – πr²h
[पाइप की लंबाई को बेलन की ऊंचाई के रूप में प्रयोग करने पर]
= πh (R² – r²)
= \(\frac{22}{7}\) × 35[(14)² – (12)²]
= 110 [196 – 144] = 110 × 52
= 5720 cm³
1 cm³ लकड़ी का द्रव्यमान = 0.6 g
5720 cm³ लकड़ी का द्रव्यमान = 0.6 × 5720 = 3432 g
= \(\frac{3432}{1000}\) kg [∵ 1000 g = 1 kg.]
= 3.432 kg.

प्रश्न 3.
एक सोफ्ट ड्रिंक (soft drink) दो प्रकार के पैकों में उपलब्ध है : (i) लंबाई 5 cm और चौड़ाई 4 cm वाले एक आयताकार आधार का टिन का डिब्बा जिसकी ऊँचाई 15 cm है और (ii) व्यास 7 cm वाले वृत्तीय आधार और 10 cm ऊँचाई वाला एक प्लास्टिक का बेलनाकार डिब्बा। किस डिब्बे की धारिता अधिक है और कितनी अधिक है ?
हल :

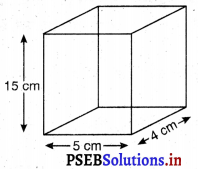
पहली स्थिति में :
आयताकार आधार की लंबाई = 5 cm
आयताकार आधार की चौड़ाई = 4 cm
टिन के डिब्बे की ऊँचाई = 15 cm
टिन के डिब्बे का आयतन = लंबाई × चौड़ाई × ऊँचाई
= 5 cm × 4 cm × 15 cm
= 300 cm³ …. (I)
दूसरी स्थिति में :

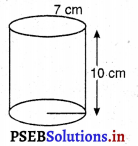
बेलन के आधार का व्यास = 7 cm
∴ बेलन के आधार की त्रिज्या ; r = \(\frac{7}{2}\) cm
बेलन की ऊँचाई ; h = 10 cm
बेलन की धारिता = बेलन का आयतन
= πr²h
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 10\)
= 11 × 7 × 5 = 385 cm³ … (II)
I और II से,
बेलनाकार डिब्बे की धारिता (385 – 300) = 85 cm³ अधिक है।

प्रश्न 4.
यदि एक बेलन का पार्श्व पृष्ठीय क्षेत्रफल 94.2 cm² है और उसकी ऊँचाई 5 cm है, तो ज्ञात कीजिए : (i) आधार की त्रिज्या (ii) बेलन का आयतन (π = 3.14 लीजिए)
हल :
बेलन का पार्श्व पृष्ठीय क्षेत्रफल = 94.2 cm² … (1)
बेलन की ऊँचाई ; h = 5 cm
मान लीजिए कि आधार की त्रिज्या = r
∴ बेलन का पार्श्व पृष्ठीय क्षेत्रफल = 2πrh
= 2 × 3.14 × r × 5
= 31.4r …. (II)
समीकरण I और II से,
31.4r = 94.2
या, r = \(\frac{94.2}{31.4}\) = 3 cm
बेलन की आयतन = πr²h
= 3.14 × 3 × 3 × 5 = 141.3 cm³.

प्रश्न 5.
10 m गहरे एक बेलनाकार बर्तन की आंतरिक वक्र पृष्ठ को पेंट कराने का व्यय 2200 रुपए है। यदि पेंट कराने की दर 20 रुपए प्रति m है, तो ज्ञात कीजिए :
(i) बर्तन की आंतरिक वक्र पृष्ठीय क्षेत्रफल
(ii) आधार की त्रिज्या
(iii) बर्तन की धारिता
हल :
बर्तन के आतंरिक वक्र पृष्ठीय क्षेत्रफल को पेंट करने पर कुल व्यय = 2200 रु०
दर = 20 रु० प्रति m²
(i) बर्तन का आंतरिक वक्र पृष्ठीय क्षेत्रफल

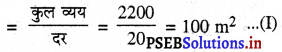
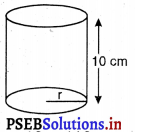
(ii) बर्तन की गहराई ; h = 10 m
मान लीजिए आधार की त्रिज्या = r
∴ बर्तन का आंतरिक पृष्ठीय क्षेत्रफल = 2πrh
= 2 × \(\frac{22}{7}\) × r × 10 …(II)
∴ I और II, से

2 × \(\frac{22}{7}\) × r × 10 = 110
या, r = 110 × \(\frac{1}{2} \times \frac{7}{22} \times \frac{1}{10}\) = 1.75 m

(iii) अब, r = 1.75 m
h = 10 m
∴ बर्तन की धारिता = बेलन का आयतन
= πr²h
= \(\frac{22}{7}\) × 1.75 × 1.75 × 10
= 96.25 m³
= 96.25 किलोलीटर
[∵ 1m³ = 1 किलो लीटर]

प्रश्न 6.
ऊँचाई 1 m वाले एक बेलनाकार बर्तन की धारिता 15.4 लीटर है। इसको बनाने के लिए कितने वर्ग मीटर धातु की शीट की आवश्यकता होगी ? (1000 l = 1m³)
हल :
बर्तन की ऊँचाई ; h = 1 m,
बर्तन की धारिता= 15.4 l
= \(\frac{15.4}{1000}\) = 0.0154 m³ …(i)
[∵ 1000 l = 1 m³]
मान लीजिए बर्तन के आधार की त्रिज्या = r
∴ πr²h = 0.0154
या, \(\frac{22}{7}\) × r² × 1 = 0.0154
या, r² = 0.0154 × \(\frac{7}{22}\)
= 0.0007 × 7 = 0.0049
या, r = \(\sqrt{0.0049}\) = 0.07 m

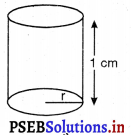
∴ बर्तन बंद बेलनाकार है।
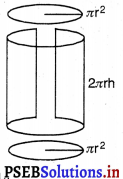
∴ बर्तन बनाने में लगी धातु का क्षेत्रफल = बर्तन का वक्र पृष्ठीय क्षेत्रफल + दो वृत्ताकार ढक्कनों का क्षेत्रफल
= 2πrh + 2πr²
= 2πr (h + r)
= 2 × \(\frac{22}{7}\) × 0.07(1 + 0.07)

= \(\frac{44}{7}\) × 0.07 × 1.07
= 44 × 0.01 × 1.07
= 0.4708 m²

प्रश्न 7.
सीसे की एक पेंसिल (lead pencil) लकड़ी के एक बेलन के अभ्यंतर में ग्रेफाइट (graphite) से बने ठोस बेलन को डाल कर बनाई गई है। पेंसिल का व्यास 7 mm है और ग्रेफाइट का व्यास 1 mm है। यदि पेंसिल की लंबाई 14 cm है, तो लकड़ी का आयतन और ग्रेफाइट का आयतन ज्ञात कीजिए।
हल :
मान लीजिए ग्रेफाइट की त्रिज्या = r
∴ व्यास 2r = 1 मिमी.

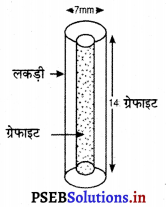
⇒ r = \(\frac{1}{2}\) mm = \(\frac{1}{2}\) × \(\frac{1}{10}\) cm = \(\frac{1}{20}\) cm
ग्रेफाइट की ऊँचाई = h = 14 cm
ग्रेफाइट का आयतन = πr²h

मान लीजिए पेंसिल की त्रिज्या = R
∴ व्यास 2R = 7 मिमी
⇒ R = \(\frac{7}{2}\) मिमी.
= \(\frac{7}{2}\) x \(\frac{1}{10}\) cm
[∵ 10 मिमी. = 1 m; ∴ 1 मिमी. = \(\frac{1}{10}\) cm]
= \(\frac{7}{20}\) cm
लकड़ी का आयतन = πR²h

= 5.39 cm³
लकड़ी का आयतन = पेंसिल का आयतन – ग्रेफाइट का आयतन
= (5.39 – 0.11) cm³
= 5.28 cm³.

प्रश्न 8.
एक अस्पताल (hospital) के एक रोगी को प्रतिदिन 7 cm व्यास वाले एक बेलनाकार कटोरे में सूप (soup) दिया जाता है। यदि यह कटोरा सूप से 4 cm ऊँचाई तक भरा जाता है, तो इस अस्पताल में 250 रोगियों के लिए प्रतिदिन कितना सूप तैयार किया जाता है ?
हल :
मान लीजिए बेलनाकार कटोरे के वृत्तीय आधार की त्रिज्या = r
∴ व्यास ; 2r = 7 cm

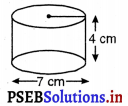
⇒ r = \(\frac{7}{2}\) cm
कटोरे की ऊँचाई = h = 4 cm
बेलनाकार कटोरे का आयतन = πr2h

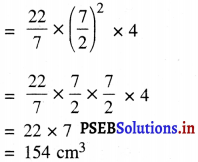
कटोरा पूरी तरह सूप से भरा हुआ है
∴ एक कटोरे में भरे गये सूप की मात्रा = 154 cm³
ऐसे 250 कटोरे रोगियों को दिए जाते हैं
अतः, अस्पताल द्वारा तैयार किए गए सूप की कुल मात्रा
= (250 × 154) cm³
= 38500 cm³
= \(\frac{38500}{1000}\) लीटर
[∵ लीटर = 1000 cm³]
= 38.5 लीटर