PSEB 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.8

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.8 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.8

जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) लीजिए।

प्रश्न 1.
उस गोले का आयतन ज्ञात कीजिए जिसकी त्रिज्या निम्न है ?
(i) 7 cm
(ii) 0.63 cm
हल :
(i) गोले की त्रि ज्या ; R = 7 cm
गोले का आयतन = \(\frac{4}{3}\)πR³
= \(\frac{4}{3} \times \frac{22}{7}\) × 7 × 7 × 7
= \(\frac{4312}{3}\) cm³
= 1437 \(\frac{1}{3}\) cm³

(ii) गोले की त्रिज्या ; R = 0.63 m
गोले का आयतन = \(\frac{4}{3}\) πr³
= \(\frac{4}{3} \times \frac{22}{7}\) × 0.63 × 0.63 × 0.63 m³

= 1.047816 m³
= 1.05m³ (लगभग)

प्रश्न 2.
एक ठोस गोलाकार गेंद द्वारा हटाए गए (विस्थापित ) पानी का आयतन ज्ञात कीजिए, जिसका व्यास निम्न है :
(i) 28 cm
(ii) 0.21 m
हल :
(i) गोलाकार गेंद का व्यास = 28 cm
गोलाकार गेंद की त्रिज्या = \(\frac{28}{2}\) = 14 cm
[∵ व्यास = 2 त्रिज्या]
विस्थापित पानी गेंद के आयतन के बराबर होगा।
∴ विस्थापित पानी का आयतन = गोलाकार गेंद का आयतन
= \(\frac{4}{3}\) πr³
= \(\frac{4}{3} \times \frac{22}{7}\) × 14 × 14 × 14 cm³
= \(\frac{88}{3}\) × 2 × 14 × 14
= \(\frac{34496}{3}\) cm³ = 11498 \(\frac{2}{3}\) cm³

(ii) गेंद का व्यास = 0.21 m
गेंद की त्रिज्या ; R = \(\frac{0.21}{2}\) m
[∵ व्यास = 2 त्रिज्या]
विस्थापित पानी का आयतन = गोलाकार गेंद का आयतन

प्रश्न 3.
धातु की एक गेंद का व्यास 4.2 cm है। यदि इस धातु का घनत्व 8.9 ग्राम प्रति cm है, तो इस गेंद का द्रव्यमान ज्ञात कीजिए।
हल :
धातु की गेंद का व्यास = 4.2 cm
धातु की गेंद की त्रिज्या ; R = \(\frac{4.2}{2}\) = 2.1 cm
[∵ व्यास = 2 त्रिज्या]
धातु का आयतन = गेंद का आयतन
= \(\frac{4}{3}\) × πr³
= \(\frac{4}{3} \times \frac{22}{7}\) × 2.1 × 2.1 × 2.1 cm³
= \(\frac{88}{21} \times \frac{21}{10} \times \frac{21}{10} \times \frac{21}{10}\) cm³
= 38.808 cm³
धातु का घनत्व = 8.9 ग्राम प्रति cm³
∴ 1 cm = 8.9g
38.808 cm³ का द्रव्यमान = 8.9 × 38.808 ग्राम
=345.3912 g
=345.39 g (लगभग)

प्रश्न 4.
चंद्रमा का व्यास पृथ्वी के व्यास का लगभग एक चौथाई है। चंद्रमा का आयतन पृथ्वी के आयतन की कौन-सी भिन्न है ?
हल :
मान लीजिए पृथ्वी का व्यास = x
∴ पृथ्वी की त्रिज्या R = \(\frac{x}{2}\)
∵ पृथ्वी गोलाकार है।
∴ पृथ्वी का आयतन = \(\frac{4}{3}\) πr³

∴ चंद्रमा का आयतन पृथ्वी के आयतन का \(\frac{1}{64}\) वाँ भाग है।

प्रश्न 5.
व्यास 10.5 cm वाले एक अर्धगोलाकार कटोरे में कितने लीटर दूध आ सकता है ?
हल :
अर्धगोलाकार कटोरे का व्यास = 10.5 cm³
अर्धगोलाकार कटोरे की त्रिज्या R = \(\frac{10.5}{2}\) = 5.25
[∵ व्यास = 2 त्रिज्या]
अर्धगोलाकार कटोरे में दूध का आयतन = अर्धगोले का आयतन
= \(\frac{2}{3}\) × πR³

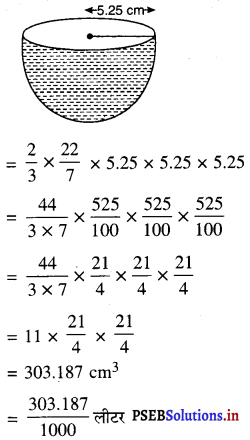
[∵ 1000 cm³ = 1 लीटर]
= 0.303187 लीटर
= 0.303 लीटर

प्रश्न 6.
एक अर्धगोलाकार टंकी 1 cm³ मोटी एक लोहे की चादर (sheet) से बनी है। यदि इसकी आंतरिक त्रिज्या 1 m है तो टंकी के बनाने में लगे लोहे का आयतन ज्ञात कीजिए।
हल :
अर्धगोलाकार टंकी की आंतरिक त्रिज्या = 1m
r = 100 cm³
चादर की मोटाई = 1 cm
∴ अर्धगोलाकार टंकी की बाह्य त्रिज्या
R = 100 + 1 = 101 cm
टंकी को बनाने में प्रयुक्त लोहे का आयतन = बाह्य अर्धगोले का आयतन – आंतरिक अर्धगोले का आयतन

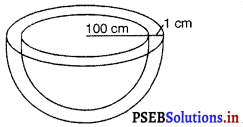
= \(\frac{2}{3}\) × πR³ – \(\frac{2}{3}\) πr³

प्रश्न 7.
उस गोले का आयतन ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 154 cm² है।
हल :
गोले का पृष्ठीय क्षेत्रफल = 154 cm²
मान लीजिए गोले की त्रिज्या = R
∴ 4πR² = 154

प्रश्न 8.
किसी भवन का गुंबद एक अर्धगोले के आकार का है। अंदर से, इसमें सफेदी कराने में ₹ 498.96 रुपए व्यय हुए। यदि सफेदी कराने की दर ₹ 2 रुपये प्रति वर्ग मीटर है, तो ज्ञात कीजिए :
(i) गुंबद का आंतरिक वक्र पृष्ठीय क्षेत्रफल
(ii) गुंबद के अंदर की हवा का आयतन
हल :
सफेदी कराने में कुल व्यय = 498.96 रु
सफेदी कराने की दर = 2.00 रु० प्रति m²
∴ सफेदी किए गए कुल भाग का क्षेत्रफल

∴ गुंबद के आंतरिक पृष्ठीय क्षेत्रफल = 249.48m²
मान लीजिए गुंबद की आंतरिक त्रिज्या = R

गुंबद के अंदर की हवा का आयतन = गोलार्ध गुंबद का आयतन
= \(\frac{2}{3}\) × πR³
= \(\frac{2}{3} \times \frac{22}{7}\) × 6.3 × 6.3 × 6.3
= 44 × 2.1 × 0.9 × 6.3 m³
= 523.9 m³

प्रश्न 9.
लोहे के सत्ताइस ठोस गोलों को पिघलाकर, जिनमें से प्रत्येक की त्रिज्या है और पृष्ठीय क्षेत्रफल S है, एक बड़ा गोला बनाया जाता है जिसका पृष्ठीय क्षेत्रफल S’ है। ज्ञात कीजिए :
(i) नए गोले की त्रिज्या r’
(ii) S और S’ का अनुपात
हल :
गोलों की संख्या = 27
प्रत्येक गोले की त्रिज्या = r
∴ 1 गोले का आयतन = \(\frac{4}{3}\)πr³
गोलों का आयतन = 27 × \(\frac{4}{3}\)πr3 = 36πr³ …(I)
अब इन ठोस गोलों को पिघलाकर r’ त्रिज्या का एक नया गोला बनाया गया है।
∴ नये गोले का आयतन = \(\frac{4}{3}\)πr’³ … (II)
∵ नये गोले का आयतन = 27 गोलों का आयतन
∴ I और II से

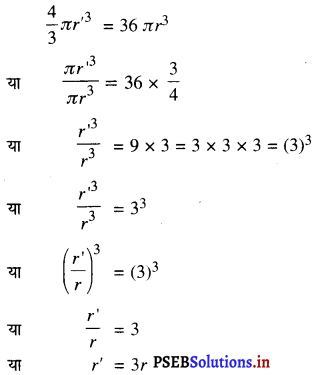
∴ नये गोले की त्रिज्या = 3r
अब दिए गए गोले का पृष्ठीय क्षेत्रफल S और त्रिज्या r है
∴ S = 4πr² …(III)
नये गोले का पृष्ठीय क्षेत्रफल S’ और त्रिज्या r’ है।
∴ S’ = 4 πr’² = 4π (3r)²
[∵ r’ = 3r]
S’ = 4 π × 3r × 3r = 3πr² … (IV)
अब
\(\frac{4}{3}\)
अब
\(\frac{S}{S^{\prime}}=\frac{4 \pi r^2}{36 \pi r^2}=\frac{4}{36}=\frac{1}{9}\)
S : S’ = 1 : 9

प्रश्न 10.
दवाई का एक कैपसूल (capsule) 3.5 mm व्यास का एक गोला (गोली) है। इस कैपसूल को भरने के लिए कितनी दवाई (mm³में) की आवश्यकता होगी ?
हल :
मान लीजिए कैपसूल की त्रिज्या = r
∴ व्यास ; 2 r = 3.5 mm
⇒ r = \(\frac{3.5}{2}\) mm
⇒ r = \(\frac{35}{20}\)
⇒ r = \(\frac{7}{4}\) mm
कैपसूल को भरने के लिए आवश्यक दवाई (mm³ में) = गोले का आयतन