Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 14 सांख्यिकी Ex 14.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 14 सांख्यिकी Ex 14.1
प्रश्न 1.
उन आँकड़ों के पाँच उदाहरण दो जिन्हें आप अपने दैनिक जीवन से एकत्रित कर सकते हो ?
उत्तर :
अपने दैनिक जीवन से एकत्रित किए जाने वाले आँकड़ों में से पाँच आँकड़े निम्नलिखित हैं :
- हमारी कक्षा में छात्रों की संख्या।
- हमारे विद्यालय में पंखों की संख्या।
- हमारे घर का पिछले दो वर्षों से बिजली का बिल।
- टेलीविज़न या समाचार-पत्रों से प्राप्त मतदान परिणाम।
- शैक्षिक सर्वे से प्राप्त साक्षरता दर के आँकड़े।
- आपकी कक्षा के 20 बच्चों की लंबाई।
- टेलीविजन से प्राप्त किसी विशेष सप्ताह में दिनों का अधिकतम तापमान।
इनके और भी विभिन्न उत्तर हो सकते हैं।
![]()
प्रश्न 2.
ऊपर दिए गिए प्रश्न 1 के आँकड़ों को प्राथमिक आँकड़ों या गौण आँकड़ों में वर्गीकृत करो।
हल :
प्राथमिक आँकड़े : (i), (ii), (iii), (vi)
गौण आँकड़े : (iv), (v), (vii)
प्राथमिक आँकड़े : यदि कोई अनुसंधानकर्ता किसी उद्देश्य या योजना को ध्यान में रखकर स्वयं आँकड़ों का संग्रह करता है, तो इन आँकड़ों को प्राथमिक आँकड़े (Primary data) कहते हैं।
गौण आँकड़े : यदि कोई अनुसंधानकर्ता किसी अन्य उद्देश्य के लिए संग्रह किए गए आँकड़ों को अपने अनुसंधान में प्रयोग कर ले तो उन आँकड़ों को गौण आँकड़े (Secondary Data) कहा जाता है। प्राथमिक आँकड़े बहुत अधिक विश्व सनीय और प्रासंगिक होते हैं क्योंकि इन आँकड़ों का संग्रह एक निश्चित योजना या विधि को मन में रखकर प्रेक्षक करता है।
आँकड़ों का प्रस्तुतिकरण (Presentation of Data) : जैसे ही आँकड़ों को एकत्रित करने का कार्य पूरा हो जाता है तो अन्वेषक उसे किसी अर्थपूर्ण और सुगम रूप प्रस्तुत करने की योजना बनाता है।
अपरिष्कृत /अवर्गीकृत आँकड़े : यदि इकट्ठे किए गए आँकड़ों को विधिपूर्वक किसी क्रम में न रखा गया हो तो इन आँकड़ों को अपरिष्कृत/अवर्गीकृत आँकड़े कहा जाता है।
सारणीबद्ध आँकड़े : यदि आँकड़ों को आरोही या अवरोही क्रम में रखा जाए तो उन्हें सारणीबद्ध आँकड़े कहा जाता है।
बारंबारता बंटन सारणी बनाना : बारंबारता बंटन सारणी दिए गए आँकड़ों में भिन्न-भिन्न मानों की बारंबारता दर्शाती है। बारंबारता बंटन सारणी (i) आँकड़ों का विश्लेषण तथा (ii) भिन्न-भिन्न सांख्यिकीय मापों का परिकलन करने के लिए बनाई जाती है।
अवर्गीकृत आँकड़े (खंडित श्रृंखला) :
इस प्रकार के आँकड़ों में विचर का मान भिन्नात्मक नहीं हो सकता। यह मान एक या दो हो सकता है परंतु 1\(\frac{1}{2}\) नहीं हो सकता जितनी बार कोई संख्या आँकड़ों में होती है उसकी गिनती संख्या के सामने लिख दी जाती है। इस गिनती को उसको बारंबारता कहते हैं।
वर्गीकृत आँकड़े (सतत श्रृंखला) [Grouped data (Continuous Series)] :
इन आँकड़ों में विचर आय, भार, लाभ, लंबाई आदि के मान हो सकते हैं, क्योंकि इनके मान भिन्नात्मक हो सकते हैं।
उदाहरण :
| दैनिक आय (रु. में) | 0 – 100 | 100 – 200 | 200 – 300 | 300 – 400 | 400 – 500 |
| व्यक्तियों की संख्या | 15 | 7 | 25 | 10 | 6 |
वर्ग :
प्रत्येक अंतराल जैसे 0-100, 100-200 आदि को वर्ग कहा जाता है।
वर्ग सीमाएँ :
प्रत्येक वर्ग की दो सीमाएँ होती हैं। किसी वर्ग के निम्न मान को निम्न सीमा तथा ऊपरी मान को ऊपरी सीमा कहा जाता है। अर्थात् वर्ग (0-100) में निम्न सीमा 0 तथा ऊपरी सीमा 100 है।
वर्ग-अंतराल या वर्ग आमाप किसी वर्ग की ऊपरी सीमा (U) और निम्न सीमा (L) के अंतर को वर्ग अंतराल कहा जाता है। अर्थात्
i = U – L
उदाहरण : वर्ग (0 – 100) में
i = 100 – 0 = 100
केंद्रीय मान या वर्ग चिहन किसी वर्ग की निम्न सीमा और ऊपरी सीमा के मध्यमानं को उस वर्ग का केंद्रीय मान या वर्ग चिह्न कहा जाता है।
वर्ग चिहन = \(\frac{\mathrm{U}+\mathrm{L}}{2}\)
उदाहरण :
वर्ग (100 – 200) में
वर्ग चिह्न = \(\frac{200+100}{2}\)
= \(\frac{300}{2}\)
= 150
वर्ग बारंबारता :
किसी विशेष वर्ग के आँकड़ों की संख्या, उस वर्ग की बारंबारता कहलाती है। बारंबारता को f से प्रकट किया जाता है। सभी वर्गों की बारंबारता के योग को Zf या N द्वारा दर्शाया जाता है।
वर्गीकृत आँकड़ों के प्रकार :
वर्गीकृत आँकड़े मुख्यतः निम्नलिखित प्रकार के होते
- अनतिव्यापी वर्ग (Inclusive series)
- सतत वर्ग (Exclusive series)
- संचयी बारंबारता सारणी (Cumulative frequency distribution)
- समान वर्ग अंतराल सारणी (Equal class interval series).
अनतिव्यापी वर्गों में पहले वर्ग की ऊपरी सीमा उससे अगले वर्ग की निम्न सीमा से कम होती है। इस सारणी में निम्न सीमा और ऊपरी सीमा वाले आँकड़ों की गिनती वर्ग अंतराल में की जाती है।
| मजदूरी (रु. में) | 10-19 | 20-29 | 30-39 | 40-49 |
| मजदूरों की संख्या (बारंबारता) | 5 | 10 | 12 | 13 |
उदाहरणतया दी गई सारणी में 19, 29, 39 और 49 जिस वर्ग में आते हैं ये उसी वर्ग में आँकड़ों के रूप में ही लिए जाएंगे। इस प्रकार की सारणी में 19 और 20, 29 और 30, 39 और 40 के बीच भिन्नात्मक मानों को नहीं गिना जा सकता।
सतत वर्ग अंतरालों में एक वर्ग की ऊपरी सीमा अगले वर्ग की निम्न सीमा होती है। इसलिए वर्ग की ऊपरी सीमा को उस वर्ग में नहीं गिना जाता और उसे अगले वर्ग में गिना जाता है जिसकी वह निम्न सीमा होती है।
| मजदूरी (रु. में) | 10-20 | 20-30 | 30-40 | 40-50 |
| मजदूरी की संख्या (बारंबारता) | 5 | 10 | 12 | 13 |
अब पहले वर्ग में ऊपरी सीमा 20 से कम मानी जाती है अर्थात् (19.999 …..00) और 20 को इस वर्ग मे नहीं लिया जाता किंतु इसे अगले वर्ग में लिया जाता है। इसी प्रकार हम दूसरे वर्गों के लिए करते हैं।
अनतिव्यापी वर्ग को सतत वर्ग में बदलना (Conversion of Inclusive Series into Exclusive Series) :
अनतिव्यापी वर्गों को सतत वर्गों में बदलने के लिए “वास्तविक सीमाएँ तय करने के कारक” का प्रयोग किया जाता है।
वास्तविक सीमा तय करने का कारक (d)
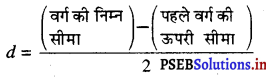
इस प्रकार प्राप्त कारक (d) को क्रमशः प्रत्येक वर्ग की निम्न सीमा में से घटा कर और ऊपरी सीमा में जोड़कर सतत वर्ग बनाए जा सकते हैं।
अनतिव्यापी सारणी
| X | 10-19 | 20-29 | 30-39 | 40-49 |
| f | 5 | 3 | 2 | 1 |
ऊपर दी गई सारणी में कारक d इस प्रकार है :
d = \(\frac{20-19}{2}\) = \(\frac{30-29}{2}\)
= \(\frac{40-39}{2}\)
= \(\frac{1}{2}\)
= 0.5
नई सतत सारणी निम्नलिखित है :
| निम्न सीमा – d | ऊपरी सीमा + d | वर्ग सीमाएँ | f |
| 10 – 0.5 = 9.5 | 19 + 0.5 = 19.5 | 9.5 – 19.5 | 5 |
| 20 – 0.5 = 19.5 | 29 + 0.5 = 29.5 | 19.5 – 29.5 | 3 |
| 30 – 0.5 = 29.5 | 39 + 0.5 = 39.5 | 29.5 – 39.5 | 2 |
| 40 – 0.5 = 39.5 | 49 + 0.5 = 49.5 | 39.5 – 49.5 | 1 |
समान और असमान वर्ग अंतराल श्रृंखला :
(i) समान वर्ग अंतराल श्रृंखला (Equal Class Interval Series) : जब किसी श्रृंखला में वर्गों के एक समान-अंतराल (चौड़ाई) हों, तो यह श्रृंखला समान अंतराल श्रृंखला कहलाती है।
(ii) असमान वर्ग अंतराल श्रृंखला (Unequal Class Interval Series)-जब किसी श्रृंखला में वर्गों की चौड़ाई एक जैसी न हो तो यह असमान वर्ग अंतराल श्रृंखला कहलाती है।
