Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 14 सांख्यिकी Ex 14.4 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 14 सांख्यिकी Ex 14.4
प्रश्न 1.
एक टीम ने फुटबाल के 10 मैचों में निम्नलिखित गोल किए:
2, 3, 4, 5, 0, 1, 3,3,4,3
इन गोलों के माध्य, माध्यक और बहुलक ज्ञात कीजिए।
हल :
जैसा कि हमें ज्ञात है कि
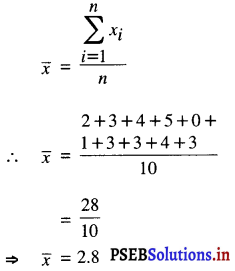
माध्यक के लिए :
दिए गए आंकड़ों को आरोही क्रम में लिखने पर हमें प्राप्त होता है।
0, 1, 2, 3, 3, 3, 3, 4, 4, 5
यहां n = 10, एक सम संख्या है।
∴ माध्यक = \(\frac{n}{2}\) वे और \(\left(\frac{n}{2}+1\right)\) वें प्रेक्षणों का माध्य या 5वें और 6वें प्रेक्षण का माध्य
∴ माध्यक = \(\frac{3+3}{2}=\frac{6}{2}\) = 3
बहुलक के लिए :
दिए गए प्रेक्षणों के लिए बारंबारता सारणी बनाने पर हमें प्राप्त होता है :
| गोल | 0 | 1 | 2 | 3 | 4 | 5 |
| बारंबारता | 1 | 1 | 1 | 4 | 2 | 1 |
यहां पर प्रेक्षण अर्थात् गोलों की अधिकतम बारंबारता 4 है। इसलिए बहुलक = 3.
![]()
प्रश्न 2.
णित की परीक्षा में 15 विद्यार्थियों ने (100 में से) निम्नलिखित अंक प्राप्त किए :-
41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 40, 42, 52, 60
इन आँकड़ों के माध्य, माध्यक और बहुलक ज्ञात कीजिए।
हल :
जैसा कि हमें ज्ञात है कि

माध्यक के लिए:
दिए गए आँकड़ों को आरोही क्रम में लिखने पर हमें प्राप्त होता है :
39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62, 96, 98
यहां n = 15, एक विषय संख्या है।
∴ माध्यक = \(\left(\frac{n+1}{2}\right)\) वाँ प्रेक्षण
= \(\left(\frac{15+1}{2}\right)\) वाँ प्रेक्षण = 8वाँ प्रेक्षण।
= 52
अतः, माध्यक = 52
बहुलक के लिए
दिए गए प्रेक्षणों के लिए बारंबारता सारणी बनाने पर हमें प्राप्त होता है :
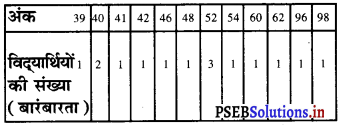
यहाँ अंक 52 की अधिकतम बारंबारता 3 है।
इसलिए, बहुलक = 52.
प्रश्न 3.
निम्नलिखित प्रेक्षणों को आरोही क्रम में व्यवस्थित किया गया है। यदि आँकड़ों का माध्यक 63 हो,तो x का मान ज्ञात कीजिए:
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
हल:
दिए गए आँकड़े आरोही क्रम में हैं और यहाँ n = 10 एक सम संख्या है।
∴ माध्यक = \(\left(\frac{n}{2}\right)\) वें और \(\left(\frac{n}{2}+1\right)\) वें प्रेक्षणों का माध्य अर्थात् 5वें और 6 प्रेक्षणों का माध्य
∴ माध्यक = \(\frac{x+(x+2)}{2}\)
⇒ 63 = x + 1
[∵ माध्यक = 63 दिया है]
⇒ x + 1 = 63
⇒ x = 62
![]()
प्रश्न 4.
आँकड़ों 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18 का बहुलक ज्ञात कीजिए।
हल :
हमें प्राप्त है :
(i) 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18
बारंबारता सारणी बनाने पर हम प्राप्त करते हैं :
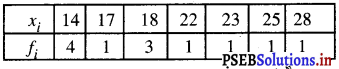
यहां प्रेक्षण 14 की अधिकतम बारंबारता 4 है।
इसलिए बहुलक = 14
प्रश्न 5.
निम्न सारणी से एक फैक्टरी में काम कर रहे 60 कर्मचारियों का माध्य वेतन मान ज्ञात कीजिए।
| वेतन (रुपयों में) | कर्मचारियों की संख्या |
| 3000 | 16 |
| 4000 | 12 |
| 5000 | 10 |
| 6000 | 8 |
| 7000 | 6 |
| 8000 | 4 |
| 9000 | 3 |
| 10000 | 1 |
| कुल योग | 60 |
हल :
|
वेतमान (रु. में) |
व्यक्तियों की संख्या fi |
fixi |
| 3000 | 16 | 48000 |
| 4000 | 12 | 48000 |
| 5000 | 10 | 50000 |
| 6000 | 8 | 48000 |
| 7000 | 6 | 42000 |
| 8000 | 4 | 32000 |
| 9000 | 3 | 27000 |
| 10000 | 1 | 10000 |
| कुल योग | Σfi = N = 60 | Σfixi = 305000 |
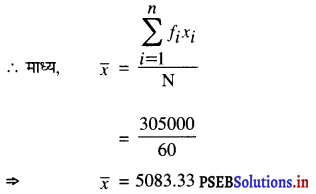
अतः, मध्य वेतन 5083.33 रु. है।
![]()
प्रश्न 6.
निम्न स्थिति पर आधारित एक उदाहरण दीजिए
(i) माध्य की केंद्रीय प्रवृत्ति का उपयुक्त माप है।
(ii) माध्य केंद्रीय प्रवृत्ति का उपयुक्त माप नहीं है, जबकि माध्यक एक उपयुक्त माप है।
हल :
(i) माध्य केंद्रीय प्रवृत्ति का उपयुक्त माप है क्योंकि इसके परिकलन में प्रत्येक पद लिया जाता है, यह हरेक मद द्वारा प्रभावित होता है। इसका उपयोग अधिकतर विभिन्न आँकड़ों के समूहों की तुलना करने के लिए किया जाता है।
उदाहरण के लिए 7 विद्यार्थियों द्वारा प्राप्त अंक है, 10, 15, 14, 18, 26, 24, 20, 14 और 27
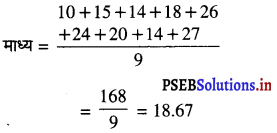
परंतु 10, 14, 14, 15, 18, 20, 24, 26 और 27 का माध्य 18 है। और बहुलक 14 है।
उपरोक्त उदाहरण से हम इस निष्कर्ष पर पहुंचते हैं कि 18.67 9 विद्यार्थियों के प्रदर्शन को निरूपित करता है। पंरतु माध्यक और बहुलक नहीं।
(ii) (a) माध्य चरम मानों से प्रभावित होता है परंतु माध्यक चरम मानों से प्रभावित नहीं होते।
उदाहरण के लिए यदि 5 मान है :
4, 7, 12, 18, 19.
इस स्थिति में माध्य (\(\overline{\mathbf{X}}\)) 12 है और माध्यक भी 12 है।
यदि हम इसमें दो मान 450 और 1000 जोड़ दें तो नया माध्यम है :
= \(\frac{4+7+12+18+19+450+1000}{7}\)
= \(\frac{1510}{7}\)
= 215.7
यह पहले पाँच मानों के माध्य की तुलना एक महान् परिवर्तन है परंतु
4, 7, 12, 18, 19, 450, 1000
का नया माध्यक 18 है जिसमें पहले 5 की तुलना में अधिक परिवर्तन नहीं है।
अतः हम इस निष्कर्ष पर पहुंचते है कि माध्य चरम मानों से प्रभावित होता है।
(b) कई बार माध्य असंभव निष्कर्ष निकालता है उदाहरण के लिए यदि 3 कक्षाओं में यदि 60, 50 और 42 विद्यार्थी हो, तो विद्यार्थियों का माध्य \(\frac{60+50+42}{3}\) = 50.67, जोकि असंभव है क्योकि 3 विद्यार्थी भिन्नों में नहीं हो सकते।
परंतु 42, 50 और 60 का माध्यक 50 है।
