PSEB 9th Class Maths Solutions Chapter 2 बहुपद Ex 2.4

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 2 बहुपद Ex 2.4 Textbook Exercise Questions and Answers

PSEB Solutions for Class 9 Maths Chapter 2 बहुपद Ex 2.4

प्रश्न 1.
बताइए कि निम्नलिखित बहुपदों में से किस बहुपद का एक गुणनखंड x + 1 है।
(i) x³ + x² + x + 1
(ii) x⁴ + x³ + x² + x + 1
(iii) x⁴ + 3x³ + 3x² + x + 1
(iv) x³ – x² – (2 + √2)x + 2
हल :
(i) मान लीजिए : p (x) = x³ + x² + x + 1
x = – 1 को p (x) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
p (-1) = (- 1)³ + (- 1)² + (- 1) + 1
= – 1 + 1 – 1 + 1 = 0
अतः, गुणनखंड प्रमेय द्वारा x + 1 बहुपद x³ + x² + x + 1 का एक गुणनखंड है।

(ii) मान लीजिए p (x) = x⁴ + x³ + x² + x + 1 1
x = – 1 को p (x) में प्रतिस्थापित करने पर हमें प्राप्त
होता है : p (- 1) = (-1)⁴ + (- 1)³ + (- 1)²+ (- 1) + 1
= 1 – 1 + 1 – 1 + 1
= 1 ≠ 0
अतः, गुणनखंड प्रमेय द्वारा x + 1 बहुपद x⁴ + x³ + x² + x + 1 का एक गुणनखंड नहीं है।

(iii) मान लीजिए p (x) = x⁴ + 3x³ + 3x² + x + 1
x = – 1 को p (x) में प्रस्थापित करने पर हमें प्राप्त होता है :
p (- 1) = (- 1)⁴ + 3(- 1)³ + 3(- 1)² + (- 1) + 1
= 1 – 3 + 3 – 1 + 1
= 1 ≠ 0
अतः, गुणनखंड प्रमेय द्वारा x + 1 बहुपद x⁴ + 3x³ + 3x² + x + 1 का गुणनखंड नहीं है

(iv) x³ – x² – (2 + √2 ) x + √2
x = – 1 को p (x) में प्रस्थापित करने पर हमें प्राप्त होता है :
p (- 1) = (- 1)³ – (- 1)³ – (2 + √2 ) (- 1) + – √2
= – 1 – 1 + 2 + √2 + √2
= 2√2 + 0
अतः, गुणनखंड प्रमेय द्वारा x + 1 बहुपद x³ – x² – (2 + √2) x + √2 का गुणनखंड नहीं है।

प्रश्न 2.
गुणनखंड प्रमेय लागू करके बताइए कि निम्नलिखित स्थितियों में से प्रत्येक स्थिति में g (x), p (x) का एक गुणनखंड है या नहीं
(i) p (x) = 2x³ + x² – 2x – 1, g (x) = x + 1
(ii) p (x) = x³ + 3x² + 3x + 1,g (x) = x + 2
(iii) p (x) = x³ – 4x² + x + 6, g (x) = x – 3.
हल :
(i) हमें प्राप्त है
p (x) = 2x³ + x² – 2x – 1 और भाजक
g(x) = x + 1
(x + 1) = 0 लीजिए
⇒ x = -1
x = – 1 को p (x), में प्रस्थापित करने पर हमें प्राप्त होता है
p (- 1) = 2 (- 1)³ + (- 1)² – 2(- 1) – 1
= – 2 + 1 + 2 – 1 = 0
अतः, गुणनखंड प्रमेय द्वारा x + 1 अर्थात् g (x) बहुपद 2x³ + x² – 2x – 1 का गुणनखंड है।

(ii) हमें प्राप्त है :
p(x) = x³ + 3x² + 3x + 1 और भाजक
g(x) = x + 2
x + 2 = 0 लीजिए
⇒ x = – 2
x = – 2 को p (x) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
p (- 2) = (- 2)³ + 3(- 2)² + 3(- 2) + 1
= – 8 + 12 – 6 + 1 = – 1 ≠ 0
अतः, गुणनखंड प्रमेय द्वारा x + 2 अर्थात् g (x) बहुपद x³ + 3x² + 3x + 1 का गुणनखंड नहीं है।

(iii) हमें प्राप्त है :
p (x) = x³ – 4x² + x + 6 और भाजक
g (x) = x – 3
x – 3 = 0 लीजिए
x = 3
x = 3 को p (x), में प्रतिस्थापित करने पर हमें प्राप्त | होता है
p (3) = (3)³ – 4 (3)² + 3 + 6
= 27 – 36 + 3 + 6
= 36 – 36 = 0
अतः, गुणनखंड प्रमेय द्वारा x – 3, अर्थात् g (x) बहुपद x³ – 4x² + x + 6 का गुणनखंड है।

प्रश्न 3.
k का मान ज्ञात कीजिए जबकि निम्नलिखित स्थितियों में से प्रत्येक स्थिति में (x – 1), p (x) का एक गुणनखंड हो :
(i) P (x) = x² + x + k
(ii) p (x) = 2x² + kx + √2
(iii) p (x) = kx² – √2x +1
(iv) p(x) = kx² – 3x + k.
हल :
(i) क्योंकि x – 1 बहुपद p (x) = x² + x + k का गुणनखंड है।
∴ गुणनखंड प्रमेय द्वारा p (1) = 0
⇒ (1)² + 1 + k = 0
⇒ 1 + 1 + k = 0
⇒ 2 + k = 0
⇒ k = – 2

(ii) क्योंकि x – 1 बहुपद p (x) = 2x² + kx + √2 का गुणनखंड है।
∴ गुणनखंड प्रमेय द्वारा p (1) = 0
⇒ 2(1)∴ + k (1) + – 2
⇒ 2 + k + √2 = 0
k = – 2 – √2
k = – (2 + √2)

(iii) क्योंकि x – 1 बहुपद
p (x) = kx² – √2x + 1 का गुणनखंड है।
∴ गुणनखंड प्रमेय द्वारा, p (1) = 0
⇒ k (1)² – √2 (1) + 1 = 0 +
k – √2 + 1 = 0
k = √2 – 1

(iv) क्योंकि x – 1 बहुपद p (x) = kx² – 3x + k का गुणनखंड है।
∴ गुणनखंड प्रमेय द्वारा,
p (1) = 0
⇒ k (1)² – 3(1) + k = 0
⇒ k – 3 + k = 0
⇒ 2k = 3
k = \(\frac{3}{2}\)

प्रश्न 4.
गुणनखंड ज्ञात कीजिए :
(i) 12x² – 7x + 1
(ii) 2x² + 7x + 3
(iii) 6x² + 5x – 6
(iv) 3x² – x – 4.
हल :
(i) 12x² – 7x + 1 = 12x² – 3x – 4x + 1
[∵ योग = – 3 – 4 = – 7 और गुणनफल (- 3) (- 4) = 12 L सिरों के पदों का गुणनफल]
12 × 1 = 12
3x (4x – 1) – 1 (4x – 1) = (4x – 1) (3x – 1)
⇒ 12x² – 7x + 1 = (4x – 1) (3x – 1)

(ii) 2x² + 7x + 3
= 2x² + 6x + x + 3
= 2x (x + 3) + 1 (x + 3)
= (x + 3)(2x + 1)

(iii) 6x² + 5x – 6
= 6x² + 9x – 4x – 6
= 3x (2x +3) – 2 (2x + 3)
= (2x + 3)(3x – 2)

(iv) 13x² – x – 4 = 3x² – 4x + 3x.- 4
= x (3x – 4) + 1 (3x – 4)
= (3x – 4) (x + 1)

प्रश्न 5.
गुणनखंड ज्ञात कीजिए
(i) x³ – 2x² – x + 2
(ii) x³ – 3x² – 9x – 5
(iii) x³ + 13x² + 32x + 20
(iv) 2y³ + y² – 2y – 1.
हल :
(i) हमें प्राप्त है : x³ – 2x² – x + 2
आइए दी हुई बहुपद को p(x) से निरूपित करें
इसलिए, p(x) = x³ – 2x² – x – 2
– 2 के सभी गुणनखंड हैं ± 1, ± 2
निरीक्षण द्वारा
p(- 1) = (- 1)³ – 2(- 1)² – (- 1) – 2
= – 1 – 2 + 1 + 2
⇒ p(- 1) = 0
इसलिए गुणनखंड प्रमेय से (x + 1) बहुपद p(x) का एक गुणनखंड है।
अब p(x) को (x + 1) से विभक्त कीजिए :

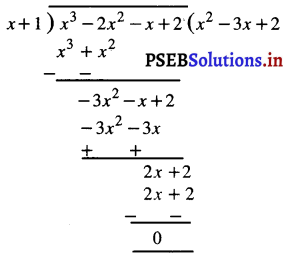
अतः x³ – 2x² – x + 2 = (x – 1) (x² – 3x + 2)
अब x² – 3x + 2 के गुणनखंड मध्य वाले पद को दो भागों में बाँटकर या गुणनखंड प्रमेय का प्रयोग करके प्राप्त कर सकते हैं :
मध्य के पद को दो भागों में बाँटने पर हमें प्राप्त है :
x² – 3x + 2 = x² – x- 2x + 2
= x(x – 1) – 2 (x – 1)
= (x – 1) (x – 2)
इसलिए, x³ – 2x² – x + 2 = (x + 1) (x – 1) (x-2)

(ii) आइए दी हुई बहुपद को p (x) से निरूपित करें :
p(x) = x³ – 3x² – 9x – 5
– 5 के सभी गुणनखंड हैं ± 1, ± 5
निरीक्षण द्वारा p(- 1) = (- 1)³ – 3 (- 1)² – 9 (- 1) – 5
= – 1 – 3 + 9 – 5
= 9 – 9 = 0
इसलिए, गुणनखंड प्रमेय द्वारा x + 1 बहुपद p(x) का गुणनखंड है।
अब p(x) को x + 1 से भाग दीजिए।

अत: x³ – 3x² – 9x – 5 = (x + 1) (x² – 4x – 5)
मध्य के पद को दो भागों में बाँटकर x² – 4x – 5 के गुणनखंड है :
x² – 4x – 5 = x² – 5x + x – 5
= x(x – 5) + 1 (x – 5)
= (x – 5) (x + 1)
इसलिए, x³ – 3x² – 9x – 5 = (x + 1) (x – 5) (x + 1)
= (x + 1) (x + 1) (x – 5)

(iii) आइए हम दी गई बहुपद को p (x) से निरूपित करें :
p(x) = x³ + 13x² + 32x + 20 20 के सभी गुणनखंड हैं ± 1, ± 2, ± 4, ± 5, ± 10, ± 20
निरीक्षण द्वारा
p(- 1) = (- 1)³ + 13 (- 1)² + 32 (- 1) + 20
= – 1 + 13 – 32 + 20
= 33 – 33
⇒ p(- 1) = 0
इसलिए, गुणनखंड प्रमेय द्वारा x + 1 बहुपद p(x) का गुणनखंड है।
अब p(x) को (x + 1) से भाग दीजिए :

अत: x³ + 13x² + 32x + 20 = (x + 1) (x² + 12x + 20)
x² + 12x + 20 के गुणनखंड मध्य के पद को दो भागों में बाँटने पर
x² + 12x + 20 = x² + 2x + 10x + 20
= x(x + 2) + 10 (x + 2)
= (x + 2) (x + 10)
इसलिए, x³ + 13x² + 32 x + 20 = (x + 1) (x + 2) (x + 10)

(iv) आइए हम दी गई बहुपद को p (y) से इस प्रकार निरूपित करें
p(y) = 2y³ + y² – 2y – 1
– 1 का गुणनखंड + 1है। निरीक्षण द्वारा
p(1) = 2(1)³ + (1)² – 2(1) – 1
= 2 + 1 – 2 – 1
= 3 – 3
⇒ p(1) = 0
इसलिए गुणनखंड प्रमेय से ; y – 1 बहुपद p(y) का गुणनखंड है।
अब p(x) को y – 1 से भाग दीजिए :

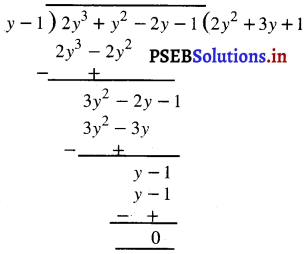
अतः 2y³ + y² – 2y – 1 = (y – 1) (2y² + 3y + 1)
2y² + 3y + 1 के गुणनखंड मध्य भाग को दो भागों के नीचे दिए अनुसार बाँटने पर;
2y² + 3y + 1 = 2y² + 2y + y + 1
= 2y (y + 1) + 1 (y + 1)
= (y + 1) (2y + 1)
इसलिए, 2y³ + y² – 2y – 1 = (y – 1) (y + 1) (2y + 1)