Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 6 रेखाएँ और कोण Ex 6.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 6 रेखाएँ और कोण Ex 6.1
प्रश्न 1.
आकृति में, रेखाएँ AB और CD बिंदु O पर प्रतिच्छेद करती हैं। यदि ∠AOC + ∠BOE = 70° है और ∠BOD = 40° है, तो ∠BOE और प्रतिवर्ती ∠COE ज्ञात कीजिए।
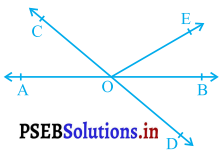
हल:
∠AOC + ∠COE + ∠BOE = 180° (रैखिक युग्म)
या (∠AOC + ∠BOE) + ∠COE = 180°
⇒ 70° + ∠COE = 180°
⇒ ∠COE = 180° – 70°
⇒ ∠COE = 110° … (i)
प्रतिवर्ती ∠COE
= 360° – ∠COE
= 360° – 110°
= 250°
इसलिए प्रतिवर्ती ∠COE = 250°
साथ ही, ∠COE + ∠BOE + ∠BOD = 180° (रैखिक युग्म)
110° + ∠BOE + 40° = 180°
⇒ ∠BOE = 180° – 110° – 40°
⇒ ∠BOE = 30°
वैकल्पिक विधि
∠AOC = ∠BOD (शीर्षाभिमुख कोण)
⇒ ∠AOC = 40°
[∵ ∠BOD = 40° (दिया है)]
अब ∠AOC + ∠BOE = 70° (दिया है)
⇒ 40° + ∠BOE = 70°
⇒ ∠BOE = 70° – 40°
⇒ ∠BOE = 30° उत्तर
प्रतिवर्ती ∠COE
= 360° – ∠COE
= 360° – 110°
= 250°
अतः प्रतिवर्ती ∠COE = 250°
![]()
प्रश्न 2.
आकृति में, रेखाएँ XY और MN बिंदु O पर प्रतिच्छेद करती हैं। यदि ∠POY = 90° और a : b = 2 : 3 है, तो c ज्ञात कीजिए।
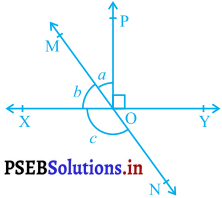
हल :
∠POX + ∠POY = 180° (रैखिक युग्म)
⇒ ∠POX + 90° = 180°
⇒ ∠POX = 180° – 90°
⇒ ∠POX = 90°
अब मान लीजिए a = 2k और b = 3k
जहाँ k अचर है और k > 0
∠POX = 90°
⇒ a + b = 90°
⇒ 2k + 3k = 90°
⇒ 5k = 90°
⇒ k = \(\frac {90°}{5}\)
⇒ k = 18°
इसलिए a = 2k
⇒ a = 2 × 18
⇒ a = 36°
और b = 3k
⇒ b = 3 × 18
⇒ b = 54°
अब ∠MOX + ∠NOX = 180° (रैखिक युग्म)
⇒ b + c = 180°
⇒ 54° + c = 180°
⇒ c = 180° – 54°
⇒ c = 126°
अतः, अभीष्ट c का माप 126° हैं।
प्रश्न 3.
आकृति में, यदि ∠PQR = ∠PRQ है, तो सिद्ध कीजिए कि ∠PQS = ∠PRT है।

हल :
दी गई आकृति के अनुसार ∠PQS + ∠PQR = 180° (रैखिय युग्म) ……… (i)
साथ ही, ∠PRT + ∠PRQ = 180° (रैखिक युग्म) … (ii)
(i) और (ii) से हमें प्राप्त होता है।
∠PQS + ∠PQR = ∠PRT + ∠PRQ … (iii)
परंतु ∠PQR = ∠PRQ (दिया है)
इसलिए हम (iii) को इस प्रकार लिख सकते हैं।
∠PQS + ∠PQR = ∠PRT + ∠PQR
⇒ ∠PQS = ∠PRT + ∠PQR – ∠PQR
⇒ ∠PQS = ∠PRT
![]()
प्रश्न 4.
आकृति में, यदि x + y = w + z है, तो सिद्ध कीजिए कि AOB एक रेखा है।

हल :
दी गई आकृति के अनुसार ∠AOC + ∠BOC + ∠DOB + ∠AOD = 360°
⇒ x + y + w + z = 360°
⇒ x + y + x + y = 360°
[∵ x + y = w + z (दिया है)]
⇒ 2x + 2y = 360°
⇒ 2 (x + y) = 360
⇒ x + y = \(\frac {360°}{2}\)
⇒ x + y = 180° (रैखिक युग्म)
या ∠BOC + ∠AOC = 180°
यह दर्शाता है कि OC, ∠AOC और ∠BOC की उभयनिष्ठ भुजा है जो रैखिक युग्म बनाते हैं।
अत: AOB एक रेखा है।
प्रश्न 5.
आकृति में POQ एक रेखा है। किरण OR रेखा PQ पर लंब है। किरणों OP और OR के बीच में OS एक अन्य किरण है। सिद्ध कीजिए :
∠ROS = \(\frac {1}{2}\) (∠QOS – ∠POS)

हल:
दी गई आकृति के अनुसार
∠QOR + ∠POR = 180° (रैखिक युग्म)
⇒ 90° + ∠POR = 180°
⇒ ∠POR = 180° – 90°
⇒ ∠POR = 90°
या ∠ROS + ∠POS = 90°
⇒ ∠ROS = 90° – ∠POS … (i)
पुन: ∠QOS + ∠POS = 180° (रैखिक युग्म) …. (ii)
2∠POS को (ii) के दोनों ओर से घटाने पर
∠QOS + ∠POS – 2∠POS
= 180°- 2∠POS
⇒ ∠QOS – ∠POS = 2 (90° – ∠POS)
या \(\frac {1}{2}\) (∠QOS – ∠POS) = 90° – ∠POS …….. (iii)
(i) और (iii) से हमें प्राप्त होता है:
∠ROS = \(\frac {1}{2}\) (∠QOS – ∠POS)
![]()
प्रश्न 6.
यह दिया है कि ∠XYZ = 64° है और XY को बिंदु P तक बढ़ाया गया है। दी हुई सूचना से एक आकृति खींचिए। यदि किरण YQ, ∠ZYP को समद्विभाजित करती है, तो ∠XYQ और प्रतिवर्ती ∠QYP के मान ज्ञात कीजिए।
हल :
XY की बिंदु P तक बढ़ाया गया है।
∴ XP एक सरल रेखा है।
अत: ∠XYZ + ∠ZYP = 180° (रैखिक युग्म)
⇒ 64° + ∠ZYP = 180°
⇒ ∠ZYP = 180° – 64°
⇒ ∠ZYP = 116° … (i)
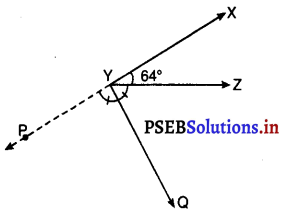
दिया है कि YQ, ∠ZYP का समद्विभाजक है।
∴ ∠ZYQ = ∠QYP = \(\frac {1}{2}\) ∠ZYP
⇒ ∠ZYQ = ∠QYP = \(\frac {1}{2}\) × 116° [(i) का प्रयोग करने पर]
⇒ ∠ZYQ = ∠QYP = 58° … (ii)
⇒ ∠QYP = 58°
अब ∠XYQ = ∠XYZ + ∠ZYQ
⇒ ∠XYQ = 64° + 58°
⇒ ∠XYQ = 122°
(ii) से हमें प्राप्त हैं : ∠ZYQ = ∠QYP
∵ ∠XYZ = 64° (दिया है)
और ∠ZYQ = 58°
∴ प्रतिवर्ती ∠QYP = 360° – ∠QYP
⇒ प्रतिवर्ती ∠QYP = 360° – 58°
⇒ प्रतिवर्ती ∠QYP = 302°
