Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 7 त्रिभुज Ex 7.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.3
प्रश्न 1.
ΔABC और ΔDBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए आकृति)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि,
(i) ΔABD ≅ ΔACD
(ii) ΔABP ≅ ΔACP
(iii) AP कोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP रेखाखंड BC का लंब समद्विभाजक है।
हल:
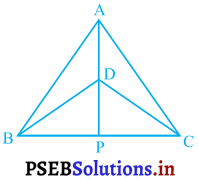
ΔABC एक समद्विबाहु त्रिभुज है।
∴ AB = AC
ΔDBC एक समद्विबाहु त्रिभुज है।
∴ BD = CD
अब, ΔABD और ΔACD में,
AB = AC (दिया है)
BD = CD (दिया है)
AD = AD (उभयनिष्ठ)
∴ ΔABD ≅ ΔACD
(SSS सर्वांगसमता नियम से)
भाग (i) सिद्ध हुआ
⇒ ∠BAD = ∠CAD …………. (a)
[सर्वांगसम त्रिभुज के संगत भाग]
(ii) अब, ΔABP और ΔACP में,
AB = AC (दिया है)
∠BAD = ∠CAD
[(a) का प्रयोग करने पर]
AP = AP (उभयनिष्ठ)
∴ ΔABP ≅ ΔACP
(SAS सर्वांगसमता नियम से)
(iii) दूसरे भाग में हमने सिद्ध किया है कि
ΔABP ≅ ΔACP
इसलिए, ∠BAP= ∠CAP
(सर्वांगसम त्रिभुजों के संगत भांग)
⇒ AP, ∠A को समद्विभाजित करता है।
भाग (i) में हमने सिद्ध किया है कि
ΔABD ≅ ΔACD
इसलिए, ∠ADB = ∠ADC ………….(b)
(सर्वांगसम त्रिभुजों के संगत भाग)
∠ADB + ∠BDP = 180°
(रैखिक युग्म) …… (c)
∠ADC + ∠CDP = 180° …………..(d) (रैखिक युग्म)
(c) और (d), से हमें प्राप्त होता है।
∠ADB + ∠BDP = ∠ADC + ∠CDP
या ∠ADB + ∠BDP = ∠ADB + ∠CDP
[(b) के प्रयोग करने पर]
⇒ ∠BDP = ∠CDP
⇒ DP, ∠D को समद्विभाजित करता है।
अर्थात् हम कह सकते हैं कि AP, ∠D को समद्विभाजित करता है।
(iv) भाग (ii) में हमने सिद्ध किया है कि
ΔABP ≅ ΔACP
∴ BP = PC ….(e)
(सर्वांगसम त्रिभुजों के संगत भाग)
और ∠APB = ∠APC …………(f)
(सर्वांगसम त्रिभुजों के संगत भाग)
अब, ∠APB + ∠APC = 180° (रैखिक युग्म)
⇒∠APB + ∠APB = 180°
[(f) का प्रयोग करने पर]
⇒ 2∠APB = 180°
⇒ ∠APB = \(\frac {180°}{2}\)
⇒ ∠APB = 90°
⇒ AP ⊥ BC … (g)
(e) से हम प्राप्त करते हैं BP = PC और (g),से हमने सिद्ध किया है कि AP ⊥ BC । दोनों को इकट्ठा लेने पर हम कह सकते हैं कि AP, BC का लंब समद्विभाजक है।
![]()
प्रश्न 2.
AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलंब है, जिसमें AB = AC है। दर्शाइए कि
(i) AD रेखा खंड BC को समद्विभाजित करता है।
(ii) AD कोण A को समद्विभाजित करता है।
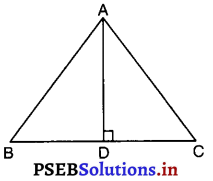
हल :
ΔABD और ΔACD में,
AB = AC (दिया है)
∠ADB = ∠ADC (प्रत्येक = 90°)
[∵ AD ⊥ BC (दिया है)]
AD = AD (उभयनिष्ठ)
∴ ΔABD ≅ ΔACD
(RHS सर्वांगसमता नियम से)
इसलिए, BD = DC
(सर्वांगसम त्रिभुजों के संगत भाग)
⇒ AD; BC, को समद्विभाजित करती है।
(भाग (i) सिद्ध हुआ है)
साथ ही, ∠BAD = ∠CAD (सर्वांगसम त्रिभुजों के संगत भाग)
⇒ AD, ∠A को समद्विभाजित करती है।
प्रश्न 3.
एक त्रिभुज ABC की दो भुजाएँ AB और BC तथा माध्यिका AM क्रमशः एक-दूसरे त्रिभुज की भुजाओं PQ और QR तथा माध्यिका PN के बराबर है (देखिए आकृति)। दर्शाइए कि
(i) ΔABM ≅ ΔPQN
(ii) ΔABC ≅ ΔPQR
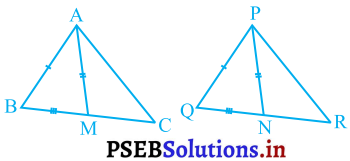
हल :
AM, ΔABC की माध्यिका है।
∴ BM = MC = \(\frac {1}{2}\) BC ……….(a)
PN, ΔPQR की माध्यिका है।
∴ QN = NR = \(\frac {1}{2}\) OR ……. (b)
अब, BC = QR (दिया है)
⇒ \(\frac {1}{2}\)BC = \(\frac {1}{2}\)QR
इसलिए, BM = QN ……. (c)
[(a) और (b) का प्रयोग करने पर]
(i) अब, ΔABM और ΔPQN में,
AB = PQ (दिया है)
AM = PN (दिया है)
BM = QN
[भाग (c) में सिद्ध किया है]
∴ ΔΑΒΜ ≅ ΔΡQN
(sss सर्वांगसमता नियम से)
इसलिए, ∠B = ∠Q ……….(d)
(सर्वांगसम त्रिभुजों के संगत भाग)
(ii) ΔABC और ΔPQR में,
AB = PQ (दिया है)
∠B = ∠Q
[भाग (d) प्रयोग करने पर]
BC = QR (दिया है)
∴ ΔABC ≅ ΔPQR ,
(SAS सर्वांगसमता नियम से)
प्रश्न 4.
BE और CF एक त्रिभुज ABC के दो बराबर शीर्षलंब हैं| RHS सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है।
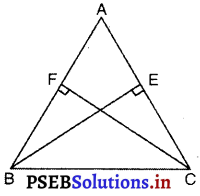
हल :
ΔBEC और ΔCFB में,
∠BEC = ∠CFB (प्रत्येक = 90°)
[∵ BE ⊥ AC और CF ⊥ AB]
BC = BC (उभयनिष्ठ)
BE = CF (दिया है)
∴ ΔBEC ≅ ΔCFB
(RHS सर्वांगसमता नियम से)
इसलिए, EC = FB …………(i)
(सर्वांगसम त्रिभुजों के संगत भाग)
अब ΔAEB और ΔAFC में,
∠A = ∠A (उभयनिष्ठ)
∠AEB = ∠AFC
(प्रत्येक = 90°) [दिया है।
EB = FC (दिया है)
∴ ΔAEB ≅ ΔAFC
(AAS सर्वांगसमता नियम से)
इसलिए, AE = AF …………..(ii)
(सर्वांगसम त्रिभुजों के संगत भाग)
(i) और (ii), को जोड़ने पर हमें प्राप्त होता है।
EC + AE = FB + AF
⇒ AC = AB
अब ΔABC में, हमें प्राप्त है
AB = AC
⇒ ΔABC एक समद्विबाहु त्रिभुज है।
![]()
प्रश्न 5.
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP ⊥ BC खींच कर दर्शाइए कि ∠B = ∠C है।
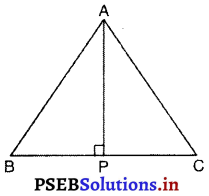
हल :
दिया है : ABC एक समद्विबाहु त्रिभुज है जिसमें
AB = AC
सिद्ध करना है : ∠B = ∠C
रचना : AP ⊥ BC खींचिए।
उपपत्ति : ΔABP और ΔACP में
∠APB = ∠APC
(प्रत्येक = 90°) [रचना से]
AB = AC (दिया है)
AP = AP (उभयनिष्ठ)
∴ ΔABP ≅ ΔACP
(RHS सर्वांगसमता नियम से)
इसलिए, ∠B = ∠C
(सर्वांगसम त्रिभुजों के संगत भाग)
