Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 7 त्रिभुज Ex 7.4 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.4
प्रश्न 1.
दर्शाइए कि समकोण त्रिभुज में कर्ण सबसे लंबी भुजा होती है।
हल :
मान लीजिए ABC एक समकोण त्रिभुज है जिसमें B पर समकोण है।
हमने सिद्ध करना है कि कर्णAC, सबसे लंबी भुजा होती है।
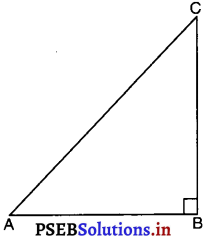
समकोण ΔABC में,
⇒ ∠A + ∠B + ∠C = 180°
∠A + 90°+ ∠C = 180° [∵ ∠B = 90°]
⇒ ∠A + ∠C = 180° – 90° = 90°
अब ∠A + ∠C = 90°
और ∠B = 90°
⇒ ∠B > ∠C और ∠B > ∠A
जैसा कि हम जानते हैं कि बड़े कोण के सम्मुख भुजा बड़ी होती है।
AC > AB और AC > BC
दूसरे शब्दों में, ∠B सबसे बड़ा होने के कारण इसकी सम्मुख भुजा AC अर्थात् कर्ण बड़ा होता है।
![]()
प्रश्न 2.
आकृति में, ΔABC की भुजाओं AB और AC को क्रमशः बिंदुओं P और Q तक बढ़ाया गया है। साथ ही, ∠PBC < ∠QCB है। दर्शाइए कि AC > AB है।
हल:
∠ABC + ∠PBC = 180° …..(i) (रैखिक युग्म)
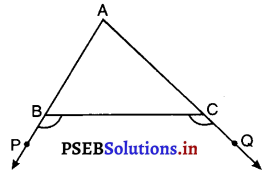
∠ACB + ∠QCB = 180° ………(ii)
(रैखिक युग्म अभिगृहीत)
(i) और (ii), से हमें प्राप्त होता है ।
∠ABC + ∠PBC = ∠ACB + ∠QCB ….(iii)
परंतु ∠PBC ∠ ∠QCB (दिया है) …(iv)
∴ (iv) को (iii) में, प्रयोग करने पर
∠ABC > ∠ACB
अब ΔABC में,
∠ABC > ∠ACB
[ऊपर (iv) में सिद्ध किया है।
∴ AC > AB [∵ बड़े कोण के सम्मुख भुजा बड़ी होती है]
प्रश्न 3.
आकृति में, ∠B < ∠A और ∠C < ∠D है। दर्शाइए कि AD < BC है।
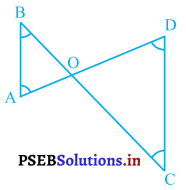
हल :
ΔAOB में,
∠B < ∠A (दिया है) या, ∠A > ∠B
इसलिए, OB > OA ……..(i) [∵ बड़े कोण के सम्मुख भुजा बड़ी होती है]
ΔCOD में,
∠C < ∠D (दिया है) या, ∠D > ∠C
∴ OC > OD ………..(ii)
[∵ बड़े कोण के सम्मुख भुजा बड़ी होती है]
(i) और (ii), को जोड़ने पर हमें प्राप्त होता है :
OB + OC > OA + OD
⇒ BC > AD
या, AD < BC (सिद्ध किया है)
![]()
प्रश्न 4.
AB और CD क्रमशः एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजाएँ हैं ( देखिए आकृति)। दर्शाइए कि ∠A > ∠C और ∠B > ∠D
हल :
दिया है : ABCD एक चतुर्भुज है। AB सबसे छोटी भुजा और CD सबसे बड़ी भुजा है।
सिद्ध करना है : ∠A > ∠C और ∠B > ∠D.
रचना : A और C तथा B और D को मिलाइए।
उपपत्ति : ΔABC में AB सबसे छोटी भुजा है
∴ BC > AB
⇒ ∠1 > ∠2 …………(i)
[ बड़ी भुजा के सम्मुख कोण बड़ा होता है।]
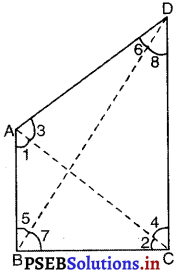
ΔADC में, CD सबसे बड़ी भुजा है।
∴ CD > AD
⇒ ∠3 > ∠4 …………(ii)
(i) और (ii), को जोड़ने पर
∠1 + ∠3 > ∠2 + ∠4
⇒ ∠A > ∠C
[इति सिद्धम् भाग (1)]
अब ΔADB में, AB सब से छोटी भुजा है।
∴ AD > AB
⇒ ∠5 > ∠6 ……..(iii)
और ΔBCD में, CD सबसे बड़ी भुजा है।
∴ CD > BC
⇒ ∠7 > ∠8 ……..(iv)
(iii) और (iv), को जोड़ने पर
∠5 + ∠7 > ∠6 + ∠8
∠B > ∠D [इति सिद्धम् (2)]
अतः, ∠A > ∠C और ∠B > ∠D(इति सिद्धम्)
प्रश्न 5.
आकृति में PR > PQ है और PS कोण QPR को समद्विभाजित करता है। सिद्ध कीजिए कि ∠PSR > ∠PSQ है।
हल:
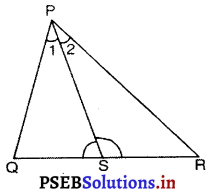
ΔPQR में,
PR > PQ (दिया है)
∴ ∠PQR > ∠PRQ (बड़ी भुजा के सम्मुख कोण बड़ा होता है) …….(1)
पुनः ∠1 = ∠2
[∵ PS, ∠P का समद्विभाजक है] …(2)
∴ ∠PQR + ∠1 > ∠PRQ + ∠2 …(3)
परंतु ∠PQS + ∠1 + ∠PSQ = ∠PRS + ∠2 + ∠PSR = 180°
[त्रिभुज के कोणों का योगफल 180° होता है।]
⇒ ∠PQR + ∠1 + ∠PSQ = ∠PRQ + ∠2 + ∠PSR …(4) [∵ ∠PRS = ∠PRQ और ∠PQS = ∠PQR]
(3) और (4), से हमें प्राप्त होता है
∠PSQ < ∠PSR या, ∠PSR > ∠PSQ
![]()
प्रश्न 6.
दर्शाइए कि एक रेखा पर एक दिए हुए बिंदु से, जो उस रेखा पर स्थित नहीं है, जितने रेखाखंड खींचे जा सकते हैं उनमें लंब रेखाखंड सबसे छोटा होता है।
हल :
दिया है : l एक रेखा है और P एक बिंदु है जो l पर स्थित नहीं है। PM ⊥ l है।
M से भिन्न कोई बिंदु N; रेखा l पर है।
(आकृति देखिए)
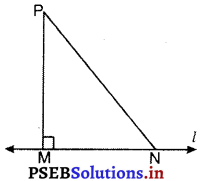
सिद्ध करना है : PM < PN उपपत्ति : ΔPMN में, ∠M एक समकोण है। N एक न्यूनकोण है। (त्रिभुज का कोण गुणधर्म) ∴ ∠M > N
∴ PN > PM
(बड़े कोण की सम्मुख भुजा)
या, PM < PN.
अतः, एक रेखाखंड पर एक दिए बिंदु से जो उस रेखा पर नहीं है, खींचे गए सभी रेखा खंडों में लंब रेखा खंड सबसे छोटा होता है।
