Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 7 Triangles Ex 7.5 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 7 Triangles Ex 7.5
Question 1.
ABC is a triangle. Locate a point in the interior of ∆ ABC which is equidistant from all the vertices of ∆ ABC.
Answer:
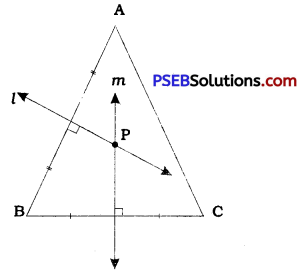
In ∆ ABC, draw l, the perpendicular bisector of side AB and m, the perpendicular bisector of side BC. Name the point of intersection of l and m as P.
P is a point on the perpendicular bisector of AB. Hence, P is equidistant from A and B.
∴ PA = PB
P is a point on the perpendicular bisector of BC. Hence, P is equidistant from B and C.
∴ PB = PC
Thus, PA = PB = PC
Hence, P is the required point which is equidistant from all the vertices of ∆ ABC.
Note: Since ∆ ABC given here is an acute angled triangle, point P lies in the interior of ∆ ABC. If ∆ ABC is a right angled Mangle, point P lies on the hypotenuse. Actually, in that case, point P will be the midpoint of the hypotenuse. Lastly, if ∆ ABC is an obtuse angled triangle, point P lies in the exterior of ∆ ABC. This point P is called the circumcentre of ∆ ABC.
![]()
Question 2.
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
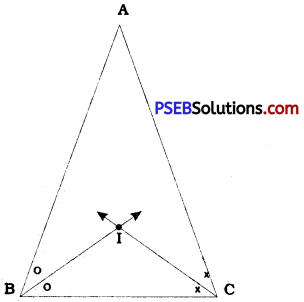
Answer:
In ∆ ABC, draw the bisectors of ∠B and ∠C to intersect each other at point I.
I is a point on the bisector of ∠ B. Hence, I is equidistant from sides BA and BC. Similarly, I is a point on the bisector of ZC. Hence, I is equidistant from sides BC and CA.
Thus, point I is the required point which is equidistant from all the three sides AB, BC and CA of ∆ ABC.
This point I is called the incentre of ∆ ABC. It always lies in the interior of ∆ ABC irrespective of the type of ∆ ABC.
Question 3.
In a huge park, people are concentrated at three points (see the given figure):

A: where there are different slides and swings for children.
B: near which a man-made lake is situated.
C: which is near to a large parking and exit.
Where should an ice cream parlour be set up so that maximum number of persons can approach it ?
(Hint: The parlour should be equidistant from A, B and C.)
Answer:
First of all, construct ∆ ABC with the given points A, B and C as vertices. Then, as shown in example 1, draw the perpendicular s bisectors of any two sides of ∆ ABC and name their point of intersection as P.
Now, the ice cream parlour should be set up at the location given by point P as it is equidistant from all the three places (points) A, B and C.
![]()
Question 4.
Complete the hexagonal and star shaped < Rangolies [see figure (1) and (2)] by filling them with as many equilateral triangles of > side 1 cm as you can. Count the number < of triangles in each case. Which has more triangles?
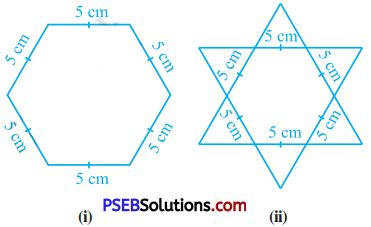
Answer:
In figure (1), if we join the opposite vertices, we get three longest diagonals of hexagon ABCDEE By the intersection of these diagonals we get point O and six equilateral triangles – ∆ OAB, ∆ OBC, ∆ OCD, ∆ ODE, ∆ OEF and ∆ OFA. Each side of all these equilateral triangles will measure 5 cm. In each of these six triangles, we can fill 25 (1 + 3 + 5 + 7 + 9) equilateral triangles with side 1 cm each. Hence in the hexagonal Rangoli ABCDEF, we can fill 25 × 6 = 150 triangles.
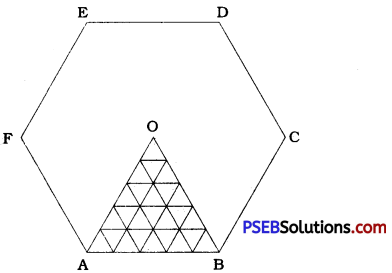
Similarly, in figure (2), we can fill 150 triangles in the inner hexagon and 150 triangles in the six triangles on the boundary of the hexagon. Thus, in figure (2), 150 + 150 = 300 triangles can be filled.
Hence, more triangles can be filled in figure (2).
