Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 7 त्रिभुज Ex 7.5 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.5
प्रश्न 1.
ABC एक त्रिभुज है। इसके अभ्यंतर में एक ऐसा बिंदु ज्ञात कीजिए जो ΔABC के तीनों शीर्षों से समदूरस्थ है।
हल :
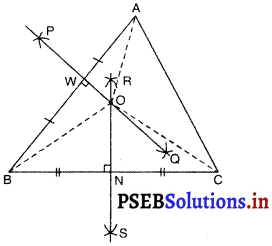
मान लीजिए ABC एक त्रिभुज है।
इसकी भुजाओं AB और BC के लंब समद्विभाजित क्रमश: PQ और RS खींचिए। मान लीजिए PQ. AB को M पर समद्विभाजित करता है और RS, BC को बिंदु N पर समद्विभाजित करता है।
मान लीजिए PQ और RS बिंदु O पर पर प्रतिच्छेद करते हैं।
OA, OB और OC को मिलाइए।
अब, ΔAOM और BOM में
AM = MB (रचना से)
∠AMO = ∠BMO (प्रत्येक = 90°) [रचना से] (उभयनिष्ठ)
OM = OM
∴ ΔAOM ≅ ΔBOM
(SAS सर्वांगसमता नियम)
इसलिए. OA = OB (सर्वांगसम. त्रिभुजों के संगत भाग)….(i)
इसी तरह, ΔBON ≅ ΔCON
⇒ OB =OC
(सर्वांगसम त्रिभुजों के संगत भाग)……..(ii)
(i) और (ii) से हम देखते हैं कि
OA = OB = OC
अतः, ΔABC की किन्हीं दो भुजाओं के लंब समद्विभाजकों का प्रतिच्छेद बिंदु O, इसके तीनों शीर्षों से समदूरस्थ है।
![]()
प्रश्न 2.
किसी त्रिभुज के अभ्यांतर में एक ऐसा बिंदु ज्ञात कीजिए जो त्रिभुज की सभी भुजाओं से समदूरस्थ हों।
हल :
मान लीजिए ABC एक त्रिभुज है।
∠B और ∠C के समद्विभाजक खींचिए।
मान लीजिए ये कोण समद्विभाजक परस्पर बिंदु I पर प्रतिच्छेद करते हैं।
IK ⊥ BC खींचिए।
साथ ही, IJ ⊥ AB
और IL ⊥ AC खींचिए।
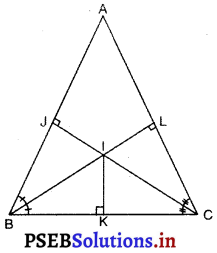
AI को मिलाइए।
ΔBIK और ΔBIJ में,
∠IKB = ∠IJB (प्रत्येक = 90°)
(रचना से)
∠IBK = ∠IBJ [∵ BI ∠B का समद्विभाजक है]
(रचना से)
BI = BI (उभयनिष्ठ)
∴ ΔBIK ≅ ΔBIJ
(AAS सर्वांगसमता नियम)
∴ IK = IJ
(सर्वांगसम त्रिभुजों के संगत भाग) ….(i)
इसी प्रकार, ΔCIK ≅ ΔCIL
इसलिए, IK = IL
(सर्वांगसम त्रिभुजों के संगत भाग)….(ii)
(i) और (ii), से हमें प्राप्त होता है
IJ = IK = IL;
अतः, ΔABC के किन्हीं दो कोणों को समद्विभाजकों का प्रतिच्छे बिंदु I इसकी भुजाओं से समदूरस्थ है।
प्रश्न 3.
एक बड़े पार्क में लोग तीन बिंदुओं (स्थानों) पर केंद्रित हैं (देखिए आकृति)।
A : जहाँ बच्चों के लिए फिसल पट्टी और झूले
B: जिसके पास मानव-निर्मित एक झील है।
C: जो एक बड़े पार्किंग स्थल और बाहर निकलने के रास्ते के निकट है। एक आइसक्रीम का स्टाल कहाँ लगाना चाहिए ताकि वहाँ लोगों की अधिकतम संख्या पहुंच सके ?

हल :
स्टाल A, B और C से समदूरस्थ होना चाहिए। इसके लिए हम बिंदुओं B और C को मिलाने वाली रेखा का लंब समद्विभाजक l और बिंदुओं A और C को मिलाने वाली रेखा का लंब समद्विभाजक m खींचते हैं।
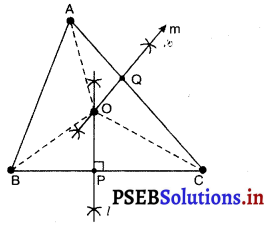
मान लीजिए l और m परस्पर बिंदु O पर प्रतिच्छेद करते हैं।
अब बिंदु O बिंदुओं A, B और C से समदूरस्थ हैं। OA, OB और OC को मिलाइए।
उपपत्ति : ΔBOP और ΔCOP में,
OP = OP (उभयनिष्ठ)
∠OPB = ∠OPC (प्रत्येक = 90°) (रचना से)
BP = PC
[∵ P, BC का मध्य-बिंदु है]
∴ ΔBOP ≅ ΔCOP
[SAS सर्वांगसमता नियम]
इसलिए, OB = OC
(सर्वांगसम त्रिभुजों के संगत भाग)…(i)
इसी तरह, ΔAOQ ≅ ΔCOQ
⇒ OA = OC
(सर्वांगसम त्रिभुजों के संगत भाग) ..(ii)
(i) और (ii) से हमें प्राप्त होता है
OA = OB = OC
हम देखते हैं कि इन बिंदुओं को मिलाने से प्राप्त तीन भुजाओं में से किन्हीं दो भुजाओं के लंब समद्विभाजकों का प्रतिच्छेद बिंदु O ही वह बिंदु है जहाँ पर आइसक्रीम स्टाल लगाना चाहिए।
![]()
प्रश्न 4.
षड्भुजीय और तारे के आकार की रंगोलियों (देखिए आकृति (i) और (ii)] को 1 cm भुजा वाले समबाहु त्रिभुजों से भर कर पूरा कीजिए। प्रत्येक स्थिति में, त्रिभुजों की संख्या गिनिए। किसमें अधिक त्रिभुज हैं?
हल :
षड्भुजीय रंगोली में : प्रत्येक 5 cm भुजा वाली समबाहु त्रिभुजों की संख्या
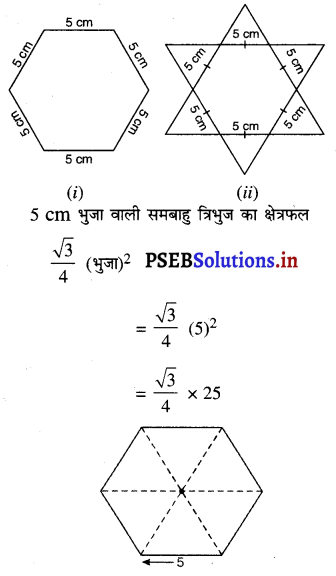
षड्भुजीय रंगोली का क्षेत्रफल = 6 × एक समबाहु त्रिभुज का क्षेत्रफल
= 6 × \(\frac{\sqrt{3}}{4}\) × 25
= 150 × \(\frac{\sqrt{3}}{4}\) cm2 …(i)
1 cm भुजा वाली समबाहु त्रिभुज का क्षेत्रफल
= \(\frac{\sqrt{3}}{4}\) (1)2
= \(\frac{\sqrt{3}}{4}\) cm2 ………. (ii)
षड्भुजीय रंगोली में 1 cm भुजा वाले समबाहु त्रिभुजों की संख्या = 150\(\frac{\sqrt{3}}{4}\) ÷ \(\frac{\sqrt{3}}{4}\)
= 150 \(\frac{\sqrt{3}}{4}\) × \(\frac{4}{\sqrt{3}}\)
= 150 ….(iii)
अब तारे के आकार की रंगोली में
प्रत्येक 5 cm भुजा वाली समबाहु त्रिभुजों की संख्या = 12
इसलिए तारे के आकार वाली रंगोली का कुल क्षेत्रफल = 12 × 5 cm भुजा वाली एक समबाहु त्रिभुज का क्षेत्रफल
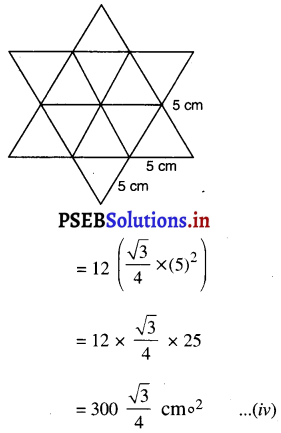
तारे के आकार वाली रंगोली में 1 cm भुजा वाली त्रिभुजों की संख्या
= 300 \(\frac{\sqrt{3}}{4}\) ÷ \(\frac{\sqrt{3}}{4}\)
[ (iv) को (ii) से भाग देने पर]
= 300 \(\frac{\sqrt{3}}{4}\) × \(\frac{4}{\sqrt{3}}\)
= 300 …….(v)
(iii) और (v) से हम देखते हैं कि तारे के आकार वाली रंगोली में 1 cm भुजा वाली समबाहु त्रिभुजों की संख्या अधिक है।
