Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 8 चतुर्भुज Ex 8.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 8 चतुर्भुज Ex 8.2
प्रश्न 1.
ABCD एक चतुर्भुज है जिसमें P, Q, R और क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं (आकृति देखिए)।
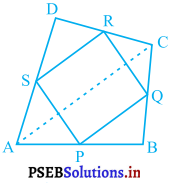
AC उसका एक विकर्ण है।
दर्शाइए कि
(i) SR || AC और SR = \(\frac {1}{2}\)AC है।
(ii) PQ = SR है।
(iii) PQRS एक समांतर चतुर्भुज है।
हल:
ΔABC में,
P, AB का मध्य-बिंदु है और Q, BC का मध्यबिंदु है।
तो PQ || AC और PQ = \(\frac {1}{2}\)AC
[मध्य-बिंदु प्रमेय]
(i) ΔACD में
R, CD का मध्य-बिंदु है और S, AD का मध्यबिंदु है।
तो SR || AC और SR = \(\frac {1}{2}\)AC
(मध्य-बिंदु प्रमेय)
(ii) हमने सिद्ध किया है कि
PQ = \(\frac {1}{2}\)AC
और SR = \(\frac {1}{2}\)AC
∴ PQ = \(\frac {1}{2}\)AC = SR
या PQ = SR
(iii) हमने सिद्ध किया है कि
PQ || AC
और SR || AC
⇒ PQ || SR [∵ दो रेखाएँ जो दी गई रेखा के समांतर होती है परस्पर समांतर होती हैं।]
अब,
PQ = SR
और PQ || SR
जैसा कि हम जानते हैं कि यदि चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर और समांतर होता है तो यह एक समांतर चतुर्भुज होता है।
∴PQRS एक समांतरचतुर्भुज है।
![]()
प्रश्न 2.
ABCD एक समचतुर्भुज हैं और P, Q, R, S क्रमशः भुजाओं AB, BC, CD और DA के मध्यबिंदु है। दर्शाइए कि PQRS एक आयत है।
दिया है : P, Q, R और S समचतुर्भुज ABCD की भुजाओं क्रमश: AB, BC, CD और DA के मध्य-बिंदु हैं। PQ, QR, RS और SP को मिलाया गया है।
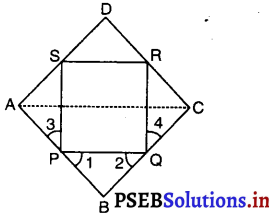
सिद्ध करना है : PQRS एक आयत है।
रचना : A और C को मिलाइए।
उपपति : ΔABC में, P, AB का और Q, BC का मध्य बिंदु है।
∴ मध्य-बिंदु प्रमेय से,
PQ || AC और PQ = \(\frac {1}{2}\)AC ……(i)
ΔADC में, R, CD का और S, AD का मध्यबिंदु है।
∴ SR || AC और SR = \(\frac {1}{2}\)AC ……(ii)
(i) और (ii) से हमें प्राप्त होता है।
PQ || SR और PQ = SR
∴ PQRS एक समांतर चतुर्भुज है।
[∵ चतुर्भुज PQRS में सम्मुख भुजाओं PQ और SR एक युग्म बराबर और समांतर है।]
अब, ABCD एक समचतुर्भुज है। (दिया है)
∴ AB = BC
⇒ \(\frac {1}{2}\)AB = \(\frac {1}{2}\)BC
⇒ PB = BQ
∴ ∠1 = ∠2 [∵ त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।]
अब, ΔAPS और ΔCQR में,
AP = CQ
[∵ AB = BC ⇒ \(\frac {1}{2}\)AB = \(\frac {1}{2}\)BC
⇒ AP = CQ जहाँ P और Q, AB और BC के मध्य-बिंदु हैं।]
इसी प्रकार, AS = CR
PS = QR
[|| gm PQRS की सम्मुख भुजाएँ।
∴ ΔAPS ≅ ΔCQR
[SSS सर्वांगसमता से]
∴ ∠3 = ∠4
(सर्वांगसम त्रिभुजों के संगत भाग)
अब, ∠1 + ∠SPQ + ∠3 = 180°
और ∠2 + ∠PQR + ∠4 = 180°
(रैखिक युग्म]
∴ ∠1 + ∠SPQ + ∠3 = ∠2 + ∠PQR + ∠4
क्योंकि ∠1 = ∠2 और ∠3 = ∠4
(उपरोक्त में प्रमाणित)
∴ ∠SPQ = ∠PQR …………..(iii)
अब, PQRS एक समांतर चतुर्भुज है।
(उपरोक्त में प्रमाणित)
∴ ∠SPQ + ∠PQR = 180° … (iv)
[∵ SP || RQ और PQ इनको काटती है और तिर्यक रेखा के एक ही ओर के अंत: कोणों का योगफल 180° होता है।]
(iii) को (iv) में प्रयोग करने पर हमें प्राप्त होता है।
∠SPQ + ∠SPQ = 180°
⇒ 2∠SPQ = 180°
⇒ ∠SPQ = 90°
इस प्रकार PQRS एक समांतर चतुर्भुज है जिसमें ∠SPQ = 90°
अतः, PQRS एक आयत है।
प्रश्न 3.
ABCD एक आयत है, जिसमें P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य| बिंदु हैं। दर्शाइए कि PQRS एक समचतुर्भुज है
हल :
दिया है : आयत ABCD में P, Q, R और S क्रमश: भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं। PQ, QR, RS और SP को मिलाया गया है।
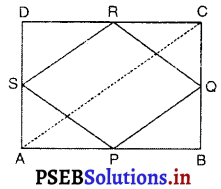
सिद्ध करना है : PQRS एक समचतुर्भुज है।
रचना: AC को मिलाइए
उपपत्ति : ΔABC में P ओर Q क्रमशः भुजाओं AB, BC के मध्य-बिंदु हैं।
∴ PQ || AC और PQ = \(\frac {1}{2}\)AC …(i)
ΔADC में R और S, क्रमशः CD और AD के मध्य-बिंदु हैं।
∴ SR || AC और SR = \(\frac {1}{2}\)AC ……(ii)
(i) और (ii) से हमें प्राप्त होता है।
PQ || SR और PQ = SR ……(iii)
⇒ PQRS एक समांतर चतुर्भुज है।
ABCD एक आयत है। (दिया है)
⇒ AD = BC
⇒ \(\frac {1}{2}\)AD = \(\frac {1}{2}\)BC
⇒ AS = BQ …. (iv)
ΔAPS और ΔBPQ में,
AP = BP
[∵ P, AB का मध्य-बिंदु है।]
∠PAS = ∠PBQ [प्रत्येक 90°]
और AS = BQ [(iv)से]
∴ ΔAPS ≅ ΔBPQ
[SAS सर्वांगसमता नियम)
⇒ PS = PQ ………(v)
[सर्वांगसम त्रिभुजों के संगत भाग]
(iii) और (v) से PQRS एक ऐसा समांतर चतुर्भुज है जिसमें
PS = PQ
अर्थात्, दो आसन्न भुजाएँ बराबर हैं।
अतः, PQRS एक समचतुर्भुज है।
![]()
प्रश्न 4.
ABCD एक समलंब है, जिसमें AB || DC है । साथ ही BD एक विकर्ण है और E भुजा AD का मध्य-बिंदु है। E से होकर एक रेखा AB के समांतर खींची गई है, जो BC को F पर प्रतिच्छेद करती है। (देखिए आकृति)। दर्शाइए कि F भुजा BC का मध्य-बिंदु है।
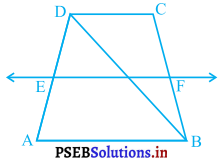
हल :
मान लीजिए विकर्ण BD रेखा EF को बिंदु P पर प्रतिच्छेद करता है।
ΔDAB में,
E, AB का मध्य-बिंदु है और EP || AB है। [∵ EF || AB (दिया है) और P, EF का एक भाग है।]
∴ P, ΔDAB की दूसरी भुजा BD का मध्य-बिंदु है।
[∵ त्रिभुज की एक भुजा के मध्य-बिंदु से दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को मध्य बिंदु पर प्रतिच्छेद करती है।]
अब, ΔBCD में,
P, BD का मध्य बिंदु है और PF || DC
[∵ EF || AB और AB || DC (दिया है)
∴ EF || DC और PF, EF का ही एक भाग है।]
∴ F, ΔBCD की भुजा BC का भाग है [मध्य-प्रमेय के विलोम से]
प्रश्न 5.
एक समांतर चतुर्भुज ABCD मे, E और F क्रमशः भुजाओं AB और ACD के मध्य-बिंदु हैं (देखिए आकृति)। दर्शाइए कि रेखाखंड AF और EC विकर्ण BD को समत्रिभाजित करते हैं।
हल :
क्योंकि E और F क्रमश: AB और CD के मध्य-बिंदु हैं।
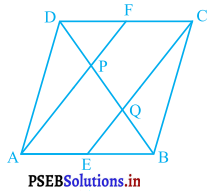
AE = \(\frac {1}{2}\)AB और CF = \(\frac {1}{2}\)CD ………..(i)
परंतु ABCD एक समांतर चतुर्भुज है।
⇒ AB = CD और AB || DC
⇒ \(\frac {1}{2}\)AB = \(\frac {1}{2}\)CD और AB || DC
⇒ AE = FC और AE || FC [(i) से]
⇒ AECF एक समांतर चतुर्भुज है
⇒ FA || CE
⇒ FP || CQ [∵ FP, FA का एक भाग है और CQ, CE का एक का भाग है।] … (ii)
हम जानते हैं कि त्रिभुज की एक भुजा के मध्य-बिंदु से खींची रेखा तीसरी भुजा को समद्विभाजित करती है।
ΔDCQ में, F, CD का मध्य-बिंदु है और FP || CQ [(ii) से]
∴ P, DQ का मध्य-बिंदु है।
⇒ DP = PQ …… (iii)
इसी प्रकार, ΔABQ में, E, AB का मध्य-बिंदु है और EQ || AP
∴ Q, BP का मध्य-बिंदु है।
⇒ BQ = PQ … (iv)
(iii) और (iv) से
DP = PQ = BQ … (v)
अब, BD = BQ + PQ + DP
= BQ + BQ + BQ
⇒ BD = 3BQ
3BQ = BD
⇒ BQ = \(\frac {1}{3}\) BD … (vi)
(v) और (vi) से हमें प्राप्त होता है।
DP = PQ = BQ = \(\frac {1}{3}\)BD
⇒ बिंदु P और Q, BD को तीन भागों में विभाजित करते हैं।
⇒ AF और CE, BD को तीन भागों में विभाजित करते हैं।
![]()
प्रश्न 6.
दर्शाइए कि किसी चतुर्भुज की सम्मुख भुजाओं के मध्य-बिंदुओं को मिलाने वाले रेखाखंड परस्पर समद्विभाजित करते हैं।
हल :
दिया है: चतुर्भुज ABCD में, EG और FH, सम्मुख भुजाओं के मध्य-बिंदुओं को मिलाने से प्राप्त रेखाखंड है।
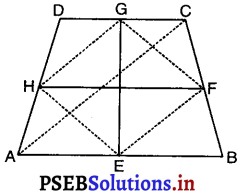
सिद्ध करना है : EG और FH परस्पर समद्विभाजित करते हैं।
रचना : AC, EF, FG, GH और HE को मिलाइए
उपपति : ΔABC में E और F क्रमशः भुजाओं AB और BC के मध्य-बिंदु हैं।
∴ EF || AC और EF = \(\frac {1}{2}\)AC ……. (i)
इसीतरह ΔADC में,
G और H क्रमशः भुजाओं CD और AD के मध्य बिंदु हैं।
∴ HG || AC और HG = \(\frac {1}{2}\)AC …… (ii)
(i) और (ii) से हमें प्राप्त होता है।
EF || HG और EF = HG
∴ EFGH एक समांतर चतुर्भुज है।
[∵ यदि किसी चतुर्भुज की सम्मुख भुजाओं का एक युग्म समान और समांतर हो तो वह समांतर चतुर्भुज होता है।]
जैसा कि हम जानते हैं कि समांतर चतुर्भुज के विकर्ण परस्पर समद्विभाजक होते हैं। इसलिए समांतर चतुर्भुज EFGH के विकर्ण अर्थात् रेखाखंड EG और FH परस्पर समद्विभाजित होते हैं।
प्रश्न 7.
ABC एक त्रिभुज है जिसका कोण C समकोण है। कर्ण AB के मध्य-बिंदु M से होकर BC के समांतर खींची गई रेखा AC को D पर प्रतिच्छेद करती है।
दर्शाइए कि
(i) D भुजा AC का मध्य-बिंदु है।
(ii) MD ⊥ AC है।
(ii) CM = MA = \(\frac {1}{2}\)AB है।
हल:
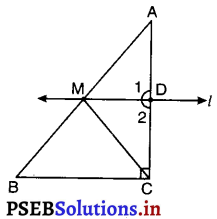
(i) ΔABC में, M, AB का मध्य-बिंदु है। (दिया है)
MD || BC
∴ AD = DC
[मध्य-बिंदु प्रमेय का विलोम]
इस प्रकार, D, AC का मध्य-बिंदु है।
(ii) l || BC (दिया है)
मान लीजिए AC एक तिर्यक रेखा है।
∴ ∠1 = ∠C (संगत कोण)
⇒ ∠1 = 90°
[∵ ∠C = 90° (दिया है)]
इस प्रकार, MD ⊥ AC.
(ii) ΔAMD और ΔCMD में,
AD = DC (ऊपर सिद्ध किया है।)
∠1 = ∠2 (प्रत्येक = 90°) [ऊपर सिद्ध किया है।]
MD = MD (उभयनिष्ठ)
ΔAMD ≅ ΔCMD
(SAS सर्वांगसमता नियम)
इसलिए, AM = CM
(सर्वांगसम त्रिभुजों के संगत भाग) ……. (a)
दिया है कि M, AB का मध्य-बिंदु है।
∴ AM = \(\frac {1}{2}\)AB … (b)
(a) और (b), का प्रयोग करने पर हमें प्राप्त होता है:
CM = AM = \(\frac {1}{2}\)AB.
