Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.2
प्रश्न 1.
आकृति में, ABCD एक समांतर चतुर्भुज है, AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 cm, AE = 8 cm और CF = 10 cm है, तो AD ज्ञात कीजिए।
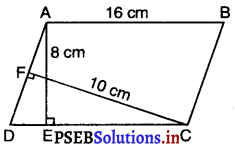
हल :
ABCD एक समांतर चतुर्भुज है।
∴ DC = AB
⇒ DC = 16 सेमी
AE ⊥ DC (दिया है)
समांतर चतुर्भुज ABCD का क्षेत्रफल
= DC × AE [∵ ar (|| gm) = आधार × संगत ऊँचाई]
= 16cm × 8 cm
= 128 cm2
आधार AD और ऊँचाई CF का प्रयोग करने पर; समांतर चतुर्भुज का क्षेत्रफल = AD × CF
⇒ 128 cm2 = AD × 10 cm
या AD × 10 cm = 128 cm2
⇒ AD = \(\frac {128}{10}\) cm
⇒ AD = 12.8 cm
![]()
प्रश्न 2.
यदि E, F, G और H क्रमशः समांतर चतुर्भुज ABCD की भुजाओं के मध्य-बिंदु हैं, तो दर्शाइए कि ar (EFGH) = \(\frac {1}{2}\)ar (ABCD) है।
हल :
दिया है : ABCD एक समांतर चतुर्भुज है और E, F, G और H क्रमश: भुजाओं AB, BC, CD और DA के मध्य-बिंदु है।
सिद्ध करना है : ar (EFGH) = \(\frac {1}{2}\)ar (ABCD)
रचना . AC और HF को मिलाइए।
उपपत्ति : ΔABC में, E भुजा AB का मध्य-बिंदु है और F भुजा BC का मध्य-बिंदु हैं।
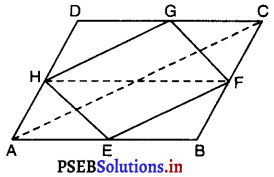
∴ EF = \(\frac {1}{2}\)AC और EF || AC …….(1)
इसी प्रकार ΔADC में,
GH = \(\frac {1}{2}\)AC और GH || AC ….(2)
∴ GH = EF और GH || EF
[(1) और (2) से]
∴ चतुर्भुज EFGH एक ||gm है। [यदि चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर और समांतर हो, तो यह समांतर चतुर्भुज होती हैं।]
|| gm ABCD में,
AD = BC और AD || BC
[|| gm की सम्मुख भुजाएँ]
∴ \(\frac {1}{2}\)AD = \(\frac {1}{2}\)BC और AD || FC
⇒ HD = FC और HD || FC
∴ HDCF एक || gm है
क्योंकि ΔHGF और ||gm HDCF एक ही आधार HF और एक ही समांतर रेखाओं के बीच है।
∴ ar (ΔHGF) = \(\frac {1}{2}\)ar (|| gm HDCF) …(3)
इसी प्रकार,
ar (ΔHEF) = \(\frac {1}{2}\)ar (|| gm HABF) ….(4)
(3) और (4) को जोड़ने से हमें प्राप्त होता है।
ar (ΔHGF) + ar (ΔHEF)
= \(\frac {1}{2}\)[ar (||gm HDCF) + ar (||gm HABF)]
अतः, ar (|| gm EFGH) = \(\frac {1}{2}\)ar (||gm ABCD).
प्रश्न 3.
P और Q क्रमश: समांतर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित बिंदु हैं। दर्शाइए कि ar (APB) = ar (BQC) है।
हल :
दिया है : ABCD एक समांतर चतुर्भुज है। P, DC पर स्थित हैऔर Q, AD पर स्थित बिंदु है।
सिद्ध करना है : ar (ΔAPB) = ar (ΔBQC)
रचना : PM | BC और QN |DC खींचिए।
उपपत्ति : क्योंकि QC, || gm QNCD का विकर्ण है।
∴ ar (ΔQNC) = \(\frac {1}{2}\)ar (|| gm QNCD) ……(1)
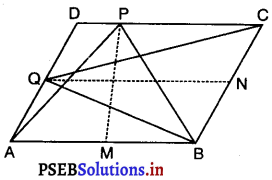
पुनः, BQ || gm ABNQ का विकर्ण है।
∴ ar (ΔBQN) = \(\frac {1}{2}\)ar (|| gm ABNQ) ….(2)
(1) और (2) को जोड़ने पर हमें प्राप्त होता है ) ar (ΔQNC) + ar (ΔBQN)
= \(\frac {1}{2}\)ar (|| gm QNCD) + \(\frac {1}{2}\)ar (|| gm ABNQ)
⇒ ar (ΔBQC) = \(\frac {1}{2}\)ar (|| gm ABCD) ….(3)
पुनः, AP, ||gm AMPD का विकर्ण है।
∴ ar (ΔAPM) = \(\frac {1}{2}\)ar (|| gm AMPD) ….(4 )
और PB, ||gm PCBM का विकर्ण है।
∴ ar (ΔPBM) = \(\frac {1}{2}\)ar (||gm PCBM) ….(5 )
(4) और (5) को जोड़ने पर हमें प्राप्त होता है:
ar (ΔAPM) + ar (ΔPBM)
= \(\frac {1}{2}\)ar (||gm AMPD) + \(\frac {1}{2}\)ar (||gm PCBM)
⇒ ar (ΔAPB) = \(\frac {1}{2}\)ar (||gm ABCD) ……(6)
(3) और (6) से हमें प्राप्त होता है
ar (ΔBQC) = ar (ΔAPB)
या ar (ΔAPB) = ar (ΔBQC)
इति सिद्धम
![]()
प्रश्न 4.
आकृति में, P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है। दर्शाइए कि
(i) ar (APB) + ar (PCD) = \(\frac {1}{2}\)ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
हल:
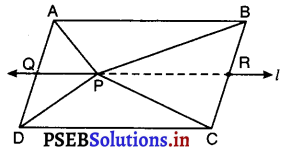
(i) P से होकर AB के समांतर एक रेखा l खींचिए जो AD को Q पर तथा BC को R पर प्रतिच्छेदित करे।
अब ΔAPB और ||gm ABRQ एक ही आधार AB तथा एक ही समांतर रेखाओं AB और QR के बीच स्थित हैं।
∴ ar (ΔAPB) = \(\frac {1}{2}\)ar (||gm ABRQ) …….(1)
साथ ही APCD और ||gm DCRQ एक ही आधार DC तथा एक ही समांतर रेखाओं DC और QR के बीच स्थित हैं।
∴ ar (ΔPCD) = \(\frac {1}{2}\)ar (||gm DCRQ) …..(2)
(1) और (2) को जोड़ने पर हमें प्राप्त होता है। ar (ΔAPB) + ar (ΔPCD)
= \(\frac {1}{2}\)ar (||gm ABRQ) + \(\frac {1}{2}\)ar (||gm DCRQ)
⇒ ar (ΔAPB) + ar (ΔPCD)
= \(\frac {1}{2}\)ar (||gm ABCD) ……….. (3)
(ii) P से होकर AD के समांतर एक रेखा m खींचिए जो AB को M पर तथा DC को N पर प्रतिच्छेद करे।
अब ΔAPD और ||gm AMND एक ही आधार AD तथा एक ही समांतर रेखाओं AD और MN के बीच स्थित हैं।
∴ ar (ΔAPD) = \(\frac {1}{2}\)ar (||gm AMND) ………….(4)
साथ ही, Δ(PBC) और ||gm MNCB एक ही आधार BC तथा एक ही समांतर रेखाओं BC और MN के बीच स्थित हैं।
∴ ar (ΔPBC) = \(\frac {1}{2}\)ar (||gm MNCB) …..(5)
(4) और (5) को जोड़ने पर हमें प्राप्त होता है :
ar (ΔAPD) + ar (ΔPBC)
= \(\frac {1}{2}\) ar (||gm AMND) + \(\frac {1}{2}\)ar (||gm MNCB)
⇒ ar (ΔAPD) + ar (ΔPBC)
= \(\frac {1}{2}\) ar (ABCD) ……..(6)
(5) और (6) से हमें प्राप्त होता है :
ar (ΔAPB) + ar (ΔPCD) = ar (ΔAPD) + ar (ΔPBC)
या, ar (ΔAPD) + ar (ΔPBC) = ar (ΔAPB) + ar (ΔPCD)
इति सिद्धम
प्रश्न 5.
आकृति में, PORS और ABRS समांतर चतुर्भज हैं तथा X भुजा BR पर स्थत कोई बिंदु है। दर्शाइए कि
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = \(\frac {1}{2}\)ar (PQRS)
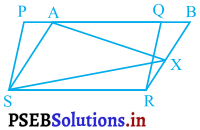
हल:
(i) समांतर चतुर्भुज PQRS और ABRS एक ही आधार SR तथा एक ही समांतर रेखाओं SR और PB के बीच स्थित हैं।
∴ ar (||gm PQRS) = ar (||gm ABRS) ……(1)
[∵ एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित समांतर चतुर्भुज क्षेत्रफल में बराबर होते हैं।]
(ii) ΔAXS और ||gm ABRS एक ही आधार AS तथा एक ही समांतर रेखाओं AS और BR के बीच स्थित
∴ ar (AAXS) = \(\frac {1}{2}\)(||gm ABRS) ….(2)
(1) का (2) में प्रयोग करने पर हमें प्राप्त होता हैं,
ar (ΔAXS) = \(\frac {1}{2}\)ar (||gm PQRS)
![]()
प्रश्न 6.
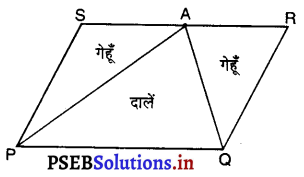
एक किसान के पास समांतर चतुर्भुज PQRS के रूप का एक खेत था। उसने RS पर स्थित कोई बिंदु A लिया और उसे P और Q से मिला दिया। खेत कितने भागों में विभाजित हो गया है? इन भागों के आकार क्या हैं? वह किसान खेत में गेहूँ और दालें बराबर-बराबर भागों में अलग-अलग बोना चाहती है। वह ऐसा कैसे करे ?
हल:
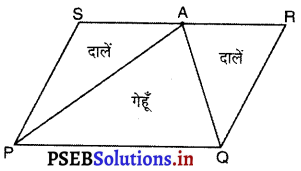
जब A को P और Q से मिलाया जाता है, तो खेत तीन भागों, जैसे : ΔPAS, ΔAPQ और ΔAQR में विभाजित हो जाता है।
ΔAPQ और समांतर चतुर्भुज PQRS एक ही आधार PQ तथा एक ही समांतर रेखाओं PQ और SR के बीच स्थित है।
∴ ar (ΔAPQ) = \(\frac {1}{2}\)ar (||gm PQRS)
अतः, त्रिभुजाकार भाग APQ, समांतर चतुर्भुज PQRS के रूप के खेत का आधा भाग है।
इसलिए किसान यदि त्रिभुजाकार खेत APQ में गेहूँ
बोती है, तो दूसरे दो त्रिभुजाकार भागों PAS और AQR में उसे दालें बोनी पड़ेंगी।
अथवा
जब वह त्रिभुजाकार खेत APQ में दालें बोती हैं तो दूसरे दो त्रिभुजाकार भागों PAS और AQR में उसे अवश्य ही गेहूँ बोना पड़ेगा।