PSEB 9th Class Science Important Questions Chapter 10 Gravitation

Punjab State Board PSEB 9th Class Science Important Questions Chapter 10 Gravitation Important Questions and Answers.

PSEB 9th Class Science Important Questions Chapter 10 Gravitation

Long Answer Type Questions:

Question 1.
Define Newton’s universal law of gravitation and establish mathematical formula for force of attraction between two objects.
Answer:
Newton’s universal law of gravitation-Every particle in this universe attracts each and every particle, the force of attraction is:
1. directly proportional to the product of both the masses.
2. Inversely proportional of the square of the distance between the two. This force always acts along the line joining the two masses.

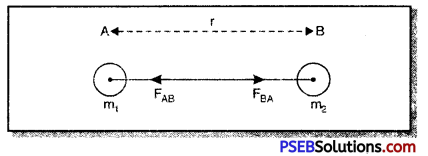
Derivation of Mathematical Formula: From the fig. Jet there are two balls A and B having masses m₁ and m₂ distance between them is ‘r’.
According to Newton’s third law of motion ball A exerts a force FAB on the ball B and ball B exerts a force FBA on the ball A. These forces are equal and opposite

where G is universal gravitational constant. This is named so since its numerical value remains constant in whole of the universe and the formula is known as Newton’s universal law’ of gravitation.
Value of G
G = 6.67 × 10^-11 Nm²/kg²

Question 2.
Write Kepler’s law in context with the motion of planets.
Answer:

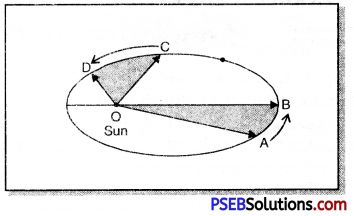
By the 16th centuary, a lot of data on the motion of planets had been collected by many astronomers. Johannes Kepler derived three law s based on these data. These are known as Kepler’s laws. These are:
1. Law of orbits (First laws): The orbit of a planet is an ellipse and the sun is at one of the foci, as shown in fig. In this fig. Sun is shown at O.

2. Law of area (Second laws): The line joining the planet and sun sweep equal areas in equal interv als of time. Thus, time taken for the motion from A to B is same as for the motion from C to D and area OAB and OCD are equal.

3. Law of time period (Third law): The cube of mean distance of a planet from the sun is directly proportional to square of its orbital time period
T² ∝ r³
But Kepler could not give a theory which explained the motion of planets.
Newton showed that due to motion of planets sun exerts force of gravtation on them.
i.e. T²/r³ = constant.

Question 3.
How did Robert Boyle proved experimentally that all bodies fall in vacuum with same acceleration?
Or
How did Robert Boyle show experimentally that a coin and a piece of paper when dropped simultaneously from same height in vacuum fall with same acceleration?
Answer:
Boyle’s Experiment: As shown in fig. Robert Boyle took a long glass tube. A heavy coin and a piece of paper were placed inside the tube. The ends of the tube were closed. Air from the tube was removed with the help of a vacuum pump.

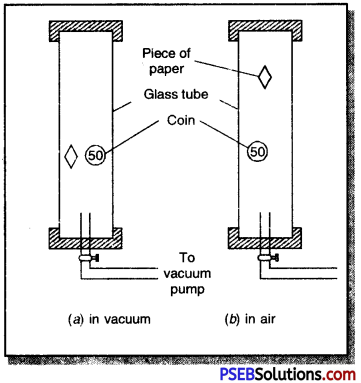
When the tube was quickly inverted it was seen that coin and a piece of paper hit the bottom of the tube at the same time. Now the experiment was repeated with air inside the glass tube. This time it was observed that a piece of paper falls slowly whereas the coin immediately hit the bottom of glass tube. This experiment proves that in vacuum all bodies irrespective of their masses (both light and heavy) fall towards earth with same acceleration

Question 4.
(a) Prove that acceleration due to gravity is independent of mass.
(b) Find the value of ‘g’.
Answer:
(a) Consider a body of mass ‘m’ lying on the surface of earth. Suppose M and R are respectively mass and radius of earth.
Let F be the force of gravity acting on the body

This acceleration is called acceleration due to gravity
∴ g = \(\frac{G M}{R^{2}}\)
This equation is free from mass ‘m’. This shows that due to force of gravity the acceleration produced in an object is independent of its mass.

(b) To find the value of ‘g’
G = 6.67 × 10 “n Nm2/kg2
R = 6400 km
= 6400 × 1000 m
= 64 × 105 m
= 6.4 × 106 m
Mass of the earth(M) = 6 × 1024 kg
But g = \(\frac{G M}{R^{2}}\)
= \(\frac{6.67 \times 10^{-11} \times 6 \times 10^{24}}{\left(6.4 \times 10^{6}\right)^{2}}\)
or g = 9.8 ms^-2

Question 5.
Describe those factors which are responsible for variation in the value of acceleration due to gravity ‘g’?
Answer:
Variation in the value of acceleration due to following factors:
Variation in g with altitude-Value of ‘g’ is maximum on the surface of earth. As we move in the upward direction (higher altitudes) value of ‘g’ goes on decreasing. We can calculate value of ‘g at altitude using mathematical formula. If
g_e = acceleration due to gravity on the surface of earth
g_h = acceleration due to gravity at height h
R = radius of earth
we know g_h = g_e\(\left[\frac{\mathrm{R}^{2}}{(\mathrm{R}+h)^{2}}\right]\)
If we know value of h, we can calculate g_h.
Special case-If ‘h’ is half the value of radius of earth i.e. h = \(\frac {R}{2}\) then

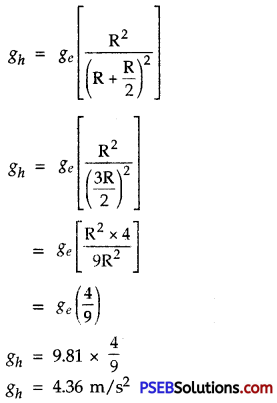
Another interesting fact that value of ‘g’ is zero at the centre of earth.

2. Variation in g due to shape of earth-
Earth is not exactly spherical. It is somewhat egg-shaped. Its radius at poles is less than that at equator as shown in fig.

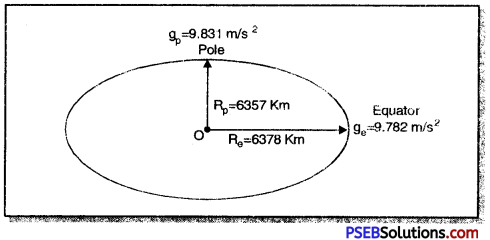
As shown in fig. radius of earth at equator is 6378 km and radius of earth at poles is 6357 km. Thus, value of g at poles is g_p = 9.831 m s_-2 (maximum) and minimum value at equator is g_e = 9.782 m s_-2. We use average value of g calculated from g_e, and g_p.

3. Effect of depth: If we go deep under the earth e.g. in caves or in mines, value of ‘g’ i’ decreased. Value of g goes on decreasing, if depth goes on increasing. At the centre of earth, value of g is zero.
\(\frac{\mathrm{W}_{d}}{\mathrm{~W}_{e}}=\frac{g_{d}}{g_{e}}=\left[1-\frac{d}{\mathrm{R}}\right]\)

Question 6.
Establish the relation between ‘g’ and ‘G’.
Or
Deduce an expression for it in terms of mass of the earth ‘M’ and universal gravitational constant ‘G’.
Or
Show that the acceleration due to gravity of an object is independent of its mass.
Answer:

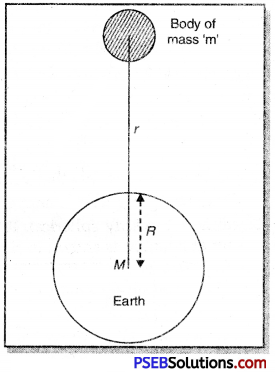
Relation between ‘g’ and ‘G’. Suppose the earth is a sphere of mass M and radius R, Consider a body of mass m lying at a distance ‘r’ from the centre of the earth. According to Newton’s law of gravitation, the force of attraction between the earth and the body,
F = \(\frac{\mathrm{GM} m}{r^{2}}\) ……………… (i)
Tills force of gravity produces an acceleration ‘g’, is the body of mass m.
Hence, from Newton’s second law,
F = Mass × Acceleration
F = m × g ……………..(ii)
From equations (i) and (ii) we get
mg = \(\frac{\mathrm{GM} m}{r^{2}}\)
or g = \(\frac{\mathrm{GM}}{r^{2}}\) ………..(iii)
This equation gives relation between acceleration due to gravity ‘g’ at points far away from the earth and gravitational constant ‘G’.
Since (3) does not involve’m’ it is therefore eviden t that ‘g’ does not depend upon the mass of the body.

Question 7.
What is Archimedes principle? How can you verify it experimentally? Also write applications of Archimedes principle.
Answer:
Archimedes Principle: According to this principle when a solid body is immersed either completely or partially in a liquid, it experiences an upward thrust which is equal to the weight of the liquid displaced by the immersed part of the body.”

Experimental Verification: Take a stone piece and tie it to the hook of a spring balance. Hold the spring balance in your hand or support it from the stand so as to suspend the stone piece as shown in fig.

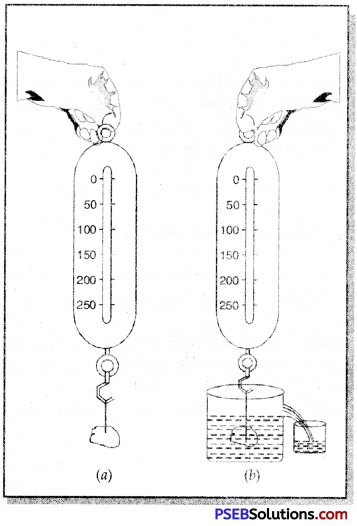
Note, the reading on the spring balance to know the weight of the stone. Now pour some water a beaker with and slowly immerse the stone in the water while remaining tied with the hook of spring balance as shown in fig. (b). You will see that spring balance shows a decreased reading i.e. weight of stone is decreased after it is immersed in the water.

Subtract the two readings to know the decrease in the weight of stone. As soon as the stone is immersed in the water it displaces water equal to its own volume. Collect this water in other beaker and measure its weight. You will find that this weight of water is equal to the decrease of weight of the stone. Thus Archimedes principle is proved.

Applications of Archimedes’ Principle:

1. Archimedes principle is used in designing ships and submarines.
2. Lactometers are constructed on Archimedes’ Principle which are used to measure puritv of a sample of milk.
3. Hydrometers used to measure density of liquid are also based on Archimedes principle.

Short Answer Type Questions:

Question 1.
Which one is greater-the gravitational force of the earth on 1 kg iron or the force of gravitation applied by 1 kg on earth?
Answer:
According to Newton’s law of Gravitation there exists of mutual force of attraction between two objects. Since the mass of iron is less than the mass of the earth, therefore earth attracts 1 kg mass towards it with a greater force which is noticeable.

Question 2.
Why is G called universal gravitational constant?
Answer:
G is called universal gravitational constant because its numerical value is same in the whole universe. This value is G = 6.67 x 10^-11 Nm²/kg².

Question 3.
Is the value of ‘g’ at a given place same for different bodies or it is variable?
Answer:
From the relation between the acceleration due to gravity ‘g’ and universal gravitational constant G, we know g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
From this equation it is evident that the value of ‘g’ does not depend upon the mass of the body. Thus we reach a conclusion that at a given place the value of g is same for different bodies.

Question 4.
Why does a body becomes weightless at the centre of earth?
Answer:
We know value of g goes on decreasing as we continue moving deep into the earth and value of acceleration due to gravity (g) = 0 at the centre of earth. Thus, a body whose mass is m,
Weight of body = m × 0 = 0
Therefore, body becomes weightless.

Question 5.
A tennis ball jumps higher at hills than at planes. Explain.
Answer:
Value of g decreases with altitude, thus gravitational force acting on ball at hills is less as a result ball jumps higher at hills than at planes.

Question 6.
The weight of an object on the surface of earth is 9.8 N. What does this statement mean?
Answer:
We know that value of ‘g’ on the surface of earth is 9.8 m/s² and the relation for weight of an object is:
w = m × g
9.8 = m × 9.8
or m = \(\frac {9.8}{9.8}\)
∴ m = 1 kg
The given statement therefore means the mass of the object on earth is 1 kg.

Question 7.
What type of motion a freely falling body execute under gravity?
Answer:
A body falling freely under gravity executes uniform accelerated motion. If bodies with different masses and different shapes are allowed to fall freely in vacuum, they all will have same acceleration due to gravity.

Question 8.
Give points of difference between Acceleration due to gravity (g) and Universal gravitational constant'(G).
Answer:
Difference between g and G:

Acceleration due to gravity (g)	Gravitational constant (G)
1. It represents acceleration acquired by the body due to gravity.	It represents force of attraction between two masses of 1 kg each lying 1 m apart.
2. Its value is different at different places on earth surface.	Its value is constant at all places. Thus, it is called universal constant.
3. Its value at the surface of earth is 9.8 m/s2.	Its value is 9.67 × 10-11 Nm2kg-2.
4. It is a vector quantity.	It is a scalar quantity.

Question 9.
You buy W weight of sugar at a place situated on equitorial line and then take it to Antarctica. Will that sugar weigh same there? If not whether it would be more or less.
Answer:
The value of ‘g’ at Antarctica is not same as on equator. The value of ‘g’ increases on Antarctica therefore, sugar bought at any place on equitorial line when taken to Antarctica would have more weight but its mass will remain the same because mass is a constant quantity.

Question 10.
Why cannot we move a finger without disturbing all the stars?
Answer:
When we move our finger, then distance between finger and all other things in the universe change and as a result force of gravitation also changes. Thus, all the things get disturbed, although this disturbance is negligible.

Question 11.
Distinguish between Gravitation and Gravity.
Answer:

• Gravitation: Gravitation is the force of attraction between any two bodies in the universe. The attraction between the sun and the earth, the attraction between a table and a chair are examples of gravitation.
• Gravity: Gravity is a special case of gravitation when one of the two bodies is the earth. Gravity is the attraction between the earth and any object lying on or near its surface. A ball thrown upward falls back on the surface of the earth due to earth’s force of gravity.

Question 12.
Explain why a small piece of stone is not attracted towards another big place of stone on the earth’s surface?
Answer:
Because of very small value of G, the force of attraction between any two such ordinary sized bodies is so small that it cannot produce motion in them.

Question 13.
The earth attracts an apple. Does the apple also attract with earth? If it does, why does the earth not move towards the apple?
Answer:
The apple also attracts the earth with an equal and opposite force. The mass of the earth is very large compared to that of apple. So, the acceleration produced in earth is very small as compared to that in the apple. Hence, the motion of the earth towards the apple is not appreciable and therefore, is not noticeable.

Question 14.
If the force of gravity somehow vanishes today, why would we be sent being in space?
Answer:
In the absence of force of gravity, the centripetal force required to keep us rotating along the earth would not be available. As a result would fly off along the tangent to with into the space.

Question 15.
What is meant by density and relative density?
Answer:
Density of a substance is defined as the mass of a substance contained in a unit volume.
Density = \(\frac{\text { Mass }}{\text { Volume }}\)
Its SI unit is kg m^-3.

Relative density or specific gravity is the ratio of density of substance to the density of same volume of water
R.D or S.G = \(\frac{\text { Density of substance }}{\text { Density of water }}\)

Density of water is 1,000 kg m^-3 in SI.
According to Archimedes’ principle, when a body is immersed in water, the loss of weight in water is equal to the weight of an equal volume of water, i.e., weight of water displaced. Hence R.D. can be written as
R.D = \(\frac{\text { Weight of substance }}{\text { Loss of weight of body in water }}\)

Question 16.
What do you mean by buoyancy and centre of buoyancy? In which direction does the buoyant force on an object immersed in a liquid act?
Answer:
Buoyancy: When a body is immersed partially or wholly in a fluid (liquid or gas), it displaces fluid. The displaced fluid exerts an upward force on the body.

The upward force acting on a body imnu rsed in a fluid is called upthrust or force of buoyancy and the phenomenon is called buoyancy. The buoyancy acts through the centre of gravity of the displaced fluid which is called centre of buoyancy.

Question 17.
State Archimedes’ principle.
Answer:
Archimedes’ Principle. When a solid body is immersed completely or partially in a fluid, it experiences an upward thrust which is equal to the weight of the fluid displaced by the immersed part of the body.

Question 18.
Name two forces which act on a body immersed in a liquid. Give the directions in which they act.
Answer:
Two forces which act on a body immersed in a liquid are:

• Weight of the body acting downward.
• An upthrust due to displaced liquid.

Question 19.
How is submarine able to move on water surface as well as go under water?
Answer:
To move submarine under water, water is pumped in its special tanks. This causes a net increase in weight and thus submarine goes down in water.

To bring the submarine upon the surface of sea, the water from the tanks is thrown out by pumps. When water from the tanks of submarine is taken out, the net weight of the submarine decreases without any change in its volume and it comes up on the surface of water.

Question 20.
Give reason when Big buildings and dams have wide foundations for safety.
Answer:
Dams and big buildings have wide foundations for safety, because they may not collapse under high pressure of the building.

Question 21.
A steel needle sinks in water but a steel ship floats. Explain how?
Answer:
A steel needle sinks in water because it displaces less weight of water which provides less buoyant force than the actual weight of the needle. On the other hand, steel ship floats because it displaces a large weight of water which provides a greater buoyant force to keep it a float.

Question 22.
Give reasons for the following :
(a) A sharp blade is more effective in cutting an object than a blunt blade.
(b) A cork piece floats but an iron piece sinks in water.
Answer:
(a) We know Pressure = \(\frac{\text { Thrust }}{\text { Area }}\). For the given thrust, pressure ∝ \(\frac{\text { 1 }}{\text { Area }}\). Thus the effect of the same magnitude of force is more when the area of surface in contact is less. Hence a sharp blade is more effective in cutting an object than a blunt blade.
(b) The density of the cork piece is less than the density of water, and the. density of the iron piece is more than the density of water. Hence, the cork piece floats but the iron piece sinks in water.

Question 23.
Explain the following:
(a) Swimmers are provided with an inflated rubber jacket.
(b) It is easier of swim in sea water than in river water.
Answer:
(a) Swimmers are provided with an inflated rubber jacket to increase the volume such that density is decreased, which is helpful for swimming.
(b) It is easier to swim in sea water than in river water because density of sea water is more than water of the needle sinks in a river while a ship float on it.

Question 24.
Why is the pressure on ground more when a man is walking than when he is standing?
Answer:
When the man stands he exerts a force on the ground equal to his own weight. But when he walks, he pushes the ground backward and exerts an additional force on the ground. That is why pressure on the ground is more when a man is walking than when he is standing.

Question 25.
Why a bucket of water is lighter when in water than when it is taken out of water?
Answer:
Inside water, the bucket experiences upthrust exerted by displaced water, so its apparent weight becomes less than the actual weight. When bucket is taken out of water, upthrust on the bucket disappears and it feels heavier.

Question 26.
If a fresh egg is put into a beaker filled with water, it sinks. On dissolving a lot of salt in the water, the egg begins to rise and floats. Why?
Answer:
The average density of a fresh egg is more than that of pure water but less than that water in which salt is dissolved. So a fresh egg sinks in pure water while it floats in salty water.

Important Formulae:

1. F = G\(\frac{\mathrm{M} m}{\mathrm{R}^{2}}\)
2. F = mg
3. g = G\(\frac{\mathrm{M}}{\mathrm{R}^{2}}\)
4. υ = u +gt
5. υ² = u² + 2gh
6. h = ut + \(\frac {1}{2}\)gt²
7. g_m = \(\frac {1}{6}\)g_e
   (g_m = Acceleration due to gravity on moon , g_e = Acceleration due to gravity on earth)

Necessary Data-
Earth
Mass = 6 × 10²⁴ Kg
Radius = 6.4 × 10⁶ m (6400 Km)
Distance from Sun = 1.5 × 10¹¹ m
Moon
Mass = 7.3 × 10²² Kg

Numerical Problems (Solved):

Question 1.
Two spheres of 1 kg mass each are separated by 3 m. Calculate the gravitational force between then. Given G = 6.67 × 10^-11 Nm²/kg².
Solution:
Here m₁= m₂ = 1 kg
Distance between two spheres, (r) = 3 m
Gravitational constant (G) = 6.67 × 10^-11 Nm²/kg²
We know

Question 2.
The radius of moon is 1.7 × 10⁶ m and its mass is 7.35 × 10²² kg. What is the acceleration due to gravity on the surface of moon? Given G = 6.67 × 10^-11 Nm²/kg²
Solution:
Radius of moon, (R) = 1.7 × 10⁶ m
Mass of moon, (M) = 7.35 × 10²² kg
Gravitational constant, (G) = 6.67 × 10^-11 Nm²/kg² (Given)
We know, Acceleration due to gravity on moon

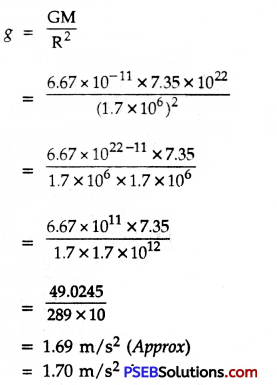
Question 3.
Find the change in weight percentage of a body when it is taken from equator to poles. Polar radius is 6357km and equitorial radius is 6378km.
Solution:
Polar radius, (r) = 6357 km
Equitorial radius (R) = 6378 km
∴ h = R – r
⇒ h = (6378 – 6357)km
h = 21km
R = 6400 km(Approx)

Question 4.
At what height above the earth surface, the acceleration due to gravity will be half that on the surface of earth? Suppose R is the radius of earth.
Solution:
Let h be the height above earth surface where

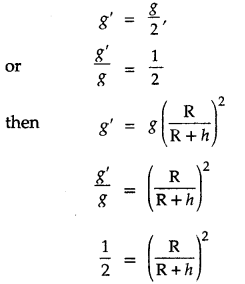
Question 5.
A ball is dropped from top of 40 m high tower. What will be its velocity after covering a distance of 20 m ? What will be its velocity on striking the earth?
Answer:
1. Here, height of the tower, (h) = 40 m
Initial velocity, (u) = 0
Acceleration due to gravity, (g) = 10m/s²
Distance covered (S) = 20m

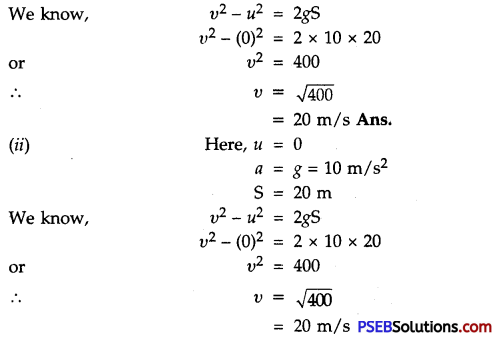
i.e. Velocity of ball when it strikes the earth. = 20 m/s

Question 6.
If weight of an object is 49 N then what will be its mass?
Solution:
Weight of the object W = 49 N
g = 9.8 m s^-2
We know, weight = Mass × acceleration due to gravity
W = m × g
49 = m × 9.8
or m = \(\frac {49}{9.8}\)
∴ m = 5 kg

Question 7.
Ah object is projected vertically upward with a velocity of 50 m/s. After what time the object will attain the maximum height.
Solution:
Initial velocity of the object (u) = 50 m/s [upward direction]
Acceleration due to gravity, (g) = – 10 ms^-2 [object comes to rest]
Velocity of the object at maximum height,
(υ) = 0
Time taken (t) =?
We know, υ = u + gt
0 = 50 + (-10) × t
0 = 50 – 10t
or 10t = 50
∴ t = \(\frac {50}{10}\) = 5s
So the object will attain its maximum height after 5 seconds.

Question 8.
A stone is dropped from the edge of a rooftop. If it crosses 2 m high window in 0.1 second then what is the distance between the upper end of window and the roof?
Solution:

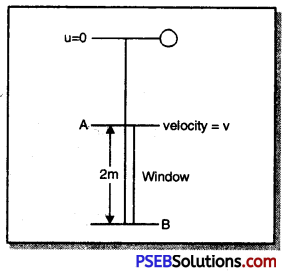
Distance covered in crossing the window
(S) = 2 m
g = 9.8 ms^-2
t = 0.1 s
Let υ be the velocity of the stone when it reaches the upper edge A of the window.

Question 9.
A helicopter drops food packet for people caught in stationary boat. This is moving at a height of 20 m with a horizontal velocity of 2 m/s. When food packet is dropped the nearest end of the boat is just below the helicopter. If boat is 5 m long shall people caught in the boat receive the dropped food packets?
Solution:
h = 20 m, u = 2 m/s g = 10ms^-2
Vertical Range (R) = \(\frac{2 \sqrt{2 h}}{g}\)
= \(\frac{2 \sqrt{2 \times 20}}{10}\)
= 2\( \sqrt{{4}} \)
= 2 × 2 = 4 m
But lenght of boat, = 5m
So people caught in the boat will receive food packets.

Question 10.
An object of volume V is immersed in a liquid of density ρ. Calculate the magnitude of buoyant force acting on the object due to the liquid.
Solution:
By Archimedes’ principle, the magnitude of buoyant force,
U.F. = Weight of liquid displaced = Volume × Density × g or
or U.F. = Vρg

Question 11.
The pressure exerted by the weight of a cubical block of side 4 cm on the surface is 10 pascal. Calculate the weight of the block.
Solution:
Here pressure exerted, P = 10 pascal = 10 Nm^-2,
Area, A = 4 cm × 4 cm
= 16 × 10^-4 m²
As P = \(\frac {F}{A}\)
= \(\frac {W}{A}\)
W = P × A
= 10 Nm^-2 × 16 × 10^-4m²
= 1.6 × 10^-2 N

Question 12.
The volume of a 500 g sealed packet is 350 cm³. Will the packet float or sink in water if the density of water is 1 g cm^-3? What will be the piass of the water displaced by this packet?
Solution:
Mass of packet = 500 g
Volume of packet = 350 cm³.
Density of packet = \(\frac{\text { Mass }}{\text { Volume }}\)
= \(\frac{500 \mathrm{~g}}{350 \mathrm{~cm}^{3}}\)
= 1.43 g cm^-3
Since its density (1.43 g cm^-3) is more than that of water (1 g cm^-3) thus, the sealed packet will sink in water
Volume of water displaced = Volume of packet
= 350 cm³
Mass of water displaced = Volume × Density
= 350 cm³ × 1gcm^-3
= 350 g

Question 13.
A block of wood is kept on the table top. The mass of wooden block is 5 kg and its dimensions are 40 cm × 20 cm × 10 cm. Find the pressure exerted by the wooden block on the table top if it is made to lie on the table top with its sides of dimensions (a) 20 cm × 10 cm and (b) 40 cm × 20 cm.
Solution:
Here, M = 5kg and g = 9.9 ms^-2
Weight = force exerted on table top
= mg
= 5 × 9.8
= 49 N

Question 14.
A solid body floating in water has \(\frac {1}{6}\)th of its volume above the surface.
What fraction of its volume will project upwards if it floats in a liquid of density 1,020 km m^-3?
Solution:
Let V be the volume of the body
Volume inside water = V – \(\frac {V}{6}\)
= (1 – \(\frac {1}{6}\))V
= \(\frac {5}{6}\)V
Upward thrust in water = \(\frac {5}{6}\) × 1,000 × g N ……………..(i)
where density of water is 1,000 kg m^-3
Let υ be the volume of the body outside the liquid of density, 1,020 kg m^-3.
∴ Volume inside the liquid = (V – υ)
Upward thrust in liquid = (V – υ) × 1,020 × g N ……….(ii)
Upward thrust in two cases must be the same and must be equal to the weight of the body.

Very Short Answer Type Questions:

Question 1.
What is g on the moon as compared to that on earth?
Answer:
Nearly \(\frac {1}{6}\)th of its value on earth.

Question 2.
What is unit of G?
Answer:
It is Nm² kg^-2.

Question 3.
What is the mass of the earth?
Answer:
It is about 6 × 10²⁴ kg.

Question 4.
What is essential property of matter-mass or weight?
Answer:
Mass is the basic and essential property. It is constant everywhere. Weight of a body varies from place to place.

Question 5.
What is SI unit of weight of a body?
Answer:
It is newton (N).

Question 6.
The earth’s gravitational force causes an acceleration of 5 m s^-2 on a 1 kg mass somewhere in the space. How much will be the acceleration of a 3 kg mass at that place?
Answer:
Same i.e., 5ms^-2 since g at a place is independent of mass of the body.

Question 7.
Why one can jump higher on the surface of moon than on the earth?
Answer:
The g at moon surface is nearly 1/6th of that at the surface of earth. Hence one can jump six times higher on the moon with a given initial velocity.

Question 8.
Give the value of universal gravitational constant in S.I. units.
Answer:
(G) = 6.67 × 10^-11 Nm²/kg²
The value of gravitational constant.

Question 9.
The value of ‘G’ on the surface of earth is 6.67 × 10^-11 Nm²/kg². What is its value on the surface of moon?
Answer:
Since G is universal constant so its value on moon surface will be same as on the earth surface i.e. G = 6.67 × 10^-11 Nm²/kg² .

Question 10.
State two factors on which the gravitational force between two objects depends.
Answer:
The gravitational force between two objects depends on: (i) their masses (ii) distance between them.

Question 11.
Write the formula to find the magnitude of gravitational force between the earth and an object on the surface of the earth.
Answer:
F = \(\mathrm{G} \frac{\mathrm{Mm}}{r^{2}}\)

Question 12.
Can the mass of a body be zero.
Answer:
No, mass of body can never be zero.

Question 13.
Mass of an object on the earth is 600g. What will be its mass on moon?
Answer:
Mass of the object on moon will be same i.e. 600 g.

Question 14.
You find your mass to be 42 kg on a weighing machine. Is your mass more or less than 42 kg?
Answer:
Mass is a constant quantity. So, it can not be more or less than 42 kg.

Question 15.
How does the value of ‘g’ vary from equator to poles?
Answer:
The value of ‘g’ increases as we move from equator to poles.

Question 16.
What will be the weight of an object on the earth whose mass is 10 kg?
Answer:
Weight of the object on earth
(W) = m x g
= 10 kg × 10 m s^-2
= 100 N

Question 17.
Write the S.I. unit of G.
Answer:
Nm²/kg².

Question 18.
When does an object float when placed on the surface of water?
Answer:
If the density of object is less than water, it will float.

Question 19.
While swimming why do we feel light?
Answer:
The swimmer experiences an upward force by water, this causes buoyancy and makes the swimmer feel light.

Question 20.
Why does a truck or a motor-bus has much wider tyres?
Answer:
So that pressure acting on the road due to weight of truck or motor-bus may be small.

Question 21.
An army tank weighing more than a hundred tonne move conveniently on an earthen road. How?
Answer:
The army tank rests upon a continuous broad chain. So, the total surface area is large and pressure on road due to weight of tank is not very high.

Question 22.
What is the unit of relative density? Why?
Answer:
Relative density has no unit because it is a ratio of two terms having same units. So relative density is expressed in numbers only.

Question 23.
The weight of an object on the moon is ………………. of its weight on the earth.
Answer:
The weight of an object on the moon is 1/6th of its weight on the earth.