PSEB 9th Class Science Important Questions Chapter 11 ਕਾਰਜ ਅਤੇ ਊਰਜਾ

Punjab State Board PSEB 9th Class Science Important Questions Chapter 11 ਕਾਰਜ ਅਤੇ ਊਰਜਾ Important Questions and Answers.

PSEB 9th Class Science Important Questions Chapter 11 ਕਾਰਜ ਅਤੇ ਊਰਜਾ

ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Long Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਸਥਿਤਿਜ ਊਰਜਾ ਕਿਸ ਨੂੰ ਆਖਦੇ ਹਨ ? ਸਥਿਤਿਜ ਊਰਜਾ ਲਈ ਗਣਿਤਿਕ ਫਾਰਮੂਲਾ ਸਥਾਪਿਤ ਕਰੋ ਅਤੇ ਯਇਸ ਉਰਜਾ ਦੀਆਂ ਵਿਵਹਾਰਿਕ ਉਦਾਹਰਨਾਂ ਦਿਓ ।
ਉੱਤਰ-
ਸਥਿਤਿਜ ਉਰਜਾ (Potential Energy)-“ਇਹ ਕਿਸੇ ਵਸਤੂ ਵਿੱਚ ਉਸ ਦੇ ਆਕਾਰ ਜਾਂ ਉਸ ਦੀ ਧਰਤੀ ਦੀ ਸੜਾ ਤੋਂ ਉੱਪਰ ਜਾਂ ਹੇਠਾਂ ਸਥਿਤੀ ਕਾਰਨ ਉਪਸਥਿਤ ਉਰਜਾ ਹੁੰਦੀ ਹੈ ।”
ਗਣਿਤਿਕ ਫਾਰਮੂਲਾ-
ਮੰਨ ਲਓ ਅਤੇ ਪੁੰਜ ਵਾਲਾ ਇੱਕ ਪੱਥਰ ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਤੋਂ ਉੱਚਾਈ ‘h’ ਤੀਕ ਉੱਪਰ ਵੱਲ ਨੂੰ ਚੁੱਕਿਆ ਜਾਂਦਾ ਹੈ ਅਜਿਹਾ ਕਰਨ ਲਈ ਧਰਤੀ ਦੀ ਗੁਰੂਤਾ ਵਿਰੁੱਧ ਪੱਥਰ ਉੱਪਰ ਕਾਰਜ ਕਰਨਾ ਪਵੇਗਾ ।
ਇਸ ਲਈ ਕੀਤਾ ਕਾਰਜ W = ਬਲ × ਉੱਚਾਈ
ਜਾਂ W = F × h
ਪਰੰਤੂ ਪੱਥਰ ਦਾ ਭਾਰ W = mg × h
ਪੱਥਰ ਉੱਪਰ ਕੀਤਾ ਗਿਆ ਇਹ ਕਾਰਜ ਉਸ ਪੱਥਰ ਅੰਦਰ ਸਥਿਤਿਜ ਊਰਜਾ (P.E.) ਦੇ ਰੂਪ ਵਿੱਚ ਸਟੋਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
∴ ਸਥਿਤਿਜ ਉਰਜਾ (P.E.) = mgh
ਇਸ ਸਮੀਕਰਨ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਜਿੰਨੀ ਜ਼ਿਆਦਾ ਉਚਾਈ ਹੋਵੇਗੀ ਓਨੀ ਹੀ ਜ਼ਿਆਦਾ ਪੱਥਰ ਵਿੱਚ ਸਥਿਤਿਜ ਉਰਜਾ ਸਟੋਰ ਹੋ ਜਾਵੇਗੀ ।

ਵਿਵਹਾਰਿਕ ਉਦਾਹਰਨਾਂ-
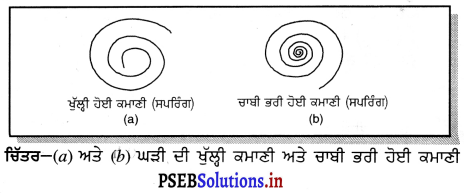
ਪੁਰਾਣੇ ਜ਼ਮਾਨੇ ਦੀਆਂ ਘੜੀਆਂ, ਡਿਜੀਟਲ ਨਹੀਂ ਹੁੰਦੀਆਂ ਸਨ ।ਉਨ੍ਹਾਂ ਘੜੀਆਂ ਨੂੰ ਚਲਾਉਣ ਲਈ ਚਾਬੀ ਭਰਨੀ ਪੈਂਦੀ ਸੀ । ਜਦੋਂ ਘੜੀ ਦੀ ਕਮਾਣੀ ਪੂਰੀ ਤਰ੍ਹਾਂ ਖੁੱਲ੍ਹੀ ਹੁੰਦੀ ਹੈ, ਤਾਂ ਘੜੀ ਨਹੀਂ ਚਲਦੀ, ਪਰੰਤੂ ਜਦੋਂ ਅਸੀਂ ਇਸ ਦੀ ਕਮਾਣੀ ਨੂੰ ਚਾਬੀ ਭਰਦੇ ਹਾਂ, ਤਾਂ ਅਸੀਂ ਕੁੱਝ ਕਾਰਜ ਕਰਦੇ ਹਾਂ, ਚਿੱਤਰ (b) ਵਿੱਚ ਵਿਖਾਏ ਅਨੁਸਾਰ ਚਾਬੀ ਭਰਨ ਨਾਲ ਕਮਾਣੀ ਸੁੰਗੜਦੀ ਜਾਂਦੀ ਹੈ ਜਿਸ ਕਰਕੇ ਇਸ ਵਿੱਚ ਸਥਿਤਿਜ ਊਰਜਾ ਸਟੋਰ ਹੁੰਦੀ ਜਾਂਦੀ ਹੈ । ਸਟੋਰ ਕੀਤੀ ਗਈ ਇਹ ਸਥਿਤਿਜ ਉਰਜਾ ਘੜੀ ਦੀਆਂ ਸੂਈਆਂ ਨੂੰ ਡਾਇਲ ਉੱਪਰ ਚਲਾਉਣ ਵਿੱਚ ਮੱਦਦ ਕਰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਗਤਿਜ ਊਰਜਾ ਕਿਸ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ? ਗਤਿਜ ਊਰਜਾ ਲਈ ਗਣਿਤਿਕ ਸਮੀਕਰਨ ਦੀ ਵਿਉਂਤ ਪੇਸ਼ ਕਰੋ ਅਤੇ ਵਿਹਾਰਿਕ ਉਦਾਹਰਨਾਂ ਵੀ ਦਿਓ ।
ਉੱਤਰ-
ਗਤਿਜ ਊਰਜਾ (Kinetic Energy) – “ਕਿਸੇ ਵਸਤੂ ਵਿੱਚ ਗਤੀ ਕਾਰਨ ਪੈਦਾ ਹੋਈ ਊਰਜਾ ਨੂੰ ਗਤਿਜ ਊਰਜਾ ਕਹਿੰਦੇ ਹਨ ।”
ਜੇਕਰ ਕੋਈ ਵਸਤੁ ਗਤੀਸ਼ੀਲ ਨਹੀਂ, ਤਾਂ ਇਸ ਵਿੱਚ ਤਿਜ ਉਰਜਾ ਨਹੀਂ ਹੁੰਦੀ ।
ਗਣਿਤਿਕ ਸਮੀਕਰਨ – ਮੰਨ ਲਓ ਕਿ ਆ ਪੁੰਜ ਵਾਲੀ ਇੱਕ ਫੁੱਟਬਾਲ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਹੈ ਜਿਸ ਉੱਤੇ ਬਲ F ਲਗਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਬਲ ਕਾਰਨ ਫੁੱਟਬਾਲ ਸਮੇਂ ਵਿੱਚ S ਦੁਰੀ ਤੈਅ ਕਰਦੀ ਹੋਈ ਵੇਗ ॥ ਪ੍ਰਾਪਤ ਕਰ ਲੈਂਦੀ ਹੈ । ਇਸ ਲਈ ਇਸ ਵਿੱਚ ਪ੍ਰਵੇਗ ‘a’ ਉਤਪੰਨ ਹੁੰਦਾ ਹੈ ।

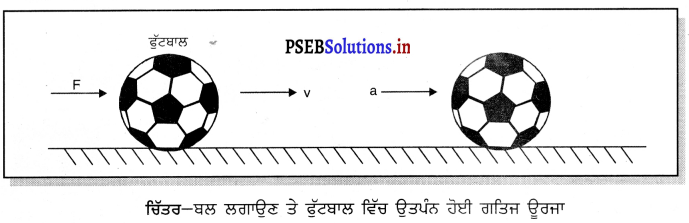
ਫੁੱਟਬਾਲ ‘ਤੇ ਕੀਤਾ ਗਿਆ ਕਾਰਜ W = F × S ………… (1)
ਨਿਊਟਨ ਦੇ ਗਤੀ ਦੇ ਦੁਜੇ ਨਿਯਮ ਅਨੁਸਾਰ, F = m × a ……………. (2)
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਗਤੀ ਦੀ ਇੱਕ ਰੇਖੀ ਸਮੀਕਰਨ
S = ut + 1/2 at² ………….. (3)
ਅਤੇ
v = u + at ……………. (4)
ਫੁੱਟਬਾਲ ਵਿਰਾਮ ਅਵਸਥਾ ਤੋਂ ਹੀ ਚੱਲੀ ਹੈ, ਇਸ ਲਈ u = 0
ਹੁਣ ਸਮੀਕਰਨ (3) ਅਤੇ (4) ਵਿੱਚ u = 0 ਰੱਖ ਕੇ
S = 1/2 at² …………(5)
ਅਤੇ
υ = 0+ at = at ……………. (6)
ਸਮੀਕਰਨ (1) ਵਿੱਚ ਸਮੀਕਰਨ (2), (5) ਅਤੇ (6) ਤੋਂ ਮੁੱਲ ਰੱਖਣ ਮਗਰੋਂ
w = (ma) (1/2 at²)
= 1/2 ma²t²
W = 1/2 m (at)² …………….. (7)
ਸਮੀਕਰਨ (6) ਨੂੰ ਸਮੀਕਰਨ (7) ਵਿੱਚ ਭਰਨ ‘ਤੇ W = 1/2 mv² ……………. (8)

ਸਮੀਕਰਨ (8) ਸਿੱਧ ਕਰਦੀ ਹੈ ਕਿ ਫੁੱਟਬਾਲ ‘ਤੇ ਕੀਤਾ ਗਿਆ ਕਾਰਜ ਉਸ ਅੰਦਰ ਗਤਿਜ ਊਰਜਾ ਦੇ ਰੂਪ ਵਿੱਚ ਸਟੋਰ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸ ਲਈ ਕੀਤਾ ਗਿਆ ਕਾਰਜ = ਸਟੋਰ ਕੀਤੀ ਗਈ ਗਤਿਜ ਉਰਜਾ = 1/2mv²
ਗਤਿਜ ਊਰਜਾ ਦੀ ਇਕਾਈ ਜੁਲ (J) ਹੈ ।
ਸਮੀਕਰਨ (8) ਵਿੱਚ ਸਿੱਧ ਹੋ ਗਿਆ ਹੈ ਕਿ ਇੱਕ ਗਤੀਸ਼ੀਲ ਵਸਤੂ ਦੀ ਗਤਿਜ ਊਰਜਾ
(i) ਵਸਤੂ ਦੇ ਪੁੰਜ ਦੇ ਸਿੱਧਾ ਅਨੁਪਾਤੀ ਹੁੰਦੀ ਹੈ ਅਰਥਾਤ ਭਾਰੀਆਂ ਵਸਤਾਂ ਵਿੱਚ ਹੌਲੀਆਂ ਵਸਤਾਂ ਨਾਲੋਂ ਜ਼ਿਆਦਾ ਗਤਿਜ ਊਰਜਾ ਹੁੰਦੀ ਹੈ ।
(ii) ਵਸਤੂ ਦੇ ਵੇਗ ਦੇ ਵਰਗ ਦੇ ਸਿੱਧਾ ਅਨੁਪਾਤੀ ਹੁੰਦੀ ਹੈ ਅਰਥਾਤ ਵਸਤੂ ਦੀ ਜਿੰਨੀ ਜ਼ਿਆਦਾ ਚਾਲ ਹੋਵੇਗੀ ਓਨੀ ਹੀ ਜ਼ਿਆਦਾ ਉਸ ਦੀ ਗਤਿਜ ਉਰਜਾ ਹੋਵੇਗੀ ।

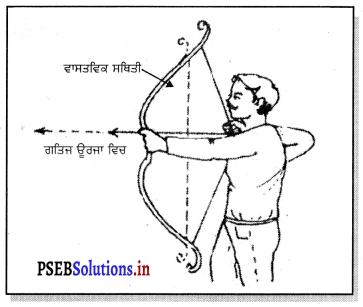
ਵਿਵਹਾਰਿਕ ਉਦਾਹਰਨ – ਆਓ ਇੱਕ ਤੀਰ ਅਤੇ ਕਮਾਨ ਬਾਰੇ ਵਿਚਾਰ ਕਰੀਏ । ਸਾਧਾਰਨ ਅਵਸਥਾ ਵਿੱਚ ਤੀਰ ਅਤੇ ਕਮਾਨ ਵਿੱਚ ਕੋਈ ਵੀ ਉਰਜਾ ਨਹੀਂ ਹੁੰਦੀ । ਜਦੋਂ ਅਸੀਂ ਤੀਰ ਨੂੰ ਕਮਾਨ ਵਿੱਚ ਖਿੱਚਦੇ ਹਾਂ ਤਾਂ ਅਸੀਂ ਕਮਾਨ ਉੱਤੇ ਕਾਰਜ ਕਰਦੇ ਹਾਂ । ਇਹ ਕਾਰਜ ਤੀਰ-ਕਮਾਨ ਸਿਸਟਮ ਵਿੱਚ ਸਥਿਤਿਜ ਉਰਜਾ ਵਜੋਂ ਸਟੋਰ ਹੋ ਜਾਂਦਾ ਹੈ । ਤੀਰ ਨੂੰ ਛੱਡਣ ਤੇ ਤਾਂ ਸਟੋਰ ਕੀਤੀ ਸਥਿਤਿਜ ਉਰਜਾ ਤੀਰ ਦੀ ਗਤਿਜ ਉਰਜਾ ਵਿੱਚ ਤਬਦੀਲ ਹੋ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਊਰਜਾ ਸੁਰੱਖਿਅਣ ਨਿਯਮ ਕੀ ਹੈ ? ਇਸ ਦੀ ਸੱਚਾਈ ਨੂੰ ਸਾਬਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਊਰਜਾ ਦਾ ਸੁਰੱਖਿਅਣ ਨਿਯਮ – ਇਸ ਨਿਯਮ ਅਨੁਸਾਰ ਊਰਜਾ ਦੀ ਮਾਤਰਾ ਹਮੇਸ਼ਾਂ ਹੀ ਸਥਿਰ ਰਹਿੰਦੀ ਹੈ, ਅਰਥਾਤ ਕੁੱਲ ਊਰਜਾ ਹਮੇਸ਼ਾ ਹੀ ਓਨੀ ਰਹਿੰਦੀ ਹੈ ਭਾਵੇਂ ਇਹ ਇੱਕ ਰੂਪ ਤੋਂ ਦੂਜੇ ਰੂਪ ਵਿੱਚ ਬਦਲ ਜਾਂਦੀ ਹੈ । ਊਰਜਾ ਰੂਪਾਂਤਰਨ ਦੀ ਕਿਸੇ ਵੀ ਸਥਿਤੀ ਵਿੱਚ ਊਰਜਾ ਦਾ ਰੂਪ ਹੀ ਬਦਲਦਾ ਹੈ ਪਰ ਇਸ ਦੀ ਮਾਤਰਾ ਨਹੀਂ । ਕਾਰਜ, ਸਥਿਤਿਜ ਉਰਜਾ ਅਤੇ ਤਿਜ ਉਰਜਾ ਆਪਸ ਵਿੱਚ ਪਰਿਵਰਤਨਸ਼ੀਲ ਹਨ ।

ਗਣਿਤਿਕ ਤੌਰ ‘ ਤੇ ਨਿਯਮ ਦੀ ਪੁਸ਼ਟੀ ਕਰਨਾ
ਮੰਨ ਲਉ 10 ਕਿਲੋ ਪੁੰਜ ਵਾਲੀ ਇੱਕ ਗੇਂਦ ਫ਼ਰਸ਼ ਤੋਂ 30 ਮੀਟਰ ਦੀ ਉੱਚਾਈ ‘ਤੇ ਸਥਿਤ ਇੱਕ ਬਿੰਦੂ A ਤੋਂ ਹੇਠਾਂ ਵੱਲ ਸੁੱਟੀ ਗਈ ਹੈ ।

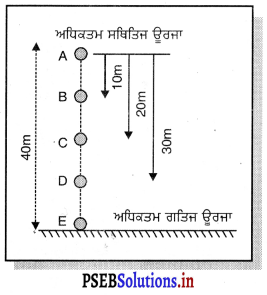
ਬਿੰਦੂ A ਉੱਤੇ
ਗੇਂਦ ਦੀ ਸਥਿਤਿਜ ਉਰਜਾ = m × g × h.
ਅਧਿਕਤਮ ਸਥਿਤਿਜ ਊਰਜਾ = 10 × 10 × 30
= 3000 J
ਕਿਉਂ ਜੋ ਗੇਂਦ ਬਿੰਦੂ A ਤੇ ਸ਼ੁਰੂ ਵਿੱਚ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਸੀ, ਇਸ ‘ ਲਈ ਗੇਂਦ ਦੀ ਗਤਿਜ ਊਰਜਾ = 0
∴ ਯੰਤਰਿਕ ਊਰਜਾ = ਸਥਿਤਿਜ ਊਰਜਾ + ਗਤਿਜ ਊਰਜਾ
= 3000 J + 0 ……… (1)
= 3000 J

ਬਿੰਦੂ B ਉੱਤੇ
B ਉੱਤੇ ਸਥਿਤਿਜ ਉਰਜਾ = m × g × h.
= 10 × 10 × 20 = 2000 J
ਸਮੀਕਰਨ v² = u² + 2gh ਦੀ ਵਰਤੋਂ ਕਰਨ ਨਾਲ
v² = 0 + 2 × 10 × 10
∴ v² = 200
∴ ਬਿੰਦੂ B ਤੇ ਗਤਿਜ ਊਰਜਾ = 1/2mv
= 1/2 × 10 × (200)
= 1000 J
∴ ਬਿੰਦੂ B ਤੇ ਕੁੱਲ ਯੰਤਰਿਕ ਊਰਜਾ = ਸਥਿਤਿਜ ਊਰਜਾ + ਗਤਿਜ ਊਰਜਾ
= 2000 J+ 1000 J = 3000 J ………… (2)
ਇਸੇ ਤਰ੍ਹਾਂ ਬਿੰਦੂ C ਅਤੇ D ਉੱਤੇ ਵੀ ਕੁੱਲ ਊਰਜਾ ਦੀ ਗਣਨਾ 3000 ਜੂਲ ਹੀ ਹੋਵੇਗੀ । ਸਮੀਕਰਨਾਂ (1) ਅਤੇ (2) ਤੋਂ ਇਹ ਸਿੱਧ ਹੁੰਦਾ ਹੈ ਕੁੱਲ ਊਰਜਾ ਹਮੇਸ਼ਾਂ ਸੁਰੱਖਿਅਤ ਰਹਿੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਜੇਕਰ ਕਿਸੇ ਵਸਤੂ ‘ਤੇ ਲੱਗ ਰਿਹਾ ਬਲ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਨਾ ਲੱਗੇ ਤਾਂ ਕੀਤੇ ਗਏ ਕਾਰਜ ਦੀ ਪਰਿਕਲਪਨਾ ਕਿਵੇਂ ਕਰੋਗੇ ? ਉਦਾਹਰਨ ਦੇ ਕੇ ਸਪੱਸ਼ਟ ਕਰੋ ਅਤੇ ਇਹ ਵੀ ਦੱਸੋ ਕਿ ਕਾਰਜ ਕਦੋਂ ਨਿਊਨਤਮ ਅਤੇ ਕਦੋਂ ਅਧਿਕਤਮ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਜਦੋਂ ਵਸਤੂ ‘ਤੇ ਲਗ ਰਿਹਾ ਬਲ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਨਹੀਂ ਹੁੰਦਾ-ਮੰਨ ਲਉ ਇੱਕ ਮਾਲੀ ਘਾਹ ਕੱਟਣ ਵਾਲੀ ਮਸ਼ੀਨ ਨੂੰ ਲਾਨ ਉੱਤੇ ਅਗਾਂਹ ਵੱਲ ਨੂੰ ਚਲਾਉਂਦਾ ਹੈ । ਉਹ ਮਸ਼ੀਨ, ਮਸ਼ੀਨ ਦੇ ਹੈਂਡਲ HH₁ ਉੱਪਰ F ਬਲ ਲਗਾਉਂਦਾ ਹੈ ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਤੋਂ ਸਪੱਸ਼ਟ ਹੈ । ਮਾਲੀ ਖਿਤਿਜ ਦਿਸ਼ਾ ਦੇ ਨਾਲ ਬਲ ਨਹੀਂ ਲਗਾ ਰਿਹਾ ਸਗੋਂ ਖਿਤਿਜ ਨਾਲ ਕੋਣ θ ਬਣਾਉਂਦੀ ਦਿਸ਼ਾ ਵੱਲ ਲਗਾਉਂਦਾ ਹੈ | ਅਜਿਹੀ ਸਥਿਤੀ ਵਿੱਚ ਮਸ਼ੀਨ ਉੱਪਰ ਲੱਗਣ ਵਾਲਾ ਬਲ ਜਿਹੜਾ ਇਸ ਨੂੰ ਸਥਿਤੀ A ਤੋਂ B ਵੱਲ ਖਿਤਿਜ ਦਿਸ਼ਾ ਵੱਲ ਚਲਾਉਂਦਾ ਹੈ F ਨਹੀਂ ਹੈ ਸਗੋਂ ਬਲ ਦਾ ਖਿਤਿਜ ਘਟਕ = F cos θ ਹੁੰਦਾ ਹੈ ।

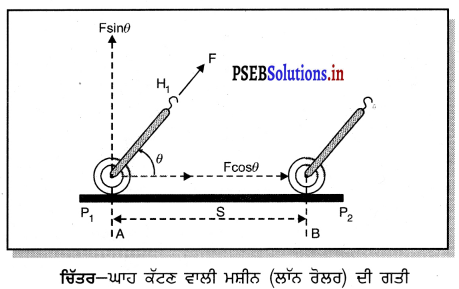
ਇੱਥੇ ਵਿਸਥਾਪਨ ਘਟਕ, F sin θ ਘਾਹ ਕੱਟਣ ਵਾਲੀ ਮਸ਼ੀਨ ਦੇ ਭਾਰ ਨੂੰ ਸੰਤੁਲਿਤ ਕਰਦਾ ਹੈ ।
ਇਸ ਲਈ ਮਸ਼ੀਨ ਦੁਆਰਾ ਕੀਤਾ ਕਾਰਜ W = (ਬਲ ਘਟਕ) × (ਵਿਸਥਾਪਨ)
w = F cos θ × s
(i) ਜਦੋਂ ਬਲ ਵਸਤੂ ਦੀ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਵਿਚ ਕਾਰਜ ਕਰਦਾ ਹੈ, ਤਾਂ θ = 0° ਅਤੇ cos θ = 1
ਕਾਰਜ W = F cos θ × S
= FS
ਇਹ W ਦਾ ਅਧਿਕਤਮ ਮਾਨ ਹੈ ।

(ii) ਜਦੋਂ ਬਲ ਵਸਤੂ ਦੀ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਦੇ ਲੰਬਾਤਮਕ ਲੱਗਦਾ ਹੈ, ਤਾਂ θ = 90°, cos 90° = 0
W = F cos 90° × S
= F × 0 × S.
= 0
ਇਸ ਲਈ ਜਦੋਂ ਬਲ ਲੰਬਾਤਮਕ ਹੁੰਦਾ ਹੈ ਤਾਂ ਕਾਰਜ ਜ਼ੀਰੋ ਹੁੰਦਾ ਹੈ ।

ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Short Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਕਾਰਜ ਕਿਸ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ? ਇਸ ਦੀ ਗਣਨਾ ਕਿਵੇਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ? ਕਾਰਜ ਦੀ ਇਕਾਈ ਵੀ ਲਿਖੋ ।
ਉੱਤਰ-
ਕਾਰਜ (Work) – “ਕਿਸੇ ਬਲ ਦੁਆਰਾ ਕੀਤਾ ਕਾਰਜ ਵਸਤੁ ਉੱਤੇ ਲੱਗ ਰਹੇ ਬਲ ਅਤੇ ਬਲ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਉਸ ਵਸਤੁ ਦੁਆਰਾ ਉਤਪੰਨ ਵਿਸਥਾਪਨ ਦੇ ਗੁਣਨਫਲ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।”

ਗਣਿਤਿਕ ਤੌਰ ‘ ਤੇ
ਜੇਕਰ F = ਵਸਤੂ ਉੱਤੇ ਲੱਗ ਰਿਹਾ ਬਲ
ਅਤੇ S = ਵਸਤੁ ਦੁਆਰਾ ਬਲ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਹੋਇਆ ਵਿਸਥਾਪਨ
ਤਾਂ ਬਲ ਦੁਆਰਾ ਕੀਤਾ ਕਾਰਜ ; W = F × S ………….. (1)
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਜਦੋਂ ਕਿਸੇ ਵਸਤੂ ‘ਤੇ ਕੋਈ ਬਲ ਲੱਗਦਾ ਹੈ, ਤਾਂ ਉਸ ਵਸਤੂ ਵਿੱਚ ਪ੍ਰਵੇਗ ਉਤਪੰਨ ਹੁੰਦਾ ਹੈ, ਇਸ ਲਈ ਜੇਕਰ m = ਵਸਤੂ ਦਾ ਪੁੰਜ
ਅਤੇ a = ਵਸਤੂ ਵਿੱਚ ਉਤਪੰਨ ਹੋਇਆ ਪ੍ਰਵੇਰਾ
ਨਿਊਟਨ ਦੇ ਦੂਜੇ ਨਿਯਮ ਅਨੁਸਾਰ, F = [m × a] ……………… (2)
ਸਮੀਕਰਨ (1) ਅਤੇ (2) ਤੋਂ
W = m × a × S …………….. (3)
ਕਾਰਜ ਦੀ ਇਕਾਈ
ਜਦੋਂ ਬਲ ਨਿਊਟਨ ਵਿੱਚ ਹੋਵੇ ਅਤੇ ਦੂਰੀ ਮੀਟਰਾਂ ਵਿੱਚ, ਤਾਂ
ਕਾਰਜ = ਨਿਊਟਨ × ਮੀਟਰ
= ਨਿਊਟਨ – ਮੀਟਰ
= ਜੂਲ
ਜੂਲ ਕਾਰਜ ਦੀ SI ਇਕਾਈ ਹੈ C.G.S. ਪ੍ਰਣਾਲੀ ਵਿੱਚ ਕਾਰਜ ਦੀ ਇਕਾਈ ਅਰਗ (erg) ਹੈ ।
1 ਜੂਲ = 10⁷ ਅਰਗ (erg)

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਉਦਾਹਰਨ ਦੇ ਕੇ ਸਮਝਾਓ ਕਿ ਜੇਕਰ ਕਿਸੇ ਵਸਤੂ ਤੇ ਲੱਗ ਰਿਹਾ ਬਲ ਵਸਤੂ ਵਿੱਚ ਵਿਸਥਾਪਨ ਨਹੀਂ ਪੈਦਾ ਕਰਦਾ, ਤਾਂ ਕੀਤਾ ਗਿਆ ਕਾਰਜ ਜ਼ੀਰੋ ਹੋਵੇਗਾ ।
ਉੱਤਰ-
ਇਸ ਤੱਥ ਨੂੰ ਨਿਮਨਲਿਖਿਤ ਉਦਾਹਰਨ ਦੁਆਰਾ ਸਮਝਿਆ ਜਾ ਸਕਦਾ ਹੈ-
ਮੰਨ ਲਓ ਇੱਕ ਬੱਚਾ ਕਾਰ ਨੂੰ ਧੱਕਾ ਲਗਾਉਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦਾ ਹੈ, ਪਰੰਤੁ ਕਾਰ ਇੱਕ ਸੈਂਟੀਮੀਟਰ ਵੀ ਨਹੀਂ ਹਿਲਦੀ ਅਤੇ ਬੱਚਾ ਥੱਕ ਜਾਂਦਾ ਹੈ । ਭੌਤਿਕ ਵਿਗਿਆਨ ਦੀ ਭਾਸ਼ਾ ਵਿੱਚ ਅਸੀਂ ਕਹਾਂਗੇ ਕਿ ਉਸਨੇ ਕੋਈ ਵੀ ਕਾਰਜ ਨਹੀਂ ਕੀਤਾ । ਇਸ ਸਥਿਤੀ ਵਿੱਚ ਮੰਨ ਲਓ ਬੱਚੇ ਨੇ ਕਾਰ ਤੇ ਬਲ F ਲਗਾਇਆ ਹੈ ਅਤੇ ਉਸ ਵਿੱਚ ਵਿਸਥਾਪਨ S = 0 ਹੈ ਤਾਂ
ਕਾਰਜ W = F × S
= F × 0
ਜਾਂ W = 0

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਪੱਥਰ ਨੂੰ ਧਾਗੇ ਨਾਲ ਬੰਨ੍ਹ ਕੇ ਚੱਕਰ ਵਿੱਚ ਘੁਮਾਇਆ ਗਿਆ ਹੈ । ਦੱਸੋ ਇਸ ਚੱਕਰੀ ਗਤੀ ਵਿੱਚ ਅਭਿਕੇਂਦਰੀ ਬਲ ਕਿੰਨਾ ਕਾਰਜ ਕਰ ਰਿਹਾ ਹੈ ?
ਉੱਤਰ-

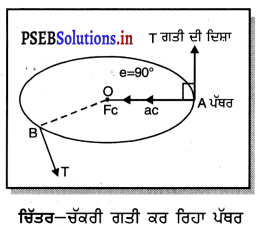
ਇੱਕ ਪੱਥਰ ਨੂੰ ਜਦੋਂ ਚਿੱਤਰ ਵਿੱਚ ਵਿਖਾਏ ਅਨੁਸਾਰ ਗੋਲ ਚੱਕਰ (ਵਿਤ) ਵਿੱਚ ਘੁਮਾਇਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਜਿਸ ਉਂਗਲੀ ਨਾਲ ਤੁਸੀਂ ਧਾਗੇ ਨੂੰ ਪਕੜਿਆ ਹੈ, ਉਸ ਉੱਪਰ ਤੁਸੀਂ ਕੁੱਝ ਬਲ ਲਗ ਰਿਹਾ ਅਨੁਭਵ ਕਰੋਗੇ । ਘੁੰਮ ਰਹੇ ਪੱਥਰ ਉੱਪਰ ਲਗ ਰਹੇ ਬਲ ਨੂੰ ਅਭਿਕੇਂਦਰੀ ਬਲ (Centripetal force) ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਹ ਬਲ ਚੱਕਰੀ ਪੱਥ ਦੇ ਅਰਧਵਿਆਸ ਦੇ ਨਾਲ ਅੰਦਰ ਕੇਂਦਰ ਵੱਲ ਨੂੰ ਲੱਗਦਾ ਹੈ । ਜੇਕਰ ਕਿਸੇ ਸਥਿਤੀ ਵਿੱਚ ਪੱਥਰ ਧਾਗੇ ਤੋਂ ਖੁੱਲ੍ਹ ਜਾਵੇ, ਤਾਂ ਇਹ AT ਜਾਂ BT ਸਪਰਸ਼ ਰੇਖਾ ਦੇ ਨਾਲ ਬਾਹਰ ਵੱਲ ਨੂੰ ਉੱਡ ਜਾਵੇਗਾ ਕਿਉਂ ਜੋ ਅਭਿਕੇਂਦਰੀ ਬਲ ਪੱਥਰ ਤੀ ਦੀ ਲਬਾਤਮਕ ਦਿਸ਼ਾ ਵਿਚ ਲਗਦਾ ਹੈ, ਇਸ ਲਈ ਅਭਕਦਰੀ ਚਿੱਤਰ-ਚੱਕਰੀ ਗਤੀ ਕਰ ਰਿਹਾ ਪੱਥਰ ਬਲ ਦੁਆਰਾ ਕੋਈ ਵੀ ਕਾਰਜ ਨਹੀਂ ਹੁੰਦਾ ।

ਪ੍ਰਸ਼ਨ 4.
ਊਰਜਾ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਉ । ਤੁਸੀਂ ਉਦਾਹਰਨ ਦੇ ਕੇ ਕਿਵੇਂ ਸਮਝਾਉਗੇ ਕਿ ਊਰਜਾ ਅਤੇ ਕਾਰਜ ਇੱਕ-ਦੂਜੇ ਵਿੱਚ ਪਰਿਵਰਤਨਸ਼ੀਲ ਹਨ ?
ਉੱਤਰ-
ਊਰਜਾ (Energy) – “ਕਿਸੇ ਵਸਤੂ ਦੀ ਕਾਰਜ ਕਰਨ ਦੀ ਸਮਰੱਥਾ ਨੂੰ ਉਰਜਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।” ਉਰਜਾ ਅਤੇ ਕਾਰਜ ਦੋਵੇਂ ਹੀ ਪਰਿਵਰਤਨਸ਼ੀਲ ਹਨ । ਇਹ ਤੱਥ ਹੇਠ ਲਿਖੀ ਉਦਾਹਰਨ ਦੁਆਰਾ ਹੋਰ ਵੀ ਸਪੱਸ਼ਟ ਹੋ ਜਾਂਦਾ ਹੈ-
ਊਰਜਾ ਅਤੇ ਕਾਰਜ ਆਪਸ ਵਿੱਚ ਪਰਿਵਰਤਨਸ਼ੀਲ-ਹੇਠਾਂ ਦਿੱਤੀ ਉਦਾਹਰਨ ਨਾਲ ਇਸ ਵਿਹਾਰਿਕ ਤੱਥ ਦੀ ਅਸੀਂ ਵਿਆਖਿਆ ਕਰ ਸਕਦੇ ਹਾਂ ;

ਜੇਕਰ ਤੁਸੀਂ ਇੱਕ ਗੇਂਦ ਨੂੰ ਧਰਤੀ ਤੋਂ ਉੱਪਰ ਦਿਸ਼ਾ ਵੱਲ ਨੂੰ ਸੁੱਟਦੇ ਹੋ, ਤੁਸੀਂ ਗੇਂਦ ਉੱਪਰ ਧਰਤੀ ਦੇ ਗੁਰੂਤਾਆਕਰਸ਼ਣ ਦੇ ਵਿਰੁੱਧ ਕੋਈ ਕਾਰਜ ਕੀਤਾ ਹੈ । ਜਿਉਂ-ਜਿਉਂ ਗੇਂਦ ਉੱਪਰ ਵੱਲ ਨੂੰ ਜਾਂਦੀ ਹੈ ਇਹ ਗੁਰੂਤਾ-ਆਕਰਸ਼ਣ ਦੇ ਵਿਰੁੱਧ ਊਰਜਾ ਪ੍ਰਾਪਤ ਕਰਦੀ ਹੈ । ਇਹ ਗੇਂਦ ਦੁਆਰਾ ਪ੍ਰਾਪਤ ਕੀਤੀ ਉਹ ਊਰਜਾ ਗੇਂਦ ਨੂੰ ਆਪਣੀ ਅਧਿਕਤਮ ਉੱਚਾਈ ਤਕ ਪੁੱਜਣ ਤੋਂ ਬਾਅਦ ਧਰਤੀ ਵੱਲ ਹੇਠਾਂ ਡਿੱਗਣ ਲਈ ਮੱਦਦ ਕਰਦੀ ਹੈ ।

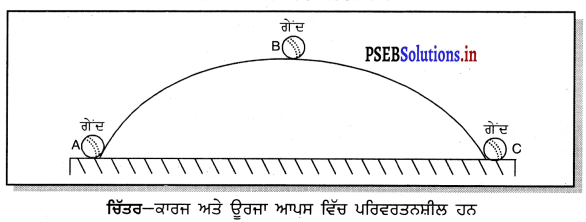
ਜਦੋਂ ਗੇਂਦ ਸਥਿਤੀ A ਤੋਂ ਉੱਚਤਮ ਬਿੰਦੂ B ਤਕ ਪਹੁੰਚਦੀ ਹੈ, ਤਾਂ ਗੇਂਦ ਉੱਪਰ ਕੀਤਾ ਕਾਰਜ ਗੇਂਦ ਅੰਦਰ ਉਰਜਾ ਦੇ ਰੂਪ ਵਿੱਚ ਸਟੋਰ ਹੋ ਜਾਂਦਾ ਹੈ । ਜਦੋਂ ਗੇਂਦ ਪੱਥ BC ਰਾਹੀਂ ਧਰਤੀ ਤੇ ਵਾਪਸ ਡਿੱਗਦੀ ਹੈ, ਤਾਂ ਜਿਹੜਾ ਕਾਰਜ ਗੇਂਦ ਅੰਦਰ ਊਰਜਾ ਦੇ ਰੂਪ ਵਿੱਚ ਸਟੋਰ ਹੋ ਗਿਆ ਸੀ, ਉਹ ਕਾਰਜ ਹੁਣ ਦ ਦੁਆਰਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

ਇਸ ਕਾਰਨ ਕਰਕੇ ਅਸੀਂ ਕਹਿੰਦੇ ਹਾਂ ਕਿ ਉਰਜਾ ਅਤੇ ਕਾਰਜ ਆਪਸ ਵਿੱਚ ਪਰਿਵਰਤਨਸ਼ੀਲ ਹਨ ।

ਪ੍ਰਸ਼ਨ 5.
ਸ਼ਕਤੀ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ? ਇਸਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਉ ਅਤੇ ਸ਼ਕਤੀ ਦੀ SI ਇਕਾਈ ਲਿਖੋ ।
ਉੱਤਰ-
ਸ਼ਕਤੀ (Power) – ਹਰੀਸ਼ ਅਤੇ ਕਰਣ 60-60 ਅੰਬ ਤੋੜਨ ਲਈ ਅੰਬ ਦੇ ਇੱਕ ਦਰੱਖ਼ਤ ‘ਤੇ ਚੜ੍ਹੇ । ਦੋਹਾਂ ਨੇ ਇੱਕੋ ਹੀ ਵੇਲੇ ਚੜ੍ਹਨਾ ਸ਼ੁਰੂ ਕੀਤਾ । ਹਰੀਸ਼ ਨੇ ਆਪਣੇ ਹਿੱਸੇ ਦੇ 60 ਸੇਬ 30 ਮਿੰਟਾਂ ਵਿੱਚ ਹੀ ਤੋੜ ਲਏ ਪਰ ਕਰਣ ਨੇ ਆਪਣਾ ਇਹ ਕੰਮ 60 ਮਿੰਟਾਂ ਵਿੱਚ ਪੂਰਾ ਕੀਤਾ । ਇਸ ਦਾ ਅਰਥ ਹੈ ਕਿ ਕਰਣ ਨੇ ਜ਼ਿਆਦਾ ਸਮਾਂ ਲਗਾਇਆ | ਹਰੀਸ਼ ਅਤੇ ਕਰਣ ਨੇ ਇੱਕੋ ਜਿੰਨਾ ਕਾਰਜ ਕੀਤਾ, ਦੋਹਾਂ ਵਿੱਚ ਇੱਕੋ ਜਿੰਨੀ ਹੀ ਸਮਰੱਥਾ ਅਰਥਾਤ ਉਰਜਾ ਹੈ, ਪਰੰਤੂ ਉਨ੍ਹਾਂ ਵਿੱਚ ਸ਼ਕਤੀ ਬਰਾਬਰ ਨਹੀਂ । ਹਰੀਸ਼ ਦੀ ਕਰਣ ਤੋਂ ਜ਼ਿਆਦਾ ਸ਼ਕਤੀ ਹੈ ਕਿਉਂਕਿ ਉਸ ਨੇ ਆਪਣਾ ਕੰਮ ਪਹਿਲਾਂ ਸਮਾਪਤ ਕਰ ਲਿਆ ਹੈ ।

ਪਰਿਭਾਸ਼ਾ – “ਕਿਸੇ ਵਸਤੂ ਜਾਂ ਮਸ਼ੀਨ ਦੀ ਸ਼ਕਤੀ, ਉਸ ਦੁਆਰਾ ਕਾਰਜ ਕਰਨ ਦੀ ਦਰ ਹੁੰਦੀ ਹੈ ।” ਅਰਥਾਤ ਇਕਾਈ ਸਮੇਂ ਵਿੱਚ ਕੀਤੇ ਗਏ ਕਾਰਜ ਨੂੰ ਸ਼ਕਤੀ ਕਹਿੰਦੇ ਹਨ ।

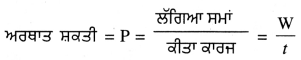
ਜੇਕਰ ਕਾਰਜ ‘ਜੂਲ’ ਵਿੱਚ ਅਤੇ ‘ਸਮਾਂ ਸੈਕਿੰਡ’ ਵਿੱਚ ਮਿਲਿਆ ਜਾਵੇ, ਤਾਂ ਸ਼ਕਤੀ ‘‘ਵਾਟ’’ ਵਿੱਚ ਮਿਣੀ ਜਾਂਦੀ ਹੈ ।
ਅਰਥਾਤ 1 ਵਾਟ = 1 ਜੁਲ/1 ਸੈਕਿੰਡ
ਸ਼ਕਤੀ ਦੀ ਵਪਾਰਕ ਇਕਾਈ ‘ਕਿਲੋਵਾਟ` ਹੈ,
1 ਕਿਲੋਵਾਟ = 1000 ਵਾਟ = 1000 ਜੂਲ/ਸੈਕਿੰਡ

ਪ੍ਰਸ਼ਨ 6.
ਊਰਜਾ ਰੂਪਾਂਤਰਨ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ? ਸਥਿਤਿਜ ਊਰਜਾ ਦਾ ਗਤਿਜ ਊਰਜਾ ਵਿੱਚ ਰੂਪਾਂਤਰਨ ਸਮਝਾਉਣ ਲਈ ਇੱਕ ਉਦਾਹਰਨ ਦਿਓ ।
ਉੱਤਰ-
ਊਰਜਾ ਰੂਪਾਂਤਰਨ ਦੇ ਨਿਯਮ ਅਨੁਸਾਰ, “ਉਰਜਾ ਦਾ ਨਾ ਤਾਂ ਸਿਰਜਨ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ਅਤੇ ਨਾ ਹੀ ਨਸ਼ਟ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਇਸ ਨੂੰ ਸਿਰਫ਼ ਇੱਕ ਰੂਪ ਤੋਂ ਦੂਜੇ ਰੂਪ ਵਿੱਚ ਬਦਲਿਆ ਜਾ ਸਕਦਾ ਹੈ ।” ਇਸ ਨੂੰ ਉਰਜਾ ਰੁਪਾਂਤਰਨ ਕਹਿੰਦੇ ਹਨ ।

ਉਦਾਹਰਨ – ਜਦੋਂ, ਅਸੀਂ ਕਮਾਨ ਵਿੱਚ ਤੀਰ ਖਿੱਚਦੇ ਹਾਂ, ਤਾਂ ਕਮਾਨ ਦੀ ਸ਼ਕਲ ਬਦਲ ਜਾਂਦੀ ਹੈ । ਕਮਾਨ ਉੱਪਰ ਕੀਤਾ ਗਿਆ ਕਾਰਜ਼ ਤੀਰ-ਕਮਾਨ ਸਿਸਟਮ ਵਿੱਚ ਸਥਿਤਿਜ ਉਰਜਾ ਵਜੋਂ ਸਟੋਰ ਹੋ ਜਾਂਦਾ ਹੈ । ਜਦੋਂ ਤੀਰ ਛੱਡਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਇਸ ਸਥਿਤਿਜ ਉਰਜਾ ਦਾ ਕੁੱਝ ਭਾਗ ਤੀਰ ਦੀ ਗਤਿਜ ਉਰਜਾ ਵਿੱਚ ਤਬਦੀਲ ਹੋ ਜਾਂਦਾ ਹੈ । ਜਦੋਂ ਇਹ ਤੀਰ ਕਿਸੇ ਨਿਸ਼ਾਨੇ ਵਿੱਚ ਧੱਸ ਜਾਂਦਾ ਹੈ ਤਾਂ ਇਹ ਕੁਝ ਕਾਰਜ ਕਰਦਾ ਹੈ ਅਰਥਾਤ ਤੀਰ ਦੀ ਗਤਿਜ ਉਰਜਾ, ਕਾਰਜ ਵਿੱਚ ਬਦਲ ਜਾਂਦੀ ਹੈ । ਇਸ ਕਾਰਜ ਦਾ ਕੁੱਝ ਹਿੱਸਾ ਨਿਸ਼ਾਨੇ ਅੰਦਰ ਗਰਮੀ ਪੈਦਾ ਕਰਦਾ ਹੈ ਅਰਥਾਤ ਤਾਪ ਉਰਜਾ ਵਿੱਚ ਪਰਿਵਰਤਿਤ ਹੁੰਦਾ ਹੈ ਅਤੇ ਬਾਕੀ ਬਚਿਆ ਕਾਰਜ ਆਵਾਜ਼ ਪੈਦਾ ਕਰਦਾ ਹੈ ਅਰਥਾਤ ਧੁਨੀ-ਉਰਜਾ ਵਿੱਚ ਰੂਪਾਂਤਰਿਤ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਪਾਣੀ ਦੁਆਰਾ ਬਿਜਲੀ ਕਿਵੇਂ ਪੈਦਾ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ?
ਜਾਂ
ਪਣ-ਬਿਜਲੀ ਕੇਂਦਰਾਂ ਤੇ ਬਿਜਲੀ ਕਿਵੇਂ ਪੈਦਾ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਡੈਮਾਂ ਵਿੱਚ ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ਤੋਂ ਕਾਫ਼ੀ ਉੱਚਾਈ ‘ਤੇ ਬਹੁਤ ਜ਼ਿਆਦਾ ਮਾਤਰਾ ਵਿੱਚ ਪਾਣੀ ਇਕੱਠਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਬੰਨ੍ਹ ਕੇ ਰੱਖਿਆ ਇਹ ਪਾਣੀ ਇੱਕ ਨਿਯੰਤ੍ਰਿਤ ਤਰੀਕੇ ਨਾਲ ਛੱਡਿਆ ਜਾਂਦਾ ਹੈ | ਸਟੋਰ ਕੀਤੀ ਇਹ ਸਥਿਤਿਜ ਊਰਜਾ ਹੁਣ ਗਤਿਜ ਊਰਜਾ ਵਿੱਚ ਬਦਲ ਜਾਂਦੀ ਹੈ । ਇਹ ਗਤਿਜ ਊਰਜਾ ਜੈਨਰੇਟਰਾਂ ਦੀਆਂ ਸਾਫ਼ਟਾਂ ਨੂੰ ਚਲਾਉਣ ਵਿੱਚ ਸਹਾਈ ਹੁੰਦੀ ਹੈ, ਜਿਸ ਤੋਂ ਇਹ ਬਿਜਲੀ ਉਰਜਾ ਵਿੱਚ ਬਦਲ ਜਾਂਦੀ ਹੈ ।

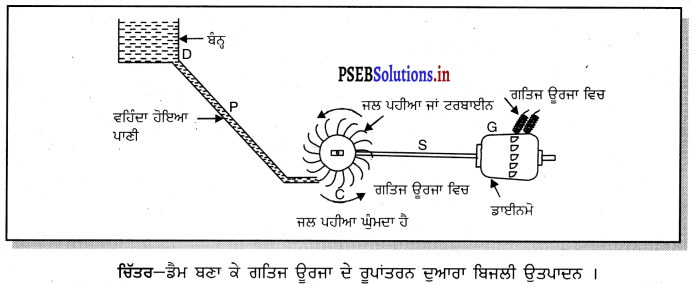
ਪ੍ਰਸ਼ਨ 8.
ਇੱਕ ਪ੍ਰਯੋਗ ਦੁਆਰਾ ਸਿੱਧ ਕਰੋ ਕਿ ਯੰਤਰਿਕ ਉਰਜਾ ਨੂੰ ਤਾਪ ਊਰਜਾ ਵਿੱਚ ਬਦਲਿਆ ਜਾ ਸਕਦਾ ਹੈ ?
ਜਾਂ
ਜਦੋਂ ਅਸੀਂ ਲੱਕੜੀ ਦੇ ਤਖ਼ਤੇ ਵਿੱਚ ਹਥੌੜੇ ਨਾਲ ਕਿੱਲ ਗੱਡਦੇ ਹਾਂ ਤਾਂ ਕਿੱਲ ਗਰਮ ਕਿਉਂ ਹੋ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਇੱਕ ਲੱਕੜੀ ਦਾ ਤਖ਼ਤਾ ਲੈ ਕੇ ਇਸ ਉੱਪਰ ਇੱਕ ਕਿੱਲ ਰੱਖ ਕੇ ਇਸ ਉੱਪਰ ਹਥੌੜਾ ਮਾਰੋ ਤਾਂ ਕਿੱਲ ਦਾ ਕੁੱਝ ਹਿੱਸੇ ‘ਤੇ ਫਿਰ ਹੋਰ ਹਥੌੜਾ ਮਾਰਨ ਨਾਲ ਸਾਰੀ ਕਿੱਲ ਤਖ਼ਤੇ ਵਿੱਚ ਗੱਡੀ ਜਾਂਦੀ ਹੈ । ਹੁਣ ਇਸ ਤੋਂ ਬਾਅਦ ਹਥੌੜਾ ਮਾਰਨ ਤੇ ਕਿੱਲ, ਹਥੌੜਾ ਅਤੇ ਤਖਤਾ ਗਰਮ ਹੋ ਜਾਂਦੇ ਹਨ । ਇਸ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਜਦੋਂ ਅਸੀਂ ਹਥੌੜਾ ਉੱਪਰ ਚੁੱਕਦੇ ਹਾਂ ਤਾਂ ਉਸ ਵਿੱਚ ਉਸ ਦੀ ਸਥਿਤੀ ਦੇ ਕਾਰਨ ਸਥਿਤਿਜ ਊਰਜਾ ਸਟੋਰ ਹੋ ਜਾਂਦੀ ਹੈ । ਜਦੋਂ ਇਹ ਕਿੱਲ ‘ਤੇ ਡਿੱਗਦਾ ਹੈ ਤਾਂ ਇਸ ਦੀ ਸਾਰੀ ਉਰਜਾ ਕਿੱਲ ਵਿੱਚ ਸਥਾਨਾਂਤਰਿਤ ਹੋ ਜਾਂਦੀ ਹੈ । ਇਸ ਕਾਰਨ ਕਿੱਲ ਨੂੰ ਗਤਿਜ ਊਰਜਾ ਮਿਲਦੀ ਹੈ ਤੇ ਉਹ ਲੱਕੜੀ ਵਿੱਚ ਗੱਡਿਆ ਜਾਂਦਾ ਹੈ । ਜਦੋਂ ਕਿੱਲ ਪੂਰੀ ਤਰ੍ਹਾਂ ਗੱਡਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਹੁਣ ਹਥੌੜੇ ਦੀ ਯੰਤਰਿਕ ਊਰਜਾ, ਤਾਪ ਉਰਜਾ ਵਿੱਚ ਬਦਲ ਜਾਂਦੀ ਹੈ ਤੇ ਕਿੱਲ, ਹਥੌੜਾ ਅਤੇ ਤਖ਼ਤਾ ਗਰਮ ਹੋ ਜਾਂਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 9.
ਗਤਿਜ ਊਰਜਾ ਅਤੇ ਸਥਿਤਿਜ ਊਰਜਾ ਵਿੱਚ ਅੰਤਰ ਦੱਸੋ ।
ਉੱਤਰ-
ਗਤਿਜ ਊਰਜਾ ਅਤੇ ਸਥਿਤਿਜ ਊਰਜਾ ਵਿੱਚ ਅੰਤਰ-

ਗਤਿਜ ਊਰਜਾ (K.E.)	ਸਥਿਤਿਜ ਊਰਜਾ (PE)
(1) ਕਿਸੇ ਵਸਤੂ ਦੀ ਗਤਿਜ ਊਰਜਾ ਉਸ ਦੀ ਗਤੀ ਕਾਰਨ ਹੁੰਦੀ ਹੈ ।	(1) ਕਿਸੇ ਵਸਤੂ ਦੀ ਸਥਿਤਿਜ ਊਰਜਾ ਉਸ ਦੀ ਸਥਿਤੀ ਜਾਂ ਆਕਾਰ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ ।
(2) ਗਤਿਜ ਊਰਜਾ = \(\frac {1}{2}\)mv2	(2) ਸਥਿਤਿਜ ਊਰਜਾ = mgh
(3) ਕਿਸੇ ਵਸਤੂ ਦੀ ਗਤਿ ਊਰਜਾ ਉਸ ਵਸਤੂ ਦੀ ਗਤੀ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ ।	(3) ਸਥਿਤਿਜ ਊਰਜਾ ਵਸਤੂ ਦੀ ਉੱਚਾਈ ਜਾਂ ਡੂੰਘਾਈ ਜੋ ਧਰਤੀ ਦੇ ਸਤਹ ਤੋਂ ਮਾਪੀ ਜਾਂਦੀ ‘ਤੇ ਨਿਰਭਰ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਇੱਕ ਘੋੜਾ ਅਤੇ ਇੱਕ ਕੁੱਤਾ ਸਮਾਨ ਚਾਲ ਨਾਲ ਦੌੜ ਰਹੇ ਹਨ । ਜੇ ਘੋੜੇ ਦਾ ਭਾਰ ਕੁੱਤੇ ਦੇ ਭਾਰ ਨਾਲੋਂ ਦਸ ਗੁਣਾ ਹੋਵੇ ਤਾਂ ਉਹਨਾਂ ਦੀ ਗਤਿਜ ਊਰਜਾ ਦਾ ਕੀ ਅਨੁਪਾਤ ਹੋਵੇਗਾ ?
ਉੱਤਰ-
ਮੰਨ ਲਓ m ਕੁੱਤੇ ਦਾ ਪੁੰਜ ਹੈ
∴ ਘੋੜੇ ਦਾ ਪੁੰਜ = 10 m
ਘੋੜੇ ਦਾ ਵੇਗ = ਕੁੱਤੇ ਦਾ ਵੇਗ = υ (ਮੰਨ ਲਉ)
ਘੋੜੇ ਦੀ ਗਤਿਜ ਊਰਜਾ = \(\frac {1}{2}\)(10m) υ²
ਕੁੱਤੇ ਦੀ ਗਤਿਜ ਊਰਜਾ = \(\frac {1}{2}\)mυ²

ਘੋੜੇ ਦੀ ਗਤਿਜ ਊਰਜਾ : ਕੁੱਤੇ ਦੀ ਗਤਿਜ ਊਰਜਾ = \(\frac {1}{2}\) x 10m x υ²: \(\frac {1}{2}\) x m x υ²
= \(\frac{\frac{1}{2} \times 10 m \times v^{2}}{\frac{1}{2} \times m \times v^{2}}\)
= \(\frac{10}{1}\)
= 10 : 1

ਪ੍ਰਸ਼ਨ 11.
(i) ਜੇ ਕਿਸੇ ਵਸਤੂ ਦਾ ਪੁੰਜ ਤਿੰਨ ਗੁਣਾ ਹੋ ਜਾਵੇ, ਤਾਂ ਉਸ ਦੀ ਗਤਿਜ ਊਰਜਾ ਵਿੱਚ ਕੀ ਪਰਿਵਰਤਨ ਹੋਵੇਗਾ ?
(ii) ਜੇ ਵਸਤੂ ਦੀ ਗਤੀ ਨੂੰ ਤਿੰਨ ਗੁਣਾ ਕਰ ਦਿੱਤਾ ਜਾਵੇ, ਤਾਂ ਉਸ ਦੀ ਗਤਿਜ ਊਰਜਾ ਵਿੱਚ ਕੀ ਪਰਿਵਰਤਨ ਆਏਗਾ ?
ਹੱਲ:
(i) K.E. = \(\frac {1}{2}\)mυ²
ਜੇ υ ਪਰਿਵਰਤਿਤ ਨਾ ਹੋਵੇ, ਤਾਂ
K.E. ∝ m
ਇਸ ਲਈ ਪੁੰਜ ਨੂੰ ਤਿੰਨ ਗੁਣਾ ਕਰਨ ‘ਤੇ ਗਤਿਜ ਊਰਜਾ ਵੀ ਤਿੰਨ ਗੁਣਾ ਹੋ ਜਾਵੇਗੀ ।

(ii) KE. = \(\frac {1}{2}\)mυ² ਜੇ ਪੁੰਜ ਸਥਿਰ ਰਹੇ, ਤਾਂ KE. ∝ υ²
ਜੇ ਵੇਗ ਤਿੰਨ ਗੁਣਾ ਹੋ ਜਾਵੇ, ਤਾਂ ਗਤਿਜ ਊਰਜਾ ਨੌਂ ਗੁਣਾ ਹੋ ਜਾਵੇਗੀ ।

ਪ੍ਰਸ਼ਨ 12.
ਬਰਾਬਰ ਪੁੰਜ ਦੀਆਂ ਦੋ ਵਸਤੂਆਂ ਨੂੰ h ਅਤੇ 2h ਦੀ ਉੱਚਾਈ ‘ਤੇ ਰੱਖਿਆ ਗਿਆ ਹੈ । ਦੱਸੋ ਉਨ੍ਹਾਂ ਵਿੱਚ ਸਥਿਤਿਜ ਊਰਜਾ ਵਿੱਚ ਕੀ ਅਨੁਪਾਤ ਹੈ ?
ਹੱਲ:
ਮੰਨ ਲਉ ਦੋਹਾਂ ਵਸਤੂਆਂ A ਅਤੇ B ਦਾ ਬਰਾਬਰ ਪੁੰਜ m ਹੈ, ਜਿਨ੍ਹਾਂ ਨੂੰ h ਅਤੇ 2h ਉੱਚਾਈ ‘ਤੇ ਰੱਖਿਆ ਗਿਆ ਹੈ ।
A ਦੀ ਸਥਿਤਿਜ ਊਰਜਾ, P_A = mgh
B ਦੀ ਸਥਿਤਿਜ ਊਰਜਾ, P_B = mg (2h)
\(\frac{\mathrm{P}_{\mathrm{A}}}{\mathrm{P}_{\mathrm{B}}}\) = \(\frac{m g h}{m g(2 \mathrm{~h})}\) = \(\frac{1}{2}\)
ਦੋਹਾਂ ਦੀ ਸਥਿਤਿਜ ਉਰਜਾ ਦਾ ਅਨੁਪਾਤ = 1 : 2

ਪ੍ਰਸ਼ਨ 13.
ਬਰਾਬਰ ਪੁੰਜ ਦੀਆਂ ਦੋ ਵਸਤੂਆਂ υ ਅਤੇ 2υ ਵੇਗ ਨਾਲ ਚੱਲ ਰਹੀਆਂ ਹਨ । ਉਨ੍ਹਾਂ ਦੀ ਗਤਿਜ ਊਰਜਾ ਦਾ ਅਨੁਪਾਤ ਗਿਆਤ ਕਰੋ ।
ਉੱਤਰ-
ਮੰਨ ਲਉ ਵਸਤੂ A ਅਤੇ B ਦਾ ਬਰਾਬਰ ਪੁੰਜ m ਹੈ ਅਤੇ ਕ੍ਰਮਵਾਰ ਵੇਗ υ ਅਤੇ 2υ ਹੈ ।
∴ A ਦੀ ਗਤਿਜ ਊਰਜਾ, K_A = \(\frac{1}{2}\)mυ²
B ਦੀ ਗਤਿਜ ਊਰਜਾ, K_B = \(\frac{1}{2}\)m (2υ)²
= \(\frac{4}{2}\)mυ²
= 2mυ²
K_A : K_B = 1 : 4

ਪ੍ਰਸ਼ਨ 14.
ਇੱਕ ਵਿਅਕਤੀ ਸੂਟਕੇਸ ਚੁੱਕ ਕੇ ਖੜਾ ਹੈ । ਕੀ ਉਹ ਕੋਈ ਕਾਰਜ ਕਰ ਰਿਹਾ ਹੈ ?
ਉੱਤਰ-
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਕਿਸੇ ਵਸਤੂ ਦੁਆਰਾ ਕੀਤਾ ਗਿਆ ਕਾਰਜ ਉਸ ਵਸਤੂ ਉੱਤੇ ਲੱਗ ਰਹੇ ਬਲ ਅਤੇ ਬਲ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਉਤਪੰਨ ਹੋਏ ਵਿਸਥਾਪਨ ਦੇ ਗੁਣਨਫਲ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ । ਇਸ ਸਥਿਤੀ ਵਿੱਚ ਵਿਅਕਤੀ ਦੁਆਰਾ ਚੁੱਕੇ ਗਏ ਸੂਟਕੇਸ ਤੇ ਗੁਰੂਤਵੀ ਬਲ ਦੇ ਬਰਾਬਰ ਬਲ ਕਿਰਿਆ ਕਰ ਰਿਹਾ ਹੈ ਪਰ ਇਸ ਬਲ ਦੁਆਰਾ ਸੂਟਕੇਸ ਵਿੱਚ ਕੋਈ ਵਿਸਥਾਪਨ ਉਤਪੰਨ ਨਹੀਂ ਹੋਇਆ ਹੈ । ਇਸ ਲਈ ਵਿਅਕਤੀ ਨੇ ਕੋਈ ਕਾਰਜ ਨਹੀਂ ਕੀਤਾ ਹੈ ।
ਇੱਥੇ F = mg
ਵਿਸਥਾਪਨ S = 0
∴ W = F × S
= mg × 0
ਅਰਥਾਤ W = 0

ਪ੍ਰਸ਼ਨ 15.
ਪਾਣੀ ਦੀ ਬਾਲਟੀ ਚੁੱਕ ਕੇ ਇੱਕ ਵਿਅਕਤੀ ਇੱਕ ਸਮਤਲ ਸੜਕ ਉੱਤੇ ਇੱਕਸਮਾਨ ਵੇਗ ਨਾਲ ਤੁਰ ਰਿਹਾ ਹੈ । ਉਹ ਕਿੰਨਾ ਕਾਰਜ ਕਰ ਰਿਹਾ ਹੈ ?
ਉੱਤਰ-
ਜਦੋਂ ਪਾਣੀ ਦੀ ਬਾਲਟੀ ਚੁੱਕ ਕੇ ਇੱਕ ਵਿਅਕਤੀ ਇੱਕ ਸਮਤਲ ਸੜਕ ਉੱਤੇ ਇੱਕਸਮਾਨ ਵੇਗ ਨਾਲ ਤੁਰਦਾ ਹੈ ਤਾਂ ਉਸ ਵੇਲੇ ਉਸ ਦੁਆਰਾ ਲਗਾਇਆ ਗਿਆ ਬਲ ਬਾਲਟੀ ਦੇ ਭਾਰ ਦੇ ਬਰਾਬਰ ਉੱਪਰ ਵੱਲ ਹੁੰਦਾ ਹੈ । ਇਸ ਅਵਸਥਾ ਵਿੱਚ ਬਲ ਅਤੇ ਵਿਸਥਾਪਨ ਦੀ ਦਿਸ਼ਾ ਵਿਚਕਾਰ ਕੋਣ θ = 90° ਹੁੰਦਾ ਹੈ ਅਰਥਾਤ ਬਲ, ਵਿਸਥਾਪਨ ਦਿਸ਼ਾ ਦੇ ਲੰਬਾਤਮਕ ਰੂਪ ਵਿੱਚ ਕਿਰਿਆ ਕਰਦਾ ਹੈ ।

ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਜੇਕਰ ਬਲ ਅਤੇ ਵਿਸਥਾਪਨ ਦਿਸ਼ਾ ਵਿਚਕਾਰ ਕੋਣ θ ਹੋਵੇ, ਤਾਂ ਬਲ ਦੁਆਰਾ ਕੀਤਾ ਗਿਆ ਕਾਰਜ
W = F cos θ × S
∴ ਵਿਅਕਤੀ ਦੁਆਰਾ ਕੀਤਾ ਗਿਆ ਕਾਰਜ = mg × cos 90° × S
= mg × 0 × S
= 0

ਪ੍ਰਸ਼ਨ 16.
ਉਹ ਸਥਿਤੀ ਦੱਸੋ ਜਦੋਂ ਬਲ ਦੁਆਰਾ ਕੋਈ ਕਾਰਜ ਨਹੀਂ ਕੀਤਾ ਜਾਂਦਾ ।
ਉੱਤਰ-
(i) ਜੇਕਰ ਵਸਤੂ ‘ਤੇ ਲਗ ਰਿਹਾ ਬਲ ਉਸ ਵਸਤੂ ਵਿੱਚ ਬਿਲਕੁਲ ਥੋੜ੍ਹਾ ਜਿਹਾ ਵਿਸਥਾਪਨ ਪੈਦਾ ਕਰਨ ਵਿੱਚ ਅਸਫਲ ਹੋਵੇ, ਤਾਂ ਉਸ ਵਸਤੂ ਤੇ ਲਗ ਰਹੇ ਬਲ ਦੁਆਰਾ ਕੋਈ ਕਾਰਜ ਨਹੀਂ ਹੁੰਦਾ ਹੈ ।
(ii) ਜੇਕਰ ਵਸਤੂ ’ਤੇ ਲੱਗ ਰਿਹਾ ਬਲ ਉਸ ਵਸਤੂ ਵਿੱਚ ਹੋਏ ਵਿਸਥਾਪਨ ਤੇ ਲੰਬਰੂਪ ਹੋਵੇ, ਤਾਂ ਬਲ ਦੁਆਰਾ ਕੋਈ ਕਾਰਜ ਨਹੀਂ ਹੁੰਦਾ ਹੈ । ਇਸ ਸਥਿਤੀ ਵਿੱਚ θ = 90°, :: cos θ = cos 90° = 0
∴ ਬਲ ਦੁਆਰਾ ਕੀਤਾ ਗਿਆ ਕਾਰਜW = F cos θ × S
= F cos 90° × S
= F × 0 × S
ਅਰਥਾਤ W = 0

ਪ੍ਰਸ਼ਨ 17.
ਜਦੋਂ ਇੱਕ ਗੇਂਦ ਨੂੰ ਉੱਪਰ ਵੱਲ ਨੂੰ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ, ਕਿਸ ਬਿੰਦੂ ਤੇ ਸਥਿਤਿਜ ਊਰਜਾ ਅਤੇ ਗਤਿਜ ਊਰਜਾ ਅਧਿਕਤਮ ਹੋਣਗੀਆਂ ?
ਉੱਤਰ-
ਜਦੋਂ ਇੱਕ ਗੇਂਦ ਨੂੰ ਉੱਪਰ ਵੱਲ ਨੂੰ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਸ਼ੁਰੂ ਵਿੱਚ ਇਸ ਦਾ ਵੇਗ ਅਧਿਕਤਮ ਹੁੰਦਾ ਹੈ ਜਿਸ ਕਰਕੇ ਇਸ ਦੀ ਗਤਿਜ ਉਰਜਾ ਅਧਿਕਤਮ ਹੁੰਦੀ ਹੈ ਜਦਕਿ ਸਥਿਤਿਜ ਉਰਜਾ ਘੱਟ ਹੁੰਦੀ ਹੈ । ਗੇਂਦ ਜਿਉਂ-ਜਿਉਂ ਉੱਪਰ ਵੱਲ ਜਾਂਦੀ ਹੈ ਤਾਂ ਇਹ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ ਪਰ ਘੱਟ ਰਹੇ ਵੇਗ ਨਾਲ । ਇਸ ਤਰ੍ਹਾਂ ਸਮੇਂ ਦੇ ਨਾਲ ਸਥਿਤਿਜ ਊਰਜਾ ਵੱਧਦੀ ਹੈ ਪਰ ਗਤਿਜ ਉਰਜਾ ਘੱਟਦੀ ਹੈ । ਗੇਂਦ ਵਲੋਂ ਅਧਿਕਤਮ ਉੱਚਾਈ ਤੇ ਪਹੁੰਚ ਕੇ ਇਸ ਦੀ ਸਥਿਤਿਜ ਉਰਜਾ ਅਧਿਕਤਮ ਹੋ ਜਾਂਦੀ ਹੈ ਜਦੋਂ ਕਿ ਗਤਿਜ ਉਰਜਾ ਜ਼ੀਰੋ ਹੋ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 18.
ਉਹ ਸਥਿਤੀ ਦੱਸੋ ਜਦੋਂ ਕਿਸੇ ਵਸਤੂ ਦੁਆਰਾ ਕੀਤਾ ਗਿਆ ਕਾਰਜ ਜ਼ੀਰੋ ਹੋਵੇਗਾ, ਭਾਵੇਂ ਉਸ ਉੱਪਰ ਬਲ ਲੱਗ ਰਿਹਾ ਹੋਵੇ ।
ਉੱਤਰ-
ਅਜਿਹਾ ਦੋ ਸਥਿਤੀਆਂ ਵਿੱਚ ਸੰਭਵ ਹੈ ਕਿ ਵਸਤੂ ਉੱਪਰ ਬਲ ਲੱਗ ਰਿਹਾ ਹੋਵੇ, ਪਰ ਕੀਤਾ ਗਿਆ ਕਾਰਜ ਜ਼ੀਰੋ ਹੋਵੇ ।
(i) ਜਦੋਂ ਵਸਤੂ ’ਤੇ ਲੱਗ ਰਿਹਾ ਬਲ ਅਤੇ ਬਲ ਦੁਆਰਾ ਵਸਤੂ ਵਿੱਚ ਉਤਪੰਨ ਹੋਇਆ ਵਿਸਥਾਪਨ ਇੱਕ-ਦੂਜੇ ਨੂੰ ਲੰਬਾਤਮਕ ਹੋਣ । ਅਜਿਹੀ ਸਥਿਤੀ ਵਿੱਚ ਕੋਣ θ = 90° ਹੈ ।
∴ cos θ = cos 90° = 0 ਹੋਵੇਗਾ ।
ਵਸਤੂ ਦੁਆਰਾ ਕੀਤਾ ਗਿਆ ਕਾਰਜ (W) = F cos θ × ਵਿਸਥਾਪਨ
= F cos 90° × ਵਿਸਥਾਪਨ
= F × 0 × ਵਿਸਥਾਪਨ ਅਰਥਾਤ
W = 0

(ii) ਜੇਕਰ ਵਸਤੂ ‘ਤੇ ਲੱਗ ਰਿਹਾ ਬਲ ਵਸਤੂ ਨੂੰ ਥੋੜ੍ਹਾ ਜਿਹਾ ਵੀ ਵਿਸਥਾਪਿਤ ਨਾ ਕਰੇ, ਤਾਂ ਵਸਤੂ ਦੁਆਰਾ ਕੀਤਾ ਗਿਆ ਕਾਰਜ ਜ਼ੀਰੋ ਹੋਵੇਗਾ |
ਹੁਣ ਬਲ = F
ਵਿਸਥਾਪਨ (S) = 0
∴ ਕਾਰਜ (w) = F × S
= F × 0 = 0

ਪ੍ਰਸ਼ਨ 19.
ਊਰਜਾ ਅਤੇ ਸ਼ਕਤੀ ਵਿੱਚ ਕੀ ਅੰਤਰ ਹੈ ? ਉਦਾਹਰਨ ਦੇ ਕੇ ਸਮਝਾਉ ।
ਉੱਤਰ-
ਊਰਜਾ-ਕੀਤੇ ਜਾ ਸਕਣ ਵਾਲੇ ਕਾਰਜ ਦਾ ਮੁੱਲ ਪਰਿਮਾਣ) ਉਰਜਾ ਕਹਾਉਂਦਾ ਹੈ । ਇਸ ਦਾ ਸਮੇਂ ਨਾਲ ਕੋਈ ਸੰਬੰਧ ਨਹੀਂ ਹੈ ।

ਸ਼ਕਤੀ (ਸਮਰੱਥਾ)-ਕਾਰਜ ਕਰਨ ਦੀ ਦਰ ਨੂੰ ਸ਼ਕਤੀ ਜਾਂ ਸਮਰੱਥਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਅਰਥਾਤ ਇਕਾਈ ਸਮੇਂ ਵਿੱਚ ਕੀਤਾ ਗਿਆ ਕਾਰਜ ਸ਼ਕਤੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਦਾ ਕਾਰਜ ਦੇ ਕੁੱਲ ਪਰਿਮਾਣ ਨਾਲ ਕੋਈ ਸੰਬੰਧ ਨਹੀਂ ਹੁੰਦਾ ਹੈ ।

ਉਦਾਹਰਨ – ਇੱਕ ਮਜ਼ਦੂਰ ਇੱਕ ਕੰਮ ਨੂੰ 1 ਘੰਟੇ ਵਿੱਚ ਪੂਰਾ ਕਰ ਲੈਂਦਾ ਹੈ । ਉਸੇ ਕੰਮ ਨੂੰ ਇੱਕ ਦੁਸਰਾ ਮਜ਼ਦੂਰ 2 ਘੰਟੇ ਵਿੱਚ ਕਰਦਾ ਹੈ । ਇਸ ਹਾਲਤ ਵਿੱਚ ਦੋਨਾਂ ਮਜ਼ਦੂਰਾਂ ਨੇ ਬਰਾਬਰ ਕੰਮ ਕੀਤਾ ਹੈ ਅਰਥਾਤ ਦੋਨਾਂ ਨੇ ਬਰਾਬਰ ਊਰਜਾ ਦੀ ਮਾਤਰਾ ਖ਼ਰਚ ਕੀਤੀ ਹੈ ਪਰ ਪਹਿਲੇ ਮਜ਼ਦੂਰ ਨੇ ਅੱਧੇ ਸਮੇਂ ਵਿੱਚ ਕੰਮ ਕੀਤਾ ਹੈ ਜਦਕਿ ਦੂਸਰੇ ਮਜ਼ਦੂਰ ਨੇ ਪਹਿਲੇ ਨਾਲੋਂ ਦੁੱਗਣਾ ਸਮਾਂ ਲਿਆ ਹੈ । ਇਸ ਲਈ ਪਹਿਲੇ ਮਜ਼ਦੂਰ ਦੀ ਦੂਸਰੇ ਮਜ਼ਦੂਰ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਦੁੱਗਣੀ ਕਾਰਜ ਸਮਰੱਥਾ (ਸ਼ਕਤੀ ਹੈ ।

ਮਹੱਤਵਪੂਰਨ ਸੂਤਰ (Important Formulae)

(1) ਗਤਿਜ ਊਰਜਾ = \(\frac {1}{2}\)mv²
(2) ਸਥਿਤਿਜ ਊਰਜਾ = mgh
ਇੱਥੇ m = ਵਸਤੂ ਦਾ ਪੁੰਜ ; g = ਗੁਰੂਤਵੀ ਵੇਗ ਅਤੇ h = ਉੱਚਾਈ
(3) ਕਾਰਜ (W) = ਬਲ (F) × ਵਿਸਥਾਪਨ (S)
(4) ਸ਼ਕਤੀ (P) =
(5) 1 ਜੂਲ = 1 ਨਿਊਟਨ × 1 ਮੀਟਰ
(6) 1 ਵਾਟ =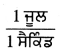
(7) ਘੋੜ ਸ਼ਕਤੀ (Horse Power) = = 746 ਵਾਟ
(8) 1 ਕਿਲੋਵਾਟ-ਘੰਟਾ = 36,00,000 ਜੂਲ = 3.6 × 10⁶ ਜੂਲ
(9) 1 ਵਾਟ-ਘੰਟਾ = 3600 ਜੂਲ

ਸੰਖਿਆਤਮਕ ਪ੍ਰਸ਼ਨ (Numerical Problems)

ਪ੍ਰਸ਼ਨ 1.
ਇੱਕ ਇਸਤਰੀ 10 m ਡੂੰਘੇ ਖੂਹ ਵਿੱਚੋਂ 5 kg ਭਾਰੀ ਪਾਣੀ ਦੀ ਬਾਲਟੀ 10 s ਵਿੱਚ ਖਿੱਚਦੀ ਹੈ, ਉਸਦੀ ਸ਼ਕਤੀ ਦੀ ਗਣਨਾ ਕਰੋ ।
ਹੱਲ:
ਪਾਣੀ ਨਾਲ ਭਰੀ ਬਾਲਟੀ ਦਾ ਪੁੰਜ (m) = 5 kg
ਖੂਹ ਦੀ ਡੂੰਘਾਈ (h) = 10 m
ਗੁਰੂਤਵੀ ਵੇਗ (g) = 10 m/s²
ਸਮਾਂ (t) = 10 s.
ਇਸਤਰੀ ਦੀ ਸ਼ਕਤੀ (P) = ?
ਇਸਤਰੀ ਦੁਆਰਾ ਕੀਤਾ ਗਿਆ ਕਾਰਜ (W) = m × g × h
= 5 × 10 × 10
= 500 ਜੂਲ

= 50 ਵਾਟ ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 2.
25 km ਦੀ ਉੱਚਾਈ ਤੇ ਇੱਕ ਰਾਕੇਟ ਨੂੰ 1km/s ਦੇ ਵੇਗ ਨਾਲ ਉਤਾਂਹ ਵੱਲ ਦਾਗਿਆ ਗਿਆ ਹੈ । ਜੇਕਰ ਰਾਕੇਟ ਦਾ ਪੁੰਜ 3 × 10⁶ kg ਹੋਵੇ, ਤਾਂ ਇਸ ਦੀ ਸਥਿਤਿਜ ਅਤੇ ਗਤਿਜ ਉਰਜਾ ਦੀ ਗਣਨਾ ਕਰੋ । (g = 10 m/s² )
ਹੱਲ:
ਇੱਥੇ
ਰਾਕੇਟ ਦਾ ਪੁੰਜ (m) = 3 × 10⁶ kg
ਰਾਕੇਟ ਦਾ ਵਗ (0) = 1 km/s
= 1000 m/s
ਉੱਚਾਈ (h) = 25 km
= 25 × 1000 m
25,000 m ਗੁਰੂਤਵੀ ਵੇਗ
(g) = 10 m/s²

(i) ਰਾਕੇਟ ਦੀ ਸਥਿਤਿਜ ਊਰਜਾ (P.E.) = m × g × h
= (3 × 10⁶ ) × 10 × 25000
= 75 × 10¹⁰ ਜੂਲ ਵਾਟ ਉੱਤਰ

(ii) ਰਾਕੇਟ ਦੀ ਗਤਿਜ ਊਰਜਾ (K.E.) = \(\frac {1}{2}\) × m × υ²
\(\frac {1}{2}\) × (3 × 10⁶ ) × (1000)²
= \(\frac {1}{2}\) × 3 × 10⁶ × 1000 × 1000
= 1.5 × 10¹² ਜਲ ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 3.
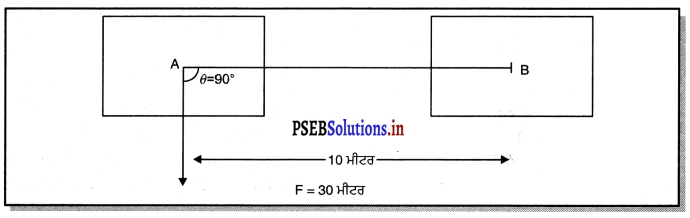
ਇੱਕ ਵਿਅਕਤੀ 30 ਕਿਲੋਗ੍ਰਾਮ ਭਾਰਾ ਬਕਸਾ ਸਿਰ ‘ਤੇ ਚੁੱਕ ਕੇ
(i) ਉੱਪਰ ਵੱਲ ਨੂੰ
(ii) ਖਿਤਿਜ ਦਿਸ਼ਾ ਵਿੱਚ, 10 ਮੀਟਰ ਦੀ ਦੂਰੀ ਤੈਅ ਕਰਦਾ ਹੈ । ਉਸ ਵੱਲੋਂ ਕਿੰਨਾ ਕਾਰਜ ਕੀਤਾ ਗਿਆ ਹੈ ?
ਹੱਲ:
ਬਕਸੇ ਦਾ ਪੁੰਜ (m) = 30 ਕਿਲੋਗ੍ਰਾਮ
ਵਿਸਥਾਪਨ (S) = 10 ਮੀਟਰ
ਗੁਰੂਤਵੀ ਵੇਗ (g) = 9.8 m/s²

(i) ਉੱਪਰ ਵੱਲ ਨੂੰ ਵਿਅਕਤੀ ਦੁਆਰਾ ਕੀਤਾ ਗਿਆ ਕਾਰਜ = m × g × S
= 30 × 9.8 × 10
= 30 × 98 ਜੁਲ
= 2940 ਜੂਲ ਉੱਤਰ

(ii) ਖਿਤਿਜ ਦਿਸ਼ਾ ਵਿੱਚ ਕੀਤਾ ਗਿਆ ਕਾਰਜ = F cos θ × S
= m × g cos θ × S
= 30 × 9.8 × cos 90° × 10
= 294 × 0 × 10 [∵ cos 90° = 0]
= 0 (ਜ਼ੀਰੋ) ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 4.
1000 kg ਦੀ 30 m/s ਦੀ ਚਾਲ ਨਾਲ ਚੱਲ ਰਹੀ ਕਾਰ ਬਰੇਕ ਲਗਾਉਣ ਤੇ ਇੱਕਸਮਾਨ ਵੇਗ ਨਾਲ 50 m ਦੀ ਦੂਰੀ ‘ਤੇ ਰੁੱਕ ਜਾਂਦੀ ਹੈ । ਬਰੇਕ ਦੁਆਰਾ ਕਾਰ ‘ਤੇ ਲੱਗੇ ਬਲ ਅਤੇ ਕਾਰਜ ਦਾ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਇੱਥੇ υ = 30 ms^-1
v = 0
S = 50 m
ਹੁਣ v² – ² = 2 as
(0)² – (30)² = 2 × a × 50
– (30 × 30) = 100 × a
∴ a = \(\frac{-900}{100}\)
-9 m/s²
ਬਲ F = m × a = 1000 × 9
9000 ਨਿਊਟਨ ਉੱਤਰ
ਬਰੇਕ ਦੁਆਰਾ ਕੀਤਾ ਗਿਆ ਕਾਰਜ = F × S
= 9000 × 50
= 45 × 10000
= 4.5 × 10⁵ J

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਮਜ਼ਦੂਰ 10 kg ਭਾਰੀ ਟੋਕਰੀ ਆਪਣੇ ਸਿਰ ‘ਤੇ ਰੱਖ ਕੇ ਪੱਧਰੀ ਸੜਕ ਤੇ 100 ਮੀਟਰ ਖਿਤਿਜ ਦਿਸ਼ਾ ਵਿੱਚ ਚਲ ਰਿਹਾ ਹੈ । ਉਸਦੇ ਦੁਆਰਾ ਗੁਰੂਤਵੀ ਬਲ ਦੇ ਵਿਰੁੱਧ ਕੀਤਾ ਕਾਰਜ ਪਤਾ ਕਰੋ । (g = 9.8 ms²)
ਹੱਲ:
ਟੋਕਰੀ ਦਾ ਭਾਰ = mg = 10 × 9.8 = 98 N (ਹੇਠਾਂ ਵੱਲ)
ਗੁਰੂਤਵੀ ਬਲ ਦੀ ਦਿਸ਼ਾ (ਹੇਠਾਂ ਵੱਲ)
ਵਿੱਚ ਵਿਸਥਾਪਨ = 0
ਕਾਰਜ = ਬਲ × ਵਿਸਥਾਪਨ
= 98 × 0 = 0

ਪ੍ਰਸ਼ਨ 6.
ਇੱਕ ਕਾਰ 54 km/hr ਵੇਗ ਨਾਲ ਚੱਲਦੀ ਹੈ । ਇਸ ਵਿੱਚ ਬੈਠੇ 40 kg ਦੇ ਲੜਕੇ ਦੀ ਤਿਜ ਊਰਜਾ ਕੀ ਹੋਵੇਗੀ ?
ਹੱਲ:
ਲੜਕੇ ਦਾ ਵੇਗ, (v) = ਕਾਰ ਦਾ ਵੇਗ
= 54 km/hr.
= \(\frac{54 \times 1000}{60 \times 60}\)
= 15 m/s
ਲੜਕੇ ਦਾ ਪੁੰਜ (m) = 40 kg
ਲੜਕੇ ਦੀ ਗਤਿਜ ਊਰਜਾ (K.E.) = \(\frac {1}{2}\)mυ²
= \(\frac {1}{2}\) × 40 × (15)²
= 4500 ਜੂਲ ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 7.
ਦਿਲ ਦੀ ਇੱਕ ਧੜਕਨ ਲਈ 1 ਜੂਲ ਊਰਜਾ ਦਾ ਖ਼ਰਚ ਹੁੰਦਾ ਹੈ । ਦਿਲ ਦੀ ਸ਼ਕਤੀ ਪਤਾ ਕਰੋ ਜੇ ਇੱਕ ਮਿੰਟ ਵਿੱਚ ਇਹ 72 ਵਾਰ ਧੜਕੇ ।
ਹੱਲ:
ਦਿਲ ਦੀ ਧੜਕਨ ਦੁਆਰਾ ਕੀਤਾ ਕਾਰਜ = 1 ਜੁਲ
72 ਧੜਕਨ ਵਿੱਚ ਕੀਤਾ ਕਾਰਜ = 72 × 1
= 72 ਜੁਲ
ਸਮਾਂ =1 ਮਿੰਟ
= 60 ਸੈਕਿੰਡ

= \(\frac{72}{60}\) = 1.2 ਜੂਲ / ਸੈਕਿੰਡ
= 1.2 ਵਾਟ ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 8.
60 W ਦਾ ਇੱਕ ਬਿਜਲੀ ਬਲਬ ਪ੍ਰਤੀਦਿਨ 6 ਘੰਟੇ ਉਪਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਬਲਬ ਦੁਆਰਾ ਇੱਕ ਦਿਨ ਵਿੱਚ ਖਰਚ ਕੀਤੀ ਗਈ ਊਰਜਾ ਦੀ ‘‘ਯੂਨਿਟ’’ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਬਲਬ ਦੀ ਸ਼ਕਤੀ (P) = 60 W
ਜਿੰਨੇ ਸਮੇਂ ਲਈ ਬਲਬ ਜਗਿਆ (t) = 6 ਘੰਟੇ
ਖਪਤ ਹੋਈ ਉਰਜਾ (E) = P x t
= 60 W X 6 h
= 360 Wh
= \(\frac{360}{1000}\) kWh
= 0.36 kWh
= 0.36 ਯੂਨਿਟ ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 9.
ਦੋ ਬਰਾਬਰ ਪੁੰਜ ਵਾਲੇ ਪਿੰਡ ਕੁਮਵਾਰ : ਇੱਕ ਸਮਾਨ ਵੇਗ υ ਅਤੇ 3υ ਨਾਲ ਗਤੀਸ਼ੀਲ ਹਨ । ਇਹਨਾਂ ਪਿੰਡਾਂ ਦੀ ਗਤਿਜ ਊਰਜਾਵਾਂ ਦਾ ਅਨੁਪਾਤ ਗਿਆਤ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਹਰੇਕ ਪਿੰਡ ਦਾ ਪੁੰਜ ਅ ਹੈ ।

ਪਹਿਲੇ ਪਿੰਡ ਦੀ ਗਤਿਜ ਊਰਜਾ (E_k1) = \(\frac {1}{2}\) mυ …………… (i)
ਦੂਜੇ ਪਿੰਡ ਦੀ ਗਤਿਜ ਊਰਜਾ (E_k2) = \(\frac {1}{2}\) m(3υ)²
\(\frac {1}{2}\) m × 9υ²
= 9 × \(\frac {1}{2}\)mυ² ………… (ii)
(i) ਪਹਿਲੇ ਪਿੰਡ ਦੀ ਗਤਿਜ ਊਰਜਾ (E_k1 = \(\frac {1}{2}\)mυ²
(ii) ਦੂਜੇ ਪਿੰਡ ਦੀ ਗਤਿਜ ਊਰਜਾ (E_k2) = 9 × \(\frac {1}{2}\)mυ²
E_k1 : E_k2 = \(\frac {1}{9}\) = 1 : 9

ਪ੍ਰਸ਼ਨ 10.
ਇੱਕ 2 kg ਪੁੰਜ ਵਾਲੀ ਵਸਤੁ ਵਿਰਾਮ ਅਵਸਥਾ ਤੋਂ ਹੇਠਾਂ ਧਰਤੀ ‘ਤੇ ਡਿੱਗਦੀ ਹੈ ਡਿੱਗਣ ਤੋਂ 2s ਬਾਅਦ ਵਸਤੂ ਦੀ ਗਤਿਜ. ਊਰਜਾ ਕਿੰਨੀ ਹੋਵੇਗੀ ? g ਦਾ ਮਾਨ 10 m/s² ਲਵੋ ।
ਹੱਲ:
ਇੱਥੇ ਪੁੰਜ (m) = 2 kg
ਆਰੰਭਿਕ ਵੇਗ (u) = 0 (ਵਿਰਾਮ ਅਵਸਥਾ)
ਸਮਾਂ (t) = 2 s
ਅੰਤਿਮ ਵੇਗ (υ) = ?
ਗੁਰੂਤਵੀ ਵੇਗ (g) = 10 m/s²
υ = u + gt ਦੀ ਵਰਤੋਂ ਕਰਕੇ
υ = 0 + 10 × 2
∴ υ = 20 m/s
ਹੁਣ 2 ਸੈਕਿੰਡ ਬਾਅਦ ਵਸਤੂ ਦੀ ਗਤਿਜ ਊਰਜਾ (E_k) = \(\frac {1}{2}\)mυ²
= \(\frac {1}{2}\) × 2 × (20)²
= \(\frac {1}{2}\) × 2 × 20 × 20
= 400 J

ਪ੍ਰਸ਼ਨ 11.
ਇੱਕ ਸਮਤਲ ਸੜਕ ਤੇ ਸਕੂਟਰ ਚਾਲਕ ਬਰੇਕ ਲਗਾ ਕੇ ਸਕੂਟਰ ਦੀ ਚਾਲ ਨੂੰ 36 km/h ਤੋਂ ਘਟਾ ਕੇ 18 km/h ਕਰ ਦਿੰਦਾ ਹੈ । ਦੱਸੋ ਬਰੇਕ ਦੁਆਰਾ ਕਿੰਨਾ ਕਾਰਜ ਕੀਤਾ ਗਿਆ, ਜੇਕਰ ਖ਼ਾਲੀ ਸਕੂਟਰ ਦਾ ਪੁੰਜ 86 kg ਅਤੇ ਚਾਲਕ ਅਤੇ ਪੈਟਰੋਲ ਦਾ ਪੁੰਜ 64 kg ਹੋਵੇ ।
ਹੱਲ:
ਕੁੱਲ ਪੁੰਜ (m) = m₁ + m₂
= ਸਕੂਟਰ ਦਾ ਪੁੰਜ + ਚਾਲਕ ਅਤੇ ਪੈਟਰੋਲ ਦਾ ਪੁੰਜ
= 86 kg +64 kg
= 150 kg
ਆਰੰਭਿਕ ਵੇਗ (u) = 36 km/h
= 36 × \(\frac{5}{18}\) m/s [∵ 1km/h = \(\frac{5}{18}\) m/s
= 10 m/s
ਅੰਤਿਮ ਵੇਗ (υ) = 18 km/h
= 18 × \(\frac{5}{18}\)
5 m/s

ਬਰੇਕ ਦੁਆਰਾ ਕੀਤਾ ਗਿਆ ਕਾਰਜ = ਸਕੂਟਰ ਦੁਆਰਾ ਗਤਿਜ ਊਰਜਾ ਦੀ ਹਾਨੀ
= ਆਰੰਭਿਕ ਗਤਿਜ ਊਰਜਾ – ਅੰਤਿਮ ਗਤਿਜ ਊਰਜਾ
= (\(\frac {1}{2}\)mu² – \(\frac {1}{2}\)mv²)
= \(\frac {1}{2}\)m(u² – v²)
= \(\frac {1}{2}\) m (u + v) (u – v)
= \(\frac {1}{2}\) × 150 × (10 + 5) (10 – 5)
= \(\frac {1}{2}\) × 150 × 15 × 5
= 75 × 75
5625 J

ਪ੍ਰਸ਼ਨ 12.
ਮੰਨ ਲਓ ਤੁਹਾਡੇ ਹੱਥ ਵਿੱਚ 1 kg ਪੁੰਜ ਵਾਲੀ ਵਸਤੂ ਹੈ । ਤੁਸੀਂ ਇਸ ਨੂੰ ਕਿੰਨੀ ਉੱਚਾਈ ਤਕ ਚੁੱਕੋਗੇ, ਤਾਂ ਜੋ ਗੁਰੂਤਵੀ ਸਥਿਤਿਜ ਊਰਜਾ 1J ਪ੍ਰਾਪਤ ਕਰ ਲਵੇ । g = 10 ms^-2)
ਹੱਲ:
ਇੱਥੇ ਸਥਿਤਿਜ ਊਰਜਾ (p) = 1 J
ਪੁੰਜ (m) = 1 kg
ਗੁਰੂਤਵੀ ਵੇਗ (g) = 10 ms^-2
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, ਸਥਿਤਿਜ ਊਰਜਾ (p) = mgh
1 = 1 × 10 × h
∴ h = \(\frac {1}{10}\)m
= 0.1 m
= 10 cm

ਪ੍ਰਸ਼ਨ 13.
ਇੱਕ 1000 w ਬਿਜਲੀ ਹੀਟਰ ਨੂੰ ਹਰ ਰੋਜ਼ 2 ਘੰਟੇ ਉਪਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । 28 ਦਿਨਾਂ ਦੇ ਮਹੀਨਾ ਭਰ ਉਪਯੋਗ ਕਰਨ ਵਿੱਚ ਕਿੰਨੀ ਊਰਜਾ ਦਾ ਖ਼ਰਚਾ ਹੋਵੇਗਾ, ਜੇਕਰ ਊਰਜਾ ਦੀ ਦਰ 3.00 ਰੁਪਏ ਪ੍ਰਤੀ ਯੂਨਿਟ ਹੋਵੇ ।
ਹੱਲ:
ਹੀਟਰ ਦੀ ਸ਼ਕਤੀ (P) = 1000 W = 1 kW
∴ ਕੁੱਲ ਸਮਾਂ (t) = 2 × 28 = 56 h
ਊਰਜਾ ਦੀ ਖ਼ਪਤ (E) = P × t
= 1 kW × 56 h
= 56 kWh
= 56 ਯੂਨਿਟ
ਊਰਜਾ ਦੀ ਦਰ = 3.00 ਰੁਪਏ ਪ੍ਰਤੀ ਯੂਨਿਟ
∴ ਕੁੱਲ ਖ਼ਰਚਾ = 56 × 3.00 ਰੁਪਏ
= 168.00 ਰੁਪਏ ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 14.
1 ਕਿਲੋਗ੍ਰਾਮ ਪਿੰਡ ਦੀ ਗਤਿਜ ਊਰਜਾ 1 ਜੁਲ ਹੈ । ਇਸ ਦੀ ਚਾਲ ਕਿੰਨੀ ਹੋਵੇਗੀ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ, ਪਿੰਡ ਦਾ ਪੁੰਜ (m) = 1 kg
ਪਿੰਡ ਦੀ ਗਤਿਜ ਊਰਜਾ (E_K) = 1 ਜੂਲ
ਵੇਗ (v) = ?
ਗਤਿਜ ਊਰਜਾ (E_k) = \(\frac {1}{2}\)mv² ਤੋਂ
1 = \(\frac {1}{2}\) × 1 × v²
v² = 2
∴ v = √2
= 1.414 ms^-1

ਪ੍ਰਸ਼ਨ 15.
50 kg ਪੁੰਜ ਦਾ ਇੱਕ ਲੜਕਾ ਦੌੜ ਕੇ 45 ਪੌੜੀਆਂ 9 s ਵਿੱਚ ਚੜ੍ਹਦਾ ਹੈ । ਜੇਕਰ ਹਰੇਕ ਪੌੜੀ ਦੀ ਉੱਚਾਈ । ‘ 15 cm ਹੋਵੇ, ਤਾਂ ਉਸ ਦੀ ਸ਼ਕਤੀ ਦਾ ਪਰਿਕਲਨ ਕਰੋ । g ਦਾ ਮਾਨ 10 ms^-2 ਲਓ ।
ਹੱਲ:
ਲੜਕੇ ਦਾ ਭਾਰ = mg
= 50 kg × 10 ms^-2
= 500 N
ਕੁੱਲ ਉੱਚਾਈ (h) = ਪੌੜੀਆਂ ਦੀ ਸੰਖਿਆ × ਇੱਕ ਪੌੜੀ ਦੀ ਉੱਚਾਈ
= 45 × 15 cm
= 675 cm
= 6.75 m
ਲੱਗਿਆ ਸਮਾਂ (t) = 9

= 375 W

ਪ੍ਰਸ਼ਨ 16.
ਇੱਕ ਕੁਲੀ 10 kg ਦਾ ਬੋਝ ਧਰਤੀ ਤੋਂ 1.5 m ਉੱਪਰ ਉਠਾ ਕੇ ਆਪਣੇ ਸਿਰ ਉੱਤੇ ਰੱਖਦਾ ਹੈ । ਉਸਦੇ ਦੁਆਰਾ ਬੋਝ ਉੱਤੇ ਕੀਤਾ ਗਿਆ ਕਾਰਜ ਦਾ ਪਰਿਕਲਨ ਕਰੋ ।
ਹੱਲ:
ਬੋਝ ਦਾ ਭਾਰ (m) = 10 kg ਅਤੇ
ਵਿਸਥਾਪਨ (S) = 1.5 m
ਕੀਤਾ ਗਿਆ ਕਾਰਜ (W) = F × S
= mg × S
= 10 kg × 10 ms^-2 × 1.5 m
= 150 Nm = 225 J

ਪ੍ਰਸ਼ਨ 17.
ਜੇਕਰ ਕਿਸੀ ਕਾਰ ਦਾ ਪੁੰਜ 1500 kg ਹੈ, ਤਾਂ ਉਸਦੇ ਵੇਗ ਨੂੰ 30 kmh^-1 ਤੋਂ 60 kmh^-1 ਤੱਕ ਵਧਾਉਣ ਵਿੱਚ ਕਿੰਨਾ ਕਾਰਜ (w) ਕਰਨਾ ਪਵੇਗਾ ।
ਹੱਲ:
ਕਾਰ ਦਾ ਮਾਨ (m) = 1500 kg
ਕਾਰ ਦਾ ਆਰੰਭਿਕ ਵੇਗ (u) = 30 km h^-1
= \(\frac{30 \times 1000 \mathrm{~m}}{60 \times 60 \mathrm{~s}}\)
= 8.33 ms^-1
ਕਾਰ ਦਾ ਅੰਤਿਮ ਵੇਗ (υ) = 60 km h^-1
= 16.67 ms^-1
ਇਸ ਲਈ ਕਾਰ ਦੀ ਆਰੰਭਿਕ ਗਤਿਜ ਊਰਜਾ
(E_Ki) = \(\frac {1}{2}\)mu²
\(\frac {1}{2}\) × 1500 kg × (8.33 ms^-1)²
= 52041.68 J
ਕਾਰ ਦੀ ਅੰਤਿਮ ਗਤਿਜ ਊਰਜਾ (E_Kf)= \(\frac {1}{2}\) mυ²
= \(\frac {1}{2}\) × 1500 × (16.67 ms^-1)²
= 208416.68 J
ਕੀਤਾ ਗਿਆ ਕਾਰਜ = ਗਤਿਜ ਊਰਜਾ ਵਿੱਚ ਪਰਿਵਰਤਨ
E_Kf – E_Ki
= 208416.68 J – 52041.68 J
= 156375 J

ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Very Short Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਕਾਰਜ ਦੀ SI ਇਕਾਈ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਜੁਲ ।

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਕਿਲੋਗ੍ਰਾਮ ਪੱਥਰ ਦੇ ਕਿਸੇ ਟੁਕੜੇ ਨੂੰ ਇੱਕ ਮੀਟਰ ਉੱਚਾਈ ਤਕ ਚੁੱਕਣ ਵਿੱਚ ਕਿੰਨੀ ਊਰਜਾ ਦੀ ਲੋੜ ਹੋਵੇਗੀ ?
ਉੱਤਰ-
9.8 ਜੂਲ ਹੱਲ :
W = mgh
= 1 × 9.8 × 1
= 9.8 J

ਪ੍ਰਸ਼ਨ 3.
ਕਿਸੇ ਵਸਤੂ ਦੇ ਵੇਗ ਵਿੱਚ ਕੀ ਪਰਿਵਰਤਨ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ, ਜਿਸ ਨਾਲ ਵਸਤੂ ਦਾ ਪੁੰਜ ਚਾਰ ਗੁਣਾ ਵਧਾਉਣ ਤੇ ਵੀ ਉਸ ਦੀ ਗਤਿਜ ਊਰਜਾ ਵਿੱਚ ਕੋਈ ਪਰਿਵਰਤਨ ਨਾ ਆਵੇ ?
ਉੱਤਰ-
ਵੇਗ ਅੱਧਾ ਕਰਨਾ ਪਵੇਗਾ ।

ਪ੍ਰਸ਼ਨ 4.
ਯੰਤਰਿਕ ਊਰਜਾ ਦੀਆਂ ਕਿਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ –

1. ਸਥਿਤਿਜ ਊਰਜਾ
2. ਗਤਿਜ ਊਰਜਾ ।

ਪ੍ਰਸ਼ਨ 5.
ਊਰਜਾ ਦੀ SI ਇਕਾਈ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਜੁਲ ।

ਪ੍ਰਸ਼ਨ 6.
ਸ਼ਕਤੀ ਦੀ sI ਇਕਾਈ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਵਾਟ ।

ਪਸ਼ਨ 7.
ਵਪਾਰਕ ਪੱਧਰ ਤੇ ਉਰਜਾ ਦੀ ਇਕਾਈ ਦਾ ਨਾਂ ਲਿਖੋ ਅਤੇ ਉਸ ਦੀ ਪਰਿਭਾਸ਼ਾ ਵੀ ਦਿਓ ।
ਉੱਤਰ-
ਵਪਾਰਕ ਪੱਧਰ ਤੇ ਊਰਜਾ ਦੀ ਇਕਾਈ ਕਿਲੋਵਾਟ ਘੰਟਾ ਹੈ ।

ਕਿਲੋਵਾਟ ਘੰਟਾ-ਜੇ ਇੱਕ ਕਿਲੋਵਾਟ ਸ਼ਕਤੀ ਦਾ 1 ਘੰਟਾ ਉਪਯੋਗ ਕੀਤਾ ਜਾਵੇ, ਤਾਂ ਊਰਜਾ ਦੀ ਪੂਰਤੀ 1 ਕਿਲੋਵਾਟ ਘੰਟਾ ਦੇ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਚਾਬੀ ਵਾਲੇ ਖਿਡੌਣੇ ਨੂੰ ਚਲਾਉਣ ਵਿੱਚ ਕਿਹੜੀ ਊਰਜਾ ਕਿਹੜੀ ਊਰਜਾ ਵਿੱਚ ਤਬਦੀਲ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਆਕਾਰ ਪਰਿਵਰਤਨ ਦੇ ਕਾਰਨ ਸਥਿਤਿਜ ਉਰਜਾ, ਗਤਿਜ ਉਰਜਾ ਵਿੱਚ ਬਦਲਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਹਥੇਲੀਆਂ ਨੂੰ ਆਪਸ ਵਿੱਚ ਰਗੜਨ ਨਾਲ ਉਹ ਗਰਮ ਕਿਉਂ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਹਥੇਲੀਆਂ ਦੀ ਗਤਿਜ ਊਰਜਾ, ਤਾਪ ਊਰਜਾ ਵਿੱਚ ਬਦਲ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਪੌਣ ਚੱਕੀ ਦੁਆਰਾ ਊਰਜਾ ਦਾ ਕਿਹੜਾ ਰੂਪ ਕਾਰਜ ਵਿੱਚ ਪਰਿਵਰਤਿਤ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਗਤਿਜ ਉਰਜਾ ।

ਪ੍ਰਸ਼ਨ 11.
ਸ਼ਕਤੀ, ਊਰਜਾ ਅਤੇ ਸਮੇਂ ਦਾ ਆਪਸੀ ਸੰਬੰਧ ਦੱਸੋ ।
ਉੱਤਰ-

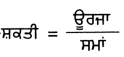
ਪ੍ਰਸ਼ਨ 12.
ਸਥਿਤਿਜ ਊਰਜਾ ਕਿਹੜੇ ਦੋ ਕਾਰਕਾਂ ‘ਤੇ ਨਿਰਭਰ ਹੈ ?
ਉੱਤਰ-
ਪੁੰਜ ਅਤੇ ਉੱਚਾਈ ।

ਪ੍ਰਸ਼ਨ 13.
ਬੰਨ੍ਹ ਤੇ ਇਕੱਠੇ ਕੀਤੇ ਗਏ ਪਾਣੀ ਵਿੱਚ ਕਿਹੜੀ ਊਰਜਾ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਸਥਿਤਿਜ ਉਰਜਾ ।

ਪ੍ਰਸ਼ਨ 14.
ਜਦੋਂ ਅਸੀਂ ਪੌੜੀਆਂ ਚੜ੍ਹਦੇ ਹਾਂ, ਤਾਂ ਕਿਹੜੀ ਊਰਜਾ ਦੀ ਵਰਤੋਂ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਮਾਸਪੇਸ਼ੀਆਂ ਦੀ ਉਰਜਾ ਦੀ ਵਰਤੋਂ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 15.
ਤੇਜ਼ ਹਨੇਰੀ ਵਾਲੇ ਦਿਨ ਕਈ ਮਕਾਨਾਂ ਦੀਆਂ ਛੱਤਾਂ ਕਿਉਂ ਉੱਡ ਜਾਂਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਤੇਜ਼ ਹਵਾ ਦੀ ਗਤਿਜ ਊਰਜਾ ਕਾਰਨ ।

ਪ੍ਰਸ਼ਨ 16.
ਇੱਕ ਕਿਲੋਗ੍ਰਾਮ ਪਾਣੀ 5 ਮੀ: ਉੱਪਰ ਚੁੱਕਣ ‘ਤੇ ਕਿੰਨਾ ਕਾਰਜ ਕਰਨਾ ਪਵੇਗਾ ?
ਉੱਤਰ-
ਪਾਣੀ ਚੁੱਕਣ ਲਈ ਕਾਰਜ = ਸਥਿਤਿਜ ਊਰਜਾ
= mgh
= 1 × 10 × 5 = 50 ਜੁਲ

ਪ੍ਰਸ਼ਨ 17.
ਜੇ ਕਿਸੇ ਵਸਤੂ ਦਾ ਵੇਗ ਤਿੰਨ ਗੁਣਾਂ ਵੱਧ ਜਾਵੇ, ਤਾਂ ਉਸਦੀ ਗਤਿਜ ਊਰਜਾ ‘ ਤੇ ਕੀ ਪ੍ਰਭਾਵ ਪਏਗਾ ?
ਉੱਤਰ-
∴ K.E. α v²
∴ ਇਹ 9 ਗੁਣਾ ਵੱਧ ਜਾਵੇਗੀ ।

ਪ੍ਰਸ਼ਨ 18.
ਸਪਰਿੰਗ ਕਮਾਨੀ) ਨੂੰ ਦਬਾਉਣ ਨਾਲ ਉਸ ਵਿੱਚ ਕਿਹੋ ਜਿਹੀ ਊਰਜਾ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਸਥਿਤਿਜ ਉਰਜਾ ।

ਪ੍ਰਸ਼ਨ 19.
ਇੱਕ ਅਜਿਹੀ ਉਦਾਹਰਨ ਦਿਓ ਜਦੋਂ ਵਸਤੂ ਵਿੱਚ ਗਤਿਜ ਊਰਜਾ ਅਤੇ ਸਥਿਤਿਜ ਊਰਜਾ ਦੋਨੋਂ ਮੌਜੂਦ ਹੋਣ ।
ਉੱਤਰ-
ਉੱਚਾਈ ਤੇ ਉੱਡ ਰਹੇ ਜਹਾਜ਼ ਵਿੱਚ ਦੋਨੋਂ ਸਥਿਤਿਜ ਊਰਜਾ ਅਤੇ ਗਤਿਜ ਊਰਜਾ ਹੁੰਦੀਆਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 20.
ਇੱਕ ਅਜਿਹੀ ਉਦਾਹਰਨ ਦਿਉ ਜਦੋਂ ਵਸਤੂ ਦੀ ਸ਼ਕਲ ਵਿੱਚ ਹੋਏ ਪਰਿਵਰਤਨ ਕਾਰਨ ਸਥਿਤਿਜ ਊਰਜਾ ਹੋਵੇ ।
ਉੱਤਰ-
ਖਿੱਚੇ ਹੋਏ ਕਮਾਨ ਵਿੱਚ ਸ਼ਕਲ (ਆਕ੍ਰਿਤੀ) ਪਰਿਵਰਤਨ ਦੇ ਪਰਿਣਾਮ ਵਜੋਂ ਸਥਿਤਿਜ ਊਰਜਾ ਪੈਦਾ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 21.
ਊਰਜਾ ਸੁਰੱਖਿਅਣ ਕਿਸਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਊਰਜਾ ਸੁਰੱਖਿਅਣ ਕਿਸਮ- “ਊਰਜਾ ਨਾ ਤਾਂ ਪੈਦਾ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ਅਤੇ ਨਾ ਹੀ ਨਸ਼ਟ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ । ਉਰਜਾ ਸਿਰਫ਼ ਇੱਕ ਰੂਪ ਤੋਂ ਦੂਸਰੇ ਰੂਪ ਵਿੱਚ ਰੂਪਾਂਤਰਿਤ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ।” ਅਰਥਾਤ ਉਰਜਾ ਰੁਪਾਂਤਰਨ ਦੌਰਾਨ ਸਿਸਟਮ ਦੀ ਕੁੱਲ ਊਰਜਾ ਨਿਯਤ ਰਹਿੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 22.
ਕਿਹੜਾ ਯੰਤਰ ਬਿਜਲੀ ਊਰਜਾ ਨੂੰ ਯੰਤਰਿਕ ਊਰਜਾ ਵਿੱਚ ਰੂਪਾਂਤਰਿਤ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ-
ਬਿਜਲਈ ਮੋਟਰ ।

ਪ੍ਰਸ਼ਨ 23.
ਬਿਜਲੀ ਪੱਖੇ ਵਿੱਚ ਕਿਹੜੀ ਊਰਜਾ ਕਿਸ ਊਰਜਾ ਵਿੱਚ ਰੂਪਾਂਤਰਿਤ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਬਿਜਲੀ ਉਰਜਾ ਦਾ ਯਾਤਿਕ ਉਰਜਾ ਵਿੱਚ ਰੂਪਾਂਤਰਣ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 24.
ਹਾਈਇਲੈੱਕਟ੍ਰਿਕ ਪਾਵਰ ਸਟੇਸ਼ਨ ਤੇ ਕਿਸ ਤਰ੍ਹਾਂ ਦੀ ਊਰਜਾ ਦਾ ਰੂਪਾਂਤਰਣ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਡਿੱਗਦੇ ਹੋਏ ਪਾਣੀ ਦੀ ਸਥਿਤਿਜ ਊਰਜਾ ਦਾ ਰੂਪਾਂਤਰਣ ਗਤਿਜ ਊਰਜਾ ਵਿੱਚ ਅਤੇ ਫਿਰ ਬਿਜਲੀ ਊਰਜਾ ਵਿੱਚ ਰੂਪਾਂਤਰਣ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 25.
ਵਾਟ ਅਤੇ ਕਿਲੋਵਾਟ ਵਿੱਚ ਕੀ ਸੰਬੰਧ ਹੈ ?
ਉੱਤਰ-
1 ਕਿਲੋਵਾਟ = 1000 ਵਾਟ ।

ਪ੍ਰਸ਼ਨ 26.
ਉਰਜਾ ਦੇ S.I. ਮਾਤ੍ਰਿਕ ਅਤੇ 1 kWh ਵਿੱਚ ਸੰਬੰਧ ਦੱਸੋ ।
ਉੱਤਰ-
ਊਰਜਾ ਦਾ S.I. ਮਾਤਿਕ ਜੁਲ (J) ਹੈ ।
∴ 1 kWh = 3.6 × 10⁶ਜੂਲ ।