PSEB 9th Class Science Important Questions Chapter 9 ਬਲ ਅਤੇ ਗਤੀ ਦੇ ਨਿਯਮ

Punjab State Board PSEB 9th Class Science Important Questions Chapter 9 ਬਲ ਅਤੇ ਗਤੀ ਦੇ ਨਿਯਮ Important Questions and Answers.

PSEB 9th Class Science Important Questions Chapter 9 ਬਲ ਅਤੇ ਗਤੀ ਦੇ ਨਿਯਮ

ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Long Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਬਲ ਕਿੰਨੇ ਕਿਸਮ ਦਾ ਹੁੰਦਾ ਹੈ ? ਹਰੇਕ ਕਿਸਮ ਦੀ ਉਦਾਹਰਨ ਸਹਿਤ ਵਿਆਖਿਆ ਕਰੋ । ਕਿਸੇ ਇੱਕ ਕਿਸਮ ਦੇ ਬਲ ਦੀਆਂ ਸ਼ਰਤਾਂ ਅਤੇ ਪ੍ਰਭਾਵ ਵੀ ਦੱਸੋ ।
ਉੱਤਰ-
ਬਲ ਦੀਆਂ ਕਿਸਮਾਂ-ਬਲ ਦੋ ਕਿਸਮ ਦੇ ਹੁੰਦੇ ਹਨ-
(i) ਸੰਤੁਲਿਤ ਬਲ
(ii) ਅਸੰਤੁਲਿਤ ਬਲ ।

(i) ਸੰਤੁਲਿਤ ਬਲ – ਜਦੋਂ ਕਿਸੇ ਵਸਤੂ ’ਤੇ ਇੱਕੋ ਸਮੇਂ ਬਹੁਤ ਸਾਰੇ ਬਲ ਕਿਰਿਆ ਕਰ ਰਹੇ ਹੋਣ ਅਤੇ ਉਨ੍ਹਾਂ ਦਾ ਪਰਿਣਾਮੀ ਬਲ ਨੈੱਟ ਬਲ ਜ਼ੀਰੋ ਹੋਵੇ, ਤਾਂ ਉਹਨਾਂ ਬਲਾਂ ਨੂੰ ਸੰਤੁਲਿਤ ਬਲ ਕਹਿੰਦੇ ਹਨ । ਬਲਾਂ ਦੀ ਸੰਤੁਲਿਤ ਹੋਣ ਦੀ ਅਵਸਥਾ ਵਿੱਚ ਜੇ ਕੋਈ ਵਸਤੂ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਹੈ, ਤਾਂ ਉਹ ਬੱਲਾਂ ਦੇ ਲੱਗਣ ਦੇ ਬਾਵਜੂਦ ਵੀ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਹੀ ਰਹੇਗੀ ਅਤੇ ਜੇਕਰ ਇਕ ਸਮਾਨ ਗਤੀ ਨਾਲ ਚਲ ਰਹੀ ਹੈ, ਤਾਂ ਉਸੇ ਇਕ ਸਮਾਨ ਗਤੀ ਨਾਲ ਗਤੀਸ਼ੀਲ ਰਹੇਗੀ, ਜਿਵੇਂ ਕਿ ਉਸ ਉੱਤੇ ਕੋਈ ਬਲ ਕਿਰਿਆ ਕਰ ਹੀ ਨਹੀਂ ਰਿਹਾ । ਇਸ ਤਰ੍ਹਾਂ ਸੰਤੁਲਿਤ ਬਲਾਂ ਦੇ ਪ੍ਰਭਾਵ ਕਾਰਨ ਵਸਤੂ ਦੀ ਸਥਿਤੀ ਵਿੱਚ ਪਰਿਵਰਤਨ ਨਹੀਂ ਹੁੰਦਾ ਹੈ । ਸੰਤੁਲਿਤ ਬਲਾਂ ਨਾਲ ਵਸਤੂ ਦੀ ਸ਼ਕਲ ਬਦਲ ਜਾਂਦੀ ਹੈ, ਜਿਵੇਂ-ਜੇਕਰ ਰਬੜ ਦੀ ਇੱਕ ਗੇਂਦ ਨੂੰ ਹਥੇਲੀਆਂ ਦੇ ਵਿਚਕਾਰ ਰੱਖ ਕੇ ਦਬਾਇਆ ਜਾਵੇ, ਤਾਂ ਸਮਾਨ ਅਤੇ ਵਿਪਰੀਤ ਦਿਸ਼ਾ ਵਿੱਚ ਬਲ ਲਗਾਏ ਜਾਂਦੇ ਹਨ ਜਿਸ ਨਾਲ ਗੇਂਦ ਦੀ ਸ਼ਕਲ ਬਦਲ ਜਾਂਦੀ ਹੈ । ਗੇਂਦ ਗੋਲ ਨਾ ਰਹਿ ਕੇ ਚਪਟੀ ਹੋ ਜਾਂਦੀ ਹੈ ।

ਉਦਾਹਰਨ – ਰੱਸਾਕਸ਼ੀ ਦੀ ਖੇਡ ਵਿੱਚ ਜਦੋਂ ਦੋਨੋਂ ਟੀਮਾਂ ਰੱਸੀ ਨੂੰ ਬਰਾਬਰ ਬਲ ਨਾਲ ਖਿੱਚਦੇ ਹਨ, ਤਾਂ ਪਰਿਣਾਮੀ ਬਲ ਜ਼ੀਰੋ ਹੁੰਦਾ ਹੈ । ਇਸ ਲਈ ਦੋਨੋਂ ਟੀਮਾਂ ਆਪਣੀ-ਆਪਣੀ ਥਾਂ ‘ਤੇ ਸਥਿਰ ਰਹਿੰਦੀਆਂ ਹਨ । ਇਸ ਅਵਸਥਾ ਵਿੱਚ ਦੋਨੋਂ ਟੀਮਾਂ ਦੁਆਰਾ ਰੱਸੀ ਉੱਪਰ ਸੰਤੁਲਿਤ ਬਲ ਲਗਾਇਆ ਗਿਆ ਹੈ ।

ਦੋ ਬਲਾਂ ਦੇ ਸੰਤੁਲਿਤ ਹੋਣ ਦੀ ਸ਼ਰਤ – ਦੋ ਸਮਾਨ ਅਤੇ ਵਿਪਰੀਤ ਦਿਸ਼ਾ ਵਿੱਚ ਕਿਰਿਆ ਕਰ ਰਹੇ ਬਲ ਉਸ ਵੇਲੇ ਸੰਤੁਲਿਤ ਹੁੰਦੇ ਹਨ ਜੇ ਉਹ ਇੱਕ ਰੇਖਾ ‘ਤੇ ਕਿਰਿਆ ਕਰ ਰਹੇ ਹੋਣ ।

ਸੰਤੁਲਿਤ ਬਲਾਂ ਦਾ ਪ੍ਰਭਾਵ – ਕਿਸੇ ਵਸਤੂ ‘ਤੇ ਕਿਰਿਆ ਕਰ ਰਹੇ ਬਲ ਜੇਕਰ ਇਸ ਨੂੰ ਵਿਰਾਮ ਜਾਂ ਗਤੀਸ਼ੀਲ ਅਵਸਥਾ ਵਿੱਚ ਪਰਿਵਰਤਨ ਨਹੀਂ ਕਰ ਸਕਦੇ, ਤਾਂ ਇਹ ਉਸ ਵਸਤੂ ਦੀ ਸ਼ਕਲ ਨੂੰ ਜ਼ਰੂਰ ਹੀ ਬਦਲ ਦੇਣਗੇ ।

(ii) ਅਸੰਤੁਲਿਤ ਬਲ – ਜਦੋਂ ਕਿਸੇ ਵਸਤੁ ’ਤੇ ਲੱਗ ਰਹੇ ਬਹੁਤ ਸਾਰੇ ਬਲਾਂ ਦਾ ਪਰਿਣਾਮੀ ਬਲ ਨੈੱਟ ਬਲ ਜ਼ੀਰੋ ਨਹੀਂ ਹੁੰਦਾ, ਤਾਂ ਉਹਨਾਂ ਬਲਾਂ ਨੂੰ ਅਸੰਤੁਲਿਤ ਬਲ ਕਹਿੰਦੇ ਹਨ । ਇਹ ਅਸੰਤੁਲਿਤ ਬਲ ਵਸਤੂ ਦੀ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਅਤੇ ਦਿਸ਼ਾ ਵਿੱਚ ਪਰਿਵਰਤਨ ਕਰਦਾ ਹੈ ।

ਉਦਾਹਰਨ – ਮੰਨ ਲਓ ਦੋ ਬੱਚੇ ਇੱਕ ਬੱਕਸੇ ਨੂੰ ਖੁਰਦਰੇ ਫਰਸ਼ ‘ਤੇ ਬਕਸੇ ਨੂੰ ਧਕੇਲਦੇ ਹਨ, ਤਾਂ ਜੋ ਬਕਸਾ ਨਹੀਂ ਖਿਸਕਦਾ ਹੈ, ਕਿਉਂਕਿ ਰਗੜ ਬਲ ਧਕੇਲਣ ਤੋਂ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਕੰਮ ਕਰ ਰਿਹਾ ਹੈ । (ਚਿੱਤਰ a) ਇਹ ਰਗੜ ਬਲ ਬਕਸੇ ਦੀ ਹੇਠਲੀ ਸਤਹਿ ਅਤੇ ਖੁਰਦਰੀ ਸਤਹਿ ਦੇ ਵਿਚਕਾਰ ਪੈਦਾ ਹੁੰਦਾ ਹੈ । ਇਹ ਰਗੜ ਬਲ, ਧਕੇਲਣ ਲਈ ਲੱਗੇ ਬਲ ਨੂੰ ਸੰਤੁਲਿਤ ਕਰਦਾ ਹੈ ਅਤੇ ਇਹੀ ਕਾਰਨ ਹੈ ਕਿ ਬਕਸਾ ਨਹੀਂ ਖਿਸਕਦਾ ਹੈ । ਹੁਣ ਬੱਚੇ ਬਕਸੇ ਨੂੰ ਵੱਧ ਜ਼ੋਰ ਲਗਾ ਕੇ ਧਕੇਲਦੇ ਹਨ ਪਰੰਤੁ ਬਕਸਾ ਫਿਰ ਵੀ ਨਹੀਂ ਖਿਸਕਦਾ ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ (b) ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ । ਅਜਿਹਾ ਇਸ ਲਈ ਕਿ ਰਗੜ ਬਲ ਅਜੇ ਵੀ ਧਕੇਲ ਬਲ ਨੂੰ ਸੰਤੁਲਿਤ ਕਰ ਰਿਹਾ ਹੈ ।

ਹੁਣ ਬੱਚੇ ਪਹਿਲਾਂ ਨਾਲੋਂ ਵੱਧ ਜ਼ੋਰ ਲਗਾ ਕੇ ਧਕੇਲਦੇ ਹਨ, ਤਾਂ ਜੋ ਧਕੇਲਣ ਵਾਲਾ ਬਲ ਰਗੜ ਬਲ ਤੋਂ ਵੱਧ ਹੋ ਜਾਂਦਾ ਹੈ । (ਚਿੱਤਰ c) ਇੱਥੇ ਅਸੰਤੁਲਿਤ ਬਲ ਦੇ ਕਾਰਨ ਬਕਸਾ ਖਿਸਕਣਾ ਸ਼ੁਰੂ ਕਰਦਾ ਹੈ ।

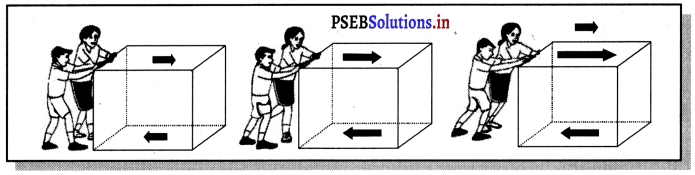
ਪ੍ਰਸ਼ਨ 2.
ਨਿਊਟਨ ਦੇ ਪਹਿਲੇ ਗਤੀ ਨਿਯਮ ਦੀ ਪਰਿਭਾਸ਼ਾ ਲਿਖੋ ਅਤੇ ਇਸ ਦੀ ਵਿਆਖਿਆ ਕਰੋ ।
ਉੱਤਰ-
ਨਿਊਟਨ ਦਾ ਪਹਿਲਾ ਗਤੀ ਨਿਯਮ-ਇਸ ਨਿਯਮ ਅਨੁਸਾਰ, “ਕੋਈ ਵਸਤੂ ਵਿਰਾਮ ਜਾਂ ਸਰਲ-ਰੇਖੀ ਗਤੀ ਦੀ ਮੁਲ ਅਵਸਥਾ ਵਿੱਚ ਉਦੋਂ ਤਕ ਰਹਿੰਦੀ ਹੈ ਜਦੋਂ ਤਕ ਉਸ ਉੱਪਰ ਕੋਈ ਬਾਹਰੀ ਬਲ ਕਿਰਿਆ ਨਹੀਂ ਕਰਦਾ ।”

ਕਥਨ ਦਾ ਅਰਥ-ਨਿਊਟਨ ਦੇ ਪਹਿਲੇ ਗਤੀ ਨਿਯਮ ਦੇ ਅਰਥ ਨੂੰ ਦੋ ਭਾਗਾਂ ਵਿੱਚ ਸਮਝਿਆ ਜਾ ਸਕਦਾ ਹੈ
(i) ਨਿਯਮ ਦੇ ਪਹਿਲੇ ਭਾਗ ਅਨੁਸਾਰ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਪਈ ਇੱਕ ਵਸਤੁ ਹਮੇਸ਼ਾਂ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਰਹੇਗੀ ਜਦੋਂ ਤਕ ਕਿ ਇਸ ਨੂੰ ਹਿਲਾਉਣ ਲਈ ਕੋਈ ਬਾਹਰੀ ਯਤਨ ਨਾ ਕੀਤਾ ਜਾਵੇ । ਇਸ ਦਾ ਅਰਥ ਇਹ ਹੋਇਆ ਕਿ ਬਾਹਰੀ ਯਤਨ, ਜਿਸਨੂੰ ਅਸੀਂ ਬਲ ਕਹਿੰਦੇ ਹਾਂ, ਨਾਲ ਸਥਿਰ ਵਸਤੂ ਨੂੰ ਕਿਸੇ ਤਰ੍ਹਾਂ ਦੀ ਵੀ ਗਤੀ ਵਿੱਚ ਲਿਆਂਦਾ ਜਾ ਸਕਦਾ ਹੈ ।

ਉਦਾਹਰਨ – ਮੰਨ ਲਉ ਇੱਕ ਵਿਦਿਆਰਥੀ ਕਿਸੇ ਮੇਜ਼ ਉੱਪਰ ਇੱਕ ਕਿਤਾਬ ਰੱਖ ਦਿੰਦਾ ਹੈ । ਇਹ ਕਿਤਾਬ ਉਦੋਂ ਤਕ ਮੇਜ਼ ਉੱਪਰ ਹੀ ਪਈ ਰਹੇਗੀ ਜਦੋਂ ਤਕ ਵਿਦਿਆਰਥੀ ਜਾਂ ਕੋਈ ਹੋਰ ਇਸ ਨੂੰ ਨਹੀਂ ਉਠਾਏਗਾ । ਇਸ ਦਾ ਅਰਥ ਇਹ ਹੋਇਆ ਕਿ ਕਿਤਾਬ ਆਪਣੇ-ਆਪ ਆਪਣੀ ਵਿਰਾਮ ਦੀ ਅਵਸਥਾ ਬਦਲਣ ਦੇ ਯੋਗ ਨਹੀਂ ਹੈ ।

(ii) ਨਿਯਮ ਦੇ ਦੂਜੇ ਭਾਗ ਅਨੁਸਾਰ ਇੱਕ ਸਮਾਨ ਸਰਲ-ਰੇਖੀ ਗਤੀ ਕਰ ਰਹੀ ਵਸਤੁ ਹਮੇਸ਼ਾਂ ਗਤੀ ਕਰਦੀ ਰਹੇਗੀ। ਜਦੋਂ ਤਕ ਕਿ ਇਸਨੂੰ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਲਿਆਉਣ ਲਈ ਕੋਈ ਬਾਹਰੀ ਬਲ ਇਸ ਉੱਪਰ ਕਿਰਿਆ ਨਹੀਂ ਕਰਦਾ ।

ਉਦਾਹਰਨ – ਤੁਸੀਂ ਇੱਕ ਕ੍ਰਿਕੇਟ ਗੇਂਦ ਨੂੰ ਪਹਿਲਾਂ ਸੀਮਿੰਟ ਦੇ ਫ਼ਰਸ਼ ਉੱਪਰ ਅਤੇ ਫਿਰ ਮਾਰਬਲ ਦੇ ਫਰਸ਼ ਉੱਪਰ ਸੁੱਟੋ | ਗੇਂਦ ਰੁਕਣ ਲਈ ਵੱਖ-ਵੱਖ ਸਮਾਂ ਲਵੇਗੀ । ਤੁਸੀਂ ਵੇਖਦੇ ਹੋ ਕਿ ਗੇਂਦ ਰੁਕ ਜਾਂਦੀ ਹੈ । ਇਸ ਦਾ ਕਾਰਨ ਇੱਕ ਵਿਰੋਧੀ ਬਲ ਹੈ ਜਿਸਨੂੰ ਰਗੜ ਬਲ ਕਹਿੰਦੇ ਹਨ | ਰਗੜ ਬਲ ਸੰਪਰਕ ਵਿੱਚ ਆਉਣ ਵਾਲੀਆਂ ਦੋ ਸਤਾਵਾਂ ਦੇ ਦਰਮਿਆਨ ਖੁਰਦਰੇਪਣ ਕਰਕੇ ਹੁੰਦਾ ਹੈ । ਮਾਰਬਲ ਦਾ ਫ਼ਰਸ਼ ਪੱਧਰਾ ਹੋਣ ਕਰਕੇ ਘੱਟ ਵਿਰੋਧੀ ਬਲ ਲਗਾਉਂਦਾ ਹੈ ਅਤੇ ਗੇਂਦ ਵੱਧ ਦੂਰੀ ਤਕ ਜਾਂਦੀ ਹੈ ਜਦ ਕਿ ਸੀਮਿੰਟ ਦਾ ਫ਼ਰਸ਼ ਖੁਰਦਰਾ ਹੋਣ ਕਰਕੇ ਵੱਧ ਵਿਰੋਧੀ ਬਲ ਲਗਾਉਂਦਾ ਹੈ ਅਤੇ ਗੇਂਦ ਘੱਟ ਦੂਰੀ ਤਕ ਜਾਂਦੀ ਹੈ ।

ਪਸ਼ਨ 3.
ਜਤਾ ਕਿਸ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ? ਜੜਤਾ ਦੀਆਂ ਵਿਭਿੰਨ ਕਿਸਮਾਂ ਦੱਸੋ ਅਤੇ ਹਰੇਕ ਲਈ ਉਦਾਹਰਨਾਂ ਵੀ ਦਿਉ ।
ਉੱਤਰ-
ਜੜ੍ਹਤਾ – ਜੜ੍ਹਤਾ ਵਸਤੂ ਦਾ ਉਹ ਗੁਣ ਹੈ ਜਿਸ ਦੇ ਸਿੱਟੇ ਵਜੋਂ ਵਸਤੂ ਆਪਣੀ ਵਿਰਾਮ ਅਵਸਥਾ ਜਾਂ ਸਰਲ ਰੇਖੀ ਗਤੀ ਦੀ ਅਵਸਥਾ ਨੂੰ ਬਦਲਣ ਵਿੱਚ ਸਮਰੱਥ ਹੁੰਦੀ ਹੈ । ਜੜ੍ਹਤਾ ਵਸਤੂ ਦੇ ਪੁੰਜ ਉੱਪਰ ਨਿਰਭਰ ਕਰਦੀ ਹੈ, ਪਰ ਪੁੰਜ, ਜੜ੍ਹਤਾ ਉੱਪਰ ਨਿਰਭਰ ਨਹੀਂ ਕਰਦਾ | ਕਾਰ ਦੀ ਜੜ੍ਹਤਾ, ਸਕੂਟਰ ਦੀ ਜੜ੍ਹਤਾ ਨਾਲੋਂ ਵੱਧ ਹੁੰਦੀ ਹੈ ਕਿਉਂਕਿ ਕਾਰ ਦਾ ਪੁੰਜ, ਸਕੂਟਰ ਦੇ ਪੁੰਜ ਤੋਂ ਵੱਧ ਹੁੰਦਾ ਹੈ । ਪੁੰਜ ਅਤੇ ਜੜ੍ਹਤਾ ਦੋਵੇਂ ਇੱਕੋ ਇਕਾਈ ਵਿੱਚ ਮਾਪੇ ਜਾਂਦੇ ਹਨ ।

ਇਸੇ ਗੁਣ ਕਾਰਨ ਨਿਉਟਨ ਦੇ ਪਹਿਲੇ ਗਤੀ ਨਿਯਮਾਂ ਨੂੰ ਜੜ੍ਹਤਾ ਦਾ ਨਿਯਮ ਕਿਹਾ ਜਾਂਦਾ ਹੈ-
ਜੜ੍ਹਤਾ ਦੀਆਂ ਵਿਭਿੰਨ ਕਿਸਮਾਂ-ਜੜ੍ਹਤਾ ਤਿੰਨ ਪ੍ਰਕਾਰ ਦੀ ਹੁੰਦੀ ਹੈ ।
1. ਵਿਰਾਮ ਜਤਾ – ਇਸ ਦਾ ਅਰਥ ਹੈ ਕਿ ਜਿਹੜੀ ਵਸਤੁ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਹੈ, ਉਹ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਰਹਿਣ ਦਾ ਯਤਨ ਕਰਦੀ ਹੈ ।
ਇਸ ਨੂੰ ਹੇਠ ਦਿੱਤੀਆਂ ਉਦਾਹਰਨਾਂ ਦੁਆਰਾ ਵਿਰਾਮ ਜੜ੍ਹਤਾ ਦੇ ਸੰਕਲਪ ਨੂੰ ਸਪੱਸ਼ਟ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ-
ਉਦਾਹਰਨ – ਬੱਸ ਜਾਂ ਰੇਲ ਗੱਡੀ ਜਦੋਂ ਅਚਾਨਕ ਚਲਦੀ ਹੈ, ਤਾਂ ਉਹ ਖੜੀ ਬੱਸ ਜਾਂ ਰੇਲ ਗੱਡੀ ਵਿੱਚ ਆਰਾਮ ਨਾਲ ਬੈਠਾ ਵਿਅਕਤੀ ਪਿੱਛੇ ਵੱਲ ਡਿੱਗਦਾ ਹੈ । ਇਸ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਵਿਅਕਤੀ ਦਾ ਹੇਠਲਾ ਹਿੱਸਾ ਤਾਂ ਗਤੀ ਵਿੱਚ ਆ ਜਾਂਦਾ ਹੈ ਪਰ ਉਸ ਦਾ ਉੱਪਰਲਾ ਹਿੱਸਾ ਜੜਤਾ ਕਾਰਨ ਵਿਰਾਮ ਵਿੱਚ ਰਹਿਣ ਦਾ ਯਤਨ ਕਰਦਾ ਹੈ ।

2. ਗਤੀ-ਜਤਾ – ਇਸ ਦਾ ਅਰਥ ਇਹ ਹੈ ਕਿ ਜਿਹੜੀ ਵਸਤੁ ਗਤੀਸ਼ੀਲ ਹੈ ਉਹ ਉਸੇ ਦਰ ਨਾਲ ਗਤੀ ਵਿੱਚ ਰਹਿਣ ਦਾ ਯਤਨ ਕਰਦੀ ਹੈ ।
ਉਦਾਹਰਨ-

• ਚਲ ਰਹੀ ਬੱਸ ਜਾਂ ਗੱਡੀ ਵਿੱਚ ਬੈਠਾ ਯਾਤਰੀ ਬੱਸ ਜਾਂ ਗੱਡੀ ਦੇ ਇੱਕਦਮ ਰੁਕ ਜਾਣ ‘ਤੇ ਅੱਗੇ ਵੱਲ ਡਿੱਗਦਾ ਹੈ । ਅਜਿਹੀ ਅਵਸਥਾ ਵਿੱਚ ਯਾਤਰੀ ਦੇ ਸਰੀਰ ਦਾ ਹੇਠਲਾ ਹਿੱਸਾ ਗੱਡੀ ਦੇ ਰੁਕਦੇ ਹੀ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਆ ਜਾਂਦਾ ਹੈ, ਪਰ ਉਸ ਦੇ ਸਰੀਰ ਦਾ ਉੱਪਰਲਾ ਹਿੱਸਾ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਗਤੀਸ਼ੀਲ ਰਹਿਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦਾ ਹੈ ।
• ਲੰਬੀ ਛਾਲ ਮਾਰਨ ਵਾਲਾ ਐਥਲੀਟ ਕੁੱਝ ਦੂਰੀ ਦੌੜ ਕੇ ਛਾਲ ਮਾਰਦਾ ਹੈ, ਤਾਂ ਜੋ ਉਸ ਦੇ ਸਰੀਰ ਦੀ ਗਤੀ-ਜਤਾ ਛਾਲ ਮਾਰਦੇ ਸਮੇਂ ਉਸ ਦੇ ਪੇਸ਼ੀ ਬਲ ਦੀ ਸਹਾਇਤਾ ਕਰੇ ।

3. ਦਿਸ਼ਾਈ ਜਤਾ-ਵਸਤੂ ਦਾ ਇਹ ਗੁਣ ਵਸਤੂ ਨੂੰ ਆਪਣੀ ਦਿਸ਼ਾ ਸਥਿਰ ਰੱਖਣ ਵਿੱਚ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ ।
ਉਦਾਹਰਨ-
(i) ਪਹੀਏ ਤੇ ਮਡਗਾਰਡ (Mud Guard) ਦਿਸ਼ਾਈ ਜਤਾ ਕਾਰਨ ਸਪਰਸ਼ ਰੇਖੀ ਦਿਸ਼ਾ ਵਿੱਚ ਆ ਰਹੇ ਚਿੱਕੜ ਤੋਂ ਬਚਾਓ ਲਈ ਲਗਾਏ ਜਾਂਦੇ ਹਨ । (ii) ਇੱਕ ਧਾਗੇ ਨਾਲ ਬੰਨ੍ਹੇ ਇੱਕ ਪੱਥਰ ਤੇ ਵਿਚਾਰ ਕਰੋ, ਜਿਹੜਾ ਖਿਤਿਜੀ ਚੱਕਰ ਵਿੱਚ ਘੁੰਮ ਰਿਹਾ ਹੈ । ਜੇਕਰ ਅਜਿਹਾ ਕਰਦੇ ਸਮੇਂ ਇਹ ਧਾਗਾ ਟੁੱਟ ਜਾਵੇ, ਤਾਂ ਦਿਸ਼ਾਈ ਜਤਾ ਕਾਰਨ ਪੱਥਰ ਚੱਕਰ ਦੀ ਸਪਰਸ਼ ਰੇਖੀ ਦਿਸ਼ਾ ਵਿੱਚ ਉੱਡ ਕੇ ਸਰਲ ਰੇਖੀ ਦਿਸ਼ਾ ਵਿੱਚ ਗਤੀਸ਼ੀਲ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਨਿਊਟਨ ਦੇ ਦੂਜੇ ਗਤੀ ਨਿਯਮ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ ਅਤੇ ਇਸ ਦੀ ਵਿਆਖਿਆ ਕਰੋ ।
ਉੱਤਰ-
ਨਿਊਟਨ ਦਾ ਦੂਜਾ ਗਤੀ ਨਿਯਮ (Newton’s Second Law of Motion) – ਨਿਊਟਨ ਦਾ ਦੂਜਾ ਗਤੀਨਿਯਮ ਕਿਸੇ ਵਸਤੂ ਨੂੰ ਗਤੀ ਵਿੱਚ ਲਿਆਉਣ ਲਈ ਲੋੜੀਂਦੇ ਬਲ ਦੀ ਮਾਤਰਾ ਮਾਲੂਮ ਕਰਨ ਵਿੱਚ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ ।

ਕਥਨ – “ਕਿਸੇ ਵਸਤ ਦੇ ਸੰਵੇਗ ਵਿੱਚ ਤਬਦੀਲੀ ਦੀ ਦਰ, ਲਗਾਏ ਗਏ ਬਾਹਰੀ ਬਲ ਦੇ ਸਿੱਧੇ ਅਨੁਪਾਤ ਵਿੱਚ ਹੁੰਦੀ ਹੈ, ਅਤੇ ਸੰਵੇਗ ਵਿੱਚ ਤਬਦੀਲੀ ਦੀ ਦਿਸ਼ਾ, ਲਗਾਏ ਗਏ ਬਲ ਦੀ ਦਿਸ਼ਾ ਹੀ ਹੁੰਦੀ ਹੈ ।
ਨਿਯਮ ਨੂੰ ਦੋ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ-

• ਕਿਸੇ ਵਸਤੂ ਦੀ ਸੰਵੇਗ ਪਰਿਵਰਤਨ ਦੀ ਦਰ ਉਸ ’ਤੇ ਕਿਰਿਆ ਕਰ ਰਹੇ ਬਲ ਦੇ ਸਿੱਧੇ ਅਨੁਪਾਤ ਵਿੱਚ ਹੁੰਦੀ ਹੈ । ਅਤੇ
• ਬਾਹਰੀ ਬਲ ਕਾਰਨ ਹੋ ਰਿਹਾ ਸਵੇਗ ਪਰਿਵਰਤਨ ਲਗਾਏ ਗਏ ਬਲ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਕਿਰਿਆ ਕਰਦਾ ਹੈ ।
  ਅਰਥਾਤ ਇਸ ਨਿਯਮ ਦੇ ਅਨੁਸਾਰ, “ਕਿਸੇ ਵਸਤੂ ’ਤੇ ਬਾਹਰੋਂ ਲਗਾਇਆ ਗਿਆ ਬਲ ਉਸ ਵਸਤੂ ਦੇ ਪੁੰਜ ਅਤੇ ਉਸ ਵਸਤੂ ਵਿੱਚ ਬਲ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਪੈਦਾ ਹੋਏ ਵੇਗ ਦੇ ਗੁਣਨਫਲ ਦਾ ਅਨੁਕੂਮਾਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ ।”

ਵਿਆਖਿਆ – ਜਦੋਂ ਕੋਈ ਬਲ ਕਿਸੇ ਵਸਤੂ ‘ਤੇ ਕਿਰਿਆ ਕਰਦਾ ਹੈ, ਤਾਂ ਇਹ ਵਸਤੂ ਦੇ ਸੰਵੇਗ ਵਿੱਚ ਪਰਿਵਰਤਨ ਕਰਦਾ ਹੈ । ਜੇਕਰ ਬਲ ਦੁੱਗਣਾ ਹੁੰਦਾ ਹੈ, ਤਾਂ ਸੰਵੇਗ ਵਿੱਚ ਵੀ ਦੁੱਗਣਾ ਪਰਿਵਰਤਨ ਹੁੰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਜਿੰਨਾ ਵੱਧ ਬਲ ਲਗਾਇਆ ਜਾਂਦਾ ਹੈ, ਸੰਵੇਗ ਪਰਿਵਰਤਨ ਦੀ ਦਰ ਵੀ ਉੱਨੀ ਹੀ ਅਧਿਕ ਹੁੰਦੀ ਹੈ । ਸੰਵੇਗ, ਵਸਤ ਦੇ ਪੰਜ ਅਤੇ ਵੇਗ ਦਾ ਗੁਣਨਫਲ ਹੈ । ਆਮ ਤੌਰ ‘ਤੇ ਪੁੰਜ ਨਹੀਂ ਬਦਲਦਾ । ਇਸ ਲਈ ਸਵੇਗ ਪਰਿਵਰਤਨ ਦੀ ਦਰ ਅਸਲ ਵਿੱਚ ਵੇਗ ਪਰਿਵਰਤਨ ਦੀ ਦਰ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਲਗਾਇਆ ਗਿਆ ਬਲ ਪ੍ਰਵੇਗ ਦੇ ਸਮਾਨ ਅਨੁਪਾਤੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਗਤੀ ਦੇ ਦੂਜੇ ਨਿਯਮ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਬਲ ਦਾ ਗਣਿਤਿਕ ਪਰਿਮਾਣ ਗਿਆਤ ਕਰਨ ਲਈ ਸੂਤਰ ਦਾ ਵਿਉਂਤਪਨ ਕਰੋ ।
ਉੱਤਰ-
ਨਿਉਟਨ ਦੇ ਦੂਜੇ ਗਤੀ ਨਿਯਮ ਤੋਂ ਬਲ ਦਾ ਗਣਿਤਿਕ ਮਾਪ-
ਮੰਨ ਲਓ ਪੁੰਜ ਅ ਦੀ ਇੱਕ ਵਸਤੂ ਦਾ ਮੁੱਢਲਾ ਵੇਗ u ਹੈ । ਇਸ ਉੱਪਰ ਬਲ F, t ਸਮੇਂ ਲਈ ਲਗਾਇਆ ਜਾਂਦਾ ਹੈ ਜਿਸ ਕਰਕੇ ਇਸ ਦਾ ਵੇਗ ਵੱਧ ਜਾਂਦਾ ਹੈ । ਮੰਨ ਲਓ, ਅੰਤਿਮ ਵੇਗ vਹੈ ।
ਮੁੱਢਲਾ ਸੰਵੇਗ = P₁ = mu
ਅੰਤਿਮ ਸੰਵੇਗ = p₂ = mυ
ਕਿਉਂਕਿ ਅੰਤਿਮ ਵੇਗ υ ਮੁੱਢਲੇ ਵੇਗ u ਤੋਂ ਵੱਧ ਹੈ, ਇਸ ਲਈ ਅੰਤਿਮ ਸੰਵੇਗ p₂, ਮੁੱਢਲਾ ਸੰਵੇਗ = p₁ ਤੋਂ ਵੱਧ ਹੋਵੇਗਾ ।
∴ ਸੰਵੇਗ ਵਿੱਚ ਤਬਦੀਲੀ = (p₁ – p₂)
= mυ – mu
= m (υ – u) ਨਿਯਮ ਦੇ ਅਨੁਸਾਰ ਬਾਹਰੀ ਬਲ F ∝ ਸੰਵੇਗ ਵਿੱਚ ਤਬਦੀਲੀ ਦੀ ਦਰ
ਅਰਥਾਤ F ∝ \(\frac{\left(p_{2}-p_{1}\right)}{t}\)
F ∝ \(\frac{m(v-u)}{t}\)
सां
F = k \(\frac{m(v-u)}{t}\) ਜਿੱਥੇ (k) ਇੱਕ ਅਨੁਪਾਤੀ ਸਥਿਰ-ਅੰਕ ਹੈ । ………………. (1)
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਵੇਗ ਵਿੱਚ ਤਬਦੀਲੀ ਦੀ ਦਰ ਨੂੰ ਪ੍ਰਵੇਗ ਕਹਿੰਦੇ ਹਨ ।
∴ \(\frac{v-u}{t}\) = a
ਇਸ ਤਰ੍ਹਾਂ ਸਮੀਕਰਨ (1) ਤੋਂ
F = k m a …………………. (2)
F, m ਅਤੇ a ਦੇ ਇਕਾਈ ਮੁੱਲ ਲਈ k = 1
ਸਮੀਕਰਨ (2) ਤੋਂ F = ma
ਬਲ = ਪੁੰਜ × ਵੇਗ
ਇਹ ਨਿਊਟਨ ਦਾ ਗਣਿਤਿਕ ਮਾਪ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਨਿਊਟਨ ਦੇ ਤੀਜੇ ਗਤੀ ਨਿਯਮ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਉ ਅਤੇ ਇਸ ਦੀ ਵਿਆਖਿਆ ਕਰੋ ।
ਉੱਤਰ-
ਨਿਊਟਨ ਦਾ ਤੀਜਾ ਗਤੀ ਨਿਯਮ (Newton’s Third Law of Motion) – ਇਸ ਨਿਯਮ ਅਨੁਸਾਰ, “ਹਰ ਕਿਰਿਆ (ਬਲ) ਲਈ, ਉਸਦੇ ਬਰਾਬਰ ਅਤੇ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਇੱਕ ਪ੍ਰਤੀਕਿਰਿਆ (ਬਲ) ਹੁੰਦੀ ਹੈ ।” ਇਸ ਨਿਯਮ ਅਨੁਸਾਰ, ਇੱਕ ਬਲ ਦੀ ਕਦੇ ਕੋਈ ਹੋਂਦ ਨਹੀਂ ਹੁੰਦੀ । ਬਲ ਹਮੇਸ਼ਾ ਜੋੜਿਆਂ ਵਿੱਚ ਹੁੰਦਾ ਹੈ ਅਰਥਾਤ ਕਿਰਿਆ ਅਤੇ ਪ੍ਰਤੀਕਿਰਿਆ ਦੇ ਬਲ ਹਮੇਸ਼ਾ ਦੋ ਵੱਖ-ਵੱਖ ਵਸਤੂਆਂ ‘ਤੇ ਕੰਮ ਕਰਦੇ ਹਨ ।

ਵਿਆਖਿਆ ਲਈ ਉਦਾਹਰਨ-
ਦੋ ਇੱਕ ਸਮਾਨ ਸਪਰਿੰਗ ਬੈਲੈਂਸ ਬਾਰੇ ਵਿਚਾਰ ਕਰੋ, ਜਿਹੜੇ ਇੱਕ-ਦੂਜੇ ਦੀ ਹੁੱਕ ਵਿੱਚ ਹਿੱਕ ਪਾਈ ਜੁੜੇ ਹੋਏ ਹਨ । ਸਪਰਿੰਗ ਬੈਲੇਂਸ A ਦਾ ਇੱਕ ਸਿਰਾ ਸਥਿਰ ਸਹਾਰੇ ਨਾਲ ਬੰਨ੍ਹਿਆ ਹੋਇਆ ਹੈ । ਬੈਲੇਂਸ B ਦੇ ਸੁਤੰਤਰ ਸਿਰੇ ਨੂੰ ਸੱਜੇ ਪਾਸੇ ਖਿੱਚੋ । ਤੁਸੀਂ ਦੇਖੋਗੇ ਕਿ ਦੋਵੇਂ ਬੈਸ ਸਮਾਨ ਪੜਤ ਦਰਸਾਉਂਦੇ ਹਨ । ਬੈਲੇਸ A ਬੈਲੈਂਸ B ਨੂੰ ਉਸੇ ਬਲ ਨਾਲ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਖਿੱਚਦਾ ਹੈ । ਅਜਿਹਾ ਚਿੱਤਰ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ ।

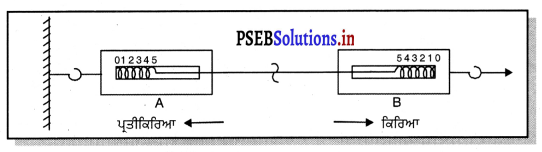
ਵਿਵਹਾਰਿਕ ਉਦਾਹਰਨਾਂ –
(i) ਜਦੋਂ ਲਾਨ-ਸਟ੍ਰਿਕਲਰ ਦੀਆਂ ਕਰ ਨੋਜ਼ਲਾਂ ਵਿੱਚੋਂ ਪਾਣੀ ਬਾਹਰ ਆਉਂਦਾ ਹੈ, ਤਾਂ ਇਹ ਪਿੰਕਲਰ ਦੇ ਪਿੱਛੇ ਵੱਲ ਬਰਾਬਰ ਬਲ ਲਗਾਉਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਸਰਿੰਕਲਰ ਘੁੰਮਣਾ ਸ਼ੁਰੂ ਕਰ ਦਿੰਦਾ ਹੈ ਅਤੇ ਪਾਣੀ ਦਾ ਸਾਰੀਆਂ ਦਿਸ਼ਾਵਾਂ ਵਿੱਚ ਛਿੜਕਾਓ ਹੋਣ ਲੱਗਦਾ ਹੈ ।
(ii) ਜਦੋਂ ਅਸੀਂ ਸੜਕ ਉੱਪਰ ਚੱਲਦੇ ਹਾਂ, ਤਾਂ ਸਾਡੇ ਪੈਰ ਸੜਕ । ਨੂੰ ਪਿੱਛੇ ਵੱਲ ਧੱਕਦੇ ਹਨ । ਪ੍ਰਤੀਕਿਰਿਆ ਵਜੋਂ ਸੜਕ ਸਾਡੇ ਪੈਰਾਂ ਨੂੰ ਅੱਗੇ ਵੱਲ ਧੱਕਦੀ ਹੈ । ਸੜਕ ਦੁਆਰਾ ਸਾਡੇ ਪੈਰਾਂ ‘ਤੇ ਹੋਈ ਪ੍ਰਤੀਕਿਰਿਆ ਦੇ ਸਿੱਟੇ ਵਜੋਂ ਹੀ ਅਸੀਂ ਚੱਲ ਸਕਦੇ ਹਾਂ ।

ਪ੍ਰਸ਼ਨ 7.
ਸੰਵੇਗ ਦੇ ਸੁਰੱਖਿਅਣ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? ਸੰਵੇਗ ਸੁਰੱਖਿਅਣ ਨਿਯਮ ਨੂੰ ਨਿਊਟਨ ਦੇ ਗਤੀ ਦੇ ਦੂਜੇ ਅਤੇ ਤੀਜੇ ਨਿਯਮ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਗਣਿਤਿਕ ਤੌਰ ‘ਤੇ ਸਿੱਧ ਕਰੋ ।
ਉੱਤਰ-
ਸੰਵੇਗ ਦਾ ਸੁਰੱਖਿਅਣ (Conservation of Momentum) – ਸੰਵੇਗ ਦਾ ਸੁਰੱਖਿਅਣ’ ਸ਼ਬਦ ਦਾ ਅਰਥ ਹੈ ਕਿ ਵਸਤੂਆਂ ਤੋਂ ਮਿਲ ਕੇ ਬਣੇ ਸਿਸਟਮ ਦਾ ਕੁੱਲ ਸੰਵੇਗ ਨਸ਼ਟ ਨਹੀਂ ਹੁੰਦਾ ਹੈ ।

ਨਿਊਟਨ ਦੇ ਦੂਜੇ ਨਿਯਮ ਅਨੁਸਾਰ,
F = k\(\frac{m(v-u)}{t}\)
F = k\(\frac{(m v-m u)}{t}\)
F = k\(\frac{\left(p_{2}-p_{1}\right)}{t}\)
ਜਿੱਥੇ ਮੁੱਢਲਾ ਸੰਵੇਗ p₁ = mu
ਅੰਤਿਮ ਸੰਵੇਗ p₂ = mυ ਹੈ ।
ਜੇਕਰ ਵਸਤੂ ਉੱਪਰ ਕੋਈ ਬਾਹਰੀ ਬਲ ਨਾ ਲੱਗ ਰਿਹਾ ਹੋਵੇ, ਤਾਂ F = 0 (ਸਿਫ਼ਰ)
∴ k\(\frac{\left(p_{2}-p_{1}\right)}{t}\) = 0
ਜਾਂ p₂ = p₁ …………….. (1)

ਸੰਗ ਸੁਰੱਖਿਅਣ ਨਿਯਮ ਦਾ ਕਥਨ – “ਜਦੋਂ ਦੋ ਜਾਂ ਦੋ ਤੋਂ ਵੱਧ ਵਸਤੂਆਂ ਕਿਸੇ ਬਾਹਰੀ ਬਲ ਦੀ ਸਹਾਇਤਾ ਤੋਂ ਬਗੈਰ ਆਪਸ ਵਿੱਚ ਟਕਰਾਉਂਦੀਆਂ ਹਨ, ਤਾਂ ਟੱਕਰ ਤੋਂ ਪਹਿਲਾਂ ਤੇ ਬਾਅਦ ਵਿੱਚ ਉਨ੍ਹਾਂ ਦਾ ਕੁੱਲ ਸੰਵੇਗ ਬਰਾਬਰ ਰਹੇਗਾ ।”

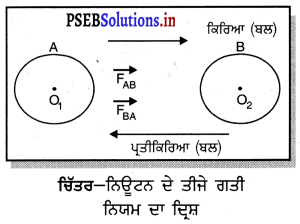
ਗਣਿਤਿਕ ਪ੍ਰਮਾਣ – ਮੰਨ ਲਓ ਪੁੰਜ m₁ ਅਤੇ m₂ ਦੀਆਂ ਦੋ ਰਬੜ-ਗੇਂਦਾਂ A ਅਤੇ B ਕੁਮਵਾਰ ਮੁੱਢਲੇ ਵੇਗ u₁ ਅਤੇ u₂, ਨਾਲ ਗਤੀ ਕਰ ਰਹੀਆਂ ਹਨ । ਉਨ੍ਹਾਂ ਦੇ ਆਪਸ ਵਿੱਚ ਟਕਰਾਉਣ ਤੋਂ ਬਾਅਦ t ਸਮੇਂ ਵਿੱਚ ਉਨ੍ਹਾਂ ਦਾ ਅੰਤਿਮ ਵੇਗ υ₁ ਅਤੇ υ₂ ਹੋ ਜਾਂਦਾ ਹੈ ।

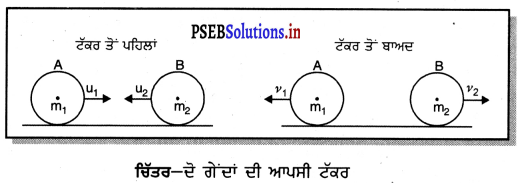
ਨਿਊਟਨ ਦੇ ਦੂਜੇ ਨਿਯਮ ਤੋਂ
ਗੇਂਦ A ਦੁਆਰਾ ਗੇਂਦ B ‘ਤੇ ਲਗਾਇਆ ਬਲ, F_AB = ਗੇਂਦ A ਦੇ ਸੰਵੇਗ ਵਿੱਚ ਤਬਦੀਲੀ ਦੀ ਦਰ
= \(\frac{m_{1} v_{1}-m_{1} u_{1}}{t}\)
F_AB = \(\frac{m_{1}\left(v_{1}-u_{1}\right)}{t}\) …………. (2)
ਨਿਊਟਨ ਦੇ ਤੀਜੇ ਗਤੀ ਨਿਯਮ ਤੋਂ
ਗੇਂਦ A ਦੁਆਰਾ ਗੇਂਦ B ਉੱਪਰ ਪ੍ਰਤੀਕਿਰਿਆ ਬਲ, F_BA = ਗੇਂਦ B ਦੇ ਸੰਵੇਗ ਵਿੱਚ ਤਬਦੀਲੀ ਦੀ ਦਰ
= \(\frac{m_{2} v_{2}-m_{2} u_{2}}{t}\)
F_BA = \(\frac{m_{2}\left(v_{2}-u_{2}\right)}{t}\) ……………. (3)
ਨਿਊਟਨ ਦੇ ਤੀਜੇ ਗਤੀ ਨਿਯਮ ਅਨੁਸਾਰ F_AB = – F_BA
ਸਮੀਕਰਨ (2) ਅਤੇ (3) ਤੋਂ
\(\frac{m_{1}\left(v_{1}-u_{1}\right)}{t}\) = –\(\frac{m_{2}\left(v_{2}-u_{2}\right)}{t}\)
ਜਾਂ m₁ υ₁ – m₁u₁ = -m₂υ₂ + m₂u₂
ਜਾਂ (m₁u₁ – m₂u₂ = (m₁υ₁ + m₂υ₂) ………… (4)

ਅਰਥਾਤ ਟੱਕਰ ਤੋਂ ਪਹਿਲਾਂ ਗੇਂਦਾਂ A ਅਤੇ B ਦਾ ਕੁੱਲ ਸੰਵੇਗ = ਟੱਕਰ ਤੋਂ ਬਾਅਦ ਗੇਂਦ A ਅਤੇ B ਗੇਂਦ ਦਾ ਕੁੱਲ ਸੰਵੇਗ ਇਸ ਤੋਂ ਇਹ ਸਿੱਧ ਹੁੰਦਾ ਹੈ ਕਿ ਦੋਵਾਂ ਗੇਂਦਾਂ ਦਾ ਕੁੱਲ ਸੰਵੇਗ ਸੁਰੱਖਿਅਤ ਰਹਿੰਦਾ ਹੈ ।

ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Short Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਬਲ ਕਿਸ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ? ਬਲ ਦੀਆਂ ਇਕਾਈਆਂ ਦਿਉ ।
ਉੱਤਰ-
ਬਲ (Force) – ‘‘ਬਲ ਉਹ ਬਾਹਰੀ ਕਾਰਕ ਹੈ, ਜੋ ਜਦੋਂ ਕਿਸੇ ਵਸਤੂ ’ਤੇ ਕਿਰਿਆ ਕਰਦਾ ਹੈ, ਤਾਂ ਇਹ ਉਸ ਵਸਤੂ ਦੀ (ਉ) ਵਿਰਾਮ-ਅਵਸਥਾ ਨੂੰ ਗਤੀ ਵਿੱਚ (ਅ) ਗਤੀ ਨੂੰ ਵਿਰਾਮ-ਅਵਸਥਾ ਵਿੱਚ (ੲ) ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਬਦਲ ਸਕਦਾ ਜਾਂ ਨਹੀਂ ਬਦਲ ਸਕਦਾ ਹੈ ।”

ਬਲ ਵਿੱਚ ਪਰਿਮਾਣ ਤੇ ਦਿਸ਼ਾ ਦੋਵੇਂ ਹੋਣ ਕਾਰਨ, ਇੱਕ ਵੈਕਟਰ ਰਾਸ਼ੀ ਹੈ ।
ਬਲੇ ਦੀਆਂ ਇਕਾਈਆਂ (Units of Force) – ਬਲ ਦੀ ਇਕਾਈ ਪੁੰਜ ਅਤੇ ਪ੍ਰਵੇਗ ਦੀ ਇਕਾਈ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਬਲ ਦੀ C.G.S. ਇਕਾਈ ਡਾਈਨ (Dyne) ਅਤੇ S.I. ਇਕਾਈ ਨਿਊਟਨ (Newton) ਹੈ । 1N = 10⁵ dyne.

ਪ੍ਰਸ਼ਨ 2.
ਜਦੋਂ ਇੱਕ ਦੌੜਦਾ ਹੋਇਆ ਘੋੜਾ ਅਚਾਨਕ ਰੁਕ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਘੋੜਸਵਾਰ ਅੱਗੇ ਵੱਲ ਨੂੰ ਕਿਉਂ ਡਿੱਗ ਪੈਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਜਦੋਂ ਇੱਕ ਦੌੜਦਾ ਹੋਇਆ ਘੋੜਾ ਅਚਾਨਕ ਰੁਕ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਘੋੜ-ਸਵਾਰ ਅੱਗੇ ਵੱਲ ਡਿੱਗਦਾ ਹੈ । ਇਹ ਇਸ ਕਾਰਨ ਹੁੰਦਾ ਹੈ ਕਿ ਜਦੋਂ ਘੋੜਾ ਅਚਾਨਕ ਰੁਕਦਾ ਹੈ, ਤਾਂ ਘੋੜ-ਸਵਾਰ ਦੇ ਸਰੀਰ ਦਾ ਹੇਠਲਾ ਭਾਗ ਰੁਕ ਜਾਂਦਾ ਹੈ । ਪਰ ਸਰੀਰ ਦਾ ਉੱਪਰਲਾ ਭਾਗ ਪਹਿਲਾਂ ਵਾਂਗ ਗਤੀ ਵਿੱਚ ਰਹਿਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਜਦੋਂ ਘੋੜਾ ਅਚਾਨਕ ਦੌੜਨਾ ਸ਼ੁਰੂ ਕਰ ਦੇਵੇ, ਤਾਂ ਘੋੜਸਵਾਰ ਪਿੱਛੇ ਵੱਲ ਕਿਉਂ ਡਿੱਗਦਾ ਹੈ ?
ਉੱਤਰ-
ਘੋੜਾ ਅਤੇ ਘੋੜਸਵਾਰ ਇੱਕ ਪ੍ਰਣਾਲੀ (ਸਿਸਟਮ) ਹੈ । ਸ਼ੁਰੂ ਵਿੱਚ ਦੋਵੇਂ ਵਿਰਾਮ ਦੀ ਅਵਸਥਾ ਵਿੱਚ ਹੁੰਦੇ ਹਨ । ਜਦੋਂ ਅਚਾਨਕ ਘੋੜਾ ਦੌੜਨ ਲਗਦਾ ਹੈ, ਤਾਂ ਘੋੜੇ ਦੇ ਨਾਲ ਹੀ ਘੋੜਸਵਾਰ ਦੇ ਸਰੀਰ ਦਾ ਹੇਠਲਾ ਭਾਗ ਵੀ ਅੱਗੇ ਵੱਲ ਗਤੀਸ਼ੀਲ ਹੋ ਜਾਂਦਾ ਹੈ, ਪਰ ਸਰੀਰ ਦਾ ਉੱਪਰਲਾ ਭਾਗ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਰਹਿਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦਾ ਹੈ । ਕਿਸੇ ਕਾਰਨ ਘੋੜੇ ਦੇ ਅਚਾਨਕ ਦੌੜਨ ਤੇ ਘੋੜਸਵਾਰ ਪਿੱਛੇ ਵੱਲ ਡਿੱਗਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਚਲਦੀ ਬੱਸ ਵਿੱਚੋਂ ਛਾਲ ਮਾਰਦੇ ਸਮੇਂ ਸਵਾਰੀ ਅੱਗੇ ਵੱਲ ਡਿੱਗ ਪੈਂਦੀ ਹੈ, ਕਿਉਂ ?
ਉੱਤਰ-
ਚਲਦੀ ਹੋਈ ਬੱਸ ਵਿੱਚੋਂ ਛਾਲ ਮਾਰਦੇ ਸਮੇਂ ਸਵਾਰੀ ਅੱਗੇ ਵੱਲ ਡਿੱਗ ਪੈਂਦੀ ਹੈ । ਜਦੋਂ ਸਵਾਰੀ ਥੱਲੇ ਪੈਰ ਰੱਖਦੀ ਹੈ, ਤਾਂ ਧਰਤੀ ਨੂੰ ਛੂਹਣ ਨਾਲ ਸਵਾਰੀ ਦੇ ਸਰੀਰ ਦਾ ਹੇਠਲਾ ਹਿੱਸਾ (ਪੈਰ) ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਆ ਜਾਂਦਾ ਹੈ ਪਰ ਉੱਪਰਲਾ ਹਿੱਸਾ ਗਤੀ ਵਿੱਚ ਹੀ ਰਹਿੰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਸਵਾਰੀ ਅੱਗੇ ਵੱਲ ਡਿੱਗ ਪੈਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਸੰਵੇਗ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਉ । ਇਸ ਦੀ ਇਕਾਈ ਵੀ ਲਿਖੋ ।
ਉੱਤਰ-
ਸੰਵੇਗ (Momentum) – ਕਿਸੇ ਵਸਤੂ ਦੇ ਪੁੰਜ ਅਤੇ ਵੇਗ, ਜਿਸ ਨਾਲ ਉਹ ਗਤੀ ਕਰ ਰਹੀ ਹੈ, ਦੇ ਗੁਣਨਫਲ ਨੂੰ ਸੰਵੇਗ ਕਹਿੰਦੇ ਹਨ ।
ਜੇਕਰ ਕਿਸੇ ਵਸਤੂ ਦਾ ਪੁੰਜ m ਅਤੇ ਵੇਗ υ ਹੋਵੇ, ਤਾਂ ਉਸ ਵਸਤੁ ਦਾ ਸੰਵੇਗ = m × υ
ਸੰਵੇਗ ਨੂੰ ਅੱਖਰ p ਨਾਲ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ ।
∴ \(\vec{p}=\overrightarrow{m v}\)
ਸੰਵੇਗ ਹਮੇਸ਼ਾਂ ਗਤੀਸ਼ੀਲ ਵਸਤੁ ਦਾ ਹੀ ਹੁੰਦਾ ਹੈ ।
ਸੰਵੇਗ ਦੀਆਂ ਇਕਾਈਆਂ – CGS ਪ੍ਰਣਾਲੀ ਵਿੱਚ gm cms^-1 ਅਤੇ SI ਪ੍ਰਣਾਲੀ ਵਿੱਚ kg ms^-1 ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਜੇਕਰ ਗਤੀਸ਼ੀਲ ਸਾਈਕਲ ਦੀ ਅੱਗੇ ਵਾਲੀ ਬੇਕ ਲਗਾਈਏ, ਤਾਂ ਅਸੀਂ ਅੱਗੇ ਵੱਲ ਡਿੱਗ ਪੈਂਦੇ ਹਾਂ, ਕਿਉਂ ?
ਉੱਤਰ-
ਜੇਕਰ ਗਤੀ ਕਰ ਰਹੇ ਸਾਈਕਲ ਦੇ ਅਗਲੇ ਪਹੀਏ ਵਾਲੀ ਬ੍ਰੇਕ ਲਗਾਈਏ, ਤਾਂ ਅੱਗੇ ਵੱਲ ਨੂੰ ਝਟਕਾ ਲਗਦਾ ਹੈ । ਅੱਗੇ ਵਾਲੀ ਬੇਕ ਲਗਾਉਣ ਨਾਲ ਸਾਈਕਲ ਇੱਕਦਮ ਰੁਕ ਜਾਂਦਾ ਹੈ, ਇਸ ਤਰ੍ਹਾਂ ਤੁਹਾਡੇ ਸਰੀਰ ਦਾ ਹੇਠਲਾ ਹਿੱਸਾ ਵੀ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਆ ਜਾਂਦਾ ਹੈ, ਪਰ ਤੁਹਾਡਾ ਉੱਪਰਲਾ ਸਰੀਰ ਗਤੀ-ਜੜ੍ਹਤਾ ਕਾਰਨ ਪਹਿਲਾਂ ਵਾਲੀ (ਗਤੀ ਵਾਲੀ ਅਵਸਥਾ ਵਿੱਚ ਰਹਿਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦਾ ਹੈ ਅਤੇ ਤੁਸੀਂ ਅੱਗੇ ਵੱਲ ਡਿੱਗ ਪੈਂਦੇ ਹੋ । ਇਸ ਲਈ ਇਹ ਸਲਾਹ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ਕਿ ਗਤੀਸ਼ੀਲ ਸਾਈਕਲ ਦੇ ਅਗਲੇ ਪਹੀਏ ਵਾਲੀ ਬੇਕ ਨਹੀਂ ਲਗਾਉਣੀ ਚਾਹੀਦੀ ।

ਪ੍ਰਸ਼ਨ 7.
ਬਲ ਦਾ ਕਿਸੇ ਵਸਤੂ ‘ ਤੇ ਕੀ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਬਲ ਦੇ ਪ੍ਰਭਾਵ-

1. ਇਹ ਵਸਤੂ ਦੀ ਗਤੀ ਨੂੰ ਘੱਟ ਜਾਂ ਵੱਧ ਕਰਕੇ ਇਸਦੀ ਚਾਲ ਵਿੱਚ ਪਰਿਵਰਤਨ ਲਿਆਉਂਦਾ ਹੈ ।
2. ਇਹ ਵਸਤੁ ਦੀ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਨੂੰ ਬਦਲ ਦਿੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਇੱਕ ਕਾਰ ਅਤੇ ਇੱਕ ਟਰੱਕ ਦੋਵੇਂ ਬਰਾਬਰ ਵੇਗ ਨਾਲ ਚਲ ਰਹੇ ਹਨ । ਇਨ੍ਹਾਂ ਵਿੱਚੋਂ ਕਿਸ ਦਾ ਸੰਵੇਗ ਵੱਧ ਹੋਵੇਗਾ ਅਤੇ ਰੋਕਣ ਲਈ ਕਿਸ ਵਿੱਚ ਵਧੇਰੇ ਬਲ ਦੀ ਲੋੜ ਹੋਵੇਗੀ ?
ਉੱਤਰ-

1. ਕਾਰ ਅਤੇ ਟਰੱਕ ਦੋਵੇਂ ਸਮਾਨ ਵੇਗ ਨਾਲ ਚਲ ਰਹੇ ਹਨ । ਇਨ੍ਹਾਂ ਦੋਹਾਂ ਵਿੱਚੋਂ ਕਾਰ ਦਾ ਪੁੰਜ ਘੱਟ ਹੁੰਦਾ ਹੈ । ਇਸ ਲਈ ਕਾਰ ਦਾ ਸੰਵੇਗ ਘੱਟ ਹੋਵੇਗਾ ਜਦੋਂ ਕਿ ਟਰੱਕ ਦਾ ਸੰਵੇਗ ਵੱਧ ਹੋਵੇਗਾ ।
2. ਜੇ ਦੋਹਾਂ ਨੂੰ ਰੋਕਿਆ ਜਾਵੇ, ਤਾਂ ਦੋਹਾਂ ਦਾ ਅੰਤਿਮ ਸੰਵੇਗ ਤਾਂ ਸਿਫ਼ਰ ਹੋ ਜਾਵੇਗਾ ਪਰੰਤ ਟਰੱਕ ਦਾ ਸੰਵੇਗ ਵੱਧ ਹੋਣ ਦੇ ਕਾਰਨ ਟਰੱਕ ਦੇ ਸੰਵੇਗ ਵਿੱਚ ਪਰਿਵਰਤਨ ਕਾਰ ਦੇ ਮੁਕਾਬਲੇ ਹੋਵੇਗਾ । ਇਸ ਲਈ ਟਰੱਕ ਨੂੰ ਰੋਕਣ ਲਈ ਕਾਰ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਵੱਧ ਬਲ ਲਗਾਉਣਾ ਪਵੇਗਾ ।

ਪ੍ਰਸ਼ਨ 9.
ਤੇਜ਼ ਗਤੀ ਨਾਲ ਆ ਰਹੀ ਗੋਲੀ ਖਿੜਕੀ ਦੇ ਸ਼ੀਸ਼ੇ ਵਿੱਚ ਗੋਲ ਛੇਕ ਬਣਾ ਦਿੰਦੀ ਹੈ, ਜਦਕਿ ਪੱਥਰ ਮਾਰਨ ਨਾਲ ਸ਼ੀਸ਼ਾ ਤਿੜਕ ਜਾਂਦਾ ਹੈ, ਕਿਉਂ ?
ਉੱਤਰ-
ਜਦੋਂ ਖਿੜਕੀ ਵਿੱਚ ਲੱਗੇ ਸ਼ੀਸ਼ੇ ਉੱਤੇ ਪੱਥਰ ਮਾਰਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਉਹ ਟੁੱਕੜੇ-ਟੁੱਕੜੇ ਹੋ ਜਾਂਦਾ ਹੈ, ਜਦਕਿ ਤੇਜ਼ ਆਉਂਦੀ ਗੋਲੀ ਲੱਗਣ ਨਾਲ ਇਸ ਵਿੱਚ ਛੇਕ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਛੇਕ ਦੇ ਨੇੜੇ ਵਾਲੇ ਸ਼ੀਸ਼ੇ ਦੇ ਕਣ ਤੇਜ਼ ਆਉਂਦੀ ਗੋਲੀ ਦੀ ਗਤੀ ਨੂੰ ਵਿਰਾਮ ਜੜ੍ਹਤਾ ਕਾਰਨ ਪ੍ਰਾਪਤ ਨਹੀਂ ਕਰਦੇ ਅਤੇ ਇਸ ਲਈ ਨਹੀਂ ਖਿਲਰਦੇ ।

ਪ੍ਰਸ਼ਨ 10.
ਵਿਆਖਿਆ ਕਰੋ ਕਿ ਜਦੋਂ ਪੱਥਰ ਖਿੜਕੀ ਦੇ ਸ਼ੀਸ਼ੇ ਨਾਲ ਟਕਰਾਉਂਦਾ ਹੈ, ਤਾਂ ਉਹ ਟੁੱਕੜੇ-ਟੁੱਕੜੇ ਹੋ ਕੇ ਕਿਉਂ ਖਿੰਡ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਜਦੋਂ ਕੋਈ ਪੱਥਰ ਦਾ ਟੁੱਕੜਾ ਖਿੜਕੀ ਦੇ ਸ਼ੀਸ਼ੇ ਨਾਲ ਟਕਰਾਉਂਦਾ ਹੈ, ਤਾਂ ਉਹ ਹਿੱਸਾ ਜਿੱਥੇ ਪੱਥਰ ਟਕਰਾਇਆ ਵੱਧ ਗਤੀ ਵਿੱਚ ਆ ਜਾਂਦਾ ਹੈ ਪਰ ਸ਼ੀਸ਼ੇ ਦਾ ਬਾਕੀ ਹਿੱਸਾ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਹੀ ਰਹਿੰਦਾ ਹੈ । ਪੱਥਰ ਦੇ ਟੁੱਕੜੇ ਦਾ ਵੇ ਘੱਟ ਹੋਣ ਕਾਰਨ, ਪੱਥਰ ਦੇ ਆਰ-ਪਾਰ ਜਾਣ ਤੋਂ ਪਹਿਲਾਂ ਹੀ ਸ਼ੀਸ਼ੇ ਦਾ ਬਾਕੀ ਹਿੱਸਾ ਵੇਗ ਲੈ ਲੈਂਦਾ ਹੈ ਤੇ ਟੁੱਟ ਕੇ ਖਿੰਡ-ਪੁੰਡਰ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
ਇੱਕ ਟਰੱਕ ਅਤੇ ਕਾਰ ਵੇਗ ‘ ਨਾਲ ਚੱਲਦੇ ਹੋਏ ਇੱਕ-ਦੂਜੇ ਨਾਲ ਆਹਮੋ-ਸਾਹਮਣੇ ਟਕਰਾਉਂਦੇ ਹਨ ਅਤੇ ਰੁਕ ਜਾਂਦੇ ਹਨ । ਜੇਕਰ ਟੱਕਰ 10 ਸੈਕਿੰਡ ਲਈ ਹੋਈ ਹੋਵੇ, ਤਾਂ ?
(i) ਕਿਸ ਗੱਡੀ ‘ ਤੇ ਵੱਧ ਬਲ ਲੱਗਿਆ ?
(ii) ਕਿਸ ਗੱਡੀ ਦੇ ਸੰਵੇਗ ਵਿੱਚ ਵੱਧ ਤਬਦੀਲੀ ਆਈ ?
(iii) ਕਿਹੜੀ ਗੱਡੀ ਵੱਧ ਗਿਤ ਹੋਈ ?
(iv) ਟਰੱਕ ਨਾਲੋਂ ਕਾਰ ਦਾ ਵੱਧ ਨੁਕਸਾਨ ਕਿਉਂ ਹੋਇਆ ਹੋਵੇਗਾ ?
ਉੱਤਰ-
(i) ਕਾਰ ‘ਤੇ ਬਲ ਦਾ ਪ੍ਰਭਾਵ ਵੱਧ ਹੋਵੇਗਾ ਕਿਉਂਕਿ ਉਸਦਾ ਪੁੰਜ ਘੱਟ ਹੈ ।
(ii) ਟਰੱਕ ਦੇ ਸੰਵੇਗ ਵਿੱਚ ਵੱਧ ਪਰਿਵਰਤਨ ਹੋਵੇਗਾ ।
(iii) ਕਾਰ ਵਿੱਚ ਵੱਧ ਵੇਗ ਹੋਵੇਗਾ ।
(iv) ਟਰੱਕ ਨਾਲੋਂ ਕਾਰ ਦਾ ਵੱਧ ਨੁਕਸਾਨ ਹੋਵੇਗਾ ਕਿਉਂਕਿ ਕਾਰ ‘ਤੇ ਵਧੇ ਬਲ ਲੱਗੇਗਾ |

ਪ੍ਰਸ਼ਨ 12.
ਸੰਵੇਗ ਸੁਰੱਖਿਅਣ ਦਾ ਨਿਯਮ ਲਿਖੋ ।
ਉੱਤਰ-
ਸੰਵੇਗ ਸੁਰੱਖਿਅਣ ਦਾ ਨਿਯਮ-ਜਦੋਂ ਦੋ ਜਾਂ ਦੋ ਤੋਂ ਵੱਧ ਵਸਤੂਆਂ ਇੱਕ-ਦੂਜੇ ‘ਤੇ ਕਿਰਿਆ ਕਰਦੀਆਂ ਹਨ, ਤਾਂ ਉਨ੍ਹਾਂ ਦਾ ਕੁੱਲ ਸੰਵੇਗ ਹਮੇਸ਼ਾ ਬਰਾਬਰ ਰਹਿੰਦਾ ਹੈ ਜਦੋਂ ਤੱਕ ਕੋਈ ਬਾਹਰੀ ਬਲ ਕਿਰਿਆ ਇਸ ‘ਤੇ ਨਹੀਂ ਕਰਦਾ । ਭਾਵ ਜੇ ਬਾਹਰੀ ਬਲ ਜ਼ੀਰੋ ਹੋਵੇ, ਤਾਂ ਸਿਸਟਮ ਦਾ ਕੁੱਲ ਸੰਵੇਗ ਸਥਿਰ ਰਹਿੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 13.
ਜੇ ਕਿਰਿਆ ਅਤੇ ਪ੍ਰਤੀਕਿਰਿਆ ਬਰਾਬਰ ਹੁੰਦੀਆਂ ਹਨ, ਤਾਂ ਇੱਕ ਘੋੜੇ ਦੁਆਰਾ ਖਿੱਚਿਆ ਰੇਹੜਾ ਅੱਗੇ ਵੱਲ ਕਿਉਂ ਚਲ ਪੈਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਨਿਊਟਨ ਦੇ ਤੀਸਰੇ ਗਤੀ ਨਿਯਮ ਅਨੁਸਾਰ ਕਿਰਿਆ ਅਤੇ ਪ੍ਰਤੀਕਿਰਿਆ ਇੱਕ ਸਮਾਨ ਤਾਂ ਹੁੰਦੀਆਂ ਹਨ ਪਰ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਅਤੇ ਵੱਖ-ਵੱਖ ਵਸਤੂਆਂ ‘ਤੇ ਲਗਦੀਆਂ ਹਨ । ਜਦੋਂ ਰੇਹੜੇ ਨੂੰ ਘੋੜਾ ਖਿੱਚਦਾ ਹੈ ਤਾਂ ਉਹ ਪੈਰਾਂ ਨਾਲ ਧਰਤੀ ਨੂੰ ਪਿੱਛੇ ਵੱਲ ਨੂੰ ਧੱਕਦਾ ਹੈ ਜਿਸ ਨੂੰ ਕਿਰਿਆ ਕਹਿੰਦੇ ਹਾਂ ਅਤੇ ਧਰਤੀ ਪ੍ਰਤੀਕਿਰਿਆ ਵਜੋਂ ਉੱਪਰ ਵੱਲ ਨੂੰ ਬਲ ਲਗਾਉਂਦੀ ਹੈ । ਇਹ ਪ੍ਰਤੀਕਿਰਿਆ ਬਲ ਦੋ ਹਿੱਸਿਆਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ, ਇੱਕ ਹਿੱਸਾ ਧਰਤੀ ਦੇ ਲੰਬ- ਵੱਤ ਹੋ ਕੇ ਘੋੜੇ ਦੇ ਭਾਰ ਨੂੰ ਸੰਤੁਲਿਤ ਕਰਦਾ ਹੈ ਤੇ ਦੂਸਰਾ ਹਿੱਸਾ ਧਰਤੀ ਦੇ ਸਮਾਨਾਂਤਰ ਹੋ ਕੇ ਰੇਹੜੇ ਨੂੰ ਅੱਗੇ ਵੱਲ ਨੂੰ ਧੱਕਦਾ ਹੈ । ਰੇਹੜੇ ਦੇ ਪਹੀਏ ਅਤੇ ਸੜਕ ਵਿਚਕਾਰ ਰਗੜ ਬਲ ਗਤੀ ਦੇ ਉਲਟ ਕਾਰਜ ਕਰਦਾ ਹੈ । ਜਦੋਂ ਘੋੜੇ ਵੱਲੋਂ ਲਗਾਇਆ ਬਲ ਰਗੜ ਬਲ ਤੋਂ ਵੱਧ ਜਾਂਦਾ ਹੈ ਤਾਂ ਰੇਹੜਾ ਚੱਲਣ ਲੱਗ ਪੈਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 14.
ਸੜਕ ਉੱਤੇ ਚੱਲਣ ਵਾਲੇ ਵਾਹਨਾਂ ਦੇ ਟਾਇਰਾਂ ਨੂੰ ਖੁਰਦਰਾ ਅਤੇ ਲਹਿਰਦਾਰ ਕਿਉਂ ਬਣਾਇਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਸੜਕਾਂ ਉੱਤੇ ਵਾਹਨਾਂ ਦਾ ਚੱਲਣਾ ਵਾਹਨਾਂ ਦੇ ਟਾਇਰਾਂ ਅਤੇ ਸੜਕ ਦੇ ਵਿਚਕਾਰ ਰਗੜ ਦੇ ਕਾਰਨ ਹੀ ਹੁੰਦਾ ਹੈ । ਜੇ ਟਾਇਰ ਚੀਕਨੇ ਹੋਣਗੇ, ਤਾਂ ਸੜਕ ਅਤੇ ਟਾਇਰਾਂ ਦੇ ਵਿਚਕਾਰ ਰਗੜ ਬਲ ਘੱਟ ਹੋਵੇਗਾ ਜਿਸ ਨਾਲ ਵਾਹਨਾਂ ਦੀ ਗਤੀ ਉੱਤੇ ਕਾਬੂ ਪਾਉਣਾ ਔਖਾ ਹੁੰਦਾ ਹੈ ਅਤੇ ਦੁਰਘਟਨਾ ਵਾਪਰ ਸਕਦੀ ਹੈ । ਇਨ੍ਹਾਂ ਦੁਰਘਟਨਾਵਾਂ ਤੋਂ ਬਚਣ ਲਈ ਵਾਹਨਾਂ ਦੇ ਟਾਇਰਾਂ ਨੂੰ ਖੁਰਦਰਾ ਅਤੇ ਲਹਿਰਦਾਰ ਬਣਾਇਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਜੋ ਸੜਕ ਅਤੇ ਟਾਇਰਾਂ ਵਿਚਕਾਰ ਰਗੜ ਵੱਧ ਜਾਏ ਜਿਸ ਨਾਲ ਟਾਇਰਾਂ ਦੀ ਸੜਕ ਨਾਲ ਪਕੜ ਚੰਗੀ ਹੋਵੇ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਤਿਲਕਣ ਤੋਂ ਰੋਕਿਆ ਜਾ ਸਕੇ ।

ਪ੍ਰਸ਼ਨ 15.
ਕੇਲੇ ਦੇ ਛਿੱਲੜ੍ਹ ਤੋਂ ਅਚਾਨਕ ਤਿਲਕ ਜਾਣ ਕਾਰਨ ਸਾਨੂੰ ਆਪਣੇ ਸਰੀਰ ਨੂੰ ਸੰਭਾਲਣਾ ਮੁਸ਼ਕਿਲ ਕਿਉਂ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਜਦੋਂ ਸਾਡਾ ਪੈਰ ਅਚਾਨਕ ਕੇਲੇ ਦੇ ਛਿੱਲੜ੍ਹ ’ਤੇ ਪੈ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਉਸਦੇ ਚੀਕਨੇਪਣ ਕਾਰਨ ਰਗੜ ਬਲ ਘੱਟ ਜਾਂਦਾ ਹੈ ਜਿਸ ਕਰਕੇ ਸਾਨੂੰ ਆਪਣੇ ਸਰੀਰ ਨੂੰ ਸੰਭਾਲਣਾ ਮੁਸ਼ਕਿਲ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 16.
ਵਿਆਖਿਆ ਕਰੋ ਕਿ ਇੱਕ ਧੂੜ ਭਰਿਆ ਕੰਬਲ ਇੱਕ ਜਾਂ ਦੋ ਵਾਰੀ ਜ਼ੋਰ ਨਾਲ ਛੱਡਣ ‘ਤੇ ਧੂੜ ਰਹਿਤ ਕਿਵੇਂ ਹੋ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਜਦੋਂ ਕੰਬਲ ਨੂੰ ਜ਼ੋਰ ਨਾਲ ਛੱਡਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਇਸ ਵਿਚਲੇ ਧੂੜ ਕਣ ਥੱਲੇ ਡਿੱਗ ਪੈਂਦੇ ਹਨ, ਕਿਉਂਕਿ ਛੰਡਣ ਸਮੇਂ ਧੂੜ ਦੇ ਕਣ ਵਿਰਾਮ ਦੀ ਜੜ੍ਹਤਾ ਕਾਰਨ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਹੀ ਰਹਿਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦੇ ਹਨ ਜਦੋਂ ਕਿ ਕੰਬਲ ਗਤੀ ਵਿੱਚ ਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਦੇ ਸਿੱਟੇ ਵਜੋਂ ਕੰਬਲ ਧੂੜ ਰਹਿਤ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 17.
ਕੀ ਕਿਸੇ ਵਸਤੂ ਨੂੰ ਇੱਕ ਸਮਾਨ ਵੇਗ ਨਾਲ ਚਲਦੇ ਰਹਿਣ ਲਈ ਬਲ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਵੇਗ ਦੀ ਦਰ ਨੂੰ ਪਵੇਗ ਕਹਿੰਦੇ ਹਨ | ਜਦੋਂ ਕੋਈ ਵਸਤੁ ਇੱਕ ਸਮਾਨ ਵੇਗ ਨਾਲ ਚਲਦੀ ਹੈ, ਤਾਂ ਉਸ ਵਿੱਚ ਪ੍ਰਵੇਗ ਉਤਪੰਨ ਨਹੀਂ ਹੁੰਦਾ ਹੈ । ਵਸਤੂ ਦਾ ਵੇਗ, ਬਲ ਦੇ ਸਮਾਨੁਪਾਤੀ ਹੈ ਅਰਥਾਤ ਵਸਤੂ ਵਿੱਚ ਉਤਪੰਨ ਹੋਇਆ ਵੇਗ ਉਸ ਉੱਪਰ ਲਗ ਰਹੇ ਬਲ ‘ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ । ਇਸ ਲਈ ਕਿਸੇ ਵਸਤੂ ਨੂੰ ਇੱਕ ਸਮਾਨ ਵੇਗ ਨਾਲ ਚਲਦਾ ਰਹਿਣ ਲਈ ਬਲ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 18.
ਕਿਸੇ ਵਸਤੂ ਦੀ ਜੜ੍ਹਤਾ ਅਤੇ ਉਸ ਦੇ ਪੁੰਜ ਵਿੱਚ ਕੀ ਸੰਬੰਧ ਹੈ ?
ਉੱਤਰ-
ਕਿਸੇ ਵਸਤੂ ਵਿੱਚ ਉਪਸਥਿਤ ਪਦਾਰਥ ਦੀ ਮਾਤਰਾ ਉਸਦਾ ਪੁੰਜ ਅਖਵਾਉਂਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਪੰਜ ਵਸਤੂ ਦੀ ਜੜ੍ਹਤਾ ਦਾ ਮਾਪ ਹੈ, ਅਰਥਾਤ ਵਸਤੂ ਦੀ ਜੜ੍ਹਤਾ ਉਸਦੇ ਪੁੰਜ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਵਸਤੂ ਦਾ ਪੁੰਜ ਜਿੰਨਾ ਜ਼ਿਆਦਾ ਹੋਵੇਗਾ, ਉਸ ਦੀ ਜੜ੍ਹਤਾ ਵੀ ਉੱਨੀ ਵੱਧ ਹੋਵੇਗੀ ਅਤੇ ਘੱਟ ਪੰਜ ਵਾਲੀ ਵਸਤੂ ਦੀ ਜੜ੍ਹਤਾ ਘੱਟ ਹੁੰਦੀ ਹੈ ।

ਉਦਾਹਰਨ – ਜੇ ਅਸੀਂ ਕਿਸੇ ਫੁਟਬਾਲ ਨੂੰ ਕਿੱਕ ਮਾਰਦੇ ਹਾਂ, ਤਾਂ ਉਹ ਬਹੁਤ ਦੂਰ ਚਲੀ ਜਾਂਦੀ ਹੈ, ਪਰ ਜੇ ਅਸੀਂ ਉਸੇ ਆਕਾਰ ਦੇ ਇੱਕ ਪੱਥਰ ਦੇ ਟੁੱਕੜੇ ਨੂੰ ਕਿੱਕ ਮਾਰਦੇ ਹਾਂ, ਤਾਂ ਉਹ ਆਪਣੀ ਥਾਂ ਤੋਂ ਨਹੀਂ ਹਿਲਦਾ ਅਤੇ ਪੈਰ ਨੂੰ ਸੱਟ ਵੀ ਲੱਗਦੀ ਹੈ । ਇਸ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਪੱਥਰ ਵਿੱਚ ਗਤੀ ਦੇ ਪਰਿਵਰਤਨ ਨੂੰ ਰੋਕਣ ਦੀ ਵੱਧ ਸਮਰੱਥਾ ਹੁੰਦੀ ਹੈ ਅਰਥਾਤ ਪੱਥਰ ਦੀ ਜੜ੍ਹਤਾ ਵੱਧ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 19.
ਪੱਖੇ ਦਾ ਸਵਿੱਚ ਬੰਦ ਕਰਨ ਤੋਂ ਬਾਅਦ ਵੀ ਕੁਝ ਸਮੇਂ ਤੱਕ ਪੱਖਾ ਕਿਉਂ ਘੁੰਮਦਾ ਰਹਿੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਪੱਖਾ ਗਤੀ ਵਿੱਚ ਹੁੰਦਾ ਹੈ । ਗਤੀ ਜੜ੍ਹਤਾ ਕਾਰਨ ਸਵਿੱਚ ਆਫ਼ ਕਰਨ ਤੋਂ ਬਾਅਦ ਵੀ ਪੱਖਾ ਗਤੀ ਵਿੱਚ ਰਹਿਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦਾ ਹੈ, ਪਰ ਹਵਾ ਦੇ ਰਗੜ ਬਲ ਦੇ ਵਿਰੋਧ ਕਾਰਨ ਇਹ ਕੁੱਝ ਸਮੇਂ ਤੱਕ ਹੀ ਘੁੰਮਦਾ ਰਹਿੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 20.
ਇੱਕ ਕ੍ਰਿਕੇਟ ਗੇਂਦ ਨਾਲੋਂ ਰਬੜ ਦੀ ਗੇਂਦ ਨੂੰ ਪਕੜਨਾ ਸੌਖਾ ਹੁੰਦਾ ਹੈ, ਭਾਵੇਂ ਦੋਨੋਂ ਇੱਕੋ ਵੇਗ ਨਾਲ ਚੱਲ ਰਹੀਆਂ ਹੋਣ । ਕਿਉਂ ?
ਉੱਤਰ-
ਭਾਵੇਂ ਕ੍ਰਿਕੇਟ ਗੇਂਦ ਅਤੇ ਰਬੜ ਦੀ ਗੇਂਦ ਦਾ ਵੇਗ ਇੱਕੋ ਜਿੰਨਾ ਹੈ, ਪਰ ਉਨ੍ਹਾਂ ਦੇ ਪੁੰਜ ਵੱਖ-ਵੱਖ ਹਨ । ਕ੍ਰਿਕਟ ਗੇਂਦ ਦਾ ਪੁੰਜ ਰਬੜ ਦੀ ਗੇਂਦ ਨਾਲੋਂ ਵੱਧ ਹੋਣ ਕਰਕੇ ਕ੍ਰਿਕੇਟ ਦੀ ਗੇਂਦ ਦਾ ਸੰਵੇਗ ਅਧਿਕ ਹੈ ਜਿਸ ਕਰਕੇ ਇਹ ਹੱਥ ਉੱਪਰ ਸੱਟ ਮਾਰਦਾ ਹੈ । ਇਸ ਲਈ ਕ੍ਰਿਕੇਟ ਗੇਂਦ ਨਾਲੋਂ ਰਬੜ ਦੀ ਗੇਂਦ ਨੂੰ ਪਕੜਨਾ ਸੌਖਾ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 21.
ਵੱਧ ਪੁੰਜ ਵਾਲੀਆਂ ਵਸਤੂਆਂ ਨੂੰ ਗਤੀਸ਼ੀਲ ਕਰਨ ਲਈ ਜ਼ਿਆਦਾ ਆਰੰਭਿਕ ਬਲ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ । ਕਿਉਂ ?
ਉੱਤਰ-
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਕਿਸੇ ਵਸਤੂ ਦੀ ਜੜ੍ਹਤਾ ਉਸਦੇ ਪੁੰਜ ’ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ | ਇਸ ਲਈ ਵੱਧ ਪੁੰਜ ਵਾਲੀ ਵਸਤੁ ਦੀ ਵਿਰਾਮ ਜਤਾ ਵੱਧ ਹੋਵੇਗੀ ਅਤੇ ਉਸ ਨੂੰ ਗਤੀਸ਼ੀਲ ਕਰਨ ਲਈ ਅਧਿਕ ਆਰੰਭਿਕ ਬਲ ਦੀ ਲੋੜ ਪਵੇਗੀ ।

ਪ੍ਰਸ਼ਨ 22.
ਜਦੋਂ ਬੰਦੁਕ ਵਿੱਚੋਂ ਗੋਲੀ ਦਾਗੀ ਜਾਂਦੀ ਹੈ, ਤਾਂ ਬੰਦੁਕ ਪਿੱਛੇ ਵੱਲ ਨੂੰ ਧੱਕਾ ਮਾਰਦੀ ਹੈ । ਵਿਆਖਿਆ ਕਰੋ, ਕਿਉਂ ?
ਉੱਤਰ-
ਜਦੋਂ ਅਜੇ ਬੰਦੂਕ ਵਿੱਚੋਂ ਗੋਲੀ ਨਹੀਂ ਦਾਗੀ ਗਈ, ਤਾਂ ਬੰਦੁਕ ਅਤੇ ਗੋਲੀ ਦੋਨੋਂ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਹੁੰਦੇ ਹਨ ਜਿਸ ਕਰਕੇ ਦੋਨਾਂ ਦਾ ਵੱਖ-ਵੱਖ ਅਤੇ ਫਿਰ ਦੋਨਾਂ ਦਾ ਕੁੱਲ ਸੰਵੇਗ ਸਿਫ਼ਰ ਹੁੰਦਾ ਹੈ । ਬੰਦੁਕ ਚਲਾਉਣ ਤੋਂ ਬਾਅਦ ਗੋਲੀ ਬਹੁਤ ਤੇਜ਼ ਵੇਗ ਨਾਲ ਬੰਦੂਕ ਵਿੱਚੋਂ ਅੱਗੇ ਵੱਲ ਨੂੰ ਨਿਕਲਦੀ ਹੈ ਅਰਥਾਤ ਇਸ ਦਾ ਬਹੁਤ ਜ਼ਿਆਦਾ ਸੰਵੇਗ ਹੁੰਦਾ ਹੈ । ਸੰਵੇਗ ਸੁਰੱਖਿਅਣ ਨਿਯਮ ਅਨੁਸਾਰ ਹੁਣ ਵੀ ਕੁੱਲ ਸੰਵੇਗ ਸਿਫ਼ਰ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ, ਜਿਵੇਂ ਕਿ ਗੋਲੀ ਚਲਾਉਣ ਤੋਂ ਪਹਿਲਾਂ ਸੀ । ਇਸ ਲਈ ਗੋਲੀ ਦੇ ਅਗਾਂਹ ਵੱਲ ਦੇ ਸੰਵੇਗ ਨੂੰ ਸੰਤੁਲਨ ਕਰਨ ਲਈ ਬੰਦੂਕ ਦਾ ਸੰਵੇਗ ਬਰਾਬਰ ਅਤੇ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਹੀ ਕਾਰਨ ਹੈ ਕਿ ਬੰਦੂਕ ਗੋਲੀ ਦੇ ਮੁਕਾਬਲੇ ਬਹੁਤ ਭਾਰੀ ਹੋਣ ਕਰਕੇ ਥੋੜੇ ਵੇਗ ਨਾਲ ਪਿਛਾਂਹ ਵੱਲ ਗਤੀ ਕਰੇਗੀ ਅਰਥਾਤ ਪਿਛਾਂਹ ਵੱਲ ਧੱਕਾ ਮਾਰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 23.
ਜਦੋਂ ਕੋਈ ਵਿਅਕਤੀ ਕਿਸ਼ਤੀ ਤੋਂ ਕਿਨਾਰੇ ਵੱਲ ਨੂੰ ਛਾਲ ਮਾਰਦਾ ਹੈ, ਤਾਂ ਕਿਸ਼ਤੀ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਚਲਦੀ ਹੈ । ਵਿਆਖਿਆ ਕਰੋ, ਕਿਉਂ ?
ਉੱਤਰ-
ਜਦੋਂ ਕੋਈ ਵਿਅਕਤੀ ਕਿਸ਼ਤੀ ਤੋਂ ਕਿਨਾਰੇ ਵੱਲ ਨੂੰ ਛਾਲ ਮਾਰਦਾ ਹੈ, ਤਾਂ ਉਹ ਕਿਸ਼ਤੀ ਨੂੰ ਆਪਣੇ ਪੈਰਾਂ ਨਾਲ ਪਿਛਾਂਹ ਵੱਲ ਧੱਕਦਾ ਹੈ ਜੋ ਕਿ ਕਿਰਿਆ ਹੈ । ਹੁਣ ਗਤੀ ਦੇ ਤੀਜੇ ਨਿਯਮ ਅਨੁਸਾਰ ਕਿਸ਼ਤੀ ਉਸ ਦੇ ਪੈਰਾਂ ਨੂੰ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਪ੍ਰਤੀਕਿਰਿਆ ਬਲ ਲਗਾ ਕੇ ਧੱਕਦੀ ਹੈ । ਇਸ ਪ੍ਰਤੀਕਿਰਿਆ ਦੇ ਸਿੱਟੇ ਵਜੋਂ ਵਿਅਕਤੀ ਅੱਗੇ ਵੱਲ ਨੂੰ ਗਤੀ ਕਰਦਾ ਹੈ ਜਦਕਿ ਕਿਸ਼ਤੀ ਪਿਛਾਂਹ ਵੱਲ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਚਲਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 24.
ਜਦੋਂ ਤੁਸੀਂ ਕਿਤਾਬ ਥੱਲੇ ਪਏ ਕਾਗਜ਼ ਨੂੰ ਤੇਜ਼ੀ ਨਾਲ ਝਟਕਾ ਮਾਰ ਕੇ ਚੁੱਕਦੇ ਹੋ, ਤਾਂ ਕਿਤਾਬ ਬਿਲਕੁਲ ਨਹੀਂ ਹਿੱਲਦੀ । ਕਿਉਂ ?
ਉੱਤਰ-
ਜਦੋਂ ਅਸੀਂ ਕਿਤਾਬ ਥੱਲੇ ਪਏ ਕਾਗਜ਼ ਨੂੰ ਤੇਜ਼ੀ ਨਾਲ ਝਟਕਾ ਮਾਰ ਕੇ ਚੁੱਕਦੇ ਹਾਂ, ਤਾਂ ਕਿਤਾਬ ਬਿਲਕੁਲ ਨਹੀਂ ਹਿੱਲਦੀ । ਇਸ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਬਾਹਰੀ ਬਲ (ਝਟਕਾ ਮਾਰਨ ਵੇਲੇ ਲੱਗਿਆ ਬਲ) ਸਿਰਫ਼ ਕਿਤਾਬ ਥੱਲੇ ਪਏ ਕਾਗਜ਼ ਉੱਪਰ ਲੱਗਿਆ, ਜਿਸ ਕਰਕੇ ਕਾਗਜ਼ ਬਾਹਰ ਨਿਕਲ ਗਿਆ, ਪਰੰਤੂ ਕਿਤਾਬ ਵਿਰਾਮ ਜੜ੍ਹਤਾ ਕਾਰਨ ਉਸੇ ਹਾਲਤ ਵਿੱਚ ਹੀ ਰਹਿੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 25.
ਜੜ੍ਹਤਾ ਕੀ ਹੈ ? ਜਤਾ ਦਾ ਮਾਪ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਜਤਾ (Inertia) – ਕਿਸੇ ਵਸਤੂ ਦੀ ਗਤੀ ਅਵਸਥਾ ਤੋਂ ਵਿਰਾਮ ਅਵਸਥਾ ਜਾਂ ਵਿਰਾਮ ਅਵਸਥਾ ਤੋਂ ਗਤੀ ਵਿੱਚ ਜਾਂ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਤਬਦੀਲੀ, ਆਪਣੇ-ਆਪ ਕਰ ਸਕਣ ਦੀ ਅਯੋਗਤਾ ਨੂੰ ਜੜ੍ਹਤਾ ਕਹਿੰਦੇ ਹਨ ।

ਸੁਭਾਵਿਕ ਤੌਰ ‘ਤੇ, ਇੱਕ ਵਸਤੂ ਆਪਣੀ ਉਸ ਅਵਸਥਾ ਵਿੱਚ ਉਦੋਂ ਤਕ ਰਹਿੰਦੀ ਹੈ ਜਦੋਂ ਤਕ ਕਿ ਉਸ ਉੱਪਰ ਕੋਈ ਬਾਹਰੀ ਬਲ ਨਾ ਲਗਾਇਆ ਜਾਵੇ ।
ਜੜ੍ਹਤਾ ਤਿੰਨ ਤਰ੍ਹਾਂ ਦੀ ਹੁੰਦੀ ਹੈ-

1. ਵਿਰਾਮ-ਜੜ੍ਹਤਾ (Inertia of Rest)
2. ਗਤੀ-ਜਤਾ (inertia of Motion)
3. ਦਿਸ਼ਾ-ਜੜ੍ਹਤਾ (Inertia of Direction) ।
   ਜੜ੍ਹਤਾ ਦਾ ਮਾਪ-ਜੜ੍ਹਤਾ ਵਸਤੂ ਦੇ ਪੁੰਜ ਉੱਪਰ ਨਿਰਭਰ ਕਰਦੀ ਹੈ ਅਰਥਾਤ ਜੜ੍ਹਤਾ ਦੀ ਇਕਾਈ ਕਿਲੋਗ੍ਰਾਮ ਹੈ ।

ਪ੍ਰਸ਼ਨ 26.
ਸਪੱਸ਼ਟ ਕਰੋ ਕਿ ਗਤੀ ਦੇ ਦੂਜੇ ਨਿਯਮ F = m × a ਵਿੱਚ ਨਿਊਟਨ ਦਾ ਗਤੀ ਦਾ ਪਹਿਲਾ ਨਿਯਮ ਮੌਜੂਦ (ਨਿਹਿਤ) ਹੈ ।
ਉੱਤਰ-
ਨਿਊਟਨ ਦੇ ਗਤੀ ਦੇ ਦੂਜੇ ਨਿਯਮ ਤੋਂ F = m × a
ਜੇਕਰ F = 0 ਹੋਵੇ ਤਾਂ a = 0

ਅਰਥਾਤ ਜੇਕਰ ਵਸਤੂ ‘ਤੇ ਬਾਹਰੀ ਬਲ ਨਾ ਲਗਾਇਆ ਜਾਵੇ, ਤਾਂ ਵਸਤੂ ਵਿੱਚ ਪ੍ਰਵੇਗ ਵੀ ਉਤਪੰਨ ਨਹੀਂ ਹੋਵੇਗਾ । ਪ੍ਰਵੇਗ ਦਾ ਜ਼ੀਰੋ ਹੋਣ ਤੇ ਜਾਂ ਤਾਂ ਵਸਤੁ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਹੋਵੇਗੀ ਜਾਂ ਫਿਰ ਇੱਕ ਸਮਾਨ ਵੇਗ ਨਾਲ ਗਤੀਸ਼ੀਲ ਰਹੇਗੀ । ਇਹੀ ਨਿਊਟਨ ਦਾ ਗਤੀ ਦਾ ਪਹਿਲਾ ਨਿਯਮ ਕਹਿੰਦਾ ਹੈ । ਇਸ ਲਈ ਨਿਉਟਨ ਦੇ ਗਤੀ ਦੇ ਦੂਜੇ ਨਿਯਮ ਵਿੱਚ ਪਹਿਲਾ ਨਿਯਮ ਮੌਜੂਦ ਹੈ ।

ਪ੍ਰਸ਼ਨ 27.
ਸੰਤੁਲਿਤ ਬਲ ਅਤੇ ਅਸੰਤੁਲਿਤ ਬਲ ਵਿੱਚ ਅੰਤਰ ਲਿਖੋ ।
ਉੱਤਰ-
ਸੰਤੁਲਿਤ ਬਲ ਅਤੇ ਅਸੰਤੁਲਿਤ ਬਲ ਵਿੱਚ ਅੰਤਰ-

ਸੰਤੁਲਿਤ ਬਲ	ਅਸੰਤੁਲਿਤ ਬਲ
(1) ਸੰਤੁਲਿਤ ਬਲ ਜਦੋਂ ਕਿਸੇ ਵਸਤੂ ਤੇ ਇੱਕੋ ਸਮੇਂ ਕਿਰਿਆ ਕਰਦੇ ਹਾਂ, ਤਾਂ ਉਹਨਾਂ ਸਾਰੇ ਬਲਾਂ ਦਾ ਪਰਿਣਾਮੀ ਬਲ ਜ਼ੀਰੋ ਹੁੰਦਾ ਹੈ ।	(1) ਅਸੰਤੁਲਿਤ ਬਲ ਜਦੋਂ ਵਸਤੂ ‘ਤੇ ਇੱਕੋ ਸਮੇਂ ਕਿਰਿਆ ਕਰਦੇ ਹਨ, ਤਾਂ ਉਹਨਾਂ ਦਾ ਨੈੱਟ (ਪਰਿਣਾਮੀ) ਬਲ ਜ਼ੀਰੋ ਨਹੀਂ ਹੁੰਦਾ ਹੈ ।
(2) ਸੰਤੁਲਿਤ ਬਲ ਵਸਤੂ ਨੂੰ ਗਤੀ ਨਹੀਂ ਪ੍ਰਦਾਨ ਕਰਦੇ ਹਨ ।	(2) ਜੇਕਰ ਕੋਈ ਵਸਤੁ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਹੈ, ਤਾਂ ਅਸੰਤੁਲਿਤ ਬਲ ਉਸ ਵਸਤੂ ਨੂੰ ਗਤੀ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ ।
(3) ਸੰਤੁਲਿਤ ਬਲ ਗਤੀਸ਼ੀਲ ਵਸਤੂ ਦੀ ਚਾਲ ਅਤੇ ਦਿਸ਼ਾ ਵਿੱਚ ਪਰਿਵਰਤਨ ਨਹੀਂ ਕਰ ਸਕਦਾ ।	(3) ਅਸੰਤੁਲਿਤ ਬਲ ਵਸਤੂ ਦੀ ਦਿਸ਼ਾ ਅਤੇ ਚਾਲ ਵਿੱਚ ਪਰਿਵਰਤਨ ਕਰ ਸਕਦਾ ਹੈ ।
(4) ਸੰਤੁਲਿਤ ਬਲ ਵਸਤੂ ਦੀ ਸ਼ਕਲ ਅਤੇ ਸਾਈਜ਼ ਵਿੱਚ ਪਰਿਵਰਤਨ ਕਰ ਸਕਦਾ ਹੈ ।	(4) ਅਸੰਤੁਲਿਤ ਬਲ ਵਸਤੁ ਦੀ ਸ਼ਕਲ ਅਤੇ ਸਾਈਜ਼ ਵਿੱਚ ਪਰਿਵਰਤਨ ਨਹੀਂ ਕਰ ਸਕਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 28.
ਕਿਸ਼ਤੀ ਨੂੰ ਅੱਗੇ ਚਲਾਉਣ ਲਈ ਕਿਸ਼ਤੀ ਚਾਲਕ ਨੂੰ ਉਲਟੀ ਦਿਸ਼ਾ ਵਿੱਚ ਚੱਪੂ ਨੂੰ ਕਿਉਂ ਚਲਾਉਣਾ ਪੈਂਦਾ ਹੈ ।
ਉੱਤਰ-
ਉਹ ਬਲ ਜੋ ਕਿਸੇ ਦਿਸ਼ਾ ਵਿੱਚ ਗਤੀ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ, ਸਾਡੇ ਦੁਆਰਾ ਲਗਾਏ ਗਏ ਬਲ ਦੀ ਪ੍ਰਤੀਕਿਰਿਆ ਹੁੰਦੀ ਹੈ । ਕਿਸ਼ਤੀ ਨੂੰ ਅੱਗੇ ਲਿਜਾਣ ਲਈ ਕਿਸ਼ਤੀ ਚਾਲਕ ਨੂੰ ਚੱਪੂ ਨਾਲ ਪਾਣੀ ਨੂੰ ਪਿਛਾਂਹ ਵੱਲ ਧੱਕਣਾ ਪੈਂਦਾ ਹੈ । ਇਸ ਬਲ ਦੀ ਪ੍ਰਤੀਕਿਰਿਆ ਨਾਲ ਕਿਸ਼ਤੀ ਅੱਗੇ ਵੱਲ ਨੂੰ ਜਾਂਦੀ ਹੈ ਕਿਉਂਕਿ ਕਿਰਿਆ ਅਤੇ ਪ੍ਰਤੀਕਿਰਿਆ ਸਮਾਨ ਅਤੇ ਵਿਪਰੀਤ ਦਿਸ਼ਾ ਵਿੱਚ ਹੁੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 29.
ਰਗੜ ਬਲ ਦਾ ਕੀ ਕਾਰਨ ਹੈ ?
ਉੱਤਰ-
ਠੋਸ ਵਸਤੁਆਂ ਦੇ ਤਲ ਸਮਤਲ ਨਹੀਂ ਹੁੰਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਵਿੱਚ ਕੁੱਝ ਅਨਿਯਮਿਤਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ । ਜਦੋਂ ਵਸਤੂ A ਦੀ ਤਲ ਵਸਤੂ B ਦੇ ਤਲ ਉੱਪਰ ਖਿਸਕਦਾ ਹੈ । ਇੱਕ ਤਲ ਦੇ ਓਬੜ-ਖਾਬੜ ਦੂਜੇ ਤਲ ਦੀਆਂ ਵਿੱਥਾਂ ਵਿੱਚ ਫਸ ਜਾਂਦੇ ਹਨ । ਇਸ ਜਕੜਣ ਨੂੰ ਤੋੜਨ ਲਈ ਬਹੁਤ ਜ਼ਿਆਦਾ ਬਲ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ । ਇਸ ਵਿਰੋਧੀ ਬਲ ਨੂੰ ਰਗੜ ਬਲ ਕਹਿੰਦੇ ਹਨ । ਰਗੜ ਬਲ ਹਮੇਸ਼ਾਂ ਗਤੀ ਦੇ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਕਾਰਜ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 30.
ਕ੍ਰਿਕੇਟ ਦੇ ਖਿਡਾਰੀ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਆ ਰਹੀ ਗੇਂਦ ਨੂੰ ਪਕੜਣ ਸਮੇਂ ਆਪਣੇ ਹੱਥ ਪਿਛਾਂਹ ਵੱਲ ਕਿਉਂ ਖਿੱਚ ਲੈਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਇਸ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਜੇਕਰ ਖਿਡਾਰੀ ਹੱਥ ਨੂੰ ਸਥਿਰ ਰੱਖ ਕੇ ਗੇਂਦ ਨੂੰ ਪਕੜਦਾ ਹੈ, ਤਾਂ ਗੇਂਦ ਨੂੰ ਰੋਕਣ ਵਿੱਚ ਘੱਟ ਸਮਾਂ ਲੱਗੇਗਾ ਜਿਸ ਕਰਕੇ ਵੇਗ ਪਰਿਵਰਤਨ ਦੀ ਦਰ (ਅਰਥਾਤ ਮੰਦਨ) ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ਖਿਡਾਰੀ ਨੂੰ ਗੇਂਦ ਰੋਕਣ ਲਈ ਵੱਧ ਬਲ ਲਗਾਉਣਾ ਪੈਂਦਾ ਹੈ ਜਿਸ ਕਰਕੇ ਖਿਡਾਰੀ ਦੀ ਹਥੇਲੀ ਨੂੰ ਸੱਟ ਲੱਗ ਸਕਦੀ ਹੈ । ਇਸ ਸੱਟ ਤੋਂ ਬਚਣ ਲਈ ਖਿਡਾਰੀ ਨੂੰ ਗੇਂਦ ਰੋਕਣ ਲਈ ਜ਼ਿਆਦਾ ਸਮਾਂ ਲਗਾਉਣਾ ਹੋਵੇਗਾ ਜਿਸ ਕਰਕੇ ਉਹ ਆਪਣੇ ਹੱਥ ਪਿਛਾਂਹ ਵੱਲ ਖਿੱਚਦਾ ਹੈ, ਤਾਂ ਜੋ ਵੇਗ-ਪਰਿਵਰਤਨ ਦੀ ਦਰ ਘੱਟ ਸਕੇ ਅਤੇ ਉਸ ਨੂੰ ਘੱਟ ਬਲ ਲਗਾਉਣਾ ਪਵੇ । ਇਸ ਤਰ੍ਹਾਂ ਖਿਡਾਰੀ ਸੱਟ ਲੱਗਣ ਤੋਂ ਬੱਚ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 31.
ਰਗੜ ਬਲ ਦੇ ਕੀ ਲਾਭ ਹਨ ?
ਉੱਤਰ-
ਰਗੜ ਬਲ ਦੇ ਲਾਭ-

1. ਰਗੜ ਬਲ ਕਾਰਨ ਹੀ ਅਸੀਂ ਸਿੱਧੇ ਖੜ੍ਹੇ ਰਹਿ ਸਕਦੇ ਹਾਂ ।
2. ਰਗੜ ਬਲ ਵਾਹਨਾਂ ਨੂੰ ਸੜਕ ਉੱਪਰ ਤਿਲਕਣ ਤੋਂ ਰੋਕਦਾ ਹੈ ।
3. ਰਗੜ ਨਾ ਹੋਣ ਦੀ ਸਥਿਤੀ ਵਿੱਚ ਮਸ਼ੀਨਾਂ ਨਹੀਂ ਚੱਲ ਸਕਦੀਆਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 32.
ਜੈਵਲਿਨ ਥੋ ਵਿੱਚ ਜੇਕਰ ਖਿਡਾਰੀ ਕਿਸੇ ਨਿਸ਼ਚਿਤ ਰੇਖਾ ਨੂੰ ਲੰਘ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਉਹ ਫਾਉਲ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ, ਪਰੰਤੂ ਆਮ ਤੌਰ ‘ਤੇ ਖਿਡਾਰੀ ਇਸ ਰੇਖਾ ‘ਤੇ ਰੁਕਣ ਲਈ ਅਸਫਲ ਰਹਿੰਦੇ ਹਨ । ਸਪੱਸ਼ਟ ਕਰੋ ਕਿਉਂ ?
ਉੱਤਰ-
ਜੈਵਲਿਨ ਥੋ ਵਿੱਚ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਭਾਲਾ ਸੁੱਟਣ ਲਈ ਖਿਡਾਰੀ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਅੱਗੇ ਵੱਲ ਨੂੰ ਦੌੜਦਾ ਹੈ । ਇਸ ਲਈ ਖਿਡਾਰੀ ਨਿਸਚਿਤ ਰੇਖਾ ‘ਤੇ ਪਹੁੰਚਣ ਸਮੇਂ ਤੀਬਰ ਗਤੀ ਦੀ ਅਵਸਥਾ ਵਿੱਚ ਹੁੰਦਾ ਹੈ ਅਤੇ ਸਰੀਰ ਗਤੀ ਜਤਾ ਕਾਰਨ ਗਤੀ ਵਿੱਚ ਰਹਿਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦੀ ਹੈ । ਇਸ ਲਈ ਨਿਸਚਿਤ ਰੇਖਾ ‘ਤੇ ਰੁਕਣ ਵਿੱਚ ਅਸਫਲ ਹੁੰਦਾ ਹੈ ।

ਮਹੱਤਵਪੂਰਨ ਸੂਤਰ (Important Formulae)

1. ਬਲ, F = m × a
2. ਪ੍ਰਵੇਗ, a = \(\frac{\mathrm{F}}{m}\)
3. ਪ੍ਰਵੇਗ, a = \(\frac{v-u}{t}\)
4. ਸੰਵੇਗ, p = m × υ
5. ਦਬਾਉ p =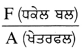

ਸੰਖਿਆਤਮਕ ਪ੍ਰਸ਼ਨ (Numerical Problems)

ਪ੍ਰਸ਼ਨ 1.
3 kg ਪੁੰਜ ਤੇ 12 ਨਿਊਟਨ ਬਲ ਕਿਰਿਆ ਕਰਾਉਣ ‘ਤੇ ਕਿੰਨਾ ਵੇਗ ਪੈਦਾ ਹੋਵੇਗਾ ?
ਹੱਲ: ਬਲ, F = 12 ਨਿਊਟਨ
ਪੁੰਜ, ਅ = 3kg
F = m × a
12 = 3 × a
∴ a = \(\frac{12}{3}\) = 4 ms^-2

ਪ੍ਰਸ਼ਨ 2.
6 kg ਪੰਜ ਵਾਲੀ ਗੇਂਦ ਨੂੰ 4 m/s² ਦਾ ਵੇਗ ਦੇਣ ਲਈ ਕਿੰਨੇ ਬਲ ਦੀ ਲੋੜ ਪਵੇਗੀ ?
ਹੱਲ: ਪੁੰਜ,
m = 6 kg
ਪ੍ਰਵੇਗ, a = 4ms^-2
F = ?
F = m × a
= 6 × 4 = 24 N

ਪ੍ਰਸ਼ਨ 3.
0.5 m/s ਦੇ ਵੇਗ ਨਾਲ ਸੁੱਟੀ ਗਈ, 70g ਪੁੰਜ ਦੀ, ਕ੍ਰਿਕੇਟ ਦੀ ਗੇਂਦ ਨੂੰ ਇੱਕ ਖਿਡਾਰੀ 0.5 s ਵਿੱਚ ਰੋਕਦਾ ‘ ਹੈ । ਗੇਂਦ ਨੂੰ ਰੋਕਣ ਲਈ ਖਿਡਾਰੀ ਨੇ ਕਿੰਨਾ ਬਲ ਲਗਾਇਆ ?
70
ਹੱਲ:
ਗੇਂਦ ਦਾ ਪੁੰਜ, (m) = 70 g = \(\frac{70}{1000}\) = 0.07 kg
u = 0.5 m/s
t = 0.5 s
υ = 0
υ = u + at
0.5 + a × 0.5
a = –\(\frac{0.5}{0.5}\) = -1m/s²
ਬਲ, F = m × a
= 0.07 × (-1) = -0.07 N

ਪ੍ਰਸ਼ਨ 4.
10kg ਪੁੰਜ ਵਾਲੀ ਇੱਕ ਵਸਤੂ ਤੇ ਕੋਈ ਬਲ 10s ਲਈ ਕਿਰਿਆ ਕਰਦਾ ਹੈ ਅਤੇ ਉਸ ਤੋਂ ਬਾਅਦ ਬਲ ਹਟਾ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਵਸਤੂ ਅਗਲੇ 5s ਵਿੱਚ 50 m ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ । ਬਲ ਗਿਆਤ ਕਰੋ ।
ਹੱਲ:
ਇੱਥੇ, ਵਸਤੂ ਦਾ ਆਰੰਭਿਕ ਵੇਗ (u) = 0
ਵਸਤੂ ਦਾ ਪੁੰਜ (m) = 10kg
ਸਮਾਂ (t) = 10s
ਮੰਨ ਲਓ ਵਸਤੂ ‘ਤੇ ਲਗ ਰਿਹਾ ਬਲ F ਹੈ ।
ਬਲ ਹਟਾਉਣ ਤੋਂ ਮਗਰੋਂ ਤੈਅ ਕੀਤੀ ਗਈ ਦੁਰੀ = 50 m
50 m ਦੀ ਦੂਰੀ ਤੈਅ ਕਰਨ ਲਈ ਲੱਗਿਆ ਸਮਾਂ = 5s

= \(\frac{50 m}{5 s}\)
υ = 10m/s
ਹੁਣ υ = u + at ਲਗਾ ਕੇ
10 = 0 + a × 10
∴ a = \(\frac{10}{10}\)
= 1m/s²
ਪਰ F = m × a
= 10 × 1
∴ F = 10 N

ਪ੍ਰਸ਼ਨ 5.
12 m/s ਦੇ ਵੇਗ ਨਾਲ ਚੱਲ ਰਹੀ 0.25 kg ਪੁੰਜ ਵਾਲੀ ਇੱਕ ਵਸਤੂ ਨੂੰ 0.6 N ਦਾ ਬਲ ਲਗਾ ਕੇ ਰੋਕ ਲਿਆ ਗਿਆ ਹੈ | ਵਸਤੂ ਨੂੰ ਰੋਕਣ ਲਈ ਲੱਗਿਆ ਸਮਾਂ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਆਰੰਭਿਕ ਵੇਗ (u) = 12 m/s
ਅੰਤਿਮ ਵੇਗ (υ) = 0 (∵ ਵਸਤੂ ਅਖੀਰ ਵਿੱਚ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਆ ਜਾਂਦੀ ਹੈ)
ਵਸਤੂ ਦਾ ਪੁੰਜ (m) = 0.25 kg
ਵਸਤੁ ਤੇ ਲੱਗ ਰਿਹਾ ਬਲ (F) = 0.6 N
ਵਸਤੂ ਨੂੰ ਰੋਕਣ ਲਈ ਲੱਗਿਆ ਸਮਾਂ (t) = ?
ਮੰਨ ਲਉ ਵਸਤੂ ਅੰਦਰ ਪੈਦਾ ਹੋਇਆ ਵੇਗ ‘a’ ਹੈ ।
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, F = m × (-a)
ਜਾਂ -a = \(\frac{\mathrm{F}}{m}\)
= \(\frac{0.6}{0.25}=\frac{60}{25}\)
∴ a = -2.4 m/s²

ਸਮਾਂ (t) = 5 ਸੈਕਿੰਡ

ਪ੍ਰਸ਼ਨ 6.
ਇੱਕ ਕਾਰ 108 km/h ਦੇ ਵੇਗ ਨਾਲ ਚੱਲ ਰਹੀ ਹੈ ਅਤੇ ਬਰੇਕ ਲਗਾਉਣ ਤੋਂ ਬਾਅਦ ਇਹ ਰੁਕਣ ਵਿੱਚ 4s ਦਾ ਸਮਾਂ ਲੈਂਦੀ ਹੈ । ਕਾਰ ਤੇ ਬਰੇਕ ਦੁਆਰਾ ਲਗਾਏ ਗਏ ਬਲ ਦਾ ਮਾਨ ਪਤਾ ਕਰੋ | ਯਾਤਰੀਆਂ ਸਮੇਤ ਕਾਰ ਦਾ ਕੁੱਲ ਪੁੰਜ 1000 kg ਹੈ ।
ਹੱਲ:
ਕਾਰ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (u) = 108 km/h
= \(\frac{108 \times 1000 m}{60 \times 60 s}\)
= 30 m/s
ਕਾਰ ਦਾ ਅੰਤਿਮ ਵੇਗ (υ) = 0 m/s
ਕਾਰ ਦਾ ਕੁੱਲ ਪੁੰਜ (m) = 1000 kg
ਕਾਰ ਨੂੰ ਰੋਕਣ ਲਈ ਗਿਆ ਸਮਾਂ (t) = 4s
ਬਰੇਕ ਨਾਲ ਲਗ ਰਹੇ ਬਲ ਦਾ ਪਰਿਮਾਣ (F) = \(\frac{m(v-u)}{t}\)
= 1000\(\frac{(0-30)}{4}\)
= -7500 kg – m/s²
= -7500 N
ਰਿਣਾਤਮਕ ਚਿੰਨ੍ਹ ਇਹ ਦਰਸਾਉਂਦਾ ਹੈ ਕਿ ਬਰੇਕ ਦੁਆਰਾ ਲਗਾਇਆ ਗਿਆ ਬਲ ਕਾਰ ਦੀ ਗਤੀ ਦੇ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਲੱਗਿਆ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
1000kg ਪੁੰਜ ਦੀ ਕਿਸੇ ਕਾਰ ਨੂੰ ਅਤੇ 10000kg ਨਾਲ ਲੱਦੇ ਹੋਏ ਕਿਸੇ ਟਰੱਕ ਨੂੰ 2 ਸੈਕਿੰਡ ਵਿੱਚ ਰੋਕਣ ਲਈ ਕੁਮਵਾਰ ਕਿੰਨੇ ਬਲ ਦੀ ਲੋੜ ਪਵੇਗੀ, ਜੇਕਰ ਦੋਨੋਂ 5 m/s ਦੇ ਵੇਗ ਨਾਲ ਗਤੀਸ਼ੀਲ ਹੋਣ ?
ਹੱਲ:
u = 5 m/s
υ = 0
t = 2s
υ = u + at
0 = 5 + a × 2
∴ a = \(\frac{-5}{2}\) m/s²
ਕਾਰ ਨੂੰ ਰੋਕਣ ਲਈ ਬਲ F₁ = m₁ × a₁
= 1000 × (\(\frac{-5}{2}\))
=-2500 N
ਟਰੱਕ ਨੂੰ ਰੋਕਣ ਲਈ ਬਲ F₂ = m₂ × a₂
– 10000 × (\(\frac{-5}{2}\))
= -25000 N

ਪ੍ਰਸ਼ਨ 8.
ਕਿਸ ਨੂੰ ਜ਼ਿਆਦਾ ਬਲ ਦੀ ਲੋੜ ਪਵੇਗੀ; 2 ਕਿਲੋਗ੍ਰਾਮ ਪੰਜ ਵਾਲੀ ਕਿਸੇ ਵਸਤੂ ਨੂੰ 5 ਮੀਟਰ/ਸੈਕਿੰਡ ਦੀ ਦਰ ਨਾਲ ਵੇਰਿਤ ਕਰਨ ਸਮੇਂ ਜਾਂ 4 ਕਿਲੋਗ੍ਰਾਮ ਪੰਜ ਵਾਲੀ ਵਸਤੂ ਨੂੰ 2 ਮੀਟਰ/ਸੈਕਿੰਡ ਦੀ ਦਰ ਨਾਲ ਪ੍ਰਵੇਗਿਤ ਕਰਨ ਲਈ ?
ਹੱਲ:
ਪਹਿਲੀ ਵਸਤੂ ਲਈ
ਦਿੱਤਾ ਹੈ
m₁ = 2 kg
a₁ = 5 m/s²
F₁ = m₁ × a₁
= 2 kg × 5 m/s²
∴ F₁ = 10 ਨਿਊਟਨ

ਦੂਜੀ ਵਸਤੂ ਲਈ
m₂ = 4 kg
a₂ = 2 m/s²
F₂ = m₂ × a₂
=4 kg × 2 m/s²
∴ F₂ = 8 ਨਿਊਟਨ
F₁ > F₂
ਇਸ ਤੋਂ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਪਹਿਲੀ ਵਸਤੂ ਨੂੰ ਪ੍ਰਵੇਗਿਤ ਕਰਨ ਲਈ ਵੱਧ ਬਲ ਦੀ ਲੋੜ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
3 ਕਿਲੋਗ੍ਰਾਮ ਦੀ ਇੱਕ ਰਾਇਫ਼ਲ ਤੋਂ 0.03 ਕਿਲੋਗ੍ਰਾਮ ਦੀ ਇੱਕ ਗੋਲੀ ਚਲਾਈ ਗਈ ਜੋ 100 ਮੀਟਰ/ਸੈਕਿੰਡ ਵੇਗ ਨਾਲ ਨਾਲੀ ਤੋਂ ਬਾਹਰ ਨਿਕਲੀ । ਜੇਕਰ ਗੋਲੀ ਨੂੰ ਨਲੀ ਤੋਂ ਬਾਹਰ ਨਿਕਲਣ ਲਈ 0.003 ਸੈਕਿੰਡ ਲੱਗੇ ਹੋਣ, ਤਾਂ ਰਾਇਫ਼ਲ ਤੇ ਲੱਗੇ ਬਲ ਦੀ ਗਣਨਾ ਕਰੋ ।
ਹੱਲ:
m₁ = 3 ਕਿਲੋਗ੍ਰਾਮ,
m₂ = 0.03 ਕਿਲੋਗ੍ਰਾਮ
u₁ = u₂ = 0
υ₁ = ?
υ₂ = 100 ਮੀਟਰ/ਸੈਕਿੰਡ

ਸੰਵੇਗ ਸੁਰੱਖਿਅਣ ਨਿਯਮ ਅਨੁਸਾਰ,
m₁u₁ + m₂u₂ = m₁υ₁ + m₂υ₂
= 3 × 0 + 0.03 × 0 = 3 × υ₁ + 0.03 × 100
υ₁ = \(-\frac{100 \times 0.03}{3}\)
= -1 ਮੀਟਰ/ਸੈਕਿੰਡ
ਰਿਣਾਤਮਕ ਚਿੰਨ੍ਹ ਰਾਇਫ਼ਲ ਦਾ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਧੱਕਾ ਲਾਉਣਾ ਦਰਸਾਉਂਦਾ ਹੈ ।

-1000 ਕਿਲੋਗ੍ਰਾਮ/ਸੈਕਿੰਡ²
= -1000 N

ਪ੍ਰਸ਼ਨ 10.
5000g ਪੁੰਜ ਵਾਲੀ ਇੱਕ ਬੰਦੂਕ 20g ਦੀ ਗੋਲੀ 500 ms^-1 ਦੀ ਵੇਗ ਨਾਲ ਚਲਾਉਂਦੀ ਹੈ । ਬੰਦੂਕ ਦੁਆਰਾ ਧੱਕਾ ਬਲ ਗਿਆਤ ਕਰੋ ।
ਹੱਲ:
ਗੋਲੀ ਦਾ ਪੁੰਜ, m = 20g
ਗੋਲੀ ਦਾ ਵੇਗ, υ = 500 ms^-1
ਬੰਦੂਕ ਦਾ ਪੁੰਜ, M = 5000g
ਸੰਵੇਗ ਸੁਰੱਖਿਆ ਦੇ ਨਿਯਮ ਅਨੁਸਾਰ,
ਗੋਲੀ ਚੱਲਣ ਤੋਂ ਪਹਿਲੇ ਦਾ ਸੰਵੇਗ = ਗੋਲੀ ਚੱਲਣ ਤੋਂ ਬਾਅਦ ਦਾ ਸੰਵੇਗ
0 = MV + mv
V = –\(\frac{m v}{\mathrm{M}}\)
= –\(\frac{20 \times 500}{1000 \times 5}\)
V = – 2 ms^-1
ਰਿਣਾਤਮਕ ਚਿੰਨ੍ਹ ਬੰਦੂਕ ਦੇ ਪਿੱਛੇ ਵੱਲ ਧੱਕਾ ਮਾਰਨ ਦਾ ਸੰਕੇਤ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
2kg ਦੀ ਇੱਕ ਪਿਸਤੌਲ ਵਿੱਚੋਂ 20g ਪੁੰਜ ਦੀ ਗੋਲੀ ਸਮਤਲ ਲੇਟਵੀ) ਦਿਸ਼ਾ ਵਿੱਚ 150 ms^-1 ਦੇ ਵੇਗ ਨਾਲ ਛੱਡੀ ਜਾਂਦੀ ਹੈ । ਪਿਸਤੌਲ ਦਾ ਪਿੱਛੇ ਵੱਲ ਦਾ ਵੇਗ ਕਿੰਨਾ ਹੋਵੇਗਾ ? ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਗੋਲੀ ਦਾ ਪੁੰਜ (m₁) = 20g = 0.02kg
ਪਿਸਤੌਲ ਦਾ ਪੁੰਜ (m₂) = 2kg
ਗੋਲੀ ਦਾ ਆਰੰਭਿਕ ਵੇਗ (u₁) ਅਤੇ ਪਿਸਤੌਲ ਦਾ
ਆਰੰਭਿਕ ਵੇਗ (u₂) ਜ਼ੀਰੋ ਹਨ ।
ਅਰਥਾਤ u₁ = u₂ = 0
ਗੋਲੀ ਦਾ ਅੰਤਿਮ ਵੇਗ (υ₁) = +150 ms^-1
ਮੰਨ ਲਓ ਪਿਸਤੌਲ ਦੀ ਖੇਪਿਤ ਵੇਗ υ ਹੈ ।

ਗੋਲੀ ਚੱਲਣ ਤੋਂ ਪਹਿਲਾਂ
ਗੋਲੀ ਅਤੇ ਪਿਸਤੌਲ ਦਾ ਕੁੱਲ ਸੰਵੇਗ = (0.02 × 0 + 2 × 0)
= 0 kg-ms^-1

ਗੋਲੀ ਚੱਲਣ ਤੋਂ ਬਾਅਦ
ਗੋਲੀ ਅਤੇ ਪਿਸਤੌਲ ਦਾ ਕੁੱਲ ਸੰਵੇਗ = (0.02 × 150) + (2 × υ) kg-ms^-1
ਸੰਵੇਗ ਸੁਰੱਖਿਅਣ ਨਿਯਮ ਅਨੁਸਾਰ, = 3 + 2υ
ਗੋਲੀ ਚੱਲਣ ਤੋਂ ਪਹਿਲਾਂ, ਗੋਲੀ ਅਤੇ ਪਿਸਤੌਲ ਦਾ ਕੁੱਲ ਸੰਵੇਗ = ਗੋਲੀ ਚੱਲਣ ਤੋਂ ਬਾਅਦ ਗੋਲੀ ਅਤੇ ਪਿਸਤੌਲ ਦਾ ਕੁੱਲ ਸੰਵੇਗ
0 = 3 + 2υ
∴ υ = \(\frac{-3}{2}\)
υ = – 1.5 ms^-1
ਰਿਣਾਤਮਕ ਚਿੰਨ੍ਹ ਦਰਸਾਉਂਦਾ ਹੈ ਕਿ ਪਿਸਤੌਲ ਦਾ ਵੇਗ ਗੋਲੀ ਦੇ ਵੇਗ ਦੀ ਦਿਸ਼ਾ ਤੋਂ ਉਲਟ ਹੈ ।

ਪ੍ਰਸ਼ਨ 12.
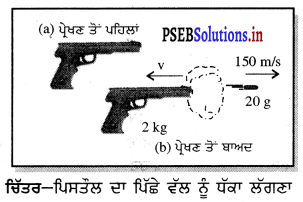
ਹਾਕੀ ਦੀ ਵਿਰੋਧੀ ਟੀਮਾਂ ਦੇ ਦੋ ਖਿਡਾਰੀ ਗੇਂਦ ਨੂੰ ਹਿੱਟ ਮਾਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਵਿੱਚ ਆਪਸ ਵਿੱਚ ਟਕਰਾ ਜਾਂਦੇ ਹਨ ਅਤੇ ਆਪਸ ਵਿੱਚ ਉਲਝ ਜਾਂਦੇ ਹਨ । ਇੱਕ ਖਿਡਾਰੀ 60kg ਦਾ ਹੈ ਅਤੇ ਉਹ 5.0 ms^-1 ਦੇ ਵੇਗ ਨਾਲ ਗਤੀ ਵਿੱਚ ਸੀ ਜਦਕਿ ਦੂਜਾ ਖਿਡਾਰੀ, ਜਿਸਦਾ ਪੁੰਜ 55kg ਹੈ 6.0 ms-^-1ਦੇ ਵੇਗ ਨਾਲ ਪਹਿਲੇ ਖਿਡਾਰੀ ਵੱਲ ਗਤੀ ਕਰ ਰਿਹਾ ਸੀ । ਟਕਰਾ ਕੇ ਉਲਝਣ ਤੋਂ ਬਾਅਦ ਉਹ ਦੋਵੇਂ ਕਿਸ ਦਿਸ਼ਾ ਵਿੱਚ ਕਿਸ ਵੇਗ ਨਾਲ ਗਤੀ ਕਰਨਗੇ । ਮੰਨ ਲਉ ਕਿ ਦੋਨਾਂ ਖਿਡਾਰੀਆਂ ਦੇ ਪੈਰਾਂ ਅਤੇ ਜ਼ਮੀਨ ਵਿਚਕਾਰ ਰਗੜ ਬਲ ਨਾ ਹੋਣ ਦੇ ਬਰਾਬਰ ਹੈ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਪਹਿਲਾ ਖਿਡਾਰੀ ਖੱਬੇ ਪਾਸਿਓਂ ਸੱਜੇ ਵੱਲ ਦੌੜ ਰਿਹਾ ਹੈ ਅਤੇ ਇਸ ਦਿਸ਼ਾ ਨੂੰ ਧਨਾਤਮਕ ਅਤੇ ਇਸਦੇ ਉਲਟ ਸੱਜੇ ਪਾਸਿਓਂ ਖੱਬੇ ਵੱਲ ਦੀ ਦਿਸ਼ਾ ਨੂੰ ਰਿਣਾਤਮਕ ਮੰਨਿਆ ਗਿਆ ਹੈ ।
ਦਿੱਤਾ ਹੈ, ਪਹਿਲੇ ਖਿਡਾਰੀ ਲਈ m₁ = 60kg, u₁ = +5 ms^-1
ਅਤੇ ਦੂਜੇ ਖਿਡਾਰੀ ਲਈ m₂ = 55kg, u₂ = -6 ms^-1
ਟੱਕਰ ਤੋਂ ਪਹਿਲਾਂ ਦੋਨਾਂ ਖਿਡਾਰੀਆਂ ਦਾ ਕੁੱਲ ਸੰਵੇਗ= m₁μ₁ + m₂μ₂
= [60 × 5 + 55 × (-6)] kg-ms^-1
= (300 – 330) kg ms^-1
= – 30 kg-ms^-1

ਮੰਨ ਲਓ ਟਕਰਾਉਣ ਤੋਂ ਬਾਅਦ ਦੋਨਾਂ ਖਿਡਾਰੀਆਂ ਦਾ ਇੱਕ ਸਮਾਨ ਵੇਗ ‘ ਹੈ ।
ਅਰਥਾਤ υ₁ = υ ਅਤੇ υ₂ = υ
∴ ਟੱਕਰ ਤੋਂ ਬਾਅਦ ਦੋਨਾਂ ਖਿਡਾਰੀਆਂ ਦਾ ਕੁੱਲ ਸੰਵੇਗ = m₁υ₁ + m₂υ₂
= 60 × υ + 55 × υ
= (60 + 55) × 0 kg-ms^-1
= 115υ kg-ms^-1
ਸੰਵੇਗ ਸੁਰੱਖਿਅਣ ਨਿਯਮ ਅਨੁਸਾਰ -30 = 115 υ
υ = \(\frac{-30}{115}\) = -0.26 ms^-1
ਦੋਨੋਂ ਖਿਡਾਰੀ ਉਲਝਣ ਤੋਂ ਬਾਅਦ ਖੱਬਿਓਂ ਸੱਜੇ ਵੱਲ ਨੂੰ 0.26 ms^-1 ਦੇ ਵੇਗ ਨਾਲ ਗਤੀਸ਼ੀਲ ਉੱਤਰ ।

ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Very Short Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਕਿਸੇ ਵਸਤੂ ਦੀ ਦਿਸ਼ਾ ਬਦਲਣ ਲਈ ਕਿਹੋ ਜਿਹੇ ਬਲ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ-ਸੰਤੁਲਿਤ ਬਲ ਜਾਂ ਅਸੰਤੁਲਿਤ ਬਲ ?
ਉੱਤਰ-
ਅਸੰਤੁਲਿਤ ਬਲ ।

ਪ੍ਰਸ਼ਨ 2.
ਕੋਈ ਵਸਤੁ ਕੁੱਝ ਦੂਰੀ ਤਕ ਲੁਢਕਣ ਤੋਂ ਬਾਅਦ ਕਿਉਂ ਰੁੱਕ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਰਗੜ ਬਲ ਕਾਰਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਰਗੜ ਬਲ ਕਿਵੇਂ ਘੱਟ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ?
ਉੱਤਰ-
ਸਮਤਲ ਸਤਹਿ ਉੱਪਰ ਲੁਬੀਐਂਟ ਦਾ ਲੇਪ ਕਰਕੇ ।

ਪ੍ਰਸ਼ਨ 4.
ਗਤੀ ਦੇ ਤਿੰਨ ਨਿਯਮ ਕਿਸ ਵਿਗਿਆਨਿਕ ਨੇ ਪੇਸ਼ ਕੀਤੇ ਸੀ ?
ਉੱਤਰ-
ਨਿਊਟਨ ਨੇ ।

ਪ੍ਰਸ਼ਨ 5.
ਨਿਊਟਨ ਦਾ ਪਹਿਲਾ ਗਤੀ ਦਾ ਨਿਯਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਨਿਊਟਨ ਦਾ ਪਹਿਲਾ ਗਤੀ ਦਾ ਨਿਯਮ – ਹਰੇਕ ਵਸਤੂ ਆਪਣੀ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਜਾਂ ਫਿਰ ਸਰਲ ਰੇਖਾ ਵਿੱਚ ਇੱਕਸਮਾਨ ਵੇਗ ਨਾਲ ਗਤੀਸ਼ੀਲ ਅਵਸਥਾ ਵਿੱਚ ਬਣੀ ਰਹਿੰਦੀ ਹੈ ਜਦੋਂ ਤਕ ਉਸ ਉੱਤੇ ਕੋਈ ਬਾਹਰੀ ਬਲ ਨਹੀਂ ਲਗਾਇਆ ਜਾਂਦਾ ।

ਪ੍ਰਸ਼ਨ 6.
ਜੜ੍ਹਤਾ ਕਿਸ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਜਤਾ-ਕਿਸੇ ਵਸਤੂ ਦਾ ਵਿਰਾਮ ਅਵਸਥਾ ਜਾਂ ਇੱਕ ਸਮਾਨ ਵੇਗ ਨਾਲ ਗਤੀ ਕਰਦੇ ਰਹਿਣ ਦੀ ਪ੍ਰਵਿਰਤੀ ਨੂੰ ਜੜ੍ਹਤਾ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 7.
ਗਤੀ ਦਾ ਪਹਿਲਾ ਨਿਯਮ ਕਿਸ ਹੋਰ ਨਾਂ ਨਾਲ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਜੜ੍ਹਤਾ ਦੇ ਨਿਯਮ ਨਾਲ ।

ਪ੍ਰਸ਼ਨ 8.
ਅਚਾਨਕ ਬ੍ਰੇਕ ਲਗਾਉਣ ‘ਤੇ ਗੱਡੀ ਵਿੱਚ ਬੈਠੀਆਂ ਹੋਈਆਂ ਸਵਾਰੀਆਂ ਨੂੰ ਝਟਕਾ ਕਿਉਂ ਲਗਦਾ ਹੈ ?
ਉੱਤਰ-
ਸਵਾਰੀਆਂ ਦਾ ਸਰੀਰ ਗਤਿਜ ਜਤਾ ਵਿੱਚ ਬਣਿਆ ਰਹਿਣ ਦੀ ਪ੍ਰਵਿਰਤੀ ਰੱਖਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਮੋਟਰ ਗੱਡੀਆਂ ਜਾਂ ਕਾਰਾਂ ਵਿੱਚ ਸੁਰੱਖਿਆ ਬੈਲਟ ਦਾ ਉਪਯੋਗ ਕਿਉਂ ਕਰਦੇ ਹਨ ?
ਉੱਤਰ-
ਇਹਨਾਂ ਕਾਰਨ ਸਾਡੀ ਅੱਗੇ ਵੱਧਣ ਦੀ ਗਤੀ ਹੌਲੀ ਹੋ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਬਲ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ ।
ਉੱਤਰ-
ਬਲ – ਬਲ ਉਹ ਬਾਹਰੀ ਕਾਰਕ ਹੈ ਜੋ ਕਿਸੇ ਵਸਤੂ ਦੀ ਵਿਰਾਮ ਅਵਸਥਾ ਜਾਂ ਗਤੀਸ਼ੀਲ ਵਸਤੂ ਦੀ ਚਾਲ ਜਾਂ ਦਿਸ਼ਾ ਨੂੰ ਬਦਲਣ ਜਾਂ ਬਦਲਣ ਦੀ ਪ੍ਰਵਿਰਤੀ ਰੱਖਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
ਸੰਤੁਲਿਤ ਬਲ ਕਿਸਨੂੰ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਸੰਤੁਲਿਤ ਬਲ – ਜੇਕਰ ਵਸਤੂ ਉੱਪਰ ਲੱਗਣ ਵਾਲੇ ਸਾਰੇ ਬਲਾਂ ਦਾ ਪਰਿਣਾਮੀ (ਨੈੱਟ) ਬਲ ਜ਼ੀਰੋ ਹੋਵੇ, ਤਾਂ ਵਸਤੁ ’ਤੇ ਲੱਗਣ ਵਾਲੇ ਸਾਰੇ ਬਲ ਸੰਤੁਲਿਤ ਬਲ ਕਹਾਉਂਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 12.
ਅਸੰਤੁਲਿਤ ਬਲ ਕਿਸ ਨੂੰ ਆਖਦੇ ਹਨ ?
ਉੱਤਰ-
ਅਸੰਤੁਲਿਤ ਬਲ – ਜੇਕਰ ਵਸਤੂ ‘ਤੇ ਲੱਗਣ ਵਾਲੇ ਸਾਰੇ ਬਲਾਂ ਦਾ ਪਰਿਣਾਮੀ ਬਲ ਨੈੱਟ ਬਲ ਜ਼ੀਰੋ ਨਾਂ ਹੋਵੇ, ਤਾਂ ਬਲ ਅਸੰਤੁਲਿਤ ਬਲ ਅਖਵਾਉਂਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 13.
ਰਬੜ ਦੀ ਗੇਂਦ ਨੂੰ ਹੱਥਾਂ ਦੀਆਂ ਹਥੇਲੀਆਂ ਵਿੱਚ ਰੱਖ ਕੇ ਦਬਾਉਣ ਸਮੇਂ ਕਿਸ ਤਰ੍ਹਾਂ ਦਾ ਬਲ ਲਗਦਾ ਹੈਸੰਤੁਲਿਤ ਜਾਂ ਅਸੰਤੁਲਿਤ ਬਲ ?
ਉੱਤਰ-
ਸੰਤੁਲਿਤ ਬਲ ।

ਪ੍ਰਸ਼ਨ 14.
ਰਗੜ ਦੀ ਪਰਿਭਾਸ਼ਾ ਲਿਖੋ ।
ਉੱਤਰ-
ਰਗੜ – ਜਦੋਂ ਕੋਈ ਵਸਤੂ ਕਿਸੇ ਹੋਰ ਵਸਤੂ ਦੇ ਸੰਪਰਕ ਵਿੱਚ ਰਹਿੰਦੇ ਹੋਏ ਗਤੀ ਕਰਦੀ ਹੈ, ਤਾਂ ਉਸ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਦੇ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਇੱਕ ਹੋਰ ਬਲ ਕਿਰਿਆ ਕਰਦਾ ਹੈ ਜਿਸਨੂੰ ਰਗੜ ਬਲ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 15.
ਜਦੋਂ ਅਸੀਂ ਸਾਈਕਲ ਨੂੰ ਪੈਡਲ ਮਾਰਨਾ ਬੰਦ ਕਰ ਦਿੰਦੇ ਹਾਂ, ਤਾਂ ਸਾਈਕਲ ਕੁੱਝ ਦੂਰੀ ਚੱਲਣ ਤੋਂ ਬਾਅਦ ਰੁਕ ਜਾਂਦੀ ਹੈ, ਕਿਉਂ ?
ਉੱਤਰ-
ਸਾਈਕਲ ਦੇ ਟਾਇਰ ਅਤੇ ਸੜਕ ਦੀ ਸਤਹਿ ਵਿਚਕਾਰ ਲੱਗਣ ਵਾਲਾ ਵਿਰੋਧੀ ਰਗੜ ਬਲ ਸਾਈਕਲ ਦੀ ਗਤੀ ਨੂੰ ਘੱਟ ਕਰ ਦਿੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 16.
ਸੰਵੇਗ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਸੰਵੇਗ – ਕਿਸੇ ਗਤੀਸ਼ੀਲ ਵਸਤੂ ਦਾ ਸੰਵੇਗ ਉਸਦੇ ਪੁੰਜ ਅਤੇ ਵੇਗ ਦਾ ਗੁਣਨਫਲ ਹੁੰਦਾ ਹੈ ।
∴ ਸੰਵੇਗ = ਪੁੰਜ × ਵੇਗ ।

ਪ੍ਰਸ਼ਨ 17.
ਨਿਊਟਨ ਦਾ ਦੂਜਾ ਗਤੀ ਦਾ ਨਿਯਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਨਿਊਟਨ ਦਾ ਦੂਜਾ ਗਤੀ ਦਾ ਨਿਯਮ-ਕਿਸੇ ਵਸਤੂ ’ਤੇ ਕਿਰਿਆ ਕਰ ਰਿਹਾ ਬਲ ਉਸ ਵਸਤੂ ਦੇ ਪੁੰਜ ਅਤੇ ਪ੍ਰਵੇਗ ਦੇ ਅਨੁਮਾਨੁਪਾਤੀ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 18.
ਨਿਊਟਨ ਦੇ ਗਤੀ ਦਾ ਤੀਜਾ ਨਿਯਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਨਿਊਟਨ ਦੀ ਗਤੀ ਦਾ ਤੀਜਾ ਨਿਯਮ – ਕਿਰਿਆ ਅਤੇ ਪ੍ਰਤੀਕਿਰਿਆ ਬਰਾਬਰ ਪਰੰਤੂ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਹੁੰਦੀਆਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 19.
ਸੰਵੇਗ ਇੱਕ ਸਦਿਸ਼ ਰਾਸ਼ੀ ਹੈ ਜਾਂ ਅਦਿਸ਼ ਰਾਸ਼ੀ ?
ਉੱਤਰ-
ਸੰਵੇਗ ਇੱਕ ਸਦਿਸ਼ ਰਾਸ਼ੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 20.
ਗੋਲੀ ਚਲਣ ਤੋਂ ਬਾਅਦ ਗੋਲੀ ਅਤੇ ਬੰਦੂਕ ਦਾ ਕੁੱਲ ਸੰਵੇਗ ਕਿੰਨਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਜ਼ੀਰੋ ।

ਪ੍ਰਸ਼ਨ 21.
ਬਲ ਦਾ ਮਾਨਕ ਮਾੜਕ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਨਿਊਟਨ ।

ਪ੍ਰਸ਼ਨ 22.
ਜੇਕਰ ਕਿਸੇ ਵਸਤੂ ’ਤੇ ਕਿਰਿਆ ਕਰ ਰਿਹਾ ਪਰਿਣਾਮੀ (ਨੈੱਟ) ਬਲ ਜ਼ੀਰੋ ਹੋਵੇ, ਤਾਂ ਬਲ ਸੰਤੁਲਿਤ ਹੋਵੇਗਾ ਜਾਂ ਅਸੰਤੁਲਿਤ ? ਆ !
ਉੱਤਰ-
ਬਲ ਸੰਤੁਲਿਤ ਹੋਵੇਗਾ ।

ਪ੍ਰਸ਼ਨ 23.
ਜੇਕਰ 1kg ਪੁੰਜ ਤੇ 1 ਨਿਊਟਨ ਬਲ ਲਗਾਇਆ ਜਾਵੇ, ਤਾਂ ਕਿੰਨਾ ਵੇਗ ਉਤਪੰਨ ਹੋਵੇਗਾ ?
ਉੱਤਰ-F = m × a
1 = 1 × a
∴ a = 1 ms^-2

ਪ੍ਰਸ਼ਨ 24.
ਹਲਕੀਆਂ ਅਤੇ ਭਾਰੀਆਂ ਵਸਤੂਆਂ ਵਿੱਚੋਂ ਕਿਸਦੀ ਜੜ੍ਹਤਾ ਵੱਧ ਹੋਵੇਗੀ ?
ਉੱਤਰ-
ਭਾਰੀਆਂ ਵਸਤੂਆਂ ਦੀ ਜੜਤਾ ਵੱਧ ਹੁੰਦੀ ਹੈ ਕਿਉਂਕਿ ਜਤਾ ਦਾ ਮਾਪ ਪੁੰਜ ਹੈ ।

ਪ੍ਰਸ਼ਨ 25.
ਸੰਵੇਗ ਦਾ S.I. ਮਾਤ੍ਰਿਕ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਸੰਵੇਗ ਦਾ S.I. ਮਾਤ੍ਰਿਕ ਕਿਲੋਗ੍ਰਾਮ ਮੀਟਰ ਪ੍ਰਤੀ ਸੈਕਿੰਡ ਹੈ । (kg-m/s)

ਪ੍ਰਸ਼ਨ 26.
ਨਿਊਟਨ ਬਲ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ ।
ਉੱਤਰ-
ਨਿਊਟਨ ਬਲ – ਉਹ ਬਲ ਹੈ ਜੋ 1 ਕਿਲੋਗ੍ਰਾਮ ਪੁੰਜ ਵਾਲੀ ਵਸਤੂ ‘ਤੇ ਲੱਗਣ ਮਗਰੋਂ ਉਸ ਵਿੱਚ 1 ਮੀਟਰ ਪ੍ਰਤੀ ਸੈਕਿੰਡ ਵੇਗ ਉਤਪੰਨ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 27.
ਬੰਦੂਕ ਚਲਾਉਣ ‘ਤੇ ਗੋਲੀ ਅੱਗੇ ਵੱਲ ਗਤੀ ਕਰਦੀ ਹੈ ਪਰ ਬੰਦੂਕੇ ਪਿਛਾਂਹ ਵੱਲ ਕਿਉਂ ਧੱਕਾ ਮਾਰਦੀ ਹੈ ?
ਉੱਤਰ-
ਸੰਵੇਗ ਸੁਰੱਖਿਅਣ ਨਿਯਮ ਕਾਰਨ ਬੰਦੂਕ ਪਿਛਾਂਹ ਵੱਲ ਗਤੀ ਕਰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 28.
ਤੈਰਨ ਦੌਰਾਨ ਕੋਈ ਤੈਰਾਕ ਪਾਣੀ ਨੂੰ ਆਪਣੇ ਹੱਥਾਂ ਨਾਲ ਪਿਛਲੇ ਪਾਸੇ ਕਿਉਂ ਧੱਕਦਾ ਹੈ ?
ਉੱਤਰ-
ਉਹ ਪਾਣੀ ਨੂੰ ਪਿੱਛੇ ਵੱਲ ਧੱਕਦਾ ਹੈ, ਤਾਂ ਜੋ ਉਸ ਦੀ ਪ੍ਰਤੀਕਿਰਿਆ ਬਲ ਉਸ ਨੂੰ ਅੱਗੇ ਵੱਲ ਲੈ ਜਾਵੇ ।

ਪ੍ਰਸ਼ਨ 29.
ਕੈਰਮ ਖੇਡਦੇ ਸਮੇਂ ਕੈਰਮ ਬੋਰਡ ‘ਤੇ ਪਾਊਡਰ ਕਿਉਂ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਰਗੜ ਬਲ ਨੂੰ ਘੱਟ ਕਰਨ ਲਈ ।

ਪ੍ਰਸ਼ਨ 30.
ਦਰੀ ਨੂੰ ਛੜੀ ਨਾਲ ਕੁੱਟਣ ‘ਤੇ ਧੂੜ ਕਿਉਂ ਝੜ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਵਿਰਾਮ ਜੜ੍ਹਤਾ ਕਾਰ ।

ਪ੍ਰਸ਼ਨ 31.
ਖਿਡਾਰੀ ਛਲਾਂਗ ਲਗਾਉਣ ਤੋਂ ਪਹਿਲਾਂ ਕੁੱਝ ਦੂਰੀ ਕਿਉਂ ਦੌੜਦਾ ਹੈ ?
ਉੱਤਰ-
ਸੰਵੇਗ ਵਧਾਉਣ ਲਈ, ਤਾਂ ਜੋ ਲੰਬੀ ਛਲਾਂਗ ਲਗਾ ਸਕੇ ।

ਪ੍ਰਸ਼ਨ 32.
ਸੰਵੇਗ ਸੁਰੱਖਿਅਣ ਨਿਯਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਸੰਵੇਗ ਸੁਰੱਖਿਅਣ ਨਿਯਮ – ਦੋ ਵਸਤੂਆਂ ਦਾ ਕੁੱਲ ਸੰਵੇਗ ਉਹਨਾਂ ਦੇ ਆਪਸ ਵਿੱਚ ਟਕਰਾਉਣ ਤੋਂ ਪਹਿਲਾਂ ਅਤੇ ਬਾਅਦ ਵਿੱਚ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ, ਜਦੋਂ ਕਿ ਉਹਨਾਂ ਉੱਪਰ ਕੋਈ ਸੰਤੁਲਿਤ ਬਲ ਕਿਰਿਆ ਨਾ ਕਰ ਰਿਹਾ ਹੋਵੇ ।

ਪ੍ਰਸ਼ਨ 33.
ਬਲ ਦਾ ਮਾਤ੍ਰਿਕ ਲਿਖੋ ।
ਉੱਤਰ-
ਨਿਊਟਨ ।

ਪ੍ਰਸ਼ਨ 34.
ਬਲ ਕਿਸ ਤਰ੍ਹਾਂ ਦੀ ਰਾਸ਼ੀ ਹੈ-ਸਦਿਸ਼ ਜਾਂ ਅਦਿਸ਼ ?
ਉੱਤਰ-
ਸਦਿਸ਼ ਰਾਸ਼ੀ ।

ਪ੍ਰਸ਼ਨ 35.
ਇੱਕ ਬੱਸ ਅਤੇ ਇੱਕ ਗੇਂਦ ਸਮਾਨ ਚਾਲ ਨਾਲ ਚਲ ਰਹੇ ਹਨ । ਦੋਨਾਂ ਵਿੱਚੋਂ ਕਿਸ ਨੂੰ ਰੋਕਣ ਲਈ ਵਧੇਰੇ ਬਲ ਦੀ ਲੋੜ ਪਵੇਗੀ ?
ਉੱਤਰ-
ਬੱਸ ਦਾ ਅਧਿਕ ਸੰਵੇਗ (m × υ) ਹੋਣ ਕਾਰਨ ਬੱਸ ਨੂੰ ਰੋਕਣ ਲਈ ਵਧੇਰੇ ਬਲ ਦੀ ਲੋੜ ਪਵੇਗੀ ।

ਪ੍ਰਸ਼ਨ 36.
1 ਕਿਲੋਗ੍ਰਾਮ ਭਾਰ ਕਿੰਨੇ ਨਿਊਟਨ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
1 ਕਿਲੋਗ੍ਰਾਮ ਭਾਰ = 9.8 ਨਿਊਟਨ ।

ਪ੍ਰਸ਼ਨ 37.
1 ਨਿਊਟਨ ਕਿੰਨੇ ਕਿਲੋਗ੍ਰਾਮ ਭਾਰ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
1 ਨਿਊਟਨ = 0.102 ਕਿਲੋਗ੍ਰਾਮ ਭਾਰ ।

ਪ੍ਰਸ਼ਨ 38.
ਜੜ੍ਹਤਾ ਕਿਸ ਭੌਤਿਕ ਰਾਸ਼ੀ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ ?
ਉੱਤਰ-
ਪੁੰਜ ’ਤੇ ।

ਪ੍ਰਸ਼ਨ 39.
ਕਿਸੇ ਵਸਤੂ ‘ਤੇ ਲੱਗ ਰਹੇ ਬਲ (F), ਪੁੰਜ (m) ਅਤੇ ਵੇਗ (a) ਦਾ ਆਪਸੀ ਸੰਬੰਧ ਦੱਸੋ ।
ਉੱਤਰ-
ਬਲ (F) = ਪੁੰਜ (m) × ਪਵੇਗ (a) ।

ਪ੍ਰਸ਼ਨ 40.
ਪਦਾਰਥ ਦਾ ਕਿਹੜਾ ਗੁਣ ਹੈ ਜਿਹੜਾ ਪਦਾਰਥ ਦੀ ਅਵਸਥਾ ਪਰਿਵਰਤਨ ਦਾ ਵਿਰੋਧ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ-
ਜੜ੍ਹਤਾ ਦਾ ਗੁਣ ।

ਪ੍ਰਸ਼ਨ 41.
ਰਾਕੇਟ ਦਾ ਸਿਧਾਂਤ ਨਿਊਟਨ ਦੇ ਗਤੀ ਦੇ ਕਿਸ ਕਿਸਮ ‘ਤੇ ਆਧਾਰਿਤ ਹੈ ?
ਉੱਤਰ-
ਨਿਊਟਨ ਦੇ ਗਤੀ ਦੇ ਤੀਜੇ ਨਿਯਮ ‘ਤੇ ।

ਪ੍ਰਸ਼ਨ 42.
ਕਿਸੇ ਵਸਤੂ ਦੇ ਪੁੰਜ ਅਤੇ ਵੇਗ ਦੇ ਗੁਣਨਫਲ ਨੂੰ ਕੀ ਨਾਂ ਦਿੱਤਾ ਗਿਆ ਹੈ ?
ਉੱਤਰ-
ਸੰਵੇਗ ।