Punjab State Board PSEB 9th Class Science Important Questions Chapter 9 Force and Laws of Motion Important Questions and Answers.
PSEB 9th Class Science Important Questions Chapter 9 Force and Laws of Motion
Long Answer Type Questions:
Question 1.
What are the different types of Forces? Explain each with the help of example
Answer:
Types of forces. There are two types of forces:
1. Balanced forces
2. Unbalanced Forces.
1. Balanced Forces: When several forces are acting simultaneously on a body and their resultant is zero, the forces are said to be balanced forces.
In the case of balanced forces if some body is at rest then it will remain at rest and if it is moving with uniform speed then it will continue to move with the same speed, as if no force is doing any work. In this way with the effect of balanced forces. There does not take place any change in position of the body.
Balanced forces change the shape of the objects, e.g. if a rubber ball is pressed between palms by applying equal and opposite forces then the shape of the ball changes. This ball no longer remains round and instead becomes flat.
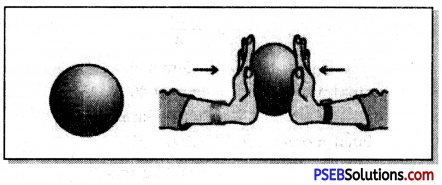
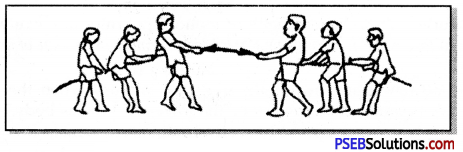
Example: In a tug of war, when both teams pull the rope with equal force, then resultant forces becomes zero. Therefore, both teams remain in their places. In this situation the forces applied by the two teams are equal and opposite so get balanced.
Condition for forces to be balanced.
Two equal forces acting in the opposite direction become balanced if they act along the same line and their magnitudes are equal.
Effect of Balanced Forces: Forces acting on any object if do not change its state of rest or its motion then these do change the shape of the object.
2. Unbalanced Forces: If the resultant of the several forces acting on a body is not zero, the forces are said to be unbalanced forces. Unbalanced forces produce change in the direction of uniform motion of the body or its state of rest.
Example:
In a tug-of-war, when one of the two teams pulls the rope with a larger force, it is able to pull the weaker team towards it. Here two forces are not balanced. Therefore, it results in the motion of the weaker team towards the larger force along the rope.
![]()
Question 2.
State and explain the Newton’s First Law of Motion.
Answer:
Newton’s First Law of Motion. This law states that “In this universe all bodies will remain in their state of rest or of uniform motion in a straight line until some external force is applied to bring about change in their state.
According to this law, motion can be divided into two parts:
1. First part says that a body at rest continues in its state of rest unless some external force is applied to bring change in its state of rest. We find a book lying on the table keeps lying in the same state unless someone applies force on it to pick it up.
2. Second part says that a body jn uniform motion continues moving in straight line path with a uniform speed unless someone applies external force to stop it. But in our daily life it appears but different.
As for example when we stop pedalling a bicycle the moving bicycle stops. After studying minutely it is found that between tyres of bicycle and ground there acts a force of friction which is an external force which opposes the motion. The resistance of air also opposes the motion of bicycle. So, moving bicycle stops moving due to these two forces.
Question 3.
What is inertia? What are its different types? Give examples for each one of them.
Answer:
Inertia: It is the property of matter by virtue ofivhich an object is unable to change by itself its state of rest or of uniform motion in a straight line.
Because of this property Newton’s First Law of Motion is also called the law of Inertia.
Types of Inertia Inertia is of three types:
1. Inertia of Rest: It means a body at rest tends to remain in its position of rest. i.e. a body at rest opposes the forces which try to move it. It can be understood clearly by the following example.
A man standing in a stationary bus or train falls backward when the bus or train suddenly starts moving forward. When the bus moves, the lower part (limbs) of his body begins to move along with the bus while his upper-part tends remain at rest due to inertia.
2. Inertia of Motion: This means a body in motion continues to move with uniform
motion in a straight line. i.e. it is the tendency of a body to remain in its state of uniform motion in a straight line.
Example: 1. A person sitting in moving bus falls forward when the moving bus suddenly stops. It is because as the bus stops the lower part of his body comes to rest along with the bus while upper part of his body continues to remain in motion due to inertia of motion.
2. An athelete runs for some distance before taking a jump so that his inertia of motion may help his muscular force to a longer jump.
3. Inertia of Direction. It is the property of a body which helps to maintain its direction i.e. it is inability of a body to change by itself its direction of motion.
Example: The mudguard is fitted in the wheel of a bicycle to protect from mud particles and water drops sticking to its wheel leaving it tangentially.
Imagine a stone tied to the end of a thread moving in a horizontal circle, while doing so, if the thread breaks then due to inertia of direction the stone flies off tangentially in a straight line.
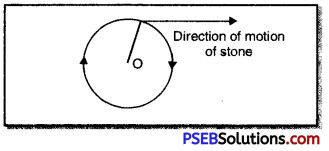
Question 4.
State and explain Newton’s Second Law of motion with the help of this law how can we measure force.
Answer:
Newton’s Second Law of Motion. Newton’s second Law of motion helps to calculate the force required to bring a body in motion. It consists of two parts
1. The rate of change of momentum of a body is directly proportional to the applied unbalanced force and
2. the change in momentum due to the external applied force takes place in the direction of force.
i.e. According to this law “the external force applied in the body is directly proportional to the product of mass of the body and the acceleration produced in the direction of force.
Explanation: When a force acts on a body, it produces change in its momentum. If the force is doubled then the change in momentum also gets doubled. The more the force applied; the more is the change in momentum produced. Momentum is the product of mass of the body and its velocity. Generally no change in mass occurs. Therefore, the rate of change of momentum is actually the rate of change of velocity. Thus the applied force is proportional to the acceleration.
When an external force acts on a body at rest, it begins to move in the direction of force. When force acts in the direction of motion of the body then its momentum gets increased. But when force acts in a direction opposite to the direction of motion, its momentum gets reduced.
Force (F) ∝ mass (m) × acceleration (a)
or F = k × m × a ….(i)
(where k is a constant of proportionality)
If we choose the unit of force in such a way that as unit of force produces unit acceleration in a body of unit mass, then
Substituting F = 1, m = 1 and a = 1 in (1)
1 = k × 1 × 1
or k = 1
∴ from equation (i), F = 1 × m × a
or F = m × a
Force = Mass × Acceleration
![]()
Question 5.
Derive the mathematical relation for magnitude of force from Newton’s Second Law of Motion.
Answer:
Measurement of Magnitude of Force from Newton’s Law of Motion. Suppose force F acts on a body of mass’m’ for Y seconds which changes its velocity from u to υ, then
Initial momentum of body, p1 = mu
Final momentum of body, p1 = mυ
Now because final velocity (υ) is more than the initial velocity (u), therefore final momentum (p2) will be more than the initial momentum (p1) change in momentum,
p = p2 – p1
= mυ – mu
= m (υ – u)
According to second law of motion,

Question 6.
State and explain Newton’s third Law of motion.
Answer:
Newton’s third Law of Motion. This law states that “Every action has equal and opposite reaction” According to this law, there does not exist one force in isolation. Force always exists in pair i.e. forces of action and reaction always act on different bodies.
Explanation: (1) Consider two similar spring balances attached to each other through their hooks. One end of spring balance A is fastened to the fixed support. Pull the free end of spring balance B to right side. Note the readings of both the spring balances. Both will read the same as shown in fig. It is because read.
A and B pull each other in opposite direction with same force.
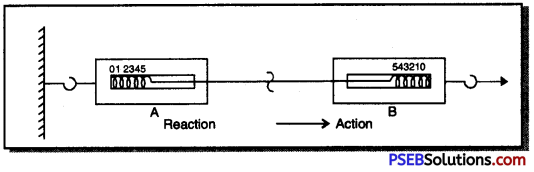
(2) Keep two balls A and B on a table at some distance from each other. When you push the ball. A towards B then the ball A acts on ball B. This force is represented by
FA→B According to Newton’s third law of motion, the ball B also reacts and applies
force on ball A. This force is represented as FB→A. if both the balls are similar then the magnitudes of action and reaction will be equal.
∴ FA→B = – FB→A
Action and reaction forces always act in the direction opposite to each other.
![]()
Question 7.
What is meant by the Law of Conservation of Momentum? Deduce this law mathematically with the help of Newton’s second and third law of motion.
Answer:
Law of Conservation of Momentum. For a system of bodies, the total vector sum of momenta of all the bodies due to mutual action and reaction remain unchanged so long as no external force acts on the system.”
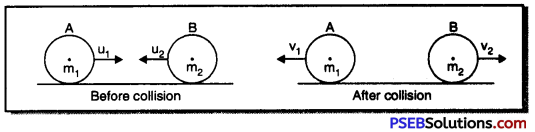
Mathematical Derivation: Consider two rubber balls of masses m1, m2 and initial velocities u1, u2 respectively. Let these collide and their velocities after collisions be υ1 and υ2 respectively. If A applies a force F on B also for time t; B also applies a force F on A for same time t.
From Newton’s Second Law of Motion:

i.e. total momentum of balls A and B before collision
= Total momentum of balls A and B after collision
This proves the law of conservation of momentum that is the total momentum remains conserved.
Short Answer Type Questions:
Question 1.
What is force? Give its units.
Answer:
Force. Force is an agent which
- produces or tends to produce motion in the body
- stops the moving body or tends to stop
- increases the speed of the body or tries to increase the speed therefore,
Force may be defined is as physical cause (a push or a pull) which changes or tends to change the state of rest or uniform motion or direction of motion of a body. The force exerted by the engine makes the train to move from its actual position of rest while the force exerted by the brakes slows down or stops the moving train. The force exerted on the steering wheel of a car changes its direction of motion.
Force is a vector quantity.
Units of force: The unit of force depends upon the unit of mass and acceleration. S.I. unit of force is Newton and C.G.S. unit is Dyne
1N = 105 Dynes
![]()
Question 2.
Why does the horse rider fall forward when a running horse suddenly stops?
Answer:
When horse is running, both the horse and the rider are in motion. When the horse suddenly stops, the lower part of the rider and horse come in the state of rest while the upper part of the rider remains in motion so that he falls forward.
Question 3.
When a horse suddenly gallops, the rider falls backward. Why?
Answer:
The horse and the rider form one system. Initially both are at rest. When the horse suddenly gallops then the horse and the lower part of the rider come into motion in the forward direction while the upper part of the rider’s body tends to remain at rest. Therefore, the rider falls backward.
Question 4.
Why does a passenger fall forwaid when he alights from the moving bus?
Answer:
While alighting from the moving bus the passenger falls forward because when the feet of the passenger touch the ground, his lower part suddenly comes to rest while the upper part still remains in motion. In this way the passenger falls forward.
Question 5.
Define momentum of a body. Also give its units.
Answer:
Momentum. It is defined as the quantity of motion possessed by the body. It is measured by the product of the mass and velocity of the body.

![]()
Question 6.
A fast-moving bullet when hits the windowpane makes a round hole while a stone strikes and shatters it, why?
Answer:
If stone piece strikes window pane glass, it gets shattered while a fast-moving bullet when strikes the windowpane a round hole is formed. The reason is that small particle of glass around and near the hole do not move due to inertia along with the bullet and threfore, do not scatter.
Question 7.
Explain how a dirty blanket becomes dust-free if it is jerked once or twice?
Answer:
If a dirty blanket is beaten with a stick or is given a jerk then dust particles get separated from it because when we beat or give a jerk to the blanket it comes in motion but due to inertia of rest, dust particles remained at rest and get separated and the blanket becomes dust-free.
Question 8.
Why a fan continues to rotate for sometime even after it is switched off?
Answer:
When a fan is rotating, then because of inertia of motion it continues it rotation for some time even if we switch if off. Due to friction on resistance of air it comes to rest after few seconds.
Question 9.
Why does a gun recoil when a bullet is fired from the gun? Explain.
Answer:
When bullet is not fired, then gun and bullet both are at rest, thus total momentum of both together is zero. When a bullet is fired from the gun the bullet moves with very high speed in the forward direction i.e. its momentum is very high. Now according to law of conservation of momentum, total momentum should still be zero as was before the firing of the bullet. Thus to balance the momentum of bullet in the forward direction gun recoil.
Question 10.
Why a cricket player lowers his hand while taking of catch of cricket ball?
Answer:
A lot of force is needed to stop a fast moving ball. If we lower our hands while catching the ball, acceleration of the ball is decreased and we have to apply less force of stop the ball.
![]()
Question 11.
Write differences between balanced and unbalanced forces.
Answer:
Differences between balanced forces and unbalanced forces:
| Balanced forces | Unbalanced forces |
| 1. When balanced forces act simultaneously on a body then their net resultant is zero. | When unbalanced forces act simultaneously on a body then their net resultant is not zero. |
| 2. Balanced forces are acting on a body which is at rest, these can not bring it in motion. | Unbalanced forces act on a body at rest, these can bring it in motion. |
| 3. These forces cannot bring a change in speed or direction of the motion. | This force can bring change in the speed of direction of motion. |
| 4. This force can make a change in the shape of the body. | This force can not make a change in the shape of the body. |
Question 12.
Why a boatman exists a force on water with his oars in the opposite direction to move forward?
Answer:
That force, which causes motion in any direction, is the reaction of the applied force. To move the boat in forward direction boatman exerts a force on water with his oars in the opposite direction. As a reaction to this force boat moves in forward direction because action and reaction are equal and opposite to each other.
Important Formulae:
- Force (F) = m × a
- Acceleration (a) = \(\frac {F}{m}\)
- Acceleration (a) = \(\frac {υ – u}{t}\)
- Momentum(p) = m × υ
- Pressure (P) = \(\frac {F(force)}{A(Area)}\)
Numerical Problems (Solved):
Question 1.
What acceleration will be produced in a body of mass 3 kg, when a force of 12 N is applied?
Solution:
Here, Force (F) = 12 N
Mass (m) = 3 kg
Acceleration (a) =?
We know F = m × a
12 = 3 × a
or a = \(\frac {12}{3}\)
∴ a = 4 m s-2
![]()
Question 2.
How much force will be required to produce an acceleration of 4 m s-2 in a ball of mass 6 kg?
Solution:
Mass of the ball (m) = 6 kg
Acceleration produced in the ball (a) = 4ms-2
Force (F) = ?
We know, F = m × a
= 6 × 4
Force (F) = 24 N
Question 3.
A man throws a ball of mass 0.5 kg vertically upwards with a velocity of 10 m s-1. What will be its initial momentum? What would be its momentum at the highest point of its reach?
Solution:
Mass of the ball (m) = 0.5 kg
Initial velocity of ball (u) = 10 m s-1
Final velocity of the ball (v) = 0 (At highest point the ball comes to rest)
Initial momentum of the ball = m × u
= 0.5 × 10
= 5 kg – m/s
Final momentunvof the ball = m × υ
= 0.5 × 0 = 0
Question 4.
A steam engine of mass 3 × 104 kg pulls two wagons each of mass 2 × 104 kg with an acceleration of 0.2 m s-2. Neglecting frictional force, calculate the:
1. force exerted by the engine.
2. force experienced by each wagon.
Solution:
Mass of steam engine (m1) = 3 × 104 kg
Mass of two wagons (m2) = 2 × (2 × 104 kg)
Total mass of the engine and wagons (m) = m1 + m2
= 3 × 104 + 4 × 104
= (3 + 4) × 104 kg
= 7 × 104 kg
Acceleration (a) = 0.2 ms-2
1. We know, F = m × a
= 7 × 104 × 0.2
= 1.4 × 104 N
2. Force experienced by each wagon = 1.4 × 104 N
![]()
Question 5.
A bullet of mass 20 g moving with a speed of 500 ms-1 strikes a wooden block of mass 1 kg and gets embedded in it. Find the speed with which block moves along with the bullet.
Solution:
Suppose the final velocity of the bag with bullet embedded in it is υ.
For Bullet, m1 = 20 g = 0.02 kg, u1 = 500 m s-1, υ1 = υ
For Block, m2 = 1 kg, u2 = 0, υ2 = υ
According to the law of conservation of momentum,
Total momentum before collision = Total momentum after collision

Question 6.
A car travelling at the speed of 108 km/h takes 4 s to stop on applying brakes. Calculate the force acting on the car after applying brakes. Total mass of the car (including passengers) is 1000 kg.
Solution:
Inital velocity of the car (u) = 108 km/h
= 108 × \(\frac {5}{18}\)
= 30 ms-1
Final velocity of the car (υ) = 0 ms-1
Total mass of the car (m) = 1000kg
Time taken to stop the car (t) = 4s
Force ‘F’ due to application of brakes = m\(\frac {υ – u}{t}\)
= 1000kg × \(\frac {0 – 30}{4s}\)ms-1
= – 750 kg – ms-2
= – 750 N
Negative sign shows that the force applied by the brakes is acting in a direction opposite to the direction of motion of the car.
Question 7.
Which one requires more force, a body of mass 2 kg accelerated at the rate 5 m s-2 or a body of mass 4 kg accelerated at 2 m s-2
Solution:
Given:
m1 = 2kg, a1 = 5 ms-2
m2 = 4kg, a2 = 2 ms-2
Force required for first body, F1 = m1 × a1
= 2kg × 5ms-2
Force required for second body, F2 = m2 × a2
= 4kg × 2ms-2 = 8N
F1 > F2
From this, it is clear that the first body would require more force.
![]()
Question 8.
A bullet of mass 0.03 kg is fired from a gun of mass 3 kg which leaves the muzzle of the gun write a velocity of 100 ms-1. If bullet takes 0.003 s to come out of the gun then calculate the force acting on the gun.
Solution:
Mass of the gun (m1) = 3 kg
Mass of the bullet (m2) = 0.03 kg
Before firing, both the gun and the bullet are at rest
∴ Initial velocity of the gun (u1) = 0
Initial velocity of the bullet (u2) = 0
After firing. Final velocity of the gun (υ1) =?
Final velocity of the bullet (υ2) = 100 m s-1
According to the law of conservation of momentum

Negative sign shows that the gun moves backward and experiences a force of 1000 N
Question 9.
From a rifle of mass 5000 g a bullet of 20 g is fired with a velocity of 500 ms-1 with respect to the ground. Find the velocity of recoil of the rifle.
Solution:
According to law of conservation of momentum,
MV + mυ = 0
V = – \(\frac {mυ}{M}\)
Now m = 0.02 kg, υ = 500 ms-1 and M = 5 kg
∴ \(\frac {20×500}{5000}\)
or V = – 2ms-1
Negative sign shows recoiling of the rifle.
Question 10.
A girl of 40 kg mass jumps with a horizontal velocity of 5 ms-1 on a stationary trolley. The wheels of the skate are frictionless. What will be the velocity of the girl in the position of start of the trolley. Suppose no unbalanced force is acting in the horizontal direction.
Solution:
Suppose in the initial motion of the trolley, the velocity of the trolley and the girl is υ
Total initial momentum of the girl and trolley = 40 kg × 5 m s-1 + 3 kg × 0 ms-1
= 200 kg ms-1 + 0
= 200 kg – ms-1
Total momentum of the girl and trolley after she jumps on the trolley.
= 40 kg × υ ms-1 + 3 kg × υ m s-1
= (40 + 3) × υ kg – ms-1
= 43 υ kg – ms-1
According to the law of conservation of momentum.
43υ = 200
υ = \(\frac {200}{43}\)
= 4.65 ms-1
The girl boarding on the trolley will move with a velocity of 4.65 m s-1 in the direction of jump.
![]()
Question 11.
The following is the distance-time table of an object in motion.
| Time in seconds | Distance in metres |
| 0 | 0 |
| 1 | 1 |
| 2 | 8 |
| 3 | 27 |
| 4 | 64 |
| 5 | 125 |
| 6 | 216 |
| 7 | 343 |
(a) What conclusion can you draw about acceleration? Is it constant, increasing, decreasing or zero?
(b) What do vou infer about forces acting on obiect?
Solution:
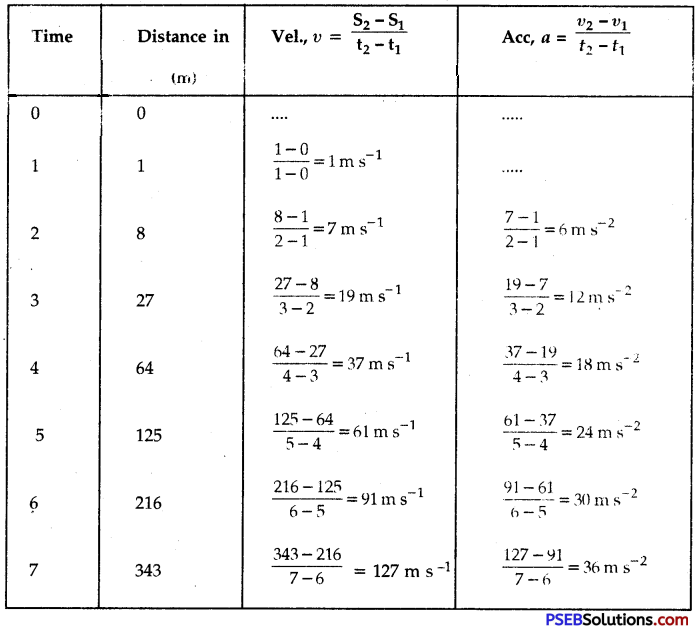
(a) Table shows that the motion is accelerated and acceleration is increasing uniformly with time i.e. acceleration is increasing by 6 ms-2 every second.
(b) Since acceleration is increasing uniformly, the force is also increasing uniformly with time.
![]()
Question 12.
Two persons manage to push a motor car of mass 1,200 kg at uniform velocity on the road. The same motor can be pushed by three persons to produce an acceleration of 0.2 ms-2. With what force does each person push the motor car? Assume that all persons push motor car with same muscular effort.
Solution:
Here, mass of the car (m) = 1200 kg
Acceleration produced in the car (a) = 0.2 ms-2
Acceleration produced by first two persons in the car = 0
It is clear that when third person pushes the car, an unbalanced force acts on the car which produces an acceleration of 0.2 ms-2
∴ Force applied by three persons together (F) = m × a
= 1200 × 0.2 = 240 N
Now because three persons together push the car using their muscular force to produce an acceleration of 0.2 ms-2
∴ Push (Force) applied by each person = \(\frac{F}{3}\)
= \(\frac{240 \mathrm{~N}}{3}\)
= 80 N
Question 13.
A hammer of mass 500 g moving at 50 ms-1, strikes a nail. The nail stops the hammer in a very short time of 0.01 s. What is the force of the nail on the hammer?
Solution:
Mass of the hammer (m) = 50 gm
= \(\frac{500}{1000}\)kg
= \(\frac{1}{2}\)kg
Initial velocity (u) = 50ms-1
Final velocity (v) = 0ms-1
Time (t) = 0.01s
Force (F) = ?
We know, υ = u + at
0 = 50 + a × 0.01
– 50 = a × \(\frac{1}{100}\)
a = – 50 × 100
∴ a = – 5000 ms-2
Here, negative sign indicates that there is retardation.
Now force applied by the nail on the hammer (F) = m × a
= \(\frac{1}{2}\) × (- 5000)
= – 2500 N
∴ Force = 2500 N
![]()
Question 14.
A motorcar of mass 1,200 kg is moving along a straight line with uniform velocity of 90 km h-1. Its velocity is slowed down to 18 km h-1 in 4 s by an unbalanced external force. Calculate the acceleration and change in momentum. Also calculate the magnitude of the force required.
Solution:
Here, mass of the car (m) = 1200 kg
Time (t) = 4 s
Initial velocity of the car (u) = 90 km/h
= \(\frac{90 \times 5}{18}\)ms-1
= 25ms-1
Final velocity of the car (υ) = 18 km/h
= 18 × \(\frac{5}{18}\)ms-1 = 5ms-1
Acceleration of the car (a) = ?
Change in momentum of the car = ?
Magnitude of the force acting on the car (F) = ?
We know, υ = u + at
5 = 25 + a × 4
– 20 = 4a
or a = \(\frac{20}{4}\)
Initial momentum = mu = 1,200 × 25 = 30,000kg ms-1
Final momentum = 1,200 × 5 = 6,000kg ms-1
Change in momentum = Final momentum – Initial momentum
= mυ – mu
= m × (υ – u)
= 1200 × (5 – 25)
= 1200 × (- 20)
= – 24000 kg ms-1
= 24000kg – ms-1 (decrease)
F = \(\frac{m×(υ – u)}{t}\)
= \(\frac{1,200×(5 – 25)}{4}\)
F = – 6,000 N
Magnitude of the force (F) = 6000N
Very Short Answer Type Questions:
Question 1.
To bring a body into motion, what is required to be done?
Answer:
It is required to be pulled, pushed or kicked.
Question 2.
Why does an object fall down?
Answer:
Due to unbalanced gravitational force.
![]()
Question 3.
Which type of force is required to change the direction of motion of the body – a balanced or unbalanced force?
Answer:
An unbalanced force is required.
Question 4.
Why does a body stop after rolling down for some time?
Answer:
Due to frictional force.
Question 5.
How can force of friction be reduced?
Answer:
By polishing/smearing the surface with a lubricant.
Question 6.
Which scientist postulated the three laws of motion?
Answer:
Newton.
Question 7.
By which other name the first law of motion is known?
Answer:
Law of Inertia.
Question 8.
Of heavy and light objects, which have more inertia?
Answer:
Heavier objects have more inertia.
Question 9.
What is the S.I unit of momentum?
Answer:
The S.I. unit of momentum is kg – ms-1.
![]()
Question 10.
Why is talcom powder sprinkled on carrom board while playing?
Answer:
In order to reduce friction.
Question 11.
Why does an athelete run before taking a high jump?
Answer:
To increase inertia in order to take high leap.
Question 12.
What is law of conservation of momentum?
Answer:
Law of conservation of momentum. The sum total of momentum of two objects before and after collision remains same unless some external force is applied.
Question 13.
A bus and a ball are moving with the same speed. To stop which one would require more force?
Answer:
Due to more inertia of bus, more force is required to be applied for stopping it.
Question 14.
A vehicle stops on applying brakes. During this activity, what happens to its momentum?
Answer:
In this activity the major part of momentum of the vehicle is transferred to the ground while the remaining part is transferred to the air molecules.
![]()
Question 15.
1 kg wt is equal to how many newtons?
Answer:
1 kg wt = 9.8 Newtons.
Question 16.
1 newton is equal to how many kg wt?
Answer:
1 newton = 0.102 kg wt.
Question 17.
On which physical quantity inertia of an object depends?
Answer:
On mass of the object.
Question 18.
On which Newton’s law of motion, the working principle of rocket is based?
Answer:
On Newton’s third law of motion.
