Punjab State Board PSEB 9th Class Science Book Solutions Chapter 11 कार्य तथा ऊर्जा Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Science Chapter 11 कार्य तथा ऊर्जा
PSEB 9th Class Science Guide कार्य तथा ऊर्जा Textbook Questions and Answers
प्रश्न 1.
निम्न सूचीबद्ध क्रियाकलापों को ध्यान से देखिए। अपनी कार्य शब्द की व्याख्या के आधार पर तर्क दीजिए कि इनमें कार्य हो रहा है अथवा नहीं।
(i) सूमा एक तालाब में तैर रही है।
(ii) एक गधे ने अपनी पीठ पर बोझा उठा रखा है।
(ii) एक पवन चक्की (विंड मिल) कुएँ से पानी उठा रही है।
(iv) एक हरे पौधे में प्रकाश-संश्लेषण की प्रक्रिया हो रही है।
(v) एक इंजन ट्रेन को खींच रहा है।
(vi) अनाज के दाने सूर्य की धूप में सूख रहे हैं।
(vii) एक पाल-नाव पवन ऊर्जा के कारण गतिशील है।
उत्तर-
(i) सूमा एक विशेष दिशा में अपना पेशीय बल लगाकर बल की दिशा में विस्थापित हो रही है। इसलिए सूमा द्वारा कार्य किया जा रहा है।
(ii) इस अवस्था में गधे की पीठ पर उठाया गया बोझ (भार) नीचे की ओर विस्थापन के लंबवत लग रहा है जिस कारण कार्य नहीं हो रहा है।
(iii) हाँ, कार्य हो रहा है क्योंकि पानी को पवन चक्की गुरुत्वाकर्षण के विपरीत दिशा में बल लगाकर उठा रही है।
(iv) हरे पौधे में प्रकाश-संश्लेषण प्रक्रिया के समय पौधे में कोई विस्थापन नहीं होता है जिस कारण कोई कार्य नहीं हो रहा है।
(v) इंजन बल लगाकर ट्रेन (गाड़ी) को बल की दिशा में खींच रहा है और ट्रेन विस्थापित होती है। इसलिए कार्य होता है।
(vi) धूप में सुखाए जा रहे अनाज के दानों में कोई विस्थापन नहीं होता है, इसलिए कोई कार्य हुआ नहीं कहा जा सकता।
(vii) पवन ऊर्जा के कारण चलती हुई पाल-नाव में बल की दिशा में विस्थापन होता है, इसलिए कार्य हो रहा
है।
प्रश्न 2.
एक पिंड को धरती से किसी कोण पर फेंका जाता है। यह एक वक्र पथ पर चलता है और वापस धरती पर आ गिरता है। पिंड के पथ क प्रारंभिक तथा अंतिम बिंदु एक ही क्षैतिज रेखा पर स्थित हैं। पिंड पर गुरुत्व बल द्वारा कितना कार्य किया गया ?
उत्तर-

जब किसी पिंड को क्षैतिज रेखा के साथ किसी कोण पर फेंका जाता है तो यह वक्रीय पथ पर जाते हुए वापिस धरती पर आ जाता है। इस व्यवस्था में कोई कार्य नहीं होता क्योंकि गुरुत्वाकर्षण बल लंबवत् नीचे की दिशा में लगता है जबकि विस्थापन क्षैतिज दिशा में होता है। इस अवस्था में θ = 90°
तथा cos θ = cos 90° = 0
∴ W = F cos θ × S
= F × o × S
W = 0
![]()
प्रश्न 3.
एक बैटरी बल्ब जलाती है। इस प्रक्रम में होने वाले ऊर्जा परिवर्तनों का वर्णन कीजिए।
उत्तर-
बैटरी में रासायनिक क्रिया होती है जिससे रासायनिक ऊर्जा विद्युत् ऊर्जा में रूपांतरित होती है। यह विद्युत् ऊर्जा बल्ब को पहले गर्म करके ताप ऊर्जा और फिर प्रकाश ऊर्जा में परिवर्तित करती है।
प्रश्न 4.
20 kg द्रव्यमान पर लगने वाला कोई बल इसके वेग को 5ms-1 से 2 ms-1 में परिवर्तित कर देता है। बल द्वारा किए गए कार्य का परिकलन कीजिए।
हल :
द्रव्यमान (m) = 20 kg
प्रारंभिक वेग (u) = 5 ms-1
अंतिम वेग (υ) = 2 ms-1
वस्तु की प्रारंभिक गतिज ऊर्जा (EK1) = \(\frac {1}{2}\)mu2
= \(\frac {1}{2}\) × 20 × (5)2
= \(\frac {1}{2}\) × 20 × 5 × 5
= 250J
वस्तु की अंतिम गतिज ऊर्जा (EK2) = \(\frac {1}{2}\)mv2
= \(\frac {1}{2}\) × 20 × (2)2
= \(\frac {1}{2}\) × 20 × 2 × 2
= 40J
∴ बल द्वारा किया गया कार्य = गतिज ऊर्जा में परिवर्तन
= अंतिम गतिज ऊर्जा – प्रारंभिक गतिज ऊर्जा
= 40J – 250J
= – 210J
ऋण चिहन से यह स्पष्ट होता है कि विरोधी बल कार्य कर रहा है।
प्रश्न 5.
10 kg द्रव्यमान का एक पिंड मेज़ पर A बिंदु पर रखा है। इसे B बिंदु पर लाया जाता है। यदि A तथा B को मिलाने वाली रेखा क्षैतिज है तो पिंड पर गुरुत्व बल द्वारा किया गया कार्य कितना होगा ? अपने उत्तर की व्याख्या कीजिए।
हल :
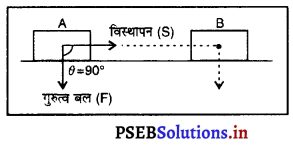
10 kg द्रव्यमान के पिंड को A से B बिंदु तक क्षैतिज दिशा में विस्थापित किया गया है परंतु गुरुत्वाकर्षण बल लंबवत नीचे की दिशा में क्रिया कर रहा है जो विस्थापन दिशा के साथ 90° का कोण बना रहा है।
∴ गुरुत्वाकर्षण बल द्वारा किया गया कार्य (W) = F cos θ × S
= F × cos 90° × S
= F × 0 × S
= 0 (शून्य) उत्तर
प्रश्न 6.
मुक्त रूप से गिरते एक पिंड की स्थितिज ऊर्जा लगातार कम होती जाती है। क्या यह ऊर्जा संरक्षण नियम का उल्लंघन करती है। कारण बताइए।
उत्तर-
नहीं, ऊर्जा संरक्षण नियम का उल्लंघन नहीं होता है। जब मुक्त रूप से गिर रहे पिंड की ऊँचाई कम होती है तो स्थितिज ऊर्जा निरंतर कम होती है परंतु गतिज ऊर्जा में वृद्धि होती है। किसी भी समय गतिज ऊर्जा तथा स्थितिज ऊर्जा का योग स्थिर रहता है।
प्रश्न 7.
जब आप साइकिल चलाते हैं तो कौन-कौन से ऊर्जा रूपांतरण करते हैं ?
उत्तर-
जब हम साइकिल चलाते हैं तो उस समय हमारी माँसपेशियों की ऊर्जा, ताप ऊर्जा और गतिज ऊर्जा में रूपांतरित होती है। यह गतिज ऊर्जा सड़क की घर्षण ऊर्जा के विरुद्ध कार्य करने में खर्च होती है।
![]()
प्रश्न 8.
जब आप अपनी सारी शक्ति लगा कर एक बड़ी चट्टान को धकेलना चाहते हैं और इसे हिलाने में असफल हो जाते हैं तो क्या इस अवस्था में ऊर्जा का स्थानांतरण होता है ? आपके द्वारा व्यय की गई ऊर्जा कहाँ चली जाती है ?
उत्तर-
जब हम अपनी सारी शक्ति लगाकर चट्टान को धकेलकर हिलाने में असफल हो जाते हैं तो उस समय कोई कार्य नहीं किया जाता है, परंतु हम अपनी पेशीय ऊर्जा का प्रयोग करते हैं। इस पेशीय ऊर्जा ने चट्टान तथा सड़क की सतह के मध्य उत्पन्न होने वाले घर्षण बल के विरोध में कार्य करने का यत्न किया तथा ताप ऊर्जा में परिवर्तित हो गई जो पसीने तथा थकान के रूप में प्रकट हुई।
प्रश्न 9.
किसी घर में एक महीने में ऊर्जा की 250 यूनिटें व्यय हुईं। यह ऊर्जा जूल में कितनी होगी ?
हल :
हम जानते हैं, 1 यूनिट ऊर्जा = 1 किलोवाट घंटा (1 kWh)
= 1 kW × 1 h
1 × 1000 वाट × 3600 सेकेण्ड
= 36 × 105 J
= 3.6 × 106 J
∴ 250 यूनिट ऊर्जा = 250 × 3.6 × 106 J
= 900 × 106 J
= 9 × 108
प्रश्न 10.
40 kg द्रव्यमान का एक पिंड धरती से 5m की ऊँचाई तक उठाया जाता है। इसकी स्थितिज ऊर्जा कितनी है ? यदि पिंड को मुक्त रूप से गिरने दिया जाए तो जब पिंड ठीक आधे रास्ते पर है उस समय इसकी गतिज ऊर्जा का परिकलन कीजिए। [g = 10 ms-2]
हल :
यहां द्रव्यमान (m) = 40 kg
ऊँचाई (h) = 5m
गुरुत्वीय त्वरण (g) = 10 ms-2
5m की ऊँचाई पर पिंड की स्थितिज ऊर्जा (Ep) = mgh
= 40 × 10 × 5J
= 32000 J
जब पिंड आधे रास्ते नीचे आ गया तो मान लो इसका वेग υ है।
अब पिंड द्वारा तय की गई दूरी (S) = \(\frac{5}{2}\) = 2.5m
υ2– u2 = 2gS का प्रयोग करके
υ2 – (0)2 = 2 × 10 × 2.5
υ2 = 2 × 25
या υ = 50
आधे रास्ते पहुँचकर पिंड की गतिज ऊर्जा (EK) = \(\frac{1}{2}\)mυ2
= \(\frac{1}{2}\) × 40 × 50
= 1000 J
प्रश्न 11.
पृथ्वी के चारों ओर घूमते हुए किसी उपग्रह पर गुरुत्व बल द्वारा कितना कार्य किया जाएगा ? अपने उत्तर को तर्क संगत बनाइए।
उत्तर-
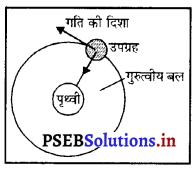
जब कोई उपग्रह पृथ्वी के चारों ओर चक्कर लगाता है तो गुरुत्व बल गति की दिशा इस वृत्तीय पथ के अर्धव्यास के साथ अंदर की ओर लगता है जबकि गति की दिशा इस पथ की स्पर्श रेखा (Tangent) जो अर्धव्यास के लंबवत् होती है। इस प्रकार गुरुत्वाकर्षण बल तथा विस्थापन परस्पर एक-दूसरे के साथ 90° का कोण बनाते हैं जिस कारण उपग्रह पर किया गया कार्य शून्य (0) होता है।
प्रश्न 12.
क्या किसी पिंड पर लगने वाले किसी भी बल की अनुपस्थिति में इसका विस्थापन हो सकता है ? सोचिए ! इस प्रश्न के बारे में अपने मित्रों तथा अध्यापकों से विचार-विमर्श कीजिए।
उत्तर-
किसी पिंड पर लगने वाले बल की अनुपस्थिति में इस पिंड का विस्थापन संभव है। यदि पिंड समान वेग से गति कर रहा है यदि पिंड विराम अवस्था में है तो बल की अनुपस्थिति में इसका विस्थापन संभव नहीं होगा।
![]()
प्रश्न 13.
कोई मनुष्य भूसे के गट्ठर को अपने सिर पर 30 मिनट तक रखे रहता है और थक जाता है। क्या उसने कुछ कार्य किया है या नहीं ? अपने उत्तर को तर्क संगत बनाइए।
उत्तर-
मनुष्य ने भूसे का गट्ठर अपने सिर पर 30 मिनट तक रखा और थक गया परंतु गुरुत्वाकर्षण बल के लगने पर भी गट्ठर में कोई विस्थापन नहीं हुआ है। इसलिए उस मनुष्य द्वारा कोई कार्य नहीं किया गया कहा जाएगा।
प्रश्न 14.
एक विद्युत् हीटर (ऊष्मक) की घोषित शक्ति 1500 w है। 10 घंटे में यह कितनी ऊर्जा उपयोग करेगा ?
हल-
यहाँ, विद्युत् हीटर की शक्ति (P) = 1500 W
जितने समय के लिए हीटर उपयोग किया गया (t) = 10 घंटे
हीटर द्वारा खर्च की गई कुल ऊर्जा (E) = P × t
= 1500 W × 10 h
= 15000 watt-hours (Wh)
यूनिट = \(\frac{15000}{1000}\)
= 15 kWh
प्रश्न 15.
जब हम किसी सरल लोलक के गोलक को एक ओर ले जाकर छोड़ते हैं तो यह दोलन करने लगता है। इसमें होने वाले ऊर्जा परिवर्तनों की चर्चा करते हुए ऊर्जा संरक्षण नियम को स्पष्ट कीजिए। गोलक कुछ समय पश्चात् विराम अवस्था में आ जाता है ? अंततः इसकी ऊर्जा का क्या होता है ? क्या यह ऊर्जा संरक्षण नियम का उल्लंघन है ?
उत्तर-
दोलित सरल लोलक में ऊर्जा का रूपांतरण – प्रारंभ में लोलक अपनी माध्य स्थिति में विराम अवस्था में होता है, इसलिए इस समय इसकी गतिज ऊर्जा शून्य होती है। इस स्थिति में हम इसकी स्थितिज ऊर्जा को भी शून्य मान लेते हैं।
जब गोलक को माध्य स्थिति से एक ओर को ले जाते हैं तो इसकी ऊँचाई बढ़ने लगती है और इस क्रिया में हमें गुरुत्वीय बल के विरुद्ध कुछ कार्य करना पड़ता है। यह कार्य गोलक की स्थितिज ऊर्जा के रूप में संचित होता जाता है। इस प्रकार माध्य स्थिति से एक तरफ का अधिकतम विस्थापन की स्थिति (आयाम) में जब गोलक को छोड़ा जाता है तो उस स्थिति में गोलक की स्थितिज ऊर्जा अधिकतम और गतिज ऊर्जा शून्य होती है। अब गोलक छोड़ने पर गोलक वापिस धीरे-धीरे माध्य स्थिति की ओर बढ़ता है जिससे गोलक की ऊँचाई कम होने लगती है अर्थात् स्थितिज ऊर्जा कम होने लगती है जबकि वेग में धीरे-धीरे वृद्धि होने के कारण गतिज ऊर्जा बढ़ना प्रारंभ करती है। क्योंकि गोलक वायु में से होकर गति करता है, इसलिए वायु के घर्षण के विरुद्ध कार्य करने से कुछ ऊर्जा व्यय हो जाती है। इससे वायु के अणुओं का वेग बढ़ने के कारण उसकी गतिज ऊर्जा बढ़ जाती है। वापिस माध्य स्थिति में पहुँचकर लोलक की गतिज ऊर्जा अधिकतम और स्थितिज ऊर्जा शून्य हो जाती है। गति जड़त्व के कारण गोलक यहाँ विराम अवस्था में नहीं आता अपितु माध्य स्थिति के दूसरी ओर गतिशील रहता है।
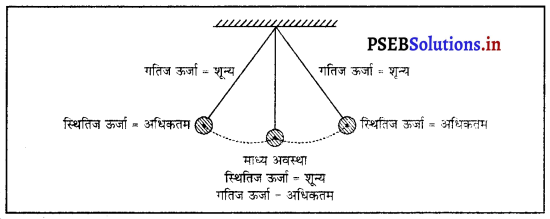
इससे गोलक की ऊँचाई बढ़ने लगती है, अत: उसकी स्थितिज ऊर्जा बढ़ने लगती है, परंतु गतिज ऊर्जा घटने लगती है। अधिकतम विस्थापन की स्थिति में गोलक की स्थितिज ऊर्जा अधिकतम तथा गतिज ऊर्जा शून्य हो जाती है। गोलक यहां रुका नहीं रहता, पुनः माध्य अवस्था की ओर लौटने लगता है। प्रत्येक स्थिति में गोलक की स्थितिज ऊर्जा, गतिज ऊर्जा तथा वायु के अणुओं को ऊर्जा का योग नियत बना रहता है। इस प्रकार सरल लोलक के दोलनों में कुल ऊर्जा संरक्षित रहती है।
गोलक का आयाम गोलक की कुल ऊर्जा पर निर्भर करता है । गोलक द्वारा वायु के अणुओं को दी गई ऊर्जा पुनः गोलक को वापिस नहीं मिल पाती। इससे गोलक की कुल ऊर्जा लगातार घटती जाती है। जब गोलक अपनी संपूर्ण ऊर्जा वायु के अणुओं को दे देता है तो उसकी कुल ऊर्जा शून्य हो जाती है और वह माध्य स्थिति में विराम अवस्था में आ जाता है।
इस प्रकार यह ऊर्जा संरक्षण के नियम का उल्लंघन नहीं है।
प्रश्न 16.
m द्रव्यमान का एक पिंड एक नियत वेग υ से गतिशील है। पिंड पर कितना कार्य करना चाहिए कि वह विराम अवस्था में आ जाए?
हल :
मान लो, पिंड का द्रव्यमान = m
पिंड का आरंभिक वेग = υ
∴ पिंड की गतिज ऊर्जा (EK) = \(\frac {1}{2}\)mυ2
m द्रव्यमान वाले पिंड का अंतिम वेग = 0 (विराम अवस्था में)
∴ पिंड पर कार्य करने की आवश्यकता = पिंड की गतिज ऊर्जा में परिवर्तन
= \(\frac {1}{2}\)mυ2 – \(\frac {1}{2}\)m (0)2
= \(\frac {1}{2}\)mυ2 – 0
= \(\frac {1}{2}\)mυ2
प्रश्न 17.
1500 kg द्रव्यमान की कार को जो 60 km/h के वेग से चल रही है, रोकने के लिए किए गए कार्य का परिकलन कीजिए।
हल :
यहाँ कार का द्रव्यमान (m) = 1500 kg
कार का प्रारंभिक वेग (u) = 60 km/h
= \(\frac{60 \times 1000}{60 \times 60}\) m/s
= \(\frac{50}{3}\) ms-1
कार का अंतिम वेग (υ) = 0 (विराम अवस्था)
कार को विराम अवस्था में लाने के लिए किया गया कार्य = कार की गतिज ऊर्जा में परिवर्तन

= 208333.3 J
= 208.33 kJ
![]()
प्रश्न 18.
निम्न में से प्रत्येक स्थिति में m द्रव्यमान के एक पिंड पर एक बल F लग रहा है। विस्थापन की दिशा पश्चिम से पूर्व की ओर है जो एक लंबे तीर से प्रदर्शित की गई है। चित्रों को ध्यानपूर्वक देखिए और बताइए कि किया गया कार्य ऋणात्मक है, धनात्मक है या शून्य है।
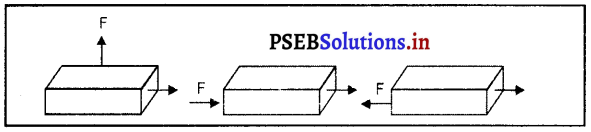
उत्तर-
(i) इस स्थिति में बल तथा विस्थापन एक-दूसरे के लंबवत हैं,
∴ θ = 90°
cos θ = cos 90° = 0
अब पिंड पर किया गया कार्य, W = F S cos θ
= F S cos 90°
= F × s × 0
= 0 (शून्य) उत्तर
(ii) इस स्थिति में बल F तथा विस्थापन एक ही दिशा में हैं।
∴ θ = 0°
cos θ = cos 0° = 1
अब पिंड पर किया गया कार्य, W = F S cos θ
= F × S × cos 0°
= F × S × 1
= FS, जोकि घनात्मक है।
(iii) इस स्थिति में पिंड पर लगाया गया बल F तथा विस्थापन विपरीत दिशा में हैं, इसलिए
θ = 180°
cos θ = cos 180° = -1
अब पिंड पर किया गया कार्य, W = FS cos θ
= FS cos 180°
= F × S × (-1)
= – FS जोकि ऋणात्मक है।
प्रश्न 19.
सोनी कहती है कि किसी वस्तु पर त्वरण शून्य हो सकता है चाहे उस पर कई बल कार्य कर रहे हों। क्या आप उससे सहमत हैं ? बताइए क्यों ?
उत्तर-
हाँ, मैं सोनी के कथन से सहमत हूँ क्योंकि यदि वस्तु पर अनेक बल एक ही समय पर लग रहे हैं तथा उनका परिणामी योग शून्य है तो वस्तु का त्वरण भी शून्य ही होगा।
a = \(\frac{\mathrm{F}}{m}\)
a = \(\frac{\mathrm{F}}{m}\) = 0
प्रश्न 20.
चार युक्तियाँ, जिनमें प्रत्येक की शक्ति 500 W है। 10 घंटे तक उपयोग में लाई जाती हैं। इनके द्वारा व्यय की गई ऊर्जा kWh में परिकलित कीजिए।
उत्तर-
एक युक्ति की शक्ति (p) = 500 W
∴ 4 युक्तियों की कुल शक्ति (P) = 500 W × 4
= 2000 W
जितने समय के लिए 4 युक्तियाँ उपयोग की गईं (t) = 10 घंटे
व्यय की गई ऊर्जा (E) = P × t
2000 W × 10 h
= 20000 Wh
= \(\frac{20000}{1000}\) = 20 kWh
प्रश्न 21.
मुक्त रूप से गिरता एक पिंड अंततः धरती तक पहुँचने पर रुक जाता है। इसकी गतिज ऊर्जा का क्या होता है ?
उत्तर-
जब कोई पिंड मुक्त रूप से नीचे धरती की ओर गिरता है तो धरती पर पहुँच कर रुक जाता है तथा इसकी गतिज ऊर्जा का अन्य रूपों में रूपांतरण हो जाता है। ये ऊर्जा के रूप, ऊष्मा, ध्वनि तथा प्रकाश हैं। अंततः यह स्थितिज ऊर्जा में रूपांतरित हो जाती है।
![]()
Science Guide for Class 9 PSEB कार्य तथा ऊर्जा InText Questions and Answers
पाठ्य-पुस्तक के प्रश्नों के उत्तर
प्रश्न 1.
किसी वस्तु पर 7 N का बल लगता है। मान लीजिए बल की दिशा में विस्थापन 8m है (देखें चित्र)। मान लीजिए वस्तु के विस्थापन के समय लगातार वस्तु पर बल लगता रहता है। इस स्थिति में किया गया कार्य कितना होगा ?
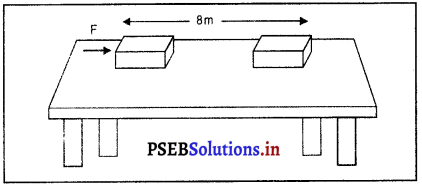
हल:
यहां बल (F) = 7 न्यूटन (N)
विस्थापन (S) = 8 m
किया गया कार्य (W) = ?
हम जानते हैं, W = F × s
= 7N × 8 m
= 56 N – m
= 56 J (जूल) उत्तर
प्रश्न 2.
हम कब कहते हैं कि कार्य किया गया है ?
उत्तर-
कार्य (Work) – जब किसी वस्तु पर बल लगाया जाता है तथा वह वस्तु बल की दिशा में विस्थापित होती है, तो बल द्वारा कार्य किया गया कहा जाता है।
∴ कार्य (W) = बल (F) × विस्थापन (S)
प्रश्न 3.
जब किसी वस्तु पर लगने वाला बल इसके विस्थापन की दिशा में हो तो किए गए कार्य का व्यंजक लिखिए।
उत्तर-
जब वस्तु में विस्थापन उस पर लगने वाले बल (F) की दिशा में हो तो,
कार्य (W) = बल (F) × विस्थापन (S)
प्रश्न 4.
1J कार्य को परिभाषित कीजिए।
उत्तर-
एक जूल कार्य किया गया कहा जाता है यदि वस्तु पर लगने वाला 1 न्यूटन बल वस्तु को अपनी ही दिशा में 1 m की दूरी से विस्थापित करे।
W = F × S
अथवा 1J = 1N × 1m
प्रश्न 5.
बैलों की एक जोड़ी खेत जोतते समय किसी हल पर 140 N बल लगाती है। जोता गया खेत 15 m लंबा है। खेत की लंबाई को जोतने में कितना कार्य किया गया ?
हल :
यहा लगाया गया बल (F) = 140 N
खेत की लंबाई (S) = 15m
किया गया कार्य (W) = ?
अब W = F × S
∴ किया गया कार्य (W) = 140 N × 15 m
= 2100 N – m
= 2100 J
![]()
प्रश्न 6.
किसी वस्तु की गतिज ऊर्जा क्या होती है ?
उत्तर-
गतिज ऊर्जा (Kinetic Energy) – किसी वस्तु की गतिज ऊर्जा उसमें उपस्थित गति के कारण होती है।
उदाहरण-
- गतिशील पत्थर।
- बहती वायु।
- घूमता हुआ पहिया।
प्रश्न 7.
किसी वस्तु की गतिज ऊर्जा के लिए व्यंजक लिखिए।
उत्तर-
एक m द्रव्यमान वाली वस्तु जो समान वेग υ से गतिशील हो, की गतिज ऊर्जा (Ek) = \(\frac {1}{2}\) × द्रव्यमान × (वेग)2
= \(\frac {1}{2}\) × m × (υ)2
∴ गतिज ऊर्जा का व्यंजक (Ek) = \(\frac {1}{2}\)mυ2
प्रश्न 8.
5ms-1 के वेग से गतिशील किसी m द्रव्यमान की वस्तु की गतिज ऊर्जा 25 J है। यदि इसके वेग को दोगुना कर दिया जाए तो इसकी गतिज ऊर्जा कितनी हो जाएगी ? यदि इसके वेग को तीन गुना बढ़ा दिया जाए तो इसकी गतिज ऊर्जा कितनी हो जाएगी?
हल :
दिया है, वस्तु का द्रव्यमान = m
वस्तु का वेग (υ) = 5 ms-1
वस्तु की गतिज ऊर्जा (EK) = 25 J
हम जानते हैं, EK = \(\frac {1}{2}\)mυ2
25 = \(\frac {1}{2}\)m × (5)2
25 = \(\frac {1}{2}\)m × 25
या m = \(\frac{25 \times 2}{25}\)
∴ m = 2 kg
(i) जब वस्तु का वेग दोगुना कर दिया जाता है, तो
m = 2 kg
υ1 = 2 × 5 ms-1
EK1 = \(\frac {1}{2}\) × m × υ12
= \(\frac {1}{2}\) × 2 × (10)2
= \(\frac {1}{2}\) × 2 × 10 × 10
= 100 J
= 4 × 25J
∴ EK1 = 4 × EK
∴ वेग दोगुना करने पर वस्तु की गतिज ऊर्जा (EK1), पहली ऊर्जा (EK = 5 J) का चार गुणा हो जायेगा।
(ii) जब वस्तु का वेग तिगुना कर दिया जाए, तो
υ2 = 3 × υ
= 3 × 5 ms-1
= 15 ms-1
.. वस्तु की गतिज ऊर्जा (EK2) = \(\frac {1}{2}\) × m × (υ2)2
= \(\frac {1}{2}\) × 2 × (15)2
= \(\frac {1}{2}\) × 2 × 15 × 15
=225J
= 9 × 25J
∴ EK2 = 9 × (EK)
अर्थात् वस्तु का वेग तिगुना करने पर वस्तु की गतिज ऊर्जा, पहली गतिज ऊर्जा (EK = 25 J) का नौ गुना हो जायेगी।
प्रश्न 9.
शक्ति क्या है ?
उत्तर-
शक्ति (Power) – कार्य करने की दर अथवा ऊर्जा रूपांतरण की दर को शक्ति कहते हैं। यदि कोई कारक (एजेंट) t समय में W कार्य करता है, तो शक्ति का मान होगा

∴ P= \(\frac{\mathrm{W}}{t}\)
प्रश्न 10.
1 वाट शक्ति को परिभाषित कीजिए।
उत्तर-
वाट (Watt) – 1 वाट उस कारक या मशीन की शक्ति है जो 1 सेकेण्ड में 1 जूल कार्य करता है।
हम इस प्रकार भी कह सकते हैं कि यदि ऊर्जा के उपयोग की दर 1 Js-1 (जूल प्रति सेकेंड) हो तो शक्ति 1 वाट (W) होगी।
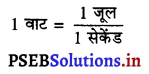
या 1 W = \(\frac{1 \mathrm{~J}}{1 \mathrm{~s}}\)
= 1 Js-1
![]()
प्रश्न 3.
एक लैंप 1000 J विद्युत् ऊर्जा 10 s में व्यय करता है। इसकी शक्ति कितनी है ?
हल :
यहाँ, W = 1000 J
t = 10s
हम जानते हैं, शक्ति (p) = \(\frac{\mathrm{E}}{t}\)
= \(\frac{1000 \mathrm{~J}}{10 s}\)
= 100 Js-1
P = 100 W
प्रश्न 11.
औसत शक्ति को परिभाषित कीजिए।
उत्तर-
औसत (मध्यमान) शक्ति (Average Power) – कुल उपयोग की गई ऊर्जा तथा कुल लगे समय के अनुपात को औसत (मध्यमान) शक्ति कहते हैं।

