PSEB 9th Class Science Solutions Chapter 11 ਕਾਰਜ ਅਤੇ ਊਰਜਾ

Punjab State Board PSEB 9th Class Science Book Solutions Chapter 11 ਕਾਰਜ ਅਤੇ ਊਰਜਾ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Science Chapter 11 ਕਾਰਜ ਅਤੇ ਊਰਜਾ

PSEB 9th Class Science Guide ਕਾਰਜ ਅਤੇ ਊਰਜਾ Textbook Questions and Answers

ਅਭਿਆਸ ਦੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਹੇਠ ਲਿਖੀਆਂ ਸੂਚੀਬੱਧ ਕਿਰਿਆਵਾਂ ਨੂੰ ਧਿਆਨ ਨਾਲ ਦੇਖੋ । ਆਪਣੀ ਕਾਰਜ ਸ਼ਬਦ ਦੀ ਵਿਆਖਿਆ ਦੇ ਆਧਾਰ ‘ਤੇ ਤਰਕ ਦਿਓ ਕਿ ਇਸ ਵਿੱਚ ਕਾਰਜ ਹੋ ਰਿਹਾ ਹੈ ਜਾਂ ਨਹੀਂ ।
(i) ਸੂਮਾ ਇੱਕ ਤਾਲਾਬ ਵਿੱਚ ਤੈਰ ਰਹੀ ਹੈ ।
(ii) ਇੱਕ ਗਧੇ ਨੇ ਆਪਣੀ ਪਿੱਠ ਉੱਤੇ ਬੋਝਾ ਉਠਾਇਆ ਹੈ ।
(iii) ਇਕ ਪਵਨ ਚੱਕੀ (ਪੌਣ ਮਿਲ) ਖੂਹ ਤੋਂ ਪਾਣੀ ਉਠਾ ਰਹੀ ਹੈ ।
(iv) ਇੱਕ ਹਰੇ ਪੌਦੇ ਵਿੱਚ ਪ੍ਰਕਾਸ਼ ਸੰਸ਼ਲੇਸ਼ਣ ਦੀ ਕਿਰਿਆ ਹੋ ਰਹੀ ਹੈ ।
(v) ਇੱਕ ਇੰਜਣ ਗੱਡੀ ਨੂੰ ਖਿੱਚ ਰਿਹਾ ਹੈ ।
(vi) ਅਨਾਜ ਦੇ ਦਾਣੇ ਸੂਰਜ ਦੀ ਧੁੱਪ ਵਿੱਚ ਸੁੱਕ ਰਹੇ ਹਨ ।
(vii) ਇੱਕ ਕਿਸ਼ਤੀ ਪਵਨ ਊਰਜਾ ਦੇ ਕਾਰਨ ਗਤੀਸ਼ੀਲ ਹੈ ।
ਉੱਤਰ-
(i) ਸੁਮਾ ਇੱਕ ਖ਼ਾਸ ਦਿਸ਼ਾ ਵਿੱਚ ਆਪਣੇ ਪੱਠਿਆਂ ਦਾ ਬਲ ਲਗਾ ਕੇ ਬਲ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਵਿਸਥਾਪਿਤ ਹੋ ਰਹੀ ਹੈ । ਇਸ ਲਈ ਸੂਮਾ ਦੁਆਰਾ ਕਾਰਜ ਕੀਤਾ ਜਾ ਰਿਹਾ ਹੈ ।

(ii) ਇਸ ਅਵਸਥਾ ਵਿਚ ਗਧੇ ਦੀ ਪਿੱਠ ‘ਤੇ ਪਿਆ ਹੋਇਆ ਭਾਰ (ਬਲ) ਥੱਲੇ ਵੱਲ, ਪਰੰਤੂ ਵਿਸਥਾਪਨ ਦੀ ਦਿਸ਼ਾ ਦੇ ਲੰਬਵਤ ਲੱਗ ਰਿਹਾ ਹੈ ਜਿਸ ਕਰਕੇ ਕਾਰਜ ਨਹੀਂ ਹੋ ਰਿਹਾ ਹੈ ।

(iii) ਹਾਂ ਕਾਰਜ ਹੋ ਰਿਹਾ ਹੈ ਕਿਉਂਕਿ ਪਾਣੀ ਨੂੰ ਗੁਰੂਤਾ ਆਕਰਸ਼ਣ ਬਲ ਦੇ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਬਲ ਲਗਾ ਕੇ ਉੱਪਰ ਚੁੱਕਿਆ ਜਾ ਰਿਹਾ ਹੈ ।

(iv) ਹਰੇ ਪੌਦੇ ਵਿੱਚ ਪ੍ਰਕਾਸ਼ ਸੰਸ਼ਲੇਸ਼ਣ ਕਿਰਿਆ ਦੌਰਾਨ ਪੌਦੇ ਵਿੱਚ ਕੋਈ ਵਿਸਥਾਪਨ ਨਹੀਂ ਹੁੰਦਾ ਹੈ, ਜਿਸ ਕਰਕੇ ਕੋਈ ਕਾਰਜ ਨਹੀਂ ਹੋ ਰਿਹਾ ਹੈ ।

(v) ਗੱਡੀ ਨੂੰ ਖਿੱਚਦੇ ਸਮੇਂ ਕਾਰਜ ਹੁੰਦਾ ਹੈ ਕਿਉਂਕਿ ਬਲ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਗੱਡੀ ਦਾ ਵਿਸਥਾਪਨ ਹੁੰਦਾ ਹੈ ।

(vi) ਧੁੱਪ ਵਿੱਚ ਪਏ ਦਾਣਿਆਂ ਵਿੱਚ ਕੋਈ ਵਿਸਥਾਪਨ ਨਹੀਂ ਹੁੰਦਾ ਹੈ, ਇਸ ਲਈ ਕੋਈ ਕਾਰਜ ਹੋਇਆ ਨਹੀਂ ਮੰਨਿਆ ਜਾ ਸਕਦਾ ।

(vii) ਚਲਦੀ ਹੋਈ ਪਵਨ ਬਲ ਲਗਾ ਕੇ ਕਿਸ਼ਤੀ ਨੂੰ ਆਪਣੀ ਦਿਸ਼ਾ ਵਿੱਚ ਵਿਸਥਾਪਿਤ ਕਰਦੀ ਹੈ, ਇਸ ਲਈ ਕਾਰਜ ਹੋ ਰਿਹਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਵਸਤੂ ਨੂੰ ਧਰਤੀ ਤੋਂ ਕਿਸੀ ਕੋਣ ’ਤੇ ਡਿਗਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਇੱਕ ਵਕਰ ਪੱਥ ਉੱਤੇ ਚੱਲਦਾ ਹੈ। ਅਤੇ ਵਾਪਸ ਧਰਤੀ ਉੱਤੇ ਆ ਡਿੱਗਦਾ ਹੈ । ਵਸਤੂ ਦੇ ਪੱਥ ਦੇ ਆਰੰਭਿਕ ਅਤੇ ਅੰਤਿਮ ਬਿੰਦੂ ਇੱਕ ਹੀ ਹੋਰੀਜ਼ੈਨਟਿਲ (ਖਿਤਿਜੀ) ਰੇਖਾ ਉੱਤੇ ਸਥਿਤ ਹੈ | ਵਸਤੁ ਉੱਤੇ ਗੁਰੁਤਾ ਬਲ ਦੁਆਰਾ ਕਿੰਨਾ ਕਾਰਜ ਕੀਤਾ ਗਿਆ ?
ਉੱਤਰ-

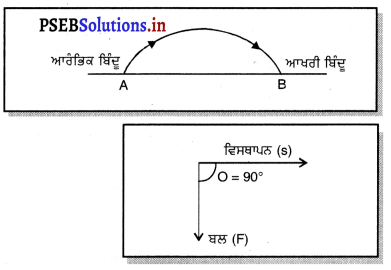
ਜਦੋਂ ਕਿਸੇ ਵਸਤੂ ਨੂੰ ਖਿਤਿਜੀ ਰੇਖਾ ਨਾਲ, ਕਿਸੇ ਕੋਣ ’ਤੇ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਇਹ ਵਕਰੀ ਪੱਥ ਵਿੱਚ ਜਾਂਦੇ ਹੋਏ ਧਰਤੀ `ਤੇ ਆ ਡਿੱਗਦੀ ਆਰੰਭਿਕ ਬਿੰਦੂ ,
ਆਖਰੀ ਬਿੰਦੂ ਹੈ । ਇਸ ਅਵਸਥਾ ਵਿੱਚ ਕੋਈ ਕਾਰਜ ਨਹੀਂ ਹੁੰਦਾ ਕਿਉਂਕਿ ਗੁਰੂਤਾ ਆਕਰਸ਼ਣ ਬਲ ਲੰਬਵਤ ਹੇਠਾਂ ਵੱਲ ਲੱਗਦਾ ਹੈ ਜਦੋਂ ਕਿ ਵਿਸਥਾਪਨ ਖਿਤਿਜ ਦਿਸ਼ਾ ਵਿੱਚ ਹੁੰਦਾ ਹੈ । ਇਸ ਹਾਲਤ ਵਿੱਚ θ = 90° ਅਤੇ cosθ = cos 90° = 0
∴ W = F cos θ × S
F × 0 × S
W = 0

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਬੈਟਰੀ ਬਲਬ ਨੂੰ ਜਲਾਉਂਦੀ ਹੈ । ਇਸ ਪ੍ਰਕਿਰਿਆ ਵਿੱਚ ਹੋਣ ਵਾਲੇ ਊਰਜਾ ਪਰਿਵਰਤਨਾਂ ਦਾ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਬੈਟਰੀ ਵਿੱਚ ਰਸਾਇਣਿਕ ਕਿਰਿਆ ਹੁੰਦੀ ਹੈ ਜਿਸ ਤੋਂ ਰਸਾਇਣਿਕ ਉਰਜਾ, ਬਿਜਲਈ ਊਰਜਾ ਵਿੱਚ ਰੂਪਾਂਤਰਿਤ ਹੁੰਦੀ ਹੈ । ਇਹ ਬਿਜਲਈ ਊਰਜਾ ਬਲਬ ਨੂੰ ਪਹਿਲਾਂ ਗਰਮ ਕਰਕੇ ਤਾਪ ਊਰਜਾ ਅਤੇ ਫਿਰ ਪ੍ਰਕਾਸ਼ ਊਰਜਾ ਵਿੱਚ ਪਰਿਵਰਤਿਤ ਕਰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
20 kg ਪੰਜ ਲੱਗਣ ਵਾਲਾ ਕੋਈ ਬਲ ਇਸਦੇ ਵੇਗ ਨੂੰ 5 ms^-1 ਤੋਂ 2 ms^-1 ਵਿੱਚ ਪਰਿਵਰਤਨ ਕਰ ਦੇਂਦਾ ਹੈ । ਬਲ ਦੁਆਰਾ ਕੀਤੇ ਗਏ ਕਾਰਜ ਦਾ ਪਰਿਕਲਨ ਕਰੋ ।
ਹੱਲ:
ਪੁੰਜ (m) = 20 kg
ਆਰੰਭਿਕ ਵੇਗ (u) = 5 ms^-1
ਅੰਤਿਮ ਵੇਗ (υ) = 2 ms^-1
ਵਸਤੂ ਦੀ ਮੁੱਢਲੀ ਗਤਿਜ ਊਰਜਾ (E_K1) = \(\frac {1}{2}\)mu²
= \(\frac {1}{2}\) × 20 × (5)²
= \(\frac {1}{2}\) × 20 × 5 × 5
= 250 J.

ਵਸਤੂ ਦੀ ਅੰਤਿਮ ਊਰਜਾ (E_K2) : \(\frac {1}{2}\)mυ²
= \(\frac {1}{2}\) × 20 × (2)²
= \(\frac {1}{2}\) × 20 × 2 × 2
= 40 J
∴ ਬਲ ਦੁਆਰਾ ਕੀਤਾ ਗਿਆ ਕਾਰਜ = ਗਤਿਜ ਊਰਜਾ ਵਿੱਚ ਪਰਿਵਰਤਨ ਅੰਤਿਮ ਗਤਿਜ ਊਰਜਾ – ਮੁੱਢਲੀ ਗਤਿਜ ਊਰਜਾ
= 40 – 250
= -210 J
ਰਿਣ ਚਿੰਨ੍ਹ ਤੋਂ ਪਤਾ ਲੱਗਦਾ ਹੈ ਕਿ ਵਿਰੋਧੀ ਬਲ ਕਾਰਜ ਕਰ ਰਿਹਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
10 kg ਮਾਨ (ਪੰਜ) ਦੀ ਇੱਕ ਵਸਤੂ ਮੇਜ਼ ਉੱਤੇ A ਬਿੰਦੂ ਉੱਤੇ ਰੱਖੀ ਗਈ ਹੈ । ਇਸਨੂੰ 8 ਬਿੰਦੂ ਤੱਕ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ A ਅਤੇ B ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੀ ਰੇਖਾ ਹੋਰੀਜ਼ੈਨਟਲ ਹੈ, ਤਾਂ ਵਸਤੂ ਉੱਤੇ ਗੁਰੂਤਵ ਬਲ ਦੁਆਰਾ ਕੀਤਾ ਗਿਆ ਕਾਰਜ ਕਿੰਨਾ ਹੋਵੇਗਾ । ਆਪਣੇ ਉੱਤਰ ਦੀ ਵਿਆਖਿਆ ਕਰੋ ।
ਹੱਲ:

10 kg ਮਾਨ (ਪੰਜ) ਵਾਲੀ ਵਸਤੂ ਨੂੰ A ਤੋਂ B ਤੱਕ ਖਿਤਿਜ ਦਿਸ਼ਾ ਵਿੱਚ ਵਿਸਥਾਪਿਤ ਕੀਤਾ ਗਿਆ ਹੈ, ਪਰੰਤੂ ਗੁਰੂਤਾ ਆਕਰਸ਼ਣ ਬਲ ਹੇਠਾਂ ਵੱਲ ਲੰਬਵਤ ਦਿਸ਼ਾ (ਲੰਬੇ ਦਾਅ) ਵਿੱਚ ਹੈ ਜੋ ਕਿ 90° ਦਾ ਕੋਣ ਬਣਾ ਰਿਹਾ ਹੈ ।
∴ ਗੁਰੂਤਾ ਆਕਰਸ਼ਣ ਬਲ ਦੁਆਰਾ ਕੀਤਾ ਗਿਆ ਕਾਰਜ
W = F S cos θ
= FS cos 90°
= F S × 0
= 0 (ਸਿਫ਼ਰ)

ਪ੍ਰਸ਼ਨ 6.
ਮੁਕਤ ਰੂਪ ਵਿੱਚ ਡਿੱਗਦੇ ਇੱਕ ਪਿੰਡ ਦੀ ਸਥਿਤਿਜ ਊਰਜਾ ਲਗਾਤਾਰ ਘੱਟ ਹੁੰਦੀ ਜਾਂਦੀ ਹੈ । ਕੀ ਇਹ ਊਰਜਾ ਸੁਰੱਖਿਅਣ ਨਿਯਮ ਦਾ ਉਲੰਘਣ ਕਰਦੀ ਹੈ ? ਕਾਰਨ ਦੱਸੋ ।
ਉੱਤਰ-
ਨਹੀਂ, ਉਰਜਾ ਸੁਰੱਖਿਅਣ ਨਿਯਮ ਦੀ ਉਲੰਘਣਾ ਨਹੀਂ ਹੁੰਦੀ ਹੈ । ਜਦੋਂ ਮੁਕਤ ਰੂਪ ਵਿੱਚ ਡਿੱਗਦੇ ਹੋਏ ਪਿੰਡ (ਵਸਤੂ ਦੀ ਉੱਚਾਈ ਘੱਟ ਹੋਣ ਕਾਰਨ ਸਥਿਤਿਜ ਊਰਜਾ ਲਗਾਤਾਰ ਘੱਟ ਹੁੰਦੀ ਹੈ, ਪਰੰਤੂ ਗਤਿਜ ਊਰਜਾ ਵੱਧਦੀ ਹੈ । ਕਿਸੇ ਵੀ ਸਮੇਂ ਗਤਿਜ ਉਰਜਾ ਅਤੇ ਸਥਿਤਿਜ ਉਰਜਾ ਦਾ ਜੋੜ ਹਮੇਸ਼ਾ ਸਥਿਰ ਰਹਿੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਜਦੋਂ ਤੁਸੀਂ ਸਾਈਕਲ ਚਲਾਉਂਦੇ ਹੋ ਤਾਂ ਕਿਥੋਂ-ਕਿਥੋਂ ਉਰਜਾ ਰੂਪਾਂਤਰਣ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਜਦੋਂ ਅਸੀਂ ਸਾਈਕਲ ਚਲਾਉਂਦੇ ਹਾਂ, ਤਾਂ ਉਸ ਸਮੇਂ ਸਾਡੀ ਪੱਠਿਆਂ ਦੀ ਊਰਜਾ, ਤਾਪ ਊਰਜਾ ਅਤੇ ਗਤਿਜ ਊਰਜਾ ਵਿੱਚ ਰੂਪਾਂਤਰਿਤ ਹੁੰਦੀ ਹੈ । ਇਹ ਗਤਿਜ ਊਰਜਾ ਸੜਕ ਦੀ ਰਗੜ ਊਰਜਾ ਦੇ ਖਿਲਾਫ਼ ਕੰਮ ਕਰਨ ਵਿੱਚ ਖ਼ਰਚ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਜਦੋਂ ਤੁਸੀਂ ਸਾਰੀ ਸ਼ਕਤੀ ਲਗਾ ਕੇ ਇੱਕ ਵੱਡੀ ਚੱਟਾਨ ਨੂੰ ਧੱਕਣਾ ਚਾਹੁੰਦੇ ਹੋ ਅਤੇ ਇਸਨੂੰ ਹਿਲਾਉਣ ਵਿੱਚ ਅਸਫਲ ਹੋ ਜਾਂਦੇ ਹੋ, ਤਾਂ ਕੀ ਇਸ ਅਵਸਥਾ ਵਿੱਚ ਊਰਜਾ ਦਾ ਸਥਾਨਾਂਤਰਣ ਹੁੰਦਾ ਹੈ ? ਆਪਣੇ ਦੁਆਰਾ ਖਰਚ ਕੀਤੀ ਗਈ ਊਰਜਾ ਕਿੱਥੇ ਚਲੀ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਜਦੋਂ ਅਸੀਂ ਸਾਰੀ ਸ਼ਕਤੀ ਲਗਾ ਕੇ ਚੱਟਾਨ ਨੂੰ ਹਿਲਾਉਣ ਵਿੱਚ ਅਸਫਲ ਹੋ ਜਾਂਦੇ ਹਾਂ, ਤਾਂ ਉਸ ਸਮੇਂ ਕੋਈ ਕੰਮ ਨਹੀਂ ਹੁੰਦਾ, ਪਰੰਤੂ ਅਸੀਂ ਆਪਣੀ ਪੱਠਿਆਂ ਦੀ ਉਰਜਾ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤਾ ਹੈ । ਇਸ ਉਰਜਾ ਨੇ ਚੱਟਾਨ ਅਤੇ ਸੜਕ ਵਿੱਚ ਪੈਦਾ ਹੋਈ ਰਗੜ ਊਰਜਾ ਦੇ ਖਿਲਾਫ਼ ਕੰਮ ਕਰਨ ਦਾ ਯਤਨ ਕੀਤਾ ਅਤੇ ਤਾਪ ਊਰਜਾ ਵਿੱਚ ਪਰਿਵਰਤਿਤ ਹੋ ਗਈ ਜਿਹੜੀ ਪਸੀਨੇ ਅਤੇ ਥਕਾਵਟ ਦੇ ਰੂਪ ਵਿੱਚ ਪ੍ਰਗਟ ਹੋ ਗਈ ।

ਪ੍ਰਸ਼ਨ 9.
ਕਿਸੀ ਘਰ ਵਿੱਚ ਇੱਕ ਮਹੀਨੇ ਵਿੱਚ ਊਰਜਾ ਦੀ 250 ਯੂਨਿਟ ਖ਼ਰਚ ਹੋਈ । ਇਹ ਊਰਜਾ ਜੂਲ ਵਿੱਚ ਕਿੰਨੀ ਹੋਵੇਗੀ ?
ਹੱਲ:
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, 1 ਯੂਨਿਟ ਊਰਜਾ = 1 kW × 1 h
= 1000 w × 3600 s
= 36 × 10⁵ J
= 3.6 × 10⁶ J
∴ 250 ਯੂਨਿਟ ਊਰਜਾ = 250 × 3.6 × 10⁶ J
= 900 × 10⁶ J
= 9 × 10⁸

ਪ੍ਰਸ਼ਨ 10.
40 kg ਪੁੰਜ ਦਾ ਇੱਕ ਪਿੰਡ ਧਰਤੀ ਤੋਂ 5 m ਦੀ ਉੱਚਾਈ ਤੱਕ ਉਠਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਦੀ ਸਥਿਤਿਜ ਉਰਜਾ ਕਿੰਨੀ ਹੈ । ਜੇਕਰ ਪਿੰਡ ਨੂੰ ਮੁਕਤ ਰੂਪ ਨਾਲ ਡਿੱਗਣ ਦਿੱਤਾ ਜਾਵੇ, ਤਾਂ ਜਦੋਂ ਪਿੰਡ ਠੀਕ ਅੱਧੇ ਰਸਤੇ ਉੱਤੇ ਹੈ ਉਸ ਸਮੇਂ ਇਸਦੀ ਗਤਿਜ ਊਰਜਾ ਦਾ ਪਰਿਕਲਨ ਕਰੋ । g = 10 ms^-2)
ਹੱਲ:
ਇੱਥੇ, m = 40 kg
h = 5 m
g = 10 ms^-2
5 m ਦੀ ਉੱਚਾਈ ‘ਤੇ ਪਿੰਡ ਦੀ ਸਥਿਤਿਜ ਊਰਜਾ
= E_p = mgh
= 40 × 10 × 5
= 2000 J

ਜਦੋਂ ਪਿੰਡ ਅੱਧੇ ਰਸਤੇ ਹੇਠਾਂ ਆ ਗਿਆ ਹੈ, ਤਾਂ ਮੰਨ ਲਓ ਇਸਦਾ ਵੇਗ υ ਹੈ,
ਹੁਣ ਦੂਰੀ S = \(\frac{5}{2}\) m
= 2.5 m
υ² – u² = 2g s ਦੀ ਵਰਤੋਂ ਕਰਕੇ
υ² – (0)² = 2 × 10 × 2.5
υ² = 2 × 25
∴ v² = 50
ਅੱਧੇ ਰਸਤੇ ਪਹੁੰਚ ਕੇ ਪਿੰਡ ਦੀ ਗਤਿਜ ਊਰਜਾ
E_K = \(\frac{1}{2}\)mv²
= \(\frac{1}{2}\) × 40 × 50
= 1000 J

ਪ੍ਰਸ਼ਨ 11.
ਪ੍ਰਿਥਵੀ ਦੇ ਚਾਰੇ ਪਾਸੇ ਘੁੰਮਦੇ ਹੋਏ ਕਿਸੀ ਉਪਗ੍ਰਹਿ ਉੱਤੇ ਗੁਰੂਤਵ ਬਲ ਦੁਆਰਾ ਕਿੰਨਾ ਕਾਰਜ ਕੀਤਾ ਜਾਵੇਗਾ ? ਆਪਣੇ ਉੱਤਰ ਨੂੰ ਤਰਕਸੰਗਤ ਬਣਾਓ ।
ਉੱਤਰ-
ਜਦੋਂ ਕੋਈ ਉਪਹਿ, ਪ੍ਰਿਥਵੀ ਦੇ ਚਾਰੇ ਪਾਸੇ ਚੱਕਰ ਲਗਾਉਂਦਾ ਹੈ, ਤਾਂ ਗੁਰੂਤਾ ਬਲ ਇਸ ਤੀ ਪੱਥ ਦੇ ਅਰਧ-ਵਿਆਸ ਦੇ ਨਾਲ ਅੰਦਰ ਵੱਲ ਨੂੰ ਲੱਗਦਾ ਹੈ ਜਦੋਂ ਕਿ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਇਸ ਪੱਥ ਦੀ ਸਪਰਸ਼ ਰੇਖਾ (Tangent) ਜੋ ਅਰਧ-ਵਿਆਸ ‘ਤੇ ਲੰਬ ਹੁੰਦੀ ਹੈ, ਦੇ ਨਾਲ-ਨਾਲ ਲੱਗਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਗੁਰੂਤਾ ਆਕਰਸ਼ਣ ਬਲ ਅਤੇ ਵਿਸਥਾਪਨ ਇਕ-ਦੂਜੇ ਨਾਲ 90° ਬਣਾਉਂਦੇ ਹਨ ਜਿਸ ਕਰਕੇ ਉਪਗ੍ਰਹਿ ਤੇ ਕੀਤਾ ਗਿਆ ਕੰਮ ਸਿਫ਼ਰ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 12.
ਕੀ ਕਿਸੇ ਪਿੰਡ ਉੱਤੇ ਲੱਗਣ ਵਾਲੇ ਕਿਸੇ ਵੀ ਬਲ ਦੀ ਅਨੁਪਸਥਿਤੀ ਵਿੱਚ, ਇਸਦਾ ਵਿਸਥਾਪਨ ਹੋ ਸਕਦਾ ਹੈ ? ਸੋਚੋ । ਇਸ ਪ੍ਰਸ਼ਨ ਦੇ ਬਾਰੇ ਵਿੱਚ ਆਪਣੇ ਮਿੱਤਰਾਂ ਅਤੇ ਅਧਿਆਪਕਾਂ ਨਾਲ ਵਿਚਾਰ-ਵਟਾਂਦਰਾ ਕਰੋ ।
ਉੱਤਰ-
ਕਿਸੇ ਵਸਤੂ (ਪਿੰਡ) ਉੱਤੇ ਲੱਗਣ ਵਾਲੇ ਬਲ ਦੀ ਅਨੁਪਸਥਿਤੀ ਵਿੱਚ ਇਸ ਵਸਤੁ (ਪਿੰਡ) ਦਾ ਵਿਸਥਾਪਨ ਸੰਭਵ ਹੈ ਜੇਕਰ ਉਹ ਪਿੰਡ ਸਮਾਨ ਵੇਗ ਨਾਲ ਗਤੀ ਕਰ ਰਿਹਾ ਹੈ । ਜੇਕਰ ਵਸਤੁ (ਪਿੰਡ) ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਹੈ, ਤਾਂ ਬਲ ਦੀ ਅਨੁਪਸਥਿਤੀ ਵਿੱਚ ਇਸ ਦਾ ਵਿਸਥਾਪਨ ਸੰਭਵ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 13.
ਕੋਈ ਮਨੁੱਖ ਘਾਹ-ਫੂਸ ਦੀ ਇੱਕ ਪੰਡ ਨੂੰ ਆਪਣੇ ਸਿਰ ਉੱਤੇ 30 ਮਿੰਟ ਤੱਕ ਰੱਖਦਾ ਹੈ ਅਤੇ ਥੱਕ ਜਾਂਦਾ ਹੈ । ਕੀ ਉਸ ਨੇ ਕੁੱਝ ਕਾਰਜ ਕੀਤਾ ਹੈ ਜਾਂ ਨਹੀਂ ? ਆਪਣੇ ਉੱਤਰ ਨੂੰ ਤਰਕ ਸੰਗਤ ਬਣਾਉ ।
ਉੱਤਰ-
ਮਨੁੱਖ ਨੇ ਘਾਹ-ਫੂਸ ਦੀ ਪੰਡ ਨੂੰ 30 ਮਿੰਟ ਲਈ ਆਪਣੇ ਸਿਰ ਉੱਪਰ ਰੱਖਿਆ ਅਤੇ ਥੱਕ ਗਿਆ ਹੈ, ਪਰੰਤੂ ਗੁਰੂਤਾ ਆਕਰਸ਼ਣ ਬਲ ਲੱਗਣ ਦੇ ਬਾਵਜੂਦ ਪੰਡ ਵਿੱਚ ਕੋਈ ਵਿਸਥਾਪਨ ਨਹੀਂ ਹੋਇਆ ਹੈ । ਇਸ ਲਈ ਉਸ ਮਨੁੱਖ ਦੁਆਰਾ ਕੋਈ ਕਾਰਜ ਨਹੀਂ ਕੀਤਾ ਗਿਆ ਮੰਨਿਆ ਜਾਵੇਗਾ ।

ਪ੍ਰਸ਼ਨ 14.
ਇੱਕ ਬਿਜਲੀ ਹੀਟਰ (ਉਸ਼ਮਕ) ਦੀ ਘੋਸ਼ਿਤ ਸ਼ਕਤੀ 1500 w ਹੈ । 10 ਘੰਟੇ ਵਿੱਚ ਇਹ ਕਿੰਨੀ ਉਰਜਾ ਉਪਯੋਗ ਕਰੇਗਾ ?
ਹੱਲ:
ਇੱਥੇ ਹੀਟਰ ਦੀ ਸ਼ਕਤੀ (P) = 1500 W
ਸਮਾਂ (t) = 10 ਘੰਟੇ
ਕੁੱਲ ਖ਼ਰਚ ਹੋਈ ਊਰਜਾ = P × t
= 1500 W × 10 h
= 15000 ਵਾਟ-ਘੰਟਾ
ਯੂਨਿਟ = \(\frac{15000}{1000}\) = 15 kWh

ਪ੍ਰਸ਼ਨ 15.
ਜਦੋਂ ਅਸੀਂ ਕਿਸੇ ਸਰਲ ਲੋਲਕ ਦੇ ਗੋਲਕ ਨੂੰ ਇੱਕ ਤਰਫ਼ ਲੈ ਕੇ ਛੱਡਦੇ ਹਾਂ, ਤਾਂ ਇਹ ਡੋਲਨ ਲੱਗਦਾ ਹੈ । ਇਸ ਵਿੱਚ ਹੋਣ ਵਾਲੇ ਊਰਜਾ ਪਰਿਵਰਤਨਾਂ ਦੀ ਚਰਚਾ ਕਰਦੇ ਹੋਏ ਊਰਜਾ ਸੁਰੱਖਿਅਣ ਦੇ ਨਿਯਮ ਨੂੰ ਸਪੱਸ਼ਟ ਕਰੋ । ਗੋਲਕ ਕੁੱਝ ਸਮੇਂ ਬਾਅਦ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਕਿਉਂ ਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਸਦੀ ਊਰਜਾ ਦਾ ਕੀ ਹੁੰਦਾ ਹੈ ? ਕੀ ਇਹ ਊਰਜਾ ਸੁਰੱਖਿਅਣ ਨਿਯਮ ਦੀ ਉਲੰਘਣਾ ਹੈ ?
ਉੱਤਰ-
ਡੋਲਨ ਕਰ ਰਹੇ ਸਰਲ ਲੋਲਕ ਵਿਚ ਉਰਜਾ ਰੂਪਾਂਤਰਨ-ਸ਼ੁਰੂ ਵਿੱਚ ਲੋਕ ਆਪਣੀ ਮੱਧ ਸਥਿਤੀ ਵਿੱਚ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਹੁੰਦਾ ਹੈ, ਇਸ ਲਈ ਇਸਦੀ ਗਤਿਜ ਉਰਜਾ ਸਿਫ਼ਰ ਹੁੰਦੀ ਹੈ । ਇਸ ਸਥਿਤੀ ਵਿੱਚ ਇਸਦੀ ਸਥਿਤਿਜ ਊਰਜਾ ਨੂੰ ਅਸੀਂ ਸਿਰ ਮੰਨ ਲੈਂਦੇ ਹਾਂ ।

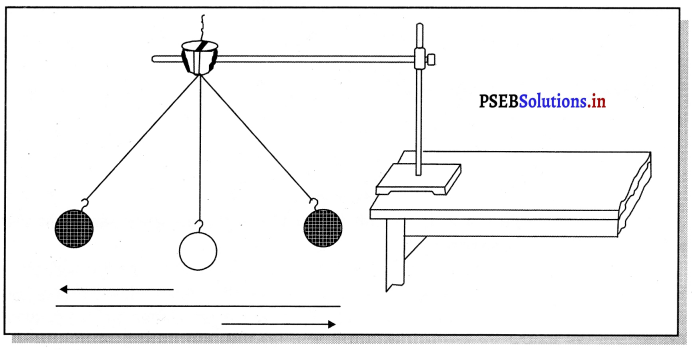
ਜਦੋਂ ਗੋਲਕ ਨੂੰ ਮੱਧ ਸਥਿਤੀ ਤੋਂ ਇੱਕ ਪਾਸੇ ਲਿਜਾਂਦੇ ਹਾਂ, ਤਾਂ ਇਸਦੀ ਉੱਚਾਈ ਵੱਧਣ ਲੱਗਦੀ ਹੈ ਅਤੇ ਇਸ ਕਿਰਿਆ ਦੌਰਾਨ ਗੁਰੂਤਵੀ ਬਲ ਦੇ ਖਿਲਾਫ਼ ਸਾਨੂੰ ਕੁੱਝ ਕਾਰਜ ਕਰਨਾ ਪੈਂਦਾ ਹੈ । ਇਹ ਕਾਰਜ ਗੋਲਕ ਦੀ ਸਥਿਤਿਜ ਉਰਜਾ ਦੇ ਰੂਪ ਵਿੱਚ ਜਮਾ ਹੁੰਦੀ ਜਾਂਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਮੱਧ ਸਥਿਤੀ ਤੋਂ ਇੱਕ ਪਾਸੇ ਵੱਧ ਤੋਂ ਵੱਧ ਵਿਸਥਾਪਨ ਦੀ (ਆਯਾਮ ਦੀ ਸਥਿਤੀ ਵਿੱਚ ਜਦੋਂ ਗੋਲਕ ਨੂੰ ਛੱਡਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਉਸ ਵੇਲੇ ਗੋਲਕ ਦੀ ਸਥਿਤਿਜ ਊਰਜਾ ਅਧਿਕਤਮ ਅਤੇ ਗਤਿਜ ਊਰਜਾ ਸਿਫ਼ਰ ਹੁੰਦੀ ਹੈ । ਹੁਣ ਗੋਲਕ ਨੂੰ ਛੱਡਣ ਨਾਲ ਗੋਲਕ ਵਾਪਸ ਹੌਲੀ-ਹੌਲੀ ਮੱਧ ਸਥਿਤੀ ਵੱਲ ਵੱਧਦਾ ਹੈ ਜਿਸ ਨਾਲ ਗੋਲਕ ਦੀ ਉੱਚਾਈ ਘੱਟ ਹੋਣ ਲੱਗਦੀ ਹੈ ਅਰਥਾਤ ਸਥਿਤਿਜ ਉਰਜਾ ਘੱਟ ਹੋਣ ਲੱਗਦੀ ਹੈ ਜਦਕਿ ਵੇਗ ਵਿੱਚ ਹੌਲੀ-ਹੌਲੀ ਵਾਧਾ ਹੁੰਦਾ ਹੈ, ਇਸ ਕਰਕੇ ਤਿਜ ਊਰਜਾ ਵੱਧਣਾ ਸ਼ੁਰੂ ਕਰਦੀ ਹੈ ਕਿਉਂਕਿ ਗੋਲਕ ਨੂੰ ਹਵਾ ਦੇ ਰਗੜ ਬਲ ਖਿਲਾਫ਼ ਕਾਰਜ ਕਰਨ ਲਈ ਕੁੱਝ ਊਰਜਾ ਖ਼ਰਚ ਕਰਨੀ ਪੈਂਦੀ ਹੈ ।

ਇਸ ਨਾਲ ਹਵਾ ਦੇ ਅਣੂਆਂ ਦਾ ਵੇਗ ਵੱਧਣ ਕਾਰਨ ਉਨ੍ਹਾਂ ਦੀ ਗਤਿਜ ਊਰਜਾ ਵੱਧ ਜਾਂਦੀ ਹੈ । ਮੱਧ ਸਥਿਤੀ ਤੇ ਪਹੁੰਚ ਕੇ ਗੋਲਕ ਦੀ ਸਥਿਤਿਜ ਉਰਜਾ ਸਿਫ਼ਰ ਹੋ ਜਾਂਦੀ ਹੈ । ਜੜ੍ਹਤਾ ਦੇ ਕਾਰਨ ਗੋਲਕ ਇੱਥੇ ਰੁੱਕਦਾ ਨਹੀਂ ਪਰੰਤੂ ਮੱਧ ਸਥਿਤੀ ਦੇ ਦੂਜੇ ਪਾਸੇ ਗਤੀਸ਼ੀਲ ਹੋ ਜਾਂਦਾ ਹੈ । ਹੁਣ ਗੋਲਕ ਦੀ ਉੱਚਾਈ ਵੱਧਣਾ ਸ਼ੁਰੂ ਕਰਦੀ ਹੈ, ਇਸ ਲਈ ਉਸਦੀ ਸਥਿਤਿਜ ਉਰਜਾ ਵੱਧਣ ਲੱਗਦੀ ਹੈ ਪਰ ਗਤਿਜ ਉਰਜਾ ਘੱਟ ਹੋਣੀ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦੀ ਹੈ । ਵੱਧ ਤੋਂ ਵੱਧ ਵਿਸਥਾਪਨ ਦੀ ਸਥਿਤੀ ਵਿੱਚ ਗੋਲਕ ਦੀ ਸਥਿਤਿਜ ਉਰਜਾ ਅਧਿਕਤਮ ਅਤੇ ਗਤਿਜ ਊਰਜਾ ਸਿਫ਼ਰ ਹੋ ਜਾਂਦੀ ਹੈ । ਗੋਲਕ ਇੱਥੇ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਨਹੀਂ ਆਉਂਦਾ ਅਤੇ ਦੁਬਾਰਾ ਮੱਧ ਸਥਿਤੀ ਵਿੱਚ ਵਾਪਸ ਆਉਣਾ ਸ਼ੁਰੂ ਕਰਦਾ ਹੈ । ਗੋਲਕ ਦੀ ਗਤੀ ਦੇ ਹਰੇਕ ਸਥਿਤੀ ਵਿੱਚ ਗਤਿਜ ਊਰਜਾ ਅਤੇ ਸਥਿਤਿਜ ਉਰਜਾ ਦਾ ਕੁੱਲ ਪਰਿਮਾਣ ਅਚਰ ਰਹਿੰਦਾ ਹੈ ।

ਗੋਲਕ ਦਾ ਆਯਾਮ ਉਸ ਦੀ ਕੁੱਲ ਊਰਜਾ ‘ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ । ਗੋਲਕ ਦੁਆਰਾ ਹਵਾ ਦੇ ਅਣੂਆਂ ਨੂੰ ਦਿੱਤੀ ਊਰਜਾ ਵਾਪਸ ਨਹੀਂ ਮਿਲਦੀ ਹੈ । ਜਦੋਂ ਲੋਕ ਆਪਣੀ ਸਾਰੀ ਉਰਜਾ ਹਵਾ ਦੇ ਅਣੂਆਂ ਨੂੰ ਦੇ ਦੇਂਦਾ ਹੈ, ਤਾਂ ਉਸਦੀ ਕੁੱਲ ਉਰਜਾ ਸਿਫ਼ਰ ਹੋ ਜਾਂਦੀ ਹੈ ਅਤੇ ਉਹ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਮੱਧ ਸਥਿਤੀ ਵਿੱਚ ਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਉਰਜਾ ਸੁਰੱਖਿਅਣ ਨਿਯਮ ਦੀ ਉਲੰਘਣਾ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 16.
m ਪੁੰਜ ਦਾ ਇੱਕ ਪਿੰਡ ਇੱਕ ਨਿਯਤ ਵੇਗ υ ਨਾਲ ਗਤੀਸ਼ੀਲ ਹੈ ।ਪਿੰਡ ਉੱਤੇ ਕਿੰਨਾ ਕਾਰਜ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਕਿ ਇਹ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਆ ਜਾਵੇ ? ਹੱਲ:
ਮੰਨ ਲਉ
ਪਿੰਡ ਦਾ ਪੁੰਜ = m
ਪਿੰਡ ਦਾ ਵੇਗ = υ
∴ ਪਿੰਡ ਦੀ ਗਤਿਜ ਊਰਜਾ E_k = \(\frac {1}{2}\)mυ²
ਪਿੰਡ ਉੱਤੇ ਕਾਰਜ ਕਰਨ ਦੀ ਲੋੜ = ਪਿੰਡ ਦੀ ਗਤਿਜ ਊਰਜਾ ਵਿੱਚ ਪਰਿਵਰਤਨ
=\(\frac {1}{2}\)mv² – \(\frac {1}{2}\) m(0)²
= \(\frac {1}{2}\)mv² – 0
\(\frac {1}{2}\)mυ²

ਪ੍ਰਸ਼ਨ 17.
1500 kg ਪੁੰਜ ਦੀ ਕਾਰ ਨੂੰ ਜੋ 60 km/h ਦੇ ਵੇਗ ਨਾਲ ਚੱਲ ਰਹੀ ਹੈ, ਨੂੰ ਰੋਕਣ ਲਈ ਕੀਤੇ ਗਏ ਕਾਰਜ ਦਾ ਪਰਿਕਲਨ ਕਰੋ ।
ਹੱਲ:
ਇੱਥੇ ਕਾਰ ਦਾ ਪੁੰਜ (m) = 1500 kg
ਕਾਰ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (υ) = 60 km/h
= \(\frac{60 \times 1000}{60 \times 60}\)
= \(\frac{50}{3}\) ms^-1
ਕਾਰ ਨੂੰ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿਚ ਲਿਆਉਣ ਲਈ ਕੀਤਾ ਗਿਆ ਕਾਰਜ
= ਕਾਰ ਦੀ ਤਿਜ ਊਰਜਾ ਵਿੱਚ ਪਰਿਵਰਤਨ
= \(\frac {1}{2}\)mυ² – \(\frac {1}{2}\) m(0)²
= \(\frac {1}{2}\)mυ²
= \(\frac {1}{2}\) × 1500 × (\(\frac{50}{3}\))²
= \(\frac {1}{2}\) × 1500 × \(\frac {50}{3}\) × \(\frac {50}{3}\)
= 208333.3 J
= 208.33 kJ

ਪ੍ਰਸ਼ਨ 18.
ਹੇਠਾਂ ਹਰੇਕ ਸਥਿਤੀ ਵਿੱਚ m ਵਮਾਨ ਦੇ ਇੱਕ ਪਿੰਡ ਉੱਤੇ ਇਕ ਬਲ F ਲੱਗ ਰਿਹਾ ਹੈ । ਵਿਸਥਾਪਨ ਦੀ ਦਿਸ਼ਾ ਪੱਛਮ ਤੋਂ ਪੂਰਬ ਵੱਲ ਹੈ ਜੋ ਇਕ ਲੰਬੇ ਤੀਰ ਨਾਲ ਪ੍ਰਦਰਸ਼ਿਤ ਕੀਤੀ ਗਈ ਹੈ । ਚਿੱਤਰਾਂ ਨੂੰ ਧਿਆਨ ਪੂਰਵਕ ਦੇਖੋ ਅਤੇ ਦੱਸੋ ਕਿ ਕੀਤਾ ਗਿਆ ਕਾਰਜ ਰਿਣਾਤਮਕ ਹੈ ਜਾਂ ਧਨਾਤਮਕ ਹੈ ਜਾਂ ਜ਼ੀਰੋ ਹੈ ?

ਉੱਤਰ-
(i) ਇੱਥੇ ਬਲ ਅਤੇ ਵਿਸਥਾਪਨ ਇੱਕ-ਦੂਜੇ ‘ਤੇ ਲੰਬ ਰੂਪ ਹਨ
∴ θ = 90°
∴ W = F S cos θ
= F S cos 90°
FS × 0
= 0

(ii) ਬਲ F ਅਤੇ ਵਿਸਥਾਪਨ – ਇੱਕ ਹੀ ਦਿਸ਼ਾ ਵਿਚ ਹਨ
∴ θ = 0°
W = F S cos θ
= FS cos θ°
= F S × 1
= FS ਜੋ ਕਿ ਧਨਾਤਮਕ ਹੈ

(iii) ਇੱਥੇ ਬਲ Fਅਤੇ ਵਿਸਥਾਪਨ S ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਹਨ।
∴ θ = 180°
cos θ = cos 180° = -1
ਪਰੰਤੂ W = F S cos θ
= F S cos 180°
= F S (-1)
= – F S ਜੋ ਕਿ ਰਿਣਾਤਮਕ ਹੈ

ਪ੍ਰਸ਼ਨ 19.
ਸੋਨੀ ਕਹਿੰਦੀ ਹੈ ਕਿ ਕਿਸੇ ਵਸਤੂ ਉੱਤੇ ਵੇਗ ਜ਼ੀਰੋ ਹੋ ਸਕਦਾ ਹੈ ਚਾਹੇ ਉਸ ਉੱਤੇ ਕੋਈ ਬਲ ਕੰਮ ਕਰ ਰਿਹਾ ਹੈ । ਕੀ ਤੁਸੀਂ ਇਸ ਨਾਲ ਸਹਿਮਤ ਹੋ ? ਦੱਸੋ ਕਿਉਂ ?
ਉੱਤਰ-
ਹਾਂ, ਮੈਂ ਸੋਨੀ ਦੇ ਕਥਨ ਨਾਲ ਸਹਿਮਤ ਹਾਂ ਕਿਉਂਕਿ ਜੇਕਰ ਵਸਤੂ ‘ਤੇ ਬਹੁਤ ਸਾਰੇ ਬਲ ਇੱਕੋ ਸਮੇਂ ਲੱਗ ਰਹੇ ਹਨ ਅਤੇ ਉਹਨਾਂ ਦਾ ਪਰਿਣਾਮੀ ਜੋੜ ਸਿਫ਼ਰ ਹੈ, ਤਾਂ ਵਸਤੁ ਦਾ ਵੇਗ ਵੀ ਜ਼ੀਰੋ ਹੋਵੇਗਾ ।
a = \(\frac{\mathrm{F}}{m}\)
a = \(\frac{0}{m}\) = 0

ਪ੍ਰਸ਼ਨ 20.
ਚਾਰ ਯੁਕਤੀਆਂ ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਹਰੇਕ ਦੀ ਸ਼ਕਤੀ 500 wਹੈ । 10 ਘੰਟੇ ਤਕ ਉਪਯੋਗ ਵਿੱਚ ਲਿਆਈ ਜਾਂਦੀ ਹੈ । ਇਸ ਦੇ ਦੁਆਰਾ ਖ਼ਰਚ ਕੀਤੀ ਗਈ ਊਰਜਾ kWh ਵਿੱਚ ਪਰਿਕਲਿਤ ਕਰੋ ।
ਹੱਲ:
ਇੱਕ ਯੁਕਤੀ (ਜੁਗਤ ਦੀ ਸ਼ਕਤੀ (p) = 500 W
4 ਯੁਕਤੀਆਂ ਦੀ ਕੁੱਲ ਸ਼ਕਤੀ (P) = 500 × 4
= 2000 W
ਸਮਾਂ (t) = 10 ਘੰਟੇ
ਖ਼ਰਚ ਕੀਤੀ ਗਈ ਊਰਜਾ = P × t
= 2000 w × 10 h
= 20000 Wh
= \(\frac{20000}{1000}\)
= 20 kWh

ਪ੍ਰਸ਼ਨ 21.
ਮੁਕਤ ਰੂਪ ਵਿੱਚ ਡਿੱਗਦਾ ਇੱਕ ਪਿੰਡ ਜੋ ਧਰਤੀ ਤੱਕ ਪਹੁੰਚਣ ਤੱਕ ਰੁੱਕ ਜਾਂਦਾ ਹੈ । ਇਸ ਦੀ ਗਤਿਜ ਊਰਜਾ ਕੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਜਦੋਂ ਕੋਈ ਪਿੰਡ ਮੁਕਤ ਰੂਪ ਵਿੱਚ ਹੇਠਾਂ ਧਰਤੀ ਵੱਲ ਡਿੱਗਦਾ ਹੈ, ਤਾਂ ਧਰਤੀ ‘ਤੇ ਪਹੁੰਚ ਕੇ ਰੁੱਕ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਸ ਦੀ ਗਤਿਜ ਊਰਜਾ ਦਾ ਹੋਰ ਊਰਜਾਵਾਂ ਵਿੱਚ ਰੂਪਾਂਤਰਨ ਹੁੰਦਾ ਹੈ । ਇਹ ਊਰਜਾਵਾਂ ਤਾਪ, ਧੁਨੀ ਅਤੇ ਪ੍ਰਕਾਸ਼ ਹਨ । ਅਖ਼ੀਰ ਵਿੱਚ ਇਹ ਸਥਿਤਿਜ ਊਰਜਾ ਵਿੱਚ ਰੂਪਾਂਤਰਿਤ ਹੋ ਜਾਂਦੀ ਹੈ ।

Science Guide for Class 9 PSEB ਕਾਰਜ ਅਤੇ ਊਰਜਾ InText Questions and Answers

ਪਾਠ-ਪੁਸਤਕ ਦੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 1.
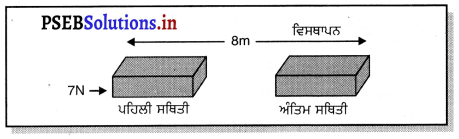
ਕਿਸੇ ਵਸਤੂ ਉੱਤੇ 7 N ਦਾ ਬਲ ਲੱਗਦਾ ਹੈ । ਮੰਨ ਲਉ ਬਲ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਵਿਸਥਾਪਨ 8 m ਹੈ । ਮੰਨ ਲਉ ਵਸਤੂ ਦੇ ਵਿਸਥਾਪਨ ਦੇ ਸਮੇਂ ਲਗਾਤਾਰ ਵਸਤੁ ਉੱਤੇ ਬਲ ਲੱਗਦਾ ਰਹਿੰਦਾ ਹੈ । ਇਸ ਸਥਿਤੀ ਵਿੱਚ ਕੀਤਾ ਗਿਆ ਕਾਰਜ ਕਿੰਨਾ ਹੋਵੇਗਾ ?

ਹੱਲ:
ਇੱਥੇ ਬਲ (F) = 7 N
ਵਿਸਥਾਪਨ (S) = 8 m
ਕੀਤਾ ਗਿਆ ਕੰਮ (W) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, W = F × S
= 7 N × 8 m
= 56 N × m
= 56 N – m
= 56 J (ਜੂਲ)

ਪ੍ਰਸ਼ਨ 2.
ਅਸੀਂ ਕਦੋਂ ਕਹਿੰਦੇ ਹਾਂ ਕਿ ਕਾਰਜ ਕੀਤਾ ਗਿਆ ਹੈ ?
ਉੱਤਰ-
ਕਾਰਜ (Work)-ਜਦੋਂ ਕਿਸੇ ਵਸਤੂ ਉੱਤੇ ਬਲ ਲੱਗੇ ਅਤੇ ਵਸਤੂ ਵਿੱਚ ਬਲ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਵਿਸਥਾਪਨ ਹੋਵੇ, ਤਾਂ ਬਲ ਦੁਆਰਾ ਕਾਰਜ ਹੋਇਆ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਕਾਰਜ (W) = ਬਲ (F) × ਵਿਸਥਾਪਨ (S)

ਪ੍ਰਸ਼ਨ 3.
ਜਦੋਂ ਕਿਸੇ ਵਸਤੂ ਉੱਤੇ ਲੱਗਣ ਵਾਲਾ ਬਲ ਇਸਦੇ ਵਿਸਥਾਪਨ ਦੀ ਦਿਸ਼ਾ ਵੱਲ ਹੋਵੇ, ਤਾਂ ਕੀਤੇ ਗਏ ਕਾਰਜ ਨੂੰ ਪ੍ਰਗਟ ਕਰੋ ।
ਉੱਤਰ-
ਜਦੋਂ ਵਸਤੂ ਉੱਤੇ ਲੱਗਣ ਵਾਲਾ ਬਲ ਵਿਸਥਾਪਨ ਦੀ ਦਿਸ਼ਾ ਵਿਚ ਹੋਵੇ, ਤਾਂ
ਕਾਰਜ (W) = ਬਲ (F) × ਵਿਸਥਾਪਨ (S).

ਪ੍ਰਸ਼ਨ 4.
1J ਕਾਰਜ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਇੱਕ ਜੂਲ ਕਾਰਜ ਹੋਇਆ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਜਦੋਂ 1 ਨਿਊਟਨ ਬਲ ਵਸਤੂ ਨੂੰ ਆਪਣੀ ਦਿਸ਼ਾ ਵਿੱਚ 1 m ਵਿਸਥਾਪਿਤ ਕਰੇ ।
W = F × S
1 J = 1 N × 1 m

ਪ੍ਰਸ਼ਨ 5.
ਬੈਲਾਂ ਦੀ ਇੱਕ ਜੋੜੀ ਖੇਤ ਨੂੰ ਜੋਤੇ ਸਮੇਂ ਕਿਸੇ ਹੱਲ ਉੱਤੇ 140 N ਬਲ ਲਗਾਉਂਦੀ ਹੈ । ਜੋਤਿਆ ਗਿਆ ਖੇਤ
ਹੱਲ:
ਇੱਥੇ, ਲਗਾਇਆ ਗਿਆ ਬਲ (F) = 140 N
ਜੋਤੇ ਗਏ ਖੇਤ ਦੀ ਲੰਬਾਈ (S) = 15 m
ਜੋਤਨ ਵਿੱਚ ਕੀਤਾ ਗਿਆ ਕਾਰਜ (w) = ?
ਹੁਣ, W = F × S
∴ ਜੋਤਨ ਵਿਚ ਕੀਤਾ ਗਿਆ ਕਾਰਜ (W) = 140 N × 15 m
= 140 × 15
= 2100 N – m
= 2100 J

ਪ੍ਰਸ਼ਨ 6.
ਕਿਸੇ ਵਸਤੂ ਦੀ ਤਿਜ ਊਰਜਾ ਕੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਗਤਿਜ ਊਰਜਾ (Kinetic Energy)-ਕਿਸੇ ਵਸਤੂ ਦੀ ਗਤਿਜ ਊਰਜਾ ਉਸ ਵਿੱਚ ਉਪਸਥਿਤ ਗਤੀ ਦੇ ਕਾਰਨ ਹੁੰਦੀ ਹੈ ।
ਉਦਾਹਰਨ-
(i) ਗਤੀਸ਼ੀਲ ਪੱਥਰ ।
(ii) ਵਗਦੀ ਹੋਈ ਹਵਾ ।
(iii) ਘੁੰਮਦਾ ਹੋਇਆ ਪਹੀਆ ।

ਪ੍ਰਸ਼ਨ 7.
ਕਿਸੇ ਵਸਤੂ ਦੀ ਗਤਿਜ ਊਰਜਾ ਦੇ ਲਈ ਸੂਤਰ ਲਿਖੋ ।
ਉੱਤਰ-
ਇੱਕ m ਪੁੰਜ ਵਾਲੀ ਵਸਤੂ ਜਿਹੜੀ ਇਕ ਸਮਾਨ ਵੇਗ υ ਨਾਲ ਗਤੀਸ਼ੀਲ ਹੈ, ਦੀ ਗਤਿਜ ਊਰਜਾ (K, E) = \(\frac {1}{2}\) ਪੁੰਜ × (ਵੇਗ)²
= \(\frac {1}{2}\) × m × υ²
∴ ਗਤਿਜ ਊਰਜਾ ਦਾ ਸੂਤਰ ਹੈ : E_k = \(\frac {1}{2}\) mυ²

ਪ੍ਰਸ਼ਨ 8.
5 ms^-1ਦੇ ਵੇਗ ਵਿੱਚ ਗਤੀਸ਼ੀਲ ਕਿਸੇ ” ਪੁੰਜ ਦੀ ਵਸਤੂ ਦੀ ਗਤਿਜ ਊਰਜਾ 25 J ਹੈ । ਜੇਕਰ ਇਸ ਦੇ ਵੇਗ ਨੂੰ ਦੁੱਗਣਾ ਕਰ ਦਿੱਤਾ ਜਾਵੇ, ਤਾਂ ਇਸਦੀ ਗਤਿਜ ਊਰਜਾ ਕਿੰਨੀ ਹੋ ਜਾਵੇਗੀ ? ਜੇਕਰ ਇਸ ਦੇ ਵੇਗ ਨੂੰ ਤਿੰਨ ਗੁਣਾ ਕਰ ਦਿੱਤਾ ਜਾਵੇ, ਤਾਂ ਇਸ ਦੀ ਤਿਜ ਊਰਜਾ ਕਿੰਨੀ ਹੋ ਜਾਵੇਗੀ ?
ਹੱਲ:
ਦਿੱਤਾ ਹੈ- ਵਸਤੂ ਦਾ ਪੁੰਜ = m
| ਵਸਤੁ ਦਾ ਵੇਗ (υ) = 5 ms^-1
ਵਸਤੂ ਦੀ ਗਤਿਜ ਉਰਜਾ (E_k) = 25 J
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, E_k = \(\frac {1}{2}\) mυ²
25 = \(\frac {1}{2}\) m(5)²
25 = \(\frac {1}{2}\) m × 25
∴ m = \(\frac{25 \times 2}{25}\)
= 2 kg

(i) ਜਦੋਂ ਵਸਤੂ ਦਾ ਵੇਗ ਦੁੱਗਣਾ ਕਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ, ਤਾਂ
m = 2 kg
υ₁ = 2 × 5 ms^-1
= 10 ms^-1
E_k1 = \(\frac {1}{2}\) × m × (υ₁)²
∴ E_k1 = \(\frac {1}{2}\) × 2 × (10)²
= \(\frac {1}{2}\) × 2 × 10 × 10
= 100 J
= 4 × 25 J
E_k1 = 4 × E_k
∴ ਵੇਗ ਦੁੱਗਣਾ ਕਰਨ ਨਾਲ ਵਸਤੂ ਦੀ ਗਤਿਜ ਊਰਜਾ (E_k1 ) ਪਹਿਲਾਂ ਦੀ ਊਰਜਾ (EE_k = 25) ਨਾਲੋਂ ਚਾਰ ਗੁਣਾ ਹੋ ਜਾਵੇਗੀ ।

(ii) ਜਦੋਂ ਵਸਤੂ ਦਾ ਵੇਗ ਤਿਗੁਣਾ ਕਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ, ਤਾਂ
υ² = 3 × υ
= 3 × 5 ms^-1
= 15 ms^-1
∴ ਵਸਤੂ ਦੀ ਗਤਿਜ ਊਰਜਾ (E_k2) = \(\frac {1}{2}\) × m × (υ₂)²
= \(\frac {1}{2}\) × 2 × (15)²
= \(\frac {1}{2}\) × 2 × 15 × 15
= 225 J
= 9 × 25 J
E_k2 = 9 × E_k
ਅਰਥਾਤ ਵਸਤੂ ਦਾ ਵੇਗ ਤਿਗੁਣਾ ਕਰਨ ‘ਤੇ ਵਸਤੂ ਦੀ ਗਤਿਜ ਊਰਜਾ (E_k2 ) , ਪਹਿਲੀ ਗਤਿਜ ਊਰਜਾ (E_k = 25 J) ਦਾ ਨੌਂ ਗੁਣਾ ਹੋ ਜਾਵੇਗੀ ।

ਪ੍ਰਸ਼ਨ 9.
ਸ਼ਕਤੀ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਸ਼ਕਤੀ (Power)-ਕਾਰਜ ਕਰਨ ਦੀ ਦਰ ਜਾਂ ਊਰਜਾ ਰੂਪਾਂਤਰਨ ਦੀ ਦਰ ਨੂੰ ਸ਼ਕਤੀ ਕਹਿੰਦੇ ਹਨ । ਜੇਕਰ ਕੋਈ ਕਾਰਕ (ਏਜੰਟ) । ਸਮੇਂ ਵਿੱਚ ਲਾ ਕਾਰਜ ਕਰਦਾ ਹੈ, ਤਾਂ ਸ਼ਕਤੀ ਦਾ ਮਾਨ ਹੋਵੇਗਾ-

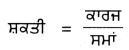
P = \(\frac{w}{t}\)

ਪ੍ਰਸ਼ਨ 10.
1 ਵਾਟ ਸ਼ਕਤੀ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਵਾਟ (Watt)-1 ਵਾਟ ਉਸ ਏਜੰਟ ਕਾਰਕ) ਦੀ ਸ਼ਕਤੀ ਹੈ ਜੋ 1 ਸੈਕਿੰਡ ਵਿੱਚ 1 ਜੂਲ ਕਾਰਜ ਕਰਦਾ ਹੈ । ਅਸੀਂ ਇੰਝ ਵੀ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਜੇਕਰ ਊਰਜਾ ਦੇ ਉਪਯੋਗ ਦੀ ਦਰ 1 Js^-1 ਹੋਵੇ, ਤਾਂ ਸ਼ਕਤੀ 1 ਵਾਟ (W) ਹੋਵੇਗੀ ।

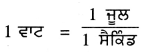
ਜਾਂ
1 W = 1 Js^-1

ਪ੍ਰਸ਼ਨ 11.
ਇਕ ਲੈਂਪ 1000 J ਬਿਜਲੀ ਊਰਜਾ 10 s ਵਿੱਚ ਵਰਤਦਾ ਹੈ । ਇਸਦੀ ਸ਼ਕਤੀ ਕਿੰਨੀ ਹੈ ?
ਹੱਲ:
ਇੱਥੇ W = 1000 J
t = 10 s
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, p = \(\frac{\mathrm{W}}{t}\)
= \(\frac{1000 \mathrm{~J}}{10 \mathrm{~s}}\)
= 100 Js^-1
= 100 W

ਪ੍ਰਸ਼ਨ 12.
ਔਸਤ ਸ਼ਕਤੀ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਔਸਤ ਸ਼ਕਤੀ (Average Power-ਕੁੱਲ ਉਪਯੋਗ ਕੀਤੀ (ਵਰਤੀ ਗਈ ਊਰਜਾ ਅਤੇ ਕੁੱਲ ਲਏ ਗਏ ਸਮੇਂ ਦੇ ਅਨੁਪਾਤ ਨੂੰ, ਔਸਤ ਸ਼ਕਤੀ ਕਹਿੰਦੇ ਹਨ ।