PSEB 10th Class Maths Solutions Chapter 8 Introduction to Trigonometry Ex 8.2

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 Introduction to Trigonometry Ex 8.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.2

Question 1.
Evaluate the following:
(i) sin 60° cos 30° + sin 30° cos 60°

(ii) 2 tan² 45° + cos² 30° – sin² 60°

(iii)

(iv)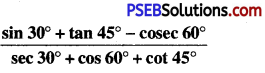

(v) $\frac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}$
Solution:
(i) sin 60° cos 30° + sin 30° cos 60°
= $\left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{3}}{2}\right)+\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)$

= $\left(\frac{\sqrt{3}}{2}\right)^{2}+\left(\frac{1}{2}\right)^{2}$
= $\frac{3}{4}+\frac{1}{4}$ = 1.

(ii) 2 tan² 45° + cos² 30° – sin² 60° = 2 (tan 45°)² + (cos 30°)² – (sin 60°)²
= 2 (1)² + ($\frac{\sqrt{3}}{2}$)² – ($\frac{\sqrt{3}}{2}$)² = 2.

(iii)
= $\frac{\frac{1}{\sqrt{2}}}{\left(\frac{2}{\sqrt{3}}\right)+(2)}=\frac{\frac{1}{\sqrt{2}}}{\frac{2+2 \sqrt{3}}{\sqrt{3}}}$

= $\frac{1}{\sqrt{2}}: \frac{\sqrt{3}}{2+2 \sqrt{3}}=\frac{\sqrt{3}}{2 \sqrt{2}(\sqrt{3}+1)}$

= $\frac{\sqrt{3}(\sqrt{3}-1)}{2 \sqrt{2}(\sqrt{3}+1)(\sqrt{3}-1)}$

= $\frac{\sqrt{2} \times \sqrt{3} \times(\sqrt{3}-1)}{4(3-1)}=\frac{3 \sqrt{2}-\sqrt{6}}{8}$.

(iv)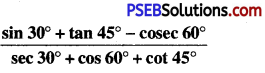

= $\frac{\frac{1}{2}+1-\frac{2}{\sqrt{3}}}{\frac{2}{\sqrt{3}}+\frac{1}{2}+1}=\frac{\frac{3}{2}-\frac{2}{\sqrt{3}}}{\frac{2}{\sqrt{3}}+\frac{3}{2}}$

= $\frac{3 \sqrt{3}-4}{4+3 \sqrt{3}}$

= $\frac{(3 \sqrt{3}-4)(3 \sqrt{3}-4)}{(3 \sqrt{3}+4)(3 \sqrt{3}-4)}$

= $\frac{27+16-24 \sqrt{3}}{27-16}$

= $\frac{43-24 \sqrt{3}}{11}$

(v) $\frac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}$

= $\begin{array}{r} 5\left(\cos 60^{\circ}\right)^{2}+4\left(\sec 30^{\circ}\right)^{2} \\ \frac{-\left(\tan 45^{\circ}\right)^{2}}{\left(\sin 30^{\circ}\right)^{2}+\left(\cos 30^{\circ}\right)^{2}} \end{array}$

= $\frac{5\left(\frac{1}{2}\right)^{2}+4\left(\frac{2}{\sqrt{3}}\right)^{2}-(1)^{2}}{\left(\frac{1}{2}\right)^{2}+\left(\frac{\sqrt{3}}{2}\right)^{2}}$

= $\frac{\frac{5}{4}+4 \times \frac{4}{3}-1}{\frac{1}{4}+\frac{3}{4}}=\frac{\frac{5}{4}+\frac{1}{3}-1}{\frac{1}{4}+\frac{3}{4}}$

= $\frac{5}{4}+\frac{16}{3}-1=\frac{15+64-12}{12}=\frac{67}{12}$.

Question 2.
Choose the correct option and justify your choice.

(i) $\frac{2 \tan 30^{\circ}}{1+\tan 30^{\circ}}$
(A) sin 60°
(B) cos 60°
(C) tan 60°
(D) sin 30°

(ii) $\frac{1-\tan ^{2} 45^{\circ}}{1+\tan 45^{\circ}}$
(A) tan 90°
(B) 1
(C) sin 45°
(D) 0.

(iii) sin 2A = 2 sin A is true when
(A) 0°
(B) 30°
(C) 45°
(D) 60°

(iv) $\frac{2 \tan 30^{\circ}}{1+\tan ^{2} 30^{\circ}}$
(A) cos 60°
(B) sin 60°
(C) tan 60°
(D) sin 30°.

Solution:
(i) $\frac{2 \tan 30^{\circ}}{1+\tan 30^{\circ}}=\frac{2\left(\frac{1}{\sqrt{3}}\right)}{1+\left(\frac{1}{\sqrt{3}}\right)^{2}}$

$\frac{\frac{2}{\sqrt{3}}}{1+\frac{1}{3}}=\frac{2}{\sqrt{3}} \times \frac{3}{4}=\frac{\sqrt{3}}{2}$ = sin 60°.
So, correct anwer is (A).

(ii) $\frac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}=\frac{1-(1)^{2}}{1+(1)^{2}}$ = 0
So, correct anwer is (D).

(iii) Here when A = 0°
L.H.S. = sin 2A = sin 0° = 0
and R.H.S. = 2 sin A = 2 sin 0°
= 2 × 0 = 0
∴ Option (A) is correct.

(iv) $\frac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}}=\frac{2\left(\frac{1}{\sqrt{3}}\right)}{1-\left(\frac{1}{\sqrt{3}}\right)^{2}}$

= $\frac{\frac{2}{\sqrt{3}}}{1-\frac{1}{3}}=\frac{2}{\sqrt{3}} \times \frac{3}{2}=\sqrt{3}$

= tan 60°
∴ Option (C) is correct.

Question 3.
If tan (A + B) = $\sqrt{3}$ and tan (A – B) = $\frac{1}{\sqrt{3}}$; 0° ∠A + B ≤ 90°; A > B. find A and B.
Solution:
tan (A + B) = $\sqrt{3}$. Given
tan (A + B) = tan 60°
⇒ A + B = 60° ……………..(1)
tan (A – B) = $\frac{1}{\sqrt{3}}$ (Given)
or tan (A – B) = tan 30°
⇒ A – B = 30° …………….(2)
On adding (1) and (2),

A = 45°

Pu value of A = 45° in (1)
45° + B = 60°
B = 60° – 45°
B = 15°
Hence A = 45° and B = 15°.

Question 4.
State whether the following are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin q increases as q increases.
(iii) The value of cos q Increases as q increases
(iv) sin q = cos q for all value of q.
(v) cot A is not defined for A = 0°.
Solution:
(i) False.
When A = 60°, B = 30°
L.H.S. = sin (A + B) = sin (60° + 30°) = sin 90° = 1
R.H.S. = sin A + sin B
= sin 60° + sin 30°
= $\frac{\sqrt{3}}{2}+\frac{1}{2}$ ≠ 1
i.e., L.H.S. ≠ R.H.S.

(ii) True, sin 30° = $\frac{1}{2}$ = 0.5,
Note that sin 0° = 0,
sin 45° = $\frac{1}{\sqrt{2}}$ = 0.7 (approx.)
sin 60° = $\frac{\sqrt{3}}{2}$ = 0.87 (approx.)
and sin 90° = 1
i.e., value of sin θ increases as θ increases from 0° to 90°.

(iii) False.
Note that cos 0° = 1,
cos 30° = $\frac{\sqrt{3}}{2}$ = 0.87(approx.)
cos 45° = $\frac{1}{\sqrt{2}}$ = 0.7.(approx.)
cos 60° = $\frac{1}{2}$ = 0.5
and cos 90° = 0.
Hence, value of θ decreases as θ increases from 0° to 90°.

(iv) False
Since sin 30° = $\frac{1}{2}$
and cos 30° = $\frac{\sqrt{3}}{2}$
or sin 30° ≠ cos 30°
Only we have: sin 45° = cos 45°.
$\frac{1}{\sqrt{2}}$ = $\frac{1}{\sqrt{2}}$

(v) True.
cot 0° = $\frac{1}{\tan 0^{\circ}}=\frac{1}{0}$, or not defined.