PSEB 12th Class Maths Solutions Chapter 13 Probability Ex 13.5

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 13 Probability Ex 13.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 13 Probability Ex 13.5

Question 1.
A die is thrown 6 times. If ‘getting an odd number’ is a success, what is the probability of
(i) 5 successes?
(ii) at least 5 successes?
(iii) at most 5 successes?
Solution.
The repeated tosses of a die are Bernoulli trials.
Let X denote the number of successes of getting odd numbers in an experiment of 6 trials.
Probability of getting an odd number in a single throw of a die is,
P = \(\frac{3}{6}=\frac{1}{2}\)

q = 1 – p = \(\frac{1}{2}\)
X has a binomial distribution.

Question 2.
A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of two successes.
Solution.
The repeated tosses of a pair of dice are Bernoulli trails.
Let X denote the number of times of getting doublets in an experiment of throwing two dice simultaneously four times.
Probability of getting doublets in a single throw of the pair of dice is
p = \(\frac{6}{36}=\frac{1}{6}\)

q = 1 – \(\frac{1}{6}\)
= \(\frac{5}{6}\)
Clearly, X has the binomial distribution with, n = 4, p = \(\frac{1}{6}\) and q = \(\frac{5}{6}\)

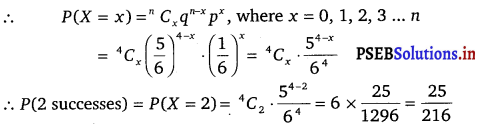
Question 3.
There are 5% defective items in a large bulk of items. What is the probability that a sample of 10 items will include not more than one defective item?
Solution.
Let X denote the number of defective items in a sample of 10 items drawn successively.
Since the drawing is done with replacement the trials are Bernoulli trials.

Question 4.
Five cards are drawn successively with replacement from a well-shuffled deck of 52 cards. What is the probability that
(i) all the five cards are spades?
(ii) only 3 cards are spades?
(iii) none is a spade?
Solution.
Let X represent the number of spade cards among the five cards drawn.
Since the drawing of card is with replacement the trials are Bernoulli trials.
In a well shuffled deck of 52 cards, there are 13 spade cards.

Question 5.
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs
(i) none
(ii) not more than one
(iii) more than one
(iv) at least one will fuse after 150 days of use.
Solution.
Probability that a bulb gets fuse after 150 days of its use = 0.05
Probability that the bulb will not fuse after 150 days of its use
=1 – 0.05
= 0.95
(i) Probability that no bulb will fuse after 150 days of its use
= P(none) = (0.95)
(ii) P (not more than one)
= P(0) + P(1)
= (0.95)⁵ + \({ }^{5} C_{1}\) × (0.95)⁴ × (0.05)
= (0.95)⁴ [0.95 + 5 × 0.05]
= (0.95)⁴ (0.95 + 0.25)
=(0.95) × 1.2

(iii) P(more than one) = P(2) + P(3) + P(4) + P(5)
= [P(0) + P(1) + P(2) + P(3) + P(4) + P(5)] – [P(0) + P(1)]
= 1 – [P(0) + P(1)]
= 1 – (0.95) × 1..2 [see part (ii)]
(iv) A(at least one) = P(1) + P(2) + P(3) + P(4) + P(5)
= 1 – P(0)
= 1 – (0.95)⁵ [From part (i)].

Question 6.
A bag consists of 10 balls each marked with one of the digits 0 to 9. If four balls are drawn successively with replacement from the bag, what is the probability that none is marked with the digit 0.
Solution.
Let X denote the number of balls marked with the digit 0 among the 4 balls drawn.
Since the balls are drawn with replacement, the trials are Bernoulli trials. X has a binomial distribution with n = 4 and p = \(\frac{1}{10}\)
∴ q = 1 – p
= 1 – \(\frac{1}{10}\) = \(\frac{9}{10}\)

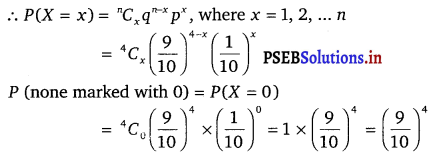
Question 7.
In an examination, 20 questions of true-false type are asked Suppose a student tosses a fair coin to determine his answer to each question. If the coin falls heads he answers, ‘ture’. If it falls tails he answers ‘false’. Find the probability that he answers at least 12 questions correctly.
Solution.
Let X represent the number of correctly answered questions out of 20 questions.
The repeated tosses of a coin are Bernoulli trails.
Since “head” on a coin represents the true answer and “tail” represents the false answer, the correctly answered questions are Bernoulli trials.

Question 8.
Suppose X has a binomial distribution B (6, \(\frac{1}{2}\)). Show that X = 3 is the most likely outcome.
[Hint : P(X = 3) is the P(X_i), X_i = 0, 1, 2, 3, 4, 5, 6]
Solution.
X is the random variable whose binomial distribution is B
Therefore, n = 6 and p = \(\frac{1}{2}\)
∴ q = 1 – p
= 1 – \(\frac{1}{2}\)
= \(\frac{1}{2}\)

The value of \({ }^{6} C_{3}\)is maximum.
Therefore, for x = 3, P(X = x) is maximum.
Thus, X = 3 is the most likely outcome.

Question 9.
On a multiple choice examination with three possible answers for each of the five questions, what is the probability that a candidate would get four or more correct answers just by guessing?
Solution.
The repeated guessing of correct answer from multiple choice questions are Bernoulli trials.
Let X represent the number of correct answers by guessing the the set of 5 multiple choice questions.
Probability of getting a correct answer is, p = \(\frac{1}{3}\)
∴ q = 1 – p
= 1 – \(\frac{1}{3}\)
= \(\frac{2}{3}\)
Clearly, X has a binomial distribution with n = 5 and p = \(\frac{1}{3}\)

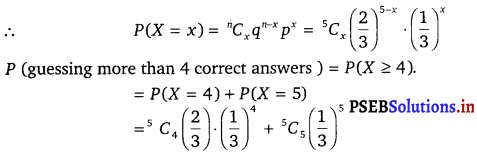
= \(5 \cdot \frac{2}{3} \cdot \frac{1}{81}+1 \cdot \frac{1}{243}\)

= \(\frac{10}{243}+\frac{1}{243}=\frac{11}{243}\)

Question 10.
A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is \(\frac{1}{100}\). What is the probability that he will in a prize
(a) at least once
(b) exactly once
(c) at least twice?
Solution.
Let X represent the number of wining prizes in 50 lotteries.
The trials are Bernoulli trials.
Clearly, X has a binomial distribution with n = 50 and p = \(\frac{1}{100}\).

Question 11.
Find the probability of getting 5 exactly twice in 7 throws of a die.
Solution.
The repeated tossing of a die are Bernoulli trials Let X, represent the number of times of getting 5 in 7 throws of the die.
Probability of getting 5 in a single throw of the die, p = \(\frac{1}{6}\)
q = 1 – p
= 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)
Clearly, X has the probability distribution with n = 7 and p = \(\frac{1}{6}\)
∴ p(X = x) = \({ }^{n} C_{x} q^{n-x} p^{x}\)

= \({ }^{7} C_{x}\left(\frac{5}{6}\right)^{7-x} \cdot\left(\frac{1}{6}\right)^{x}\)
p(getting 5 exactly twice) = P(X = 2)
= \({ }^{7} C_{2}\left(\frac{5}{6}\right)^{5} \cdot\left(\frac{1}{6}\right)^{2}\)

= \(21 \cdot\left(\frac{5}{6}\right)^{5} \cdot \frac{1}{36}=\left(\frac{7}{12}\right)\left(\frac{5}{6}\right)^{5}\).

Question 12.
Find the probability of throwing at most 2 sixes in 6 throws of a single die.
Solution.
When a die is thrown, probability of getting a six = \(\frac{1}{6}\)
Probability of not getting a six = 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)
Probability of getting atmost 2 sixes in 6 throws of a single die.
= P(0) + P(1) + P(2)

Question 13.
It is known that 10% of a certain articles manufactured are defective. What is the probability that in a random sample of 12 such articles, 9 are defective?
Solution.
The repeated selections of artides in a random sample space are Bernoulli trails.
Let X denote the number of times of selecting defective articles in a random sample space of 12 articles.
Clearly, X has a binomial distribution with n = 12 and p = 10%

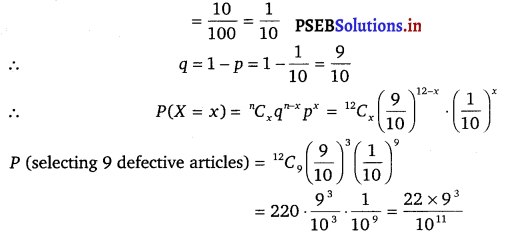
Question 14.
In a box containing 100 bulbs, 10 are defective. The probability that out of a sample of 5 bulbs, none is defective is
(A) 10^-1

() \(\left(\frac{1}{2}\right)^{5}\)

(C) \(\left(\frac{9}{10}\right)^{5}\)

(D) \(\frac{9}{10}\)
Solution.
The repeated selections of defective bulbs from a box are Bernoulli trials. Let X denote the number of defective bulbs out of a sample of 5 bulbs.

Probability of getting a defective bulb, p = \(\frac{10}{100}=\frac{1}{10}\)
q = 1 – p
= 1 – \(\frac{1}{10}\)
= \(\frac{9}{10}\)
Clearly, X has a binomial distribution with n = 5 and p = \(\frac{1}{10}\)

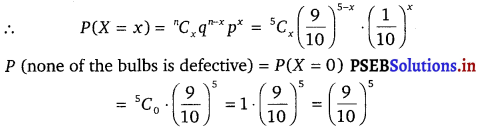
Hence, the correct answer is (C).

Question 15.
The probability that a student is not a swimmer is \(\frac{1}{5}\). Then the probability that out of five students, four are swimmers is
(A) \({ }^{5} C_{4}\left(\frac{4}{5}\right)^{4} \frac{1}{5}\)

(B) \(\left(\frac{4}{5}\right)^{4} \frac{1}{5}\)

(C) \({ }^{5} C_{1} \frac{1}{5}\left(\frac{4}{5}\right)^{4}\)

(D) None of these
Solution.
The repeated selection of students who are swimmers are Bernoulli trials.
Let X denote the number of students, out of 5 students, who are swimmers.
Probability of students who are not swimmers, q = \(\frac{1}{5}\)
p = 1 – q
= 1 – \(\frac{1}{5}\)
= \(\frac{4}{5}\)
Clearly, X has a binomial distribution with n = 5 and p = \(\frac{4}{5}\)
P(X = x) = \({ }^{n} C_{x} q^{n-x} p^{x}\)

= \({ }^{5} C_{x} \cdot\left(\frac{1}{5}\right)^{5-x} \cdot\left(\frac{4}{5}\right)^{x}\)
P (four students are swimmers) = P(X = 4)
= \({ }^{5} C_{4}\left(\frac{1}{5}\right) \cdot\left(\frac{4}{5}\right)^{4}\)
Hence, the correct answer is (A).