Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 9 Sequences and Series Ex 9.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 11 Maths Chapter 9 Sequences and Series Ex 9.3
Question 1.
Find the 20th and nth terms of the G.P. \(\frac{5}{2}, \frac{5}{4}, \frac{5}{8}, \ldots\)
Answer.
The given G.P. is \(\frac{5}{2}, \frac{5}{4}, \frac{5}{8}, \ldots\).
Here, a = first term = \(\frac{5}{2}\)
r = Common ratio = \(\frac{\frac{5}{4}}{5}=\frac{1}{2}\)
a20 = ar20 – 1
= \(\frac{5}{2}\left(\frac{1}{2}\right)^{19}\)
= \(\frac{5}{(2)(2)^{19}}=\frac{5}{(2)^{20}}\)
an = arn – 1
= \(\frac{5}{2}\left(\frac{1}{2}\right)^{n-1}\)
= \(\frac{5}{(2)(2)^{n-1}}=\frac{5}{(2)^{n}}\)
![]()
Question 2.
Find the 12th term of a G.P. whose 8th term is 192 and the common ratio is 2.
Answer.
Common ratio, r = 2
Let a be the first term of the G.P.
∴ a8 = ar8 – 1 = ar7
ar7 = 192
a(2)7 = 192
a(2)7 = (2)6 (3)
a = \(\frac{(2)^{6} \times 3}{(2)^{7}}=\frac{3}{2}\)
∴ a12 = ar12 – 1
= (\(\frac{3}{2}\)) (2)11
= (3)(2)10 = 3072
Question 3.
The 5th, 8th and 11th terms of a G.P. are p, q and s, respectively. Show that q2 =ps.
Answer.
Let a be the first term and r be the common ratio of the G.P.
According to the given condition.
a5 = ar5 – 1
= ar4 = p ………………(i)
a8 = ar8 – 1
= ar7 = q ……………(ii)
a11 = ar11 – 1
= ar10 = s ……………(iii)
Dividing equation (ii) by equation (i) we obtain
\(\frac{a r^{7}}{a r^{4}}=\frac{q}{p}\)
r3 = \(\frac{q}{p}\) ……………(iv)
Dividing equation (iii) by (ii), we obtain
\(\frac{a r^{10}}{a r^{7}}=\frac{s}{q}\)
r3 = \(\frac{s}{q}\) ……………….(v)
Equating the values of r3 obtained in eqs. (iv) and (v), we obtain
\(\frac{q}{p}=\frac{s}{q}\)
⇒ q2 = ps
Thus, the given result is proved.

Question 4.
The 4th term of a G.P. is square of its second term, and the first term is – 3. Determine its 7th term.
Answer.
Let a be the first term and r be the common ratio of the G.P.
∴ a = – 3
It is known that,
an = a rn – 1
∴ a4 = ar3
= (- 3) r3
a2 = ar1
= (- 3) r
According to the given condition.
(- 3) r3 = [(- 3) r]2
⇒ – 3r3 = 9r2
⇒ r = – 3
a7 = ar7 – 1 = ar6
= (- 3) (- 3)6
= – (3)7 = – 2187
Thus, the seventh term of the G.P. is – 2187.
Question 5.
Which term of the following sequences :
(a) 2, 2√2, 4, ……….. is 128 ?
(b) √3, 3, 3√3, ………… is 729?
(c) \(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \ldots\) is \(\frac{1}{19683}\)?
Answer.
(a) The given sequence is 2, 2√2, 4, ………..
Here, a = 2 and r = \(\frac{2 \sqrt{2}}{2}\) = √2
Let the nth term of the given sequence be 128.
an = arn – 1
⇒ (2) (√2)n – 1 = 128
⇒ (2) \(\text { (2) } \frac{n-1}{2}\) = (2)7
⇒ \(\text { (2) } \frac{n-1}{2}+1\) = (2)7
∴ \(\frac{n – 1}{2}\) + 1 = 7
\(\frac{n – 1}{2}\) = 6
⇒ n – 1 = 12
⇒ n = 13
Thus, the 13th term of the given sequence is 128.
(b) 
(c) 

Question 6.
For what values of x, the numbers – \(\frac{2}{7}\), x, – \(\frac{7}{2}\) are in GP.?
Answer.
The given numbers are – \(\frac{2}{7}\), x, – \(\frac{7}{2}\)
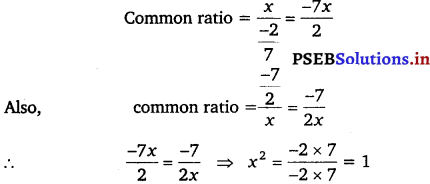
⇒ x = √1
⇒ x = ± 1
Thus, fcr x = ±1 , the given numbers will be in GP.
Question 7.
Find the sum to 20 terms In the geometric progression 0.15, 0.015, 0.0015 ………
Answer.
The given G.P. is 0.15, 0.015, 0.0015, ………..
Here, a = 0.15 and r = \(\frac{0.015}{0.15}\) = 0.1
Sn = \(\frac{a\left(1-r^{n}\right)}{1-r}\)
Sn = \(\frac{0.15\left[1-(0.1)^{20}\right]}{1-0.1}\)
= \(\frac{0.15}{0.9}\left[1-(0.1)^{20}\right]\)
= \(\frac{1}{6}\) [1 – (0.1)20].

Question 8.
Find the sum to n terms in the geometric progression √7, √21, 3√7 ……………
Answer.
The given G.P. is √7, √21, 3√7 ……………
Here, a = √7

Question 9.
Find the sum to n terms in the geometric progression 1, – a, a2, – a3 ………… (if a ≠ 1)
Answer.
The given G.P. is 1, – a, a2, – a3 …………
Here, first term = a1 = 1
Common ratio = r = – a
Sn = \(\frac{a-{n}\left(1-r^{n}\right)}{1-r}\)
∴ Sn = \(\frac{1\left[1-(-a)^{n}\right]}{1-(-a)}=\frac{\left[1-(-a)^{n}\right]}{1+a}\)
Question 10.
Find the sum to n terms in the geometric progression x3, x5, x7 … (if x ≠ ± 1).
Answer.
The given G.P. is x3, x5, x7, ………….
Here, a = x3 and r = x2
Sn = \(\frac{a\left(1-r^{n}\right)}{1-r}\)
= \(\frac{x^{3}\left[1-\left(x^{2}\right)^{n}\right]}{1-x^{2}}=\frac{x^{3}\left(1-x^{2 n}\right)}{1-x^{2}}\).
Question 11.
Evaluate \(\sum-{k=1}^{11}\) (2 + 3k)
Answer.
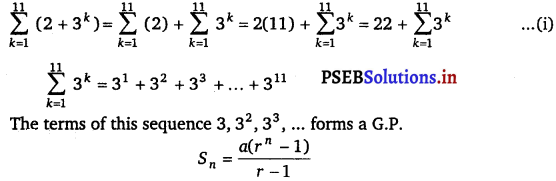
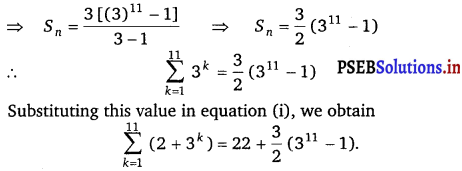

Question 12.
The sum of first three terms of a G.P. is – and their product is 1. Find the common ratio and the terms.
Answer.
Let the first three number of G.P. be \(\frac{a}{r}\), a and ar.
According to the question,
\(\frac{a}{r}\) + a + ar = \(\frac{39}{10}\) … (i)
and (\(\frac{a}{r}\)) × (a) × (ar) = 1
⇒ a3 = 1
⇒ a = 1
On putting the value of a = 1 in eq. (i), we get
\(\frac{1}{r}\) + 1 + r = \(\frac{39}{10}\)
\(\frac{1+r+r^{2}}{r}=\frac{39}{10}\)
⇒ 10 + 10r + 10r2 = 39r
⇒ 10r2 + 10r – 39r + 10 = 0
⇒ 10r2 – 29r + 10 = 0
Now, factorising it by splitting the middle term, we get
10r2 – 25r – 4r + 10 = 0
⇒ 5r (2r – 5) – 2 (2r – 5) = 0
⇒ (5r – 2)(2r – 5) = 0
⇒ 5r – 2 = 0 and 2r – 5 = 0
⇒ r = \(\frac{2}{5}\) and r = \(\frac{5}{2}\)
When a = 1 and r = \(\frac{2}{5}\), then numbers are
\(\frac{a}{r}=\frac{1}{\frac{2}{5}}=\frac{5}{2}\),
a = 1 and
ar = 1 × \(\frac{2}{5}\) = \(\frac{2}{5}\)
∴ \(\frac{5}{2}\), 1, \(\frac{2}{5}\).
When a = 1 and r = \(\frac{5}{2}\), then numbers are
\(\frac{a}{r}=\frac{1}{5}=\frac{2}{5}\);
a = 1 and ar = 1 × \(\frac{5}{2}\) = \(\frac{5}{2}\)
∴ \(\frac{2}{5}\), 1, \(\frac{5}{2}\).
Question 13.
How many terms of G.P. 3, 32, 33, …………… are needed to give the sum 120?
Answer.
The given G.P. is 3, 32, 33, …………
Let n terms of this G.P. be required to obtain the sum as 120.
Sn = \(\frac{a\left(r^{n}-1\right)}{r-1}\)
Here, a = 3 and r = 3
Sn = 120 = \(\frac{3\left(3^{n}-1\right)}{3-1}\)
⇒ 120 = \(\frac{3\left(3^{n}-1\right)}{3-1}\)
⇒ \(\frac{120 \times 2}{3}\) = 3n – 1
⇒ 3n – 1 = 80
⇒ 3n = 81
⇒ 3n = 34
∴ n = 4
Thus, four terms of the given G.P. are required to obtain the sum as 120.

Question 14.
The sum of first three terms of a G.P. is 16 andthe sum of the next three terms is 128. Determine the first term, the common ratio and the sum to n terms of the G.P.
Answer.
Let a be the first term and r be the common ratio, then

Question 15.
Given a G.P. with a = 729 and 7th term 64, determine S7.
Answer.
a = 729, a7 = 64
Let r be the common ratio of the G.P.
It is known that, an = arn – 1
a7 = ar7 – 1 (729)r6


Question 16.
Find a G.P. for which sum of the first two terms is – 4 and the fifth term is 4 times the third term.
Answer.
Let, first term = a and common ratio = r.
Given, sum of first two terms = – 4
⇒ a1 + a2 = – 4
⇒ a + ar = – 4
⇒ a (1 + r) = – 4
and fifth term = 4 × third term
a5 = 4 × a3
⇒ ar4 = 4ar2
r2 = 4
r = ± 2
When r = 2, then from eq. (i), we get
a (1 + 2) = – 4
⇒ a = – \(\frac{4}{3}\)
Then, G.P. is – \(\frac{4}{3}\), – \(\frac{4}{3}\) × 2, – \(\frac{4}{3}\) × (2)2, ……………
i.e., \(\frac{-4}{3}, \frac{-8}{3}, \frac{-16}{3}\)
When r = – 2, then from eq. (i), we get a
a (1 – 2)= – 4
⇒ – a = – 4
⇒ a = 4
Then, G.P. is 4, 4 × (- 2), 4 × (- 2)2 … i.e, 4,- 8, 16, ………..
Question 17.
If the 4th, 10th and 16th terms of a G.P. are x, y and z, respectively. Prove that x, y, z are in G.P.
Answer.
Given, 4 th term,
T4 = x
⇒ ar4 – 1 = x
⇒ ar3 = x …………………..(i)
10th term,
T10 = y
⇒ ar10 – 1 = y
⇒ ar9 = y ………………….(ii)
and 16 th term, T16 = z
⇒ ar16 – 1 = z
⇒ ar15 = z ………………(iii)
Now, multiplying eq. (j) by eq. (ill), we get
ar3 × ar15 = x × z
a2 r3 + 15 = x × z
a2 r18 = xz
(ar9)2 = xz
∴ y2 = xz [from eq. (ii)]
Therefore, x,y and z are in GP.

Question 18.
Find the sum to n terms of the sequence, 8, 88, 888, 8888 …………
Answer.
The given sequence is 8, 88, 888, 8888 ………………
This sequence is not a G.P.
However, it can be changed to G.P. by writing the terms as
Sn = 8 + 88 + 888 + 8888 + ……………. to n terms
= \(\frac{8}{9}\) [9 + 99 + 999 + 9999 + ………….to n terms]
= \(\frac{8}{9}\) [(10 – 1) + (102 – 1) + (103 – 1) + (104 – 1) + …………… to n terms]
= [(10 + 102 +………… n terrns) – (1 + 1 + 1 + ………….. n terms)]
= \(\frac{8}{9}\left[\frac{10\left(10^{n}-1\right)}{10-1}-n\right]=\frac{8}{9}\left[\frac{10\left(10^{n}-1\right)}{9}-n\right]\)
= \(\frac{80}{81}\) (10n – 1) – \(\frac{8}{9}\) n.
Question 19.
Find the sum of the products of the corresponding terms of the sequences 2, 4, 8, 16, 32 and 128, 32, 8, 2,.
Answer.


Question 20.
Show that the products of the corresponding terms of the sequences a, ar, ar2, … arn – 1 and A, AR, AR2, …….. ARn – 1 form a G.P. and find the common ratio.
Answer.
It has to be proved that the sequence, aA, arAR, ar2AR2, ………. arn – 1 ARn – 1, forms a G.P.
\(\frac{\text { Second term }}{\text { First term }}=\frac{a r A R}{a A}\) = rR
\(\frac{\text { Third term }}{\text { Second term }}=\frac{a r^{2} A R^{2}}{a r A R}\) = rR
Thus, the above sequence forms a G.P. and the common ratio is rR.
Question 21.
Find four numbers forming a geometric progression in which third term is greater than the first term by 9, and the second term is greater than the 4th by 18.
Answer.
Let a be the first term and r the common ratio of G.P.
∴ nth term = Tn = arn – 1
⇒ T2 = ar , T3 = ar2 and T4 = ar3
Since third term is greater than the first by 9.
∴ T3 = T1 + 9
⇒ ar2 = a + 9
Second term is greater than the 4th by 18.
T2 = T4 + 18
⇒ ar = ar3 + 18
⇒ ar3 = ar + 9r
From eqs. (ii) and (iii), we get
ar = ar + 9r + 18
⇒ 0 = 9r + 18
⇒ r = \(\frac{-18}{9}\) = – 2
Put = – 2 in (i), we get
a(- 2)2 = a + 9
⇒ 4a = a + 9
⇒ 3a = 9
⇒ a = 3
T2 = ar = 3 (- 2) = – 6
T3 = ar2
= 3 (- 2)2 = 12
T4 = ar3
= 3 (- 2)3 = – 24
∴ Required terms are 3, – 6, 12 and – 24.

Question 22.
If the pth, qth and rth terms of a G.P. are a, b, and c, respectively. Prove that aq – r br – p cp – q = 1.
Answer.
Let A be the first term and R be the common ratio of the G.P.
According to the given information.
ARp – 1 = a
ARq – 1 = b
ARr – 1 = c
aq – r br – p cp – q = Aq – r x R(p – 1) (q – r) x Ar – p x R(q – 1) (r – p) x Ap – q x R(r – 1) (p – q)
= Aq – r + r – p + p – q R(pq – pr – p + q) + (rq – r + p – pq) + (pr – p – qr + q)
= A0 × R0 = 1
Thus, the given result is proved.
Question 23.
If the first and the nth term of a G.P. are a and b, respectively, and if P is the product of n terms, prove that P2 = (ab)n.
Answer.
The first term of the G.P. is a and the last term is b.
Therefore, the G.P. is a, ar, ar2, ar3, …………. arn – 1, where r is the common ratio.
b = arn – 1 …………..(i)
P = Product of n terms
= (a) (ar) (ar2) … (arn – 1)
= (a × a × ……… a) (r × r2 × ……….. rn – 1)
= an r1 + 2 + ………. + (n – 1)
Here, 1, 2, ………. (n – 1) is an A.P.
∴ 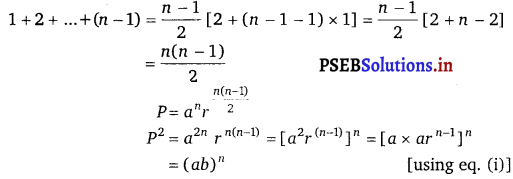
Thus, the given result is proved.

Question 24.
Show that the ratio of the sum of first n terms of a G.P. to the sum of terms from (n + 1)th to (2n)th term is \(\frac{1}{r^{n}}\).
Answer.
Let a be the first term and r be the common ratio of the G.P.
Sum of first n terms = \(\frac{a\left(1-r^{n}\right)}{(1-r)}\)
Since there are n terms from (n + 1)th to (2n)th term,
sum of terms from (n + 1)th to (2n)th term
= \(\frac{a_{n+1}\left(1-r^{n}\right)}{(1-r)}\)
= \(\frac{a r^{n}\left(1-r^{n}\right)}{(1-r)}\) [∵ an + 1 = arn + 1 – 1 = arn]
Thus, required ratio = \(\frac{a\left(1-r^{n}\right)}{(1-r)} \times \frac{(1-r)}{a r^{n}\left(1-r^{n}\right)}=\frac{1}{r^{n}}\)
Thus, the ratio of the sum of first n terms of G.P. to the sum of terms from (n + 1)th to (2n)th term is \(\frac{1}{r^{n}}\).
Question 25.
If a, b, c and d are in G.P. show that
(a2 + b2 + c2) (b2 + c2 + d2) = (ab + bc + cd)2.
Answer.
Given, a, b, c, d are in G.P.
\(\frac{b}{a}=\frac{c}{b}=\frac{d}{c}\) = r (say)
⇒ b = ar, c = br, d = cr
⇒ b = ar, c = (ar)r, d = (br)r
⇒ b = ar, c = ar2, d = br2
⇒ b = ar,c = ar2,d = (ar)r2 = ar3
Now we have to prove that
(a2 + b2 + c2) (b2 + c2 + d2) = (ab + bc + cd)2
L.H.S. = (a2 + b2 + c2) (b2 + c2 + d2)
= (a2 + a2 r2 + a2 r4) (a2 r2 + a2 r4 + a2 r6)
= a2 (1 + r2 + r4) a2 r2 (1 + r2 + r4)
= a4r2 (1 + r2 + r4)2
= [a2 r (1 + r2 + r4)]2
= [a2 r + a2r3 + a2 r5]2
=[a . ar + ar . ar2 + ar2 ar3]2
= [ab + be + cd]2 [from eq. (i)]
= R.H.S.
Hence proved.

Question 26.
Insert two numbers between 3 and 81 so that the resulting sequence is GJ*.
Answer.
Let G1 and G2 be two numbers between 3 and 81 such that the Series, 3, G1, G2, 81, forms a G.P.
Let a be the first term and r be the common ratio of the G.P.
∴ 81 = (3)(r)3
r3 = 27
∴ r = 3
For r = 3
G1 = ar = (3) (3) = 9
G2 = ar2 = (3) (3)2 = 27
Question 27.
Find the value of n so that \(\frac{a^{n+1}+b^{n+1}}{a^{n}+b^{n}}\) may be the geometric mean between a and b.
Answer.
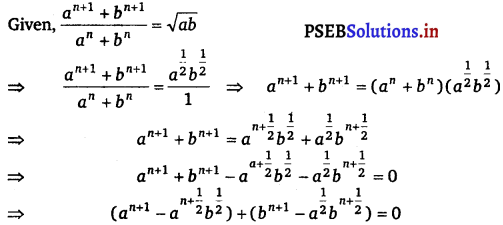
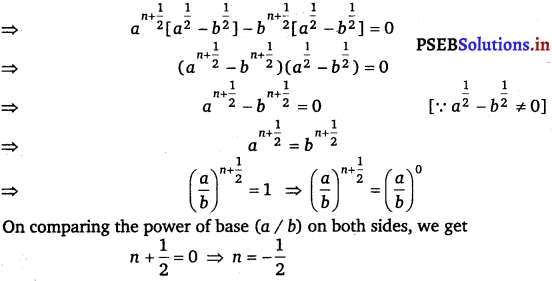
Hence proved.

Question 28.
The sum of two numbers is 6 times their geometric mean, show that numbers are in the ratio (3 + 2√2) : (3 – 2√2).
Answer.
Let the two numbers be a and b.
G.M. = √ab
According to the given condition,
a + b = √ab …………….(i)
(a + b)2 = 36(ab)
Also, (a – b)2 = (a + b)2 – 4ab
= 36ab – 4ab = 32ab
a – b = √32 √ab
= 4 √2 √ab ……………….(ii)
Adding eqs. (i) and (ii), we obtain
26 = (6 + 4√2) √ab
⇒ a = (3 + 2√2)√ab
Substituting the value of a in (i), we obtain
b = 6√ab – (3 + 2√2) √ab
⇒ b = (3 – 2√2) √ab
\(\frac{a}{b}=\frac{(3+2 \sqrt{2}) \sqrt{a b}}{(3-2 \sqrt{2}) \sqrt{a b}}=\frac{3+2 \sqrt{2}}{3-2 \sqrt{2}}\)
Thus, the required ratio is (3 + 2√2) : (3 – 2√2).

Question 29.
If A and G be AM. and G.M., respectively between two positive numbers, prove that the numbers are A ± \(\sqrt{(A+G)(A-G)}\).
Answer.
let the numbers are α and β.
Given, sum of the roots,
\(\frac{\alpha+\beta}{2}\) = A [arithmetic mean]
α + β = 2A
and product of the root,
\(\sqrt{\alpha \beta}\) = G [geometric mean]
⇒ αβ = G2
Now, quadratic equation having roots α and β is
x2 – (α + β)x + αβ = 0
⇒ x2 – 2Ax + G2 = 0
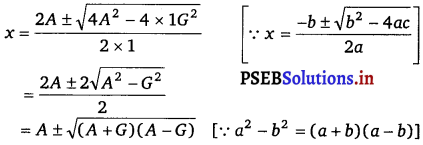
Hence proved.
Question 30.
The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th hour and nth hour?
Answer.
It is given that the number of bacteria doubles every hour.
Therefore, the number of bacteria after every hour will form a G.P.
Here, a = 30 and r = 2
∴ a3 = ar2
= (30) (2)2 = 120
Therefore, the number of bacteria at the end of 2nd hour will be 120.
a5 = ar4
= (30) (2)4 = 480
The number of bacteria at the end of 4 th hour will be 480.
an + 1 = arn = (30) 2n
Thus, number of bacteria at the end of nth hour will be 30(2)n.

Question 31.
What will Rs. 500 amounts to in 10 years after its deposit in a bank which pays annual interest rate of 10% compounded annually?
Answer.
The amount deposited in the bank is Rs. 500.
At the end of first year, amount = Rs. 500(1 + \(\frac{1}{10}\)) = Rs. 500 (1.1)
At the end of 2nd year, amount = Rs. 500 (1.1) (1.1)
At the end of 3rd year, amount = Rs. 500 (1.1) (1.1) (1.1) and so on .
Amount at the end of 10 years = Rs. 500 (1.1) (1.1) … (10 times)
= Rs. 500 (1.1)10.

Question 32.
If AM. and G.M. of roots of a quadratic equation are 8 and 5, respectively, then obtain the quadratic equation.
Answer.
Let the roots of the quadratic equation are α and β, then
(arithmetic mean) \(\frac{\alpha+\beta}{2}\) = 8 and
(geometric mean) \(\sqrt{\alpha \beta}\)= 5
⇒ α + β = 16 and αβ = 25
Now, if roots are a and p, then quadratic equation is x2 – (Sum of roots) x + Product of roots = 0
⇒ x2 – (α + β)x + αβ = 0
⇒ x2 – 16x + 25 = 0.
