PSEB 11th Class Economics Solutions Chapter 23 केंद्रीय प्रवृत्ति के माप-मध्यका

Punjab State Board PSEB 11th Class Economics Book Solutions Chapter 23 केंद्रीय प्रवृत्ति के माप-मध्यका Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 11 Economics Chapter 23 केंद्रीय प्रवृत्ति के माप-मध्यका

PSEB 11th Class Economics केंद्रीय प्रवृत्ति के माप-मध्यका Textbook Questions and Answers

I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)

प्रश्न 1.
मध्यका से क्या अभिप्राय है ?
उत्तर-
मध्यका किसी श्रेणी की वह मूल्य है जो श्रेणी को दो भागों में इस प्रकार बांटता है कि उसके एक तरफ सभी बड़े और दूसरी तरफ कम मूल्य होते हैं।

प्रश्न 2.
मध्यका का कोई एक गुण लिखो।
उत्तर-
यह एक सरल औसत है जिसे समझना तथा माप करना आसान होता है।

प्रश्न 3.
अखण्डित श्रेणी में मध्यका का माप सूत्र लिखो।
उत्तर-
M = \(\mathrm{L}_{1}+\frac{\frac{\mathrm{N}}{2}-c f p}{f} \times i\)

प्रश्न 4.
विभाजन मूल्यों से क्या अभिप्राय है ?
उत्तर-
किसी श्रेणी को दो अथवा दो से अधिक भागों में बांटने को विभाजन मूल्य कहा जाता है।

प्रश्न 5.
विभाजन मूल्य ……. को कहा जाता है।
(a) मध्यका
(b) चतुर्थक
(c) दशमक
(d) उपरोक्त सभी।
उत्तर-
(d) उपरोक्त सभी।

प्रश्न 6.
मध्यका को स्थिति की औसत कहा जाता है ?
उत्तर-
सही।

प्रश्न 7.
संचयी आवृत्ति वक्र (Ogive) द्वारा मध्यका का माप नहीं किया जा सकता।
उत्तर-
ग़लत।

II. अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
मध्यका से क्या अभिप्राय है ?
उत्तर-
केन्द्रीय प्रवृत्ति के दूसरे माप को मध्यका कहा जाता है। इस स्थिति को प्रकट करने वाली औसत होती है। जब श्रेणी की मदों को बढ़ते क्रमानुसार में कर लिया जाए तो वह मूल्य जोकि श्रेणी को दो समान भागों में विभाजित करता है, उस मूल्य को मध्यका कहा जाता है, अर्थात् मध्यका किसी श्रेणी की वह संख्या होती है, जो उस श्रेणी को दो समान भागों में विभाजित करती है। उसकी एक ओर सभी मदें उससे छोटी होती हैं तथा दूसरी ओर सभी मदें उससे बड़ी होती हैं। उदाहरणस्वरूप ग्यारहवीं कक्षा के पाँच विद्यार्थियों द्वारा प्राप्त किए अंक 60, 65.

प्रश्न 2.
मध्यका के कोई तीन गुण बताएँ।
उत्तर-
मध्यका के गुण-मध्यका के गुण इस प्रकार हैं-

1. मध्यका स्थिति की औसत होती है। इसको समझना आसान है।
2. मध्यका एक सरल विधि है। इसका माप व्यक्तिगत श्रेणी तथा खण्डित श्रेणी में आसानी से किया जा सकता है।
3. मध्यका पर सीमान्त मूल्यों का प्रभाव नहीं पड़ता। इसलिए इसके परिणाम अधिक शुद्ध होते हैं।

प्रश्न 3.
मध्यका के कोई तीन दोष बताएँ।
उत्तर-
मध्यका के दोष-मध्यका के दोष इस प्रकार हैं –

1. जब मदों के मूल्य में अन्तर बहुत अधिक होता है तो मध्यका ऐसी श्रेणी का उचित प्रतिनिधित्व नहीं करता।
2. मध्यका में बीजगणित विवेचन नहीं किया जा सकता। इसलिए इस विधि का प्रयोग अन्य सांख्यिकी संख्याओं के हल में सहायक होता है।
3. मध्यका की गणना करते समय अन्तर्गणना के सूत्र का प्रयोग किया जाता है। इसलिए गणना करने में मुश्किल का सामना करना पड़ता है।

III. लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 1.
मध्यका के गुण बताओ।
उत्तर-
मध्यका के गुण इस प्रकार हैं –

1. मध्यका स्थिति की औसत होती है। इसको समझना आसान है।
2. मध्यका एक सरल विधि है। इस का माप व्यक्तिगत श्रेणी तथा खण्डित श्रेणी में आसानी से किया जाता है।
3. मध्यका ऊपर सीमान्त मूल्य का प्रभाव नहीं पड़ता। इसके लिए इसके परिणाम अधिक शुद्ध होते हैं।
4. मध्यका श्रेणी के मूल्य में ही होती है। इसलिए इसको प्रतिनिधि औसत भी कहा जाता है।
5. मध्यका को ग्राफ विधि द्वारा भी ज्ञात किया जा सकता है।
6. अपूर्ण आंकड़ों की स्थिति में भी मध्यका का माप किया जा सकता है। यदि बीच वाले मूल्यों की जानकारी हो तो मध्यका की गणना की जा सकती है।
7. मध्यका को ग्राफ विधि द्वारा भी ज्ञात किया जा सकता है।

प्रश्न 2.
मध्यका के दोष लिखो।
उत्तर-
मध्यका के दोष निम्नलिखित अनुसार हैं –

1. जब मदों के मूल्यों में अन्तर बहुत अधिक होता है तो मध्यका ऐसी श्रेणी का उचित प्रतिनिधित्व नहीं करती।
2. मध्यका में बीजगणित विवेचन नहीं किया जा सकता। इसलिए इस विधि का प्रयोग अन्य सांख्यिकी समस्याओं के हल में कम सहायक होता है।
3. मध्य की गणना करते समय अन्तर्गणना के सूत्र का प्रयोग किया जाता है। इसलिए गणना करने में मुश्किल का सामना करना पड़ता है।
4. जब मध्यका दो मूल्यों में स्थित होती है तो ऐसी स्थिति में सम्भावित मूल्य का पता किया जा सकता है। असल मध्यका का पता नहीं लगता।
5. श्रेणी में थोड़ा-सा परिवर्तन होने से मध्यका के मूल्य में काफ़ी परिवर्तन हो जाता है।

IV. दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 1.
मध्यका से क्या अभिप्राय है ? मध्यका के गुण तथा दोष बताओ।
उत्तर-
केन्द्रीय प्रवृत्ति के दूसरे माप को मध्यका कहा जाता है। इस स्थिति को प्रकट करने वाली औसत होती है। जब श्रेणी की मदों को बढ़ते क्रमानुसार अथवा घटते क्रमानुसार में कर लिया जाए तो वह मूल्य जोकि श्रेणी को दो समान भागों में विभाजित करता है, उस मूल्य को मध्यका कहा जाता है, अर्थात् मध्यका किसी श्रेणी की वह संख्या होती है, जो उस श्रेणी को दो समान भागों में विभाजित करती है। उसकी एक ओर सभी मदें उससे छोटी होती हैं तथा दूसरी ओर सभी मदें उससे बड़ी होती हैं।

उदाहरणस्वरूप ग्यारहवीं कक्षा के पाँच विद्यार्थियों द्वारा प्राप्त किए अंक 60, 65, 70, 75, 80 हैं तो मध्यका 70 अंक है। 70 अंकों से 60 तथा 65 अंक हैं, जबकि 75 तथा 80 अधिक हैं। इसलिए मध्यका बीच की स्थिति को प्रकट करने वाली औसत होती है। इसको रेखाचित्र द्वारा भी स्पष्ट किया जा सकता है।

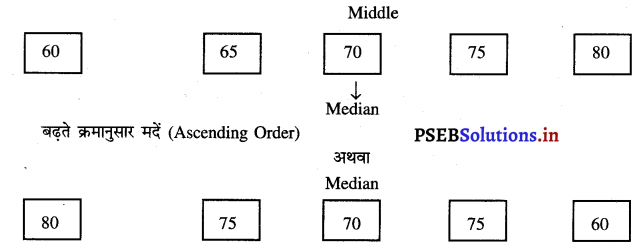
घटते क्रमानुसार मदें (Descending Order)
इस प्रकार मदों को बढ़ते क्रमानुसार अथवा घटते क्रमानुसार लिखने के पश्चात् जो मदें 70 बीच (middle) स्थित होती हैं, उस मद को मध्यका कहा जाता है।

परिभाषा (Definition)
प्रो० एल० आर० कोनर के शब्दों में, “मध्यका श्रेणी का वह मूल्य होता है जो श्रेणी को दो समान भागों में इस प्रकार विभाजित करता है कि एक भाग में सभी मूल्य मध्यका से अधिक तथा दूसरे भाग में सभी मूल्य मध्यका से कम होते हैं।”
मध्यका के गुण-मध्यका के गुण इस प्रकार हैं –

1. मध्यका स्थिति की औसत होती है। इसको समझना आसान है।
2. मध्यका एक सरल विधि है। इसका माप व्यक्तिगत श्रेणी तथा खण्डित श्रेणी में आसानी से किया जा सकता है।
3. मध्यका पर सीमान्त मूल्यों का प्रभाव नहीं पड़ता। इसलिए इसके परिणाम अधिक शुद्ध होते हैं।
4. मध्यका श्रेणी के मूल्य में ही होती है। इसीलिए इसको प्रतिनिधि औसत भी कहा जाता है।
5. मध्यका निश्चित होती है, इसलिए मध्यका का पता किया जा सकता है।
6. अपूर्ण आंकड़ों की स्थिति में भी मध्यका का माप किया जा सकता है। यदि बीच के मूल्यों की जानकारी हो तो मध्यका की गणना की जा सकती है।
7. मध्यका को ग्राफ विधि द्वारा भी ज्ञात किया जा सकता है।

मध्यका के दोष-मध्यका के दोष इस प्रकार हैं –

1. जब मदों के मूल्य में अन्तर बहुत अधिक होता है तो मध्यका ऐसी श्रेणी का उचित प्रतिनिधित्व नहीं करता।
2. मध्यका में बीजगणित विवेचन नहीं किया जा सकता। इसलिए इस विधि का प्रयोग अन्य सांख्यिकी संख्याओं के हल में कम सहायक होता है।
3. मध्यका की गणना करते समय अन्तर्गणना के सूत्र का प्रयोग किया जाता है। इसलिए गणना करने में मुश्किल का सामना करना पड़ता है।
4. जब मध्यका दो मूल्यों में स्थित होती है तो ऐसी स्थिति में सम्भावित मूल्य का ही पता किया जा सकता है। वास्तविक मध्यका का पता नहीं लगता।
5. श्रेणी में थोड़े से परिवर्तन होने से मध्यका के मूल्य में काफ़ी परिवर्तन हो जाता है।
6. यदि मध्यका का पता हो तो श्रेणी की कुल मदों का पता नहीं कर सकते।

व्यक्तिगत श्रेणी में मध्यका का माप (Calculation of Median in Individual Series)

प्रश्न 2.
निम्नलिखित श्रेणी में विद्यार्थियों के अंकों का विवरण दिया गया है। मध्यका का पता करो।
अंक 25, 20, 27, 30, 16, 40, 35, 12, 10
हल :
इन मदों को बढ़ते क्रमानुसार अथवा घटते क्रमानुसार लिखना चाहिए –

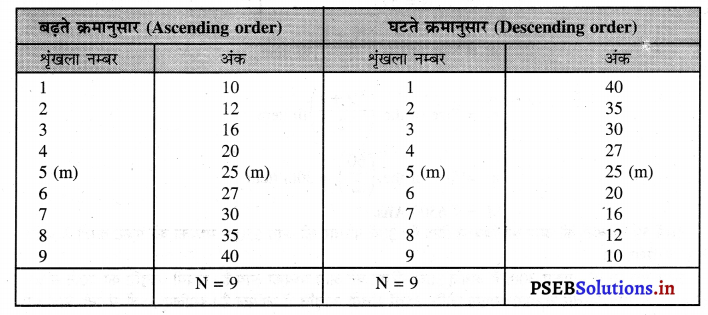
बढ़ते क्रमानुसार
m= Size of the \(\left(\frac{n+1}{2}\right)\) an item
m =\(\left(\frac{9+1}{2}\right)\)th = \(\frac{10}{2}\) = 5th item
size of the 5th item
M = 25 Marks Ans.

घटते क्रमानुसार
m = Size of the \(\left(\frac{n+1}{2}\right)\) th item
m = \(\left(\frac{9+1}{2}\right)\) th or 5th item
i.e. size of the 5th item
M = 25 Marks Ans.
समंकों को बढ़ते अथवा घटते क्रमानुसार करके मध्यका का माप किया जाता है तो 5वें विद्यार्थी के अंक 25 हैं जो कि केन्द्र में स्थित है। इसलिए 25 अंकों को मध्यका कहा जाता है।

प्रश्न 3.
निम्नलिखित आंकड़ों की मध्यका ज्ञात करो।

आय (₹) प्रति माह :	5000	5500	6000	6500	7000	7500
परिवारों की संख्या :	4	6	10	15	19	5

हल : आंकड़े बढ़ते क्रमानुसार दिए गए हैं।

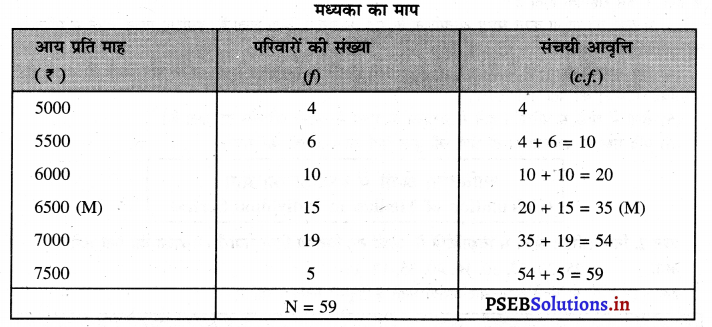
m = Size of the \(\left(\frac{\mathrm{N}+1}{2}\right)\) th item
m = Size of the \(\left(\frac{59+1}{2}\right) \)th item
m = Size of the \(\left(\frac{60}{2}\right)\) th item
m = Size of the = 30th item
M = ₹ 6500 Ans.
इसमें 59 परिवारों की आय का विवरण दिया है। 30वें परिवार की आय 6500 मध्यका को प्रकट करती है जोकि केन्द्र में स्थित है। ऊपर मध्यका का आकार 30th है अर्थात् 30वें परिवार की आय मध्यका आय है। संचयी आवृत्ति को देखने से ज्ञात होता है कि 20वें परिवार से आगे आएगा जोकि 35वीं संचयी आवृत्ति में शामिल है। इसलिए 35वीं संचयी आवृत्ति में 30वां परिवार होने के कारण इस आकार को (m) द्वारा लिखा जाता है। इस आकार (m) के सामने 6500 रु० प्रति माह आय दिखाई गई है। इसलिए मध्यका (Median) ₹ 6500 होगा।

प्रश्न 4.
निम्नलिखित आंकड़ों की मध्यका का पता करो।

अंक :	0-10	10-20	20-30	30-40	40-50	50-60
विद्यार्थियों की संख्या :	8	12	20	35	15	6

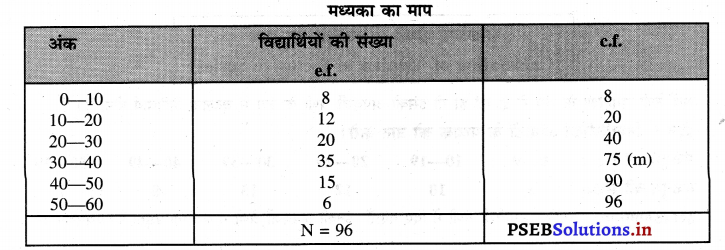
m = Size of the \(\left(\frac{n}{2}\right)\) th item.
m = Size of the \(\left(\frac{96}{2}\right)\) th or 48th item
मध्यक आकार से पता चलता है कि 48वां विद्यार्थी संचयी आवृत्ति 75 में शामिल है। इसको m कहा जाता है। इसके बिल्कुल सामने वर्गान्तर 30-40 है। इसको मध्यक वर्ग कहते हैं। मध्यक 30-40 के बीच है। इसका माप निम्न सूत्र द्वारा किया जा सकता है।
M = \(\mathrm{L}_{1}+\frac{\frac{\mathrm{N}}{2}-c f p}{f} \times i\)
यहां L₁ = मध्यक वर्गान्तर की निचली सीमा = 30
\(\frac{\mathrm{N}}{2}\) = मध्यक मदों का आकार (m) = 48
c.f.p = मध्यक वर्ग 30-40 से प्रथम वर्ग 20-30 की संचयी आवृत्ति = 40
f = मध्यक वर्गान्तर (40–30) = 10
इन रकमों को सूत्र में भरने से
M = \(30+\frac{\frac{96}{2}-40}{35} \times 10\)
अथवा
M = \(30+\frac{48-40}{35} \times 10\)
M = 30 + \(\frac{8}{35} \times 10\)
M = 30 + 2.285
Median = 32.285 अंक Ans. कक्षा में 48वें विद्यार्थी के अंक 32.285 हैं, इसको मध्यका कहा जाएगा।

समावेशी श्रेणी में मध्यका का माप (Calculation of Median in Inclusive Series)

जब श्रेणी समावेशी के रूप में दी गई हो तो इसको अपवर्जी श्रेणी के रूप में बदलना अनिवार्य होता है।

प्रश्न 5.
निम्नलिखित आंकड़ों के मध्यक को ज्ञात करो।

मज़दूरी (₹) :	0-9	10-19	20-29	30-39	40-49	50-59
मज़दूरों की संख्या :	8	10	12	15	8	7

हल (Solution) :
वर्गान्तर समावेशी श्रेणी में दिए गए हैं। इनको अपवर्जी श्रेणी में बदलना पड़ता है। प्रथमवर्ग की ऊपरी सीमा तथा द्वितीय वर्ग की निचली सीमा का अन्तर एक है तो इसका आधा = = 0.5 होगा। प्रत्येक वर्ग की निचली सीमा में से 0.5 घटा देना चाहिए तथा प्रत्येक वर्ग की ऊपरी सीमा में 0.5 जोड़ देना चाहिए। इसी तरह समावेशी श्रेणी अपवर्जी श्रेणी में बदल जाती है। फिर प्रश्न का हल करना चाहिए।

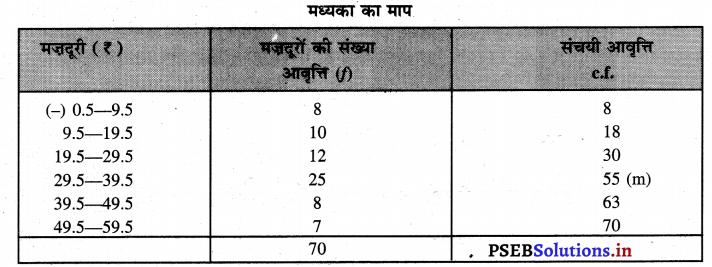
m = size of the \(\left(\frac{n}{2}\right)\) th item = \(\frac{70}{2}\) = 35th item
M = \(\mathrm{L}_{1}+\frac{\frac{n}{2}-c f p}{f} \times i\)
M = 29.5 + \(\frac{35-30}{25}\) x 10 = 29.5 + 2 = ₹ 31.5 Ans.
70 मजदूरों में से 35वें मज़दूर की मज़दूरी ₹ 31.5 है, इसको मध्यका कहा जाता है।

संचयी आवृत्ति में मध्यका का माप (Calculation of Median in Cummulative Frequency)
यदि प्रश्न में संचयी आवृत्ति दी हो तो साधारण आवृत्ति निकालकर प्रश्न का हल करना चाहिए।

प्रश्न 6.
निम्नलिखित तालिका की मध्यका ज्ञात करो।

अंक (से कम):	10	20	30	40	50	60	70	80
आवृत्ति :	15	35	60	84	96	127	198	250

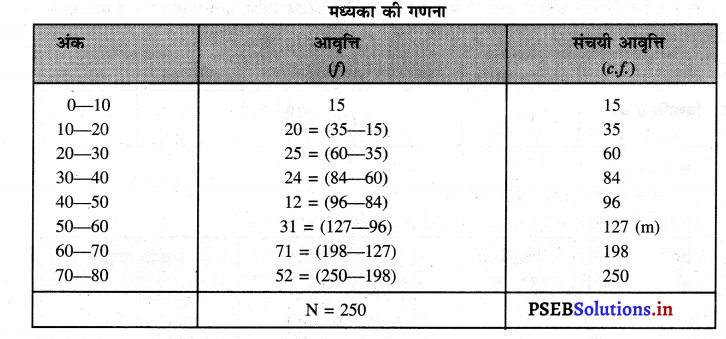
m = Size of the \(\left(\frac{n}{2}\right)\) th = \(\frac{250}{2}\) = 125th item
मध्यक वर्ग = 50-60
L₁ = 50, \(\frac{n}{2}\) = 125, c.f.p .= 96, i = (60–50) = 10, f = 31
M = \(\frac{\mathrm{Z}_{1}+\frac{\mathrm{M}}{2}-c . f \cdot p .}{f} \times i\)
M = 50 + \(\frac{125-96}{31} \times 10\)
= 50 + \(\frac{290}{31}\)
= 50 + 9.35
Median = 59.35 अंक Ans.
250 विद्यार्थियों में से केन्द्र में स्थित 125वें विद्यार्थी ने 59.35 अंक प्राप्त किए हैं। इसको मध्यका कहा जाता है, क्योंकि आधे विद्यार्थियों के अंक इस विद्यार्थी के समान अथवा कम हैं तथा आधे विद्यार्थियों के अंक इसके समान अथवा अधिक हैं।

बिन्दु रेखीय विधि द्वारा मध्यका का निर्धारण (Graphic Determination of Median)
बिन्दु रेखीय विधि द्वारा ओजाइव (Ogive) वक्र बनाकर मध्यका का माप किया जा सकता है। इसकी दो विधियां होती हैं
(i) से कम विधि (Less than Method)
(ii) से अधिक विधि (More than Method)

प्रश्न 7.
निम्नलिखित आँकड़ों द्वारा
(i) से कम विधि,
(ii) से अधिक विधि,
(ii) संयुक्त रूप में मध्यका की गणना करो।

अंक:	0-10	10-20	20 – 30	30 – 40	40-50
विद्यार्थियों की संख्या :	4	6	10	15	5

हल (Solution) –
(i) से कम विधि (Less Than Method)
इस श्रृंखला को पहले से कम आवृत्ति में बदल लें और आवृत्ति वक्र बना लें।

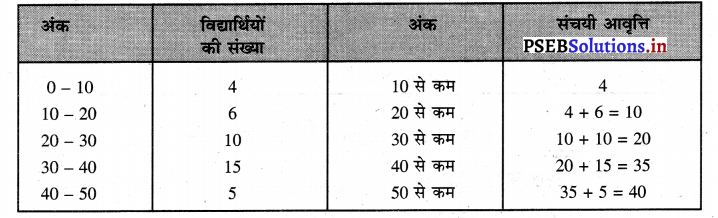
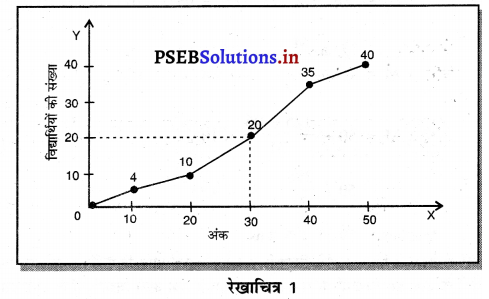
Median = \(\frac{N}{2}=\frac{40}{2}\) = 20th Student
(Ans. Median = 30 अंक)

(ii) से अधिक विधि (More than Method)


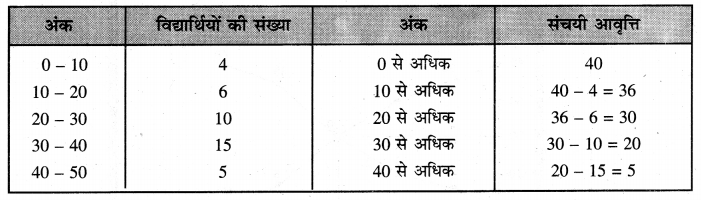
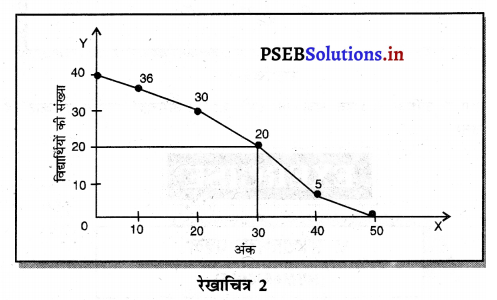
Median = \(\frac{N}{2}=\frac{40}{2}\) = 20th Student
20वें विद्यार्थी से एक लम्ब संचयी आवृत्ति रेखा की तरफ खींचते हैं। जहाँ पर यह लंब संचयी आवृत्ति रेखा को काटता है। वहाँ से Ox की तरफ लम्ब खींचते हैं। इस चित्र में 30 अंक माध्यक हैं। (Ans. Median = 30 अंक)

(iii) से कम तथा से अधिक विधि (Less than and More then Ogive) ऊपर हमने से कम विधि (Less than Method) द्वारा तथा से अधिक विधि द्वारा संचयी आवृत्ति का माप किया . है जो कि इस प्रकार है-

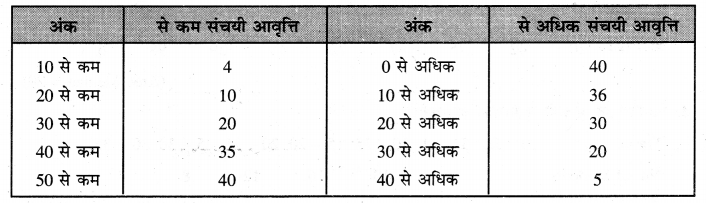
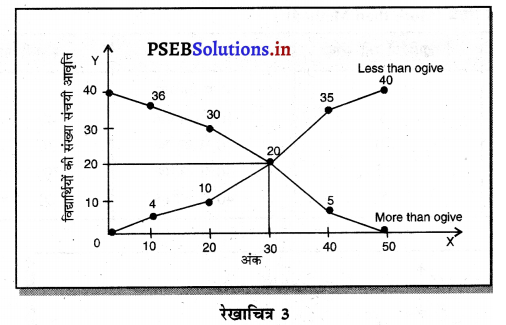
यहाँ पर से कम तथा से अधिक ओजाइव अंक एक दूसरे को 20 असंचयी आवृत्ति पर काट रहे हैं। इसलिये Median = 30 अंक उत्तर।