PSEB 9th Class Science Solutions Chapter 8 गति

Punjab State Board PSEB 9th Class Science Book Solutions Chapter 8 गति Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Science Chapter 8 गति

PSEB 9th Class Science Guide गति Textbook Questions and Answers

प्रश्न 1.
एक एथलीट वृत्तीय पथ, जिसका व्यास 200 m है, का एक चक्कर 40s में लगाता है। 2 min 20s के बाद वह कितनी दूरी तय करेगा और उसका विस्थापन क्या होगा ?
हल :

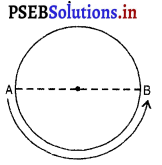
दिया है, वृत्तीय पथ का व्यास (d) = 200 m
∴ वृत्तीय पथ का अर्धव्यास = $\frac{200}{2}$ = 100m
वृत्तीय पथ की लंबाई (ce) = 2πr
= 2 × $\frac{22}{7}$ × 100
= $\frac{4400}{7}$ m
1 चक्कर पूरा करने में लगा समय (t) = 40 s
कुल समय = 2 मिनट 20 सेकंड
= ( 2 × 60 + 20) सेकंड
= (120 + 20) सेकंड
= 140 सेकंड
40 s में तय की गई दूरी = $\frac{4400 \mathrm{~m}}{7}$ (= 1 चक्कर की परिधि)
1 s में तय की गई दूरी = $\frac{4400}{7 \times 40}$
40 s में तय हुई दूरी = $\frac{4400}{7 \times 40}$ × 140
= 2200 m
= $\frac{1}{2}$ चक्कर की लंबाई
इसलिए गति के अंत में एथलीट $\frac{1}{2}$ चक्कर लगाकर वृत्त के व्यास के दूसरे सामने वाले सिरे B पर पहुँचेगा।
∴ विस्थापन AB (मूल बिंदु तथा अंतिम बिंदु के मध्य की दूरी)
= 2200 m

प्रश्न 2.
300 m सरल रेखीय पथ पर जोसेफ़ जॉगिंग करता हुआ 2 min 30s में एक सिरे A से दूसरे सिरे B पर पहुंचता है और धूपकर 1 min में 100 m पीछे बिंदु C पर पहुँचता है। जोसेफ़ की औसत चाल और औसत वेग क्या होंगे ?
(a) सिरे A से सिरे B तक तथा
(b) सिरे A से सिरे C तक।
हल :

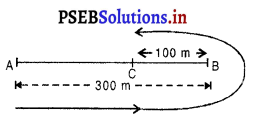
(a) सिरे A से सिरे B के बीच की लंबाई (AB) = 300 m
लगा समय (t) = 2 min 30 s
= (2 × 60 + 30) S
= (120 + 30)s
= 150 s
∴ औसत चाल = औसत वेग
=
= $\frac{300 \mathrm{~m}}{150 \mathrm{~s}}$
= 2 ms^-1

(b) A सिरे से सिरे B तक लंबाई + वापिस B से C तक की लंबाई
= AB + BC
= 300 m + 100 m
= 400 m
कुल समय = 2 min 30 s + 1 min
= 3 min 30 s
= (180 + 30)s
=210 s
औसत चाल = $\frac{400 \mathrm{~m}}{210 \mathrm{~s}}$
= $\frac{40}{21}$ ms
= 1.9 ms^-1
औसत वेग = $\frac{(300-100) \mathrm{m}}{210 \mathrm{~s}}$
= $\frac{200}{210}$ms^-1
= $\frac{20}{21}$ ms^-1
= 0. 95 ms^-1

प्रश्न 3.
अब्दुल गाड़ी से स्कूल जाने के क्रम में औसत चाल को 20 kmh^-1 पाता है। उसी रास्ते से लौटने के समय वहाँ भीड़ कम है और औसत चाल 30 kmh-1 है। अब्दुल की इस पूरी यात्रा में उसकी औसत चाल क्या है ?
हल :
मान लो घर से स्कूल की दरी = L
∴ घर से स्कूल तथा वापिस स्कूल से घर तक को दूरी = L + L = 2 L
स्कूल जाते समय औसत चाल (υ₂) = 200 kmh^-1
स्कल जाते समय औसत चाल (t₁) =
स्कूल से वापिस घर आते समय औसत चाल (v₂) = 30 kmh^-1
∴ स्कूल से वापिस घर आने में लगा समय (t₂) = $\frac{\mathrm{L}}{v_{2}}$
पूरे सफ़र के लिए लगा कुल समय = t₁ + t₂

= 24 Kmh^-1

प्रश्न 4.
कोई मोटरबोट झील में विरामावस्था से सरल रेखीय पथ पर 3.0 ms^-2 के नियत त्वरण से 8.0s तक चलती है। इस समय अंतराल में मोटरबोट कितनी दूरी तय करती है ?
हल :
यहाँ, प्रारंभिक वेग (u) = 0 (विरामावस्था)
त्वरण (a) = 3.0 ms^-2
समय (t) = 8.0 s
मोटरबोट द्वारा तय की गई दूरी (S) = ?
हम जानते हैं, S = ut + $\frac{1}{2}$ at²
= 0 × 8 + $\frac{1}{2}$ × 3 × (8)²
= 0 + $\frac{1}{2}$ × 3 × 8 × 8
S = 96 m
अर्थात् मोटरबोट जितनी दूरी तय करती है = S = 96 m

प्रश्न 5.
किसी गाड़ी का चालक 52 km h^-1 की गति से चल रही कार में ब्रेक लगाता है तथा कार विपरीत दिशा में एकसमान दर से त्वरित होती है। कार 5 s में रुक जाती है। दूसरा चालक 30 kmh-1 की गति से चलती हुई दूसरी कार पर धीमे-धीमे ब्रेक लगाता है तथा 10s में रुक जाता है। एक ही ग्राफ पेपर पर दोनों कारों के लिये चाल-समय ग्राफ़ आलेखित करें। ब्रेक लगाने के पश्चात् दोनों में से कौन-सी कार अधिक दरी तक जाएगी ?
हल-

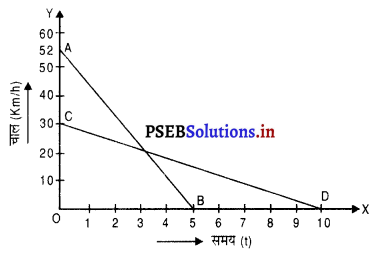
चित्र में दो कारों के चाल-समय ग्राफ़ AB तथा CD प्रदर्शित किए गए हैं जिनकी क्रमवार चाल 52 km h^-1 तथा 30 kmh^-1 है।
विरामावस्था में आने से पूर्व पहली कार द्वारा तय की गई दूरी = ΔAOB का क्षेत्रफल
= $\frac{1}{2}$ × AO × OB
= $\frac{1}{2}$ × (52 × $\frac{5}{18}$) × 5
= 36.1 m
विरामावस्था में आने से पूर्व दूसरी कार द्वारा तय की गई दूरी
= ΔCOD का क्षेत्रफल
= $\frac{1}{2}$ × CO × OD
= $\frac{1}{2}$ × (30 × $\frac{5}{18}$) × 10
= 47.2 m
इस तरह ब्रेक लगाने के पश्चात् दूसरी कार, पहली की तुलना में अधिक दूरी तय करेगी।

प्रश्न 6.
चित्र में तीन वस्तुओं A, B और C के दूरी-समय ग्राफ़ प्रदर्शित हैं। ग्राफ़ का अध्ययन करके निम्न प्रश्नों के उत्तर दीजिए :
(a) तीनों में से कौन सबसे तीव्र गति से गतिमान है ?
(b) क्या ये तीनों किसी भी समय सड़क के एक ही बिंदु पर होंगे ?
(c) जिस समय B, A से गुज़रती है उस समय तक C कितनी दूरी तय कर लेती है ?
(d) जिस समय B, C से गुजरती है तो उस समय तक यह कितनी दूरी तय कर लेती है ?

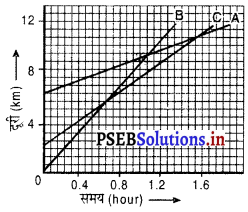
हल-

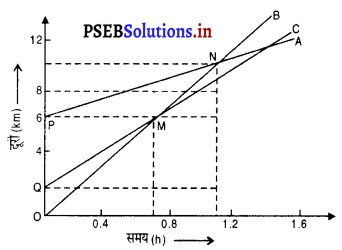
(a) A की चाल = P N की ढाल (Slope)
= $\frac{10-6}{1.1-0}$
= $\frac{40}{11}$ = 3.63km h^-1
B की चाल = OM की ढाल (slope)
= $\frac{6-0}{0.7-0}$
= $\frac{60}{7}$ = 8.57 km h^-1
C की चाल = QM की ढाल (slope)
= $\frac{6-2}{0.7-0}$
= $\frac{40}{7}$ = 5.71 kmh^-1
क्योंकि वस्तु B की ढाल (Slope) सबसे अधिक है इसलिए यह सबसे तीव्र गति से चल रही है।

(b) क्योंकि तीनों के ग्राफ़ एक बिंदु पर नहीं काटते हैं इसलिए ये तीनों किसी समय भी सड़क पर एक बिंदु पर नहीं होंगे।

(c) जब B, N बिंदु पर A को मिलता है। (1.1 घंटा पर) तब उस समय C मूल बिंदु O से लगभग 9 km की दूरी पर होगी।

(d) B बिंदु M पर C को मिलती है, उस समय B 9 km की दूरी कर लेती है।

प्रश्न 7.
20 m की ऊँचाई से एक गेंद को गिराया जाता है। यदि उसका वेग 10 ms^-2 के एकसमान त्वरण की दर से बढ़ता है तो यह किस वेग से धरातल से टकराएगी ? कितने समय पश्चात् वह धरातल से टकराएगी ?
हल :
यहाँ u = 0
S = 20 m
a = g = 10 ms^-2
v = ?
v² – u² = 2 as का प्रयोग करने पर
v² – (0)² = 2 × 10 × 20
∴ v = $\sqrt{400}$
= $\sqrt{20 \times 20}$
= 20 ms^-1
अब v = 4 + at
20 = 0 + 10 + t
∴ t = $\frac{20}{10}$
t = 2s

प्रश्न 8.
किसी कार का चाल-समय ग्राफ़ चित्र में दर्शाया गया है।

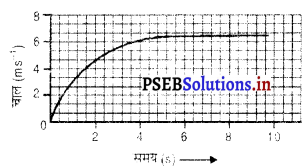
(a) पहले 4 s में कार कितनी दूरी तय करती है ? इस अवधि में कार द्वारा तय की गई दूरी को ग्राफ़ में छायांकित क्षेत्र द्वारा दर्शाइए।
(b) ग्राफ़ का कौन-सा भाग कार की एकसमान गति को दर्शाता है ?
हल :
(a) X – अक्ष के 5 छोटे चिह्न = 2s
Y – अक्ष के 3 छोटे चिह्न – 2 ms^-1
∴ 15 छोटे वर्गों का क्षेत्रफल = 2 s × 2ms^-1
= 4 m
1 छोटे वर्ग का क्षेत्रफल = $\frac{4}{15}$ m
0 से 5s के अंतर्गत चाल-समय ग्राफ़ का क्षेत्रफल
= 57 छोटे वर्ग + $\frac{1}{2}$ × 6 छोटे वर्ग
= (57 + 3) वर्ग
= 60 छोटे वर्ग
कार द्वारा 4 सेकंड में तय हुई दूरी = 60 × $\frac{4}{15}$ m
= 16 m

(b) 6 s पश्चात् कार की एकसमान गति है।

प्रश्न 9.
निम्नलिखित में से कौन-सी अवस्थाएँ संभव हैं तथा प्रत्येक के लिए एक उदाहरण दें:
(a) कोई वस्तु जिसका त्वरण नियत हो परंतु वेग शून्य हो।
(b) कोई वस्तु किसी निश्चित दिशा में गति कर रही हो तथा त्वरण उसके लंबवत् हो।
उत्तर-
(4) हाँ, यह स्थिति संभव है। जब किसी वस्तु को पृथ्वी तल से ऊपर की ओर फेंका जाता है तो अधिकतम ऊँचाई पर वस्तु का वेग शून्य होता है परंतु त्वरण स्थिर रहता है।

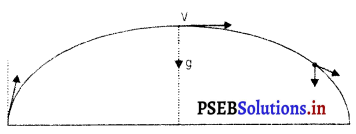
(b) हाँ, प्रक्षेप्य की अधिकतम ऊँचाई पर वेग क्षैतिज दिशा में होता है तथा त्वरण लंबवत् दिशा में जैसा कि चित्र में दिखाया गया है।

प्रश्न 10.
एक कृत्रिम उपग्रह 42250 km त्रिज्या की वृत्ताकार कक्षा में घूम रहा है। यदि वह 24 घंटे में पृथ्वी की परिक्रमा करता है तो उसकी चाल का परिकलन कीजिए।
हल :
कृत्रिम उपग्रह के वृत्ताकार पथ की त्रिज्या (r) = 42250 कि० मी०
पृथ्वी के केंद्र पर बना कोण (θ) = 2π रेडियन
पृथ्वी का एक चक्कर लगाने में उपग्रह द्वारा लिया गया समय (t) = 24 घंटे = 24 × 3600 सेकंड
= 86400 सेकंड
अत: कोणीय वेग (ω) = $\frac{\theta}{\mathrm{t}}$
= $\frac{2 \pi}{86400}$ rad/s
उपग्रह का रैखिक वेग (v) = r × ω).
= 42250 × $\frac{2 \pi}{86400}$ km/s
= $\frac{42250 \times 2 \times 3.14}{86400}$ km/s
= 3.07 km/s

Science Guide for Class 9 PSEB गति InText Questions and Answers

पाठ्य-पुस्तक के प्रश्नों के उत्तर

प्रश्न 1.
एक वस्तु के द्वारा कुछ दूरी तय की गई। क्या इसका विस्थापन शून्य हो सकता है ? अगर हाँ, तो अपने उत्तर को उदाहरण के द्वारा समझाएँ।
उत्तर-
गति के दौरान विस्थापन की मात्रा शून्य (0) हो सकती है. यदि वह वस्तु गति करते हुए अपनी आरंभिक स्थिति में आ जाये। इस अवस्था में अंतिम स्थिति, आरंभिक स्थिति से मिल जाती है।

उदाहरणार्थ – मान लो एक वस्तु मूल बिंदु O से गति आरंभ करते हुये A बिंदु तक 60 km की दूरी तय करती है। यदि वह वस्तु गति करते हुए वापस A से O बिंदु पर आ जाए तो उस अवस्था में उसका विस्थापन शून्य (0) होगा।

परंतु वस्तु द्वारा तय की गई कुल दूरी = OA + AO
= 60 km + 60 km
= 120 km होगी।

प्रश्न 2.
एक किसान 10 m की भुजा वाले एक वर्गाकार खेत की सीमा पर 40s में चक्कर लगाता है। 2 मिनट (minute) 20 सेकंड (s) बाद किसान के विस्थापन का परिमाण क्या होगा?
हल :

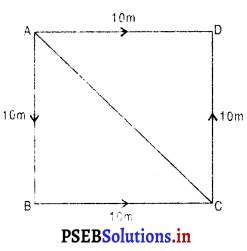
खेत की सीमा (1 चक्कर) = AB + BC + CD + DA
– 10 m + 10m + 10m + 10m
= 40m
खेत की सीमा (40m) का 1 चक्कर लगाने में लगा समय = 40s
कुल समय = 2 मिनट 20 सेकंड = (2 × 60 + 20) सेकंड
= (120 + 20) सेकंड
= 140 सेकंड
किसान 3 चक्कर लगाने के लिए जो समय लगा = 3 × 40 सेकंड
= 120 सेकंड
3 पूरे चक्कर लगाने के बाद शेष समय = (140 – 120) सेकंड
= 20 सेकंड
∴ किसान 40 s में जो दूरी तय करता है = 40 m
∴ 1 s में जो दूरी तय करेगा = 1m
20s में जो दूरी तय करेगा = 20 m
अर्थात् A से गति आरंभ करता हुआ सीमा के साथ-साथ 3 चक्कर लगाकर 2 मिनट 20 सेकंड के पश्चात् C बिंदु पर पहुँच जाएगा।
विस्थापन की मात्रा = AC (मूल बिंदु और अंतिम बिंदु के मध्य न्यूनतम दूरी)
= $\sqrt{A B^{2}+B C^{2}}$
= $\sqrt{(10)^{2}+(10)^{2}}$
= $\sqrt{100+100}$
= $\sqrt{200 \mathrm{~m}}$
= $\sqrt{100 \times 2 \mathrm{~m}}$
= 10$\sqrt{2 m}$
= 10 × 1.414 m
= 14.14 m

प्रश्न 3.
विस्थापन के लिए निम्न में कौन सही है ?
(a) यह शून्य नहीं हो सकता है।
(b) इसका परिमाण वस्तु के द्वारा तय की गई दूरी से अधिक है।
उत्तर-
(a) तथा
(b) दोनों कथनों में से कोई भी सही नहीं है।

प्रश्न 4.
चाल एवं वेग में अंतर बताइए।
उत्तर-
चाल का पूर्ण रूप से व्यक्त करने के लिए केवल परिमाण (मात्रा) की आवश्यकता होती है, जबकि वेग को पूर्ण रूप से व्यक्त करने के लिए परिमाण (मात्रा) तथा दिशा दोनों का होना आवश्यक है। इसलिए चाल एक अदिश राशि है परंतु वेग एक सदिश राशि है। चाल सदैव धनात्मक होती है परंतु वेग धनात्मक तथा ऋणात्मक दोनों प्रकार की हो सकती है। चाल किसी वस्तु की इकाई समय में तय की गई दूरी होती है दूसरी ओर यदि इसके साथ दिशा का ज्ञान भी हो तो यह वेग कहलाता है। अर्थात् एक निश्चित दिशा में चाल को वेग कहते हैं।

प्रश्न 5.
किस अवस्था में किसी वस्तु के औसत वेग का परिमाण उसकी औसत चाल के बराबर होगा ?
उत्तर-

कुल लगा समय जब वस्तु एक सीधी रेखा में परिवर्तनशील गति के साथ एक दिशा में चलती है तो कुल तय की गई दूरी तथा विस्थापन दोनों के परिमाण बराबर होते हैं। इसलिए औसत चाल तथा औसत वेग बराबर होते हैं।

प्रश्न 6.
एक गाड़ी का ओडोमीटर क्या मापता है ?
उत्तर-
गाड़ी (स्वै चालित वाहन) का ओडोमीटर उस द्वारा तय की गई दूरी को मापता है।

प्रश्न 7.
जब वस्तु एकसमान गति में होती है तब इसका मार्ग कैसा दिखाई पड़ता है ?
उत्तर-
जब वस्तु एकसमान गति में होती है तब इसका मार्ग एक सीधी सरल रेखा होता है।

प्रश्न 8.
एक प्रयोग के दौरान, अंतरिक्षयान से एक सिग्नल को पृथ्वी पर पहुँचने में 5 मिनट का समय लगता है। पृथ्वी पर स्थित स्टेशन से उस अंतरिक्षयान की दूरी क्या है ?
(सिग्नल की चाल = प्रकाश की चाल = 3 × 10⁸ ms^-1)
हल :
सिग्नल को अंतरिक्षयान से पृथ्वी तक पहुँचने में लगा समय (t) = 5 मिनट
= 5 × 60 सेकंड
= 300 सेकंड
सिग्नल की चाल (v) = 3 × 10⁸ ms^-1
अंतरिक्षयान की पृथ्वी से दूरी (S) = ?
अंतरिक्षयान की पृथ्वी से दूरी (S) = सिग्नल की चाल (v) × लगा समय (t)
= 3 × 10⁸ × 300 = 3 × 108 × 3 × 10²
= 9 × 10⁸ × 10² = 9 × 10¹⁰ m

प्रश्न 9.
आप किसी वस्तु के बारे में कब कहेंगे कि,
(i) वह एक समान त्वरण से गति में है ?
(ii) वह असमान त्वरण से गति में है ?
उत्तर-
(i) जब कोई वस्तु सरल रेखा में चलती है तब इसका वेग समान समय अंतरालों में समान मात्रा से घटता और बढ़ता है, तब उस समय वह वस्तु एक समान त्वरण से गति करती हुई कहलाती है।

(i) जब किसी वस्तु का वेग असमान दर से परिवर्तित होता है, अर्थात् उस वस्तु का वेग समान समय अंतरालों में असमान मात्रा से घटता और बढ़ता है, तो उस अवस्था में वस्तु असमान त्वरण से गति करती हुई कहलाती है।

प्रश्न 10.
एक बस की गति 5 s में 80 kmh^-1 से घटकर 60 kmh^-1 हो जाती है। बस का त्वरण ज्ञात कीजिए।
हल :
बस का प्रारंभिक वेग (u) = 80 km h^-1
= 80 × $\frac{5}{18}$ ms^-1
बस का अंतिम वेग (v) = 60 kmh^-1
60 × $\frac{5}{18}$ ms^-1
लगा हुआ समय (t) = 5s [∵ 1kmh^-1 = $\frac{5}{18}$ ms^-1]
बस का त्वरण (a) = ?

प्रश्न 11.
एक रेलगाड़ी स्टेशन से चलना प्रारंभ करती है और एकसमान त्वरण के साथ चलते हुए 10 मिनट में 40 kmh^-1 की चाल प्राप्त करती है। इसका त्वरण ज्ञात कीजिए।
हल :
रेलगाड़ी की आरंभिक चाल (u) = 0
रेलगाड़ी की अंतिम चाल (υ) = 40 kmh^-1
= 40 × $\frac{5}{18}$ ms^-1
= $\frac{100}{9}$ms^-1
समय (t) = 10 मिनट
= 10 × 60 सेकंड
= 600 सेकंड
त्वरण (a) = 7

= 0.018 ms^-2

प्रश्न 12.
किसी वस्तु के एक समान व असमान गति के लिए समय-दूरी (x-t) ग्राफ़ की प्रकृति क्या होती है ?
उत्तर-
जब कोई वस्तु बराबर समय में बराबर दूरी तय करती है तब वह एक समान गति से चलती है अर्थात् इस अवस्था में वस्तु द्वारा तय की गई दूरी लगे हुए समय के सीधा अनुपात में होती है। इसलिये एक समान गति की वस्तु के लिए दूरी-समय (x-t) ग्राफ़ एक सरल रेखीय ग्राफ़ होता है।

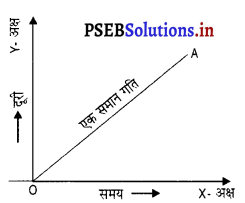
किसी वस्तु की असमान गति के लिए दूरी-समय (x-t) ग्राफ किसी आकृति का वक्र-रेखीय ग्राफ़ हो सकता है क्योंकि यह वस्तु समान समय अंतरालों में असमान दूरी तय करती है।

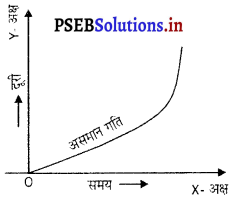
प्रश्न 13.
किसी वस्तु की गति के विषय में आप क्या कह सकते हैं, जिसका दूरी-समय ग्राफ़ (x-t) समय अंक्ष के समानांतर एक सरल रेखा है ?
उत्तर-
वह वस्तु जिसका दूरी-समय (x-t) ग्राफ़ समय अक्ष के समानांतर एक सरल रेखा है, विराम अवस्था में होगी।

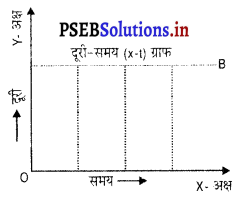
प्रश्न 14.
किसी वस्तु की गति के विषय में आप क्या कह सकते हैं, जिसका चाल-समय ग्राफ़ समय अक्ष के समानांतर एक सरल रेखा है।
उत्तर-
वह वस्तु जिसका चाल-समय (v-t) ग्राफ़ समय अक्ष के समानांतर सरल रेखा हो, एकसमान चाल से गतिमान होगी।

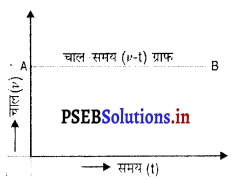
प्रश्न 15.
वेग-समय ग्राफ़ के नीचे के क्षेत्र से मापी गई राशि क्या होती है ?
उत्तर-
वेग-समय ग्राफ़ के नीचे घिरा हुए क्षेत्र द्वारा एक निश्चित समय में तय की गई दूरी मापता है।

प्रश्न 16.
कोई बस विरामावस्था से चलना प्रारंभ करती है तथा 2 मिनट तक 0.1 ms^-2 के एकसमान चरण से चलती है। परिकलन कीजिए,
(a) प्राप्त की गई चाल तथा
(b) तय की गई दूरी।
हल :
(i) बस का प्रारंभिक वेग (u) = 0 (विरामावस्था)
समय (t) = 2 मिनट
= 2 × 60 सेकंड
= 120 सेकंड
बस का अंतिम वेग (v) = ?
बस द्वारा तय की गई दूरी (S) = ?
हम जानते हैं, v = u + at
v = 0+ 0.1 × 120
v = 1 × 12
v = 12 ms^-1

(ii) अब v² – u² = 2 aS
(12²) – (0²) = 2 × 0.1 × 5
12 × 12 = 2 × 5
∴ S = $\frac{12 \times 12}{2}$
= $\frac{144 \times 10}{2}$
S = 720 m

प्रश्न 17.
कोई रेलगाड़ी 90 kmh^-1 के चाल से चल रही है। ब्रेक लगाए जाने पर वह – 0.5 ms^-2 का एकसमान त्वरण उत्पन्न करती है। रेलगाड़ी विरामावस्था में आने के पहले कितनी दूरी तय करेगी ?
हल :
रेलगाड़ी का प्रारंभिक वेग (u) = 90 kmh^-1
= 90 × $\frac{5}{18}$ ms^-1
= 5 × 5ms^-1
= 25 ms^-1
त्वरण (a) = – 0.5 ms^-2
अंतिम वेग (v) = 0 (विरामावस्था)
रेलगाड़ी द्वारा तय की गई दूरी (S) = ?
हम जानते हैं, v² – u² = 2 aS
(0²) – (25²) = 2 × (-0.5) × 5
– 25 × 25 = – 1 × 5
या S = 25 × 25
∴ S = 625 m

प्रश्न 18.
एक ट्रॉली एक आनत तल पर 2 ms^-2 के त्वरण से नीचे जा रही है। गति प्रारंभ करने के 3 s के पश्चात् उसका वेग क्या होगा ? हल :
यहाँ ट्राली का आरंभिक वेग (u) = 0
त्वरण (a) = 2 ms^-2
समय (T) = 3s
ट्राली का अंतिम वेग (v) = ?
V = u + at समीकरण का प्रयोग करने पर
= 0 + 2 × 3
V = 6 ms^-1

प्रश्न 19.
एक रेसिंग कार का एकसमान त्वरण 4 ms^-2 है। गति प्रारंभ करने के 10 s के पश्चात् वह कितनी दूरी तय करेगी ?
हल :
रेसिंग कार का त्वरण (a) = 4 ms^-2
कार का आरंभिक वेग (u) = 0
समय (t) = 10s
कार द्वारा तय की गई दूरी (S) = ?
रेसिंग कार का अंतिम वेग (v) = ?
हम जानते हैं, v = u + at
v = 0 + 4 × 10
∴ v = 40 ms^-1
अब v² – u² = 2aS
(40²) – (0²) = 2 × 4 × S
40 × 40 = 8 × S
S = $\frac{1600}{8}$
∴ S = 200 m

प्रश्न 20.
किसी पत्थर को ऊर्ध्वाधर ऊपर की ओर 5 ms^-1 के वेग से फेंका जाता है। यदि गति के दौरान पत्थर का नीचे की ओर दिष्ट त्वरण 10 ms^-2 है, तो पत्थर के द्वारा कितनी ऊँचाई प्राप्त की गई तथा उसे वहाँ पहुँचने में कितना समय लगा ?
हल :
यहाँ, आरंभिक वेग (u) = 5 ms^-1
गुरुत्वात्वरण (a = g) = – 10 ms^-2
अंतिम वेग (v) = 0 (अधिकतम ऊँचाई पर पहुंचकर पत्थर विरामावस्था में आ जाता है)
समय (t) = ?
ऊँचाई (h = S) = ?
हम जानते हैं, v = u + gt
0 = 5 + (-10) × t
0 = 5 – 10t
या 10t = 5
∴ t = $\frac{5}{10}$ = . 5 s
अब v² – u² = 2 gS
(0)² – (5)² = 2 × 10 × h
-5 × 5 = 20 × h
∴ h = $\frac{-5 \times 5}{-20}$
= $\frac{25}{-20}$
= $\frac{5}{4}$
∴ h = 1.25 m