Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 6 रेखाएँ और कोण Ex 6.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 6 रेखाएँ और कोण Ex 6.2
प्रश्न 1.
आकृति में, x और y के मान ज्ञात कीजिए और फिर दर्शाइए कि AB || CD है।
हल :
मान लीजिए तिर्यक रेखा l, AB और CD को क्रमश: P और Q पर प्रतिच्छेदित करती है।
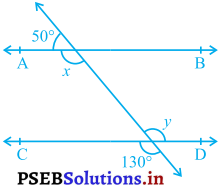
दी गई आकृति में,
50° + x = 180° (रैखिक युग्म)
⇒ x = 180° -50°
⇒ x = 130° …………. (i)
y= 130°
(शीर्षाभिमुख कोण)…….(ii)
(i) और (ii), से हम देखते हैं कि
x = y
यह दर्शाता है कि अंत: एकांतर कोण बराबर हैं।
जैसा कि हम जानते हैं कि यदि एक तिर्यक रेखा (मान लीजिए l) दो रेखाओं को इस प्रकार प्रतिच्छेदित करती है कि अंत: एकांतर कोणों के युग्म बराबर हों, तो दो रेखाएँ समांतर होती हैं।
अत: AB || CD.
![]()
प्रश्न 2.
आकृति में, यदि AB || CD, CD || EF और y : z = 3 : 7 है, तोx का मान ज्ञात कीजिए।
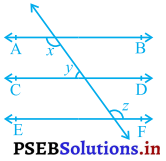
हल:
AB || CD
∴ x + y = 180° ……….(i)
[∵ दो समांतर रेखाओं के बीच एक तिर्यक रेखा के एक ओर के अंत: कोणों का योग 180° होता है।]
दिया है कि
AB || CD, CD||EF
∴ AB || EF [∵ एक ही रेखा के समांतर खींची गई दो रेखाएँ परस्पर समांतर होती हैं।]
अत: x = z (समांतर रेखाओं के लिए एकांतर अंतः कोण बराबर होते हैं।) …(ii)
(ii) से x का मान (i) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
z + y = 180° ….(iii)
दिया है कि y : z = 3 : 7
मान लीजिए कि y = 3k ∴ z = 7k
जहाँ अचर k > 0
y और z के मान (iii) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
7k + 3k = 180°
⇒ 10k = 180°
⇒ k = \(\frac {180°}{10}\)
⇒ k=18°
अत: y = 3k
⇒ y = 3 × 18°
⇒ y= 54°
⇒ z = 7k
⇒ z = 7 × 18°
⇒ z = 126°
(ii) से हमें प्राप्त होता है : x = z
∴ x = 126°
प्रश्न 3.
आकृति में, यदि AB ||CD, EF ⊥ CD और ∠GED = 126° है, तो ∠AGE, ∠GEF और ∠FGE ज्ञात कीजिए।
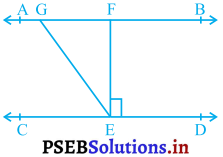
हल :
AB || CD और GE एक तिर्यक रेखा है.
∵ ∠AGE = ∠GED [एकांतर कोण]
⇒ ∠AGE = 126°
[∵ ∠GED = 126° (दिया है)]
∠GED = 126° (दिया है)
या ∠GEF + ∠FED = 126°
⇒ ∠GEF + 90° = 126°
[∵ EF ⊥ CD (दिया है)]
[∵ ∠FED = 90°]
⇒ ∠GEF = 126° – 90°
⇒ ∠GEF = 36°
अब ∠AGE + ∠FGE = 180° (रैखिक युग्म)
⇒ 126° + ∠FGE = 180°
[∵ ∠AGE = 126° (ऊपर प्राप्त किया है)]
⇒ ∠FGE = 180° – 126°
⇒ ∠FGE = 54°.
![]()
प्रश्न 4.
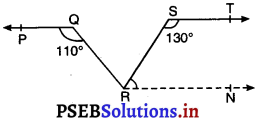
आकृति में, यदि PQ || ST, ∠PQR = 110° और ∠RST = 130° है, तो ∠QRS ज्ञात कीजिए।
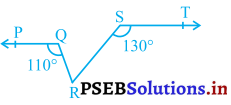
हल :
बिंदु R से होकर ST के समांतर एक रेखा RN खींचिए।
अब ST || RN
⇒ ∠RST + ∠SRN = 180°
[∵ दो समांतर रेखाओं के बीच एक तिर्यक रेखा के एक ओर के अंत:कोणों का योग 180° होता है।]
⇒ 130° + ∠SRN = 180°
⇒ ∠SRN = 180° – 130°
⇒ ∠SRN = 50° …(i)
अब PQ || ST (दिया है)
ओर RN || ST (रचना)
∴ PQ || RN [∵ दो रेखाएँ जो एक ही रेखा के समांतर हों परस्पर समांतर हैं]
अब PQ || RN और QR एक तिर्यक रेखा है।
∴ ∠QRN = ∠PQR (एकांतर कोण)
⇒ ∠QRN = 110°
[∵ ∠PQR = 110° (दिया है)]
∠QRN = 110°
⇒ ∠QRS + ∠SRN= 110°
⇒ ∠QRS + 50° = 110°
[(i) का प्रयोग करने पर]
⇒ ∠QRS = 110° – 50°
⇒ ∠QRS = 60°.
प्रश्न 5.
आकृति में, यदि AB || CD, ∠APQ = 50° और ∠PRD = 127° है, तो x और y ज्ञात कीजिए।
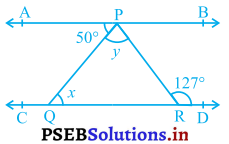
हल :
AB || CD; PQ एक तिर्यक रेखा है
∴ x = ∠APQ (एकांतर कोण)
⇒ x = 50°
[∵ ∠APQ = 50° (दिया है)]
AB || CD; PR एक तिर्यक रेखा है।
∴ ∠APR = ∠PRD (एकांतर कोण)
⇒ ∠APQ + ∠QPR = ∠PRD
⇒ 50° + y = 127°
⇒ y = 127° – 50°
⇒ y = 77°
![]()
प्रश्न 6.
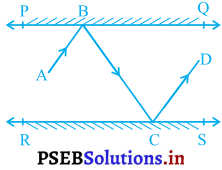
आकृति में, PQ और RS दो दर्पण हैं जो एक दूसरे के समांतर रखे गए हैं। एक आपतन किरण (incident ray) AB, दर्पण PQ से B पर टकराती है और परवर्तित किरण (Reflected ray) पथ BC पर चल कर दर्पण RS से C पर टकराती हैं तथा पुन: CD के अनुदिश परावर्तित हो जाती है। सिद्ध कीजिए कि AB || CD है।
हल :
दी गई आकृति के अनुसार PQ और RS दो दर्पण हैं जो एक दूसरे के समांतर हैं। एक आपतन किरण AB, दर्पण PQ से B पर टकराती है। CD एक परावर्तित किरण है जो दर्पण RS से परावर्तित होती है।
हमने सिद्ध करना है
AB || CD
उपपति : जैसा कि हम जानते हैं कि
आपतन कोण = परावर्तित कोण
∴ ∠1 = ∠2 और ∠3 = ∠4 ………….(i)
[∴ ∠1 आपाती किरण AB और अभिलंब BL]
∴ ∠1 एक आपतन कोण है, ∠2 परावर्तित किरण BC और अभिलंब BL के बीच स्थित है। इसलिए ∠2 परावर्तित कोण है। इसी तरह ∠3 और ∠4 क्रमश: आपतन कोण और परावर्तित कोण हैं।
∴ PQ || RS और BL ⊥ PQ
और CM ⊥ RS
BL || CM
अब समांतर रेखाएँ BL और CM हैं। एक तिर्यक रेखा BC इन्हें प्रतिच्छेद करती है।
∴ ∠2 = ∠3 (एकांतर कोण) …(ii)
अब ∠ABC = ∠1 + ∠2
⇒ ∠ABC = ∠2 + ∠2 [∵ ∠1 = ∠2]
⇒ ∠ABC = 2∠2
और ∠BCD = ∠3 + ∠4
⇒ ∠BCD = ∠3 + ∠3
⇒ [∵ ∠3 = ∠4]
⇒ ∠BCD = 2∠3
परंतु (ii), से हमें प्राप्त होता है
⇒ ∠2 = ∠3
⇒ 2∠2 = 2∠3
⇒ ∠ABC = ∠BCD
ये एकांतर कोण हैं। BC एक तिर्यक रेखा है।
अत: AB || CD.
