Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 8 चतुर्भुज Ex 8.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 8 चतुर्भुज Ex 8.1
प्रश्न 1.
एक चतुर्भुज के कोण 3 : 5 : 9 : 13 के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए ।
हल :
मान लीजिए ABCD एक चतुर्भुज है। इसलिए,
∠A = 3x
∠B = 5x
∠C = 9x
∠D = 13x
जहाँ x एक घनात्मक अचर है।
अब, ∠A + ∠B + ∠C + ∠D = 360°
[चतुर्भुज का कोण योग गुण]
⇒ 3x + 5x + 9x + 13x = 360°
⇒ 30x = 360°
⇒ x = \(\frac {360°}{30°}\)
⇒ x = 12°
अब
∠A = 3x ⇒ ∠A = 3 × 12° ⇒ ∠A = 36°
∠B = 5x ⇒ ∠B = 5 × 12° ⇒ ∠B = 60°
∠C = 9x ⇒ ∠C = 9 × 12° ⇒ ∠C = 108°
और ∠D = 13x ⇒ ∠D = 13 × 12° = 156°
अतः, दी गई चतुर्भुज के कोण क्रमशः 36°, 60°, 108° और 156° हैं।
![]()
प्रश्न 2.
यदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है।
हल :
दिया है : ABCD एक || gm है जिसमें
विकर्ण AC = विकर्ण BD
सिद्ध करना है : ABCD एक आयत है।

उपपत्ति : ΔABC और ΔABD में,
AB = AB … (उभयनिष्ठ)
AC = BD (दिया है)
और AD = BC (||gm की सम्मुख भुजाएँ)
∴ ΔABC ≅ ΔBAD
[SSS सर्वांगसमता नियम से]
⇒ ∠DAB = ∠CBA …………….(i)
(सर्वांगसम त्रिभुजों के संगत भाग)
परंतु ∠DAB + ∠CBA = 180° …..(ii) [∵ AD || BC और AB इनको काटती है। तिर्यक रेखा के एक ओर के अंतः कोणों का योगफल 180° होता है।]
(i) और (ii) से हमें प्राप्त होता है;
∠DAB = ∠CBA = एक समकोण
अतः, ABCD एक आयत है। [∵ यदि || gm का एक कोण 90°का हो, तो वह आयत होता है।]
इति सिद्धम
प्रश्न 3.
दर्शाइए कि यदि एक चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करें, तो वह एक समचतुर्भुज होता है।
हल :
मान लीजिए ABCD एक चतुर्भुज है।।
मान लीजिए इसके विकर्ण AC और BD परस्पर समकोण पर, बिंदु O पर समद्विभाजित करते हैं।
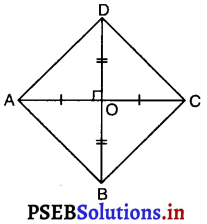
∴ OA = OC, OB = OD
और ∠AOB = ∠BOC = ∠COD
= ∠AOD = 90°
हमने सिद्ध करना है कि ABCD एक समचतुर्भुज हैं।
ΔAOD और ΔBOC में,
OA = OC (दिया है)
∠AOD = ∠BOC
(प्रत्येक = 90°) [दिया है।
OD = OB (दिया है)
∴ ΔAOD ≅ ΔCOB
(SAS सर्वांगसमता नियम से)
इसलिए, AD = CB
(सर्वांगसम त्रिभुजों के संगत भाग) …..(i)
ΔAOB और ΔCOD में,
OA = OC (दिया है)
∠AOB = ∠COD
(प्रत्येक = 90°) [दिया है।]
OB = OD (दिया है)
∴ ΔAOB ≅ ΔCOD
[SAS सर्वांगसमता नियम से] इसलिए, AB = CD
(सर्वांगसम त्रिभुजों के संगत भाग) … (ii)
अब, ΔAOB और ΔBOC में,
AO = OC (दिया है)
∠AOB = ∠BOC
(प्रत्येक = 90°) (दिया है)
OB = OB (उभयनिष्ठ)
∴ ΔAOB ≅ ΔBOC
(SAS सर्वांगसमता नियम से)
इसलिए, AB = BC
(सर्वांगसम त्रिभुजों के संगत भाग) … (iii)
(i), (ii) और (iii) से हमें प्राप्त होता है
AD = BC = CD = AB
इस प्रकार दिए गए प्रतिबंध कि चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं, के साथ-साथ हमने यह भी प्राप्त किया है कि इसकी सभी भुजाएँ बराबर हैं।
अतः, चतुर्भुज उन सभी प्रतिबंधों को, जो एक समचतुर्भुज के लिए आवश्यक हैं, संतुष्ट करती है। अतः, दी गई चतुर्भुज समचतुर्भुज है।
![]()
प्रश्न 4.
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
हल :
दिया है : ABCD एक वर्ग है जिसमें AC और BD इसके विकर्ण हैं।
सिद्ध करना है : (i) AC = BD, (ii) AC ⊥ BD
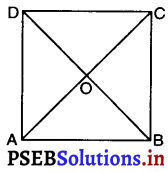
उपपत्ति : ΔABC और ΔBAD में,
AB = AB (उभयनिष्ठ)
∠ABC = ∠BAD (प्रत्येक 90°)
BC = AD (वर्ग की भुजाएँ)
∴ ΔABC ≅ ΔBAD
[SAS सर्वांगसमता नियम]
⇒ AC = BD
(सर्वांगसम त्रिभुजों के संगत भाग)
अतः, भाग (i) सिद्ध हुआ।
ΔAOB और AOD में,
AO = AO (उभयनिष्ठ)
AB = AD (वर्ग की भुजाएँ)
OB = OD (वर्ग के विकर्ण परस्पर समद्विभाजित करते हैं।)
∴ ΔAOB ≅ ΔAOD
(SSS सर्वांगसमता नियम)
∴ ∠AOB = ∠AOD
(सर्वांगसम त्रिभुजों के संगत भाग)
परंतु ∠AOB + ∠AOD = 180° [रैखिक युग्म]
∴ ∠AOB = ∠AOD = 90°
अर्थात्, OA ⊥ BD या AC ⊥ BD.
(अतः, भाग (ii) सिद्ध हुआ)
प्रश्न 5.
दर्शाइए कि यदि एक चतुर्भुज के विकर्ण बराबर हों और परस्पर समकोण पर समद्विभाजित करें, तो वह एक वर्ग होता है।
हल :
मान लीजिए ABCD एक चतुर्भुज है जिसके बराबर विकर्ण AC और BD परस्पर बिंदु O पर समद्विभाजित करते हैं।
हमें प्राप्त हैं :
AC = BD
OA = OC ………….(i)
और OB = OD …………..(ii)
AC = BD
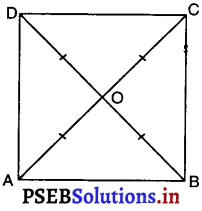
⇒ OA + OC = OB + OD
⇒ OC + OC = OB + OB
[(i) और (ii) के प्रयोग करने पर]
⇒ 2OC = 2OB
⇒ OC = OB …… (iii)
(i), (ii) और (i) से हमें प्राप्त होता है :
OA = OB = OC = OD ……… (iv)
अब, ΔAOB और ΔCOD में,
OA = OD
[भाग (iv) में दर्शाया गया है।
∠AOB = ∠COD
[शीर्षाभिमुख कोण]
OB = OC
[भाग (iv) में दर्शाया गया है।]
∴ ΔAOB ≅ ΔDOC
[SAS सर्वांगसमता नियम]
इसलिए, AB = DC ……..(v) (सर्वांगसम त्रिभुजों के संगत भाग)
इसी प्रकार, ΔBOC ≅ ΔAOD
[SAS सर्वांगसमता नियम]
इसलिए, BC = AD
(सर्वांगसम त्रिभुजों के संगत भाग)….(vi)
(v) और (vi) से परिणाम निकलता है कि चतुर्भुज ABCD की सम्मुख भुजाएँ बराबर हैं।
अतः, ABCD एक समांतर चतुर्भुज है
अब, ΔABC और ΔBAD में
AB = BA [उभयनिष्ठ]
BC = AD
[भाग (vi) में सिद्ध किया है।
AC = BD (दिया है)
∴ ΔABC ≅ ΔBAD
[SSS सर्वांगसमता नियम]
इसलिए, ∠ABC = ∠BAD …..(vii)
(सर्वांगसम त्रिभुजों के संगत भाग)
परंतु ∠ABC + ∠BAD = 180° …..(vii)] [∵ ABCD एक समांतर चतुर्भुज है।
(ऊपर प्रमाणित)
∴ AD || BC और AD एक तिर्यक रेखा है।
⇒ ∠ABC + ∠ABC = 180°
[(vii) को (viii) में प्रयोग करने पर]
⇒ 2∠ABC = 180°
⇒ ∠ABC = 90°
∴ ∠ABC = ∠BAD = 90° …. (ix)
समांतर चतुर्भुज के सम्मुख कोण बराबर हैं। परंतु ∠ABC = 90° और ∠BAD = 90°
∴ ∠ABC = ∠ADC = 90° …(x)
और ∠BAD = ∠BCD = 90° …..(xi)
हम देखते हैं कि ∠ABC = ∠ADC = ∠BAD
= ∠BCD = 90° …..(xii)
अब ΔAOB और ΔBOC में
OA = OC (दिया है)
∠AOB = ∠BOC प्रत्येक 90° (दिया है)
OB = OB (उभयनिष्ठ)
∴ ΔABC ≅ ΔCOB
(SAS सर्वांगसमता नियम)
इसलिए AB = BC …..(xiii)
(v), (vi) और (xiii) से प्राप्त है।
AB = BC = CD = AD (xiv)
(xii) और (xiv) से
अब हमें एक चतुर्भुज प्राप्त है जिसके बराबर विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं। साथ ही बराबर भुजाएँ परस्पर 90° का कोण बनाती है।
अतः, दी गई चतुर्भुज वर्ग के सभी प्रतिबंधों को संतुष्ट करती है।
![]()
प्रश्न 6.
समांतर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है ( देखिए आकृति) दर्शाइए कि
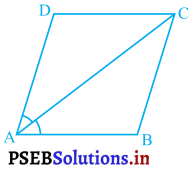
(i) यह ∠C को भी समद्विभाजित करता है।
(ii) ABCD एक समचतुर्भुज है।
हल :
यह दिया है कि समांतर चतुर्भुज ABCD में विकर्ण AC कोण A को समद्विभाजित करता है।
सिद्ध करना है : AC, ∠C को समद्विभाजित करती है।
उपपत्ति ; क्योंकि AB || DC और AC उनको प्रतिच्छेदित करती है।
∴ ∠1 = ∠3 (एकांतर कोण) (a)
इसी प्रकार ∠2 = ∠4 …………(b)
परंतु ∠1 = ∠2
[∵ AC, ∠A को समद्विभाजित करती है।] …………(c)
∠3 = ∠4
[(a), (b) और (c) का प्रयोग करने पर] अतः, AC, ∠C को समद्विभाजित करता है।
प्रश्न 7.
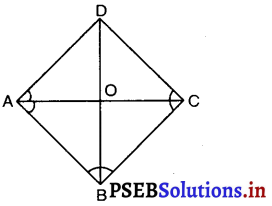
ABCD एक समचतुर्भुज है। दर्शाइए कि विकर्ण AC कोणों A और C दोनों को समद्विभाजित करता है तथा विकर्ण BD कोणों B और D दोनों को समद्विभाजित करता है।
हल :
ABCD एक समचतुर्भुज है।
∴ AB = BC = CD = AD
मान लीजिए O, विकर्ण BD का समद्विभाजक बिंदु है और OB = OD है।
ΔAOB और ΔAOD में,
OA = OA (उभयनिष्ठ)
AB = AD
[समचतुर्भुज की बराबर भुजाएँ]
OB = OD
[समचतुर्भुज के विकर्ण परस्पर समद्विभाजित करते है।]
∴ ΔAOB ≅ ΔAOD
[SSS सर्वांगसमता नियम ]
इसलिए, ∠OAD = ∠OAB
(सर्वांगसम त्रिभुजों के संगत भाग)
⇒ OA, ∠A को समद्विभाजित करता है …..(i)
इसी तरह, ΔBOC ≅ ΔDOC
(SSS सर्वांगसमता नियम)
इसलिए; ∠OCB = ∠OCD
[सवांगसम त्रिभुजों के संगत भाग]
⇒ OC, ∠C को समद्विभाजित करता है …..(ii)
(i) और (ii) से हम कह सकते हैं कि विकर्ण AC, ∠A और ∠C को समद्विभाजित करता है।
अब, ΔAOB और ΔBOC में,
OB = OB (उभयनिष्ठ)
AB = BC
[समचतुर्भुज की बराबर भुजाएँ]
OA = OC [∵ समचतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं।]
ΔAOB ≅ ΔCOB
(SSS सर्वांगसमता नियम)
इसलिए, ∠OBA = ∠OBC
(सर्वांगसम त्रिभुजों के संगत भाग)
⇒ OB, ∠B को समद्विभाजित करता है ….(iii)
इसी तरह, ΔAOD ≅ ΔCOD
(SSS सर्वांगसमता नियम)
⇒ ∠ODA = ∠ODC
(सर्वांगसम त्रिभुजों के संगत भाग)
⇒ OD, ∠D को समद्विभाजित करता है….(iv)
(iii) और (iv) से हम कह सकते हैं कि विकर्ण BD दोनों ∠B और ∠D को समद्विभाजित करता है।
![]()
प्रश्न 8.
ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है। दर्शाइए कि
(i) ABCD एक वर्ग है।
(ii) विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है।
हल :
ABCD एक आयत है ।
∴ AB = DC ……………(a)
और BC = AD
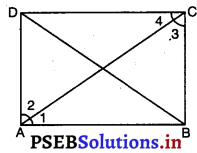
साथ ही, प्रत्येक कोण; ∠A = ∠B = ∠C = ∠D = 90°
(i) ΔABC और ΔADC में,
∠1 = ∠2.
और ∠3 = ∠4 [∵ AC दोनों कोणों ∠A और ∠C को समदविभाजित करता है (दिया है)]
AC = AC (उभयनिष्ठ)
∴ ΔABC ≅ ΔADC
(ASA सर्वांगसमता नियम)
इसलिए, AB = AD ……..(b)
(a) और (b) से हमें प्राप्त होता है
AB = BC = AD = DC
इसका अर्थ है कि आयत की सभी भुजाएँ बराबर हैं।
अतः, यह एक वर्ग है।
(ii) ΔABD और ΔBDC में,
AB = BC [∵ आयत ABCD एक वर्ग है भाग (i) में सिद्ध किया है]
AD = DC
(भाग (i) में सिद्ध किया है कि ABCD एक वर्ग है।)
BD = BD (उभयनिष्ठ)
∴ ΔABD ≅ ΔCBD
(SSS सर्वांगसमता नियम)
इसलिए, ∠ABD = ∠CBD ……(c)
(सर्वागसम त्रिभुजों के संगत भाग)
और ∠ADB = ∠CDB …….(d)
(सर्वांगसम त्रिभुजों के संगत भाग)
(c) और (d) का भाव है कि विकर्ण BD दोनों कोणों ∠B और ∠D को समद्विभाजित करता है।
प्रश्न 9.
समांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु P और Q इस प्रकार स्थित हैं कि DP = BQ है (देखिए आकृति )। दर्शाइए कि
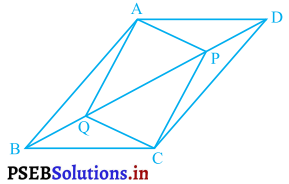
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
(v) APCQ एक समांतर चतुर्भुज है।
हल :
(i) ΔAPD और ΔCQB में,
DP = BQ (दिया है)
∠ADP = ∠QBC [∵ समांतर चतुर्भुज ABCD में AD || BC, BD एक तिर्यक रेखा है।
∴ ∠ADB = ∠DBC (एकांतर कोण) इसलिए;
∠ADP = ∠QBC]
AD = CB [∵ समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं।]
∴ ΔAPD ≅ ΔCQB
(SAS सर्वांगसमता नियम)
(ii) इसलिए ; AP = CQ
(सर्वांगसम त्रिभुजों के संगत भाग)
(iii) ΔAQB और ΔCPD में
BQ = DP (दिया है)
∠ABQ = ∠PDC [∵ समांतर चतुर्भुज ABCD में, AB || CD; BD एक तिर्यक रेखा है।]
∴ ∠ABD = ∠BDC (एकांतर कोण)
इसलिए ; ∠ABQ = ∠PDC]
AB = CD [∵ समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं।]
∴ ΔAQB ≅ ΔCPD
[SAS सर्वांगसमता नियम]
(iv) इसलिए, AQ = CP
(सर्वांगसम त्रिभुजों के संगत भाग)
(v) चतुर्भुज APCQ में, हमें प्राप्त है
AP = CQ
[भाग (ii) में सिद्ध किया है]
AQ = CP
[भाग (iv) में सिद्ध किया है]
चतुर्भुज ARCQ की सम्मुख भुजाएँ बराबर हैं
जैसा कि हम जानते हैं कि एक समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती है।
अतः, APCQ एक समांतर चतुर्भुज है।
![]()
प्रश्न 10.
ABCD एक समांतर चतुर्भुज है तथा AP, CQ शीर्षों, A और C से विकर्ण BD पर क्रमशः लम्ब हैं। ( देखिए आकृति)। दर्शाइए कि
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ
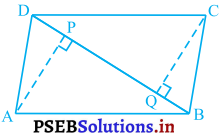
हल :
ABCD एक समांतर चतुर्भुज है।
∴ AB || DC
BD एक तिर्यक रेखा है।
इसलिए, ∠1 = ∠2 (एकांतर कोण)
(i) अब, ΔAPB और ΔCQD में,
∠APB = ∠CQD
(प्रत्येक = 90°) [दिया है]
∠1 = ∠2 (ऊपर सिद्ध किया है)
AB = CD [∵ समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं।]
∴ ΔAPB ≅ ΔCQD
[AAS सर्वांगसमता नियम]
(ii) इसलिए, AP = CQ
(सर्वांगसम त्रिभुजों के संगत भाग)
प्रश्न 11.
ΔABC और ΔDEF में, AB = DE, AB || DE, BC = EF और BC || EF है। शीर्षों A, B और C को क्रमश: शीर्षों D, E और F से जोड़ा जाता है ( देखिए आकृति)।
दर्शाइए कि
(i) चतुर्भुज ABED एक समांतर चतुर्भुज है।
(ii) चतुर्भुज BEFC एक समांतर चतुर्भुज है।
(iii) AD || CF और AD = CF है।
(iv) चतुर्भुज ACFD एक समांतर चतुर्भुज है।
(v) AC = DF है।
(vi) ΔARC ≅ ΔDEF है।
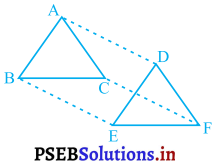
हल :
दिया है : ΔABC और ΔDEF में,
AB = DE और AB || DE.
साथ ही, त्रिभुजों में BC = EF और BC || EF है।
(i) चतुर्भुज ABED में सम्मुख भुजाओं AB और DE का एक युग्म इस प्रकार है कि AB = DE और AB || DE है।
∴ ABED एक समांतर चतुर्भुज है।
∴ AD = BE और AD || BE.
[समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती है] ……………(1)
(ii) पुनः, चतुर्भुज BEFC में,
BE = CF और BE || CF
∴ BEFC एक समांतर चतुर्भुज है।
∴ CF = BE और CF || BE ….(2)
(iii) (1) और (2) से प्राप्त होता है :
AD = CF और AD || CF
(iv) ∴ ACFD एक समांतर चतुर्भुज है। [∵ यदि चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर और समांतर हो, तो यह समांतर चतुर्भुज होती है।]
(v) अतः, AC = DF
[||gm को सम्मुख भुजाएँ].
(vi) ΔABC और ΔDEF में,
AB = DE (दिया है)
BC = EF (दिया है)
AC = DF [भाग (v) में सिद्ध किया है]
∴ ΔABC ≅ ΔDFE
(SSS सर्वांगसमता नियम)
![]()
प्रश्न 12.
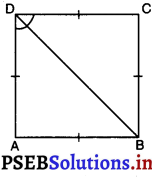
ABCD एक समलंब है, जिसमें AB || DC और AD = BC है ( देखिए आकृति)। दर्शाइए कि
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ΔABC ≅ ΔBAD
(iv) विकर्ण AC = विकर्ण BD है।
हल :
AB को बढ़ाइए और रेखा CE || AD खींचिए जैसा कि आकृति में दर्शाया गया है।
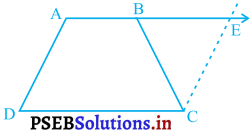
क्योंकि AD || CE और तिर्यक रेखा AE उनको क्रमश: A और E पर काटती है :
∴ ∠A + ∠E = 180°
∠A = 180° – ∠E ….(1)
⇒ क्योंकि AB || CD और AD || CE है।
∴ AECD एक समांतर चतुर्भुज है।
⇒ AD = CE
⇒ BC = CE
[∵ AD = BC (दिया है)]
इस प्रकार, ΔBCE में
BC = CE
⇒ ∠CBE = ∠CEB [बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।]
⇒ 180° – ∠B = ∠E [∵ ∠CBE + ∠ABC = 180° (रैखिक युग्म)
∴ ∠CBE = 180° – ∠ABC]
⇒ 180° – ∠E = ∠B …..(2)
(1) और (2) से हमें प्राप्त होता है : ∠A = ∠B
(ii) ABCD एक समलंब है जिसमें AB || DC
∴ ∠A + ∠D = 180° ….(a)
और ∠B + ∠C = 180° ….(b)
[∵ दो समांतर रेखाओं के लिए तिर्यक रेखा के एक ही ओर के दो अंत: कोणों का योगफल 180° होता है।]
(a) और (b) को बराबर करने पर हमें प्राप्त होता है
∠A + ∠D = ∠B + ∠C
परंतु ∠A = ∠B भाग (i) में सिद्ध किया है।
∴ ∠A + ∠D = ∠A + ∠C
⇒ ∠D = ∠C
या, ∠C = ∠D इति सिद्धम ।
(iii) ΔABC और ΔBAD में,
AB = AB (उभयनिष्ठ)
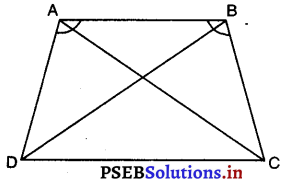
∠A = ∠B
[भाग (i) में सिद्ध किया है।]
BC = AD (दिया है)
∴ ΔABC ≅ ΔBAD
(SAS सर्वांगसमता नियम)
(iv) इसलिए, AC = BD
(सर्वांगसम त्रिभुजों के संगत भाग)
अर्थात्, समलंब ABCD में;
विकर्ण AC = विकर्ण BD.
