This PSEB 6th Class Computer Notes Chapter 1 कम्प्यूटर से जान-पहचान will help you in revision during exams.
PSEB 6th Class Computer Notes Chapter 1 कम्प्यूटर से जान-पहचान
कम्प्यूटर से जान-पहचान (Introduction to Computer)
आजकल कम्प्यूटर बहुत महत्त्वपूर्ण है। यह किसी भी काम को आसानी तथा तेज़ी से करता है। हमारी रोज़ाना की कई क्रियाएं इसी पर आधारित हैं। कम्प्यूटर का प्रयोग स्कूल, बैंक, अस्पताल, दुकानों, रेलवे तथा हवाई सेवाओं, शिक्षा तथा मनोरंजन के लिए किया जाता है।
कम्प्यूटर (Computer)-
कम्प्यूटर शब्द लेटिन भाषा के शब्द ‘कम्प्यूटरे’ से लिया गया है जिसका अर्थ है ‘गणना करना’। बिना निर्देश कम्प्यूटर कोई भी कार्य नहीं कर सकता। कम्प्यूटर एक इलैक्ट्रॉनिक यन्त्र है जो इनपुट के तौर पर डाटा प्राप्त करता है, उसे प्रोसैस करता है तथा नतीजा दिखाता है। यह यूजर से डाटा तथा निर्देश प्राप्त करता है।

- कम्प्यूटर को निर्देश तथा डाटा देने की प्रक्रिया को इनपुट कहा जाता है।
- कम्प्यूटर इनपुट को प्रोसैस करता है।
- प्रोसैसिंग के बाद हमें जो नतीजा प्राप्त होता है उसे आऊटपुट कहा जाता है।
कम्प्यूटर की परिभाषा (Definition of Computer)
“कम्प्यूटर एक इलैक्ट्रॉनिक मशीन है जो इनपुट के तौर पर यूजर से डाटा प्राप्त करती है तथा इस इनपुट किये डाटा को निर्देश अनुसार प्रोसैस करता है तथा नतीजा (आऊटपुट) प्रदान करता है। कम्प्यूटर इस आऊटपुट को भविष्य के लिए संभाल कर भी रखता है। यह नुमैरीकल (Numerical) और नान-नुमैरीकल (Non-Numerical) गणनाओं को प्रोसेस कर सकता है।”
कम्यूटर का प्रयोग (Use of Computer) हम कम्प्यूटर पर गणित की गणनाएँ, स्पैल चैक, गेम, तस्वीर बनाना, गाने सुनना, छपाई करना, टिकटें बुक करना, मौसम की जानकारी प्राप्त करना तथा नतीजे प्राप्त करना आदि कार्य कर सकते हैं।
हम कम्प्यूटर पर निम्न कार्य कर सकते हैं-
- गणितिक गणनाएं।
- टैक्सट के स्पैल चैक
- गेम खेलना
- तस्वीर बनाना।
- फिल्म देखना तथा गाने सुनना।
- किताबें तथा अखबारें छापना
- टिकट बुक करना।
- रेलगाड़ी, बसों तथा जहाज़ों के आने-जाने का पता करना।
- मौसम की जानकारी प्राप्त करना।
- स्कूल रिपोर्ट, नतीजा तथा समय सारणी तैयार करना।
- रेलवे, बस तथा हवाई जहाज़ में सफर करने के लिए टिकट बुक कराना।
- किसी जगह पहुँचने के लिए रास्ता पता करना।
![]()
कम्प्यू टर के उपयोग (Application of Computer)
कम्प्यूटर का प्रयोग, शिक्षा, सेहत, दुकानों, व्यापार, बैंकों, मनोरंजन, सरकारी सैक्टर, खेलों आदि क्षेत्रों में किया जाता है।
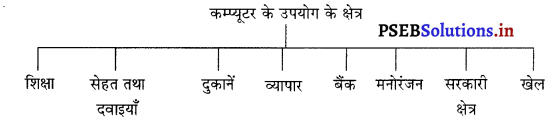
आजकल कम्प्यूटर विभिन्न क्षेत्रों में प्रयोग किया जाता है जिनका वर्णन नीचे किया गया है-
1. शिक्षा के क्षेत्र में (In Education Field)-शिक्षा में कम्प्यूटर का प्रयोग हाज़री लगाने, मार्कशीट बनाने, पेपर बनाने आदि में किया जाता है। लाइब्रेरी में भी कम्प्यूटर का प्रयोग किया जाता है। इसकी सहायता से रिज़ल्टस बनाए जाते हैं। कम्प्यूटर का प्रयोग कक्षा में पढ़ाने के लिए भी किया जाता है। प्रयोगशालाओं में भी कम्प्यूटर का प्रयोग होता है।
2. सेहत तथा दवाइयों के क्षेत्र में (In Health and Medicine field)-आजकल कम्प्यूटर का प्रयोग अस्पतालों में किया जाता है जहां डॉक्टर इसका प्रयोग मरीज की जांच करने के लिए करते हैं। इनकी सहायता से मरीज को दवाई दी जाती है तथा उनके आपरेशन भी किए जाते हैं।
3. दुकानों में (In Shops) कम्प्यूटर का प्रयोग एक दुकानदार दुकानों में अपने सामान का उपलब्ध रिकार्ड रखने में करता है। वह दुकान में हुई खरीद-बिक्री तथा टैक्स का रिकार्ड कम्प्यूटर में रख सकता है। आजकल कम्प्यूटर पर बिक्री के बिल भी तैयार किए जाते हैं।
4. व्यापार में (Trade Use)-कम्प्यूटर का प्रयोग व्यापार में हिसाब-किताब रखने के लिए किया जाता है। इसकी सहायता से खरीददारी भी की जाती है। हम घर बैठे कम्प्यूटर की सहायता से दुनिया में कहीं से भी खरीददारी कर सकते हैं। इनके प्रयोग से बिलों का भुगतान किया जा सकता है। आजकल बड़े-बड़े माल तथा शोपिंग सैंटरों में इसी का प्रयोग होता है।
5. बैंकों में (In Banks)-आजकल सभी बैंक कम्प्यूटर की सहायता से चलते हैं। ATM मशीन अपने आप में एक कम्प्यूटर है जिससे हम कभी भी पैसे निकाल सकते हैं। हम इंटरनैट की सहायता से कहीं से भी अपना पैसा कहीं भी भेज सकते हैं।
6. मनोरंजन के क्षेत्र में (In field of Entertainment) मनोरंजन क्षेत्र में भी कम्प्यूटर का प्रयोग हो रहा है। कार्टून फिल्में इसी की सहायता से बनती हैं जिन्हें बच्चे बहुत पसंद करते हैं। वीडियो गेम भी कम्प्यूटर की सहायता से चलती है। आजकल तो कई प्रकार की फिल्में भी इसी के प्रयोग से बनती हैं।
7. विभिन्न सरकारी क्षेत्रों में (In different Government Fields)-सरकार के कई विभाग कम्प्यूटर का प्रयोग अपनी योजना, नियंत्रण तथा कानून को प्रभावशाली बनाने के लिए करते हैं। कम्प्यूटर का प्रयोग ट्रैफिक, सैर-सपाटा, सूचना, शिक्षा, सेना, हवाबाज़ी तथा अन्य कई क्षेत्रों में होता है।
8. खेलों में (In Sports)- कम्प्यूटर का प्रयोग खेलों में भी होता है। क्रिकेट में आजकल बहुत प्रभावशाली स्कोर बोर्ड होते हैं। इनमें जैसे ही सूचना दाखिल की जाती है यह उसी समय दर्शकों को नतीजा दिखाता है।
9. संचार (Communication)-कम्प्यूटर का प्रयोग संचार के लिए किया जाता है । इसके द्वारा हम नए माध्यम जैसे कि वीडियो कॉल आदि का प्रयोग कर संचार कर सकते हैं।
कई तरह के – नए संचार माध्यम : जैसे-ई-मेल, चैट आदि कम्प्यूटर की ही देन है। इसका प्रयोग किसी भी स्मार्ट फोन, टेबलेट, कम्प्यूटर, लैपटाप या डैस्कटाप आदि से किया जाता है।
![]()
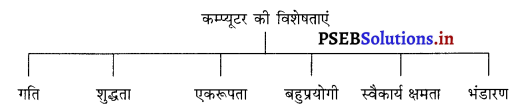
कम्प्यू टर की विशेषताएं (Characteristics of Computer)
गति, शुद्धता, एकसारता, बहुगणता, आटोमेशन तथा भण्डारण आदि कम्प्यूटर की विशेषताएं हैं।
1. गति (Speed)-कम्प्यूटर काफी तेज काम करता है। जिन गणनाओं में हम कई घंटे लगाते हैं, उन्हें यह कुछ सैकेंड में कर सकता है। कम्प्यूटर एक सैकेंड में कई लाख गणनाएं कर सकता है। आप को यह जानकर बहुत हैरानी होगी कि एक कम्प्यूटर एक सैकेण्ड में कई लाखों हिदायतों पर अमल कर सकता है।
2. शुद्धता (Accuracy)-कम्प्यूटर पर काम करने पर शुद्धता का स्तर बहुत ऊंचा होता है। कम्प्यूटर हमेशा सही कार्य करता है। अगर कोई गलती होती है तो वह इनपुट या निर्देश की होती है। जिस तरह के निर्देश या हिदायत कम्प्यूटर को दी जाती है यह वैसा ही नतीजा देता है।
3. एकसारता (Consistency)-कम्प्यूटर को कोई थकावट, ध्यान भटकना तथा काम का बोझ महसूस नहीं होता। यह बगैर ग़लती किए कई घंटों तक काम कर सकता है।
4. बहुगुणता (Versatility)-इसका अर्थ है एक समय पर विभिन्न कार्य करना। जब हम कम्प्यूटर पर गणनाएं करते हैं, ठीक उसी समय हम वस्तुओं का रिकार्ड बनाने तथा खरीद बिक्री के लिए भी इसका प्रयोग कर सकते हैं तथा साथ में हम गाने भी सुन सकते हैं।
5. आटोमेशन (Automation)-यदि एक बार कम्प्यूटर को कोई निर्देश दिया जाए, तो यह मनुष्य के हस्तक्षेप के बिना उस निर्देश पर काम करता रहता है। यह निर्देश की पूर्ति होने तक काम करता है। जब इस निर्देश को समाप्त करने के लिए कोई लॉजिकल (तार्किक) निर्देश दिया जाता है तो यह उस प्रोग्राम को समाप्त कर देता है।
6. भंडारण (Storage)-कम्प्यूटर की अपनी मैमरी होती है जिसमें वह डाटा स्टोर कर सकता है। इस डाटा को आवश्यकता अनुसार स्टोरेज उपकरण जैसे कि सी०डी०, डी०वी०डी०, यू०एस०वी० तथा पैन ड्राइव का प्रयोग करके किसी अन्य कम्प्यूटर पर भी ले जाया जा सकता है।
पोर्टेबल कम्प्यूटिंग यंत्र (Portable Computing Devices) –
पोर्टेबल कम्प्यूटिंग यंत्रों से हमारा अभिप्राय यंत्रों से है, जिनको प्रयोग करने के लिए हम आसानी से एक स्थान से दूसरे स्थान पर ले जा सकते हैं। यह यंत्र आकार में छोटा होता है। इनका भार भी कम होता है। आजकल हम कई प्रकार के पोर्टेबल कम्प्यूटिंग यंत्रों का प्रयोग कर रहे हैं। तीन प्रकार के कम्प्यूटिंग यंत्रों की व्याख्या नीचे की गई है-
1. मोबाइल फोन/स्मार्टफोन (Mobile/Smart Phone)-मोबाइल फोन या स्मार्टफोन आजकल प्रयोग में आने वाला सबसे आम पोर्टेबल कम्प्यूटिंग यंत्र है। यहां लगभग सभी लोगों के पास पाया जाता है। इसमें हम अपने सभी कार्य कर सकते हैं जिसको करने के लिए हमें एक नॉर्मल कम्प्यूटर की जरूरत पड़ती है। आजकल के मोबाइल फोन में हम गाने सुन सकते हैं। फिल्में देख सकते हैं, डॉक्यूमैंट तैयार कर सकते हैं तथा सोशल नेटवर्किंग के जरिए अपने दोस्तों तथा मित्रों से भी संपर्क बना सकते हैं। आजकल के मोबाइल फोन काफ़ी तीव्र गति से काम करते हैं तथा भंडारण के लिए भी काफी ज्यादा स्थान प्रदान करते हैं। इन मोबाइल फोनों में इंटरनेट का प्रयोग भी किया जाता है। मोबाइल फोन का प्रयोग शिक्षा व्यापार वाणिज्य मनोरंजन तथा गेम खेलने के लिए किया जा सकता है।

2. टैबलेट (Tablet)-टैबलेट कम्प्यूटर एक पतला तथा पोर्टेबल कम्प्यूटर होता है जो कि एक बैटरी की सहायता से चलता है। इस कम्प्यूटर पर टचस्क्रीन लगी होती है। इसको चलाने के लिए हमें अलग कीबोर्ड या माऊस की ज़रूरत नहीं होती। स्क्रीन को अपनी उंगली से ही चलाया जा सकता है। इस कम्प्यूटर का प्रयोग विभिन्न मंत्रों के लिए किया जा सकता है। मुख्य रूप से इसका प्रयोग उन कार्यों में होता है जहां टाइपिंग की ज्यादा जरूरत नहीं होती। टैबलेट कम्प्यूटर का अधिकतर प्रयोग शॉपिंग मॉल रेस्टोरेंट तथा शिक्षा में विद्यार्थियों द्वारा देखा जाता है।

3. पामटोप (Palmtop) यह एक छोटे प्रकार का कम्प्यूटर होता है जिसमें एक छोटी स्क्रीन लगी होती है तथा इसके साथ इसमें एक छोटा सा कीबोर्ड भी होता है। यह कम्प्यूटर में एक मोबाइल फोन की तरह लगता है। आजकल इस कम्प्यूटर का प्रयोग ज्यादा नहीं किया जाता क्योंकि इसका प्रयोग कुछ सीमित कार्यों को करने के लिए ही किया जाता है।

4. लैपटॉप (Laptop)-लैपटॉप कम्प्यूटर आजकल सभी जगह प्रयोग हो रहे हैं। यह एक छोटे आकार का तथा हल्का कम्प्यूटर होता है जिसकी बड़ी स्क्रीन होती है। इसमें एक कीबोर्ड भी लगा होता है तथा साथ में माउस चलाने के लिए एक टचपैड भी होता है। लैपटॉप कम्प्यूटर को हम अपनी गोद में रख कर आसानी से काम कर सकते हैं। अंग्रेज़ी भाषा में गोद को Lap कहते हैं। इसी कारण इस कम्प्यूटर का नाम लैपटॉप कम्प्यूटर पड़ा। यह कम्प्यूटर एक टैस्ट ऑफ कम्प्यूटर के जितना ही शक्तिशाली होता है तथा उसी प्रकार हमारे सभी कार्य कर सकता है।

5. नोट-बुक (Note-Book)-यह एक पोर्टेबल कम्प्यूटर होता है परंतु आकार में एक लैपटॉप से भी छोटा होता है। लैपटॉप कम्प्यूटर की तरह ही यह वज़न में हल्का होता है। एक नोट-बुक की अपनी बैटरी होती है जिसे आवश्यकता पड़ने पर चार्ज भी किया जाता है। एक व्यक्ति सफर के दौरान इसको साथ लेकर जा सकता है।

![]()
कम्प्यूटर की सीमाएं (Limitations of Computer)
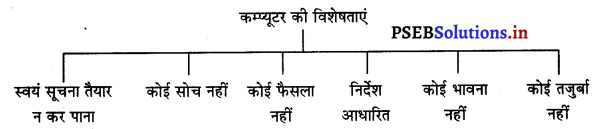
समझ न आना, स्वयं कार्य करने के योग्य न होना, भावना और तजुर्बाहीन होना आदि कम्प्यूटर की सीमाएं हैं। कम्प्यूटर की निम्नलिखित सीमाएं हैं –
- यह सिर्फ मानवीय निर्देशों पर कार्य करता है।
- इसमें अपनी सोचने-समझने की कोई शक्ति नहीं है।
- यह अपना ध्यान नहीं रख सकता।
- कम्प्यूटर की मैमरी मनुष्य की तुलना में सीमित कार्य कर सकती है।
- कम्प्यूटर में कोई भावना नहीं होती है।
- कम्प्यूटर में दूरदर्शिता की कमी होती है।
- यह सिर्फ तर्क आधारित कार्य ही कर सकते हैं।
- कम्प्यूटर हार्डवेयर में एक स्वरूपता की कमी है। विभिन्न कम्पनियों के अलग-अलग हार्डवेयर यंत्र होते हैं।
- कम्प्यूटर को कार्य करने के लिए खास वातावरण की ज़रूरत होती है। ये तापमान, नमी आदि से काफ़ी प्रभावित होते हैं।
































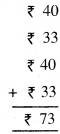

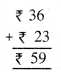


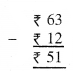

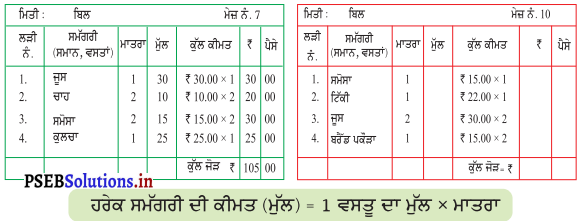
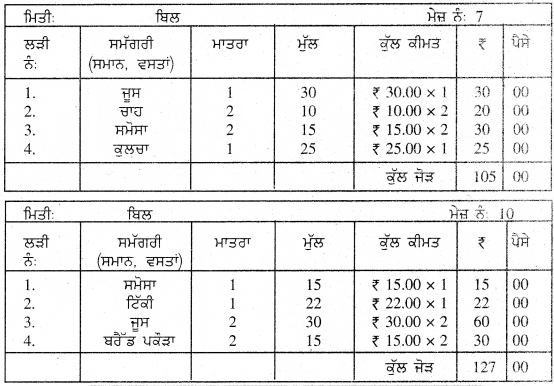






 ਰੁਪਏ = ….. ਪੈਸੇ
ਰੁਪਏ = ….. ਪੈਸੇ