Punjab State Board PSEB 5th Class Welcome Life Book Solutions Chapter 4 Keep Love in Heart Towards Them Textbook Exercise Questions and Answers.
PSEB Solutions for Class 5 Welcome Life Chapter 4 Keep Love in Heart Towards Them
Welcome Life Guide for Class 5 PSEB Keep Love in Heart Towards Them Textbook Questions and Answers
(a) Information about our state :
Our Punjab is a colorful place. It is like a Rose among other flowers. Here people never lose hope and dream new every day.
We are the natives of Punjab. Punjab is a famous state of India. Punjab has a special recognition across the world. Punjab was named after five rivers – Satluj, Beas, Raavi, Chenab and Jehlum. But two rivers – Chenab and Jhelum became the part of Pakistan at the time of Partition of India in 1947. Now, three rivers – Satluj,Beas and Raavi flow here.


Punjab is a border state. It has been facing many battles because of that. People living here have no fear of enemy. Their culture is full of bravery. Punjabis have a great contribution in the struggle of freedom for the country. These people a re famous for thei r bravery across the world.

Punjabi is the language of Punjab. Punjabi speaking people can be found even far away from Punjab. It is the lQth – llth language of the world on spoken based. Our Gurus, Suffis, Saints, Poets and singers adopted this language to raise its status. Today, Punjabi is known as a rich language.

Bhangra and Gidha is the folk dance of Punjab. Bhangra is the dance of men and Gidha is the dance of women. These dances are performed on the occasion of happiness. Singing and dancing is the food of Punjabi’s soul.


Punjab is very famous for agriculture. Its land is very fertile. There are bumper crops of wheat, rice, maize and sugarcane here. Punjab provides major share in Food store of India in spite of having less area. Animal husbandry is another main occupation here.

Punjabis are very fond of fairs. Many fairs are celebrated in the Punjab. Vaisakhi fair, chappar fair, Jarg fair, Hola mahala, Maghi fair and Prof. Pooran Singh fair are very famous among them.

Punjabis are very open – hearted, happy – go – lucky and helpful people. They have nature of helping other people and arranging Langer for needy ones.


Oral Questions:
Question 1.
How many rivers were there in ancient Punjab?
Answer:
Five.
Question 2.
Which rivers are there in Punjab these days?
Answer:
Sutlej, Bias, Ravi.
Question 3.
Which language is spoken in Punjab?
Answer:
Punjabi.
Question 4.
Which crops are cultivated in Punjab?
Answer:
Sugarcane, Wheat, Rice, Maze.

Question 5.
Which are the major occupations of Punjabis?
Answer:
Agriculture.
Question 6.
Which are main fairs of Punjab?
Answer:
Jarag, Chhappar, Hola Mohala, Vaisakhi, Pro. Mohan Singh Mela.
Question 7.
How is the nature of Punjabis?
Answer:
Broadmindedness, jolly nature and being helpful to others.
Question 8.
What is your viewpoint about Punjab?
Answer:
Very much.
(b) Love with Mother – Tongue:

Teacher : Children, today we’ll discuss about mother – tongue.
Ankur : Sir, What is mother – tongue?

Teacher : Children, Mother – tongue is that which is acquired by a child from his/her parents or his/her family from the very beginning.
Baljit : Sir, if a child learns from parents or family, then why is it called mother – tongue?
Teacher : Yes Baljit, you asked a very good question. In reality, a child lives with his/her mother most of the time from early days. May be that’s why it is named as mother – tongue.
Chandan : Sir, there is a song by Harbhajan Maan – ‘Mainu iyon na mano visaar ve main teri maa boli ha’.
(Don’t forget me from your heart. I’m your mother – tongue.)
Teacher : Well done, you reminded me a very good song.
Baljit : Sir, Satinder Sartaj also has a song – ‘Main Gurmukhi da Beta’.
Teacher : Yes son, it is also a very good song. You listen to very good songs. Son, both these songs highlighted the importance of mother – tongue. They give the message to love mother – tongue.
Savirta : Sir, Is Punjabi our mother – tongue?
Teacher : Yes, Punjabi is our mother – tongue.
Savita : Sir, What is Gurumukhi then?

Teacher : Daughter, Gurumukhi is a script of Punjabi language. The signs that are used for writing Punjabi language is called a script. Like a A e ishwrl, ibhwrl, ibMdl, it pi… The group of signs that are used to write is called a script. Gurumukhi script is used for writing Punjabi.
Savita : Sir, Why do many Hindi movies have Punjabi songs?
Teacher : Children, Punjabi is a very famous language. By the numbers of speakers, this language is on lOth/llth position among the world. Punjabi people have reached in more than 160 countries of the world. Whenever there is a Punjabi song in a Hindi movie, many Punjabis like to watch that movie. Many times, Hindi film makers add a Punjabi song in their movieto make it more popular.
Bharti : Sir, all the members in my house speak in Hindi. Our Real house is in U.P. Our relatives also speak in Hindi.
Teacher : Child, Then your mother – tongue is Hindi. No problem, Hindi and Punjabi our like sisters. Every human being must love his/her own mother – tongue. Mother – tongue has a deep and loveable relationship with our heart and mind. Whatever is listened and read in mother – tongue is easily understood.
Baljit : Yes Sir, That’s right.
Teacher : But children, it doesn’t mean that we needn’t learn other languages. Just keep in mind that other languages are not learnt by forgetting mother – tongue. Harbhajan Maan is also saying that – ‘Mainu iyon na manovisar.
Baljit : Sir, There is a song of Manmohan Waris in my father’s phone – ‘Mawan tin hundiyan ne’. (Mothers are three….)
Teacher : Baljit, your father has a good taste of music. I have also listened to that song – Mothers are three – one is Mother Earth, second is mother – tongue and third is the mother who gave us birth. Really children, these three nurture us. Their debt can’t be repaid.
Savita : Sir, my uncle reads Punjabi books.

Teacher : Yes children, Books of many famous writers like Gurdial Singh, Shiv Kumar, Surjit Patar and Narinder Kapoor are read in Punjabi.
Ankur : Sir, My brother reads Punjabi newspaper on computer.
Teacher : Yes children, many things in Punjabi are there on computer. I also read three Punjabi newspapers early in the morning – Punjabi Tribune, Nawan Jamana (The New World) and Ajit.
Children let’s stop this conversation here. What did you learn today?
Bharti : Sir, today we learnt that we should never forget our mother – tongue ever.
Teacher : Let’s finish this talk with lines of a Pakistani Poet:
ਮੈਨੂੰ ਕਈਆਂ ਨੇ ਆਖਿਆ ਕਈ ਵਾਰੀ
ਤੂੰ ਲੈਣਾ ਪੰਜਾਬੀ ਦਾ ਨਾਂ ਛੱਡ ਦੇ।
ਜਿਦੀ ਗੋਦੀ ‘ਚ ਪਲ ਕੇ ਜਵਾਨ ਹੋਇਓਂ |
ਉਹ ਮਾਂ ਛੱਡ ਦੇ ਤੇ ਗਰਾਂ ਛੱਡ ਦੇ।
ਜੇ ਪੰਜਾਬੀ-ਪੰਜਾਬੀ ਈ ਕੂਕਣਾ ਈ
ਜਿੱਥੇ ਖਲਾ ਖਲੋਤਾ ਉਹ ਥਾਂ ਛੱਡ ਦੇ।
ਮੈਨੂੰ ਇੰਝ ਲੱਗਦਾ ਲੋਕੀਂ ਆਖਦੇ ਨੇ
ਤੂੰ ਪੁੱਤਰਾ ਆਪਣੀ ਮਾਂ ਛੱਡ ਦੇ।

(Many people have asked me to stop using the name of Punjabi just as a child loves his mother and native place after growing up in the lap of his mother.)

Oral Questions:
Question 1.
Which are three mothers of a human being?
Answer:
Earth mother, mother-tongue, birth-giving mother.
Question 2.
Which language is the mother – tongue of Punjab?
Answer:
Punjabi.
Question 3.
Can Punjabi be read or written on computer?
Answer:
Yes.
Question 4.
What did we learn from today’s talk?
Answer:
We should not learn more languages after forgetting Punjabi. But we should learn other languages also so that we can get knowledge about other singers and writers.
(C) On other Languages of the country:
Other people have their mother – tongues just as Punjabi is our mother – tongue. They also love their mother – tongue as we do. Everyone has a right to love his/her own mother – tongue. Everyone must love his/her mother – tongue. Hundreds of languages and dialects are spoken in India. More spoken languages amongthem hold a place in the constitution.

You must have seen any Indian rupee – note. The amount of rupee can be found written on this in seventeen languages including Punjabi, Hindi and English. In Reality, India is a multi language country. India is a bouquet of language flowers. That’s why Indian government gives the deserved right to every language. We must love our mother – tongue but we shouldn’t condemn others’ mother – tongue. Mother – tongue is as loveable to anyone as we love ours.

We must learn as well as speak our mother – tongue very well but other languages also. It is impossible to live without learning Hindi and English. If we have to live in any other state for a longer period, then we should learn their language also. Our many problems will get solved after learning this otherwise also, if we learn as many languages as we can, many doors to knowledge will get open for us. Bangla, Assami, Marathi, Kashmiri, Bodo, Kannad, Malyalam, Gujrati, Dogri, Urdu and Tamil are other languages spoken in India.

Do you know that Munshi Premchand is a well known writer in Hindi? You must have heard the name of Rabindranath Tagore. Tagore was from Bengal. He wrote in Bangali Language. Indian National Anthem ‘JANA GANA MANA’ is written by him. So It is very important to understand the Importance of other languages.

ਦੇਸ ਮੇਰੇ ਦੀਆਂ ਸਭ ਬੋਲੀਆਂ ਨਿਆਰੀਆਂ।
ਦੇਸ ਦੀ ਅਮੀਰੀ ਇਹ ਦਿਖਾਉਣ ਸਾਰੀਆਂ।
ਜਿੰਨੀਆਂ ਭਾਸ਼ਾਵਾਂ ਅਸੀਂ ਸਿੱਖ ਲੈਂਦੇ ਹਾਂ,
ਗਿਆਨ ਦੀਆਂ ਓਨੀਆਂ ਖੁੱਲ੍ਹਣ ਬਾਰੀਆਂ।

(All the languages of my country are different. It increases the richness of the country. As many languages as we learn, more and more windows get open to acquire knowledge.
Oral Questions:
Question 1.
Hundred languages are spoken in India. True Or False?
Answer:
Right.
Question 2.
Write any two languages other than Punjabi, Hindi and English?
Answer:
Marathi, Bodo, Kashmiri.
Question 3.
Where did Rabindranath Tagore belongto?
Answer:
In Bengal.

Question 4.
Learning more languages is beneficial or not?
Answer:
More doors of knowledge are opened for us.
(d) Love with people of the country:
It is a very high human trait of having true love for country. It is not a wholly love for things of the country. Real love for country is a love for its people. People of the country means all the people that belong to that country. Till we don’t love all people of the country, we can’t say that we love our country. As you know that we all are human beings. That’s why the feeling of hatred or partiality shouldn’t exist in our heart.
Any citizen irrespective of his state, religion, caste or language, is a part of the country. Any kind of partiality must not be done with him. We should not have any feelings of superiority or inferiority. Every citizen should be helpful to others. Nobody should think about other’s loss. Nobody should cheat anyone. This is the love for the people of the country.
The most important thing is to think about the rights of poor people in the country. We should try to make poor people’s life prosper. They should be helped in education. A nation can prosper only, if all the people are happy and have essential facilities for life. A Real courtesy is to take weak people along with us. Let’s read a poem :
ਆਓ, ਸਾਰੇ ਲੋਕਾਂ ਨੂੰ ਪਿਆਰ ਕਰੀਏ,
ਦਿਲਾਂ ਚ ਕਦੇ ਨਾਨਫ਼ਰਤ ਭਰੀਏ ।
ਸਾਰੇ ਹੀਨੇ ਆਪਣੇ, ਬੇਗਾਨਾ ਕੋਈਨਾ,
ਪਿਆਰ ਜਿਹਾ ਜੱਗ ਚ ਤਰਾਨਾ ਕੋਈ।
ਸੱਚੇ-ਸੁੱਚੇ ਦਿਲ ’ਚ ਵਿਚਾਰ ਰੱਖੀਏ,
ਦਿਲ ’ਚ ਨਾਕਦੇ ਹੰਕਾਰ ਰੱਖੀਏ।
ਵੰਡੀਆਂਦਿਲਾਂ ਦੇ ਵਿੱਚ ਆਉਣ ਦੇਈਏ ਨਾ,
ਝਗੜਾ ਕਿਸੇ ਨੂੰ ਕਦੇ ਪਾਉਣ ਦੇਈਏ ਨਾ।


(Let us love all the people and never have feeling of hatred in our hearts. All are ours, nobody is strange and nothing is more beautiful song than love in the world. We should keep good and pure thoughts in our hearts in place of pride. We should restrict people to make divisions and stop fighting.)
Oral Questions:
Question 1.
Are we all India ns united?
Answer:
Yes, all Indians are one.
Question 2.
Should we help others or harm others?
Answer:
We should help others.
Question 3.
What are the benefits of living with love?
Answer:
Country and all the people in the country make progress.
Question 4.
The country is also a big family. True or False?
Answer:
Right.

Question 5.
Do all human being’s blood similaror different?
Answer:
Alike.
Question 6.
Is it a good thing to fight on the basis of religion, caste or region?
Answer:
No, it is very bad.
Question 7.
After growing up would you teach people to live with love?
Answer:
Yes, I will start from now.
PSEB 5th Class Welcome Life Guide Keep Love in Heart Towards Them Important Questions and Answers
Multiple Choice Questions :
Question 1.
Which river is not included in Punjab at Present ?
(a) Sutlej
(b) Jhelum
(c) Bias
(d) Ravi.
Answer:
(b) Jhelum.

Question 2.
When did country get freedom ?
(a) 1950
(b) 1947
(c) 1974
(d) 1945.
Answer:
(b) 1947.
Question 3.
Which type of state is Punjab ?
(a) Borderline
(b) Near the sea
(c) Sandy
(d) All are wrong.
Answer:
(a) Borderline.
Question 4.
How many languages are there on the Indian rupee ?
(a) 10
(b) 17
(c) 11
(d) 21
Answer:
(b) 17.
Question 5.
In which language Tagore used to Write ?
(a) Punjabi
(b) Bengali
(c) Urdu
(d) Hindi.
Answer:
(b) Bengali.

Question 6.
Who was Munshi Prem Chand ?
(a) Writer
(b) Poet
(c) Actor
(d) Singer.
Answer:
(a) Writer.
Question 7.
Who has written the national Anthem of India ?
(a) Tagore
(b) Munshi Prem Chand
(c) Amrita Pritam
(d) None of the above.
Answer:
(a) Tagore.
Question 8.
In how many countries have Punjabi people reached ?
(a) More than 160
(b) Less than 95
(c) 340
(d) 460.
Answer:
(a) More than 160.

Question 9.
Who has said in the song that mothers are three in number ?
(a) Sartaj
(b) Batalavi
(c) Manmohan Wans
(d) Harbhajan Mann.
Answer:
(c) Manmohan Waris.
Question 10.
Famous writer is :
(a) Shiv Kumar Batalavi
(b) Narinder Singh Kapoor
(c) Gurdial Singh
(d) All are correct.
Answer:
(d) All are correct.
Question 11.
We should ……….. our mother-tongue.
(a) Love
(b) Partiality
(c) Hate
(d) All of the above.
Answer:
(a) Love

Question 12.
Which newspaper does our teacher read in computer ?
(a) Punjabi Tribune
(b) Nawan Jamana
(c) Ajit
(d) All are correct.
Answer:
(d) All are correct.
Fill in the blanks :
1. We are the citizens of ……………………………… State.
2. People of Punjab are famous all over the world for their …………………………….. .
3. On the basis of number of Punjabi-speaking people in the world, Punjabi is on the ……………………………… number.
4. Punjab has always to face wars due to ……………………………… state.
5. Punjab is very famous for …………………………….. .
6. National Anthem of India ‘Jana Gana Mann’ is written by …………………………….. .
7. To support the ……………………………… person is real goodness.
Answer:
1. Punjab
2. bravery
3. tenth-eleventh
4. borderline
5. agriculture
6. Rabindranath Tagore
7. weak.

Tick Right (✓) or Wrong (✗) :
1. Punjab has got its name by seven rivers.
2. Punjab is at borderline. That is why it always remains peaceful.
3. The language of Punjab is Dogri.
4. Dancing and singing is the diet of souls of Punjabis.
5. Wheat, rice, maze and sugarcane are grown at large scale in Punjab.
6. Amount of note is written in 17 languages on the Indian rupee.
7. Munshi Prem Chand is a great writer of Hindi.
8. There should not be any feeling of casteism.
Answer:
1. ✗
2. ✗
3. ✗
4. ✓
5. ✓
6. ✓
7. ✓
8. ✓
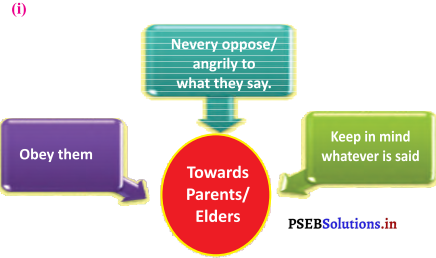
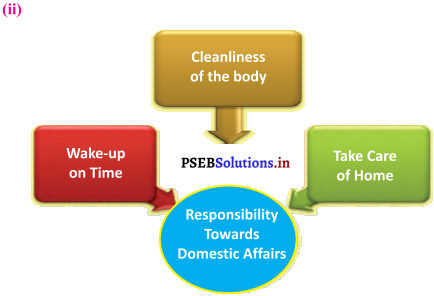
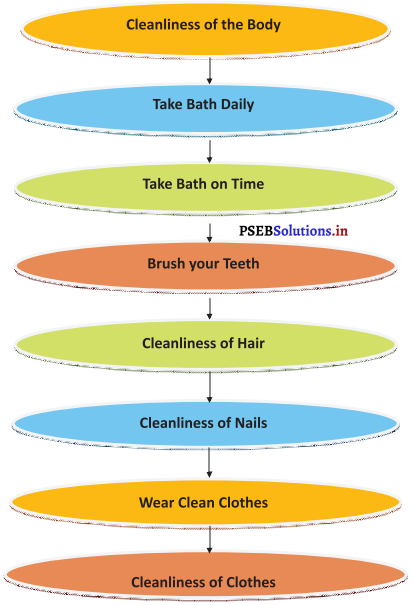
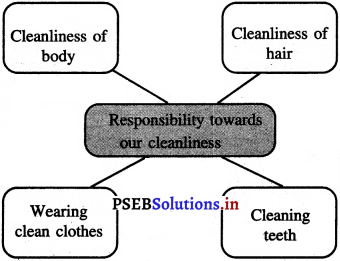
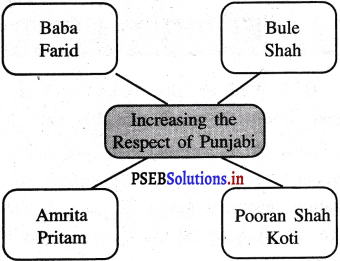
Mind Mapping :

Answer:

Match the following :
1. Punjab (a) Tagore
2. Fair of Punjab (b) Surjeet Pattar
3. Punjabi Poet (c) Borderline State
4. Bengali Writer (d) Jarag.
Answer:
1. (c)
2. (d)
3. (b)
4. (a)
Short Answer Type Questions
Question 1.
Name five rivers on the basis of which Punjab has got its name ?
Answer:
Sutlej, Bias, Ravi, Chenab and Jhelum.
Question 2.
How many rivers are there in Punjab nowadays ?
Question 3.
How two rivers of Punjab are excluded from it ?
Answer:
At the time of division of 1947, two rivers were included in Pakistan.
Question 4.
What are the folk dances of Punjab ?
Answer:
Bhangra of men and Giddha of women.
Question 5.
Give names of martyrs of Punjab.
Answer:
Shaheed Bhagat Singh, Shaheed Kartar Singh Sarabha, Shaheed Udam Singh.

Question 6.
What is the language of Punjab ?
Answer:
Language of Punjab is Punjabi.
Question 7.
Language of Punjab stands at which number in the world ?
Answer:
On the basis of number of Punjabi-speaking people in the world, Punjabi stands at the tenth-eleventh number.
Question 8.
What is Mother-tongue?
Answer:
Mother-tongue is that language which a child learns from his/her parents or family.
Question 9.
What are the two songs in which mother-tongue is used ?
Answer:
Harbhajan Mann’s ……… Mainu Eyu na Mono Visar, Ve main Teri maa di Boli haan.
Satinder Sartaj’s ……… Main Gurmukhi da Beta.
Question 10.
What is Gurmukhi ?
Answer:
It is the script of Punjabi language.

Question 11.
According to Manmohan Waris’s song, which are the three mothers ?
Answer:
Mother earth, Mother-tongue, Birth giving mother.
![]()

![]()
![]()
![]()
![]()
![]()
![]()