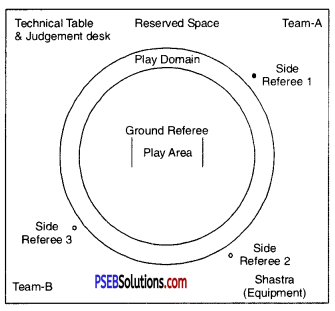
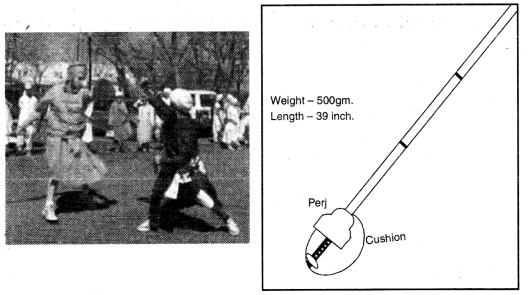
Punjab State Board PSEB 10th Class Physical Education Book Solutions योग (Yoga) Game Rules.
योग (Yoga) Game Rules – PSEB 10th Class Physical Education
प्रश्न
योग का इतिहास और नियम लिखें।
उत्तर-
योग का इतिहास
(History of Yoga)
‘योग’ का इतिहास वास्तव में बहुत पुराना है। योग के उद्भव के बारे में दृढ़तापूर्वक व स्पष्टता से कुछ भी नहीं कहा जा सकता। केवल यह कहा जा सकता है कि योग का उद्भव भारतवर्ष में हुआ था। उपलब्ध तथ्य यह दर्शाते हैं कि योग सिन्धु घाटी सभ्यता से सम्बन्धित है। उस समय व्यक्ति योग किया करते थे। गौण स्रोतों के आधार पर यह कहा जा सकता है कि योग का उद्भव भारतवर्ष में लगभग 3000 ई० पू० हुआ था। 147 ई० पू० पतंजलि (Patanjali) के द्वारा योग पर प्रथम पुस्तक लिखी गई थी। वास्तव में योग संस्कृत भाषा के ‘युज्’ शब्द से लिया गया है। जिसका अभिप्राय है ‘जोड़’ या ‘मेल’। आजकल योग पूरे विश्व में प्रसिद्ध हो चुका है। आधुनिक युग को तनाव, दबाव व चिंता का युग कहा जा सकता है। इसलिए अधिकतर व्यक्ति खुशी से भरपूर व फलदायक जीवन नहीं गुजार रहे हैं। पश्चिमी देशों में योग जीवन का एक भाग बन चुका है। मानव जीवन में योग बहुत महत्त्वपूर्ण है।
यौगिक व्यायाम के नये नियम
(New Rules of Yogic Exercise)
- यौगिक व्यायाम करने का स्थान समतल होना चाहिए। ज़मीन पर दरी या कम्बल डाल कर यौगिक व्यायाम करने चाहिए।
- यौगिक व्यायाम करने का स्थान एकान्त, हवादार और सफाई वाला होना चाहिए।
- यौगिक व्यायाम करते हुए श्वास और मन को शान्त रखना चाहिए।
- भोजन करने के बाद कम-से-कम चार घण्टे के पश्चात् यौगिक आसन करने चाहिए।
- यौगिक आसन धीरे-धीरे करने चाहिए और अभ्यास को धीरे-धीरे बढ़ाना चाहिए।
- अभ्यास प्रतिदिन किसी योग्य प्रशिक्षक की देख-रेख में करना चाहिए।
- दो आसनों के मध्य में थोड़ा विश्राम शव आसन द्वारा कर लेना चाहिए।
- शरीर पर कम-से-कम कपड़े पहनने चाहिए, लंगोट, निक्कर, बनियान आदि, और सन्तुलित भोजन करना चाहिए।
बोर्ड द्वारा निर्धारित पाठ्यक्रम में निम्नलिखित यौगिक व्यायाम सम्मिलित किए गए हैं जिनके दैनिक अभ्यास द्वारा एक साधारण व्यक्ति का स्वास्थ्य बना रहता है—
- ताड़ासन
- अर्द्धचन्द्रासन
- भुजंगासन
- शलभासन
- धनुरासन
- अर्द्धमत्स्येन्द्रासन
- पश्चिमोत्तानासन
- पद्मासन
- स्वास्तिकासन
- सर्वांगासन
- मत्स्यासन
- हलासन
- योग मुद्रा
- मयूरासन
- उड्डियान
- प्राणायाम : अनुलोम विलोम
- सूर्य नमस्कार
- शवासन
![]()
प्रश्न
ताड़ासन और भुजंगासन की विधि बताकर इनके लाभ लिखें।
उत्तर-
ताड़ासन (Tarasan) इस आसन में खड़े होने की स्थिति में धड़ को ऊपर की ओर खींचा जाता है।
ताड़ासन की स्थिति (Position of Tarasan)—इस आसन में स्थिति ताड़ के वृक्ष जैसी होती है।
ताड़ासन की विधि (Technique of Tarasan)-खड़े होकर पांव की एड़ियों और अंगुलियों को जोड़ कर भुजाओं को ऊपर सीधा करें। हाथों की अंगुलियां एक-दूसरे हाथ में फंसा लें। हथेलियां ऊपर और नज़र सामने हो। अपना पूरा सांस अन्दर की ओर खींचें। एड़ियों को ऊपर उठा कर शरीर का सारा भार पंजों पर ही डालें। शरीर को ऊपर की ओर खींचे। कुछ समय के बाद सांस छोड़ते हुए शरीर को नीचे लाएं। ऐसा दस पन्द्रह बार करो।
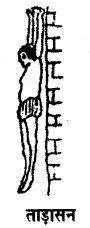
ताड़ासन ताड़ासन के लाभ (Advantages of Tarasan)-
- इससे शरीर का मोटापा दूर होता है।
- इससे कब्ज दूर होती है।
- इससे आंतों के रोग नहीं लगते।
- प्रतिदिन ठण्डा पानी पी कर इस आसन को करने से पेट साफ रहता है।
भुजंगासन (Bhujangasana)-इसमें चित्त लेट कर धड़ को ढीला किया जाता है।
भुजंगासन की विधि (Technique of Bhujangasana)-इसे सर्पासन भी कहते हैं। इसमें शरीर की स्थिति सर्प के आकार जैसी होती है। सासन करने के लिए भूमि पर पेट के बल लेटें। दोनों हाथ कन्धों के बराबर रखो। धीरे-धीरे टांगों को अकड़ाते हुए हथेलियों के बल छाती को इतना ऊपर उठाएं कि भुजाएं बिल्कुल सीधी हो जाएं। पंजों को अन्दर की ओर करो और सिर को धीरे-धीरे पीछे की ओर लटकाएं। धीरे-धीरे पहली स्थिति में लौट आएं। इस आसन को तीन से पांच बार करें।
लाभ (Advantages)—
- भुजंगासन से पाचन शक्ति बढ़ती है।
- जिगर और तिल्ली के रोगों से छुटकारा मिलता है।
- रीढ़ की हड्डी और मांसपेशियां मज़बूत बनती हैं।
- कब्ज दूर होती है।
- बढ़ा हुआ पेट अन्दर को धंसता है।
- फेफड़े शक्तिशाली होते हैं।
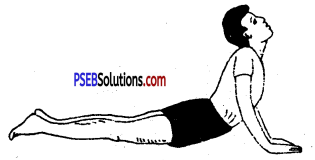
भुजंगासन
![]()
प्रश्न
धनुरासन, अर्द्धमत्स्येन्द्रासन और पश्चिमोत्तानासन की विधि और लाभ लिखें।
उत्तर-
धनुरासन (Dhanurasana)-इसमें चित्त लेट कर और टांगों को ऊपर खींच कर पांवों को हाथों से पकड़ा जाता है।
धनुरासन की विधि (Technique of Dhanurasana)-इससे शरीर की स्थिति कमान की तरह होती है। धनुरासन करने के लिए पेट के बल भूमि पर लेट जाएं। घुटनों को पीछे की ओर मोड़ कर रखें। टखनों के समीप पांवों को हाथ से पकड़ें। लम्बी सांस
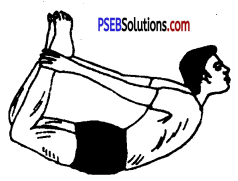
धनुरासन
लेकर छाती को जितना हो सके ऊपर की ओर उठाएं। अब पांव अकड़ायें जिससे शरीर का आकार कमान की तरह बन जाए। जितने समय तक सम्भव हो ऊपर वाली स्थिति में रहें। सांस छोड़ते समय शरीर को ढीला रखते हुए पहले वाली स्थिति में आ जाएं। इस आसन को तीन-चार बार करें। भुजंगासन और धनुरासन दोनों ही आसन बारी-बारी करने चाहिए।
लाभ (Advantages)—
- इस आसन से शरीर का मोटापा कम होता है।
- इससे पाचन शक्ति बढ़ती है।
- गठिया और मूत्र रोगों से छुटकारा मिलता है।
- मेहदा तथा आंतें अधिक ताकतवर बनती हैं।
- रीढ़ की हड्डी तथा मांसपेशियां मज़बूत और लचकीली बनती हैं।
अर्द्धमत्स्येन्द्रासन (Ardhmatseyandrasana)-इसमें बैठने की स्थिति में धड़ को पाश्र्यों की ओर धंसा जाता है।
विधि-ज़मीन पर बैठकर बाएं पांव की एड़ी को दाईं ओर नितम्ब के पास ले जाओ। जिससे एड़ी का भाग गुदा के निकट लगे। दायें पांव को ज़मीन पर बायें पांव के घुटने के निकट रखो फिर वक्षस्थल के निकट बाईं भुजा को लाएं, दायें पांव के घुटने के नीचे अपनी जंघा पर रखें, पीछे की ओर से दायें हाथ द्वारा कमर को लपेट कर नाभि को स्पर्श करने का यत्न करें। फिर पांव बदल कर सारी क्रिया को दोहराएँ।
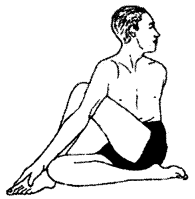
अर्द्धमत्स्येन्द्रासन
लाभ—
- इस आसन द्वारा मांसपेशियां और जोड़ अधिक लचीले रहते हैं और शरीर में शक्ति आती है।
- यह आसन वायु विकार और मधुमेह दूर करता है तथा आन्त उतरने (Hernia) में लाभदायक है।
- यह आसन मूत्राशय, अमाशय, प्लीहादि के रोगों में लाभदायक है।
- इस आसन के करने से मोटापा दूर रहता है।
- छोटी तथा बड़ी आन्तों के रोगों के लिए बहुत उपयोगी है।।
पश्चिमोत्तानासन (Paschimotanasana)—इसमें पांवों के अंगूठों को अंगुलियों से पकड़ कर इस प्रकार बैठा जाता है कि धड़ एक ओर ज़ोर से चला जाए।
पश्चिमोत्तानासन की स्थिति (Position of Paschimotanasana)-इस आसन में सारे शरीर को फैला कर मोड़ा जाता है।
पश्चिमोत्तानासन की विधि (Technique of Paschimotansana)—दोनों टांगें आगे की ओर फैला कर भूमि पर बैठ जाएं। दोनों हाथों से पांवों के अंगूठे पकड़ कर धीरे-धीरे सांस छोड़ते हुए घुटनों को छूने की कोशिश करो। फिर धीरे-धीरे सांस लेते हुए सिर को ऊपर उठाएं और पहले वाली स्थिति में आ जाएं। यह आसन हर रोज़ 10-15 बार करना चाहिए।
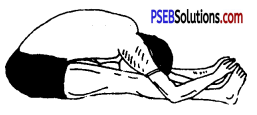
पश्चिमोत्तानासन
लाभ (Advantages)—
- इस आसन से जंघाओं को शक्ति मिलती है।
- नाड़ियों की सफाई होती है।
- पेट के अनेक प्रकार के रोगों से छुटकारा मिलता है।
- शरीर की बढ़ी हुई चर्बी कम होती है।
- पेट की गैस समाप्त होती है।
प्रश्न
पद्मासन, मयूरासन, सर्वांगासन और मत्स्यासन की विधि और लाभ बताएं।
उत्तर-
1. पद्मासन (Padamasana)—इसमें टांगों की चौंकड़ी लगा कर बैठा जाता है।
पद्मासन की विधि (Technique of Padamasana)-चौकड़ी मार कर बैठने के बाद दायां पांव बाईं जांघ पर इस तरह रखें कि दायें पांव की एड़ी बाईं जांघ पर पेड्र हड्डी को छुए। इसके पश्चात् बायें पांव को उठा कर उसी प्रकार दायें पांव की जांघ पर रख लें। रीढ़ की हड्डी बिल्कुल सीधी रहनी चाहिए। बाजुओं को तान कर हाथों को घुटनों पर रखो। कुछ दिनों के अभ्यास द्वारा इस आसन को बहुत ही आसानी से किया जा सकता है।
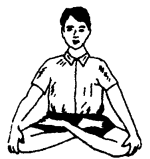
पद्मासन
लाभ (Advantages)—
- इस आसन में पाचन शक्ति बढ़ती है।
- यह आसन मन की एकाग्रता के लिए सर्वोत्तम है।
- कमर दर्द दूर होता है।
- दिल के तथा पेट के रोग नहीं लगते।
- मूत्र के रोगों को दूर करता है।
2. मयूरासन (Mayurasana)
विधि (Technique)—पेट के बल ज़मीन पर लेट कर दोनों पांवों के पंजों को मिलाओ। दोनों कहनियों को आपस में मिला कर ज़मीन पर ले जाओ। सम्पूर्ण शरीर का भार कुहनियों पर दे कर घुटनों और पैरों को जमीन से उठाए रखो।

मयूरासन
लाभ (Advantages)—
- यह आसन फेफड़ों की बीमारी दूर करता है। चेहरे को लाली प्रदान करता है।
- पेट की सभी बीमारियां इससे दूर होती हैं और बांहों तथा हाथों को बलवान बनाता है।
- इस आसन से आंखों की नज़र पास की व दूर की ठीक रहती है।
- इस आसन से मधुमेह रोग नहीं होता यदि हो जाए तो दूर हो जाता है।
- यह आसन रक्त संचार को नियमित करता है।
3. सर्वांगासन (Sarvangasana)—इसमें कन्धों पर खड़ा हुआ जाता है।
सर्वांगासन की विधि (Technique of Sarvangasana)-सर्वांगासन में शरीर की स्थिति अर्द्ध हल आसन की भान्ति होती है। इस आसन के लिए शरीर को सीधा करके पीठ के बल ज़मीन पर लेट जाएं। हाथों को जंघाओं के बराबर रखें। दोनों पांवों को एक बार उठा कर हथेलियों द्वारा पीठ को सहारा देकर कुहनियों को ज़मीन पर टिकाएँ। सारे
सर्वांगासन
शरीर को सीधा रखें। शरीर का भार कन्धों और गर्दन पर रहे। ठोडी कण्ठकूप से लगी रहे। कुछ समय इस स्थिति में रहने के पश्चात् धीरे-धीरे पहली स्थिति में आएं। आरम्भ में आसन का समय बढ़ा कर 5 से 7 मिनट तक किया जा सकता है। जो व्यक्ति किसी कारण शीर्षासन नहीं कर सकते उन्हें सर्वांगासन करना चाहिए।
लाभ (Advantages)—
- इस आसन से कब्ज दूर होती है, भूख खूब लगती है।
- बाहर को बढ़ा हुआ पेट अन्दर धंसता है।
- शरीर के सभी अंगों में चुस्ती आती है।
- पेट की गैस नष्ट होती है।
- रक्त का संचार तेज़ और शुद्ध होता है।
- बवासीर के रोग से छुटकारा मिलता है।
4. मत्स्यासन (Matsyasana)-इसमें पद्मासन में बैठकर Supine लेते हुए और पीछे की ओर arch बनाते हैं।
विधि (Technique)—पद्मासन लगा कर सिर को इतना पीछे ले जाओ जिससे सिर की चोटी का भाग ज़मीन पर लग जाए और पीठ का भाग ज़मीन से ऊपर उठा हो। दोनों हाथों से दोनों पैरों के अंगूठे पकड़ें।

मत्स्यासन
लाभ (Advantages)—
- वह आसन चेहरे को आकर्षक बनाता है। चर्म रोग को दूर करता है।
- यह आसन टांसिल, मधुमेह, घुटनों तथा कमर दर्द के लिए लाभदायक है। शुद्ध रक्त का निर्माण तथा संचार करता है।
- इस आसन द्वारा मेरूदण्ड में लचक आती है, कब्ज दूर होती है, भूख बढ़ती है, पेट की गैस को नष्ट करके भोजन पचाता है।
- यह आसन फेफड़ों के लिए लाभदायक है, श्वास सम्बन्धी रोग जैसे खांसी, दमा, श्वास नली की बीमारी आदि दूर करता है। नेत्र दोषों को दूर करता है।
- यह आसन टांगों और भुजाओं की शक्ति को बढ़ाता है और मानसिक दुर्बलता को दूर करता है।
![]()
प्रश्न
हलासन और शवासन की विधि और लाभ बताएं।
उत्तर-
हलासन (Halasana)—इसमें Supine लेते हुए, टांगें उठा कर और सिर से परे रखी जाती हैं।

हलासन
विधि (Technique)-दोनों टांगों को ऊपर उठाएं, सिर को पीछे रखें और दोनों पांवों को सिर के पीछे ज़मीन पर रखें। पैरों के अंगूठे जमीन को छू लें। यह स्थिति जब तक हो सके रखें। इसके पश्चात् अपनी टांगें पहले वाले स्थान पर लाएं जहां से आरम्भ किया था।
लाभ (Advantages)—
- हल आसन औरतों और मर्दो के लिए हर आयु में लाभदायक है।
- यह आसन रक्त के दबाव अधिक और कम के लिए भी फायदेमंद है। जिस व्यक्ति को दिल की बीमारी हो उसके लिए भी लाभदायक है।
- रक्त का दौरा नियमित हो जाता है।
- इस आसन को करने से व्यक्ति की वसा कम हो जाती है और कमर व पेट पतले हो जाते हैं।
- रीढ़ की हड्डी लचकदार हो जाती है।
शवासन (Shavasana)-चित्त लेट कर मीटर को ढीला छोड़ दें।
शवासन की विधि (Technique of Shavasana)-शवासन में पीठ के बल सीधा लेट कर शरीर को पूरी तरह ढीला छोड़ा जाता है। शवासन करने के लिए जमीन पर पीठ के बल लेट जाओ और शरीर के अंगों को ढीला छोड़ दें। धीरे-धीरे लम्बे सांस लो। बिल्कुल चित्त लेट कर सारे शरीर के अंगों को ढीला छोड़ दो। दोनों पांवों के बीच एक डेढ़ फुट की दूरी होनी चाहिए। हाथों की हथेलियों को आकाश की ओर करके शरीर से दूर रखो। आंखें बन्द कर अन्तर्ध्यान हो कर सोचो कि शरीर ढीला हो रहा है। अनुभव करो कि शरीर विश्राम की स्थिति में है। यह आसन 3 से 5 मिनट तक करना चाहिए। इस आसन का अभ्यास प्रत्येक आसन के शुरू या अन्त में करना ज़रूरी है।

शवासन
महत्त्व (Importance)—
- शवासन से उच्च रक्त चाप और मानसिक तनाव से छुटकारा मिलता है।
- यह दिल और दिमाग को ताज़ा करता है।
- इस आसन द्वारा शरीर की थकावट दूर होती है।
योग मुद्रा (Yog Mudra)—इसमें व्यक्ति पद्मासन में बैठता है, धड़ को झुकाता है और भूमि पर सिर को विश्राम देता है।
मयूरासन (Mayurasana)-इसमें शरीर को क्षैतिज रूप में कुहनियों पर सन्तुलित किया जाता है। हथेलियां भूमि पर टिकाई होती हैं।
उड्डियान (Uddiyan)-पांवों को अलग-अलग करके खड़ा होकर धड़ को आगे की ओर झुकाएं। हाथों को जांघों पर रखें। सांस बाहर निकालें और पसलियों के नीचे अन्दर को सांस खींचने की नकल करें।
प्राणायाम : अनुलोम विलोम (Pranayam : Anulom Vilom)-बैठकर निश्चित अवधि के लिए बारी-बारी सांस को अन्दर खींचें, ठोडी की सहायता से सांस रोकें और सांस बाहर निकालें।
लाभ (Advantages—प्राणायाम आसन द्वारा रक्त, नाड़ियों और मन की शुद्धि होती है।
सूर्य नमस्कार (Surya Namaskar)—सूर्य नमस्कार के 16 अंग हैं परन्तु 16 अंगों वाला सूर्य सम्पूर्ण सृष्टि के लय होने के समय प्रकट होता है। साधारणतया इसके 12 अंगों का ही अभ्यास किया जाता है।
लाभ (Advantages)—यह श्रेष्ठ यौगिक व्यायाम है। इससे व्यक्ति को आसन, मुद्रा और प्राणायाम के लाभ प्राप्त होते हैं। अभ्यासी का शरीर सूर्य के समान चमकने लगता है। चर्म सम्बन्धी रोगों से बचाव होता है। कोष्ठ बद्धता दूर होती है। मेरूदण्ड और कमर लचकीली होती है। गर्भवती स्त्रियों और हर्निया के रोगियों को इसका अभ्यास नहीं करना चाहिए।
![]()
प्रश्न
वज्रासन, शीर्षासन, चक्रासन, और गरुड़ासन की विधि एवं लाभ लिखें।
उत्तर-
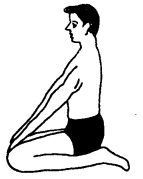
वज्रासन (Vajur Asana)-पैरों को पीछे की ओर मोड़ कर बैठना और हाथों को घुटनों पर रखना इसकी स्थिति है।
विधि (Technique)—
- घुटने मोड़ कर पैरों को पीछे की ओर करके पैरों के तलुओं के भार बैठो।
- नीचे पैर इस प्रकार हों कि पैर के अंगूठे एक दूसरे से मिले हों।
- दोनों घुटने भी मिले हों और कमर तथा पीठ दोनों एकदम सीधे रहें।
- दोनों हाथों को तान कर घुटनों के पास रखो।
- सांसें लम्बी-लम्बी और साधारण हों।
- यह आसन प्रतिदिन 3 मिनट से लेकर 20 मिनट तक करना चाहिए।
लाभ (Advantages)—
वज्रासन
- शरीर में स्फूर्ति आती है।
- शरीर का मोटापा दूर हो जाता है।
- शरीर स्वस्थ रहता है।
- मांसपेशियां मज़बूत होती हैं।
- इससे स्वप्न दोष दूर हो जाता है।
- पैरों का दर्द दूर हो जाता है।
- मानसिक शांति प्राप्त होती है।
- मनुष्य निश्चिंत हो जाता है।
- इससे मधुमेह की बीमारी में लाभ पहुंचता है।
- पाचन क्रिया ठीक रहती है।
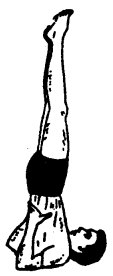
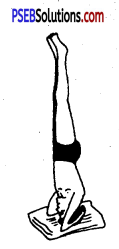
शीर्षासन (Shirsh Asana)-इस आसन में सिर नीचे और पैर ऊपर की ओर होते
विधि (Technique)—
- एक दरी या कम्बल बिछा कर घुटनों के भार बैठो।
- दोनों हाथों की अंगुलियां कस कर बांध लो। दोनों हाथों को कोणदार बना कर कम्बल या दरी पर रखो।
- सिर का सामने वाला भाग हाथों में इस प्रकार जमीन पर रखो कि दोनों अंगूठे सिर के पिछले हिस्से को दबाएं।
- टांगों को धीरे-धीरे अन्दर की ओर मोड़ते हुए शरीर को सिर और दोनों हाथों के सहारे आसमान की ओर उठाओ।
- पैरों को धीरे-धीरे ऊपर उठाओ। पहले एक यंग को सीधा करो, फिर दूसरी को।
- शरीर को बिल्कुल सीधा रखो।
- शरीर का सारा भार बांहों और सिर पर बराबर पड़े।
- दीवार या साथी का सहारा लो।
लाभ (Advantages)—
शीर्षासन
- यह आसन भूख बढ़ाता है।
- इससे स्मरण-शक्ति बढ़ती है।
- मोटापा दूर हो जाता है।
- जिगर ठीक प्रकार से कार्य करता है।
- पेशाब की बीमारियां दूर हो जाती हैं।
- बवासीर आदि बीमारियां दूर हो जाती हैं।
- इस आसन का प्रतिदिन अभ्यास करने से कई मानसिक बीमारियां दूर हो जाती हैं।
सावधानियां (Precautions)-
- जब आंखों में लाली आ जाए तो बन्द कर दो।
- सिर चकराने लगे तो आसन बन्द कर दें।
- कानों में सां-सां की ध्वनि सुनाई दे तो शीर्षासन बन्द कर दें।
- नाक बन्द हो जाए तो यह आसन बन्द कर दें।
- यदि शरीर भार सहन न कर सके तो आसन बन्द कर दें।
- पैरों व बांहों में कम्पन होने लगे तो आसन बन्द कर दो।
- यदि दिल घबराने लगे तो भी आसन बन्द कर दो।
- शीर्षासन सदैव एकान्त स्थान पर करना चाहिए।
- आवश्यकता होने पर दीवार का सहारा लेना चाहिए।
- यह आसन केवल एक मिनट से पांच मिनट तक करो। इससे अधिक शरीर के लिए हानिकारक है।
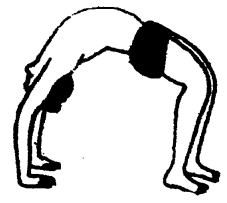
चक्रासन (Chakar Asana) की स्थिति-इस आसन में शरीर को गोल चक्र जैसा बनाना पड़ता है।
चक्रासन
विधि (Technique)—
- पीठ के भार लेट कर, घुटनों को मोड़ कर, पैरों के तलवों को ज़मीन से लगाओ। दोनों पैरों के बीच में एक से डेढ़ फुट का अन्तर रखो।
- हाथों को पीछे की ओर ज़मीन पर रखो। तलवों और अंगुलियों को दृढ़ता के साथ ज़मीन से लगाए रखो।
- अब हाथ-पैरों के सहारे पूरे शरीर को चक्रासन या चक्र की शक्ल में ले जाओ।
- सारे शरीर की स्थिति गोलाकार होनी चाहिए।
- आंखें बन्द रखो ताकि श्वास की गति तेज़ हो सके।
लाभ (Advantages)—
- शरीर की सारी कमजोरियां दूर हो जाती हैं।
- शरीर के सारे अंगों को लचीला बनाता है।
- हर्निया तथा गुर्दो के रोग दूर करने में लाभदायक होता है।
- पाचन शक्ति को बढ़ाता है।
- पेट की वायु विकार आदि बीमारियां दूर हो जाती हैं।
- रीढ़ की हड्डी मज़बूत हो जाती है।
- जांघ तथा बाहें शक्तिशाली बनती हैं।
- गुर्दे की बीमारियां घट जाती हैं।
- कमर दर्द दूर हो जाता है।
- शरीर हल्कापन अनुभव करता है।
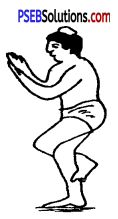
गरुड़ आसन (Garur Asana) की स्थिति- गरुड़ आसन में शरीर की स्थिति गरुड़ पक्षी की भांति पैरों पर सीधे खड़ा होना होता है।
विधि (Technique)—
गरुड़ासन
- सीधे खड़े होकर बायें पैर को उठा कर दाहिनी टांग में बेल की तरह लपेट लो।
- बाईं जांघ दाईं जांघ पर आ जायेगी तथा बाईं जांघ पिंडली को ढांप देगी।
- शरीर का सारा भार एक ही टांग पर कर दो।
- बाएं बाजू को दायें बाजू से दोनों हथेलियों को नमस्कार की स्थिति में ले जाओ।
- इसके बाद बाईं टांग को थोड़ा सा झुका कर शरीर को बैठने की स्थिति में ले जाओ। इस प्रकार शरीर की नसें खिंच जाती हैं। अब शरीर को सीधा करो और सावधान की स्थिति में हो जाओ।
- अब हाथों और पैरों को बदल कर पहली वाली स्थिति में पुनः दोहराओ।
लाभ (Advantages)—
- शरीर के सभी अंगों को शक्तिाली बनाता है।
- शरीर स्वस्थ हो जाता है।
- यह बांहों को ताकतवर बनाता है।
- यह हर्निया रोग से मनुष्य को बचाता है।
- टांगें शक्तिशाली हो जाती हैं।
- शरीर हल्कापन अनुभव करता है।
- रक्त संचार तेज़ हो जाता है।
- गरुड़ आसन करने से मनुष्य बहुत-सी बीमारियों से बच जाता है।
![]()
प्रश्न
प्राणायाम क्या है ? प्राणायाम के भेद और करने की विधियां लिखें।
उत्तर-
प्राणायाम
(Pranayama)
प्राणायाम दो शब्दों के मेल से बना है “प्राण” का अर्थ है ‘जीवन’ और ‘याम’ का अर्थ है, ‘नियन्त्रण’ जिससे अभिप्राय है जीवन पर नियन्त्रण अथवा सांस पर नियन्त्रण।
प्राणायाम वह क्रिया है जिससे जीवन की शक्ति को बढ़ाया जा सकता है और इस पर नियन्त्रण किया जा सकता है।
मनु-महाराज ने कहा है, “प्राणायाम से मनुष्य के सभी दोष समाप्त हो जाते हैं और कमियां पूरी हो जाती हैं।”
प्राणायाम के आधार
(Basis of Pranayama)
सांस को बाहर की ओर निकालना तथा फिर अन्दर की ओर करना और अन्दर ही कुछ समय रोक कर फिर कुछ समय के बाद बाहर निकालने की तीनों क्रियाएं ही प्राणायाम का आधार हैं।
रेचक-सांस बाहर को छोड़ने की क्रिया को ‘रेचक’ कहते हैं।
पूरक-जब सांस अन्दर खींचते हैं तो इसे पूरक कहते हैं।
कुम्भक-सांस को अन्दर खींचने के बाद उसे वहां ही रोकने की क्रिया को कुम्भक कहते हैं।
प्राण के नाम
(Name of Prana)
व्यक्ति के सारे शरीर में प्राण समाया हुआ है। इसके पांच नाम हैं—
- प्राण-यह गले से दिल तक है। इसी प्राण की शक्ति से सांस शरीर में नीचे जाता है।
- अप्राण-नाभिका से निचले भाग में प्राण को अप्राण कहते हैं। छोटी और बडी आन्तों में यही प्राण होता है। यह टट्टी, पेशाब और हवा को शरीर में से बाहर निकालने के लिए सहायता करता है।
- समान-दिल और नाभिका तक रहने वाली प्राण क्रिया को समान कहते हैं। यह प्राण पाचन क्रिया और एडरीनल ग्रन्थि की कार्यक्षमता में वृद्धि करता है।
- उदाना- गले से सिर तक रहने वाले प्राण को उदान कहते हैं। आंखों, कानों, नाक, मस्तिष्क इत्यादि अंगों का काम इसी प्राण के कारण होता है।
- ध्यान-यह प्राण शरीर के सभी भागों में रहता है और शरीर का अन्य प्राणों से मेल-जोल रखता है। शरीर के हिलने-जुलने पर इसका नियन्त्रण होता है।
प्राणायाम के भेद
(Kinds of Pranayama)
शास्त्रों में प्राणायाम कई प्रकार के दिये गए हैं, परन्तु प्राय: यह आठ होते हैं—
- सूर्य-भेदी प्राणायाम
- उजयी प्राणायाम
- शीतकारी प्राणायाम
- शीतली प्राणायाम
- भस्त्रिका प्राणायाम
- भ्रमरी प्राणायाम
- मुर्छा प्राणायाम
- कपालभाती प्राणायाम
प्राणायाम करने की विधि
(Technique of doing Pranayama)
प्राणायाम श्वासों पर नियन्त्रण करने के लिए किया जाता है। इस क्रिया से श्वास अन्दर की ओर खींच कर रोक लिया जाता है और कुछ समय रोकने के बाद फिर छोड़ा जाता है। इस प्रकार सांस धीरे-धीरे नियन्त्रण करने के समय को बढ़ाया जा सकता है। अपनी दाईं नासिका को बन्द करके, बाईं से आठ गिनते समय तक सांस खींचो। फिर नौ और दस गिनते हुए सांस रोको। इससे पूरा सांस बाहर निकल जाएगा। फिर दाईं नासिका से गिरते हुए सांस खींचो। नौ-दस तक रोके। फिर दाईं नासिका बन्द करके बाईं से आठ तक गिनते हुए सांस बाहर निकालो तथा नौ-दस तक रोको।