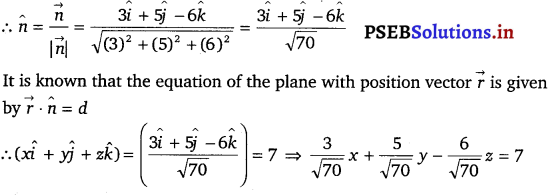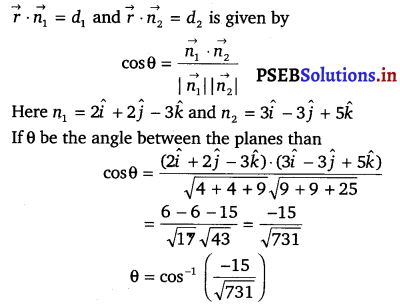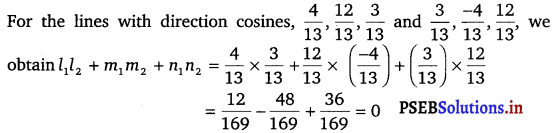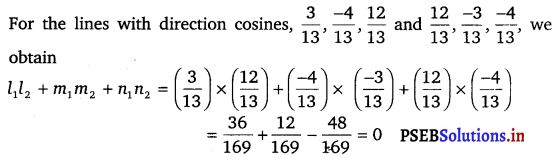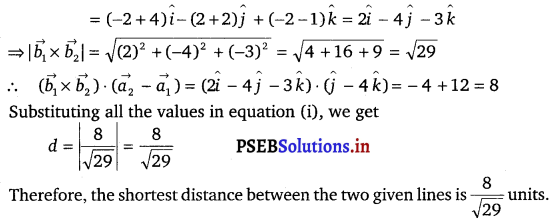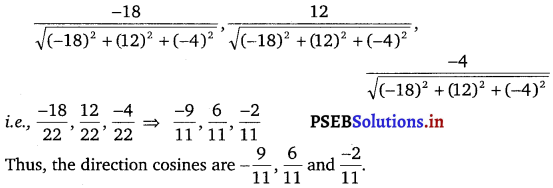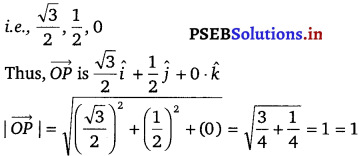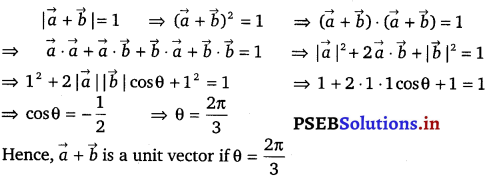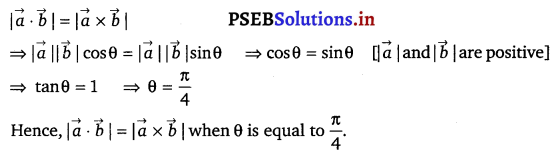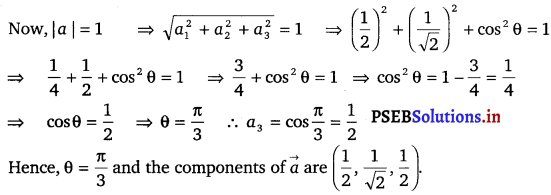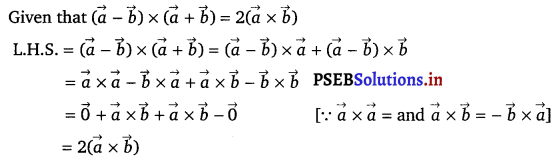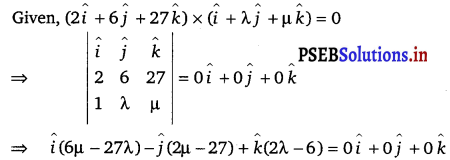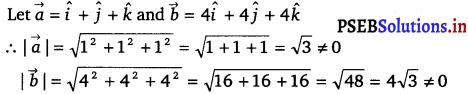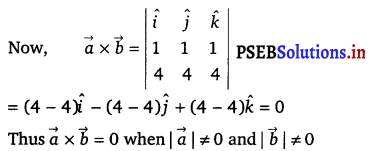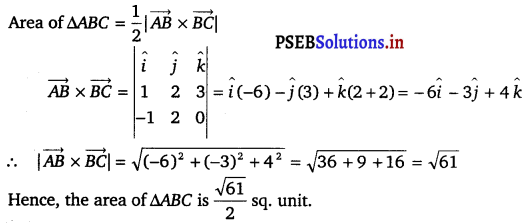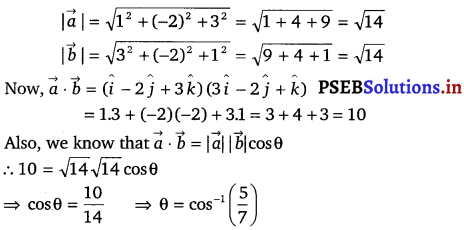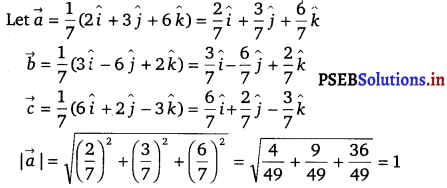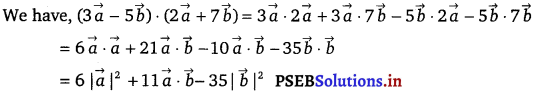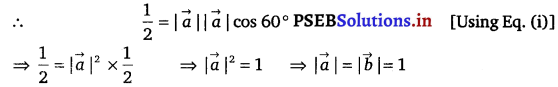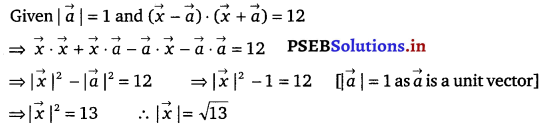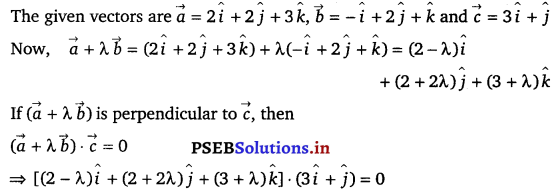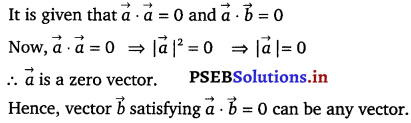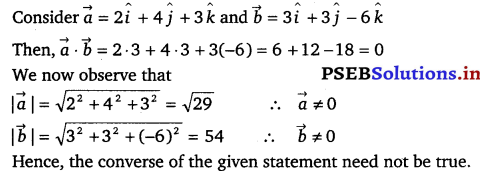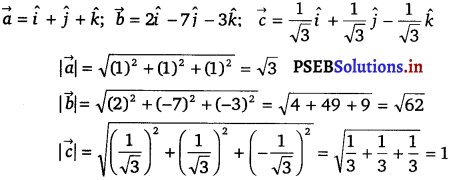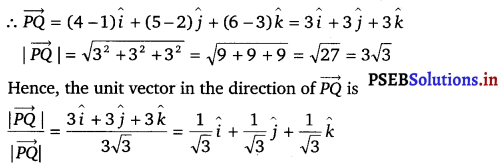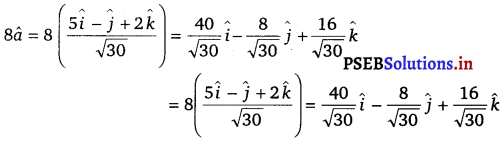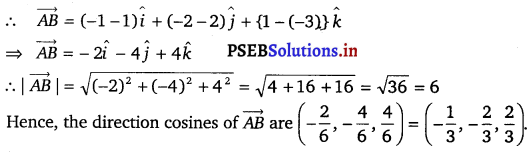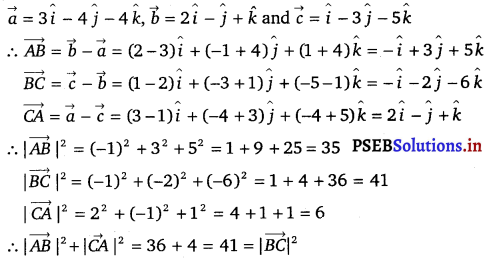Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 11 Three Dimensional Geometry Miscellaneous Exercise Questions and Answers.
PSEB Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry Miscellaneous Exercise
Question 1.
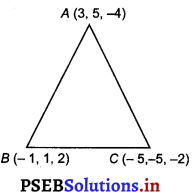
Show that the line joining the origin to the point (2, 1, 1) is perpendicular to the line determined by the points (3, 5,-1), (4, 3,-1).
Solution.
Let OA be the line joining the origin, 0(0, 0, 0), and the point, A(2, 1, 1).
Also, let BC be the line joining the points, B (3, 5, – 1) and C(4, 3, – 1).
The direction ratios of OA are 2, 1 and 1 and of BC are (4 – 3) = 1, (3 – 5) = – 2 and (- 1 + 1) = 0
OA is perpendicular to BC, if a<sub1a2 + b1b2 + c1c2 = 0
∴ a1a2 + b1b2 + c1c2 = 2 × 1 + 1 (- 2) + 1 × 0
= 2 – 2 = 0
Thus, OA is perpendicular to BC.
![]()
Question 2.
If l1, m1 and n1 and l2, m2, n2 are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are m1n2 – m2n1, n1l2 – n2l1, l1m2 – l2m1.
Solution.
Given, lines are respectively parallel to unit vector
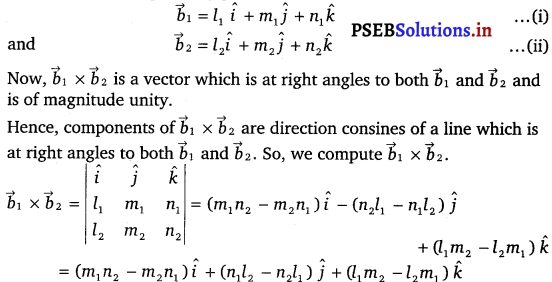
Question 3.
Find the angle between the lines whose direction ratios are a, b, c and b – c, c – a, a – b.
Solution.
The angle θ between the lines with direction cosines, a, b, c and b – c, c – a, a – b is given by
cos θ = \(\frac{a(b-c)+b(c-a)+c(a-b)}{\sqrt{a^{2}+b^{2}+c^{2}}+\sqrt{(b-c)^{2}+(c-a)^{2}+(a-b)^{2}}}\)
⇒ cos θ = 0
⇒ θ = cos-1 0
⇒ θ = 90°
Thus, the angle between the lines is 90°.
![]()
Question 4.
Find the equation of a line parallel to x-axis and passing through the origin.
Solution.
The line parallel to x-axis and passing through the origin is x-axis itself.
Let A be a point on x-axis.
Therefore, the coordinates of A are given by (a, 0,0), where a ∈ R.
Direction ratios of OA are (a – 0), 0, 0 = a, 0,0
The equation of OA is given by,
\(\frac{x-0}{a}=\frac{y-0}{0}=\frac{z-0}{0}\)
⇒ \(\frac{x}{1}=\frac{y}{0}=\frac{z}{0}\) = a
Thus, the equation of line parallel to x-axis and passing through origin is \(\frac{x}{1}=\frac{y}{0}=\frac{z}{0}\) = a
Question 5.
If the coordinates of the points A, B, C,D be (1, 2, 3), (4, 5, 7), (- 4, 3, – 6) and (2, 9, 2) respectively, then find the angle between the lines AB and CD.
Solution.
The coordinates of A, B, C and D are (1, 2, 3),(4, 5, 7), (- 4, 3, – 6)and (2, 9, 2) respectively.
The direction ratios of AB are (4 – 1) = 3, (5 – 2) = 3 and (7 – 3) = 4
The direction ratios of CD are (2 – (- 4)) = 6, (9 – 3) = 6 and (2 – (- 6)) = 8
It can be seen that,
Therefore, AB is parallel to CD.
Thus, the angle between AB and CD is either 0° or 180°.
![]()
Question 6.
If the lines \(\frac{x-1}{-3}=\frac{y-2}{2 k}=\frac{z-3}{2}\) and \(\frac{x-1}{3 k}=\frac{y-1}{1}=\frac{z-6}{-5}\) are perpendicular, find the value of k.
Solution.
The direction of ratios of the lines, \(\frac{x-1}{-3}=\frac{y-2}{2 k}=\frac{z-3}{2}\) and \(\frac{x-1}{3 k}=\frac{y-1}{1}=\frac{z-6}{-5}\) are – 3, 2k, 2 and 3k, 1, – 5 respectively.
Itis known that two lines with direction ratios, a1, b1, c1 and a2, b2, c2 are perpendicular, if
a1a2 + b1b2 + c1c2 = 0
∴ – 3 (3k) + 2k × 1 + 2 (- 5) = 0
⇒ – 9k + 2k – 10 = 0
⇒ 7k = – \(\frac{10}{7}\)
⇒ k = – \(\frac{10}{7}\)
Therefore, for k = – \(\frac{10}{7}\), the given lines are perpendicular to each other.
Question 7.
Find the vector equation of the line passing through (1, 2, 3) and perpendicular to the plane \(\vec{r}\) . (î + 2ĵ – 5k̂) + 9 = 0.
Solution.
Direction ratios of the normal of the plane \(\vec{r}\) . (î + 2ĵ – 5k̂) + 9 = 0 are 1, 2, – 5.
The equation of line passing through \(\overrightarrow{r_{1}}\) and with direction ratios b1, b2, b3 is
\(\vec{r}=\vec{r}_{1}+\lambda\left(b_{1} \hat{i}+b_{2} \hat{j}+b_{3} \hat{k}\right)\)
Hence, the line passing through (1, 2, 3) and having the direction ratios 1, 2, – 5 is \(\vec{r}\) = î + 2ĵ + 3k̂ + λ (î + 2ĵ – 5k̂)
Question 8.
Find the equation of the plane passing through (a, b, c) and parallel to the plane \(\vec{r}\) . (î + ĵ + k̂) = 2.
Solution.
Any plane parallel to the plane, \(\overrightarrow{r_{1}}\) . [(î + ĵ + k̂) = 2, is of the form
\(\vec{r}\) . (î + ĵ + k̂) = λ …………….(i)
The plane passes through the point (a, b, c).
Therefore, the position vector \(\vec{r}\) of this point is \(\vec{r}\) = aî + bĵ + ck̂
Therefore, equation (i) becomes
(aî + bĵ + ck̂) . (î + ĵ + k̂) = λ
⇒ a + b + c = λ
Substituting λ = a + b + c in equation (i), we get
\(\vec{r}\) . (î + ĵ + k̂) = a + b + c …(ii)
This is the vector equation of the required plane.
Substituting \(\vec{r}\) = xî + yĵ + zk̂ in equation (ii), we get
(xî + yĵ + zk̂) . (î + ĵ + k̂) = a + b + c
⇒ x + y + z = a + b + c.
![]()
Question 9.
Find the Shortest distance between lines \(\vec{r}\) = 6î + 2ĵ + 2k̂ + λ (î – 2ĵ + 2k̂) and r = – 4î – k̂ + μ (3î – 2ĵ – 2k̂).
Solution.

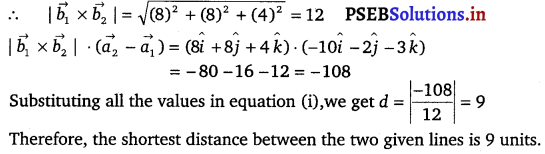
![]()
Question 10.
Find the coordinates of the point where the line through (5, 1, 6) and (3, 4, 1) crosses the YZ-plane.
Solution.
It is known that the equation of the line passing through the points, (x1, y1, z1) and (x2, y2, z2) is
The line passing through the points, (5, 1, 6) and (3, 4, 1), is given by \(\frac{x-5}{3-5}=\frac{y-1}{4-1}=\frac{z-6}{1-6}\)
⇒ \(\frac{x-5}{-2}=\frac{y-1}{3}=\frac{z-6}{-5}\)= k (say)
⇒ x = 5 – 2k, y = 3k + 1, z = 6 – 5k
Any point on the line is of the form (5 – 2k, 3k + 1, 6 – 5k).
The equation of YZ-plane is x = 0
Since the line passes through YZ-plane.
5 – 2k = 0
⇒ k = \(\frac{5}{2}\)
⇒ 3k + 1 = 3 × \(\frac{5}{2}\) + 1 = \(\frac{17}{2}\);
6 – 5k = 6 – 5 × \(\frac{5}{2}\) = – \(\frac{13}{2}\)
Therefore, the required point is (0, \(\frac{17}{2}\), \(-\frac{13}{2}\)).
Question 11.
Find the coordinates of the point where the line through (5, 1, 6) and (3, 4, 1) crosses the ZX-plane.
Solution.
It is known that the equation of the ime passing through the points, (x1, y1, z1) and (x2, y2, z2) is \(\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{z-z_{1}}{z_{2}-z_{1}}\)
The line passing through the points, (5, 1, 6) and (3, 4, 1), is given by \(\frac{x-5}{3-5}=\frac{y-1}{4-1}=\frac{z-6}{1-6}\)
⇒ \(\frac{x-5}{-2}=\frac{y-1}{3}=\frac{z-6}{-5}\) = k(say)
⇒ x = 5 – 2k, y = 3k + 1, z = 6 – 5k
Any point on the line is of the form (5 – 2k, 3k + 1, 6 – 5k).
Since the line passes through ZX-plane.
3k + 1 = 0
⇒ k = – \(\frac{1}{3}\)
⇒ 5 – 2k = 5 – 2(- \(\frac{1}{3}\)) = \(\frac{17}{3}\);
6 – 5k = 6 – 5(- \(\frac{1}{3}\)) = \(\frac{23}{3}\)
Therefore, the required point is (\(\frac{17}{3}\), 0, \(\frac{23}{3}\)).
![]()
Question 12.
Find the coordinates of the point where the line through (3, – 4, – 5) and (2, – 3, 1) crosses the plane 2x + y + z = 7.
Solution.
It is known that the equation of the line through the points, (x1, y1, z1) and (x2, y2, z2)
Since the line passing through the points, (3, – 4,- 5) and (2, – 3, 1), its equation is given by \(\frac{x-3}{2-3}=\frac{y+4}{-3+4}=\frac{z+5}{1+5}\)
⇒ \(\frac{x-3}{-1}=\frac{y+4}{1}=\frac{z+5}{6}\) = k (say)
⇒ x = 3 – k, y = k – 4, z = 6k – 5
Therefore, any point on the line is of the form (3 – k, k – 4, 6 k – 5).
This point lies on the plane, 2x + y + z = 7
∴ 2 (3 – k) + (k – 4) + (6k – 5) = 7
⇒ 5k – 3 = 7
⇒ k = 2
Hence, the coordinates of the required point are (3 – 2, 2 – 4, 6 × 2 – 5), i.e., (1, – 2, 7).
Question 13.
Find the equation of the plane passing through the point (- 1, 3, 2) and perpendicular to each of the planes x + 2y + 3z = 5 and 3x + 3y + z = 0.
Solution.
The equation of the plane passing through the point (- 1, 3, 2) is
a (x + 1) + b (y – 3) + c (z- 2) = 0 ……………(i)
where, a, b, c are the direction ratios of normal to the plane.
It is known that two planes, a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2 = 0, are perpendicular, if
a1a2 + b1b2 + c1c2 = 0
Plane (i) is perpendicular to the plane, x + 2y + 3z = 5
∴ a . 1 + b . 2 + c . 3 = 0
⇒ a + 2b + 3c = 0 …………..(ii)
Also, plane (i) is perpendicular to the plane, 3x + 3y +z = 0
∴ a . 3 + b . 3 + c . 1 = 0
⇒ 3a + 3b + c = 0 …………(iii)
From equations (ii) and (iii), we get
\(\frac{a}{2 \times 1-3 \times 3}=\frac{b}{3 \times 3-1 \times 1}=\frac{c}{1 \times 3-2 \times 3}\)
⇒ \(\frac{a}{-7}=\frac{b}{8}=\frac{c}{-3}\) = k (say)
⇒ a = – 7k, b = 8k, c = – 3k -7
Substituting the value of a, b and c in equation (i), we get
– 7k (x + 1) + 8k (y – 3) – 3k(z – 2) = 0
⇒ (- 7x – 7) + (8y – 24) – 3z + 6 = 0
⇒ – 7x + 8y – 3z – 25 = 0
⇒ 7x – 8y + 3z + 25 = 0
This is the required equation of the plane.
![]()
Question 14.
If the points (1, 1, p) and (- 3, 0, 1) be equidistant from the plane \(\vec{r}\) = (3î + 4ĵ – 12k̂) + 13 = 0, then find the value of p.
Solution.
The position vector through the point (1, 1, p) is \(\overrightarrow{a_{1}}\) = î + ĵ + pk̂
Similarly, the position vector through the point (- 3, 0, 1) is \(\overrightarrow{a_{2}}\) = – 4î + k̂
The equation of the given plane is \(\vec{r}\) . (3î + 4ĵ – 12k̂) + 13 = 0

![]()
Question 15.
Find the equation of the plane passing through the line of intersection of the planes \(\vec{r}\) . (î + ĵ + k̂) = 1 and \(\vec{r}\) . (2î + 3ĵ – k̂) + 4 = 0 and parallel to x-axis.
Solution.
The given planes are \(\vec{r}\) . (î + ĵ + k̂) = 1
⇒ \(\vec{r}\) . (î + ĵ + k̂) – 1 = 0
\(\vec{r}\) . (2î + 3ĵ – k̂) + 4 = 0
The equation of any plane passing through the line of intersection of these planes is
[\(\vec{r}\) . (î + ĵ + k̂) – 1] + λ [\(\vec{r}\) . (2î + 3ĵ – k̂) + 4] = 0
\(\vec{r}\) . [(2λ + 1)î + (3λ + 1)ĵ + (1 – λ) k̂] + (4λ +1) = 0 ………….(i)
Its direction ratios are (2λ + 1), (3λ + 1) and (1 – λ)
The required plane is parallel to x-axis.
Therefore, its normal is perpendicular to x-axis.
The direction ratios of x-axis are 1, 0 and 0.
∴ 1 (2λ + 1) + 0 (3λ + 1) + 0 (1 – λ) = 0
⇒ 2λ + 1 = 0
⇒ λ = – \(\frac{1}{2}\)
Substituting λ = – \(\frac{1}{2}\) in equation (i), we get
⇒ \(\vec{r} \cdot\left[-\frac{1}{2} \hat{j}+\frac{3}{2} \hat{k}\right]\) + (- 3) = 0
⇒ \(\vec{r}\) (ĵ – 3k̂) + 6 = 0
Therefore, its Cartesian equation is y – 3z + 6 = 0.
This is the equation of the required plane.
Question 16.
If O be the origin and the coordinates of P be (1, 2,- 3), then find the equation of the plane passing through P and perpendicular to OP.
Solution.
The coordinates of the points, O and P are (0, 0, 0) and (1, 2, – 3) respectively.
Therefore, the direction ratios of OP are (1 – 0) = 1, (2 – 0) = 2 and (- 3 – 0) = – 3
Here, the direction ratios of normal are 1, 2 and – 3 and the point P is (1, 2, – 3).
Thus, the equation of the required plane is 1 (x – 1) + 2 (y – 2) – 3 (z + 3) = 0
⇒ x – 1 + 2y – 4 – 3z – 9 = 0
⇒ x + 2y – 3z – 14 = 0.
![]()
Question 17.
Find the equation of the plane which contains the line of intersec¬tion of the planes \(\vec{r}\) . (î + 2ĵ + 3k̂) – 4 = 0, \(\vec{r}\) . (2î + ĵ – k̂) + 5 = 0 and which is perpendicular to the plane \(\vec{r}\) . (5î + 3ĵ – 6k̂) + 8 = 0.
Solution.
The equations of the given planes are
\(\vec{r}\) . (î + 2ĵ + 3k̂) – 4 = 0 …………..(i)
\(\vec{r}\) . (2î + ĵ – k̂) + 5 = 0 ………….(ii)
The equation of the plane passing through the line intersection of the plane given in equation (i) and equation (ii) is
[\(\vec{r}\) . (î + 2ĵ + 3k̂) – 4 ] + λ [\(\vec{r}\) . (2î + ĵ – k̂) + 5] = 0
\(\vec{r}\) . [(2λ + 1)î + (λ + 2)ĵ + (3 – λ)k̂] + (5λ – 4) = 0 ……………(iii)
The plane in equation (iii) is perpendicular to the plane,
\(\vec{r}\) . (5î + 3ĵ – 6k̂) + 8 = 0
∴ 5(2λ + 1) + 3 (λ + 2) – 6 (3 – λ) = 0
⇒ 19λ – 7 = 0
⇒ λ = \(\frac{7}{19}\)
Sustituting λ = \(\frac{7}{19}\) in equation (iii), we get
⇒ \(\vec{r} \cdot\left[\frac{13}{19} \hat{i}+\frac{45}{19} \hat{j}+\frac{50}{19} \hat{k}\right] \frac{-41}{19}\) = 0
⇒ \(\vec{r}\) . (33î + 45ĵ + 50k̂) – 41 = 0
This is the vector equation of the required plane.
The Cartesian equation of this plane can be geted by substituting \(\vec{r}\) = xî + yĵ + zk̂ in equation (iii).
(xî + yĵ + zk̂) . (33î + 45ĵ + 50k̂) – 41 = 0
⇒ 33x + 45y + 50z – 41 = 0.
![]()
Question 18.
Find the distance of the point (- 1, – 5, 10) from the point of intersection of the line \(\vec{r}\) = 2î – ĵ + 2k̂ + λ (3î + 4ĵ + 2k̂) and the plane \(\vec{r}\) . (î – ĵ + k̂) = 5.
Solution.
The equation of the given line is
\(\vec{r}\) = 2î – ĵ + 2k̂ + λ (3î + 4ĵ + 2k̂) ………….(i)
The equation of the given plane is
\(\vec{r}\) . (î – ĵ + k̂) = 5 ………….(ii)
Substituting the value of r from equation (i) in equation (ii), we get
[2î – ĵ + 2k̂ + λ (3î + 4ĵ + 2k̂)] . (î – ĵ + k̂) = 5
⇒ (3λ + 2)î + (4λ – 1)ĵ + (2λ + 2)k̂] . (î – ĵ + k̂) = 5
⇒ (3λ + 2) – (4λ – 1) + (2λ + 2) = 5
⇒ λ = 0
Substituting this value in equation (i), we get the equation of the line as
\(\vec{r}\) = 2î – ĵ + 2k̂
And r is position vector of the point (2, – 1, 2)
The distance d between the points (2, – 1, 2) and (- 1, – 5, – 10) is
d = \(\sqrt{(-1-2)^{2}+(-5+1)^{2}+(-10-2)^{2}}\)
= \(\sqrt{9+16+144}=\sqrt{169}\)
= 13 units.
Question 19.
Find the vector equation of the line passing through (1, 2, 3) and parallel to the planes \(\vec{r}\) . (î – ĵ + 2k̂) = 5 and \(\vec{r}\) . (3î + ĵ + k̂) = 6.
Solution.
Let the required line be parallel to vector \(\vec{b}\) given by
\(\vec{b}\) = b1 î + b2 ĵ + b3 k̂
The position vector of the point (1, 2, 3) is \(\vec{a}\) = î + 2 ĵ + 3 k̂
The equation of line passing through (1, 2, 3) and parallel to \(\vec{b}\) is given by
\(\vec{r}=\vec{a}+\lambda \vec{b}\)
⇒ \(\vec{r}\) (î + 2 ĵ + 3 k̂) + λ (b1 î + b2 ĵ + b3 k̂) ……………(i)
The equations of the given planes are
\(\vec{r}\) . (î – ĵ + 2k̂) = 5 …………….(ii)
\(\vec{r}\) . (3î + ĵ + k̂) = 6 …………..(iii)
The line in equation (i) and plane in equation (ii) are parallel. Therefore, the normal to the plane of equation (ii) and the given line are perpendicular.
⇒ (î – ĵ + 2k̂) . λ (b1 î + b2 ĵ + b3 k̂) = 0
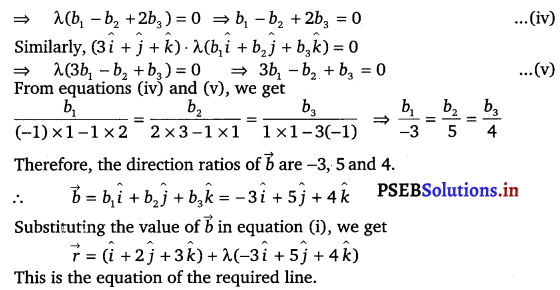
![]()
Question 20.
Find the vector equation of the line passing through the point (1, 2, – 4) and perpendicular to the two lines \(\frac{x-8}{3}=\frac{y+19}{-16}=\frac{z-10}{7}\) and \(\frac{x-15}{3}=\frac{y-29}{8}=\frac{z-5}{-5}\).
Solution.
Let the required line be parallel to the vector \(\vec{b}\) given by,

![]()
Question 21.
Prove that if a plane has the intercepts a, b, c and is at a distance of p units from the origin, then \(\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}=\frac{1}{p^{2}}\).
Solution.
The equation of a plane having Intercepts a, b, c with x, y and z axes respetively is given by \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1 …………….(i)
The distance (p) of the plane from the origin is given by
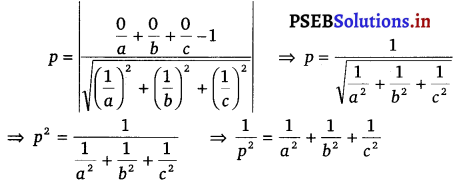
Direction (22 – 23): Choose the correct answer.
Question 22.
Distance between the two planes 2x + 3y + 4z = 4 and 4x + 6y + 8z = 12 is
(A) 2 units
(B) 4 units
(C) 8 units
(D) units
Solution.
The equations of the planes are
2x + 3y + 4z = 4 ……………(i)
4x + 6y + 8z = 112
⇒ 2x + 3y + 4z = 6 ……………(ii)
It can be seen that the given planes are parallel.
k is known that the distance between two parallel planes, ax + by + cz = d1 and ax + by + cz = d2 given by
D = \(\frac{d_{2}-d_{1}}{\sqrt{a^{2}+b^{2}+c^{2}}}\)
D = \(\left|\frac{6-4}{\sqrt{(2)^{2}+(3)^{2}+(4)^{2}}}\right|\)
D = \(\frac{2}{\sqrt{29}}\)
Thus, the distance between the lines is \(\frac{2}{\sqrt{29}}\) units.
Hence, the correct answer is (D).
Question 23.
The planes 2x – y + 4z = 5 and 5x – 25y + 10z = 6are
(A) perpendicular
(B) parallel
(C) intersect y-axis
(D) passes through (o, o, \(\frac{5}{4}\))
Solution.
The equations of the planes are
2x – y + 4z = 5 ………….(i)
5x – 25y + 10z = 6 …………(ii)
It can be seen that
\(\frac{a_{1}}{a_{2}}=\frac{2}{5}\);
\(\frac{b_{1}}{b_{2}}=\frac{-1}{-2.5}=\frac{2}{5}\);
\(\frac{c_{1}}{c_{2}}=\frac{4}{10}=\frac{2}{5}\)⇒ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\).
Therefore, the given planes are parallel.
Hence, the correct answer is (B).