PSEB 12th Class Maths Solutions Chapter 11 Three Dimensional Geometry Ex 11.1

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 11 Three Dimensional Geometry Ex 11.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry Ex 11.1

Question 1.
If a line makes angles 90°, 135°, 45° with x, y and z-axes respectively, find its direction cosines.
Solution.
Let direction cosines of the line be l, m and n.
I = cos 90° = 0, m = cos 135° = – \(\frac{1}{\sqrt{2}}\), n = cos 45° = \(\frac{1}{\sqrt{2}}\)

Therefore, the direction cosines of the line are 0, \(\frac{1}{\sqrt{2}}\) and \(\frac{1}{\sqrt{2}}\).

Question 2.
Find the direction cosines of a line which makes equal angles with the coordinate axes.
Solution.
Let the direction cosines of the line make an angle a with each of the coordinate axes.
∴ l = cos α, m = cos α, n = cos α
We know that l² + m² + n² = 1
⇒ cos² α + cos² α + cos² α = 1
⇒ 3 cos² α = 1
⇒ cos² α = \(\frac{1}{3}\)
⇒ cos α = ± \(\frac{1}{\sqrt{3}}\)
Thus, the direction cosines of the line, which is equally inclined to the coordinate axes, are ± \(\frac{1}{\sqrt{3}}\), ± \(\frac{1}{\sqrt{3}}\) and ± \(\frac{1}{\sqrt{3}}\).

Question 3.
If a line has the direction ratios -18, 12, – 4, then what are its direction cosines?
Solution.
If a line has direction ratios of – 18,12 and – 4, then its direction cosines are

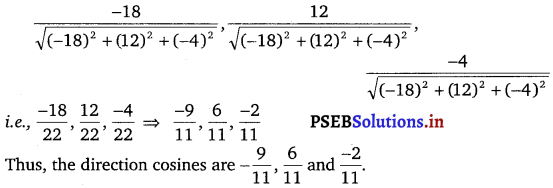
Question 4.
Show that the points (2, 3, 4), (- 1, – 2, 1), (5, 8, 7) are collinear.
Solution.
Let the given points are A (2, 3, 4), B (- 1, – 2, 1), C(5, 8, 7)
Direction ratios of AB are x₂ – x₁; y₂ – y₁, z₂ – z₁
i.e., (- 1 – 2), (- 2 – 3), (1 – 4) or – 3, – 5, – 3
Direction ratios of BC are
5 – (-1), 8 – (- 2), (7 – 1) or 6, 10, 6
which are – 2 times the direction ratios of AB.
∴ AB and BC have the same direction ratios.
∴ AB || BC, but B is a common point of AB and BC.
Hence A,B,C are collinear.

Question 5.
Find the direction cosines of the sides of the triangle whose vertices are (3, 5, – 4), (- 1, 1, 2) and (- 5, – 5,- 2).
Solution.

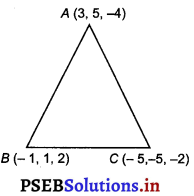
The vertices of ∆ABC are A(3, 5, – 4), B(- 2, 1, 2) and C(- 5, – 5, -2).
The direction ratios of side AB are (- 1, – 3), (1, – 5) and (2 – (- 4)) i.e„ – 4, – 4 and 6.
Then, \(\sqrt{(-4)^{2}+(-4)^{2}+(6)^{2}}\)
= \(\sqrt{16+16+36}\)
= \(\sqrt{68}=2 \sqrt{17}\)