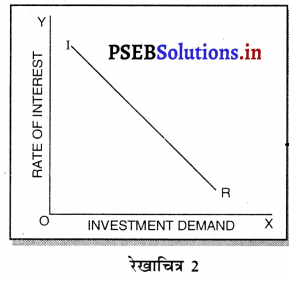
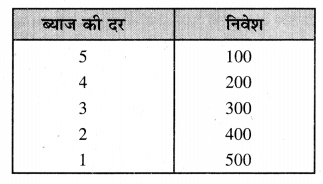
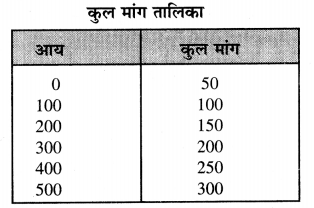
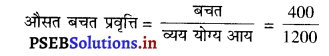Punjab State Board PSEB 12th Class History Book Solutions Chapter 12 ਅਬਦੁਸ ਸਮਦ ਖਾਂ, ਜ਼ਕਰੀਆ ਖਾਂ ਅਤੇ ਮੀਰ ਮੰਨੂੰ – ਉਨ੍ਹਾਂ ਦੇ ਸਿੱਖਾਂ ਨਾਲ ਸੰਬੰਧ Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 History Chapter 12 ਅਬਦੁਸ ਸਮਦ ਖਾਂ, ਜ਼ਕਰੀਆ ਖਾਂ ਅਤੇ ਮੀਰ ਮੰਨੂੰ – ਉਨ੍ਹਾਂ ਦੇ ਸਿੱਖਾਂ ਨਾਲ ਸੰਬੰਧ
Long Answer Type Questions
ਪ੍ਰਸ਼ਨ 1.
ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ‘ਤੇ ਇੱਕ ਨੋਟ ਲਿਖੋ । (Write a short note on Abdus Samad Khan.)
ਜਾਂ
1713 ਤੋਂ 1726 ਈ. ਦੇ ਦੌਰਾਨ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਅਤੇ ਸਿੱਖਾਂ ਦੇ ਸੰਬੰਧਾਂ ਦੀ ਵਿਆਖਿਆ ਕਰੋ । (Explain Abdus Samad Khan relations with the Sikhs from 1713 to 1726.)
ਉੱਤਰ-
ਪੰਜਾਬ ਵਿੱਚ ਸਿੱਖਾਂ ਦੀ ਵੱਧਦੀ ਹੋਈ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਲਈ ਮੁਗ਼ਲ ਬਾਦਸ਼ਾਹ ਫਰੁਖਸਿਅਰ ਨੇ 1713 ਈ. ਵਿੱਚ ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਨੂੰ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਨਿਯੁਕਤ ਕੀਤਾ । ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ 1715 ਈ. ਵਿੱਚ ਬੰਦਾ ਬਹਾਦਰ ਅਤੇ ਉਸ ਦੇ ਹੋਰ ਸਾਥੀਆਂ ਨੂੰ ਫੜਨ ਵਿੱਚ ਸਫਲ ਹੋਇਆ । ਇਸ ਤੋਂ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੇ ਹੌਸਲੇ ਬੁਲੰਦ ਹੋ ਗਏ ਅਤੇ ਉਸ ਨੇ ਸਿੱਖਾਂ ‘ਤੇ ਅੱਤਿਆਚਾਰਾਂ ਦਾ ਦੌਰ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ । ਰੋਜ਼ਾਨਾ ਸਿੱਖਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਕੇ ਲਾਹੌਰ ਲਿਜਾਇਆ ਜਾਂਦਾ ਜਿੱਥੇ ਉਨ੍ਹਾਂ ਨੂੰ ਕਤਲ ਕਰ ਦਿੱਤਾ ਜਾਂਦਾ । ਉਸ ਦੀ ਇਹ ਦਮਨਕਾਰੀ ਨੀਤੀ ਬੜੀ ਸਫਲ ਰਹੀ ਉਸ ਦੀ ਸਫਲਤਾ ਤੋਂ ਖੁਸ਼ ਹੋ ਕੇ ਮੁਗ਼ਲ ਬਾਦਸ਼ਾਹ ਫ਼ਰੁਖਸਿਅਰ ਨੇ ਉਸ ਨੂੰ ‘ਰਾਜ ਦੀ ਤਲਵਾਰ’ ਦੇ ਖ਼ਿਤਾਬ ਨਾਲ ਸਨਮਾਨਿਤ ਕੀਤਾ । ਉਸ ਦੇ ਅੱਤਿਆਚਾਰ ਤੋਂ ਬਚਣ ਲਈ ਬਹੁਤ ਸਾਰੇ ਸਿੱਖ ਜੰਗਲਾਂ ਅਤੇ ਪਹਾੜਾਂ ਵੱਲ ਦੌੜ ਗਏ ਸਨ ਪਰ ਬਾਅਦ ਵਿੱਚ ਉਨ੍ਹਾਂ ਨੇ ਮੁਗਲਾਂ ‘ਤੇ ਛਾਪੇਮਾਰ ਹਮਲੇ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੇ ਸਨ । ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਸਿੱਖਾਂ ਦੇ ਇਨ੍ਹਾਂ ਹਮਲਿਆਂ ਨੂੰ ਰੋਕਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ । ਸਿੱਟੇ ਵਜੋਂ 1726 ਈ. ਵਿੱਚ ਉਸ ਨੂੰ ਉਸ ਦੇ ਅਹੁਦੇ ਤੋਂ ਹਟਾ ਦਿੱਤਾ ਗਿਆ ।
ਪ੍ਰਸ਼ਨ 2.
ਬੰਦਈ ਖ਼ਾਲਸਾ ਅਤੇ ਤੱਤ ਖ਼ਾਲਸਾ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? ਉਨ੍ਹਾਂ ਵਿਚਾਲੇ ਮਤਭੇਦ ਕਿਵੇਂ ਖ਼ਤਮ ਹੋਏ ? (What do you mean by Bandai Khalsa and Tat Khalsa ? How were their differences resolved ?)
ਜਾਂ
ਤੱਤ ਖ਼ਾਲਸਾ ਅਤੇ ਬੰਦਈ ਖ਼ਾਲਸਾ ਵਿੱਚ ਕੀ ਮਤਭੇਦ ਸਨ ? ਇਨ੍ਹਾਂ ਵਿੱਚ ਸਮਝੌਤਾ ਕਿਸ ਨੇ ਕਰਵਾਇਆ ? (What was the difference between Tat Khalsa and Bandai Khalsa ? Who compromised them ?)
ਜਾਂ
ਬੰਦਈ ਖ਼ਾਲਸਾ ਅਤੇ ਤੱਤ ਖ਼ਾਲਸਾ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? ਚਰਚਾ ਕਰੋ । (What do you mean by Bandai Khalsa and Tat Khalsa ? Explain.)
ਉੱਤਰ-
1. ਤੱਤ ਖ਼ਾਲਸਾ-ਤੱਤ ਖ਼ਾਲਸਾ ਕੱਟੜ ਸਿੱਖਾਂ ਦਾ ਇੱਕ ਫਿਰਕਾ ਸੀ । ਇਹ ਸਭ ਤੋਂ ਵੱਧ ਸ਼ਕਤੀਸ਼ਾਲੀ ਗੁੱਟ ਸੀ । ਤੱਤ ਖ਼ਾਲਸਾ ਦੇ ਮੈਂਬਰ ਗੁਰੂ ਗ੍ਰੰਥ ਸਾਹਿਬ ਵਿੱਚ ਪੂਰਾ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ ਅਤੇ ਉਸ ਦੇ ਨਿਯਮਾਂ ਦੇ ਅਨੁਸਾਰ ਆਪਣਾ ਜੀਵਨ ਗੁਜ਼ਾਰਦੇ ਸਨ । ਉਹ ਗੁਰੂ ਗੋਬਿੰਦ ਸਿੰਘ ਜੀ ਦੁਆਰਾ ਨਿਰਧਾਰਿਤ ਨੀਲੇ ਕੱਪੜੇ ਪਾਉਂਦੇ ਸਨ । ਉਹ ਇੱਕ ਦੂਜੇ ਨੂੰ ਮਿਲਦੇ ਸਮੇਂ ‘ਵਾਹਿਗੁਰੂ ਜੀ ਕਾ ਖ਼ਾਲਸਾ, ਵਾਹਿਗੁਰੂ ਜੀ ਕੀ ਫ਼ਤਿਹ’ ਕਹਿ ਕੇ ਸੰਬੋਧਨ ਕਰਦੇ ਸਨ । ਉਹ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੁਆਰਾ ਸਿੱਖ ਧਰਮ ਵਿੱਚ ਕੀਤੇ ਗਏ ਪਰਿਵਰਤਨਾਂ ਨੂੰ ਸਵੀਕਾਰ ਨਹੀਂ ਕਰਦੇ ਸਨ । ਉਹ ਕਿਸੇ ਵੀ ਤਰ੍ਹਾਂ ਦੇ ਚਮਤਕਾਰ ਦਿਖਾਉਣ ਦੇ ਵਿਰੁੱਧ ਸਨ । ਉਹ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਨੂੰ ਗੁਰੂ ਦੀ ਪਦਵੀ ਦਿੱਤੇ ਜਾਣ ਦੇ ਵਿਰੁੱਧ ਸਨ ।
2. ਬੰਦਈ ਖ਼ਾਲਸਾ – ਬੰਦਈ ਖ਼ਾਲਸਾ ਸਿੱਖਾਂ ਦਾ ਦੂਸਰਾ ਮਹੱਤਵਪੂਰਨ ਫਿਰਕਾ ਸੀ । ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੇ ਸੈਨਿਕ ਕਾਰਨਾਮਿਆਂ ਨੇ ਉਨ੍ਹਾਂ ਦੇ ਦਿਲਾਂ ‘ਤੇ ਜਾਦੂਈ ਪ੍ਰਭਾਵ ਪਾਇਆ ਸੀ । 1716 ਈ. ਵਿਚ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੁਆਰਾ ਦਿੱਤੀ ਗਈ ਅਦੁੱਤੀ ਸ਼ਹੀਦੀ ਨਾਲ ਉਹ ਬਹੁਤ ਪ੍ਰਭਾਵਿਤ ਹੋਏ । ਇਸ ਕਾਰਨ ਬੰਦਈ ਖ਼ਾਲਸਾ ਦੇ ਲੋਕ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਨੂੰ ਗੁਰੂ ਸਮਝ ਕੇ ਉਸ ਦੀ ਪੂਜਾ ਕਰਨ ਲੱਗੇ | ਅਨੇਕਾਂ ਲੋਕਾਂ ਦਾ ਇਹ ਵਿਸ਼ਵਾਸ ਸੀ ਕਿ ਗੁਰੂ ਗੋਬਿੰਦ ਸਿੰਘ ਜੀ ਨੇ ਆਪਣੇ ਜੋਤੀ-ਜੋਤ ਸਮਾਉਣ ਤੋਂ ਪਹਿਲਾਂ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਨੂੰ ਗੁਰਗੱਦੀ ਸੌਂਪ ਦਿੱਤੀ ਸੀ ।ਉਹ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੁਆਰਾ ਦਿੱਤੇ ਗਏ ਦੋ ਨਾਅਰਿਆਂ ‘ਫ਼ਤਿਹ ਧਰਮ’ ਅਤੇ ‘ਫ਼ਤਿਹ ਦਰਸ਼ਨ’ ਵਿਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ । ਉਹ ਬੰਦਾ ਬਹਾਦਰ ਦੁਆਰਾ ਨਿਰਧਾਰਿਤ ਲਾਲ ਰੰਗ ਦੇ ਕੱਪੜੇ ਪਹਿਨਦੇ ਸਨ ।
3. ਸਮਝੌਤਾ – 1721 ਈ. ਵਿੱਚ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਦੇ ਮੁੱਖ ਗ੍ਰੰਥੀ ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੇ ਦੋਹਾਂ ਦਲਾਂ ਵਿਚਾਲੇ ਸਮਝੌਤਾ ਕਰਵਾ ਦਿੱਤਾ । ਇਸ ਸਮਝੌਤੇ ਦੇ ਸਿੱਟੇ ਵਜੋਂ ਬੰਦਈ ਖ਼ਾਲਸਾ ਅਤੇ ਤੱਤ ਖ਼ਾਲਸਾ ਇਕ ਹੋ ਗਏ । ਇਹ ਸਮਝੌਤਾ ਸਿੱਖ ਧਰਮ ਦੇ ਵਿਕਾਸ ਲਈ ਇੱਕ ਮੀਲ ਪੱਥਰ ਸਿੱਧ ਹੋਇਆ ।
![]()
ਪ੍ਰਸ਼ਨ 3.
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਨਾਲ ਨਜਿੱਠਣ ਲਈ ਕਿਸ ਤਰ੍ਹਾਂ ਕੋਸ਼ਿਸ਼ ਕੀਤੀ ? (How did Zakariya Khan try to deal with the Sikhs ?)
ਜਾਂ
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੇ ਅਧੀਨ ਸਿੱਖਾਂ ਉੱਪਰ ਜ਼ੁਲਮ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Discuss in brief the persecution of the Sikhs under Zakariya Khan.)
ਉੱਤਰ-
ਜ਼ਕਰੀਆ ਖ਼ਾਂ 1726 ਈ. ਵਿੱਚ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਬਣਿਆ ਸੀ ।
(i) ਉਸ ਨੇ ਸਿੱਖਾਂ ਦੇ ਪ੍ਰਤੀ ਦਮਨ ਦੀ ਨੀਤੀ ਅਪਣਾਈ । ਉਸ ਨੇ ਆਪਣਾ ਅਹੁਦਾ ਸੰਭਾਲਦੇ ਹੀ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਲਈ 20,000 ਸੈਨਿਕਾਂ ਨੂੰ ਭਰਤੀ ਕੀਤਾ ।
(ii) ਉਸ ਨੇ ਪਿੰਡਾਂ ਦੇ ਮੁਕੱਦਮਾਂ ਅਤੇ ਚੌਧਰੀਆਂ ਨੂੰ ਇਹ ਆਦੇਸ਼ ਦਿੱਤਾ ਕਿ ਉਹ ਆਪਣੇ ਇਲਾਕਿਆਂ ਵਿੱਚ ਸਿੱਖਾਂ ਨੂੰ ਸ਼ਰਨ ਨਾ ਲੈਣ ਦੇਣ । ਉਸ ਨੇ ਇਹ ਐਲਾਨ ਕੀਤਾ ਕਿ ਕਿਸੇ ਸਿੱਖ ਬਾਰੇ ਸੂਹ ਦੇਣ ਵਾਲੇ ਨੂੰ ‘ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਵਾਉਣ ਵਾਲੇ ਨੂੰ ‘ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਕੇ ਸਰਕਾਰ ਦੇ ਹਵਾਲੇ ਕਰਨ ਵਾਲੇ ਨੂੰ ਅਤੇ ਸਿਰ ਵੱਢ ਕੇ ਸਰਕਾਰ ਨੂੰ ਭੇਟ ਕਰਨ ਵਾਲੇ ਨੂੰ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਇਨਾਮਾਂ ਨਾਲ ਸਨਮਾਨਿਤ ਕੀਤਾ ਜਾਵੇਗਾ । ਸਿੱਟੇ ਵਜੋਂ ਸੈਂਕੜੇ ਸਿੱਖਾਂ ਨੂੰ ਰੋਜ਼ਾਨਾ ਲਾਹੌਰ ਦੇ ਦਿੱਲੀ ਗੇਟ ਵਿਖੇ ਸ਼ਹੀਦ ਕੀਤਾ ਜਾਣ ਲੱਗਾ । ਇਸ ਕਾਰਨ ਇਸ ਥਾਂ ਦਾ ਨਾਂ ‘ਸ਼ਹੀਦ ਗੰਜ ਪੈ ਗਿਆ ।
(iii) ਇਸ ਦੇ ਬਾਵਜੂਦ ਜਦੋਂ ਉਹ ਆਪਣੇ ਉਦੇਸ਼ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ ਤਾਂ ਉਸ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਖ਼ੁਸ਼ ਕਰਨ ਦੀ ਯੋਜਨਾ ਬਣਾਈ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਦੇ ਨੇਤਾ ਸਰਦਾਰ ਕਪੂਰ ਸਿੰਘ ਜੀ ਨੂੰ ਨਵਾਬ ਦਾ ਖ਼ਿਤਾਬ ਅਤੇ ਇੱਕ ਵੱਡੀ ਜਾਗੀਰ ਦਿੱਤੀ । ਸਿੱਖਾਂ ਨੇ ਇਸ ਮੌਕੇ ਦਾ ਫਾਇਦਾ ਉਠਾ ਕੇ ਆਪਣੀ ਸ਼ਕਤੀ ਨੂੰ ਮੁੜ ਸੰਗਠਿਤ ਕਰਨਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ ।
(iv) ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਇਸ ਨੂੰ ਸਹਿਨ ਕਰਨ ਲਈ ਤਿਆਰ ਨਹੀਂ ਸੀ । ਇਸ ਲਈ ਉਸ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਮੁੜ ਕੁਚਲਣ ਦਾ ਯਤਨ ਕੀਤਾ । ਉਸ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਦਿੱਤੀ ਹੋਈ ਜਾਗੀਰ ਵਾਪਸ ਲੈ ਲਈ ਅਤੇ ਸਿੱਖਾਂ ਨੂੰ ਫੜ ਕੇ ਕਤਲ ਕਰਨ ਦੇ ਹੁਕਮ ਦਿੱਤੇ । ਸਿੱਟੇ ਵਜੋਂ ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ, ਮਹਿਤਾਬ ਸਿੰਘ ਜੀ, ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਅਤੇ ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਜੀ ਵਰਗੇ ਪ੍ਰਸਿੱਧ ਵਿਅਕਤੀਆਂ ਨੂੰ ਸ਼ਹੀਦ ਕੀਤਾ ਗਿਆ । ਇਸ ਦੇ ਬਾਵਜੂਦ ਜ਼ਕਰੀਆ ਖਾਂ ਆਪਣੇ ਅੰਤ ਤਕ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ ।
ਪ੍ਰਸ਼ਨ 4.
ਤਾਰਾ ਸਿੰਘ ਵਾਂ ਕੌਣ ਸੀ ? ਉਸ ਦੀ ਸ਼ਹੀਦੀ ਦੀ ਸਿੱਖ ਇਤਿਹਾਸ ਵਿੱਚ ਕੀ ਮਹੱਤਤਾ ਹੈ ? (Who was Tara Singh Van ? What is the importance of his martyrdom in Sikh History ?)
ਉੱਤਰ-
ਤਾਰਾ ਸਿੰਘ ਅੰਮ੍ਰਿਤਸਰ ਜ਼ਿਲ੍ਹੇ ਦੇ ਪਿੰਡ ਵਾਂ ਦੇ ਵਸਨੀਕ ਸਨ । ਉਹ ਆਪਣੀ ਸਿੱਖ ਪੰਥ ਦੀ ਸੇਵਾ ਅਤੇ ਬਹਾਦਰੀ ਕਾਰਨ ਸਿੱਖਾਂ ਵਿੱਚ ਬੜਾ ਹਰਮਨ-ਪਿਆਰੇ ਸਨ । ਉਨ੍ਹਾਂ ਨੇ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੀਆਂ ਲੜਾਈਆਂ ਵਿੱਚ ਬੜਾ ਵੱਧ-ਚੜ੍ਹ ਕੇ ਹਿੱਸਾ ਲਿਆ ਸੀ । ਹੁਣ ਉਹ ਆਪਣੇ ਪਿੰਡ ਵਿੱਚ ਖੇਤੀ ਦਾ ਧੰਦਾ ਕਰਨ ਲੱਗ ਪਏ ਸਨ । ਨੌਸ਼ਹਿਰੇ ਦਾ ਚੌਧਰੀ ਸਾਹਿਬ ਰਾਏ ਸਿੱਖਾਂ ਦੇ ਖੇਤਾਂ ਵਿੱਚ ਆਪਣੇ ਘੋੜੇ ਛੱਡ ਦਿੰਦਾ ਜਿਸ ਕਾਰਨ ਉਹ ਫ਼ਸਲਾਂ ਨੂੰ ਬਰਬਾਦ ਕਰ ਦਿੰਦੇ । ਜਦੋਂ ਸਿੱਖ ਇਸ ਗੱਲ ਦਾ ਇਤਰਾਜ਼ ਕਰਦੇ ਤਾਂ ਉਹ ਸਿੱਖਾਂ ਦਾ ਘੋਰ ਅਪਮਾਨ ਕਰਦਾ । ਸਿੱਖ ਇਸ ਅਪਮਾਨ ਨੂੰ ਬਰਦਾਸ਼ਤ ਨਹੀਂ ਕਰ ਸਕਦੇ ਸਨ ।
ਇੱਕ ਦਿਨ ਤਾਰਾ ਸਿੰਘ ਵਾਂ ਨੇ ਸਾਹਿਬ ਰਾਏ ਦੀ ਇੱਕ ਘੋੜੀ ਨੂੰ ਫੜ ਕੇ ਵੇਚ ਦਿੱਤਾ ਅਤੇ ਉਨ੍ਹਾਂ ਪੈਸਿਆਂ ਦਾ ਰਾਸ਼ਨ ਖ਼ਰੀਦ ਕੇ ਲੰਗਰ ਲਈ ਦੇ ਦਿੱਤਾ । ਜਦੋਂ ਸਾਹਿਬ ਰਾਏ ਨੂੰ ਇਸ ਬਾਰੇ ਪਤਾ ਲੱਗਾ ਤਾਂ ਉਸ ਨੇ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਤੋਂ ਜਾ ਮਦਦ ਮੰਗੀ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਆਪਣੇ 2200 ਘੋੜਸਵਾਰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕਾਰਵਾਈ ਕਰਨ ਲਈ ਭੇਜੇ । ਤਾਰਾ ਸਿੰਘ ਵਾਂ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ 22 ਸਾਥੀ ਬੜੀ ਦਲੇਰੀ ਨਾਲ ਮੁਗਲਾਂ ਦਾ ਮੁਕਾਬਲਾ ਕਰਦੇ ਹੋਏ ਸ਼ਹੀਦ ਹੋ ਗਏ । ਇਹ ਘਟਨਾ ਫ਼ਰਵਰੀ, 1726 ਈ. ਦੀ ਹੈ । ਤਾਰਾ ਸਿੰਘ ਵਾਂ ਦੀ ਸ਼ਹੀਦੀ ਨੇ ਸਿੱਖਾਂ ਵਿੱਚ ਇੱਕ ਨਵਾਂ ਜੋਸ਼ ਪੈਦਾ ਕੀਤਾ ।
ਪ੍ਰਸ਼ਨ 5.
ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਕੌਣ ਸਨ ? ਉਨ੍ਹਾਂ ਦੀ ਸ਼ਹੀਦੀ ਦਾ ਸਿੱਖ ਇਤਿਹਾਸ ‘ ਤੇ ਕੀ ਪ੍ਰਭਾਵ ਪਿਆ ? (Who was Bhai Mani Singh Ji ? What was the impact of his martyrdom in Sikh History.)
ਜਾਂ
ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਦੀ ਸ਼ਹੀਦੀ ਦੇ ਕਾਰਨ ਲਿਖੋ । (What were the causes of the martyrdom of Bhai Mani Singh Ji ?)
ਜਾਂ
ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀ ਸ਼ਹੀਦੀ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ? (What do you know about Bhai Mani Singh Ji and his martyrdom ?)
ਜਾਂ
ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ‘ ਤੇ ਇੱਕ ਸੰਖੇਪ ਨੋਟ ਲਿਖੋ । (Write a short note on Bhai Mani Singh Ji.)
ਉੱਤਰ-
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੇ ਕਾਲ ਦੀ ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ ਘਟਨਾ ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਦੀ ਸ਼ਹੀਦੀ ਸੀ । ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਦਰਬਾਰ ਸਾਹਿਬ, ਅੰਮ੍ਰਿਤਸਰ ਵਿੱਚ ਮੁੱਖ ਗ੍ਰੰਥੀ ਸਨ । ਸਿੱਖ ਉਨ੍ਹਾਂ ਦਾ ਬਹੁਤ ਇੱਜ਼ਤ-ਮਾਣ ਕਰਦੇ ਸਨ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਉੱਤੇ ਦਰਬਾਰ ਸਾਹਿਬ ਜਾਣ ‘ਤੇ ਪਾਬੰਦੀ ਲਗਾ ਦਿੱਤੀ ਸੀ । ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੇ 5,000 ਰੁਪਏ ਦੇ ਬਦਲੇ ਦੀਵਾਲੀ ਦੇ ਮੌਕੇ ‘ਤੇ ਸਿੱਖਾਂ ਨੂੰ ਦਰਬਾਰ ਸਾਹਿਬ ਵਿੱਚ ਇਕੱਠੇ ਹੋਣ ਦੀ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਤੋਂ ਇਜਾਜ਼ਤ ਲੈ ਲਈ । ਵੱਡੀ ਗਿਣਤੀ ਵਿੱਚ ਸਿੱਖ ਅੰਮ੍ਰਿਤਸਰ ਇਕੱਠੇ ਹੋਣੇ ਸ਼ੁਰੂ ਹੋ ਗਏ | ਪਰ ਦੀਵਾਲੀ ਤੋਂ ਇੱਕ ਦਿਨ ਪਹਿਲਾਂ ਹੀ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਅੰਮ੍ਰਿਤਸਰ ‘ਤੇ ਹਮਲਾ ਕਰ ਦਿੱਤਾ । ਇਸ ਕਾਰਨ ਸਿੱਖਾਂ ਵਿੱਚ ਭਗਦੜ ਮੱਚ ਗਈ ਤੇ ਦੀਵਾਲੀ ਦਾ ਇਕੱਠ ਨਾ ਹੋ ਸਕਿਆ ।
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਅਤੇ ਉਨ੍ਹਾਂ ਤੋਂ 5,000 ਰੁਪਏ ਦੀ ਮੰਗ ਕੀਤੀ । ਮੇਲਾ ਨਾ ਹੋ ਸਕਣ ਕਾਰਨ ਉਹ ਇੰਨੀ ਵੱਡੀ ਰਕਮ ਨਹੀਂ ਦੇ ਸਕਦੇ ਸਨ । ਇਸ ਬਦਲੇ ਉਨ੍ਹਾਂ ਨੂੰ ਇਸਲਾਮ ਧਰਮ ਸਵੀਕਾਰ ਕਰਨ ਲਈ ਕਿਹਾ ਗਿਆ । ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਦੇ ਇਨਕਾਰ ਕਰਨ ‘ਤੇ 1738 ਈ. ਵਿੱਚ ਉਨ੍ਹਾਂ ਨੂੰ ਲਾਹੌਰ ਵਿਖੇ ਬੜੀ ਬੇਰਹਿਮੀ ਨਾਲ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ਗਿਆ । ਇਸ ਸ਼ਹੀਦੀ ਕਾਰਨ ਸਿੱਖ ਭੜਕ ਉੱਠੇ । ਉਨ੍ਹਾਂ ਨੇ ਹੁਣ ਮੁਗ਼ਲ ਰਾਜ ਨੂੰ ਜੜ੍ਹ ਤੋਂ ਉਖਾੜਨ ਦਾ ਫੈਸਲਾ ਕਰ ਲਿਆ ।
ਪਸ਼ਨ 6.
ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਕੌਣ ਸਨ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀ ਸ਼ਹੀਦੀ ਦੀ ਸਿੱਖ ਇਤਿਹਾਸ ਵਿੱਚ ਕੀ ਮਹੱਤਤਾ ਹੈ ? (Who was Bhai Taru Singh ? What is the significance of his martyrdom in Sikh History ?)
ਜਾਂ
ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ‘ਤੇ ਇੱਕ ਸੰਖੇਪ ਨੋਟ ਲਿਖੋ । (Write a short note on Bhai Taru Singh Ji.) ਉੱਤਰ-ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਮਾਝੇ ਦੇ ਇਲਾਕੇ ਦੇ ਪਿੰਡ ਪੂਹਲਾ ਦੇ ਰਹਿਣ ਵਾਲੇ ਸਨ । ਉਹ ਖੇਤੀਬਾੜੀ ਦਾ ਧੰਦਾ ਕਰਦੇ ਸਨ ਅਤੇ ਆਪਣੀ ਹੋਣ ਵਾਲੀ ਆਮਦਨ ਤੋਂ ਸਿੱਖਾਂ ਦੀ ਸਹਾਇਤਾ ਕਰਦੇ ਸਨ । ਸਰਕਾਰ ਦੀਆਂ ਨਜ਼ਰਾਂ ਵਿੱਚ ਇਹ ਇੱਕ ਘੋਰ ਅਪਰਾਧ ਸੀ । ਜੰਡਿਆਲਾ ਦੇ ਹਰਭਗਤ ਨਾਮੀ ਵਿਅਕਤੀ ਨੇ ਭਾਈ ਸਾਹਿਬ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਵਾ ਦਿੱਤਾ । ਉਨ੍ਹਾਂ ਨੂੰ ਲਾਹੌਰ ਲਿਆਂਦਾ ਗਿਆ । ਇੱਥੇ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਨੂੰ ਇਸਲਾਮ ਧਰਮ ਗ੍ਰਹਿਣ ਕਰਨ ਲਈ ਕਿਹਾ । ਇਸ ਦੇ ਬਦਲੇ ਉਨ੍ਹਾਂ ਨੂੰ ਦੁਨੀਆ ਭਰ ਦੀਆਂ ਖੁਸ਼ੀਆਂ ਦੇਣ ਦਾ ਲਾਲਚ ਦਿੱਤਾ ਗਿਆ । ਭਾਈ ਸਾਹਿਬ ਨੇ ਇਨ੍ਹਾਂ ਦੋਹਾਂ ਗੱਲਾਂ ਤੋਂ ਇਨਕਾਰ ਕਰ ਦਿੱਤਾ । ਇਸ ’ਤੇ ਜ਼ਾਲਮ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਜੱਲਾਦਾਂ ਨੂੰ ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਦੀ ਖੋਪੜੀ ਨੂੰ ਉਤਾਰਨ ਦਾ ਆਦੇਸ਼ ਦਿੱਤਾ ।
ਆਦੇਸ਼ ਦੀ ਪਾਲਣਾ ਕਰਦੇ ਹੋਏ ਜੱਲਾਦਾਂ ਨੇ ਭਾਈ ਸਾਹਿਬ ਦੀ ਖੋਪੜੀ ਨੂੰ ਉਤਾਰਨਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ । ਜਦੋਂ ਭਾਈ ਸਾਹਿਬ ਦੀ ਖੋਪੜੀ ਉਤਾਰੀ ਜਾ ਰਹੀ ਸੀ ਤਾਂ ਉਹ ਜਪੁਜੀ ਸਾਹਿਬ ਦਾ ਪਾਠ ਕਰ ਰਹੇ ਸਨ । ਉਨ੍ਹਾਂ ਦਾ ਸਾਰਾ ਸਰੀਰ ਲਹੂ-ਲੁਹਾਣ ਹੋ ਗਿਆ ਸੀ, ਪਰ ਉਹ ਆਪਣੇ ਸਿਦਕ ਤੋਂ ਨਾ ਡੋਲੇ । ਇਸ ਤੋਂ 22 ਦਿਨਾਂ ਬਾਅਦ 1 ਜੁਲਾਈ, 1745 ਈ. ਨੂੰ ਉਹ ਸ਼ਹੀਦ ਹੋ ਗਏ । ਇਸ ਲਾਸਾਨੀ ਸ਼ਹਾਦਤ ਨੇ ਸਿੱਖਾਂ ਵਿੱਚ ਇੱਕ ਨਵਾਂ ਜੋਸ਼ ਪੈਦਾ ਕੀਤਾ ।
![]()
ਪ੍ਰਸ਼ਨ 7.
ਨਾਦਰ ਸ਼ਾਹ ਕੌਣ ਸੀ ? ਉਸ ਦੇ ਹਮਲੇ ਦਾ ਪੰਜਾਬ ‘ਤੇ ਕੀ ਪ੍ਰਭਾਵ ਪਿਆ ?(Who was Nadir Shah ? What was the effect of his invasion on the Punjab ?)
ਜਾਂ
ਨਾਦਰ ਸ਼ਾਹ ਦੇ ਪੰਜਾਬ ਹਮਲੇ ਅਤੇ ਇਸ ਦੇ ਪ੍ਰਭਾਵਾਂ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Give a brief account of Nadir Shah’s invasion on Punjab and its impact.)
ਉੱਤਰ-
ਨਾਦਰ ਸ਼ਾਹ ਈਰਾਨ ਦਾ ਬਾਦਸ਼ਾਹ ਸੀ ।ਉਸ ਨੇ ਭਾਰਤ ‘ਤੇ 1739 ਈ. ਵਿੱਚ ਹਮਲਾ ਕੀਤਾ । ਇਸ ਹਮਲੇ ਦੌਰਾਨ ਉਸ ਨੇ ਭਾਰਤ ਦੇ ਅਨੇਕਾਂ ਸ਼ਹਿਰਾਂ ਵਿੱਚ ਭਾਰੀ ਲੁੱਟਮਾਰ ਮਚਾਈ । ਇਸ ਕਾਰਨ ਭਾਰਤ ਅਤੇ ਖ਼ਾਸ ਤੌਰ ‘ਤੇ ਪੰਜਾਬ ਵਿੱਚ ਭਾਰੀ ਬਦਅਮਨੀ ਫੈਲ ਗਈ । ਉਹ ਇੰਨਾ ਜ਼ਾਲਮ ਸੀ ਕਿ ਦੁਸ਼ਮਣ ਉਸ ਦਾ ਨਾਂ ਸੁਣਦੇ ਹੀ ਥਰ-ਥਰ ਕੰਬਣ ਲੱਗ ਜਾਂਦੇ ਸਨ । ਵਾਪਸੀ ਸਮੇਂ ਜਦੋਂ ਉਹ ਦਿੱਲੀ ਵਿੱਚ ਲੁੱਟਮਾਰ ਕਰਕੇ ਪੰਜਾਬ ਵਿੱਚੋਂ ਲੰਘ ਰਿਹਾ ਸੀ ਤਾਂ ਸਿੱਖਾਂ ਨੇ ਉਸ ‘ਤੇ ਅਚਾਨਕ ਹਮਲਾ ਕਰਕੇ ਉਸ ਦਾ ਬਹੁਤ ਸਾਰਾ ਖਜ਼ਾਨਾ ਲੁੱਟ ਲਿਆ ਸੀ । ਇਸ ਕਾਰਨ ਨਾਦਰ ਸ਼ਾਹ ਹੈਰਾਨ ਰਹਿ ਗਿਆ ।
ਉਸ ਨੇ ਇਨ੍ਹਾਂ ਸਿੱਖਾਂ ਸੰਬੰਧੀ ਪੰਜਾਬ ਦੇ ਸੂਬੇਦਾਰ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਤੋਂ ਪੁੱਛ-ਗਿੱਛ ਕੀਤੀ । ਉਸ ਨੇ ਜ਼ਕਰੀਆ ਖਾਂ ਨੂੰ ਇਹ ਚੇਤਾਵਨੀ ਦਿੱਤੀ ਕਿ ਜੇਕਰ ਉਸ ਨੇ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਵਧੇਰੇ ਸਖ਼ਤ ਕਦਮ ਨਾ ਚੁੱਕੇ ਤਾਂ ਛੇਤੀ ਹੀ ਸਿੱਖ ਪੰਜਾਬ ’ਤੇ ਆਪਣਾ ਕਬਜ਼ਾ ਕਰ ਲੈਣਗੇ । ਸਿੱਟੇ ਵਜੋਂ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਉੱਤੇ ਵਧੇਰੇ ਅੱਤਿਆਚਾਰ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੇ । ਪਰ ਨਾਦਰ ਸ਼ਾਹ ਦੇ ਹਮਲੇ ਤੋਂ ਬਾਅਦ ਪੰਜਾਬ ਵਿੱਚ ਬਦਅਮਨੀ ਫੈਲ ਗਈ ਸੀ । ਇਸ ਸਥਿਤੀ ਦਾ ਫਾਇਦਾ ਉਠਾ ਕੇ ਸਿੱਖਾਂ ਨੇ ਆਪਣੀ ਸ਼ਕਤੀ ਨੂੰ ਸੰਗਠਿਤ ਕਰਨਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ ਸੀ । ਛੇਤੀ ਹੀ ਪੰਜਾਬ ਵਿੱਚ ਉਨ੍ਹਾਂ ਦਾ ਪ੍ਰਭਾਵ ਵੱਧ ਗਿਆ ।
ਪ੍ਰਸ਼ਨ 8.
ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ‘ਤੇ ਇੱਕ ਨੋਟ ਲਿਖੋ । (Write a note on Buddha Dal and Taruna Dal.)
ਜਾਂ
ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ? (What do you know about Buddha Dal and Taruna Dal ?)
ਜਾਂ
‘ਬੁੱਢਾ ਦਲ’ ਅਤੇ ‘ਤਰੁਣਾ ਦਲ’ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? ਸੰਖੇਪ ਵਿੱਚ ਵਰਣਨ ਕਰੋ । (What do you mean by ‘Buddha Dal’ and ‘Taruna Dal’? Explain briefly.)
ਉੱਤਰ-
1733 ਈ. ਵਿੱਚ ਮੁਗ਼ਲਾਂ ਨਾਲ ਸਮਝੌਤਾ ਹੋ ਜਾਣ ਨਾਲ ਸਿੱਖਾਂ ਨੂੰ ਆਪਣੀ ਸ਼ਕਤੀ ਨੂੰ ਸੰਗਠਿਤ ਕਰਨ ਦਾ ਸੁਨਹਿਰੀ ਮੌਕਾ ਮਿਲਿਆ । ਨਵਾਬ ਕਪੂਰ ਸਿੰਘ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਇਹ ਸੁਨੇਹਾ ਭੇਜਿਆ ਕਿ ਉਹ ਜੰਗਲਾਂ ਅਤੇ ਪਹਾੜਾਂ ਨੂੰ ਛੱਡ ਕੇ ਆਪਣੇ ਘਰਾਂ ਵਿੱਚ ਆ ਜਾਣ । ਇਸ ਤਰ੍ਹਾਂ ਪਿਛਲੇ ਦੋ ਦਹਾਕਿਆਂ ਤੋਂ ਮੁਗ਼ਲਾਂ ਅਤੇ ਸਿੱਖਾਂ ਵਿਚਾਲੇ ਚਲੇ ਆ ਰਹੇ ਸੰਘਰਸ਼ ਦਾ ਅੰਤ ਹੋਇਆ ਤੇ ਸਿੱਖਾਂ ਨੂੰ ਕੁਝ ਸੁੱਖ ਦਾ ਸਾਹ ਮਿਲਿਆ । 1734 ਈ. ਵਿੱਚ ਨਵਾਬ ਕਪੂਰ ਸਿੰਘ ਨੇ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਮਜ਼ਬੂਤ ਕਰਨ ਦੇ ਉਦੇਸ਼ ਨਾਲ ਉਨ੍ਹਾਂ ਨੂੰ ਦੋ ਜੱਥਿਆਂ ਵਿੱਚ ਸੰਗਠਿਤ ਕਰ ਦਿੱਤਾ । ਇਹ ਜੱਥੇ ਸਨ-ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ।
ਬੁੱਢਾ ਦਲ ਵਿੱਚ 40 ਸਾਲਾਂ ਤੋਂ ਵਡੇਰੀ ਉਮਰ ਦੇ ਸਿੱਖਾਂ ਨੂੰ ਸ਼ਾਮਲ ਕੀਤਾ ਗਿਆ ਅਤੇ ਇਸ ਤੋਂ ਘੱਟ ਦੀ ਉਮਰ ਵਾਲੇ ਸਿੱਖਾਂ ਨੂੰ ਤਰੁਣਾ ਦਲ ਵਿੱਚ ਤਰੁਣਾ ਦਲ ਨੂੰ ਅੱਗੇ ਪੰਜ ਜੱਥਿਆਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ ਸੀ । ਹਰੇਕ ਜੱਥੇ ਵਿੱਚ 1300 ਤੋਂ ਲੈ ਕੇ 2000 ਸਿੱਖ ਸਨ । ਹਰੇਕ ਜੱਥੇ ਦਾ ਆਪਣਾ ਇੱਕ ਵੱਖਰਾ ਨੇਤਾ ਅਤੇ ਝੰਡਾ ਹੁੰਦਾ ਸੀ । ਬੁੱਢਾ ਦਲ ਧਾਰਮਿਕ ਸਥਾਨਾਂ ਦੀ ਦੇਖ-ਭਾਲ ਕਰਦਾ ਸੀ ਜਦ ਕਿ ਤਰੁਣਾ ਦਲ ਦੁਸ਼ਮਣਾਂ ਦਾ ਮੁਕਾਬਲਾ ਕਰਦਾ ਸੀ ।
ਪ੍ਰਸ਼ਨ 9.
ਯਾਹੀਆ ਖ਼ਾਂ ਕੌਣ ਸੀ ? ਉਸ ਦੇ ਸ਼ਾਸਨ ਕਾਲ ਸੰਬੰਧੀ ਜਾਣਕਾਰੀ ਦਿਓ । (Who was Yahiya Khan ? Give a brief information of his rule.)
ਉੱਤਰ-
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ ਤੋਂ ਬਾਅਦ ਯਾਹੀਆ ਖ਼ਾਂ 1746 ਈ. ਵਿੱਚ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਬਣਿਆ । ਉਹ 1747 ਈ. ਤਕ ਇਸ ਅਹੁਦੇ ‘ਤੇ ਰਿਹਾ । ਸਿੱਖਾਂ ਉੱਤੇ ਅੱਤਿਆਚਾਰ ਕਰਨ ਵਿੱਚ ਉਹ ਆਪਣੇ ਪਿਤਾ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਤੋਂ ਇੱਕ ਕਦਮ ਅੱਗੇ ਸੀ ।
1. ਸਿੱਖਾਂ ਦੀਆਂ ਕਾਰਵਾਈਆਂ – ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ ਦਾ ਲਾਭ ਉਠਾ ਕੇ ਸਿੱਖਾਂ ਨੇ ਆਪਣੀ ਸ਼ਕਤੀ ਨੂੰ ਸੰਗਠਿਤ ਕਰ ਲਿਆ ਸੀ । ਉਨ੍ਹਾਂ ਨੇ ਪੰਜਾਬ ਦੇ ਕਈ ਪਿੰਡਾਂ ਦੇ ਚੌਧਰੀਆਂ ਅਤੇ ਮੁਕੱਦਮਾਂ ਨੂੰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕਾਰਵਾਈਆਂ ਕਰਨ ਕਰਕੇ ਮੌਤ ਦੇ ਘਾਟ ਉਤਾਰ ਦਿੱਤਾ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਸਿੱਖ ਜੱਥਿਆਂ ਨੇ ਪੰਜਾਬ ਦੇ ਕਈ ਦੇਸ਼ਾਂ ਵਿਚ ਆਪਣੀਆਂ ਲੁੱਟਮਾਰ ਦੀਆਂ ਕਾਰਵਾਈਆਂ ਤੇਜ਼ ਕਰ ਦਿੱਤੀਆਂ ਸਨ ।
2. ਜਸਪਤ ਰਾਏ ਦੀ ਮੌਤ – 1746 ਈ. ਵਿੱਚ ਸਿੱਖਾਂ ਦੇ ਇੱਕ ਜੱਥੇ ਨੇ ਗੋਦਲਾਂਵਾਲਾ ਪਿੰਡ ਤੋਂ ਬਹੁਤ ਸਾਰੀਆਂ ਭੇਡਬੱਕਰੀਆਂ ਨੂੰ ਫੜ ਲਿਆ । ਲੋਕਾਂ ਦੀ ਸ਼ਿਕਾਇਤ ‘ਤੇ ਜਸਪਤ ਰਾਏ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਇਹ ਭੇਡ-ਬੱਕਰੀਆਂ ਵਾਪਸ ਕਰਨ ਦਾ ਆਦੇਸ਼ ਦਿੱਤਾ । ਸਿੱਖਾਂ ਦੇ ਇਨਕਾਰ ਕਰਨ ‘ਤੇ ਉਸ ਨੇ ਸਿੱਖਾਂ ‘ਤੇ ਹਮਲਾ ਕਰ ਦਿੱਤਾ । ਲੜਾਈ ਦੇ ਦੌਰਾਨ ਜਸਪਤ ਰਾਏ ਮਾਰਿਆ ਗਿਆ । ਇਸ ਕਾਰਨ ਮੁਗ਼ਲ ਫ਼ੌਜ ਵਿੱਚ ਭਾਜੜ ਪੈ ਗਈ ।
3. ਲਖਪਤ ਰਾਏ ਦੀ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕਾਰਵਾਈ – ਜਸਪਤ ਰਾਏ ਦੀ ਮੌਤ ਦੀ ਖ਼ਬਰ ਸੁਣ ਕੇ ਉਸ ਦੇ ਭਰਾ ਦੀਵਾਨ ਲਖਪਤ ਰਾਏ ਦਾ ਖੂਨ ਖੌਲ ਉੱਠਿਆ । ਉਸ ਨੇ ਇਹ ਪ੍ਰਣ ਕੀਤਾ ਕਿ ਉਹ ਸਿੱਖਾਂ ਦਾ ਨਾਮੋ-ਨਿਸ਼ਾਨ ਮਿਟਾ ਕੇ ਹੀ ਸੁੱਖ ਦਾ ਸਾਹ ਲਵੇਗਾ। ਉਸ ਨੇ ਸਿੱਖਾਂ ‘ਤੇ ਅਨੇਕਾਂ ਪਾਬੰਦੀਆਂ ਲੱਗਾ ਦਿੱਤੀਆਂ । ਇਨ੍ਹਾਂ ਆਦੇਸ਼ਾਂ ਦੀ ਉਲੰਘਣਾ ਕਰਨ ਵਾਲਿਆਂ ਨੂੰ ਮੌਤ ਦੀ ਸਜ਼ਾ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ ।
4. ਪਹਿਲਾ ਘੱਲੂਘਾਰਾ – 1746 ਈ. ਵਿੱਚ ਯਾਹੀਆ ਖਾਂ ਤੇ ਲਖਪਤ ਰਾਏ ਦੇ ਅਧੀਨ ਮੁਗ਼ਲ ਸੈਨਾ ਨੇ ਲਗਭਗ 15,000 ਸਿੱਖਾਂ ਨੂੰ ਕਾਹਨੂੰਵਾਨ ਵਿਖੇ ਘੇਰ ਲਿਆ । ਇਸ ਹਮਲੇ ਵਿੱਚ 7,000 ਸਿੱਖ ਸ਼ਹੀਦ ਹੋ ਗਏ ਅਤੇ 3,000 ਸਿੱਖਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਗਿਆ । ਇਨ੍ਹਾਂ ਸਿੱਖਾਂ ਨੂੰ ਲਾਹੌਰ ਵਿਖੇ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ਗਿਆ । ਇਸ ਦਰਦਨਾਕ ਘਟਨਾ ਨੂੰ ਇਤਿਹਾਸ ਵਿੱਚ ਪਹਿਲਾ ਜਾਂ ਛੋਟਾ ਘੱਲੂਘਾਰਾ ਦੇ ਨਾਂ ਨਾਲ ਯਾਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 10.
ਪਹਿਲੇ ਜਾਂ ਛੋਟੇ ਘੱਲੂਘਾਰੇ (1746 ਈ.) ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ? [What do you know about the First Holocaust (1746) or Chhota Ghallughara ?]
ਜਾਂ
‘ਛੋਟਾ ਘੱਲੂਘਾਰਾਂ’ ‘ਤੇ ਇੱਕ ਸੰਖੇਪ ਨੋਟ ਲਿਖੋ । (Write a short note on ‘Chhota Ghallughara’.)
ਉੱਤਰ-
ਸਿੱਖਾਂ ਦਾ ਮਲੀਆਮੇਟ ਕਰਨ ਲਈ ਯਾਹੀਆ ਖ਼ਾਂ ਤੇ ਲਖਪਤ ਰਾਏ ਨੇ ਇੱਕ ਭਾਰੀ ਸੈਨਾ ਤਿਆਰ ਕੀਤੀ ।ਇਸ ਸੈਨਾ ਨੇ ਲਗਭਗ 15,000 ਸਿੱਖਾਂ ਨੂੰ ਅਚਾਨਕ ਕਾਹਨੂੰਵਾਨ ਵਿਖੇ ਘੇਰ ਲਿਆ । ਸਿੱਖ ਉੱਥੋਂ ਬਚ ਕੇ ਬਸੌਲੀ ਦੀਆਂ ਪਹਾੜੀਆਂ ਵੱਲ ਚਲੇ ਗਏ । ਮੁਗ਼ਲ ਸੈਨਿਕਾਂ ਨੇ ਉਨ੍ਹਾਂ ਦਾ ਬੜੀ ਤੇਜ਼ੀ ਨਾਲ ਪਿੱਛਾ ਕੀਤਾ । ਇੱਥੇ ਸਿੱਖ ਬੜੀ ਮੁਸ਼ਕਿਲ ਵਿੱਚ ਫਸ ਗਏ । ਇੱਕ ਪਾਸੇ ਉੱਚੀਆਂ ਪਹਾੜੀਆਂ ਸਨ ਅਤੇ ਦੂਜੇ ਪਾਸੇ ਦਰਿਆ ਰਾਵੀ ਵਿੱਚ ਬੜਾ ਹੜ੍ਹ ਆਇਆ ਹੋਇਆ ਸੀ । ਪਿਛਲੇ ਪਾਸੇ ਮੁਗ਼ਲ ਸੈਨਿਕ ਉਨ੍ਹਾਂ ਦਾ ਪਿੱਛਾ ਕਰ ਰਹੇ ਸਨ ਅਤੇ ਅੱਗੇ ਵੀ ਪਹਾੜੀ ਰਾਜੇ ਅਤੇ ਲੋਕ ਉਨ੍ਹਾਂ ਦੇ ਕੱਟੜ ਦੁਸ਼ਮਣ ਸਨ ।
ਸਿੱਖਾਂ ਕੋਲ ਰਸਦ ਤਾਂ ਬਿਲਕੁਲ ਹੀ ਨਹੀਂ ਸੀ । ਚਾਰੇ ਦੀ ਘਾਟ ਕਾਰਨ ਘੋੜਿਆਂ ਦਾ ਵੀ ਭੁੱਖ ਨਾਲ ਬੁਰਾ ਹਾਲ ਸੀ । ਇਸ ਹਮਲੇ ਵਿੱਚ 7,000 ਸਿੱਖ ਸ਼ਹੀਦ ਹੋ ਗਏ ਅਤੇ ਮੁਗ਼ਲਾਂ ਨੇ 3,000 ਸਿੱਖਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ । ਇਨ੍ਹਾਂ ਸਿੱਖਾਂ ਨੂੰ ਲਾਹੌਰ ਵਿਖੇ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ਗਿਆ । ਸਿੱਖਾਂ ਦੇ ਇਤਿਹਾਸ ਵਿੱਚ ਇਹ ਪਹਿਲਾ ਮੌਕਾ ਸੀ ਜਦੋਂ ਸਿੱਖਾਂ ਦਾ ਇੱਕੋ ਵਾਰੀ ਇੰਨਾ ਭਾਰੀ ਜਾਨੀ ਨੁਕਸਾਨ ਹੋਇਆ । ਇਸ ਕਾਰਨ ਇਸ ਘਟਨਾ ਨੂੰ ਇਤਿਹਾਸ ਵਿੱਚ ਪਹਿਲਾ ਜਾਂ ਛੋਟਾ ਘੱਲੂਘਾਰਾ ਦੇ ਨਾਂ ਨਾਲ ਯਾਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਹ ਘੱਲੂਘਾਰਾ ਮਈ, 1746 ਈ. ਨੂੰ ਵਾਪਰਿਆ । ਇਸ ਵਿਨਾਸ਼ਕਾਰੀ ਘੱਲੂਘਾਰੇ ਦੇ ਬਾਵਜੂਦ ਸਿੱਖਾਂ ਦੇ ਹੌਸਲੇ ਬੁਲੰਦ ਰਹੇ ।
ਪ੍ਰਸ਼ਨ 11.
ਮੀਰ ਮੰਨੂੰ ਕੌਣ ਸੀ ? ਉਸ ਨੇ ਆਪਣੇ ਸ਼ਾਸਨ ਕਾਲ ਵਿੱਚ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕੀ ਕਾਰਵਾਈ ਕੀਤੀ ? (Who was Mir Mannu ? What steps did he take against the Sikhs during his rule ?)
ਜਾਂ
ਮੀਰ ਮੰਨੂੰ ਦਾ ਸ਼ਾਸਨ ਕਾਲ ਸਿੱਖ ਸ਼ਕਤੀ ਦੇ ਉਭਾਰ ਵਿੱਚ ਕਿਵੇਂ ਸਹਾਇਕ ਹੋਇਆ ? (How did the rule of Mir Mannu help in the rise of Sikh Power ?)
ਜਾਂ
ਮੀਰ ਮੰਨੂੰ ਦੁਆਰਾ ਸਿੱਖਾਂ ਦੇ ਦਮਨ ਦਾ ਅਧਿਐਨ ਕਰੋ । (Study the persecution of the Sikhs by Mir Mannu.)
ਜਾਂ
ਮੀਰ ਮੰਨੂੰ ਦੇ ਸਿੱਖਾਂ ਨਾਲ ਸੰਬੰਧਾਂ ਦਾ ਸੰਖੇਪ ਹਾਲ ਲਿਖੋ । (Write briefly the relations of Mir Mannu with the Sikhs.)
ਉੱਤਰ-
ਮੀਰ ਮੰਨੂੰ ਨੂੰ ਮੁਈਨ-ਉਲ-ਮੁਲਕ ਦੇ ਨਾਂ ਨਾਲ ਵੀ ਜਾਣਿਆ ਜਾਂਦਾ ਸੀ । ਉਹ 1748 ਈ. ਤੋਂ ਲੈ ਕੇ 1752 ਈ. ਤਕ ਮੁਗ਼ਲ ਬਾਦਸ਼ਾਹ ਵੱਲੋਂ ਅਤੇ 1752 ਈ. ਤੋਂ 1753 ਈ. ਤਕ ਅਹਿਮਦ ਸ਼ਾਹ ਅਬਦਾਲੀ ਵੱਲੋਂ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਰਿਹਾ । ਮੀਰ ਮੰਨੂੰ ਸਿੱਖਾਂ ਦਾ ਬੜਾ ਕੱਟੜ ਦੁਸ਼ਮਣ ਸੀ । ਇਸ ਲਈ ਉਸ ਨੇ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਆਪਣਾ ਧਿਆਨ ਸਿੱਖਾਂ ਵੱਲ ਕੀਤਾ । ਮੀਰ ਮੰਨੂੰ ਨੇ ਸਿੱਖਾਂ ਦੇ ਵਿਨਾਸ਼ ਲਈ ਪੰਜਾਬ ਦੇ ਵੱਖ-ਵੱਖ ਦੇਸ਼ਾਂ ਵਿੱਚ ਆਪਣੇ ਸੈਨਿਕ ਦਸਤੇ ਭੇਜੋ । ਉਸ ਨੇ ਜਲੰਧਰ ਦੇ ਫ਼ੌਜਦਾਰ ਅਦੀਨਾ ਬੇਗ ਨੂੰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਸਖ਼ਤ ਕਾਰਵਾਈ ਕਰਨ ਦਾ ਹੁਕਮ ਦਿੱਤਾ । ਸਿੱਖਾਂ ਨੂੰ ਰੋਜ਼ਾਨਾ ਗਿਫ਼ਤਾਰ ਕੀਤਾ ਜਾਣ ਲੱਗਾ । ਅਦੀਨਾ ਬੇਗ ਅਤੇ ਸਿੱਖਾਂ ਵਿਚਾਲੇ ਹੋਈ ਇੱਕ ਲੜਾਈ ਵਿੱਚ 600 ਸਿੱਖ ਸ਼ਹੀਦ ਹੋ ਗਏ । ਸਿੱਟੇ ਵਜੋਂ ਸਿੱਖਾਂ ਨੇ ਜੰਗਲਾਂ ਵਿੱਚ ਸ਼ਰਨ ਲਈ ।
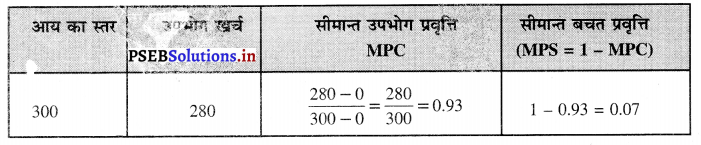
ਛੇਤੀ ਹੀ ਮੀਰ ਮੰਨੂੰ ਨੇ ਸਿੱਖਾਂ ਦਾ ਮਲੀਆਮੇਟ ਕਰਨ ਲਈ ਬੜੇ ਜ਼ੋਰਦਾਰ ਯਤਨ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੇ । ਸਿੱਖਾਂ ਦੇ ਸਿਰਾਂ ਦੇ ਮੁੱਲ ਨਿਯਤ ਕੀਤੇ ਗਏ । ਸਿੱਖਾਂ ਨੂੰ ਸ਼ਰਨ ਦੇਣ ਵਾਲਿਆਂ ਨੂੰ ਸਖ਼ਤ ਸਜ਼ਾਵਾਂ ਦਿੱਤੀਆਂ ਗਈਆਂ । ਮਾਰਚ, 1753 ਈ. ਵਿੱਚ ਜਦੋਂ ਸਿੱਖ ਹੋਲੇ-ਮਹੱਲੇ ਦੇ ਮੌਕੇ ‘ਤੇ ਮਾਖੋਵਾਲ ਵਿਖੇ ਇਕੱਠੇ ਹੋਏ ਸਨ ਤਾਂ ਅਦੀਨਾ ਬੇਗ਼ ਨੇ ਅਚਾਨਕ ਹਮਲਾ ਕਰ ਕੇ ਬਹੁਤ ਸਾਰੇ ਸਿੱਖਾਂ ਨੂੰ ਕਤਲ ਕਰ ਦਿੱਤਾ । ਸਿੱਖ ਇਸਤਰੀਆਂ ਅਤੇ ਬੱਚਿਆਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਕੇ ਲਾਹੌਰ ਲੈ ਆਂਦਾ ਗਿਆ । ਇਨ੍ਹਾਂ ਇਸਤਰੀਆਂ ਅਤੇ ਬੱਚਿਆਂ ਉੱਤੇ ਜੋ ਜ਼ੁਲਮ ਅਤੇ ਜਬਰ ਢਾਹੇ ਗਏ, ਉਨ੍ਹਾਂ ਦਾ ਸ਼ਬਦਾਂ ਵਿਚ ਵਰਣਨ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਦਾ । ਹਰੇਕ ਇਸਤਰੀ ਨੂੰ ਸਵਾ-ਸਵਾ ਮਣ ਰੋਜ਼ਾਨਾ ਅਨਾਜ ਪੀਸਣ ਨੂੰ ਦਿੱਤਾ ਜਾਂਦਾ । ਦੁੱਧ ਚੁੰਘਦੇ ਬੱਚਿਆਂ ਨੂੰ ਉਨ੍ਹਾਂ ਦੀਆਂ ਮਾਂਵਾਂ ਤੋਂ ਖੋਹ ਕੇ ਉਨ੍ਹਾਂ ਦੇ ਸਾਹਮਣੇ ਕਤਲ ਕੀਤਾ ਗਿਆ । ਇਨ੍ਹਾਂ ਘੋਰ ਤਸੀਹਿਆਂ ਦੇ ਬਾਵਜੂਦ ਸਿੱਖਾਂ ਦੀ ਗਿਣਤੀ ਘਟਣ ਦੀ ਬਜਾਏ ਵਧਦੀ ਚਲੀ ਗਈ। ਉਸ ਸਮੇਂ ਇਹ ਅਖਾਣ ਬੜਾ ਪ੍ਰਚੱਲਿਤ ਸੀ,
“ਮੰਨੂੰ ਅਸਾਡੀ ਦਾਤਰੀ, ਅਸੀਂ ਮੰਨੂੰ ਦੇ ਸੋਏ ।
ਜਿਉਂ-ਜਿਉਂ ਮੰਨੂੰ ਵੱਢਦਾ, ਅਸੀਂ ਦੂਣ ਸਵਾਏ ਹੋਏ”
![]()
ਪ੍ਰਸ਼ਨ 12.
ਮੀਰ ਮੰਨੂੰ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਕਿਉਂ ਅਸਫਲ ਰਿਹਾ ? (Why did Mir Mannu fail to crush the Sikh Power ?)
ਜਾਂ
ਮੀਰ ਮੰਨੂੰ ਦੀ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਅਸਫਲਤਾ ਦੇ ਕੀ ਕਾਰਨ ਸਨ ? ਕੋਈ ਛੇ ਕਾਰਨ ਦੱਸੋ । (What were the causes of the failure of Mir Mannu against the Sikhs ? Write any six causes.)
ਜਾਂ
ਮੀਰ ਮੰਨੂੰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕਿਉਂ ਅਸਫਲ ਰਿਹਾ ? (Why Mir Mannu was unsuccessful against the Sikhs ?) ਉੱਤਰ-
ਮੀਰ ਮੰਨੂੰ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਕੁਚਲਣ ਲਈ ਅਣਥੱਕ ਯਤਨ ਕੀਤੇ, ਪਰ ਉਹ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ । ਉਸ ਦੀ ਅਸਫਲਤਾ ਲਈ ਹੇਠ ਲਿਖੇ ਮੁੱਖ ਕਾਰਨ ਜ਼ਿੰਮੇਵਾਰ ਸਨ-
1. ਦਲ ਖ਼ਾਲਸਾ ਦੀ ਜੱਥੇਬੰਦੀ – ਮੀਰ ਮੰਨੂੰ ਦੀ ਅਸਫਲਤਾ ਦਾ ਇੱਕ ਪ੍ਰਮੁੱਖ ਕਾਰਨ ਦਲ ਖ਼ਾਲਸਾ ਦੀ ਜੱਥੇਬੰਦੀ ਸੀ । ਸਿੱਖ ਦਲ ਖ਼ਾਲਸਾ ਦਾ ਦਿਲੋਂ ਸਤਿਕਾਰ ਕਰਦੇ ਸਨ ਅਤੇ ਇਸ ਦੇ ਹੁਕਮ ‘ਤੇ ਹਰ ਕੁਰਬਾਨੀ ਦੇਣ ਲਈ ਤਿਆਰ ਰਹਿੰਦੇ ਸਨ । ਸਿੱਟੇ ਵਜੋਂ ਮੀਰ ਮੰਨੂੰ ਲਈ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣਾ ਔਖਾ ਹੋ ਗਿਆ ।
2. ਸਿੱਖਾਂ ਦੇ ਅਸਾਧਾਰਨ ਗੁਣ – ਸਿੱਖਾਂ ਵਿੱਚ ਆਪਣੇ ਪੰਥ ਲਈ ਦਿੜ ਨਿਸ਼ਚਾ, ਅਥਾਹ ਜੋਸ਼, ਦਲੇਰੀ ਅਤੇ ਕੁਰਬਾਨੀ ਦੀਆਂ ਭਾਵਨਾਵਾਂ ਸਨ ਉਹ ਭਾਰੀ ਔਕੜਾਂ ਦੇ ਬਾਵਜੂਦ ਆਪਣਾ ਹੌਸਲਾ ਕਦੇ ਨਹੀਂ ਸਨ ਛੱਡਦੇ । ਮੀਰ ਮੰਨੂੰ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਅਣਗਿਣਤ ਤਸੀਹੇ ਦਿੱਤੇ ਪਰ ਉਹ ਸਿੱਖਾਂ ਨੂੰ ਵਿਚਲਿਤ ਕਰਨ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ ।
3. ਸਿੱਖਾਂ ਦੀ ਗੁਰੀਲਾ ਯੁੱਧ ਨੀਤੀ – ਸਿੱਖਾਂ ਨੇ ਮੁਗ਼ਲ ਸੈਨਾ ਦੇ ਵਿਰੁੱਧ ਗੁਰੀਲਾ ਯੁੱਧ ਨੀਤੀ ਅਪਣਾਈ । ਇਸ ਨੀਤੀ ਅਨੁਸਾਰ ਸਿੱਖਾਂ ਨੂੰ ਜਦ ਮੌਕਾ ਮਿਲਦਾ ਉਹ ਮੁਗ਼ਲ ਫ਼ੌਜਾਂ ‘ਤੇ ਹਮਲਾ ਕਰਦੇ ਅਤੇ ਲੁੱਟਮਾਰ ਕਰਨ ਮਗਰੋਂ ਮੁੜ ਜੰਗਲਾਂ ਵਿੱਚ ਜਾ ਸ਼ਰਨ ਲੈਂਦੇ । ਇਸ ਤਰ੍ਹਾਂ ਆਹਮਣੇ-ਸਾਹਮਣੇ ਦੀ ਟੱਕਰ ਦੀ ਕਮੀ ਵਿੱਚ ਮੀਰ ਮੰਨੂੰ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ ।
4. ਦੀਵਾਨ ਕੌੜਾ ਮਲ ਦਾ ਸਿੱਖਾਂ ਨਾਲ ਸਹਿਯੋਗ – ਦੀਵਾਨ ਕੌੜਾ ਮਲ ਮੀਰ ਮੰਨੂੰ ਦਾ ਸਲਾਹਕਾਰ ਸੀ । ਸਹਿਜਧਾਰੀ ਸਿੱਖ ਹੋਣ ਕਾਰਨ ਉਹ ਸਿੱਖਾਂ ਨਾਲ ਹਮਦਰਦੀ ਰੱਖਦਾ ਸੀ । ਜਦੋਂ ਵੀ ਕਦੇ ਮੀਰ ਮੰਨੂੰ ਨੇ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕੋਈ ਸਖ਼ਤ ਕਦਮ ਚੁੱਕਣ ਦਾ ਨਿਰਣਾ ਕੀਤਾ ਤਾਂ ਕੌੜਾ ਮਲ ਉਸ ਨੂੰ ਸਿੱਖਾਂ ਨਾਲ ਸਮਝੌਤਾ ਕਰਨ ਲਈ ਮਨਾ ਲੈਂਦਾ ਸੀ । ਇਸ ਤਰ੍ਹਾਂ ਦੀਵਾਨ ਕੌੜਾ ਮਲ ਦਾ ਸਹਿਯੋਗ ਵੀ ਸਿੱਖ ਸ਼ਕਤੀ ਨੂੰ ਬਚਾਈ ਰੱਖਣ ਵਿੱਚ ਬੜਾ ਲਾਹੇਵੰਦ ਸਿੱਧ ਹੋਇਆ ।
5. ਮੀਰ ਮੰਨੂੰ ਦੀਆਂ ਸਮੱਸਿਆਵਾਂ – ਮੀਰ ਮੰਨੂੰ ਆਪਣੇ ਸ਼ਾਸਨ ਕਾਲ ਦੇ ਦੌਰਾਨ ਕਈ ਸਮੱਸਿਆਵਾਂ ਵਿੱਚ ਘਿਰਿਆ ਰਹਿਣ ਦੇ ਕਾਰਨ ਵੀ ਸਿੱਖਾਂ ਨੂੰ ਪੂਰੀ ਤਰ੍ਹਾਂ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ । ਉਸ ਦੀ ਪਹਿਲੀ ਵੱਡੀ ਸਮੱਸਿਆ ਅਹਿਮਦ ਸ਼ਾਹ ਅਬਦਾਲੀ ਦੇ ਹਮਲੇ ਸਨ । ਇਨ੍ਹਾਂ ਹਮਲਿਆਂ ਕਾਰਨ ਉਸ ਨੂੰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਆਪਣੀ ਕਾਰਵਾਈ ਸਥਗਿਤ ਕਰਨੀ ਪੈਂਦੀ ਸੀ । ਦੂਜਾ, ਦਿੱਲੀ ਦਾ ਵਜ਼ੀਰ ਸਫ਼ਦਰਜੰਗ ਵੀ ਉਸ ਨੂੰ ਅਹੁਦੇ ਤੋਂ ਹਟਾਉਣ ਲਈ ਸਾਜ਼ਸ਼ਾਂ ਕਰਦਾ ਰਹਿੰਦਾ ਸੀ । ਸਿੱਟੇ ਵਜੋਂ ਮੀਰ ਮੰਨੂੰ ਇਨ੍ਹਾਂ ਸਮੱਸਿਆਵਾਂ ਵਿੱਚ ਹੀ ਰੁੱਝਿਆ ਰਿਹਾ ।
6. ਮੀਰ ਮੰਨੂੰ ਦੇ ਅੱਤਿਆਚਾਰ – ਮੀਰ ਮੰਨੂੰ ਨੇ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਲਈ ਨਿਰਦੋਸ਼ ਲੋਕਾਂ ‘ਤੇ ਭਾਰੀ ਅੱਤਿਆਚਾਰ ਕੀਤੇ । ਇਸ ਕਾਰਨ ਇਹ ਲੋਕ ਸਿੱਖਾਂ ਨਾਲ ਮਿਲ ਗਏ । ਇਸ ਕਾਰਨ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਬਹੁਤ ਵੱਧ ਗਈ । ਇਸ ਕਾਰਨ ਮੀਰ ਮੰਨੂੰ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫ਼ਲ ਰਿਹਾ ।
ਪ੍ਰਸਤਾਵ ਰੂਪੀ ਪ੍ਰਸ਼ਨ (Essay Type Questions)
ਅਬਦੁਸ ਸਮਦ ਖਾਂ 1713-26 ਈ. (Abdus Samad Khan 1713-26 A.D.).
ਪ੍ਰਸ਼ਨ 1.
ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੀ ਸ਼ਹੀਦੀ ਦੇ ਪਿੱਛੋਂ ਸਿੱਖਾਂ ਦੀ ਹਾਲਤ ਕਿਹੋ ਜਿਹੀ ਸੀ ? ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਨੇ ਉਨ੍ਹਾਂ ਨਾਲ ਕਿਹੋ ਜਿਹਾ ਸਲੂਕ ਕੀਤਾ ? (What was the condition of the Sikhs after the martyrdom of Banda Singh Bahadur ? How did Abdus Samad Khan tackle the Sikhs ?)
ਜਾਂ
ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਨੇ 1713-1726 ਤਕ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਲਈ ਕੀ ਕਦਮ ਚੁੱਕੇ ? (What steps were taken by Abdus Samad Khan to crush the power of Sikhs during 1713-1726 ?)
ਜਾਂ
ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੇ ਸਿੱਖਾਂ ਨਾਲ 1713 ਤੋਂ 1726 ਤਕ ਦੇ ਕਿਵੇਂ ਸੰਬੰਧ ਸਨ ? (What were the relations of Abdus Samad Khan and the Sikhs from 1713 to 1726 ?)
ਉੱਤਰ-
ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਨੂੰ 1713 ਈ. ਵਿੱਚ ਮੁਗ਼ਲ ਬਾਦਸ਼ਾਹ ਫ਼ਰੁੱਖਸੀਅਰ ਦੁਆਰਾ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਨਿਯੁਕਤ ਕੀਤਾ ਗਿਆ ਸੀ । ਉਸ ਨੂੰ ਇਸ ਉਦੇਸ਼ ਨਾਲ ਇਸ ਅਹੁਦੇ ‘ਤੇ ਨਿਯੁਕਤ ਕੀਤਾ ਗਿਆ ਸੀ ਤਾਂ ਕਿ ਉਹ ਪੰਜਾਬ ਵਿੱਚੋਂ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਪੂਰੀ ਤਰ੍ਹਾਂ ਕੁਚਲ ਦੇਵੇ । ਉਸ ਨੇ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਅਤੇ ਉਸ ਨੂੰ ਦਿੱਲੀ ਲਿਆ ਕੇ 1716 ਈ. ਵਿੱਚ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ । ਫ਼ਰੁੱਖਸੀਅਰ ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਦੀ ਇਸ ਕਾਰਵਾਈ ਤੋਂ ਬਹੁਤ ਖੁਸ਼ ਹੋਇਆ । ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੇ ਸਿੱਖਾਂ ਨਾਲ ਸੰਬੰਧਾਂ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਹੇਠ ਲਿਖਿਆ ਹੈ-
1. ਫ਼ਰੁੱਖਸੀਅਰ ਦਾ ਫ਼ਰਮਾਨ (Farrukhsiyar’s Edict) – 1716 ਈ. ਵਿੱਚ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੀ ਸ਼ਹੀਦੀ ਤੋਂ ਬਾਅਦ ਮੁਗ਼ਲ ਬਾਦਸ਼ਾਹ ਫ਼ਰੁੱਖਸੀਅਰ ਨੇ ਇੱਕ ਸ਼ਾਹੀ ਫ਼ਰਮਾਨ ਜਾਰੀ ਕੀਤਾ । ਇਸ ਵਿੱਚ ਮੁਗ਼ਲ ਅਧਿਕਾਰੀਆਂ ‘ ਨੂੰ ਇਹ ਆਦੇਸ਼ ਦਿੱਤਾ ਗਿਆ ਕਿ ਜਿਹੜਾ ਵੀ ਸਿੱਖ ਤੁਹਾਡੇ ਹੱਥ ਲੱਗੇ ਉਸ ਨੂੰ ਕਤਲ ਕਰ ਦਿਓ । ਸਿੱਖਾਂ ਨੂੰ ਸਹਾਇਤਾ ਜਾਂ ਸ਼ਰਨ ਦੇਣ ਵਾਲਿਆਂ ਨੂੰ ਵੀ ਇਹੋ ਸਜ਼ਾ ਦਿੱਤੀ ਜਾਵੇ । ਜੇ ਕੋਈ ਵਿਅਕਤੀ ਸਿੱਖਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਵਾਉਣ ਵਿੱਚ ਸਰਕਾਰ ਦੀ ਮਦਦ ਕਰੇ ਤਾਂ ਉਸ ਨੂੰ ਇਨਾਮ ਦਿੱਤਾ ਜਾਵੇ ।
2. ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੁਆਰਾ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਚੁੱਕੇ ਗਏ ਕਦਮ (Steps taken by Abdus Samad Khan against the Sikhs) – ਸ਼ਾਹੀ ਫ਼ਰਮਾਨ ਦੇ ਜਾਰੀ ਹੋਣ ਤੋਂ ਬਾਅਦ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਨੇ ਸਿੱਖਾਂ ‘ਤੇ ਘੋਰ ਅੱਤਿਆਚਾਰ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੇ । ਸੈਂਕੜੇ ਨਿਰਦੋਸ਼ ਸਿੱਖਾਂ ਨੂੰ ਰੋਜ਼ਾਨਾ ਗਿਫ਼ਤਾਰ ਕਰਕੇ ਲਾਹੌਰ ਲਿਆਂਦਾ ਜਾਂਦਾ । ਜੱਲਾਦ ਇਨ੍ਹਾਂ ਸਿੱਖਾਂ ਨੂੰ ਭਾਰੀ ਤਸੀਹੇ ਦੇਣ ਮਗਰੋਂ ਸ਼ਹੀਦ ਕਰ ਦਿੰਦੇ । ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੀ ਇਸ ਸਖ਼ਤ ਨੀਤੀ ਤੋਂ ਬਚਣ ਲਈ ਬਹੁਤ ਸਾਰੇ ਸਿੱਖਾਂ ਨੇ ਲੱਖੀ ਜੰਗਲ ਅਤੇ ਸ਼ਿਵਾਲਿਕ ਦੀਆਂ ਪਹਾੜੀਆਂ ਵਿੱਚ ਜਾ ਸ਼ਰਨ ਲਈ। ਇਸ ਤਰ੍ਹਾਂ ਆਪਣੇ ਸ਼ਾਸਨ ਕਾਲ ਦੇ ਸ਼ੁਰੂ ਦੇ ਕੁਝ ਵਰਿਆਂ ਤਕ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੀ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਦਮਨ ਨੀਤੀ ਬਹੁਤ ਸਫਲ ਰਹੀ । ਇਸ ਤੋਂ ਖ਼ੁਸ਼ ਹੋ ਕੇ ਫ਼ਰੁੱਖਸੀਅਰ ਨੇ ਉਸ ਨੂੰ ‘ਰਾਜ ਦੀ ਤਲਵਾਰ ਦੀ ਉਪਾਧੀ ਨਾਲ ਸਨਮਾਨਿਤ ਕੀਤਾ ।
3. ਸਿੱਖਾਂ ਵਿੱਚ ਫੁੱਟ (Split among the Sikhs) – ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੀ ਸ਼ਹੀਦੀ ਤੋਂ ਬਾਅਦ ਸਿੱਖ ਆਪਸੀ ਫੁੱਟ ਦਾ ਸ਼ਿਕਾਰ ਹੋ ਗਏ । ਉਹ ਤੱਤ ਖ਼ਾਲਸਾ ਅਤੇ ਬੰਦਈ ਖ਼ਾਲਸਾ ਨਾਂ ਦੀਆਂ ਦੋ ਮੁੱਖ ਸੰਪਰਦਾਵਾਂ ਵਿੱਚ ਵੰਡੇ ਗਏ । ਤੱਤ ਖ਼ਾਲਸਾ ਗੁਰੂ ਗੋਬਿੰਦ ਸਿੰਘ ਜੀ ਦੇ ਧਾਰਮਿਕ ਅਸੂਲਾਂ ਦੇ ਦ੍ਰਿੜ ਸਮਰਥਕ ਸਨ । ਬੰਦਈ ਖ਼ਾਲਸਾ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਨੂੰ ਆਪਣਾ ਨੇਤਾ ਮੰਨਣ ਲੱਗ ਪਏ ਸਨ । ਤੱਤ ਖ਼ਾਲਸਾ ਵਾਲੇ ਆਪਸ ਵਿੱਚ ਮਿਲਣ ਵੇਲੇ ‘ਵਾਹਿਗੁਰੂ ਜੀ ਕਾ ਖ਼ਾਲਸਾ, ਵਾਹਿਗੁਰੂ ਜੀ ਕੀ ਫ਼ਤਹਿ’ ਕਹਿੰਦੇ ਸਨ ਜਦਕਿ ਬੰਦਈ ਖ਼ਾਲਸਾ ‘ਫ਼ਤਹਿ ਧਰਮ’ ਅਤੇ ‘ਫ਼ਤਹਿ’ ਦਰਸ਼ਨ ਸ਼ਬਦਾਂ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਸਨ । ਤੱਤ ਖ਼ਾਲਸਾ ਵਾਲੇ ਨੀਲੇ ਰੰਗ ਦੇ ਕੱਪੜੇ ਪਾਉਂਦੇ ਸਨ ਜਦਕਿ ਬੰਦਈ ਖ਼ਾਲਸਾ ਵਾਲੇ ਲਾਲ ਰੰਗ ਦੇ ਦੋਹਾਂ ਸੰਪਰਦਾਵਾਂ ਵਿਚਾਲੇ ਆਪਸੀ ਮਤਭੇਦ ਦਿਨੋ-ਦਿਨ ਵਧਦੇ ਗਏ । ਸਿੱਟੇ ਵਜੋਂ ਸਿੱਖ ਅਬਦੁਸ ਸਮਦ ਮਾਂ ਦੇ ਅੱਤਿਆਚਾਰਾਂ ਦਾ ਇਕੱਠੇ ਹੋ ਕੇ ਮੁਕਾਬਲਾ ਨਾ ਕਰ ਸਕੇ ।
4. ਹਾਲਾਤਾਂ ਵਿੱਚ ਤਬਦੀਲੀ (Change in Circumstances) – 1720 ਈ. ਤੋਂ ਬਾਅਦ ਹਾਲਾਤਾਂ ਵਿੱਚ ਕੁਝ ਤਬਦੀਲੀ ਆਉਣੀ ਸ਼ੁਰੂ ਹੋ ਗਈ ਅਤੇ ਸਿੱਖਾਂ ਦੀ ਸਥਿਤੀ ਵਿੱਚ ਸੁਧਾਰ ਹੋਣ ਲੱਗਾ | ਸ਼ਾਹੀ ਦਰਬਾਰ ਸਾਜ਼ਸ਼ਾਂ ਦਾ ਅੱਡਾ ਬਣ ਕੇ ਰਹਿ ਗਿਆ ਸੀ । ਸਿੱਟੇ ਵਜੋਂ ਕੇਂਦਰੀ ਸਰਕਾਰ ਸਿੱਖਾਂ ਵੱਲ ਆਪਣਾ ਲੋੜੀਂਦਾ ਧਿਆਨ ਨਾ ਦੇ ਸਕੀ । ਪੰਜਾਬ ਵਿੱਚ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਵੀ ਈਸਾ ਖਾਂ ਅਤੇ ਹੁਸੈਨ ਖਾਂ ਦੇ ਵਿਦਰੋਹਾਂ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਉਲਝ ਗਿਆ । 1721 ਈ. ਵਿੱਚ ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੇ ਵਿਸਾਖੀ ਵਾਲੇ ਦਿਨ ਅੰਮ੍ਰਿਤਸਰ ਵਿਖੇ ਤੱਤ ਖ਼ਾਲਸਾ ਅਤੇ ਬੰਦਈ ਖ਼ਾਲਸਾ ਵਿਚਾਲੇ ਆਪਸੀ ਸਮਝੌਤਾ ਕਰਵਾ ਦਿੱਤਾ । ਸਿੱਟੇ ਵਜੋਂ ਸਿੱਖ ਮੁੜ ਇੱਕ ਹੋ ਗਏ ।
5. ਸਿੱਖਾਂ ਦੀਆਂ ਕਾਰਵਾਈਆਂ (Activities of the Sikhs) – ਸਥਿਤੀ ਵਿੱਚ ਤਬਦੀਲੀ ਆਉਣ ਨਾਲ ਸਿੱਖਾਂ ਵਿੱਚ ਇੱਕ ਨਵਾਂ ਜੋਸ਼ ਪੈਦਾ ਹੋਇਆ । ਉਨ੍ਹਾਂ ਨੇ ਸੌ-ਸੌ ਸਿੱਖਾਂ ਦੇ ਜੱਥੇ ਬਣਾ ਲਏ ਅਤੇ ਮੁਗ਼ਲ ਪ੍ਰਦੇਸ਼ਾਂ ਵਿੱਚ ਲੁੱਟਮਾਰ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੀ । ਉਨ੍ਹਾਂ ਨੇ ਉਨ੍ਹਾਂ ਹਿੰਦੂ ਅਤੇ ਮੁਸਲਮਾਨਾਂ ਨੂੰ ਸਖ਼ਤ ਸਜ਼ਾਵਾਂ ਦੇਣੀਆਂ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੀਆਂ, ਜਿਨ੍ਹਾਂ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀਆਂ ਇਸਤਰੀਆਂ ਅਤੇ ਬੱਚਿਆਂ ਨੂੰ ਮੁਗ਼ਲਾਂ ਦੇ ਹਵਾਲੇ ਕਰ ਦਿੱਤਾ ਸੀ | ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਸਬਕ ਸਿਖਾਉਣ ਲਈ ਅਸਲਮ ਖ਼ਾਂ ਅਧੀਨ ਕੁਝ ਫ਼ੌਜ ਅੰਮ੍ਰਿਤਸਰ ਭੇਜੀ । ਸਿੱਖਾਂ ਨੇ ਇਸ ਫ਼ੌਜ ‘ਤੇ ਅਚਾਨਕ ਹਮਲਾ ਕਰਕੇ ਉਸ ਨੂੰ ਕਰਾਰੀ ਹਾਰ ਦਿੱਤੀ । ਇਸ ਲੜਾਈ ਵਿੱਚ ਅਸਲਮ ਖਾਂ ਨੂੰ ਲੜਾਈ ਦਾ ਮੈਦਾਨ ਛੱਡ ਕੇ ਨੱਸਣ ਲਈ ਮਜਬੂਰ ਹੋਣਾ ਪਿਆ ।
6. ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੀ ਅਸਫਲਤਾ (Failure of Abdus Samad Khan) – ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਆਪਣੇ ਸਾਰੇ ਯਤਨਾਂ ਦੇ ਬਾਵਜੂਦ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ । ਇਸ ਦੇ ਕਈ ਕਾਰਨ ਸਨ । ਪਹਿਲਾ, ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਬੁੱਢਾ ਹੋ ਗਿਆ ਸੀ ।ਦੂਜਾ, ਸਿੱਖਾਂ ਵਿੱਚ ਆਪਸੀ ਏਕਤਾ ਸਥਾਪਿਤ ਹੋ ਗਈ ਸੀ । ਤੀਸਰਾ, ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਨੂੰ ਮੁਗ਼ਲ ਅਧਿਕਾਰੀਆਂ ਦੀਆਂ ਸਾਜ਼ਸ਼ਾਂ ਦਾ ਸ਼ਿਕਾਰ ਹੋਣਾ ਪਿਆ । ਚੌਥਾ, ਉਸ ਨੂੰ ਕੇਂਦਰ ਤੋਂ ਲੋੜੀਂਦੀ ਸਹਾਇਤਾ ਨਾ ਪ੍ਰਾਪਤ ਹੋਈ । 1726 ਈ. ਵਿੱਚ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਨੂੰ ਉਸ ਦੇ ਅਹੁਦੇ ਤੋਂ ਹਟਾ ਦਿੱਤਾ ਗਿਆ ।
![]()
ਜ਼ਕਰੀਆ ਖਾਂ 1726-45 ਈ. (Zakariya Khan 1726-45 A.D.)
ਪ੍ਰਸ਼ਨ 2.
ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਲਈ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਕੀ ਕਦਮ ਚੁੱਕੇ ? ਉਸ ਦੀਆਂ ਕੋਸ਼ਿਸ਼ਾਂ ਵਿੱਚ ਉਸ ਨੂੰ ਕਿੱਥੋਂ ਤਕ ਸਫਲਤਾ ਪ੍ਰਾਪਤ ਹੋਈ ? (What measures were adopted by Zakariya Khan to crush the power of the Sikhs ? How far did he succeed in his efforts ?)
ਜਾਂ
ਜ਼ਕਰੀਆ ਖਾਂ ਦੇ ਸਿੱਖਾਂ ਨਾਲ ਸੰਬੰਧ ਦੀ ਚਰਚਾ ਕਰੋ । (Discuss the relations of Zakariya Khan with the Sikhs.)
ਜਾਂ
ਜ਼ਕਰੀਆਂ ਖਾਂ ਨੇ ਸਿੱਖਾਂ ਨਾਲ ਨਜਿੱਠਣ ਦੀ ਕਿਸ ਤਰ੍ਹਾਂ ਕੋਸ਼ਿਸ਼ ਕੀਤੀ ? (How did Zakariya Khan treat the Sikhs ?)
ਜਾਂ
ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਲਈ ਜ਼ਕਰੀਆਂ ਖਾਂ ਨੇ ਕੀ ਕਦਮ ਚੁੱਕੇ ? ਉਸ ਨੂੰ ਆਪਣੇ ਯਤਨਾਂ ਵਿੱਚ ਕਿੱਥੋਂ ਤਕ ਸਫ਼ਲਤਾ ਮਿਲੀ ? (What measures were adopted by Zakariya Khan to crush the power of the Sikhs ? How far did he succeed in his efforts ?)
ਉੱਤਰ-
ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਦੇ ਬਾਅਦ ਉਸ ਦਾ ਪੁੱਤਰ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਬਣਿਆ । ਉਹ ਇਸ ਅਹੁਦੇ ‘ਤੇ 1726 ਈ. ਤੋਂ 1745 ਈ. ਤਕ ਰਿਹਾ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੇ ਸ਼ਾਸਨ ਕਾਲ ਅਤੇ ਉਸ ਦੇ ਸਿੱਖਾਂ ਨਾਲ ਸੰਬੰਧਾਂ ਦਾ ਵਰਣਨ ਇਸ ਪ੍ਰਕਾਰ ਹੈ-
1. ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਸਖ਼ਤ ਕਾਰਵਾਈਆਂ (Harsh measures against the Sikhs) – ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਆਪਣਾ ਅਹੁਦਾ ਸੰਭਾਲਦੇ ਹੀ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਲਈ 20,000 ਸੈਨਿਕਾਂ ਨੂੰ ਭਰਤੀ ਕੀਤਾ । ਪਿੰਡਾਂ ਦੇ ਮੁਕੱਦਮਾਂ ਅਤੇ ਚੌਧਰੀਆਂ ਨੂੰ ਇਹ ਆਦੇਸ਼ ਦਿੱਤਾ ਗਿਆ ਕਿ ਉਹ ਆਪਣੇ ਇਲਾਕਿਆਂ ਵਿੱਚ ਸਿੱਖਾਂ ਨੂੰ ਸ਼ਰਨ ਨਾ ਲੈਣ ਦੇਣ । ਉਸ ਨੇ ਇਹ ਐਲਾਨ ਕੀਤਾ ਕਿ ਕਿਸੇ ਸਿੱਖ ਬਾਰੇ ਸੂਹ ਦੇਣ ਵਾਲੇ ਨੂੰ 10 ਰੁਪਏ, ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਵਾਉਣ ਵਾਲੇ ਨੂੰ 25 ਰੁਪਏ, ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਕੇ ਸਰਕਾਰ ਦੇ ਹਵਾਲੇ ਕਰਨ ਵਾਲੇ ਨੂੰ 50 ਰੁਪਏ ਅਤੇ ਸਿਰ ਵੱਢ ਕੇ ਸਰਕਾਰ ਨੂੰ ਭੇਟ ਕਰਨ ਵਾਲੇ ਨੂੰ 100 ਰੁਪਏ ਦਾ ਇਨਾਮ ਦਿੱਤਾ ਜਾਵੇਗਾ । ਇਸ ਤਰ੍ਹਾਂ ਸਿੱਖਾਂ ‘ਤੇ ਮੁੜ ਅੱਤਿਆਚਾਰ ਦਾ ਦੌਰ ਸ਼ੁਰੂ ਹੋ ਗਿਆ । ਸੈਂਕੜੇ ਸਿੱਖਾਂ ਨੂੰ ਲਾਹੌਰ ਦੇ ਦਿੱਲੀ ਗੇਟ ਵਿਖੇ ਸ਼ਹੀਦ ਕੀਤਾ ਜਾਣ ਲੱਗਾ। ਇਸ ਕਾਰਨ ਇਸ ਥਾਂ ਦਾ ਨਾਂ ‘ਸ਼ਹੀਦ ਗੰਜ ਪੈ ਗਿਆ ।
2. ਭਾਈ ਤਾਥਾ ਸਿੰਘ ਜੀ ਵਾਂ ਦੀ ਸ਼ਹੀਦੀ (Martyrdom of Bhai Tara Singh Ji Van) – ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਅੰਮ੍ਰਿਤਸਰ ਜ਼ਿਲ੍ਹੇ ਦੇ ਪਿੰਡ ਵਾਂ ਦੇ ਵਸਨੀਕ ਸਨ । ਉਨ੍ਹਾਂ ਨੇ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੀਆਂ ਲੜਾਈਆਂ ਵਿੱਚ ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਨਿਭਾਈ ਸੀ । ਨੌਸ਼ਹਿਰੇ ਦਾ ਚੌਧਰੀ ਸਾਹਿਬ ਰਾਏ ਸਿੱਖਾਂ ਦੇ ਖੇਤਾਂ ਵਿੱਚ ਆਪਣੇ ਘੋੜੇ ਛੱਡ ਦਿੰਦਾ ਸੀ । ਜਦੋਂ ਸਿੱਖ ਇਸ ਗੱਲ ਦਾ ਇਤਰਾਜ਼ ਕਰਦੇ ਤਾਂ ਉਹ ਸਿੱਖਾਂ ਦਾ ਅਪਮਾਨ ਕਰਦਾ । ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਵਾਂ ਲਈ ਇਹ ਗੱਲ ਅਸਹਿ ਸੀ । ਇੱਕ ਦਿਨ ਉਨ੍ਹਾਂ ਨੇ ਸਾਹਿਬ ਰਾਏ ਦੀ ਇੱਕ ਘੋੜੀ ਨੂੰ ਵੇਚ ਦਿੱਤਾ ਅਤੇ ਮਿਲੇ ਹੋਏ ਪੈਸਿਆਂ ਨੂੰ ਲੰਗਰ ਲਈ ਦੇ ਦਿੱਤਾ । ਇਸ ’ਤੇ ਸਿੱਖਾਂ ਨੂੰ ਸਬਕ ਸਿਖਾਉਣ ਲਈ ਸਾਹਿਬ ਰਾਏ ਨੇ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਤੋਂ ਮਦਦ ਮੰਗੀ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ 2200 ਘੋੜਸਵਾਰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਭੇਜੇ । ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਵਾਂ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ 22 ਸਾਥੀ ਮੁਗ਼ਲਾਂ ਦਾ ਮੁਕਾਬਲਾ ਕਰਦੇ ਹੋਏ ਸ਼ਹੀਦ ਹੋ ਗਏ । ਇਸ ਤੋਂ ਪਹਿਲਾਂ ਉਨ੍ਹਾਂ ਨੇ 300 ਮੁਗ਼ਲ ਸੈਨਿਕਾਂ ਨੂੰ ਯਮਲੋਕ ਪਹੁੰਚਾ ਦਿੱਤਾ ਸੀ । ਇਹ ਘਟਨਾ 1726 ਈ. ਦੀ ਹੈ । ਪ੍ਰਸਿੱਧ ਇਤਿਹਾਸਕਾਰ ਐੱਸ. ਐੱਸ. ਸ਼ੀਤਲ ਅਨੁਸਾਰ,
“ਉਸ (ਤਾਰਾ ਸਿੰਘ ਦੀ ਸ਼ਹੀਦੀ ਦਾ ਸਿੱਖਾਂ ਦੇ ਮਨਾਂ ‘ਤੇ ਡੂੰਘਾ ਅਸਰ ਪਿਆ ।”1
3. ਸਿੱਖਾਂ ਦੀਆਂ ਜਵਾਬੀ ਕਾਰਵਾਈਆਂ (Retaliatory measures of the Sikhs) – ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਵਾਂ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਸਾਥੀਆਂ ਦੀ ਸ਼ਹੀਦੀ ਨੇ ਸਿੱਖਾਂ ਵਿੱਚ ਇੱਕ ਨਵਾਂ ਜੋਸ਼ ਪੈਦਾ ਕਰ ਦਿੱਤਾ । ਉਨ੍ਹਾਂ ਨੇ ਛਾਪਾਮਾਰ ਯੁੱਧਾਂ ਰਾਹੀਂ ਸਰਕਾਰੀ ਖਜ਼ਾਨਿਆਂ ਨੂੰ ਲੁੱਟਣਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ । ਉਨ੍ਹਾਂ ਨੇ ਕਈ ਥਾਂਵਾਂ ‘ਤੇ ਹਮਲਾ ਕਰਕੇ ਸਰਕਾਰ ਦੇ ਪਿੱਛਲੱਗਿਆਂ ਨੂੰ ਮੌਤ ਦੇ ਘਾਟ ਉਤਾਰ ਦਿੱਤਾ । ਜਦੋਂ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਇਨ੍ਹਾਂ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਆਪਣੇ ਸੈਨਿਕਾਂ ਨੂੰ ਭੇਜਦਾ ਤਾਂ ਉਹ ਝਟ ਜੰਗਲਾਂ ਅਤੇ ਪਹਾੜਾਂ ਵਿੱਚ ਜਾ ਛਿਪਦੇ ।
4. ਹੈਦਰੀ ਝੰਡੇ ਦੀ ਘਟਨਾ (Incident of Haidri Flag) – ਮਜਬੂਰ ਹੋ ਕੇ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਦੇ ਦਮਨ ਲਈ ਜ਼ਿਹਾਦ ਦਾ ਨਾਅਰਾ ਲਗਾਇਆ । ਹਜ਼ਾਰਾਂ ਦੀ ਗਿਣਤੀ ਵਿੱਚ ਮੁਸਲਮਾਨ ਇਨਾਇਤ ਉਲਾ ਖਾਂ ਦੇ ਝੰਡੇ ਅਧੀਨ ਆਣ ਇਕੱਠੇ ਹੋਏ । ਉਨ੍ਹਾਂ ਨੂੰ ਈਦ ਦੇ ਮੁਬਾਰਕ ਦਿਨ ਇੱਕ ਹੈਦਰੀ ਝੰਡਾ ਦਿੱਤਾ ਗਿਆ ਅਤੇ ਇਹ ਐਲਾਨ ਕੀਤਾ ਗਿਆ ਕਿ ਇਸ ਝੰਡੇ ਅਧੀਨ ਲੜਨ ਵਾਲਿਆਂ ਨੂੰ ਅੱਲ੍ਹਾ ਜ਼ਰੂਰ ਫ਼ਤਹਿ ਦੇਵੇਗਾ । ਪਰ ਇੱਕ ਦਿਨ ਲਗਭਗ 7 ਹਜ਼ਾਰ ਸਿੱਖਾਂ ਨੇ ਇਨ੍ਹਾਂ ਗਾਜ਼ੀਆਂ ਉੱਤੇ ਅਚਾਨਕ ਹਮਲਾ ਕਰਕੇ ਹਜ਼ਾਰਾਂ ਗਾਜ਼ੀਆਂ ਨੂੰ ਕਤਲ ਕਰ ਦਿੱਤਾ । ਇਸ ਘਟਨਾ ਨਾਲ ਸਰਕਾਰ ਦੇ ਗੌਰਵ ਨੂੰ ਭਾਰੀ ਸੱਟ ਵੱਜੀ ।
5. ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦਾ ਸਿੱਖਾਂ ਨਾਲ ਸਮਝੌਤਾ (Agreement of Zakariya Khan with the Sikhs) – ਹੁਣ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਖੁਸ਼ ਕਰਨ ਦੀ ਨੀਤੀ ਅਪਣਾਈ । ਉਸ ਨੇ 1733 ਈ. ਵਿੱਚ ਐਲਾਨ ਕੀਤਾ ਕਿ ਜੇਕਰ ਸਿੱਖ ਸਰਦਾਰ ਵਿਰੋਧੀ ਕਾਰਵਾਈਆਂ ਨੂੰ ਬੰਦ ਕਰ ਦੇਣ ਤਾਂ ਉਨ੍ਹਾਂ ਨੂੰ ਇੱਕ ਲੱਖ ਰੁਪਏ ਸਾਲਾਨਾ ਆਮਦਨ ਵਾਲੀ ਇੱਕ ਜਾਗੀਰ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਆਗੂ ਨੂੰ “ਨਵਾਬ’ ਦਾ ਖਿਤਾਬ ਦਿੱਤਾ ਜਾਵੇਗਾ । ਪਹਿਲਾਂ ਤਾਂ ਸਿੱਖ ਇਸ ਸਮਝੌਤੇ ਦੇ ਵਿਰੁੱਧ ਸਨ ਪਰ ਬਾਅਦ ਵਿੱਚ ਉਨ੍ਹਾਂ ਨੇ ਇਸ ਨੂੰ ਸਵੀਕਾਰ ਕਰ ਲਿਆ । ਸਿੱਖਾਂ ਨੇ ਨਵਾਬ ਦੀ ਪਦਵੀ ਸਰਦਾਰ ਕਪੂਰ ਸਿੰਘ ਫ਼ੈਜ਼ਲਪੁਰੀਆ ਨੂੰ ਦਿੱਤੀ ।
6. ਬੁੱਢਾ ਦਲ ਤੇ ਤਰੁਣਾ ਦਲ ਦਾ ਸੰਗਠਨ (Organisation of Buddha Dal and Taruna Dal) – ਮੁਗਲਾਂ ਨਾਲ ਸਮਝੌਤਾ ਹੋ ਜਾਣ ਨਾਲ ਨਵਾਬ ਕਪੂਰ ਸਿੰਘ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਇਹ ਸੁਨੇਹਾ ਭੇਜਿਆ ਕਿ ਉਹ ਮੁੜ ਆਪਣੇ ਘਰਾਂ ਵਿੱਚ ਆ ਜਾਣ । 1734 ਈ. ਵਿੱਚ ਨਵਾਬ ਕਪੂਰ ਸਿੰਘ ਨੇ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਮਜ਼ਬੂਤ ਕਰਨ ਦੇ ਉਦੇਸ਼ ਨਾਲ ਉਨ੍ਹਾਂ ਨੂੰ ਦੋ ਜੱਥਿਆਂ ਵਿੱਚ ਸੰਗਠਿਤ ਕਰ ਦਿੱਤਾ । ਇਹ ਜੱਥੇ ਸਨ-ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ । ਬੁੱਢਾ ਦਲ ਵਿੱਚ 40 ਸਾਲਾਂ ਤੋਂ ਵਡੇਰੀ ਉਮਰ ਦੇ ਸਿੱਖਾਂ ਨੂੰ ਸ਼ਾਮਲ ਕੀਤਾ ਗਿਆ ਅਤੇ ਤਰੁਣਾ ਦਲ ਵਿੱਚ ਉਸ ਤੋਂ ਘੱਟ ਦੀ ਉਮਰ ਵਾਲੇ ਸਿੱਖਾਂ ਨੂੰ । ਤਰੁਣਾ ਦਲ ਨੂੰ ਅੱਗੇ ਪੰਜ ਜੱਥਿਆਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ ਸੀ । ਬੁੱਢਾ ਦਲ ਧਾਰਮਿਕ ਸਥਾਨਾਂ ਦੀ ਦੇਖਭਾਲ ਕਰਦਾ ਸੀ । ਤਰੁਣਾ ਦਲ ਦੁਸ਼ਮਣਾਂ ਦਾ ਮੁਕਾਬਲਾ ਕਰਦਾ ਸੀ ।
7. ਮੁਗ਼ਲਾਂ ਅਤੇ ਸਿੱਖਾਂ ਵਿਚਾਲੇ ਦੁਬਾਰਾ ਸੰਘਰਸ਼ (Renewed struggle between the Mughals and the Sikhs) – ਆਪਣੀ ਸ਼ਕਤੀ ਨੂੰ ਸੰਗਠਿਤ ਕਰਨ ਤੋਂ ਬਾਅਦ ਸਿੱਖਾਂ ਨੇ ਆਪਣੀਆਂ ਸੈਨਿਕ ਕਾਰਵਾਈਆਂ ਮੁੜ ਆਰੰਭ ਕਰ ਦਿੱਤੀਆਂ ਸਨ । ਉਨ੍ਹਾਂ ਨੇ ਸ਼ਾਹੀ ਖ਼ਜ਼ਾਨਿਆਂ ਨੂੰ ਮੁੜ ਲੁੱਟਣਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ ਸੀ । ਇਸ ਕਾਰਨ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਗੁੱਸੇ ਵਿੱਚ ਆ ਕੇ ਸਿੱਖਾਂ ਨੂੰ ਦਿੱਤੀ ਗਈ ਜਾਗੀਰ ਨੂੰ 1735 ਈ. ਵਿੱਚ ਜ਼ਬਤ ਕਰ ਲਿਆ । ਸਿੱਖਾਂ ਨੂੰ ਮੁੜ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਕੇ ਕਤਲ ਕਰਨਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ ਗਿਆ । ਸਿੱਟੇ ਵਜੋਂ ਸਿੱਖ ਜੰਗਲਾਂ ਵੱਲ ਚਲੇ ਗਏ । ਇਸ ਮੌਕੇ ਦਾ ਫਾਇਦਾ ਉਠਾ ਕੇ ਮੁਗ਼ਲਾਂ ਨੇ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਉੱਤੇ ਕਬਜ਼ਾ ਕਰ ਲਿਆ ।

8. ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਦੀ ਸ਼ਹੀਦੀ (Martyrdom of Bhai Mani Singh Ji) – ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ 1721 ਈ. ਤੋਂ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਦੇ ਮੁੱਖ ਗ੍ਰੰਥੀ ਚਲੇ ਆ ਰਹੇ ਸਨ ।ਉਨ੍ਹਾਂ ਨੇ 1738 ਈ. ਵਿੱਚ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੂੰ ਇਹ ਬੇਨਤੀ ਕੀਤੀ ਕਿ ਜੇਕਰ ਉਹ ਸਿੱਖਾਂ ਨੂੰ ਦੀਵਾਲੀ ਦੇ ਮੌਕੇ ‘ਤੇ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਆਉਣ ਦੀ ਇਜਾਜ਼ਤ ਦੇਵੇ ਤਾਂ ਉਹ 5,000 ਰੁਪਏ ਉਸ ਨੂੰ ਭੇਟ ਕਰਨਗੇ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਇਹ ਪੇਸ਼ਕਸ਼ ਸਵੀਕਾਰ ਕਰ ਲਈ । ਪਰ ਹਾਲੇ ਸਿੱਖ ਅੰਮ੍ਰਿਤਸਰ ਵਿੱਚ ਇਕੱਠੇ ਹੋ ਹੀ ਰਹੇ ਸਨ ਕਿ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੇ ਸੈਨਿਕਾਂ ਨੇ ਹਮਲਾ ਕਰ ਦਿੱਤਾ । ਸਿੱਟੇ ਵਜੋਂ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਵਿੱਚ ਦੀਵਾਲੀ ਦਾ ਮੇਲਾ ਨਾ ਮਨਾਇਆ ਜਾ ਸਕਿਆ । ਜ਼ਕਰੀਆ ਖਾਂ ਨੇ ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਤੋਂ 5,000 ਰੁਪਏ ਦੀ ਮੰਗ ਕੀਤੀ । ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਇਹ ਪੈਸਾ ਨਾ ਦੇ ਸਕੇ । ਇਸ ਲਈ ਉਨ੍ਹਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਕੇ ਲਾਹੌਰ ਭੇਜ ਦਿੱਤਾ ਗਿਆ | ਭਾਈ ਸਾਹਿਬ ਜੀ ਨੂੰ ਇਸਲਾਮ ਹਿਣ ਕਰਨ ਲਈ ਕਿਹਾ ਗਿਆ ਪਰ ਉਨ੍ਹਾਂ ਨੇ ਇਨਕਾਰ ਕਰ ਦਿੱਤਾ । ਸਿੱਟੇ ਵਜੋਂ ਉਨ੍ਹਾਂ ਨੂੰ 1738 ਈ. ਵਿੱਚ ਤਸੀਹੇ ਦੇ ਕੇ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ਗਿਆ । ਇਸ ਘਟਨਾ ਨਾਲ ਸਿੱਖਾਂ ਵਿੱਚ ਗੁੱਸੇ ਦੀ ਲਹਿਰ ਦੌੜ ਗਈ । ਪ੍ਰਸਿੱਧ ਇਤਿਹਾਸਕਾਰ ਖੁਸ਼ਵੰਤ ਸਿੰਘ ਦੇ ਵਿਚਾਰ ਅਨੁਸਾਰ,
‘‘ਪਵਿੱਤਰ ਅਤੇ ਪੂਜਣ ਯੋਗ ਮੁੱਖ ਪੁਜਾਰੀ (ਭਾਈ ਮਨੀ ਸਿੰਘ ਦੀ ਕੁਰਬਾਨੀ ਕਾਰਨ ਸਿੱਖ ਭੜਕ ਉਠੇ ।’’ 1
9. ਸਿੱਖਾਂ ਦਾ ਨਾਦਰ ਸ਼ਾਹ ਨੂੰ ਲੁੱਟਣਾ (Sikhs robbed Nadir Shah) – 1739 ਈ. ਵਿੱਚ ਨਾਦਰ ਸ਼ਾਹ ਦਿੱਲੀ ਵਿੱਚ ਭਾਰੀ ਲੁੱਟਮਾਰ ਕਰਕੇ ਪੰਜਾਬ ਵਿੱਚੋਂ ਹੁੰਦਾ ਹੋਇਆ ਵਾਪਸ ਈਰਾਨ ਜਾ ਰਿਹਾ ਸੀ । ਜਦੋਂ ਸਿੱਖਾਂ ਨੂੰ ਇਸ ਬਾਰੇ ਸੂਚਨਾ ਮਿਲੀ ਤਾਂ ਉਨ੍ਹਾਂ ਨੇ ਅਚਾਨਕ ਹਮਲਾ ਕਰਕੇ ਉਸ ਦਾ ਬਹੁਤ ਸਾਰਾ ਖ਼ਜ਼ਾਨਾ ਲੁੱਟ ਲਿਆ । ਨਾਦਰ ਸ਼ਾਹ ਨੇ ਜ਼ਕਰੀਆ ਖਾਂ ਨੂੰ ਇਹ ਚੇਤਾਵਨੀ ਦਿੱਤੀ ਕਿ ਛੇਤੀ ਹੀ ਸਿੱਖ ਪੰਜਾਬ ਦੇ ਸ਼ਾਸਕ ਬਣ ਜਾਣਗੇ ।
10. ਜ਼ਕਰੀਆ ਖਾਂ ਦੁਆਰਾ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਸਖ਼ਤ ਕਾਰਵਾਈਆਂ (Strong actions against the Sikhs by Zakariya Khan) – ਨਾਦਰ ਸ਼ਾਹ ਦੀ ਚੇਤਾਵਨੀ ਦਾ ਜ਼ਕਰੀਆ ਖਾਂ ਦੇ ਮਨ ’ਤੇ ਬੜਾ ਡੂੰਘਾ ਅਸਰ ਪਿਆ । ਉਸ ਨੇ ਸਿੱਖਾਂ ਦਾ ਮਲੀਆਮੇਟ ਕਰਨ ਲਈ ਅਨੇਕਾਂ ਕਦਮ ਚੁੱਕੇ । ਸਿੱਖਾਂ ਦਾ ਇੱਕ ਵਾਰੀ ਫਿਰ ਰੋਜ਼ਾਨਾ ਬੜੇ ਜ਼ਾਲਮਾਨਾ ਢੰਗ ਨਾਲ ਕਤਲ ਕੀਤਾ ਜਾਣ ਲੱਗਾ | ਕੁਝ ਪ੍ਰਸਿੱਧ ਸ਼ਹੀਦਾਂ ਦਾ ਵਰਣਨ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ-
(ੳ) ਭਾਈ ਬੋਤਾ ਸਿੰਘ ਜੀ (Bhai Bota Singh Ji) – ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਅਨੇਕਾਂ ਸਿੱਖਾਂ ਨੂੰ ਕਤਲ ਕਰਨ ਤੋਂ ਬਾਅਦ ਇਹ ਘੋਸ਼ਣਾ ਕੀਤੀ ਕਿ ਉਸ ਨੇ ਸਿੱਖਾਂ ਦਾ ਨਾਮੋ-ਨਿਸ਼ਾਨ ਖ਼ਤਮ ਕਰ ਦਿੱਤਾ ਹੈ । ਸਿੱਖਾਂ ਦੀ ਹੋਂਦ ਨੂੰ ਦਰਸਾਉਣ ਲਈ ਭਾਈ ਬੋਤਾ ਸਿੰਘ ਜੀ ਨੇ ਸਰਾਇ ਨਦੀਨ ਵਿਖੇ ਇੱਕ ਚੌਕੀ ਕਾਇਮ ਕਰ ਲਈ ਅਤੇ ਉੱਥੋਂ ਚੰਗੀ ਕਰ ਲੈਣਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਉਸ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਨ ਲਈ ਕੁਝ ਫ਼ੌਜ ਭੇਜੀ । ਭਾਈ ਬੋਤਾ ਸਿੰਘ ਜੀ ਆਪਣੇ ਦੁਸ਼ਮਣਾਂ ਦਾ ਡਟ ਕੇ ਮੁਕਾਬਲਾ ਕਰਦੇ ਹੋਏ ਸ਼ਹੀਦ ਹੋ ਗਏ ।
(ਅ) ਭਾਈ ਮਹਿਤਾਬ ਸਿੰਘ ਜੀ ਅਤੇ ਭਾਈ ਸੁੱਖਾ ਸਿੰਘ ਜੀ (Bhai Mehtab Singh Ji and Bhai Sukha Singh Ji) – ਅੰਮ੍ਰਿਤਸਰ ਜ਼ਿਲ੍ਹੇ ਦੇ ਮੰਡਿਆਲਾ ਪਿੰਡ ਦਾ ਚੌਧਰੀ ਮੱਸਾ ਰੰਗੜ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਦੀ ਪਵਿੱਤਰਤਾ ਨੂੰ ਭੰਗ ਕਰ ਰਿਹਾ ਸੀ । ਇਸ ਕਾਰਨ ਸਿੱਖ ਉਸ ਨੂੰ ਇੱਕ ਸਬਕ ਸਿਖਾਉਣਾ ਚਾਹੁੰਦੇ ਸਨ । ਇੱਕ ਦਿਨ ਭਾਈ ਮਹਿਤਾਬ ਸਿੰਘ ਜੀ ਅਤੇ ਭਾਈ ਸੁੱਖਾ ਸਿੰਘ ਜੀ ਕੁਝ ਬੋਰੀਆਂ ਵਿੱਚ ਥੱਲੇ ਪੱਥਰ ਭਰ ਕੇ ਅਤੇ ਉੱਤੇ ਕੁਝ ਸਿੱਕੇ ਭਰ ਕੇ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਪਹੁੰਚ ਗਏ | ਸੈਨਿਕਾਂ ਦੁਆਰਾ ਪੁੱਛਣ ‘ਤੇ ਉਨ੍ਹਾਂ ਨੇ ਦੱਸਿਆ ਕਿ ਉਹ ਮਾਮਲਾ ਉਗਰਾਹ ਕੇ ਲਿਆਏ ਹਨ । ਮੱਸਾ ਰੰਗੜ ਸਿੱਕੇ ਨਾਲ ਭਰੀਆਂ ਬੋਰੀਆਂ ਵੇਖ ਕੇ ਬੜਾ ਖ਼ੁਸ਼ ਹੋਇਆ । ਜਿਵੇਂ ਹੀ ਉਹ ਇਨ੍ਹਾਂ ਬੋਰੀਆਂ ਨੂੰ ਸਵੀਕਾਰ ਕਰਨ ਲਈ ਥੱਲੇ ਝੁਕਿਆ ਉਸੇ ਸਮੇਂ ਭਾਈ ਮਹਿਤਾਬ ਸਿੰਘ ਜੀ ਨੇ ਆਪਣੀ ਤਲਵਾਰ ਦੇ ਇੱਕੋ ਵਾਰ ਨਾਲ ਉਸ ਦਾ ਸਿਰ ਧੜ ਨਾਲੋਂ ਵੱਖ ਕਰ ਦਿੱਤਾ । ਬਾਅਦ ਵਿੱਚ ਭਾਈ ਮਹਿਤਾਬ ਸਿੰਘ ਜੀ ਅਤੇ ਭਾਈ ਸੁੱਖਾ ਸਿੰਘ ਜੀ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਕੇ ਬੜੀ ਬੇਰਹਿਮੀ ਨਾਲ 1740 ਈ. ਵਿੱਚ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ਗਿਆ ।
(ੲ) ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਜੀ (Bal Haqiqat Rai Ji) – ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਜੀ ਸਿਆਲਕੋਟ ਦੇ ਰਹਿਣ ਵਾਲੇ ਸਨ । ਇੱਕ ਦਿਨ ਕੁਝ ਮੁਸਲਮਾਨ ਮੁੰਡਿਆਂ ਨੇ ਹਿੰਦੂ ਦੇਵੀ-ਦੇਵਤਿਆਂ ਦੀ ਸ਼ਾਨ ਵਿੱਚ ਕੁਝ ਅਪਮਾਨ-ਜਨਕ ਸ਼ਬਦ ਕਹੇ | ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਜੀ ਇਹ ਸਹਿਣ ਨਾ ਕਰ ਸਕੇ ।ਉਨ੍ਹਾਂ ਨੇ ਹਜ਼ਰਤ ਮੁਹੰਮਦ ਬਾਰੇ ਕੁਝ ਅਯੋਗ ਸ਼ਬਦ ਕਹਿ ਦਿੱਤੇ । ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਜੀ `ਤੇ ਮੁਕੱਦਮਾ ਚਲਾਇਆ ਗਿਆ ਅਤੇ ਮੌਤ ਦੀ ਸਜ਼ਾ ਸੁਣਾਈ ਗਈ । ਇਹ ਘਟਨਾ 1742 ਈ. ਦੀ ਹੈ । ਇਸ ਘਟਨਾ ਕਾਰਨ ਲੋਕਾਂ ਨੇ ਜ਼ਾਲਮ ਮੁਗਲ ਸ਼ਾਸਨ ਦਾ ਅੰਤ ਕਰਨ ਦੀ ਸਹੁੰ ਚੁੱਕੀ ।
(ਸ) ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ Bhai Taru Singh Ji) – ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਮਾਝੇ ਦੇ ਇਲਾਕੇ ਦੇ ਪਿੰਡ ਪੂਹਲਾ ਦੇ ਨਿਵਾਸੀ ਸਨ । ਉਹ ਆਪਣੀ ਆਮਦਨ ਤੋਂ ਸਿੱਖਾਂ ਦੀ ਮੱਦਦ ਕਰਦੇ ਸਨ । ਸਰਕਾਰ ਦੀਆਂ ਨਜ਼ਰਾਂ ਵਿੱਚ ਇਹ ਇੱਕ ਘੋਰ ਅਪਰਾਧ ਸੀ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਨੂੰ ਲਾਹੌਰ ਬੁਲਾ ਕੇ ਇਸਲਾਮ ਧਰਮ ਗ੍ਰਹਿਣ ਕਰਨ ਲਈ ਕਿਹਾ । ਭਾਈ ਸਾਹਿਬ ਜੀ ਨੇ ਕਿਹਾ ਕਿ ਉਹ ਕਿਸੇ ਵੀ ਕੀਮਤ ‘ਤੇ ਸਤਿਰੂ ਦੀ ਦਿੱਤੀ ਪਵਿੱਤਰ ਦਾਤ ਕੇਸਾਂ ਨੂੰ ਨਹੀਂ ਦੇ ਸਕਦੇ ਹਾਂ ਉਹ ਆਪਣੇ ਕੇਸ ਆਪਣੀ ਖੋਪਰੀ ਨਾਲ ਹੀ ਉਤਰਵਾ ਸਕਦੇ ਹਨ । ਇਸ ’ਤੇ ਜੱਲਾਦਾਂ ਨੇ ਭਾਈ ਸਾਹਿਬ ਦੀ ਖੋਪਰੀ ਨੂੰ ਉਤਾਰ ਦਿੱਤਾ । ਜਦੋਂ ਭਾਈ ਸਾਹਿਬ ਜੀ ਦੀ ਖੋਪਰੀ ਉਤਾਰੀ ਜਾ ਰਹੀ ਸੀ ਤਾਂ ਉਹ ਜਪੁਜੀ ਸਾਹਿਬ ਦਾ ਪਾਠ ਕਰ ਰਹੇ ਸਨ । ਇਹ ਘਟਨਾ 1745 ਈ. ਦੀ ਹੈ । ਇਸ ਲਾਸਾਨੀ ਸ਼ਹਾਦਤ ਨੇ ਸਿੱਖਾਂ ਵਿੱਚ ਇੱਕ ਨਵਾਂ ਜੋਸ਼ ਪੈਦਾ ਕੀਤਾ |
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ (Death of Zakariya Khan) – ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਨਿਰਸੰਦੇਹ ਆਪਣੇ ਕਾਲ ਵਿੱਚ ਸਿੱਖਾਂ ਉੱਤੇ ਘੋਰ ਅੱਤਿਆਚਾਰ ਕੀਤੇ ।ਉਹ ਆਪਣੇ ਅਣਥੱਕ ਯਤਨਾਂ ਦੇ ਬਾਵਜੂਦ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ । 1 ਜੁਲਾਈ, 1745 ਈ. ਨੂੰ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ ਹੋ ਗਈ । ਪਤਵੰਤ ਸਿੰਘ ਦਾ ਇਹ ਕਹਿਣਾ ਬਿਲਕੁਲ ਠੀਕ ਹੈ, .
‘‘ਕਿਸੇ ਨੇ ਵੀ ਸਿੱਖਾਂ ਦਾ ਇਸ ਤੋਂ ਵੱਧ ਉਤਸ਼ਾਹ ਨਾਲ ਮਨ ਨਹੀਂ ਕੀਤਾ ਜਿੰਨਾ ਕਿ ਜ਼ਕਰੀਆ ਖਾਂ ਨੇ ।” 1
![]()
ਪ੍ਰਸ਼ਨ 3.
ਸੰਖੇਪ ਵਿੱਚ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਅਤੇ ਜ਼ਕਰੀਆ ਖਾਂ ਦੇ ਸਿੱਖਾਂ ਨਾਲ ਸੰਬੰਧਾਂ ਦੀ ਚਰਚਾ ਕਰੋ । (Briefly describe the relations of Abdus Samad Khan and Zakariya Khan with the Sikhs.)
ਉੱਤਰ-
ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਨੂੰ 1713 ਈ. ਵਿੱਚ ਮੁਗ਼ਲ ਬਾਦਸ਼ਾਹ ਫ਼ਰੁੱਖਸੀਅਰ ਦੁਆਰਾ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਨਿਯੁਕਤ ਕੀਤਾ ਗਿਆ ਸੀ । ਉਸ ਨੂੰ ਇਸ ਉਦੇਸ਼ ਨਾਲ ਇਸ ਅਹੁਦੇ ‘ਤੇ ਨਿਯੁਕਤ ਕੀਤਾ ਗਿਆ ਸੀ ਤਾਂ ਕਿ ਉਹ ਪੰਜਾਬ ਵਿੱਚੋਂ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਪੂਰੀ ਤਰ੍ਹਾਂ ਕੁਚਲ ਦੇਵੇ । ਉਸ ਨੇ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਅਤੇ ਉਸ ਨੂੰ ਦਿੱਲੀ ਲਿਆ ਕੇ 1716 ਈ. ਵਿੱਚ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ । ਫ਼ਰੁੱਖਸੀਅਰ ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਦੀ ਇਸ ਕਾਰਵਾਈ ਤੋਂ ਬਹੁਤ ਖੁਸ਼ ਹੋਇਆ । ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੇ ਸਿੱਖਾਂ ਨਾਲ ਸੰਬੰਧਾਂ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਹੇਠ ਲਿਖਿਆ ਹੈ-
1. ਫ਼ਰੁੱਖਸੀਅਰ ਦਾ ਫ਼ਰਮਾਨ (Farrukhsiyar’s Edict) – 1716 ਈ. ਵਿੱਚ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੀ ਸ਼ਹੀਦੀ ਤੋਂ ਬਾਅਦ ਮੁਗ਼ਲ ਬਾਦਸ਼ਾਹ ਫ਼ਰੁੱਖਸੀਅਰ ਨੇ ਇੱਕ ਸ਼ਾਹੀ ਫ਼ਰਮਾਨ ਜਾਰੀ ਕੀਤਾ । ਇਸ ਵਿੱਚ ਮੁਗ਼ਲ ਅਧਿਕਾਰੀਆਂ ‘ ਨੂੰ ਇਹ ਆਦੇਸ਼ ਦਿੱਤਾ ਗਿਆ ਕਿ ਜਿਹੜਾ ਵੀ ਸਿੱਖ ਤੁਹਾਡੇ ਹੱਥ ਲੱਗੇ ਉਸ ਨੂੰ ਕਤਲ ਕਰ ਦਿਓ । ਸਿੱਖਾਂ ਨੂੰ ਸਹਾਇਤਾ ਜਾਂ ਸ਼ਰਨ ਦੇਣ ਵਾਲਿਆਂ ਨੂੰ ਵੀ ਇਹੋ ਸਜ਼ਾ ਦਿੱਤੀ ਜਾਵੇ । ਜੇ ਕੋਈ ਵਿਅਕਤੀ ਸਿੱਖਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਵਾਉਣ ਵਿੱਚ ਸਰਕਾਰ ਦੀ ਮਦਦ ਕਰੇ ਤਾਂ ਉਸ ਨੂੰ ਇਨਾਮ ਦਿੱਤਾ ਜਾਵੇ ।
2. ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੁਆਰਾ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਚੁੱਕੇ ਗਏ ਕਦਮ (Steps taken by Abdus Samad Khan against the Sikhs) – ਸ਼ਾਹੀ ਫ਼ਰਮਾਨ ਦੇ ਜਾਰੀ ਹੋਣ ਤੋਂ ਬਾਅਦ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਨੇ ਸਿੱਖਾਂ ‘ਤੇ ਘੋਰ ਅੱਤਿਆਚਾਰ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੇ । ਸੈਂਕੜੇ ਨਿਰਦੋਸ਼ ਸਿੱਖਾਂ ਨੂੰ ਰੋਜ਼ਾਨਾ ਗਿਫ਼ਤਾਰ ਕਰਕੇ ਲਾਹੌਰ ਲਿਆਂਦਾ ਜਾਂਦਾ । ਜੱਲਾਦ ਇਨ੍ਹਾਂ ਸਿੱਖਾਂ ਨੂੰ ਭਾਰੀ ਤਸੀਹੇ ਦੇਣ ਮਗਰੋਂ ਸ਼ਹੀਦ ਕਰ ਦਿੰਦੇ । ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੀ ਇਸ ਸਖ਼ਤ ਨੀਤੀ ਤੋਂ ਬਚਣ ਲਈ ਬਹੁਤ ਸਾਰੇ ਸਿੱਖਾਂ ਨੇ ਲੱਖੀ ਜੰਗਲ ਅਤੇ ਸ਼ਿਵਾਲਿਕ ਦੀਆਂ ਪਹਾੜੀਆਂ ਵਿੱਚ ਜਾ ਸ਼ਰਨ ਲਈ। ਇਸ ਤਰ੍ਹਾਂ ਆਪਣੇ ਸ਼ਾਸਨ ਕਾਲ ਦੇ ਸ਼ੁਰੂ ਦੇ ਕੁਝ ਵਰਿਆਂ ਤਕ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੀ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਦਮਨ ਨੀਤੀ ਬਹੁਤ ਸਫਲ ਰਹੀ । ਇਸ ਤੋਂ ਖ਼ੁਸ਼ ਹੋ ਕੇ ਫ਼ਰੁੱਖਸੀਅਰ ਨੇ ਉਸ ਨੂੰ ‘ਰਾਜ ਦੀ ਤਲਵਾਰ ਦੀ ਉਪਾਧੀ ਨਾਲ ਸਨਮਾਨਿਤ ਕੀਤਾ ।
3. ਸਿੱਖਾਂ ਵਿੱਚ ਫੁੱਟ (Split among the Sikhs) – ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੀ ਸ਼ਹੀਦੀ ਤੋਂ ਬਾਅਦ ਸਿੱਖ ਆਪਸੀ ਫੁੱਟ ਦਾ ਸ਼ਿਕਾਰ ਹੋ ਗਏ । ਉਹ ਤੱਤ ਖ਼ਾਲਸਾ ਅਤੇ ਬੰਦਈ ਖ਼ਾਲਸਾ ਨਾਂ ਦੀਆਂ ਦੋ ਮੁੱਖ ਸੰਪਰਦਾਵਾਂ ਵਿੱਚ ਵੰਡੇ ਗਏ । ਤੱਤ ਖ਼ਾਲਸਾ ਗੁਰੂ ਗੋਬਿੰਦ ਸਿੰਘ ਜੀ ਦੇ ਧਾਰਮਿਕ ਅਸੂਲਾਂ ਦੇ ਦ੍ਰਿੜ ਸਮਰਥਕ ਸਨ । ਬੰਦਈ ਖ਼ਾਲਸਾ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਨੂੰ ਆਪਣਾ ਨੇਤਾ ਮੰਨਣ ਲੱਗ ਪਏ ਸਨ । ਤੱਤ ਖ਼ਾਲਸਾ ਵਾਲੇ ਆਪਸ ਵਿੱਚ ਮਿਲਣ ਵੇਲੇ ‘ਵਾਹਿਗੁਰੂ ਜੀ ਕਾ ਖ਼ਾਲਸਾ, ਵਾਹਿਗੁਰੂ ਜੀ ਕੀ ਫ਼ਤਹਿ’ ਕਹਿੰਦੇ ਸਨ ਜਦਕਿ ਬੰਦਈ ਖ਼ਾਲਸਾ ‘ਫ਼ਤਹਿ ਧਰਮ’ ਅਤੇ ‘ਫ਼ਤਹਿ’ ਦਰਸ਼ਨ ਸ਼ਬਦਾਂ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਸਨ । ਤੱਤ ਖ਼ਾਲਸਾ ਵਾਲੇ ਨੀਲੇ ਰੰਗ ਦੇ ਕੱਪੜੇ ਪਾਉਂਦੇ ਸਨ ਜਦਕਿ ਬੰਦਈ ਖ਼ਾਲਸਾ ਵਾਲੇ ਲਾਲ ਰੰਗ ਦੇ ਦੋਹਾਂ ਸੰਪਰਦਾਵਾਂ ਵਿਚਾਲੇ ਆਪਸੀ ਮਤਭੇਦ ਦਿਨੋ-ਦਿਨ ਵਧਦੇ ਗਏ । ਸਿੱਟੇ ਵਜੋਂ ਸਿੱਖ ਅਬਦੁਸ ਸਮਦ ਮਾਂ ਦੇ ਅੱਤਿਆਚਾਰਾਂ ਦਾ ਇਕੱਠੇ ਹੋ ਕੇ ਮੁਕਾਬਲਾ ਨਾ ਕਰ ਸਕੇ ।
4. ਹਾਲਾਤਾਂ ਵਿੱਚ ਤਬਦੀਲੀ (Change in Circumstances) – 1720 ਈ. ਤੋਂ ਬਾਅਦ ਹਾਲਾਤਾਂ ਵਿੱਚ ਕੁਝ ਤਬਦੀਲੀ ਆਉਣੀ ਸ਼ੁਰੂ ਹੋ ਗਈ ਅਤੇ ਸਿੱਖਾਂ ਦੀ ਸਥਿਤੀ ਵਿੱਚ ਸੁਧਾਰ ਹੋਣ ਲੱਗਾ | ਸ਼ਾਹੀ ਦਰਬਾਰ ਸਾਜ਼ਸ਼ਾਂ ਦਾ ਅੱਡਾ ਬਣ ਕੇ ਰਹਿ ਗਿਆ ਸੀ । ਸਿੱਟੇ ਵਜੋਂ ਕੇਂਦਰੀ ਸਰਕਾਰ ਸਿੱਖਾਂ ਵੱਲ ਆਪਣਾ ਲੋੜੀਂਦਾ ਧਿਆਨ ਨਾ ਦੇ ਸਕੀ । ਪੰਜਾਬ ਵਿੱਚ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਵੀ ਈਸਾ ਖਾਂ ਅਤੇ ਹੁਸੈਨ ਖਾਂ ਦੇ ਵਿਦਰੋਹਾਂ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਉਲਝ ਗਿਆ । 1721 ਈ. ਵਿੱਚ ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੇ ਵਿਸਾਖੀ ਵਾਲੇ ਦਿਨ ਅੰਮ੍ਰਿਤਸਰ ਵਿਖੇ ਤੱਤ ਖ਼ਾਲਸਾ ਅਤੇ ਬੰਦਈ ਖ਼ਾਲਸਾ ਵਿਚਾਲੇ ਆਪਸੀ ਸਮਝੌਤਾ ਕਰਵਾ ਦਿੱਤਾ । ਸਿੱਟੇ ਵਜੋਂ ਸਿੱਖ ਮੁੜ ਇੱਕ ਹੋ ਗਏ ।
5. ਸਿੱਖਾਂ ਦੀਆਂ ਕਾਰਵਾਈਆਂ (Activities of the Sikhs) – ਸਥਿਤੀ ਵਿੱਚ ਤਬਦੀਲੀ ਆਉਣ ਨਾਲ ਸਿੱਖਾਂ ਵਿੱਚ ਇੱਕ ਨਵਾਂ ਜੋਸ਼ ਪੈਦਾ ਹੋਇਆ । ਉਨ੍ਹਾਂ ਨੇ ਸੌ-ਸੌ ਸਿੱਖਾਂ ਦੇ ਜੱਥੇ ਬਣਾ ਲਏ ਅਤੇ ਮੁਗ਼ਲ ਪ੍ਰਦੇਸ਼ਾਂ ਵਿੱਚ ਲੁੱਟਮਾਰ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੀ । ਉਨ੍ਹਾਂ ਨੇ ਉਨ੍ਹਾਂ ਹਿੰਦੂ ਅਤੇ ਮੁਸਲਮਾਨਾਂ ਨੂੰ ਸਖ਼ਤ ਸਜ਼ਾਵਾਂ ਦੇਣੀਆਂ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੀਆਂ, ਜਿਨ੍ਹਾਂ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀਆਂ ਇਸਤਰੀਆਂ ਅਤੇ ਬੱਚਿਆਂ ਨੂੰ ਮੁਗ਼ਲਾਂ ਦੇ ਹਵਾਲੇ ਕਰ ਦਿੱਤਾ ਸੀ | ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਸਬਕ ਸਿਖਾਉਣ ਲਈ ਅਸਲਮ ਖ਼ਾਂ ਅਧੀਨ ਕੁਝ ਫ਼ੌਜ ਅੰਮ੍ਰਿਤਸਰ ਭੇਜੀ । ਸਿੱਖਾਂ ਨੇ ਇਸ ਫ਼ੌਜ ‘ਤੇ ਅਚਾਨਕ ਹਮਲਾ ਕਰਕੇ ਉਸ ਨੂੰ ਕਰਾਰੀ ਹਾਰ ਦਿੱਤੀ । ਇਸ ਲੜਾਈ ਵਿੱਚ ਅਸਲਮ ਖਾਂ ਨੂੰ ਲੜਾਈ ਦਾ ਮੈਦਾਨ ਛੱਡ ਕੇ ਨੱਸਣ ਲਈ ਮਜਬੂਰ ਹੋਣਾ ਪਿਆ ।
6. ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੀ ਅਸਫਲਤਾ (Failure of Abdus Samad Khan) – ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਆਪਣੇ ਸਾਰੇ ਯਤਨਾਂ ਦੇ ਬਾਵਜੂਦ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ । ਇਸ ਦੇ ਕਈ ਕਾਰਨ ਸਨ । ਪਹਿਲਾ, ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਬੁੱਢਾ ਹੋ ਗਿਆ ਸੀ ।ਦੂਜਾ, ਸਿੱਖਾਂ ਵਿੱਚ ਆਪਸੀ ਏਕਤਾ ਸਥਾਪਿਤ ਹੋ ਗਈ ਸੀ । ਤੀਸਰਾ, ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਨੂੰ ਮੁਗ਼ਲ ਅਧਿਕਾਰੀਆਂ ਦੀਆਂ ਸਾਜ਼ਸ਼ਾਂ ਦਾ ਸ਼ਿਕਾਰ ਹੋਣਾ ਪਿਆ । ਚੌਥਾ, ਉਸ ਨੂੰ ਕੇਂਦਰ ਤੋਂ ਲੋੜੀਂਦੀ ਸਹਾਇਤਾ ਨਾ ਪ੍ਰਾਪਤ ਹੋਈ । 1726 ਈ. ਵਿੱਚ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਨੂੰ ਉਸ ਦੇ ਅਹੁਦੇ ਤੋਂ ਹਟਾ ਦਿੱਤਾ ਗਿਆ ।
ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਦੇ ਬਾਅਦ ਉਸ ਦਾ ਪੁੱਤਰ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਬਣਿਆ । ਉਹ ਇਸ ਅਹੁਦੇ ‘ਤੇ 1726 ਈ. ਤੋਂ 1745 ਈ. ਤਕ ਰਿਹਾ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੇ ਸ਼ਾਸਨ ਕਾਲ ਅਤੇ ਉਸ ਦੇ ਸਿੱਖਾਂ ਨਾਲ ਸੰਬੰਧਾਂ ਦਾ ਵਰਣਨ ਇਸ ਪ੍ਰਕਾਰ ਹੈ-
1. ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਸਖ਼ਤ ਕਾਰਵਾਈਆਂ (Harsh measures against the Sikhs) – ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਆਪਣਾ ਅਹੁਦਾ ਸੰਭਾਲਦੇ ਹੀ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਲਈ 20,000 ਸੈਨਿਕਾਂ ਨੂੰ ਭਰਤੀ ਕੀਤਾ । ਪਿੰਡਾਂ ਦੇ ਮੁਕੱਦਮਾਂ ਅਤੇ ਚੌਧਰੀਆਂ ਨੂੰ ਇਹ ਆਦੇਸ਼ ਦਿੱਤਾ ਗਿਆ ਕਿ ਉਹ ਆਪਣੇ ਇਲਾਕਿਆਂ ਵਿੱਚ ਸਿੱਖਾਂ ਨੂੰ ਸ਼ਰਨ ਨਾ ਲੈਣ ਦੇਣ । ਉਸ ਨੇ ਇਹ ਐਲਾਨ ਕੀਤਾ ਕਿ ਕਿਸੇ ਸਿੱਖ ਬਾਰੇ ਸੂਹ ਦੇਣ ਵਾਲੇ ਨੂੰ 10 ਰੁਪਏ, ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਵਾਉਣ ਵਾਲੇ ਨੂੰ 25 ਰੁਪਏ, ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਕੇ ਸਰਕਾਰ ਦੇ ਹਵਾਲੇ ਕਰਨ ਵਾਲੇ ਨੂੰ 50 ਰੁਪਏ ਅਤੇ ਸਿਰ ਵੱਢ ਕੇ ਸਰਕਾਰ ਨੂੰ ਭੇਟ ਕਰਨ ਵਾਲੇ ਨੂੰ 100 ਰੁਪਏ ਦਾ ਇਨਾਮ ਦਿੱਤਾ ਜਾਵੇਗਾ । ਇਸ ਤਰ੍ਹਾਂ ਸਿੱਖਾਂ ‘ਤੇ ਮੁੜ ਅੱਤਿਆਚਾਰ ਦਾ ਦੌਰ ਸ਼ੁਰੂ ਹੋ ਗਿਆ । ਸੈਂਕੜੇ ਸਿੱਖਾਂ ਨੂੰ ਲਾਹੌਰ ਦੇ ਦਿੱਲੀ ਗੇਟ ਵਿਖੇ ਸ਼ਹੀਦ ਕੀਤਾ ਜਾਣ ਲੱਗਾ। ਇਸ ਕਾਰਨ ਇਸ ਥਾਂ ਦਾ ਨਾਂ ‘ਸ਼ਹੀਦ ਗੰਜ ਪੈ ਗਿਆ ।
2. ਭਾਈ ਤਾਥਾ ਸਿੰਘ ਜੀ ਵਾਂ ਦੀ ਸ਼ਹੀਦੀ (Martyrdom of Bhai Tara Singh Ji Van) – ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਅੰਮ੍ਰਿਤਸਰ ਜ਼ਿਲ੍ਹੇ ਦੇ ਪਿੰਡ ਵਾਂ ਦੇ ਵਸਨੀਕ ਸਨ । ਉਨ੍ਹਾਂ ਨੇ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੀਆਂ ਲੜਾਈਆਂ ਵਿੱਚ ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਨਿਭਾਈ ਸੀ । ਨੌਸ਼ਹਿਰੇ ਦਾ ਚੌਧਰੀ ਸਾਹਿਬ ਰਾਏ ਸਿੱਖਾਂ ਦੇ ਖੇਤਾਂ ਵਿੱਚ ਆਪਣੇ ਘੋੜੇ ਛੱਡ ਦਿੰਦਾ ਸੀ । ਜਦੋਂ ਸਿੱਖ ਇਸ ਗੱਲ ਦਾ ਇਤਰਾਜ਼ ਕਰਦੇ ਤਾਂ ਉਹ ਸਿੱਖਾਂ ਦਾ ਅਪਮਾਨ ਕਰਦਾ । ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਵਾਂ ਲਈ ਇਹ ਗੱਲ ਅਸਹਿ ਸੀ । ਇੱਕ ਦਿਨ ਉਨ੍ਹਾਂ ਨੇ ਸਾਹਿਬ ਰਾਏ ਦੀ ਇੱਕ ਘੋੜੀ ਨੂੰ ਵੇਚ ਦਿੱਤਾ ਅਤੇ ਮਿਲੇ ਹੋਏ ਪੈਸਿਆਂ ਨੂੰ ਲੰਗਰ ਲਈ ਦੇ ਦਿੱਤਾ । ਇਸ ’ਤੇ ਸਿੱਖਾਂ ਨੂੰ ਸਬਕ ਸਿਖਾਉਣ ਲਈ ਸਾਹਿਬ ਰਾਏ ਨੇ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਤੋਂ ਮਦਦ ਮੰਗੀ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ 2200 ਘੋੜਸਵਾਰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਭੇਜੇ । ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਵਾਂ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ 22 ਸਾਥੀ ਮੁਗ਼ਲਾਂ ਦਾ ਮੁਕਾਬਲਾ ਕਰਦੇ ਹੋਏ ਸ਼ਹੀਦ ਹੋ ਗਏ । ਇਸ ਤੋਂ ਪਹਿਲਾਂ ਉਨ੍ਹਾਂ ਨੇ 300 ਮੁਗ਼ਲ ਸੈਨਿਕਾਂ ਨੂੰ ਯਮਲੋਕ ਪਹੁੰਚਾ ਦਿੱਤਾ ਸੀ । ਇਹ ਘਟਨਾ 1726 ਈ. ਦੀ ਹੈ । ਪ੍ਰਸਿੱਧ ਇਤਿਹਾਸਕਾਰ ਐੱਸ. ਐੱਸ. ਸ਼ੀਤਲ ਅਨੁਸਾਰ,
“ਉਸ (ਤਾਰਾ ਸਿੰਘ ਦੀ ਸ਼ਹੀਦੀ ਦਾ ਸਿੱਖਾਂ ਦੇ ਮਨਾਂ ‘ਤੇ ਡੂੰਘਾ ਅਸਰ ਪਿਆ ।”1
3. ਸਿੱਖਾਂ ਦੀਆਂ ਜਵਾਬੀ ਕਾਰਵਾਈਆਂ (Retaliatory measures of the Sikhs) – ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਵਾਂ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਸਾਥੀਆਂ ਦੀ ਸ਼ਹੀਦੀ ਨੇ ਸਿੱਖਾਂ ਵਿੱਚ ਇੱਕ ਨਵਾਂ ਜੋਸ਼ ਪੈਦਾ ਕਰ ਦਿੱਤਾ । ਉਨ੍ਹਾਂ ਨੇ ਛਾਪਾਮਾਰ ਯੁੱਧਾਂ ਰਾਹੀਂ ਸਰਕਾਰੀ ਖਜ਼ਾਨਿਆਂ ਨੂੰ ਲੁੱਟਣਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ । ਉਨ੍ਹਾਂ ਨੇ ਕਈ ਥਾਂਵਾਂ ‘ਤੇ ਹਮਲਾ ਕਰਕੇ ਸਰਕਾਰ ਦੇ ਪਿੱਛਲੱਗਿਆਂ ਨੂੰ ਮੌਤ ਦੇ ਘਾਟ ਉਤਾਰ ਦਿੱਤਾ । ਜਦੋਂ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਇਨ੍ਹਾਂ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਆਪਣੇ ਸੈਨਿਕਾਂ ਨੂੰ ਭੇਜਦਾ ਤਾਂ ਉਹ ਝਟ ਜੰਗਲਾਂ ਅਤੇ ਪਹਾੜਾਂ ਵਿੱਚ ਜਾ ਛਿਪਦੇ ।
4. ਹੈਦਰੀ ਝੰਡੇ ਦੀ ਘਟਨਾ (Incident of Haidri Flag) – ਮਜਬੂਰ ਹੋ ਕੇ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਦੇ ਦਮਨ ਲਈ ਜ਼ਿਹਾਦ ਦਾ ਨਾਅਰਾ ਲਗਾਇਆ । ਹਜ਼ਾਰਾਂ ਦੀ ਗਿਣਤੀ ਵਿੱਚ ਮੁਸਲਮਾਨ ਇਨਾਇਤ ਉਲਾ ਖਾਂ ਦੇ ਝੰਡੇ ਅਧੀਨ ਆਣ ਇਕੱਠੇ ਹੋਏ । ਉਨ੍ਹਾਂ ਨੂੰ ਈਦ ਦੇ ਮੁਬਾਰਕ ਦਿਨ ਇੱਕ ਹੈਦਰੀ ਝੰਡਾ ਦਿੱਤਾ ਗਿਆ ਅਤੇ ਇਹ ਐਲਾਨ ਕੀਤਾ ਗਿਆ ਕਿ ਇਸ ਝੰਡੇ ਅਧੀਨ ਲੜਨ ਵਾਲਿਆਂ ਨੂੰ ਅੱਲ੍ਹਾ ਜ਼ਰੂਰ ਫ਼ਤਹਿ ਦੇਵੇਗਾ । ਪਰ ਇੱਕ ਦਿਨ ਲਗਭਗ 7 ਹਜ਼ਾਰ ਸਿੱਖਾਂ ਨੇ ਇਨ੍ਹਾਂ ਗਾਜ਼ੀਆਂ ਉੱਤੇ ਅਚਾਨਕ ਹਮਲਾ ਕਰਕੇ ਹਜ਼ਾਰਾਂ ਗਾਜ਼ੀਆਂ ਨੂੰ ਕਤਲ ਕਰ ਦਿੱਤਾ । ਇਸ ਘਟਨਾ ਨਾਲ ਸਰਕਾਰ ਦੇ ਗੌਰਵ ਨੂੰ ਭਾਰੀ ਸੱਟ ਵੱਜੀ ।
5. ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦਾ ਸਿੱਖਾਂ ਨਾਲ ਸਮਝੌਤਾ (Agreement of Zakariya Khan with the Sikhs) – ਹੁਣ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਖੁਸ਼ ਕਰਨ ਦੀ ਨੀਤੀ ਅਪਣਾਈ । ਉਸ ਨੇ 1733 ਈ. ਵਿੱਚ ਐਲਾਨ ਕੀਤਾ ਕਿ ਜੇਕਰ ਸਿੱਖ ਸਰਦਾਰ ਵਿਰੋਧੀ ਕਾਰਵਾਈਆਂ ਨੂੰ ਬੰਦ ਕਰ ਦੇਣ ਤਾਂ ਉਨ੍ਹਾਂ ਨੂੰ ਇੱਕ ਲੱਖ ਰੁਪਏ ਸਾਲਾਨਾ ਆਮਦਨ ਵਾਲੀ ਇੱਕ ਜਾਗੀਰ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਆਗੂ ਨੂੰ “ਨਵਾਬ’ ਦਾ ਖਿਤਾਬ ਦਿੱਤਾ ਜਾਵੇਗਾ । ਪਹਿਲਾਂ ਤਾਂ ਸਿੱਖ ਇਸ ਸਮਝੌਤੇ ਦੇ ਵਿਰੁੱਧ ਸਨ ਪਰ ਬਾਅਦ ਵਿੱਚ ਉਨ੍ਹਾਂ ਨੇ ਇਸ ਨੂੰ ਸਵੀਕਾਰ ਕਰ ਲਿਆ । ਸਿੱਖਾਂ ਨੇ ਨਵਾਬ ਦੀ ਪਦਵੀ ਸਰਦਾਰ ਕਪੂਰ ਸਿੰਘ ਫ਼ੈਜ਼ਲਪੁਰੀਆ ਨੂੰ ਦਿੱਤੀ ।
6. ਬੁੱਢਾ ਦਲ ਤੇ ਤਰੁਣਾ ਦਲ ਦਾ ਸੰਗਠਨ (Organisation of Buddha Dal and Taruna Dal) – ਮੁਗਲਾਂ ਨਾਲ ਸਮਝੌਤਾ ਹੋ ਜਾਣ ਨਾਲ ਨਵਾਬ ਕਪੂਰ ਸਿੰਘ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਇਹ ਸੁਨੇਹਾ ਭੇਜਿਆ ਕਿ ਉਹ ਮੁੜ ਆਪਣੇ ਘਰਾਂ ਵਿੱਚ ਆ ਜਾਣ । 1734 ਈ. ਵਿੱਚ ਨਵਾਬ ਕਪੂਰ ਸਿੰਘ ਨੇ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਮਜ਼ਬੂਤ ਕਰਨ ਦੇ ਉਦੇਸ਼ ਨਾਲ ਉਨ੍ਹਾਂ ਨੂੰ ਦੋ ਜੱਥਿਆਂ ਵਿੱਚ ਸੰਗਠਿਤ ਕਰ ਦਿੱਤਾ । ਇਹ ਜੱਥੇ ਸਨ-ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ । ਬੁੱਢਾ ਦਲ ਵਿੱਚ 40 ਸਾਲਾਂ ਤੋਂ ਵਡੇਰੀ ਉਮਰ ਦੇ ਸਿੱਖਾਂ ਨੂੰ ਸ਼ਾਮਲ ਕੀਤਾ ਗਿਆ ਅਤੇ ਤਰੁਣਾ ਦਲ ਵਿੱਚ ਉਸ ਤੋਂ ਘੱਟ ਦੀ ਉਮਰ ਵਾਲੇ ਸਿੱਖਾਂ ਨੂੰ । ਤਰੁਣਾ ਦਲ ਨੂੰ ਅੱਗੇ ਪੰਜ ਜੱਥਿਆਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ ਸੀ । ਬੁੱਢਾ ਦਲ ਧਾਰਮਿਕ ਸਥਾਨਾਂ ਦੀ ਦੇਖਭਾਲ ਕਰਦਾ ਸੀ । ਤਰੁਣਾ ਦਲ ਦੁਸ਼ਮਣਾਂ ਦਾ ਮੁਕਾਬਲਾ ਕਰਦਾ ਸੀ ।
7. ਮੁਗ਼ਲਾਂ ਅਤੇ ਸਿੱਖਾਂ ਵਿਚਾਲੇ ਦੁਬਾਰਾ ਸੰਘਰਸ਼ (Renewed struggle between the Mughals and the Sikhs) – ਆਪਣੀ ਸ਼ਕਤੀ ਨੂੰ ਸੰਗਠਿਤ ਕਰਨ ਤੋਂ ਬਾਅਦ ਸਿੱਖਾਂ ਨੇ ਆਪਣੀਆਂ ਸੈਨਿਕ ਕਾਰਵਾਈਆਂ ਮੁੜ ਆਰੰਭ ਕਰ ਦਿੱਤੀਆਂ ਸਨ । ਉਨ੍ਹਾਂ ਨੇ ਸ਼ਾਹੀ ਖ਼ਜ਼ਾਨਿਆਂ ਨੂੰ ਮੁੜ ਲੁੱਟਣਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ ਸੀ । ਇਸ ਕਾਰਨ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਗੁੱਸੇ ਵਿੱਚ ਆ ਕੇ ਸਿੱਖਾਂ ਨੂੰ ਦਿੱਤੀ ਗਈ ਜਾਗੀਰ ਨੂੰ 1735 ਈ. ਵਿੱਚ ਜ਼ਬਤ ਕਰ ਲਿਆ । ਸਿੱਖਾਂ ਨੂੰ ਮੁੜ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਕੇ ਕਤਲ ਕਰਨਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ ਗਿਆ । ਸਿੱਟੇ ਵਜੋਂ ਸਿੱਖ ਜੰਗਲਾਂ ਵੱਲ ਚਲੇ ਗਏ । ਇਸ ਮੌਕੇ ਦਾ ਫਾਇਦਾ ਉਠਾ ਕੇ ਮੁਗ਼ਲਾਂ ਨੇ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਉੱਤੇ ਕਬਜ਼ਾ ਕਰ ਲਿਆ ।

8. ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਦੀ ਸ਼ਹੀਦੀ (Martyrdom of Bhai Mani Singh Ji) – ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ 1721 ਈ. ਤੋਂ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਦੇ ਮੁੱਖ ਗ੍ਰੰਥੀ ਚਲੇ ਆ ਰਹੇ ਸਨ ।ਉਨ੍ਹਾਂ ਨੇ 1738 ਈ. ਵਿੱਚ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੂੰ ਇਹ ਬੇਨਤੀ ਕੀਤੀ ਕਿ ਜੇਕਰ ਉਹ ਸਿੱਖਾਂ ਨੂੰ ਦੀਵਾਲੀ ਦੇ ਮੌਕੇ ‘ਤੇ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਆਉਣ ਦੀ ਇਜਾਜ਼ਤ ਦੇਵੇ ਤਾਂ ਉਹ 5,000 ਰੁਪਏ ਉਸ ਨੂੰ ਭੇਟ ਕਰਨਗੇ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਇਹ ਪੇਸ਼ਕਸ਼ ਸਵੀਕਾਰ ਕਰ ਲਈ । ਪਰ ਹਾਲੇ ਸਿੱਖ ਅੰਮ੍ਰਿਤਸਰ ਵਿੱਚ ਇਕੱਠੇ ਹੋ ਹੀ ਰਹੇ ਸਨ ਕਿ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੇ ਸੈਨਿਕਾਂ ਨੇ ਹਮਲਾ ਕਰ ਦਿੱਤਾ । ਸਿੱਟੇ ਵਜੋਂ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਵਿੱਚ ਦੀਵਾਲੀ ਦਾ ਮੇਲਾ ਨਾ ਮਨਾਇਆ ਜਾ ਸਕਿਆ । ਜ਼ਕਰੀਆ ਖਾਂ ਨੇ ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਤੋਂ 5,000 ਰੁਪਏ ਦੀ ਮੰਗ ਕੀਤੀ । ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਇਹ ਪੈਸਾ ਨਾ ਦੇ ਸਕੇ । ਇਸ ਲਈ ਉਨ੍ਹਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਕੇ ਲਾਹੌਰ ਭੇਜ ਦਿੱਤਾ ਗਿਆ | ਭਾਈ ਸਾਹਿਬ ਜੀ ਨੂੰ ਇਸਲਾਮ ਹਿਣ ਕਰਨ ਲਈ ਕਿਹਾ ਗਿਆ ਪਰ ਉਨ੍ਹਾਂ ਨੇ ਇਨਕਾਰ ਕਰ ਦਿੱਤਾ । ਸਿੱਟੇ ਵਜੋਂ ਉਨ੍ਹਾਂ ਨੂੰ 1738 ਈ. ਵਿੱਚ ਤਸੀਹੇ ਦੇ ਕੇ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ਗਿਆ । ਇਸ ਘਟਨਾ ਨਾਲ ਸਿੱਖਾਂ ਵਿੱਚ ਗੁੱਸੇ ਦੀ ਲਹਿਰ ਦੌੜ ਗਈ । ਪ੍ਰਸਿੱਧ ਇਤਿਹਾਸਕਾਰ ਖੁਸ਼ਵੰਤ ਸਿੰਘ ਦੇ ਵਿਚਾਰ ਅਨੁਸਾਰ,
‘‘ਪਵਿੱਤਰ ਅਤੇ ਪੂਜਣ ਯੋਗ ਮੁੱਖ ਪੁਜਾਰੀ (ਭਾਈ ਮਨੀ ਸਿੰਘ ਦੀ ਕੁਰਬਾਨੀ ਕਾਰਨ ਸਿੱਖ ਭੜਕ ਉਠੇ ।’’ 1
9. ਸਿੱਖਾਂ ਦਾ ਨਾਦਰ ਸ਼ਾਹ ਨੂੰ ਲੁੱਟਣਾ (Sikhs robbed Nadir Shah) – 1739 ਈ. ਵਿੱਚ ਨਾਦਰ ਸ਼ਾਹ ਦਿੱਲੀ ਵਿੱਚ ਭਾਰੀ ਲੁੱਟਮਾਰ ਕਰਕੇ ਪੰਜਾਬ ਵਿੱਚੋਂ ਹੁੰਦਾ ਹੋਇਆ ਵਾਪਸ ਈਰਾਨ ਜਾ ਰਿਹਾ ਸੀ । ਜਦੋਂ ਸਿੱਖਾਂ ਨੂੰ ਇਸ ਬਾਰੇ ਸੂਚਨਾ ਮਿਲੀ ਤਾਂ ਉਨ੍ਹਾਂ ਨੇ ਅਚਾਨਕ ਹਮਲਾ ਕਰਕੇ ਉਸ ਦਾ ਬਹੁਤ ਸਾਰਾ ਖ਼ਜ਼ਾਨਾ ਲੁੱਟ ਲਿਆ । ਨਾਦਰ ਸ਼ਾਹ ਨੇ ਜ਼ਕਰੀਆ ਖਾਂ ਨੂੰ ਇਹ ਚੇਤਾਵਨੀ ਦਿੱਤੀ ਕਿ ਛੇਤੀ ਹੀ ਸਿੱਖ ਪੰਜਾਬ ਦੇ ਸ਼ਾਸਕ ਬਣ ਜਾਣਗੇ ।
10. ਜ਼ਕਰੀਆ ਖਾਂ ਦੁਆਰਾ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਸਖ਼ਤ ਕਾਰਵਾਈਆਂ (Strong actions against the Sikhs by Zakariya Khan) – ਨਾਦਰ ਸ਼ਾਹ ਦੀ ਚੇਤਾਵਨੀ ਦਾ ਜ਼ਕਰੀਆ ਖਾਂ ਦੇ ਮਨ ’ਤੇ ਬੜਾ ਡੂੰਘਾ ਅਸਰ ਪਿਆ । ਉਸ ਨੇ ਸਿੱਖਾਂ ਦਾ ਮਲੀਆਮੇਟ ਕਰਨ ਲਈ ਅਨੇਕਾਂ ਕਦਮ ਚੁੱਕੇ । ਸਿੱਖਾਂ ਦਾ ਇੱਕ ਵਾਰੀ ਫਿਰ ਰੋਜ਼ਾਨਾ ਬੜੇ ਜ਼ਾਲਮਾਨਾ ਢੰਗ ਨਾਲ ਕਤਲ ਕੀਤਾ ਜਾਣ ਲੱਗਾ | ਕੁਝ ਪ੍ਰਸਿੱਧ ਸ਼ਹੀਦਾਂ ਦਾ ਵਰਣਨ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ-
(ੳ) ਭਾਈ ਬੋਤਾ ਸਿੰਘ ਜੀ (Bhai Bota Singh Ji) – ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਅਨੇਕਾਂ ਸਿੱਖਾਂ ਨੂੰ ਕਤਲ ਕਰਨ ਤੋਂ ਬਾਅਦ ਇਹ ਘੋਸ਼ਣਾ ਕੀਤੀ ਕਿ ਉਸ ਨੇ ਸਿੱਖਾਂ ਦਾ ਨਾਮੋ-ਨਿਸ਼ਾਨ ਖ਼ਤਮ ਕਰ ਦਿੱਤਾ ਹੈ । ਸਿੱਖਾਂ ਦੀ ਹੋਂਦ ਨੂੰ ਦਰਸਾਉਣ ਲਈ ਭਾਈ ਬੋਤਾ ਸਿੰਘ ਜੀ ਨੇ ਸਰਾਇ ਨਦੀਨ ਵਿਖੇ ਇੱਕ ਚੌਕੀ ਕਾਇਮ ਕਰ ਲਈ ਅਤੇ ਉੱਥੋਂ ਚੰਗੀ ਕਰ ਲੈਣਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਉਸ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਨ ਲਈ ਕੁਝ ਫ਼ੌਜ ਭੇਜੀ । ਭਾਈ ਬੋਤਾ ਸਿੰਘ ਜੀ ਆਪਣੇ ਦੁਸ਼ਮਣਾਂ ਦਾ ਡਟ ਕੇ ਮੁਕਾਬਲਾ ਕਰਦੇ ਹੋਏ ਸ਼ਹੀਦ ਹੋ ਗਏ ।
(ਅ) ਭਾਈ ਮਹਿਤਾਬ ਸਿੰਘ ਜੀ ਅਤੇ ਭਾਈ ਸੁੱਖਾ ਸਿੰਘ ਜੀ (Bhai Mehtab Singh Ji and Bhai Sukha Singh Ji) – ਅੰਮ੍ਰਿਤਸਰ ਜ਼ਿਲ੍ਹੇ ਦੇ ਮੰਡਿਆਲਾ ਪਿੰਡ ਦਾ ਚੌਧਰੀ ਮੱਸਾ ਰੰਗੜ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਦੀ ਪਵਿੱਤਰਤਾ ਨੂੰ ਭੰਗ ਕਰ ਰਿਹਾ ਸੀ । ਇਸ ਕਾਰਨ ਸਿੱਖ ਉਸ ਨੂੰ ਇੱਕ ਸਬਕ ਸਿਖਾਉਣਾ ਚਾਹੁੰਦੇ ਸਨ । ਇੱਕ ਦਿਨ ਭਾਈ ਮਹਿਤਾਬ ਸਿੰਘ ਜੀ ਅਤੇ ਭਾਈ ਸੁੱਖਾ ਸਿੰਘ ਜੀ ਕੁਝ ਬੋਰੀਆਂ ਵਿੱਚ ਥੱਲੇ ਪੱਥਰ ਭਰ ਕੇ ਅਤੇ ਉੱਤੇ ਕੁਝ ਸਿੱਕੇ ਭਰ ਕੇ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਪਹੁੰਚ ਗਏ | ਸੈਨਿਕਾਂ ਦੁਆਰਾ ਪੁੱਛਣ ‘ਤੇ ਉਨ੍ਹਾਂ ਨੇ ਦੱਸਿਆ ਕਿ ਉਹ ਮਾਮਲਾ ਉਗਰਾਹ ਕੇ ਲਿਆਏ ਹਨ । ਮੱਸਾ ਰੰਗੜ ਸਿੱਕੇ ਨਾਲ ਭਰੀਆਂ ਬੋਰੀਆਂ ਵੇਖ ਕੇ ਬੜਾ ਖ਼ੁਸ਼ ਹੋਇਆ । ਜਿਵੇਂ ਹੀ ਉਹ ਇਨ੍ਹਾਂ ਬੋਰੀਆਂ ਨੂੰ ਸਵੀਕਾਰ ਕਰਨ ਲਈ ਥੱਲੇ ਝੁਕਿਆ ਉਸੇ ਸਮੇਂ ਭਾਈ ਮਹਿਤਾਬ ਸਿੰਘ ਜੀ ਨੇ ਆਪਣੀ ਤਲਵਾਰ ਦੇ ਇੱਕੋ ਵਾਰ ਨਾਲ ਉਸ ਦਾ ਸਿਰ ਧੜ ਨਾਲੋਂ ਵੱਖ ਕਰ ਦਿੱਤਾ । ਬਾਅਦ ਵਿੱਚ ਭਾਈ ਮਹਿਤਾਬ ਸਿੰਘ ਜੀ ਅਤੇ ਭਾਈ ਸੁੱਖਾ ਸਿੰਘ ਜੀ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਕੇ ਬੜੀ ਬੇਰਹਿਮੀ ਨਾਲ 1740 ਈ. ਵਿੱਚ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ਗਿਆ ।
(ੲ) ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਜੀ (Bal Haqiqat Rai Ji) – ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਜੀ ਸਿਆਲਕੋਟ ਦੇ ਰਹਿਣ ਵਾਲੇ ਸਨ । ਇੱਕ ਦਿਨ ਕੁਝ ਮੁਸਲਮਾਨ ਮੁੰਡਿਆਂ ਨੇ ਹਿੰਦੂ ਦੇਵੀ-ਦੇਵਤਿਆਂ ਦੀ ਸ਼ਾਨ ਵਿੱਚ ਕੁਝ ਅਪਮਾਨ-ਜਨਕ ਸ਼ਬਦ ਕਹੇ | ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਜੀ ਇਹ ਸਹਿਣ ਨਾ ਕਰ ਸਕੇ ।ਉਨ੍ਹਾਂ ਨੇ ਹਜ਼ਰਤ ਮੁਹੰਮਦ ਬਾਰੇ ਕੁਝ ਅਯੋਗ ਸ਼ਬਦ ਕਹਿ ਦਿੱਤੇ । ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਜੀ `ਤੇ ਮੁਕੱਦਮਾ ਚਲਾਇਆ ਗਿਆ ਅਤੇ ਮੌਤ ਦੀ ਸਜ਼ਾ ਸੁਣਾਈ ਗਈ । ਇਹ ਘਟਨਾ 1742 ਈ. ਦੀ ਹੈ । ਇਸ ਘਟਨਾ ਕਾਰਨ ਲੋਕਾਂ ਨੇ ਜ਼ਾਲਮ ਮੁਗਲ ਸ਼ਾਸਨ ਦਾ ਅੰਤ ਕਰਨ ਦੀ ਸਹੁੰ ਚੁੱਕੀ ।
(ਸ) ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ Bhai Taru Singh Ji) – ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਮਾਝੇ ਦੇ ਇਲਾਕੇ ਦੇ ਪਿੰਡ ਪੂਹਲਾ ਦੇ ਨਿਵਾਸੀ ਸਨ । ਉਹ ਆਪਣੀ ਆਮਦਨ ਤੋਂ ਸਿੱਖਾਂ ਦੀ ਮੱਦਦ ਕਰਦੇ ਸਨ । ਸਰਕਾਰ ਦੀਆਂ ਨਜ਼ਰਾਂ ਵਿੱਚ ਇਹ ਇੱਕ ਘੋਰ ਅਪਰਾਧ ਸੀ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਨੂੰ ਲਾਹੌਰ ਬੁਲਾ ਕੇ ਇਸਲਾਮ ਧਰਮ ਗ੍ਰਹਿਣ ਕਰਨ ਲਈ ਕਿਹਾ । ਭਾਈ ਸਾਹਿਬ ਜੀ ਨੇ ਕਿਹਾ ਕਿ ਉਹ ਕਿਸੇ ਵੀ ਕੀਮਤ ‘ਤੇ ਸਤਿਰੂ ਦੀ ਦਿੱਤੀ ਪਵਿੱਤਰ ਦਾਤ ਕੇਸਾਂ ਨੂੰ ਨਹੀਂ ਦੇ ਸਕਦੇ ਹਾਂ ਉਹ ਆਪਣੇ ਕੇਸ ਆਪਣੀ ਖੋਪਰੀ ਨਾਲ ਹੀ ਉਤਰਵਾ ਸਕਦੇ ਹਨ । ਇਸ ’ਤੇ ਜੱਲਾਦਾਂ ਨੇ ਭਾਈ ਸਾਹਿਬ ਦੀ ਖੋਪਰੀ ਨੂੰ ਉਤਾਰ ਦਿੱਤਾ । ਜਦੋਂ ਭਾਈ ਸਾਹਿਬ ਜੀ ਦੀ ਖੋਪਰੀ ਉਤਾਰੀ ਜਾ ਰਹੀ ਸੀ ਤਾਂ ਉਹ ਜਪੁਜੀ ਸਾਹਿਬ ਦਾ ਪਾਠ ਕਰ ਰਹੇ ਸਨ । ਇਹ ਘਟਨਾ 1745 ਈ. ਦੀ ਹੈ । ਇਸ ਲਾਸਾਨੀ ਸ਼ਹਾਦਤ ਨੇ ਸਿੱਖਾਂ ਵਿੱਚ ਇੱਕ ਨਵਾਂ ਜੋਸ਼ ਪੈਦਾ ਕੀਤਾ |
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ (Death of Zakariya Khan) – ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਨਿਰਸੰਦੇਹ ਆਪਣੇ ਕਾਲ ਵਿੱਚ ਸਿੱਖਾਂ ਉੱਤੇ ਘੋਰ ਅੱਤਿਆਚਾਰ ਕੀਤੇ ।ਉਹ ਆਪਣੇ ਅਣਥੱਕ ਯਤਨਾਂ ਦੇ ਬਾਵਜੂਦ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ । 1 ਜੁਲਾਈ, 1745 ਈ. ਨੂੰ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ ਹੋ ਗਈ । ਪਤਵੰਤ ਸਿੰਘ ਦਾ ਇਹ ਕਹਿਣਾ ਬਿਲਕੁਲ ਠੀਕ ਹੈ, .
‘‘ਕਿਸੇ ਨੇ ਵੀ ਸਿੱਖਾਂ ਦਾ ਇਸ ਤੋਂ ਵੱਧ ਉਤਸ਼ਾਹ ਨਾਲ ਮਨ ਨਹੀਂ ਕੀਤਾ ਜਿੰਨਾ ਕਿ ਜ਼ਕਰੀਆ ਖਾਂ ਨੇ ।” 1
![]()
ਯਾਹੀਆ ਖ਼ਾਂ 1746-47 ਈ. (Yahiya Khan 1746-47 A.D.)
ਪ੍ਰਸ਼ਨ 4.
ਯਾਹੀਆ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਦੀ ਤਾਕਤ ਨੂੰ ਕੁਚਲਣ ਲਈ ਕੀ ਕਦਮ ਚੁੱਕੇ ? (What steps were taken by Yahiya Khan to crush the power of the Sikhs ?)
ਉੱਤਰ-
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ ਤੋਂ ਬਾਅਦ ਯਾਹੀਆ ਖ਼ਾਂ ਦਿੱਲੀ ਦੇ ਵਜ਼ੀਰ ਕਮਰਉੱਦੀਨ ਦੇ ਸਹਿਯੋਗ ਸਦਕਾ 1746 ਈ. ਵਿੱਚ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਬਣਿਆ । ਉਹ 1747 ਈ. ਤਕ ਇਸ ਅਹੁਦੇ ‘ਤੇ ਰਿਹਾ । ਸਿੱਖਾਂ ਉੱਤੇ ਅੱਤਿਆਚਾਰ ਕਰਨ ਵਿੱਚ ਉਹ ਆਪਣੇ ਪਿਤਾ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਤੋਂ ਇੱਕ ਕਦਮ ਅੱਗੇ ਸੀ ।
1. ਸਿੱਖਾਂ ਦੀਆਂ ਕਾਰਵਾਈਆਂ (Activities of the Sikhs) – ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ ਦਾ ਲਾਭ ਉਠਾ ਕੇ ਸਿੱਖਾਂ ਨੇ ਆਪਣੀ ਸ਼ਕਤੀ ਨੂੰ ਸੰਗਠਿਤ ਕਰ ਲਿਆ ਸੀ ।ਉਨ੍ਹਾਂ ਨੇ ਪੰਜਾਬ ਦੇ ਕਈ ਪਿੰਡਾਂ ਦੇ ਚੌਧਰੀਆਂ ਅਤੇ ਮੁਕੱਦਮਾਂ ਨੂੰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕਾਰਵਾਈਆਂ ਕਰਨ ਕਰਕੇ ਮੌਤ ਦੇ ਘਾਟ ਉਤਾਰ ਦਿੱਤਾ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਸਿੱਖ ਜੱਥਿਆਂ ਨੇ ਪੰਜਾਬ ਦੇ ਕਈ ਦੇਸ਼ਾਂ ਵਿੱਚ ਆਪਣੀਆਂ ਲੁੱਟਮਾਰ ਦੀਆਂ ਕਾਰਵਾਈਆਂ ਤੇਜ਼ ਕਰ ਦਿੱਤੀਆਂ ਸਨ ।
2. ਜਸਪਤ ਰਾਏ ਦੀ ਮੌਤ (Death of Jaspat Rai) – 1746 ਈ. ਵਿੱਚ ਸਿੱਖਾਂ ਦੇ ਇੱਕ ਜੱਥੇ ਨੇ ਗੋਂਦਲਾਂਵਾਲਾ ਪਿੰਡ ਤੋਂ ਬਹੁਤ ਸਾਰੀਆਂ ਭੇਡ-ਬੱਕਰੀਆਂ ਨੂੰ ਫੜ ਲਿਆ । ਲੋਕਾਂ ਦੀ ਸ਼ਿਕਾਇਤ ‘ਤੇ ਜਸਪਤ ਰਾਏ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਇਹ ਭੇਡ-ਬੱਕਰੀਆਂ ਵਾਪਸ ਕਰਨ ਦਾ ਆਦੇਸ਼ ਦਿੱਤਾ । ਸਿੱਖਾਂ ਦੇ ਇਨਕਾਰ ਕਰਨ ‘ਤੇ ਉਸ ਨੇ ਸਿੱਖਾਂ ‘ਤੇ ਹਮਲਾ ਕਰ ਦਿੱਤਾ | ਲੜਾਈ ਦੇ ਦੌਰਾਨ ਜਸਪਤ ਰਾਏ ਮਾਰਿਆ ਗਿਆ । ਇਸ ਕਾਰਨ ਮੁਗ਼ਲ ਫ਼ੌਜ ਵਿੱਚ ਭਾਜੜ ਪੈ ਗਈ ।
3. ਲਖਪਤ ਰਾਏ ਦੀ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕਾਰਵਾਈ (Action of Lakhpat Rai against the Sikhs) – ਜਸਪਤ ਰਾਏ ਦੀ ਮੌਤ ਦੀ ਖ਼ਬਰ ਸੁਣ ਕੇ ਉਸ ਦਾ ਭਰਾ ਦੀਵਾਨ ਲਖਪਤ ਰਾਏ ਅੱਗ-ਬਬੂਲਾ ਹੋ ਗਿਆ । ਉਸ ਨੇ ਇਹ ਪ੍ਰਣ ਕੀਤਾ ਕਿ ਉਹ ਸਿੱਖਾਂ ਦਾ ਨਾਮੋ-ਨਿਸ਼ਾਨ ਮਿਟਾ ਕੇ ਹੀ ਸੁੱਖ ਦਾ ਸਾਹ ਲਵੇਗਾ। ਉਸ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਉਨ੍ਹਾਂ ਦੇ ਧਰਮ ਗ੍ਰੰਥ ਪੜ੍ਹਨ ‘ਤੇ ਪਾਬੰਦੀ ਲਗਾ ਦਿੱਤੀ । ਉਸ ਨੇ ਗੁਰੂ ਸ਼ਬਦ ਦੀ ਵਰਤੋਂ ਦੀ ਵੀ ਮਨਾਹੀ ਕਰ ਦਿੱਤੀ । ਇਸ ਉਦੇਸ਼ ਨਾਲ ਉਸ ਨੇ ਗੁੜ ਦੀ ਥਾਂ ਲੋਕਾਂ ਨੂੰ ਰੋੜੀ ਸ਼ਬਦ ਦੀ ਵਰਤੋਂ ਕਰਨ ਲਈ ਕਿਹਾ ਕਿਉਂਕਿ ਗੁੜ ਸ਼ਬਦ ਦੀ ਆਵਾਜ਼ ਗੁਰੂ ਦੇ ਨਾਲ ਮਿਲਦੀ-ਜੁਲਦੀ ਸੀ । ਇਸੇ ਤਰ੍ਹਾਂ ਗ੍ਰੰਥ ਦੀ ਥਾਂ ਪੋਥੀ ਸ਼ਬਦ ਦੀ ਵਰਤੋਂ ਕਰਨ ਦਾ ਆਦੇਸ਼ ਦਿੱਤਾ ਗਿਆ । ਇਨ੍ਹਾਂ ਆਦੇਸ਼ਾਂ ਦੀ ਉਲੰਘਣਾ ਕਰਨ ਵਾਲਿਆਂ ਨੂੰ ਮੌਤ ਦੀ ਸਜ਼ਾ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ । ਉਸ ਨੇ ਬਹੁਤ ਸਾਰੇ ਸਿੱਖਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਲਾਹੌਰ ਲਿਜਾ ਕੇ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ।
4. ਪਹਿਲਾ ਘੱਲੂਘਾਰਾ (First Holocaust) – 1746 ਈ. ਵਿੱਚ ਯਾਹੀਆ ਖ਼ਾਂ ਤੇ ਲਖਪਤ ਰਾਏ ਦੇ ਅਧੀਨ ਮੁਗ਼ਲ ਸੈਨਾ ਨੇ ਲਗਭਗ 15,000 ਸਿੱਖਾਂ ਨੂੰ ਕਾਹਨੂੰਵਾਨ ਵਿਖੇ ਘੇਰ ਲਿਆ । ਸਿੱਖ ਬਸੌਲੀ ਦੀਆਂ ਪਹਾੜੀਆਂ ਵੱਲ ਚਲੇ ਗਏ । ਮੁਗਲ ਸੈਨਿਕਾਂ ਨੇ ਉਨ੍ਹਾਂ ਦਾ ਪਿੱਛਾ ਕੀਤਾ । ਸਿੱਖ ਬੜੀ ਮੁਸ਼ਕਿਲ ਵਿੱਚ ਫਸ ਗਏ । ਇੱਕ ਪਾਸੇ ਉੱਚੀਆਂ ਪਹਾੜੀਆਂ ਸਨ ਅਤੇ ਦੂਜੇ ਪਾਸੇ ਦਰਿਆ ਰਾਵੀ ਵਿੱਚ ਹੜ੍ਹ ਆਇਆ ਹੋਇਆ ਸੀ । ਪਿਛਲੇ ਪਾਸੇ ਮੁਗ਼ਲ ਸੈਨਿਕ ਉਨ੍ਹਾਂ ਦਾ ਪਿੱਛਾ ਕਰ ਰਹੇ ਸਨ । ਇਸ ਹਮਲੇ ਵਿੱਚ 7,000 ਸਿੱਖ ਸ਼ਹੀਦ ਹੋ ਗਏ ਅਤੇ 3,000 ਸਿੱਖਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਗਿਆ । ਇਨ੍ਹਾਂ ਸਿੱਖਾਂ ਨੂੰ ਲਾਹੌਰ ਵਿਖੇ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ਗਿਆ । ਸਿੱਖਾਂ ਦੇ ਇਤਿਹਾਸ ਵਿੱਚ ਇਹ ਪਹਿਲਾ ਮੌਕਾ ਸੀ ਜਦੋਂ ਸਿੱਖਾਂ ਦਾ ਇੱਕੋ ਵਾਰੀ ਇੰਨਾ ਭਾਰੀ ਜਾਨੀ ਨੁਕਸਾਨ ਹੋਇਆ ਸੀ । ਇਸ ਦਰਦਨਾਕ ਘਟਨਾ ਨੂੰ ਇਤਿਹਾਸ ਵਿੱਚ ਪਹਿਲਾ ਜਾਂ ਛੋਟਾ ਘੱਲੂਘਾਰਾ ਦੇ ਨਾਂ ਨਾਲ ਯਾਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਗੁਰਬਖ਼ਸ਼ ਸਿੰਘ ਦਾ ਕਹਿਣਾ ਬਿਲਕੁਲ ਠੀਕ ਹੈ,
1746 ਦੇ ਤਬਾਹਕੁੰਨ ਝਟਕੇ ਨੇ ਸਿੱਖਾਂ ਦੇ ਇਸ ਵਿਸ਼ਵਾਸ ਨੂੰ ਹੋਰ ਬਲ ਪ੍ਰਦਾਨ ਕੀਤਾ ਕਿ ਉਹ ਅੱਤਿਆਚਾਰੀਆਂ ਦਾ ਸਰਵਨਾਸ਼ ਕਰਨ ’’ 1
5. ਯਾਹੀਆ ਖਾਂ ਦਾ ਪਤਨ (Fall of Yahiya Khan) – ਨਵੰਬਰ, 1746 ਈ. ਵਿੱਚ ਯਾਹੀਆ ਖ਼ਾਂ ਦੇ ਛੋਟੇ ਭਰਾ ਸ਼ਾਹਨਵਾਜ਼ ਖਾਂ ਨੇ ਵਿਦਰੋਹ ਕਰ ਦਿੱਤਾ । ਇਹ ਵਿਦਰੋਹ ਚਾਰ ਮਹੀਨੇ ਤਕ ਜਾਰੀ ਰਿਹਾ । ਇਸ ਵਿਦਰੋਹ ਵਿੱਚ ਸ਼ਾਹਨਵਾਜ਼ ਖਾਂ ਸਫਲ ਰਿਹਾ ਤੇ ਉਸ ਨੇ ਯਾਹੀਆ ਖ਼ਾਂ ਨੂੰ 17 ਮਾਰਚ, 1747 ਈ. ਨੂੰ ਜੇਲ੍ਹ ਵਿੱਚ ਸੁੱਟ ਦਿੱਤਾ । ਇਸ ਤਰ੍ਹਾਂ ਉਸ ਦੇ ਅੱਤਿਆਚਾਰਾਂ ਦਾ ਅੰਤ ਹੋਇਆ ।
ਪ੍ਰਸ਼ਨ 5.
1726-1746 ਤਕ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਅਤੇ ਯਾਹੀਆ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਦੀ ਤਾਕਤ ਨੂੰ ਕੁਚਲਣ ਲਈ ਕੀ ਕਦਮ ਚੁੱਕੇ ? (What steps were taken by Zakariya Khan and Yahiya Khan from 1726-1746 in order to crush the power of the Sikhs ?)
ਜਾਂ
ਜ਼ਕਰੀਆ ਖਾਂ ਅਤੇ ਯਾਹੀਆ ਖ਼ਾਂ ਦੇ ਅਧੀਨ ਸਿੱਖਾਂ ‘ਤੇ ਕੀਤੇ ਗਏ ਜ਼ੁਲਮਾਂ ਦਾ ਵਰਣਨ ਕਰੋ । (Describe the persecution of the Sikhs during the rule of Zakariya Khan and Yahiya Khan.)
ਉੱਤਰ-
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ ਤੋਂ ਬਾਅਦ ਯਾਹੀਆ ਖ਼ਾਂ ਦਿੱਲੀ ਦੇ ਵਜ਼ੀਰ ਕਮਰਉੱਦੀਨ ਦੇ ਸਹਿਯੋਗ ਸਦਕਾ 1746 ਈ. ਵਿੱਚ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਬਣਿਆ । ਉਹ 1747 ਈ. ਤਕ ਇਸ ਅਹੁਦੇ ‘ਤੇ ਰਿਹਾ । ਸਿੱਖਾਂ ਉੱਤੇ ਅੱਤਿਆਚਾਰ ਕਰਨ ਵਿੱਚ ਉਹ ਆਪਣੇ ਪਿਤਾ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਤੋਂ ਇੱਕ ਕਦਮ ਅੱਗੇ ਸੀ ।
1. ਸਿੱਖਾਂ ਦੀਆਂ ਕਾਰਵਾਈਆਂ (Activities of the Sikhs) – ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ ਦਾ ਲਾਭ ਉਠਾ ਕੇ ਸਿੱਖਾਂ ਨੇ ਆਪਣੀ ਸ਼ਕਤੀ ਨੂੰ ਸੰਗਠਿਤ ਕਰ ਲਿਆ ਸੀ ।ਉਨ੍ਹਾਂ ਨੇ ਪੰਜਾਬ ਦੇ ਕਈ ਪਿੰਡਾਂ ਦੇ ਚੌਧਰੀਆਂ ਅਤੇ ਮੁਕੱਦਮਾਂ ਨੂੰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕਾਰਵਾਈਆਂ ਕਰਨ ਕਰਕੇ ਮੌਤ ਦੇ ਘਾਟ ਉਤਾਰ ਦਿੱਤਾ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਸਿੱਖ ਜੱਥਿਆਂ ਨੇ ਪੰਜਾਬ ਦੇ ਕਈ ਦੇਸ਼ਾਂ ਵਿੱਚ ਆਪਣੀਆਂ ਲੁੱਟਮਾਰ ਦੀਆਂ ਕਾਰਵਾਈਆਂ ਤੇਜ਼ ਕਰ ਦਿੱਤੀਆਂ ਸਨ ।
2. ਜਸਪਤ ਰਾਏ ਦੀ ਮੌਤ (Death of Jaspat Rai) – 1746 ਈ. ਵਿੱਚ ਸਿੱਖਾਂ ਦੇ ਇੱਕ ਜੱਥੇ ਨੇ ਗੋਂਦਲਾਂਵਾਲਾ ਪਿੰਡ ਤੋਂ ਬਹੁਤ ਸਾਰੀਆਂ ਭੇਡ-ਬੱਕਰੀਆਂ ਨੂੰ ਫੜ ਲਿਆ । ਲੋਕਾਂ ਦੀ ਸ਼ਿਕਾਇਤ ‘ਤੇ ਜਸਪਤ ਰਾਏ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਇਹ ਭੇਡ-ਬੱਕਰੀਆਂ ਵਾਪਸ ਕਰਨ ਦਾ ਆਦੇਸ਼ ਦਿੱਤਾ । ਸਿੱਖਾਂ ਦੇ ਇਨਕਾਰ ਕਰਨ ‘ਤੇ ਉਸ ਨੇ ਸਿੱਖਾਂ ‘ਤੇ ਹਮਲਾ ਕਰ ਦਿੱਤਾ | ਲੜਾਈ ਦੇ ਦੌਰਾਨ ਜਸਪਤ ਰਾਏ ਮਾਰਿਆ ਗਿਆ । ਇਸ ਕਾਰਨ ਮੁਗ਼ਲ ਫ਼ੌਜ ਵਿੱਚ ਭਾਜੜ ਪੈ ਗਈ ।
3. ਲਖਪਤ ਰਾਏ ਦੀ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕਾਰਵਾਈ (Action of Lakhpat Rai against the Sikhs) – ਜਸਪਤ ਰਾਏ ਦੀ ਮੌਤ ਦੀ ਖ਼ਬਰ ਸੁਣ ਕੇ ਉਸ ਦਾ ਭਰਾ ਦੀਵਾਨ ਲਖਪਤ ਰਾਏ ਅੱਗ-ਬਬੂਲਾ ਹੋ ਗਿਆ । ਉਸ ਨੇ ਇਹ ਪ੍ਰਣ ਕੀਤਾ ਕਿ ਉਹ ਸਿੱਖਾਂ ਦਾ ਨਾਮੋ-ਨਿਸ਼ਾਨ ਮਿਟਾ ਕੇ ਹੀ ਸੁੱਖ ਦਾ ਸਾਹ ਲਵੇਗਾ। ਉਸ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਉਨ੍ਹਾਂ ਦੇ ਧਰਮ ਗ੍ਰੰਥ ਪੜ੍ਹਨ ‘ਤੇ ਪਾਬੰਦੀ ਲਗਾ ਦਿੱਤੀ । ਉਸ ਨੇ ਗੁਰੂ ਸ਼ਬਦ ਦੀ ਵਰਤੋਂ ਦੀ ਵੀ ਮਨਾਹੀ ਕਰ ਦਿੱਤੀ । ਇਸ ਉਦੇਸ਼ ਨਾਲ ਉਸ ਨੇ ਗੁੜ ਦੀ ਥਾਂ ਲੋਕਾਂ ਨੂੰ ਰੋੜੀ ਸ਼ਬਦ ਦੀ ਵਰਤੋਂ ਕਰਨ ਲਈ ਕਿਹਾ ਕਿਉਂਕਿ ਗੁੜ ਸ਼ਬਦ ਦੀ ਆਵਾਜ਼ ਗੁਰੂ ਦੇ ਨਾਲ ਮਿਲਦੀ-ਜੁਲਦੀ ਸੀ । ਇਸੇ ਤਰ੍ਹਾਂ ਗ੍ਰੰਥ ਦੀ ਥਾਂ ਪੋਥੀ ਸ਼ਬਦ ਦੀ ਵਰਤੋਂ ਕਰਨ ਦਾ ਆਦੇਸ਼ ਦਿੱਤਾ ਗਿਆ । ਇਨ੍ਹਾਂ ਆਦੇਸ਼ਾਂ ਦੀ ਉਲੰਘਣਾ ਕਰਨ ਵਾਲਿਆਂ ਨੂੰ ਮੌਤ ਦੀ ਸਜ਼ਾ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ । ਉਸ ਨੇ ਬਹੁਤ ਸਾਰੇ ਸਿੱਖਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਲਾਹੌਰ ਲਿਜਾ ਕੇ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ।
4. ਪਹਿਲਾ ਘੱਲੂਘਾਰਾ (First Holocaust) – 1746 ਈ. ਵਿੱਚ ਯਾਹੀਆ ਖ਼ਾਂ ਤੇ ਲਖਪਤ ਰਾਏ ਦੇ ਅਧੀਨ ਮੁਗ਼ਲ ਸੈਨਾ ਨੇ ਲਗਭਗ 15,000 ਸਿੱਖਾਂ ਨੂੰ ਕਾਹਨੂੰਵਾਨ ਵਿਖੇ ਘੇਰ ਲਿਆ । ਸਿੱਖ ਬਸੌਲੀ ਦੀਆਂ ਪਹਾੜੀਆਂ ਵੱਲ ਚਲੇ ਗਏ । ਮੁਗਲ ਸੈਨਿਕਾਂ ਨੇ ਉਨ੍ਹਾਂ ਦਾ ਪਿੱਛਾ ਕੀਤਾ । ਸਿੱਖ ਬੜੀ ਮੁਸ਼ਕਿਲ ਵਿੱਚ ਫਸ ਗਏ । ਇੱਕ ਪਾਸੇ ਉੱਚੀਆਂ ਪਹਾੜੀਆਂ ਸਨ ਅਤੇ ਦੂਜੇ ਪਾਸੇ ਦਰਿਆ ਰਾਵੀ ਵਿੱਚ ਹੜ੍ਹ ਆਇਆ ਹੋਇਆ ਸੀ । ਪਿਛਲੇ ਪਾਸੇ ਮੁਗ਼ਲ ਸੈਨਿਕ ਉਨ੍ਹਾਂ ਦਾ ਪਿੱਛਾ ਕਰ ਰਹੇ ਸਨ । ਇਸ ਹਮਲੇ ਵਿੱਚ 7,000 ਸਿੱਖ ਸ਼ਹੀਦ ਹੋ ਗਏ ਅਤੇ 3,000 ਸਿੱਖਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਗਿਆ । ਇਨ੍ਹਾਂ ਸਿੱਖਾਂ ਨੂੰ ਲਾਹੌਰ ਵਿਖੇ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ਗਿਆ । ਸਿੱਖਾਂ ਦੇ ਇਤਿਹਾਸ ਵਿੱਚ ਇਹ ਪਹਿਲਾ ਮੌਕਾ ਸੀ ਜਦੋਂ ਸਿੱਖਾਂ ਦਾ ਇੱਕੋ ਵਾਰੀ ਇੰਨਾ ਭਾਰੀ ਜਾਨੀ ਨੁਕਸਾਨ ਹੋਇਆ ਸੀ । ਇਸ ਦਰਦਨਾਕ ਘਟਨਾ ਨੂੰ ਇਤਿਹਾਸ ਵਿੱਚ ਪਹਿਲਾ ਜਾਂ ਛੋਟਾ ਘੱਲੂਘਾਰਾ ਦੇ ਨਾਂ ਨਾਲ ਯਾਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਗੁਰਬਖ਼ਸ਼ ਸਿੰਘ ਦਾ ਕਹਿਣਾ ਬਿਲਕੁਲ ਠੀਕ ਹੈ,
1746 ਦੇ ਤਬਾਹਕੁੰਨ ਝਟਕੇ ਨੇ ਸਿੱਖਾਂ ਦੇ ਇਸ ਵਿਸ਼ਵਾਸ ਨੂੰ ਹੋਰ ਬਲ ਪ੍ਰਦਾਨ ਕੀਤਾ ਕਿ ਉਹ ਅੱਤਿਆਚਾਰੀਆਂ ਦਾ ਸਰਵਨਾਸ਼ ਕਰਨ ’’ 1
5. ਯਾਹੀਆ ਖਾਂ ਦਾ ਪਤਨ (Fall of Yahiya Khan) – ਨਵੰਬਰ, 1746 ਈ. ਵਿੱਚ ਯਾਹੀਆ ਖ਼ਾਂ ਦੇ ਛੋਟੇ ਭਰਾ ਸ਼ਾਹਨਵਾਜ਼ ਖਾਂ ਨੇ ਵਿਦਰੋਹ ਕਰ ਦਿੱਤਾ । ਇਹ ਵਿਦਰੋਹ ਚਾਰ ਮਹੀਨੇ ਤਕ ਜਾਰੀ ਰਿਹਾ । ਇਸ ਵਿਦਰੋਹ ਵਿੱਚ ਸ਼ਾਹਨਵਾਜ਼ ਖਾਂ ਸਫਲ ਰਿਹਾ ਤੇ ਉਸ ਨੇ ਯਾਹੀਆ ਖ਼ਾਂ ਨੂੰ 17 ਮਾਰਚ, 1747 ਈ. ਨੂੰ ਜੇਲ੍ਹ ਵਿੱਚ ਸੁੱਟ ਦਿੱਤਾ । ਇਸ ਤਰ੍ਹਾਂ ਉਸ ਦੇ ਅੱਤਿਆਚਾਰਾਂ ਦਾ ਅੰਤ ਹੋਇਆ ।
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ ਤੋਂ ਬਾਅਦ ਯਾਹੀਆ ਖ਼ਾਂ ਦਿੱਲੀ ਦੇ ਵਜ਼ੀਰ ਕਮਰਉੱਦੀਨ ਦੇ ਸਹਿਯੋਗ ਸਦਕਾ 1746 ਈ. ਵਿੱਚ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਬਣਿਆ । ਉਹ 1747 ਈ. ਤਕ ਇਸ ਅਹੁਦੇ ‘ਤੇ ਰਿਹਾ । ਸਿੱਖਾਂ ਉੱਤੇ ਅੱਤਿਆਚਾਰ ਕਰਨ ਵਿੱਚ ਉਹ ਆਪਣੇ ਪਿਤਾ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਤੋਂ ਇੱਕ ਕਦਮ ਅੱਗੇ ਸੀ ।
1. ਸਿੱਖਾਂ ਦੀਆਂ ਕਾਰਵਾਈਆਂ (Activities of the Sikhs) – ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ ਦਾ ਲਾਭ ਉਠਾ ਕੇ ਸਿੱਖਾਂ ਨੇ ਆਪਣੀ ਸ਼ਕਤੀ ਨੂੰ ਸੰਗਠਿਤ ਕਰ ਲਿਆ ਸੀ ।ਉਨ੍ਹਾਂ ਨੇ ਪੰਜਾਬ ਦੇ ਕਈ ਪਿੰਡਾਂ ਦੇ ਚੌਧਰੀਆਂ ਅਤੇ ਮੁਕੱਦਮਾਂ ਨੂੰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕਾਰਵਾਈਆਂ ਕਰਨ ਕਰਕੇ ਮੌਤ ਦੇ ਘਾਟ ਉਤਾਰ ਦਿੱਤਾ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਸਿੱਖ ਜੱਥਿਆਂ ਨੇ ਪੰਜਾਬ ਦੇ ਕਈ ਦੇਸ਼ਾਂ ਵਿੱਚ ਆਪਣੀਆਂ ਲੁੱਟਮਾਰ ਦੀਆਂ ਕਾਰਵਾਈਆਂ ਤੇਜ਼ ਕਰ ਦਿੱਤੀਆਂ ਸਨ ।
2. ਜਸਪਤ ਰਾਏ ਦੀ ਮੌਤ (Death of Jaspat Rai) – 1746 ਈ. ਵਿੱਚ ਸਿੱਖਾਂ ਦੇ ਇੱਕ ਜੱਥੇ ਨੇ ਗੋਂਦਲਾਂਵਾਲਾ ਪਿੰਡ ਤੋਂ ਬਹੁਤ ਸਾਰੀਆਂ ਭੇਡ-ਬੱਕਰੀਆਂ ਨੂੰ ਫੜ ਲਿਆ । ਲੋਕਾਂ ਦੀ ਸ਼ਿਕਾਇਤ ‘ਤੇ ਜਸਪਤ ਰਾਏ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਇਹ ਭੇਡ-ਬੱਕਰੀਆਂ ਵਾਪਸ ਕਰਨ ਦਾ ਆਦੇਸ਼ ਦਿੱਤਾ । ਸਿੱਖਾਂ ਦੇ ਇਨਕਾਰ ਕਰਨ ‘ਤੇ ਉਸ ਨੇ ਸਿੱਖਾਂ ‘ਤੇ ਹਮਲਾ ਕਰ ਦਿੱਤਾ | ਲੜਾਈ ਦੇ ਦੌਰਾਨ ਜਸਪਤ ਰਾਏ ਮਾਰਿਆ ਗਿਆ । ਇਸ ਕਾਰਨ ਮੁਗ਼ਲ ਫ਼ੌਜ ਵਿੱਚ ਭਾਜੜ ਪੈ ਗਈ ।
3. ਲਖਪਤ ਰਾਏ ਦੀ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕਾਰਵਾਈ (Action of Lakhpat Rai against the Sikhs) – ਜਸਪਤ ਰਾਏ ਦੀ ਮੌਤ ਦੀ ਖ਼ਬਰ ਸੁਣ ਕੇ ਉਸ ਦਾ ਭਰਾ ਦੀਵਾਨ ਲਖਪਤ ਰਾਏ ਅੱਗ-ਬਬੂਲਾ ਹੋ ਗਿਆ । ਉਸ ਨੇ ਇਹ ਪ੍ਰਣ ਕੀਤਾ ਕਿ ਉਹ ਸਿੱਖਾਂ ਦਾ ਨਾਮੋ-ਨਿਸ਼ਾਨ ਮਿਟਾ ਕੇ ਹੀ ਸੁੱਖ ਦਾ ਸਾਹ ਲਵੇਗਾ। ਉਸ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਉਨ੍ਹਾਂ ਦੇ ਧਰਮ ਗ੍ਰੰਥ ਪੜ੍ਹਨ ‘ਤੇ ਪਾਬੰਦੀ ਲਗਾ ਦਿੱਤੀ । ਉਸ ਨੇ ਗੁਰੂ ਸ਼ਬਦ ਦੀ ਵਰਤੋਂ ਦੀ ਵੀ ਮਨਾਹੀ ਕਰ ਦਿੱਤੀ । ਇਸ ਉਦੇਸ਼ ਨਾਲ ਉਸ ਨੇ ਗੁੜ ਦੀ ਥਾਂ ਲੋਕਾਂ ਨੂੰ ਰੋੜੀ ਸ਼ਬਦ ਦੀ ਵਰਤੋਂ ਕਰਨ ਲਈ ਕਿਹਾ ਕਿਉਂਕਿ ਗੁੜ ਸ਼ਬਦ ਦੀ ਆਵਾਜ਼ ਗੁਰੂ ਦੇ ਨਾਲ ਮਿਲਦੀ-ਜੁਲਦੀ ਸੀ । ਇਸੇ ਤਰ੍ਹਾਂ ਗ੍ਰੰਥ ਦੀ ਥਾਂ ਪੋਥੀ ਸ਼ਬਦ ਦੀ ਵਰਤੋਂ ਕਰਨ ਦਾ ਆਦੇਸ਼ ਦਿੱਤਾ ਗਿਆ । ਇਨ੍ਹਾਂ ਆਦੇਸ਼ਾਂ ਦੀ ਉਲੰਘਣਾ ਕਰਨ ਵਾਲਿਆਂ ਨੂੰ ਮੌਤ ਦੀ ਸਜ਼ਾ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ । ਉਸ ਨੇ ਬਹੁਤ ਸਾਰੇ ਸਿੱਖਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਲਾਹੌਰ ਲਿਜਾ ਕੇ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ।
4. ਪਹਿਲਾ ਘੱਲੂਘਾਰਾ (First Holocaust) – 1746 ਈ. ਵਿੱਚ ਯਾਹੀਆ ਖ਼ਾਂ ਤੇ ਲਖਪਤ ਰਾਏ ਦੇ ਅਧੀਨ ਮੁਗ਼ਲ ਸੈਨਾ ਨੇ ਲਗਭਗ 15,000 ਸਿੱਖਾਂ ਨੂੰ ਕਾਹਨੂੰਵਾਨ ਵਿਖੇ ਘੇਰ ਲਿਆ । ਸਿੱਖ ਬਸੌਲੀ ਦੀਆਂ ਪਹਾੜੀਆਂ ਵੱਲ ਚਲੇ ਗਏ । ਮੁਗਲ ਸੈਨਿਕਾਂ ਨੇ ਉਨ੍ਹਾਂ ਦਾ ਪਿੱਛਾ ਕੀਤਾ । ਸਿੱਖ ਬੜੀ ਮੁਸ਼ਕਿਲ ਵਿੱਚ ਫਸ ਗਏ । ਇੱਕ ਪਾਸੇ ਉੱਚੀਆਂ ਪਹਾੜੀਆਂ ਸਨ ਅਤੇ ਦੂਜੇ ਪਾਸੇ ਦਰਿਆ ਰਾਵੀ ਵਿੱਚ ਹੜ੍ਹ ਆਇਆ ਹੋਇਆ ਸੀ । ਪਿਛਲੇ ਪਾਸੇ ਮੁਗ਼ਲ ਸੈਨਿਕ ਉਨ੍ਹਾਂ ਦਾ ਪਿੱਛਾ ਕਰ ਰਹੇ ਸਨ । ਇਸ ਹਮਲੇ ਵਿੱਚ 7,000 ਸਿੱਖ ਸ਼ਹੀਦ ਹੋ ਗਏ ਅਤੇ 3,000 ਸਿੱਖਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਗਿਆ । ਇਨ੍ਹਾਂ ਸਿੱਖਾਂ ਨੂੰ ਲਾਹੌਰ ਵਿਖੇ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ਗਿਆ । ਸਿੱਖਾਂ ਦੇ ਇਤਿਹਾਸ ਵਿੱਚ ਇਹ ਪਹਿਲਾ ਮੌਕਾ ਸੀ ਜਦੋਂ ਸਿੱਖਾਂ ਦਾ ਇੱਕੋ ਵਾਰੀ ਇੰਨਾ ਭਾਰੀ ਜਾਨੀ ਨੁਕਸਾਨ ਹੋਇਆ ਸੀ । ਇਸ ਦਰਦਨਾਕ ਘਟਨਾ ਨੂੰ ਇਤਿਹਾਸ ਵਿੱਚ ਪਹਿਲਾ ਜਾਂ ਛੋਟਾ ਘੱਲੂਘਾਰਾ ਦੇ ਨਾਂ ਨਾਲ ਯਾਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਗੁਰਬਖ਼ਸ਼ ਸਿੰਘ ਦਾ ਕਹਿਣਾ ਬਿਲਕੁਲ ਠੀਕ ਹੈ,
1746 ਦੇ ਤਬਾਹਕੁੰਨ ਝਟਕੇ ਨੇ ਸਿੱਖਾਂ ਦੇ ਇਸ ਵਿਸ਼ਵਾਸ ਨੂੰ ਹੋਰ ਬਲ ਪ੍ਰਦਾਨ ਕੀਤਾ ਕਿ ਉਹ ਅੱਤਿਆਚਾਰੀਆਂ ਦਾ ਸਰਵਨਾਸ਼ ਕਰਨ ’’ 1
5. ਯਾਹੀਆ ਖਾਂ ਦਾ ਪਤਨ (Fall of Yahiya Khan) – ਨਵੰਬਰ, 1746 ਈ. ਵਿੱਚ ਯਾਹੀਆ ਖ਼ਾਂ ਦੇ ਛੋਟੇ ਭਰਾ ਸ਼ਾਹਨਵਾਜ਼ ਖਾਂ ਨੇ ਵਿਦਰੋਹ ਕਰ ਦਿੱਤਾ । ਇਹ ਵਿਦਰੋਹ ਚਾਰ ਮਹੀਨੇ ਤਕ ਜਾਰੀ ਰਿਹਾ । ਇਸ ਵਿਦਰੋਹ ਵਿੱਚ ਸ਼ਾਹਨਵਾਜ਼ ਖਾਂ ਸਫਲ ਰਿਹਾ ਤੇ ਉਸ ਨੇ ਯਾਹੀਆ ਖ਼ਾਂ ਨੂੰ 17 ਮਾਰਚ, 1747 ਈ. ਨੂੰ ਜੇਲ੍ਹ ਵਿੱਚ ਸੁੱਟ ਦਿੱਤਾ । ਇਸ ਤਰ੍ਹਾਂ ਉਸ ਦੇ ਅੱਤਿਆਚਾਰਾਂ ਦਾ ਅੰਤ ਹੋਇਆ ।
![]()
ਪ੍ਰਸ਼ਨ 6.
1716 ਈ. ਤੋਂ 1747 ਈ. ਤਕ ਸਿੱਖਾਂ ਦੇ ਕਤਲੇਆਮ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Explain in brief the persecution of the Sikhs during 1716 to 1747 A.D.)
ਜਾਂ
1716-1747 ਦੇ ਸਮੇਂ ਦੌਰਾਨ ਮੁਗ਼ਲ ਗਵਰਨਰਾਂ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਕੁਚਲਣ ਲਈ ਕੀ ਯਤਨ ਕੀਤੇ ? ਮੁਗਲ ਗਵਰਨਰ ਸਿੱਖਾਂ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਕਿਉਂ ਅਸਫਲ ਰਹੇ ? (What steps did the Mughal Governors take to crush the Sikhs between 1716-1747 ? Why did the Mughal Governors fail to suppress the Sikhs ?)
ਉੱਤਰ-
ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਨੂੰ 1713 ਈ. ਵਿੱਚ ਮੁਗ਼ਲ ਬਾਦਸ਼ਾਹ ਫ਼ਰੁੱਖਸੀਅਰ ਦੁਆਰਾ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਨਿਯੁਕਤ ਕੀਤਾ ਗਿਆ ਸੀ । ਉਸ ਨੂੰ ਇਸ ਉਦੇਸ਼ ਨਾਲ ਇਸ ਅਹੁਦੇ ‘ਤੇ ਨਿਯੁਕਤ ਕੀਤਾ ਗਿਆ ਸੀ ਤਾਂ ਕਿ ਉਹ ਪੰਜਾਬ ਵਿੱਚੋਂ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਪੂਰੀ ਤਰ੍ਹਾਂ ਕੁਚਲ ਦੇਵੇ । ਉਸ ਨੇ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਅਤੇ ਉਸ ਨੂੰ ਦਿੱਲੀ ਲਿਆ ਕੇ 1716 ਈ. ਵਿੱਚ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ । ਫ਼ਰੁੱਖਸੀਅਰ ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਦੀ ਇਸ ਕਾਰਵਾਈ ਤੋਂ ਬਹੁਤ ਖੁਸ਼ ਹੋਇਆ । ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੇ ਸਿੱਖਾਂ ਨਾਲ ਸੰਬੰਧਾਂ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਹੇਠ ਲਿਖਿਆ ਹੈ-
1. ਫ਼ਰੁੱਖਸੀਅਰ ਦਾ ਫ਼ਰਮਾਨ (Farrukhsiyar’s Edict) – 1716 ਈ. ਵਿੱਚ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੀ ਸ਼ਹੀਦੀ ਤੋਂ ਬਾਅਦ ਮੁਗ਼ਲ ਬਾਦਸ਼ਾਹ ਫ਼ਰੁੱਖਸੀਅਰ ਨੇ ਇੱਕ ਸ਼ਾਹੀ ਫ਼ਰਮਾਨ ਜਾਰੀ ਕੀਤਾ । ਇਸ ਵਿੱਚ ਮੁਗ਼ਲ ਅਧਿਕਾਰੀਆਂ ‘ ਨੂੰ ਇਹ ਆਦੇਸ਼ ਦਿੱਤਾ ਗਿਆ ਕਿ ਜਿਹੜਾ ਵੀ ਸਿੱਖ ਤੁਹਾਡੇ ਹੱਥ ਲੱਗੇ ਉਸ ਨੂੰ ਕਤਲ ਕਰ ਦਿਓ । ਸਿੱਖਾਂ ਨੂੰ ਸਹਾਇਤਾ ਜਾਂ ਸ਼ਰਨ ਦੇਣ ਵਾਲਿਆਂ ਨੂੰ ਵੀ ਇਹੋ ਸਜ਼ਾ ਦਿੱਤੀ ਜਾਵੇ । ਜੇ ਕੋਈ ਵਿਅਕਤੀ ਸਿੱਖਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਵਾਉਣ ਵਿੱਚ ਸਰਕਾਰ ਦੀ ਮਦਦ ਕਰੇ ਤਾਂ ਉਸ ਨੂੰ ਇਨਾਮ ਦਿੱਤਾ ਜਾਵੇ ।
2. ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੁਆਰਾ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਚੁੱਕੇ ਗਏ ਕਦਮ (Steps taken by Abdus Samad Khan against the Sikhs) – ਸ਼ਾਹੀ ਫ਼ਰਮਾਨ ਦੇ ਜਾਰੀ ਹੋਣ ਤੋਂ ਬਾਅਦ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਨੇ ਸਿੱਖਾਂ ‘ਤੇ ਘੋਰ ਅੱਤਿਆਚਾਰ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੇ । ਸੈਂਕੜੇ ਨਿਰਦੋਸ਼ ਸਿੱਖਾਂ ਨੂੰ ਰੋਜ਼ਾਨਾ ਗਿਫ਼ਤਾਰ ਕਰਕੇ ਲਾਹੌਰ ਲਿਆਂਦਾ ਜਾਂਦਾ । ਜੱਲਾਦ ਇਨ੍ਹਾਂ ਸਿੱਖਾਂ ਨੂੰ ਭਾਰੀ ਤਸੀਹੇ ਦੇਣ ਮਗਰੋਂ ਸ਼ਹੀਦ ਕਰ ਦਿੰਦੇ । ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੀ ਇਸ ਸਖ਼ਤ ਨੀਤੀ ਤੋਂ ਬਚਣ ਲਈ ਬਹੁਤ ਸਾਰੇ ਸਿੱਖਾਂ ਨੇ ਲੱਖੀ ਜੰਗਲ ਅਤੇ ਸ਼ਿਵਾਲਿਕ ਦੀਆਂ ਪਹਾੜੀਆਂ ਵਿੱਚ ਜਾ ਸ਼ਰਨ ਲਈ। ਇਸ ਤਰ੍ਹਾਂ ਆਪਣੇ ਸ਼ਾਸਨ ਕਾਲ ਦੇ ਸ਼ੁਰੂ ਦੇ ਕੁਝ ਵਰਿਆਂ ਤਕ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੀ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਦਮਨ ਨੀਤੀ ਬਹੁਤ ਸਫਲ ਰਹੀ । ਇਸ ਤੋਂ ਖ਼ੁਸ਼ ਹੋ ਕੇ ਫ਼ਰੁੱਖਸੀਅਰ ਨੇ ਉਸ ਨੂੰ ‘ਰਾਜ ਦੀ ਤਲਵਾਰ ਦੀ ਉਪਾਧੀ ਨਾਲ ਸਨਮਾਨਿਤ ਕੀਤਾ ।
3. ਸਿੱਖਾਂ ਵਿੱਚ ਫੁੱਟ (Split among the Sikhs) – ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੀ ਸ਼ਹੀਦੀ ਤੋਂ ਬਾਅਦ ਸਿੱਖ ਆਪਸੀ ਫੁੱਟ ਦਾ ਸ਼ਿਕਾਰ ਹੋ ਗਏ । ਉਹ ਤੱਤ ਖ਼ਾਲਸਾ ਅਤੇ ਬੰਦਈ ਖ਼ਾਲਸਾ ਨਾਂ ਦੀਆਂ ਦੋ ਮੁੱਖ ਸੰਪਰਦਾਵਾਂ ਵਿੱਚ ਵੰਡੇ ਗਏ । ਤੱਤ ਖ਼ਾਲਸਾ ਗੁਰੂ ਗੋਬਿੰਦ ਸਿੰਘ ਜੀ ਦੇ ਧਾਰਮਿਕ ਅਸੂਲਾਂ ਦੇ ਦ੍ਰਿੜ ਸਮਰਥਕ ਸਨ । ਬੰਦਈ ਖ਼ਾਲਸਾ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਨੂੰ ਆਪਣਾ ਨੇਤਾ ਮੰਨਣ ਲੱਗ ਪਏ ਸਨ । ਤੱਤ ਖ਼ਾਲਸਾ ਵਾਲੇ ਆਪਸ ਵਿੱਚ ਮਿਲਣ ਵੇਲੇ ‘ਵਾਹਿਗੁਰੂ ਜੀ ਕਾ ਖ਼ਾਲਸਾ, ਵਾਹਿਗੁਰੂ ਜੀ ਕੀ ਫ਼ਤਹਿ’ ਕਹਿੰਦੇ ਸਨ ਜਦਕਿ ਬੰਦਈ ਖ਼ਾਲਸਾ ‘ਫ਼ਤਹਿ ਧਰਮ’ ਅਤੇ ‘ਫ਼ਤਹਿ’ ਦਰਸ਼ਨ ਸ਼ਬਦਾਂ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਸਨ । ਤੱਤ ਖ਼ਾਲਸਾ ਵਾਲੇ ਨੀਲੇ ਰੰਗ ਦੇ ਕੱਪੜੇ ਪਾਉਂਦੇ ਸਨ ਜਦਕਿ ਬੰਦਈ ਖ਼ਾਲਸਾ ਵਾਲੇ ਲਾਲ ਰੰਗ ਦੇ ਦੋਹਾਂ ਸੰਪਰਦਾਵਾਂ ਵਿਚਾਲੇ ਆਪਸੀ ਮਤਭੇਦ ਦਿਨੋ-ਦਿਨ ਵਧਦੇ ਗਏ । ਸਿੱਟੇ ਵਜੋਂ ਸਿੱਖ ਅਬਦੁਸ ਸਮਦ ਮਾਂ ਦੇ ਅੱਤਿਆਚਾਰਾਂ ਦਾ ਇਕੱਠੇ ਹੋ ਕੇ ਮੁਕਾਬਲਾ ਨਾ ਕਰ ਸਕੇ ।
4. ਹਾਲਾਤਾਂ ਵਿੱਚ ਤਬਦੀਲੀ (Change in Circumstances) – 1720 ਈ. ਤੋਂ ਬਾਅਦ ਹਾਲਾਤਾਂ ਵਿੱਚ ਕੁਝ ਤਬਦੀਲੀ ਆਉਣੀ ਸ਼ੁਰੂ ਹੋ ਗਈ ਅਤੇ ਸਿੱਖਾਂ ਦੀ ਸਥਿਤੀ ਵਿੱਚ ਸੁਧਾਰ ਹੋਣ ਲੱਗਾ | ਸ਼ਾਹੀ ਦਰਬਾਰ ਸਾਜ਼ਸ਼ਾਂ ਦਾ ਅੱਡਾ ਬਣ ਕੇ ਰਹਿ ਗਿਆ ਸੀ । ਸਿੱਟੇ ਵਜੋਂ ਕੇਂਦਰੀ ਸਰਕਾਰ ਸਿੱਖਾਂ ਵੱਲ ਆਪਣਾ ਲੋੜੀਂਦਾ ਧਿਆਨ ਨਾ ਦੇ ਸਕੀ । ਪੰਜਾਬ ਵਿੱਚ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਵੀ ਈਸਾ ਖਾਂ ਅਤੇ ਹੁਸੈਨ ਖਾਂ ਦੇ ਵਿਦਰੋਹਾਂ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਉਲਝ ਗਿਆ । 1721 ਈ. ਵਿੱਚ ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੇ ਵਿਸਾਖੀ ਵਾਲੇ ਦਿਨ ਅੰਮ੍ਰਿਤਸਰ ਵਿਖੇ ਤੱਤ ਖ਼ਾਲਸਾ ਅਤੇ ਬੰਦਈ ਖ਼ਾਲਸਾ ਵਿਚਾਲੇ ਆਪਸੀ ਸਮਝੌਤਾ ਕਰਵਾ ਦਿੱਤਾ । ਸਿੱਟੇ ਵਜੋਂ ਸਿੱਖ ਮੁੜ ਇੱਕ ਹੋ ਗਏ ।
5. ਸਿੱਖਾਂ ਦੀਆਂ ਕਾਰਵਾਈਆਂ (Activities of the Sikhs) – ਸਥਿਤੀ ਵਿੱਚ ਤਬਦੀਲੀ ਆਉਣ ਨਾਲ ਸਿੱਖਾਂ ਵਿੱਚ ਇੱਕ ਨਵਾਂ ਜੋਸ਼ ਪੈਦਾ ਹੋਇਆ । ਉਨ੍ਹਾਂ ਨੇ ਸੌ-ਸੌ ਸਿੱਖਾਂ ਦੇ ਜੱਥੇ ਬਣਾ ਲਏ ਅਤੇ ਮੁਗ਼ਲ ਪ੍ਰਦੇਸ਼ਾਂ ਵਿੱਚ ਲੁੱਟਮਾਰ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੀ । ਉਨ੍ਹਾਂ ਨੇ ਉਨ੍ਹਾਂ ਹਿੰਦੂ ਅਤੇ ਮੁਸਲਮਾਨਾਂ ਨੂੰ ਸਖ਼ਤ ਸਜ਼ਾਵਾਂ ਦੇਣੀਆਂ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੀਆਂ, ਜਿਨ੍ਹਾਂ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀਆਂ ਇਸਤਰੀਆਂ ਅਤੇ ਬੱਚਿਆਂ ਨੂੰ ਮੁਗ਼ਲਾਂ ਦੇ ਹਵਾਲੇ ਕਰ ਦਿੱਤਾ ਸੀ | ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਸਬਕ ਸਿਖਾਉਣ ਲਈ ਅਸਲਮ ਖ਼ਾਂ ਅਧੀਨ ਕੁਝ ਫ਼ੌਜ ਅੰਮ੍ਰਿਤਸਰ ਭੇਜੀ । ਸਿੱਖਾਂ ਨੇ ਇਸ ਫ਼ੌਜ ‘ਤੇ ਅਚਾਨਕ ਹਮਲਾ ਕਰਕੇ ਉਸ ਨੂੰ ਕਰਾਰੀ ਹਾਰ ਦਿੱਤੀ । ਇਸ ਲੜਾਈ ਵਿੱਚ ਅਸਲਮ ਖਾਂ ਨੂੰ ਲੜਾਈ ਦਾ ਮੈਦਾਨ ਛੱਡ ਕੇ ਨੱਸਣ ਲਈ ਮਜਬੂਰ ਹੋਣਾ ਪਿਆ ।
6. ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੀ ਅਸਫਲਤਾ (Failure of Abdus Samad Khan) – ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਆਪਣੇ ਸਾਰੇ ਯਤਨਾਂ ਦੇ ਬਾਵਜੂਦ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ । ਇਸ ਦੇ ਕਈ ਕਾਰਨ ਸਨ । ਪਹਿਲਾ, ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਬੁੱਢਾ ਹੋ ਗਿਆ ਸੀ ।ਦੂਜਾ, ਸਿੱਖਾਂ ਵਿੱਚ ਆਪਸੀ ਏਕਤਾ ਸਥਾਪਿਤ ਹੋ ਗਈ ਸੀ । ਤੀਸਰਾ, ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਨੂੰ ਮੁਗ਼ਲ ਅਧਿਕਾਰੀਆਂ ਦੀਆਂ ਸਾਜ਼ਸ਼ਾਂ ਦਾ ਸ਼ਿਕਾਰ ਹੋਣਾ ਪਿਆ । ਚੌਥਾ, ਉਸ ਨੂੰ ਕੇਂਦਰ ਤੋਂ ਲੋੜੀਂਦੀ ਸਹਾਇਤਾ ਨਾ ਪ੍ਰਾਪਤ ਹੋਈ । 1726 ਈ. ਵਿੱਚ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਨੂੰ ਉਸ ਦੇ ਅਹੁਦੇ ਤੋਂ ਹਟਾ ਦਿੱਤਾ ਗਿਆ ।
ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਦੇ ਬਾਅਦ ਉਸ ਦਾ ਪੁੱਤਰ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਬਣਿਆ । ਉਹ ਇਸ ਅਹੁਦੇ ‘ਤੇ 1726 ਈ. ਤੋਂ 1745 ਈ. ਤਕ ਰਿਹਾ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੇ ਸ਼ਾਸਨ ਕਾਲ ਅਤੇ ਉਸ ਦੇ ਸਿੱਖਾਂ ਨਾਲ ਸੰਬੰਧਾਂ ਦਾ ਵਰਣਨ ਇਸ ਪ੍ਰਕਾਰ ਹੈ-
1. ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਸਖ਼ਤ ਕਾਰਵਾਈਆਂ (Harsh measures against the Sikhs) – ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਆਪਣਾ ਅਹੁਦਾ ਸੰਭਾਲਦੇ ਹੀ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਲਈ 20,000 ਸੈਨਿਕਾਂ ਨੂੰ ਭਰਤੀ ਕੀਤਾ । ਪਿੰਡਾਂ ਦੇ ਮੁਕੱਦਮਾਂ ਅਤੇ ਚੌਧਰੀਆਂ ਨੂੰ ਇਹ ਆਦੇਸ਼ ਦਿੱਤਾ ਗਿਆ ਕਿ ਉਹ ਆਪਣੇ ਇਲਾਕਿਆਂ ਵਿੱਚ ਸਿੱਖਾਂ ਨੂੰ ਸ਼ਰਨ ਨਾ ਲੈਣ ਦੇਣ । ਉਸ ਨੇ ਇਹ ਐਲਾਨ ਕੀਤਾ ਕਿ ਕਿਸੇ ਸਿੱਖ ਬਾਰੇ ਸੂਹ ਦੇਣ ਵਾਲੇ ਨੂੰ 10 ਰੁਪਏ, ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਵਾਉਣ ਵਾਲੇ ਨੂੰ 25 ਰੁਪਏ, ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਕੇ ਸਰਕਾਰ ਦੇ ਹਵਾਲੇ ਕਰਨ ਵਾਲੇ ਨੂੰ 50 ਰੁਪਏ ਅਤੇ ਸਿਰ ਵੱਢ ਕੇ ਸਰਕਾਰ ਨੂੰ ਭੇਟ ਕਰਨ ਵਾਲੇ ਨੂੰ 100 ਰੁਪਏ ਦਾ ਇਨਾਮ ਦਿੱਤਾ ਜਾਵੇਗਾ । ਇਸ ਤਰ੍ਹਾਂ ਸਿੱਖਾਂ ‘ਤੇ ਮੁੜ ਅੱਤਿਆਚਾਰ ਦਾ ਦੌਰ ਸ਼ੁਰੂ ਹੋ ਗਿਆ । ਸੈਂਕੜੇ ਸਿੱਖਾਂ ਨੂੰ ਲਾਹੌਰ ਦੇ ਦਿੱਲੀ ਗੇਟ ਵਿਖੇ ਸ਼ਹੀਦ ਕੀਤਾ ਜਾਣ ਲੱਗਾ। ਇਸ ਕਾਰਨ ਇਸ ਥਾਂ ਦਾ ਨਾਂ ‘ਸ਼ਹੀਦ ਗੰਜ ਪੈ ਗਿਆ ।
2. ਭਾਈ ਤਾਥਾ ਸਿੰਘ ਜੀ ਵਾਂ ਦੀ ਸ਼ਹੀਦੀ (Martyrdom of Bhai Tara Singh Ji Van) – ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਅੰਮ੍ਰਿਤਸਰ ਜ਼ਿਲ੍ਹੇ ਦੇ ਪਿੰਡ ਵਾਂ ਦੇ ਵਸਨੀਕ ਸਨ । ਉਨ੍ਹਾਂ ਨੇ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੀਆਂ ਲੜਾਈਆਂ ਵਿੱਚ ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਨਿਭਾਈ ਸੀ । ਨੌਸ਼ਹਿਰੇ ਦਾ ਚੌਧਰੀ ਸਾਹਿਬ ਰਾਏ ਸਿੱਖਾਂ ਦੇ ਖੇਤਾਂ ਵਿੱਚ ਆਪਣੇ ਘੋੜੇ ਛੱਡ ਦਿੰਦਾ ਸੀ । ਜਦੋਂ ਸਿੱਖ ਇਸ ਗੱਲ ਦਾ ਇਤਰਾਜ਼ ਕਰਦੇ ਤਾਂ ਉਹ ਸਿੱਖਾਂ ਦਾ ਅਪਮਾਨ ਕਰਦਾ । ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਵਾਂ ਲਈ ਇਹ ਗੱਲ ਅਸਹਿ ਸੀ । ਇੱਕ ਦਿਨ ਉਨ੍ਹਾਂ ਨੇ ਸਾਹਿਬ ਰਾਏ ਦੀ ਇੱਕ ਘੋੜੀ ਨੂੰ ਵੇਚ ਦਿੱਤਾ ਅਤੇ ਮਿਲੇ ਹੋਏ ਪੈਸਿਆਂ ਨੂੰ ਲੰਗਰ ਲਈ ਦੇ ਦਿੱਤਾ । ਇਸ ’ਤੇ ਸਿੱਖਾਂ ਨੂੰ ਸਬਕ ਸਿਖਾਉਣ ਲਈ ਸਾਹਿਬ ਰਾਏ ਨੇ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਤੋਂ ਮਦਦ ਮੰਗੀ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ 2200 ਘੋੜਸਵਾਰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਭੇਜੇ । ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਵਾਂ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ 22 ਸਾਥੀ ਮੁਗ਼ਲਾਂ ਦਾ ਮੁਕਾਬਲਾ ਕਰਦੇ ਹੋਏ ਸ਼ਹੀਦ ਹੋ ਗਏ । ਇਸ ਤੋਂ ਪਹਿਲਾਂ ਉਨ੍ਹਾਂ ਨੇ 300 ਮੁਗ਼ਲ ਸੈਨਿਕਾਂ ਨੂੰ ਯਮਲੋਕ ਪਹੁੰਚਾ ਦਿੱਤਾ ਸੀ । ਇਹ ਘਟਨਾ 1726 ਈ. ਦੀ ਹੈ । ਪ੍ਰਸਿੱਧ ਇਤਿਹਾਸਕਾਰ ਐੱਸ. ਐੱਸ. ਸ਼ੀਤਲ ਅਨੁਸਾਰ,
“ਉਸ (ਤਾਰਾ ਸਿੰਘ ਦੀ ਸ਼ਹੀਦੀ ਦਾ ਸਿੱਖਾਂ ਦੇ ਮਨਾਂ ‘ਤੇ ਡੂੰਘਾ ਅਸਰ ਪਿਆ ।”1
3. ਸਿੱਖਾਂ ਦੀਆਂ ਜਵਾਬੀ ਕਾਰਵਾਈਆਂ (Retaliatory measures of the Sikhs) – ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਵਾਂ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਸਾਥੀਆਂ ਦੀ ਸ਼ਹੀਦੀ ਨੇ ਸਿੱਖਾਂ ਵਿੱਚ ਇੱਕ ਨਵਾਂ ਜੋਸ਼ ਪੈਦਾ ਕਰ ਦਿੱਤਾ । ਉਨ੍ਹਾਂ ਨੇ ਛਾਪਾਮਾਰ ਯੁੱਧਾਂ ਰਾਹੀਂ ਸਰਕਾਰੀ ਖਜ਼ਾਨਿਆਂ ਨੂੰ ਲੁੱਟਣਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ । ਉਨ੍ਹਾਂ ਨੇ ਕਈ ਥਾਂਵਾਂ ‘ਤੇ ਹਮਲਾ ਕਰਕੇ ਸਰਕਾਰ ਦੇ ਪਿੱਛਲੱਗਿਆਂ ਨੂੰ ਮੌਤ ਦੇ ਘਾਟ ਉਤਾਰ ਦਿੱਤਾ । ਜਦੋਂ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਇਨ੍ਹਾਂ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਆਪਣੇ ਸੈਨਿਕਾਂ ਨੂੰ ਭੇਜਦਾ ਤਾਂ ਉਹ ਝਟ ਜੰਗਲਾਂ ਅਤੇ ਪਹਾੜਾਂ ਵਿੱਚ ਜਾ ਛਿਪਦੇ ।
4. ਹੈਦਰੀ ਝੰਡੇ ਦੀ ਘਟਨਾ (Incident of Haidri Flag) – ਮਜਬੂਰ ਹੋ ਕੇ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਦੇ ਦਮਨ ਲਈ ਜ਼ਿਹਾਦ ਦਾ ਨਾਅਰਾ ਲਗਾਇਆ । ਹਜ਼ਾਰਾਂ ਦੀ ਗਿਣਤੀ ਵਿੱਚ ਮੁਸਲਮਾਨ ਇਨਾਇਤ ਉਲਾ ਖਾਂ ਦੇ ਝੰਡੇ ਅਧੀਨ ਆਣ ਇਕੱਠੇ ਹੋਏ । ਉਨ੍ਹਾਂ ਨੂੰ ਈਦ ਦੇ ਮੁਬਾਰਕ ਦਿਨ ਇੱਕ ਹੈਦਰੀ ਝੰਡਾ ਦਿੱਤਾ ਗਿਆ ਅਤੇ ਇਹ ਐਲਾਨ ਕੀਤਾ ਗਿਆ ਕਿ ਇਸ ਝੰਡੇ ਅਧੀਨ ਲੜਨ ਵਾਲਿਆਂ ਨੂੰ ਅੱਲ੍ਹਾ ਜ਼ਰੂਰ ਫ਼ਤਹਿ ਦੇਵੇਗਾ । ਪਰ ਇੱਕ ਦਿਨ ਲਗਭਗ 7 ਹਜ਼ਾਰ ਸਿੱਖਾਂ ਨੇ ਇਨ੍ਹਾਂ ਗਾਜ਼ੀਆਂ ਉੱਤੇ ਅਚਾਨਕ ਹਮਲਾ ਕਰਕੇ ਹਜ਼ਾਰਾਂ ਗਾਜ਼ੀਆਂ ਨੂੰ ਕਤਲ ਕਰ ਦਿੱਤਾ । ਇਸ ਘਟਨਾ ਨਾਲ ਸਰਕਾਰ ਦੇ ਗੌਰਵ ਨੂੰ ਭਾਰੀ ਸੱਟ ਵੱਜੀ ।
5. ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦਾ ਸਿੱਖਾਂ ਨਾਲ ਸਮਝੌਤਾ (Agreement of Zakariya Khan with the Sikhs) – ਹੁਣ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਖੁਸ਼ ਕਰਨ ਦੀ ਨੀਤੀ ਅਪਣਾਈ । ਉਸ ਨੇ 1733 ਈ. ਵਿੱਚ ਐਲਾਨ ਕੀਤਾ ਕਿ ਜੇਕਰ ਸਿੱਖ ਸਰਦਾਰ ਵਿਰੋਧੀ ਕਾਰਵਾਈਆਂ ਨੂੰ ਬੰਦ ਕਰ ਦੇਣ ਤਾਂ ਉਨ੍ਹਾਂ ਨੂੰ ਇੱਕ ਲੱਖ ਰੁਪਏ ਸਾਲਾਨਾ ਆਮਦਨ ਵਾਲੀ ਇੱਕ ਜਾਗੀਰ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਆਗੂ ਨੂੰ “ਨਵਾਬ’ ਦਾ ਖਿਤਾਬ ਦਿੱਤਾ ਜਾਵੇਗਾ । ਪਹਿਲਾਂ ਤਾਂ ਸਿੱਖ ਇਸ ਸਮਝੌਤੇ ਦੇ ਵਿਰੁੱਧ ਸਨ ਪਰ ਬਾਅਦ ਵਿੱਚ ਉਨ੍ਹਾਂ ਨੇ ਇਸ ਨੂੰ ਸਵੀਕਾਰ ਕਰ ਲਿਆ । ਸਿੱਖਾਂ ਨੇ ਨਵਾਬ ਦੀ ਪਦਵੀ ਸਰਦਾਰ ਕਪੂਰ ਸਿੰਘ ਫ਼ੈਜ਼ਲਪੁਰੀਆ ਨੂੰ ਦਿੱਤੀ ।
6. ਬੁੱਢਾ ਦਲ ਤੇ ਤਰੁਣਾ ਦਲ ਦਾ ਸੰਗਠਨ (Organisation of Buddha Dal and Taruna Dal) – ਮੁਗਲਾਂ ਨਾਲ ਸਮਝੌਤਾ ਹੋ ਜਾਣ ਨਾਲ ਨਵਾਬ ਕਪੂਰ ਸਿੰਘ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਇਹ ਸੁਨੇਹਾ ਭੇਜਿਆ ਕਿ ਉਹ ਮੁੜ ਆਪਣੇ ਘਰਾਂ ਵਿੱਚ ਆ ਜਾਣ । 1734 ਈ. ਵਿੱਚ ਨਵਾਬ ਕਪੂਰ ਸਿੰਘ ਨੇ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਮਜ਼ਬੂਤ ਕਰਨ ਦੇ ਉਦੇਸ਼ ਨਾਲ ਉਨ੍ਹਾਂ ਨੂੰ ਦੋ ਜੱਥਿਆਂ ਵਿੱਚ ਸੰਗਠਿਤ ਕਰ ਦਿੱਤਾ । ਇਹ ਜੱਥੇ ਸਨ-ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ । ਬੁੱਢਾ ਦਲ ਵਿੱਚ 40 ਸਾਲਾਂ ਤੋਂ ਵਡੇਰੀ ਉਮਰ ਦੇ ਸਿੱਖਾਂ ਨੂੰ ਸ਼ਾਮਲ ਕੀਤਾ ਗਿਆ ਅਤੇ ਤਰੁਣਾ ਦਲ ਵਿੱਚ ਉਸ ਤੋਂ ਘੱਟ ਦੀ ਉਮਰ ਵਾਲੇ ਸਿੱਖਾਂ ਨੂੰ । ਤਰੁਣਾ ਦਲ ਨੂੰ ਅੱਗੇ ਪੰਜ ਜੱਥਿਆਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ ਸੀ । ਬੁੱਢਾ ਦਲ ਧਾਰਮਿਕ ਸਥਾਨਾਂ ਦੀ ਦੇਖਭਾਲ ਕਰਦਾ ਸੀ । ਤਰੁਣਾ ਦਲ ਦੁਸ਼ਮਣਾਂ ਦਾ ਮੁਕਾਬਲਾ ਕਰਦਾ ਸੀ ।
7. ਮੁਗ਼ਲਾਂ ਅਤੇ ਸਿੱਖਾਂ ਵਿਚਾਲੇ ਦੁਬਾਰਾ ਸੰਘਰਸ਼ (Renewed struggle between the Mughals and the Sikhs) – ਆਪਣੀ ਸ਼ਕਤੀ ਨੂੰ ਸੰਗਠਿਤ ਕਰਨ ਤੋਂ ਬਾਅਦ ਸਿੱਖਾਂ ਨੇ ਆਪਣੀਆਂ ਸੈਨਿਕ ਕਾਰਵਾਈਆਂ ਮੁੜ ਆਰੰਭ ਕਰ ਦਿੱਤੀਆਂ ਸਨ । ਉਨ੍ਹਾਂ ਨੇ ਸ਼ਾਹੀ ਖ਼ਜ਼ਾਨਿਆਂ ਨੂੰ ਮੁੜ ਲੁੱਟਣਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ ਸੀ । ਇਸ ਕਾਰਨ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਗੁੱਸੇ ਵਿੱਚ ਆ ਕੇ ਸਿੱਖਾਂ ਨੂੰ ਦਿੱਤੀ ਗਈ ਜਾਗੀਰ ਨੂੰ 1735 ਈ. ਵਿੱਚ ਜ਼ਬਤ ਕਰ ਲਿਆ । ਸਿੱਖਾਂ ਨੂੰ ਮੁੜ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਕੇ ਕਤਲ ਕਰਨਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ ਗਿਆ । ਸਿੱਟੇ ਵਜੋਂ ਸਿੱਖ ਜੰਗਲਾਂ ਵੱਲ ਚਲੇ ਗਏ । ਇਸ ਮੌਕੇ ਦਾ ਫਾਇਦਾ ਉਠਾ ਕੇ ਮੁਗ਼ਲਾਂ ਨੇ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਉੱਤੇ ਕਬਜ਼ਾ ਕਰ ਲਿਆ ।

8. ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਦੀ ਸ਼ਹੀਦੀ (Martyrdom of Bhai Mani Singh Ji) – ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ 1721 ਈ. ਤੋਂ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਦੇ ਮੁੱਖ ਗ੍ਰੰਥੀ ਚਲੇ ਆ ਰਹੇ ਸਨ ।ਉਨ੍ਹਾਂ ਨੇ 1738 ਈ. ਵਿੱਚ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੂੰ ਇਹ ਬੇਨਤੀ ਕੀਤੀ ਕਿ ਜੇਕਰ ਉਹ ਸਿੱਖਾਂ ਨੂੰ ਦੀਵਾਲੀ ਦੇ ਮੌਕੇ ‘ਤੇ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਆਉਣ ਦੀ ਇਜਾਜ਼ਤ ਦੇਵੇ ਤਾਂ ਉਹ 5,000 ਰੁਪਏ ਉਸ ਨੂੰ ਭੇਟ ਕਰਨਗੇ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਇਹ ਪੇਸ਼ਕਸ਼ ਸਵੀਕਾਰ ਕਰ ਲਈ । ਪਰ ਹਾਲੇ ਸਿੱਖ ਅੰਮ੍ਰਿਤਸਰ ਵਿੱਚ ਇਕੱਠੇ ਹੋ ਹੀ ਰਹੇ ਸਨ ਕਿ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੇ ਸੈਨਿਕਾਂ ਨੇ ਹਮਲਾ ਕਰ ਦਿੱਤਾ । ਸਿੱਟੇ ਵਜੋਂ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਵਿੱਚ ਦੀਵਾਲੀ ਦਾ ਮੇਲਾ ਨਾ ਮਨਾਇਆ ਜਾ ਸਕਿਆ । ਜ਼ਕਰੀਆ ਖਾਂ ਨੇ ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਤੋਂ 5,000 ਰੁਪਏ ਦੀ ਮੰਗ ਕੀਤੀ । ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਇਹ ਪੈਸਾ ਨਾ ਦੇ ਸਕੇ । ਇਸ ਲਈ ਉਨ੍ਹਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਕੇ ਲਾਹੌਰ ਭੇਜ ਦਿੱਤਾ ਗਿਆ | ਭਾਈ ਸਾਹਿਬ ਜੀ ਨੂੰ ਇਸਲਾਮ ਹਿਣ ਕਰਨ ਲਈ ਕਿਹਾ ਗਿਆ ਪਰ ਉਨ੍ਹਾਂ ਨੇ ਇਨਕਾਰ ਕਰ ਦਿੱਤਾ । ਸਿੱਟੇ ਵਜੋਂ ਉਨ੍ਹਾਂ ਨੂੰ 1738 ਈ. ਵਿੱਚ ਤਸੀਹੇ ਦੇ ਕੇ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ਗਿਆ । ਇਸ ਘਟਨਾ ਨਾਲ ਸਿੱਖਾਂ ਵਿੱਚ ਗੁੱਸੇ ਦੀ ਲਹਿਰ ਦੌੜ ਗਈ । ਪ੍ਰਸਿੱਧ ਇਤਿਹਾਸਕਾਰ ਖੁਸ਼ਵੰਤ ਸਿੰਘ ਦੇ ਵਿਚਾਰ ਅਨੁਸਾਰ,
‘‘ਪਵਿੱਤਰ ਅਤੇ ਪੂਜਣ ਯੋਗ ਮੁੱਖ ਪੁਜਾਰੀ (ਭਾਈ ਮਨੀ ਸਿੰਘ ਦੀ ਕੁਰਬਾਨੀ ਕਾਰਨ ਸਿੱਖ ਭੜਕ ਉਠੇ ।’’ 1
9. ਸਿੱਖਾਂ ਦਾ ਨਾਦਰ ਸ਼ਾਹ ਨੂੰ ਲੁੱਟਣਾ (Sikhs robbed Nadir Shah) – 1739 ਈ. ਵਿੱਚ ਨਾਦਰ ਸ਼ਾਹ ਦਿੱਲੀ ਵਿੱਚ ਭਾਰੀ ਲੁੱਟਮਾਰ ਕਰਕੇ ਪੰਜਾਬ ਵਿੱਚੋਂ ਹੁੰਦਾ ਹੋਇਆ ਵਾਪਸ ਈਰਾਨ ਜਾ ਰਿਹਾ ਸੀ । ਜਦੋਂ ਸਿੱਖਾਂ ਨੂੰ ਇਸ ਬਾਰੇ ਸੂਚਨਾ ਮਿਲੀ ਤਾਂ ਉਨ੍ਹਾਂ ਨੇ ਅਚਾਨਕ ਹਮਲਾ ਕਰਕੇ ਉਸ ਦਾ ਬਹੁਤ ਸਾਰਾ ਖ਼ਜ਼ਾਨਾ ਲੁੱਟ ਲਿਆ । ਨਾਦਰ ਸ਼ਾਹ ਨੇ ਜ਼ਕਰੀਆ ਖਾਂ ਨੂੰ ਇਹ ਚੇਤਾਵਨੀ ਦਿੱਤੀ ਕਿ ਛੇਤੀ ਹੀ ਸਿੱਖ ਪੰਜਾਬ ਦੇ ਸ਼ਾਸਕ ਬਣ ਜਾਣਗੇ ।
10. ਜ਼ਕਰੀਆ ਖਾਂ ਦੁਆਰਾ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਸਖ਼ਤ ਕਾਰਵਾਈਆਂ (Strong actions against the Sikhs by Zakariya Khan) – ਨਾਦਰ ਸ਼ਾਹ ਦੀ ਚੇਤਾਵਨੀ ਦਾ ਜ਼ਕਰੀਆ ਖਾਂ ਦੇ ਮਨ ’ਤੇ ਬੜਾ ਡੂੰਘਾ ਅਸਰ ਪਿਆ । ਉਸ ਨੇ ਸਿੱਖਾਂ ਦਾ ਮਲੀਆਮੇਟ ਕਰਨ ਲਈ ਅਨੇਕਾਂ ਕਦਮ ਚੁੱਕੇ । ਸਿੱਖਾਂ ਦਾ ਇੱਕ ਵਾਰੀ ਫਿਰ ਰੋਜ਼ਾਨਾ ਬੜੇ ਜ਼ਾਲਮਾਨਾ ਢੰਗ ਨਾਲ ਕਤਲ ਕੀਤਾ ਜਾਣ ਲੱਗਾ | ਕੁਝ ਪ੍ਰਸਿੱਧ ਸ਼ਹੀਦਾਂ ਦਾ ਵਰਣਨ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ-
(ੳ) ਭਾਈ ਬੋਤਾ ਸਿੰਘ ਜੀ (Bhai Bota Singh Ji) – ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਅਨੇਕਾਂ ਸਿੱਖਾਂ ਨੂੰ ਕਤਲ ਕਰਨ ਤੋਂ ਬਾਅਦ ਇਹ ਘੋਸ਼ਣਾ ਕੀਤੀ ਕਿ ਉਸ ਨੇ ਸਿੱਖਾਂ ਦਾ ਨਾਮੋ-ਨਿਸ਼ਾਨ ਖ਼ਤਮ ਕਰ ਦਿੱਤਾ ਹੈ । ਸਿੱਖਾਂ ਦੀ ਹੋਂਦ ਨੂੰ ਦਰਸਾਉਣ ਲਈ ਭਾਈ ਬੋਤਾ ਸਿੰਘ ਜੀ ਨੇ ਸਰਾਇ ਨਦੀਨ ਵਿਖੇ ਇੱਕ ਚੌਕੀ ਕਾਇਮ ਕਰ ਲਈ ਅਤੇ ਉੱਥੋਂ ਚੰਗੀ ਕਰ ਲੈਣਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਉਸ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਨ ਲਈ ਕੁਝ ਫ਼ੌਜ ਭੇਜੀ । ਭਾਈ ਬੋਤਾ ਸਿੰਘ ਜੀ ਆਪਣੇ ਦੁਸ਼ਮਣਾਂ ਦਾ ਡਟ ਕੇ ਮੁਕਾਬਲਾ ਕਰਦੇ ਹੋਏ ਸ਼ਹੀਦ ਹੋ ਗਏ ।
(ਅ) ਭਾਈ ਮਹਿਤਾਬ ਸਿੰਘ ਜੀ ਅਤੇ ਭਾਈ ਸੁੱਖਾ ਸਿੰਘ ਜੀ (Bhai Mehtab Singh Ji and Bhai Sukha Singh Ji) – ਅੰਮ੍ਰਿਤਸਰ ਜ਼ਿਲ੍ਹੇ ਦੇ ਮੰਡਿਆਲਾ ਪਿੰਡ ਦਾ ਚੌਧਰੀ ਮੱਸਾ ਰੰਗੜ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਦੀ ਪਵਿੱਤਰਤਾ ਨੂੰ ਭੰਗ ਕਰ ਰਿਹਾ ਸੀ । ਇਸ ਕਾਰਨ ਸਿੱਖ ਉਸ ਨੂੰ ਇੱਕ ਸਬਕ ਸਿਖਾਉਣਾ ਚਾਹੁੰਦੇ ਸਨ । ਇੱਕ ਦਿਨ ਭਾਈ ਮਹਿਤਾਬ ਸਿੰਘ ਜੀ ਅਤੇ ਭਾਈ ਸੁੱਖਾ ਸਿੰਘ ਜੀ ਕੁਝ ਬੋਰੀਆਂ ਵਿੱਚ ਥੱਲੇ ਪੱਥਰ ਭਰ ਕੇ ਅਤੇ ਉੱਤੇ ਕੁਝ ਸਿੱਕੇ ਭਰ ਕੇ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਪਹੁੰਚ ਗਏ | ਸੈਨਿਕਾਂ ਦੁਆਰਾ ਪੁੱਛਣ ‘ਤੇ ਉਨ੍ਹਾਂ ਨੇ ਦੱਸਿਆ ਕਿ ਉਹ ਮਾਮਲਾ ਉਗਰਾਹ ਕੇ ਲਿਆਏ ਹਨ । ਮੱਸਾ ਰੰਗੜ ਸਿੱਕੇ ਨਾਲ ਭਰੀਆਂ ਬੋਰੀਆਂ ਵੇਖ ਕੇ ਬੜਾ ਖ਼ੁਸ਼ ਹੋਇਆ । ਜਿਵੇਂ ਹੀ ਉਹ ਇਨ੍ਹਾਂ ਬੋਰੀਆਂ ਨੂੰ ਸਵੀਕਾਰ ਕਰਨ ਲਈ ਥੱਲੇ ਝੁਕਿਆ ਉਸੇ ਸਮੇਂ ਭਾਈ ਮਹਿਤਾਬ ਸਿੰਘ ਜੀ ਨੇ ਆਪਣੀ ਤਲਵਾਰ ਦੇ ਇੱਕੋ ਵਾਰ ਨਾਲ ਉਸ ਦਾ ਸਿਰ ਧੜ ਨਾਲੋਂ ਵੱਖ ਕਰ ਦਿੱਤਾ । ਬਾਅਦ ਵਿੱਚ ਭਾਈ ਮਹਿਤਾਬ ਸਿੰਘ ਜੀ ਅਤੇ ਭਾਈ ਸੁੱਖਾ ਸਿੰਘ ਜੀ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਕੇ ਬੜੀ ਬੇਰਹਿਮੀ ਨਾਲ 1740 ਈ. ਵਿੱਚ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ਗਿਆ ।
(ੲ) ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਜੀ (Bal Haqiqat Rai Ji) – ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਜੀ ਸਿਆਲਕੋਟ ਦੇ ਰਹਿਣ ਵਾਲੇ ਸਨ । ਇੱਕ ਦਿਨ ਕੁਝ ਮੁਸਲਮਾਨ ਮੁੰਡਿਆਂ ਨੇ ਹਿੰਦੂ ਦੇਵੀ-ਦੇਵਤਿਆਂ ਦੀ ਸ਼ਾਨ ਵਿੱਚ ਕੁਝ ਅਪਮਾਨ-ਜਨਕ ਸ਼ਬਦ ਕਹੇ | ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਜੀ ਇਹ ਸਹਿਣ ਨਾ ਕਰ ਸਕੇ ।ਉਨ੍ਹਾਂ ਨੇ ਹਜ਼ਰਤ ਮੁਹੰਮਦ ਬਾਰੇ ਕੁਝ ਅਯੋਗ ਸ਼ਬਦ ਕਹਿ ਦਿੱਤੇ । ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਜੀ `ਤੇ ਮੁਕੱਦਮਾ ਚਲਾਇਆ ਗਿਆ ਅਤੇ ਮੌਤ ਦੀ ਸਜ਼ਾ ਸੁਣਾਈ ਗਈ । ਇਹ ਘਟਨਾ 1742 ਈ. ਦੀ ਹੈ । ਇਸ ਘਟਨਾ ਕਾਰਨ ਲੋਕਾਂ ਨੇ ਜ਼ਾਲਮ ਮੁਗਲ ਸ਼ਾਸਨ ਦਾ ਅੰਤ ਕਰਨ ਦੀ ਸਹੁੰ ਚੁੱਕੀ ।
(ਸ) ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ Bhai Taru Singh Ji) – ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਮਾਝੇ ਦੇ ਇਲਾਕੇ ਦੇ ਪਿੰਡ ਪੂਹਲਾ ਦੇ ਨਿਵਾਸੀ ਸਨ । ਉਹ ਆਪਣੀ ਆਮਦਨ ਤੋਂ ਸਿੱਖਾਂ ਦੀ ਮੱਦਦ ਕਰਦੇ ਸਨ । ਸਰਕਾਰ ਦੀਆਂ ਨਜ਼ਰਾਂ ਵਿੱਚ ਇਹ ਇੱਕ ਘੋਰ ਅਪਰਾਧ ਸੀ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਨੂੰ ਲਾਹੌਰ ਬੁਲਾ ਕੇ ਇਸਲਾਮ ਧਰਮ ਗ੍ਰਹਿਣ ਕਰਨ ਲਈ ਕਿਹਾ । ਭਾਈ ਸਾਹਿਬ ਜੀ ਨੇ ਕਿਹਾ ਕਿ ਉਹ ਕਿਸੇ ਵੀ ਕੀਮਤ ‘ਤੇ ਸਤਿਰੂ ਦੀ ਦਿੱਤੀ ਪਵਿੱਤਰ ਦਾਤ ਕੇਸਾਂ ਨੂੰ ਨਹੀਂ ਦੇ ਸਕਦੇ ਹਾਂ ਉਹ ਆਪਣੇ ਕੇਸ ਆਪਣੀ ਖੋਪਰੀ ਨਾਲ ਹੀ ਉਤਰਵਾ ਸਕਦੇ ਹਨ । ਇਸ ’ਤੇ ਜੱਲਾਦਾਂ ਨੇ ਭਾਈ ਸਾਹਿਬ ਦੀ ਖੋਪਰੀ ਨੂੰ ਉਤਾਰ ਦਿੱਤਾ । ਜਦੋਂ ਭਾਈ ਸਾਹਿਬ ਜੀ ਦੀ ਖੋਪਰੀ ਉਤਾਰੀ ਜਾ ਰਹੀ ਸੀ ਤਾਂ ਉਹ ਜਪੁਜੀ ਸਾਹਿਬ ਦਾ ਪਾਠ ਕਰ ਰਹੇ ਸਨ । ਇਹ ਘਟਨਾ 1745 ਈ. ਦੀ ਹੈ । ਇਸ ਲਾਸਾਨੀ ਸ਼ਹਾਦਤ ਨੇ ਸਿੱਖਾਂ ਵਿੱਚ ਇੱਕ ਨਵਾਂ ਜੋਸ਼ ਪੈਦਾ ਕੀਤਾ |
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ (Death of Zakariya Khan) – ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਨਿਰਸੰਦੇਹ ਆਪਣੇ ਕਾਲ ਵਿੱਚ ਸਿੱਖਾਂ ਉੱਤੇ ਘੋਰ ਅੱਤਿਆਚਾਰ ਕੀਤੇ ।ਉਹ ਆਪਣੇ ਅਣਥੱਕ ਯਤਨਾਂ ਦੇ ਬਾਵਜੂਦ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ । 1 ਜੁਲਾਈ, 1745 ਈ. ਨੂੰ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ ਹੋ ਗਈ । ਪਤਵੰਤ ਸਿੰਘ ਦਾ ਇਹ ਕਹਿਣਾ ਬਿਲਕੁਲ ਠੀਕ ਹੈ, .
‘‘ਕਿਸੇ ਨੇ ਵੀ ਸਿੱਖਾਂ ਦਾ ਇਸ ਤੋਂ ਵੱਧ ਉਤਸ਼ਾਹ ਨਾਲ ਮਨ ਨਹੀਂ ਕੀਤਾ ਜਿੰਨਾ ਕਿ ਜ਼ਕਰੀਆ ਖਾਂ ਨੇ ।” 1
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ ਤੋਂ ਬਾਅਦ ਯਾਹੀਆ ਖ਼ਾਂ ਦਿੱਲੀ ਦੇ ਵਜ਼ੀਰ ਕਮਰਉੱਦੀਨ ਦੇ ਸਹਿਯੋਗ ਸਦਕਾ 1746 ਈ. ਵਿੱਚ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਬਣਿਆ । ਉਹ 1747 ਈ. ਤਕ ਇਸ ਅਹੁਦੇ ‘ਤੇ ਰਿਹਾ । ਸਿੱਖਾਂ ਉੱਤੇ ਅੱਤਿਆਚਾਰ ਕਰਨ ਵਿੱਚ ਉਹ ਆਪਣੇ ਪਿਤਾ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਤੋਂ ਇੱਕ ਕਦਮ ਅੱਗੇ ਸੀ ।
1. ਸਿੱਖਾਂ ਦੀਆਂ ਕਾਰਵਾਈਆਂ (Activities of the Sikhs) – ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ ਦਾ ਲਾਭ ਉਠਾ ਕੇ ਸਿੱਖਾਂ ਨੇ ਆਪਣੀ ਸ਼ਕਤੀ ਨੂੰ ਸੰਗਠਿਤ ਕਰ ਲਿਆ ਸੀ ।ਉਨ੍ਹਾਂ ਨੇ ਪੰਜਾਬ ਦੇ ਕਈ ਪਿੰਡਾਂ ਦੇ ਚੌਧਰੀਆਂ ਅਤੇ ਮੁਕੱਦਮਾਂ ਨੂੰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕਾਰਵਾਈਆਂ ਕਰਨ ਕਰਕੇ ਮੌਤ ਦੇ ਘਾਟ ਉਤਾਰ ਦਿੱਤਾ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਸਿੱਖ ਜੱਥਿਆਂ ਨੇ ਪੰਜਾਬ ਦੇ ਕਈ ਦੇਸ਼ਾਂ ਵਿੱਚ ਆਪਣੀਆਂ ਲੁੱਟਮਾਰ ਦੀਆਂ ਕਾਰਵਾਈਆਂ ਤੇਜ਼ ਕਰ ਦਿੱਤੀਆਂ ਸਨ ।
2. ਜਸਪਤ ਰਾਏ ਦੀ ਮੌਤ (Death of Jaspat Rai) – 1746 ਈ. ਵਿੱਚ ਸਿੱਖਾਂ ਦੇ ਇੱਕ ਜੱਥੇ ਨੇ ਗੋਂਦਲਾਂਵਾਲਾ ਪਿੰਡ ਤੋਂ ਬਹੁਤ ਸਾਰੀਆਂ ਭੇਡ-ਬੱਕਰੀਆਂ ਨੂੰ ਫੜ ਲਿਆ । ਲੋਕਾਂ ਦੀ ਸ਼ਿਕਾਇਤ ‘ਤੇ ਜਸਪਤ ਰਾਏ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਇਹ ਭੇਡ-ਬੱਕਰੀਆਂ ਵਾਪਸ ਕਰਨ ਦਾ ਆਦੇਸ਼ ਦਿੱਤਾ । ਸਿੱਖਾਂ ਦੇ ਇਨਕਾਰ ਕਰਨ ‘ਤੇ ਉਸ ਨੇ ਸਿੱਖਾਂ ‘ਤੇ ਹਮਲਾ ਕਰ ਦਿੱਤਾ | ਲੜਾਈ ਦੇ ਦੌਰਾਨ ਜਸਪਤ ਰਾਏ ਮਾਰਿਆ ਗਿਆ । ਇਸ ਕਾਰਨ ਮੁਗ਼ਲ ਫ਼ੌਜ ਵਿੱਚ ਭਾਜੜ ਪੈ ਗਈ ।
3. ਲਖਪਤ ਰਾਏ ਦੀ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕਾਰਵਾਈ (Action of Lakhpat Rai against the Sikhs) – ਜਸਪਤ ਰਾਏ ਦੀ ਮੌਤ ਦੀ ਖ਼ਬਰ ਸੁਣ ਕੇ ਉਸ ਦਾ ਭਰਾ ਦੀਵਾਨ ਲਖਪਤ ਰਾਏ ਅੱਗ-ਬਬੂਲਾ ਹੋ ਗਿਆ । ਉਸ ਨੇ ਇਹ ਪ੍ਰਣ ਕੀਤਾ ਕਿ ਉਹ ਸਿੱਖਾਂ ਦਾ ਨਾਮੋ-ਨਿਸ਼ਾਨ ਮਿਟਾ ਕੇ ਹੀ ਸੁੱਖ ਦਾ ਸਾਹ ਲਵੇਗਾ। ਉਸ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਉਨ੍ਹਾਂ ਦੇ ਧਰਮ ਗ੍ਰੰਥ ਪੜ੍ਹਨ ‘ਤੇ ਪਾਬੰਦੀ ਲਗਾ ਦਿੱਤੀ । ਉਸ ਨੇ ਗੁਰੂ ਸ਼ਬਦ ਦੀ ਵਰਤੋਂ ਦੀ ਵੀ ਮਨਾਹੀ ਕਰ ਦਿੱਤੀ । ਇਸ ਉਦੇਸ਼ ਨਾਲ ਉਸ ਨੇ ਗੁੜ ਦੀ ਥਾਂ ਲੋਕਾਂ ਨੂੰ ਰੋੜੀ ਸ਼ਬਦ ਦੀ ਵਰਤੋਂ ਕਰਨ ਲਈ ਕਿਹਾ ਕਿਉਂਕਿ ਗੁੜ ਸ਼ਬਦ ਦੀ ਆਵਾਜ਼ ਗੁਰੂ ਦੇ ਨਾਲ ਮਿਲਦੀ-ਜੁਲਦੀ ਸੀ । ਇਸੇ ਤਰ੍ਹਾਂ ਗ੍ਰੰਥ ਦੀ ਥਾਂ ਪੋਥੀ ਸ਼ਬਦ ਦੀ ਵਰਤੋਂ ਕਰਨ ਦਾ ਆਦੇਸ਼ ਦਿੱਤਾ ਗਿਆ । ਇਨ੍ਹਾਂ ਆਦੇਸ਼ਾਂ ਦੀ ਉਲੰਘਣਾ ਕਰਨ ਵਾਲਿਆਂ ਨੂੰ ਮੌਤ ਦੀ ਸਜ਼ਾ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ । ਉਸ ਨੇ ਬਹੁਤ ਸਾਰੇ ਸਿੱਖਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਲਾਹੌਰ ਲਿਜਾ ਕੇ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ।
4. ਪਹਿਲਾ ਘੱਲੂਘਾਰਾ (First Holocaust) – 1746 ਈ. ਵਿੱਚ ਯਾਹੀਆ ਖ਼ਾਂ ਤੇ ਲਖਪਤ ਰਾਏ ਦੇ ਅਧੀਨ ਮੁਗ਼ਲ ਸੈਨਾ ਨੇ ਲਗਭਗ 15,000 ਸਿੱਖਾਂ ਨੂੰ ਕਾਹਨੂੰਵਾਨ ਵਿਖੇ ਘੇਰ ਲਿਆ । ਸਿੱਖ ਬਸੌਲੀ ਦੀਆਂ ਪਹਾੜੀਆਂ ਵੱਲ ਚਲੇ ਗਏ । ਮੁਗਲ ਸੈਨਿਕਾਂ ਨੇ ਉਨ੍ਹਾਂ ਦਾ ਪਿੱਛਾ ਕੀਤਾ । ਸਿੱਖ ਬੜੀ ਮੁਸ਼ਕਿਲ ਵਿੱਚ ਫਸ ਗਏ । ਇੱਕ ਪਾਸੇ ਉੱਚੀਆਂ ਪਹਾੜੀਆਂ ਸਨ ਅਤੇ ਦੂਜੇ ਪਾਸੇ ਦਰਿਆ ਰਾਵੀ ਵਿੱਚ ਹੜ੍ਹ ਆਇਆ ਹੋਇਆ ਸੀ । ਪਿਛਲੇ ਪਾਸੇ ਮੁਗ਼ਲ ਸੈਨਿਕ ਉਨ੍ਹਾਂ ਦਾ ਪਿੱਛਾ ਕਰ ਰਹੇ ਸਨ । ਇਸ ਹਮਲੇ ਵਿੱਚ 7,000 ਸਿੱਖ ਸ਼ਹੀਦ ਹੋ ਗਏ ਅਤੇ 3,000 ਸਿੱਖਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਗਿਆ । ਇਨ੍ਹਾਂ ਸਿੱਖਾਂ ਨੂੰ ਲਾਹੌਰ ਵਿਖੇ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ਗਿਆ । ਸਿੱਖਾਂ ਦੇ ਇਤਿਹਾਸ ਵਿੱਚ ਇਹ ਪਹਿਲਾ ਮੌਕਾ ਸੀ ਜਦੋਂ ਸਿੱਖਾਂ ਦਾ ਇੱਕੋ ਵਾਰੀ ਇੰਨਾ ਭਾਰੀ ਜਾਨੀ ਨੁਕਸਾਨ ਹੋਇਆ ਸੀ । ਇਸ ਦਰਦਨਾਕ ਘਟਨਾ ਨੂੰ ਇਤਿਹਾਸ ਵਿੱਚ ਪਹਿਲਾ ਜਾਂ ਛੋਟਾ ਘੱਲੂਘਾਰਾ ਦੇ ਨਾਂ ਨਾਲ ਯਾਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਗੁਰਬਖ਼ਸ਼ ਸਿੰਘ ਦਾ ਕਹਿਣਾ ਬਿਲਕੁਲ ਠੀਕ ਹੈ,
1746 ਦੇ ਤਬਾਹਕੁੰਨ ਝਟਕੇ ਨੇ ਸਿੱਖਾਂ ਦੇ ਇਸ ਵਿਸ਼ਵਾਸ ਨੂੰ ਹੋਰ ਬਲ ਪ੍ਰਦਾਨ ਕੀਤਾ ਕਿ ਉਹ ਅੱਤਿਆਚਾਰੀਆਂ ਦਾ ਸਰਵਨਾਸ਼ ਕਰਨ ’’ 1
5. ਯਾਹੀਆ ਖਾਂ ਦਾ ਪਤਨ (Fall of Yahiya Khan) – ਨਵੰਬਰ, 1746 ਈ. ਵਿੱਚ ਯਾਹੀਆ ਖ਼ਾਂ ਦੇ ਛੋਟੇ ਭਰਾ ਸ਼ਾਹਨਵਾਜ਼ ਖਾਂ ਨੇ ਵਿਦਰੋਹ ਕਰ ਦਿੱਤਾ । ਇਹ ਵਿਦਰੋਹ ਚਾਰ ਮਹੀਨੇ ਤਕ ਜਾਰੀ ਰਿਹਾ । ਇਸ ਵਿਦਰੋਹ ਵਿੱਚ ਸ਼ਾਹਨਵਾਜ਼ ਖਾਂ ਸਫਲ ਰਿਹਾ ਤੇ ਉਸ ਨੇ ਯਾਹੀਆ ਖ਼ਾਂ ਨੂੰ 17 ਮਾਰਚ, 1747 ਈ. ਨੂੰ ਜੇਲ੍ਹ ਵਿੱਚ ਸੁੱਟ ਦਿੱਤਾ । ਇਸ ਤਰ੍ਹਾਂ ਉਸ ਦੇ ਅੱਤਿਆਚਾਰਾਂ ਦਾ ਅੰਤ ਹੋਇਆ ।
![]()
ਮੀਰ ਮੰਨੂੰ 1748-53 ਈ. (Mir Mannu 1748-53 A.D.)
ਪ੍ਰਸ਼ਨ 7.
ਮੀਰ ਮੰਨੂੰ ਕੌਣ ਸੀ ? ਸਿੱਖਾਂ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਉਸ ਦੀ ਅਸਫਲਤਾ ਦੇ ਕੀ ਕਾਰਨ ਸਨ ? (Who was Mir Mannu ? What were the causes of his failure to crush the Sikhs ?)
ਜਾਂ
ਮੀਰ ਮੰਨੂੰ ਦੇ ਸਿੱਖਾਂ ਨਾਲ ਸੰਬੰਧਾਂ ਦੀ ਚਰਚਾ ਕਰੋ । (Describe Mir Mannu’s relations with the Sikhs.)
ਜਾਂ
ਮੀਰ ਮੰਨੂੰ ਨੇ ਸਿੱਖਾਂ ਨਾਲ ਨਜਿੱਠਣ ਦੀ ਕਿਵੇਂ ਕੋਸ਼ਿਸ਼ ਕੀਤੀ ? (What was the strategy of Mir Mannu to fight against the Sikhs ?)
ਉੱਤਰ-
ਮੀਰ ਮੰਨੂੰ, ਮੁਗ਼ਲ ਬਾਦਸ਼ਾਹ ਮੁਹੰਮਦ ਸ਼ਾਹ ਰੰਗੀਲਾ ਦੇ ਵਜ਼ੀਰ ਕਮਰਉੱਦੀਨ ਦਾ ਪੁੱਤਰ ਸੀ । ਉਹ ਇੱਕ ਬਹਾਦਰ, ਅਨੁਸ਼ਾਸਿਤ ਅਤੇ ਯੋਗ ਰਾਜਨੀਤੀਵਾਨ ਸੀ । ਉਸ ਦੇ ਇਨ੍ਹਾਂ ਗੁਣਾਂ ਦੇ ਕਾਰਨ ਉਸ ਨੂੰ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਨਿਯੁਕਤ ਕੀਤਾ ਗਿਆ ਸੀ । ਉਹ 1748 ਈ. ਤੋਂ 1753 ਈ. ਤਕ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਰਿਹਾ । ਹਰਬੰਸ ਸਿੰਘ ਦੇ ਅਨੁਸਾਰ,
“ਮੀਰ ਮੰਨੂੰ ਆਪਣੇ ਪੂਰਵ-ਅਧਿਕਾਰੀਆਂ ਨਾਲੋਂ ਸਿੱਖਾਂ ਦਾ ਵੱਧ ਕੱਟੜ ਦੁਸ਼ਮਣ ਸਿੱਧ ਹੋਇਆ ।’’ 1
1. ਮੀਰ ਮੰਨੂੰ ਦੀਆਂ ਔਕੜਾਂ (Difficulties of Mir Mannu) – ਮੀਰ ਮੰਨੂੰ ਜਦੋਂ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਬਣਿਆ ਤਦ ਉਸ ਦੇ ਸਾਹਮਣੇ ਪਹਾੜ ਵਰਗੀਆਂ ਔਕੜਾਂ ਸਨ । ਗੱਦੀ ਦੀ ਪ੍ਰਾਪਤੀ ਲਈ ਯਾਹੀਆ ਖ਼ਾਂ ਅਤੇ ਸ਼ਾਹਨਵਾਜ਼ ਖ਼ਾ ਵਿਚਾਲੇ ਚੱਲਣ ਵਾਲੇ ਸੰਘਰਸ਼ ਕਾਰਨ ਪੰਜਾਬ ਵਿੱਚ ਅਰਾਜਕਤਾ ਫੈਲ ਗਈ ਸੀ । ਅਹਿਮਦ ਸ਼ਾਹ ਅਬਦਾਲੀ ਦੇ ਹਮਲੇ ਨੇ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਸਥਿਤੀ ਨੂੰ ਵਧੇਰੇ ਬਦਤਰ ਬਣਾ ਦਿੱਤਾ । ਸਿੱਖਾਂ ਨੇ ਆਪਣੀਆਂ ਲੁੱਟਮਾਰ ਦੀਆਂ ਕਾਰਵਾਈਆਂ ਤੇਜ਼ ਕਰ ਦਿੱਤੀਆਂ ਸਨ । ਰਾਜ ਦਾ ਖ਼ਜ਼ਾਨਾ ਲਗਭਗ ਖ਼ਾਲੀ ਪਿਆ ਸੀ । ਮੀਰ ਮੰਨੂੰ ਨੇ ਇਨ੍ਹਾਂ ਔਕੜਾਂ ‘ਤੇ ਕਾਬੂ ਪਾਉਣ ਲਈ ਵਿਸ਼ੇਸ਼ ਕਦਮ ਉਠਾਉਣ ਦਾ ਫੈਸਲਾ ਕੀਤਾ ।
2. ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕਾਰਵਾਈ (Action against the Sikhs) – ਮੀਰ ਮੰਨੂੰ ਨੇ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਆਪਣਾ ਧਿਆਨ ਸਿੱਖਾਂ ਵੱਲ ਦਿੱਤਾ । ਮੀਰ ਮੰਨੂੰ ਨੇ ਸਿੱਖਾਂ ਦੇ ਵਿਨਾਸ਼ ਲਈ ਪੰਜਾਬ ਦੇ ਵੱਖ-ਵੱਖ ਦੇਸ਼ਾਂ ਵਿੱਚ ਆਪਣੇ ਸੈਨਿਕ ਦਸਤੇ ਭੇਜੇ । ਉਸ ਨੇ ਜਲੰਧਰ ਦੇ ਫ਼ੌਜਦਾਰ ਅਦੀਨਾ ਬੇਗ਼ ਨੂੰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਸਖ਼ਤ ਕਾਰਵਾਈ ਕਰਨ ਦਾ ਹੁਕਮ ਦਿੱਤਾ । ਸਿੱਖਾਂ ਨੂੰ ਰੋਜ਼ਾਨਾ ਗ੍ਰਿਫ਼ਤਾਰ ਕੀਤਾ ਜਾਣ ਲੱਗਾ । ਅਦੀਨਾ ਬੇਗ਼ ਅਤੇ ਸਿੱਖਾਂ ਵਿਚਾਲੇ ਹੋਈ ਇੱਕ ਲੜਾਈ ਵਿੱਚ 600 ਸਿੱਖ ਸ਼ਹੀਦ ਹੋ ਗਏ । ਸਿੱਟੇ ਵਜੋਂ ਸਿੱਖਾਂ ਨੇ ਜੰਗਲਾਂ ਵਿੱਚ ਸ਼ਰਨ ਲਈ ।
3. ਰਾਮਰੌਣੀ ਦਾ ਘੇਰਾ (Siege of Ram Rauni) – ਸਿੱਖ ਅਕਤੂਬਰ, 1748 ਈ. ਵਿੱਚ ਦੀਵਾਲੀ ਦੇ ਮੌਕੇ ‘ਤੇ ਅੰਮ੍ਰਿਤਸਰ ਵਿਖੇ ਇਕੱਠੇ ਹੋਏ । ਜਦੋਂ ਮੀਰ ਮੰਨੂੰ ਨੂੰ ਇਹ ਸੂਚਨਾ ਮਿਲੀ ਤਾਂ ਉਹ ਇੱਕ ਵਿਸ਼ਾਲ ਸੈਨਾ ਨਾਲ ਅੰਮ੍ਰਿਤਸਰ ਵੱਲ ਵਧਿਆ । ਸਿੱਖਾਂ ਨੇ ਰਾਮਰੌਣੀ ਕਿਲ੍ਹੇ ਵਿੱਚ ਜਾ ਸ਼ਰਨ ਲਈ । ਮੀਰ ਮੰਨੂੰ ਨੇ ਰਾਮਰੌਣੀ ਕਿਲ੍ਹੇ ਨੂੰ ਘੇਰਾ ਪਾ ਲਿਆ । ਇਹ ਘੇਰਾ ਚਾਰ ਮਹੀਨਿਆਂ ਤਕ ਜਾਰੀ ਰਿਹਾ | ਅਜਿਹੇ ਸਮੇਂ ਜੱਸਾ ਸਿੰਘ ਰਾਮਗੜ੍ਹੀਆ ਆਪਣੇ ਸੈਨਿਕਾਂ ਸਮੇਤ ਸਿੱਖਾਂ ਦੀ ਮਦਦ ਲਈ ਪਹੁੰਚਿਆ । ਇਸੇ ਸਮੇਂ ਮੀਰ ਮੰਨੂੰ ਨੂੰ ਇਹ ਸੂਚਨਾ ਮਿਲੀ ਕਿ ਅਹਿਮਦ ਸ਼ਾਹ ਅਬਦਾਲੀ ਪੰਜਾਬ ਉੱਤੇ ਹਮਲਾ ਕਰਨ ਵਾਲਾ ਹੈ । ਸਿੱਟੇ ਵਜੋਂ ਮੀਰ ਮੰਨੂੰ ਨੇ ਸਿੱਖਾਂ ਨਾਲ ਸਮਝੌਤਾ ਕਰ ਲਿਆ ਅਤੇ ਘੇਰੇ ਨੂੰ ਚੁੱਕ ਲਿਆ । ਸਮਝੌਤੇ ਦੇ ਅਨੁਸਾਰ ਮੀਰ ਮੰਨੂੰ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਪੱਟੀ ਵਿਖੇ ਇੱਕ ਜਾਗੀਰ ਦਿੱਤੀ ਤਾਂ ਕਿ ਉਹ ਸ਼ਾਂਤੀ ਨਾਲ ਰਹਿਣ ।
4. ਅਬਦਾਲੀ ਦਾ ਦੂਜਾ ਹਮਲਾ (Second Invasion of Abdali) – ਅਹਿਮਦ ਸ਼ਾਹ ਅਬਦਾਲੀ ਨੇ ਦਸੰਬਰ, 1748 ਈ. ਵਿੱਚ ਪੰਜਾਬ ਉੱਤੇ ਦੂਜੀ ਵਾਰ ਹਮਲਾ ਕੀਤਾ । ਮੀਰ ਮੰਨੂੰ ਨੇ ਸਿਆਣਪ ਤੋਂ ਕੰਮ ਲੈਂਦਿਆਂ ਅਬਦਾਲੀ ਨਾਲ ਸੰਧੀ ਕਰ ਲਈ । ਇਸ ਅਨੁਸਾਰ ਮੀਰ ਮੰਨੂੰ ਨੇ ਚਾਰ ਮਹੱਲਾਂ-ਸਿਆਲਕੋਟ, ਗੁਜਰਾਤ, ਪਸਰੂਰ ਅਤੇ ਔਰੰਗਾਬਾਦ ਦਾ ਲਗਾਨ ਅਬਦਾਲੀ ਨੂੰ ਦੇਣਾ ਮੰਨ ਲਿਆ । ਇਨ੍ਹਾਂ ਮਹੱਲਾਂ ਦਾ ਸਲਾਨਾ ਲਗਾਨ 14 ਲੱਖ ਰੁਪਏ ਸੀ ।
5. ਨਾਸਿਰ ਖ਼ਾਂ ਅਤੇ ਸ਼ਾਹ ਨਵਾਜ਼ ਸ਼ਾਂ ਦੇ ਵਿਦਰੋਹ (Revolts of Nasir Khan and Shah Nawaz Khan) – ਦਿੱਲੀ ਦੇ ਵਜ਼ੀਰ ਸਫ਼ਦਰਜੰਗ ਦੇ ਉਕਸਾਉਣ ‘ਤੇ ਫ਼ੌਜਦਾਰ ਨਾਸਿਰ ਖ਼ਾਂ ਤੇ ਮੁਲਤਾਨ ਦੇ ਸੂਬੇਦਾਰ ਸ਼ਾਹਨਵਾਜ਼ ਮਾਂ ਨੇ ਮੀਰ ਮੰਨੂੰ ਵਿਰੁੱਧ ਵਿਦਰੋਹ ਕਰ ਦਿੱਤਾ । ਸ਼ਾਹਨਵਾਜ਼ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਲਾਹੌਰ ਦੇ ਆਲੇ-ਦੁਆਲੇ ਦੇ ਖੇਤਰਾਂ ਵਿੱਚ ਅਸ਼ਾਂਤੀ ਫੈਲਾਉਣ ਲਈ ਉਕਸਾਇਆ । ਮੀਰ ਮੰਨੂੰ ਇਹ ਕਿਵੇਂ ਬਰਦਾਸ਼ਤ ਕਰ ਸਕਦਾ ਸੀ । ਉਸ ਨੇ ਕੌੜਾ ਮੱਲ ਨੂੰ ਸ਼ਾਹਨਵਾਜ਼ ਖਾਂ ਦੇ ਵਿਦਰੋਹ ਨੂੰ ਕੁਚਲਣ ਲਈ ਭੇਜਿਆ । ਇਸ ਲੜਾਈ ਵਿੱਚ ਸ਼ਾਹਨਵਾਜ਼ ਖਾਂ ਮਾਰਿਆ ਗਿਆ ।
6. ਅਬਦਾਲੀ ਦਾ ਤੀਸਰਾ ਹਮਲਾ (Third Invasion of Abdali) – ਅਬਦਾਲੀ ਨੇ 1751 ਈ. ਦੇ ਅਖੀਰ ਵਿੱਚ ਪੰਜਾਬ ਉੱਤੇ ਤੀਜੀ ਵਾਰ ਹਮਲਾ ਕਰ ਦਿੱਤਾ 16 ਮਾਰਚ, 1752 ਈ. ਨੂੰ ਅਹਿਮਦ ਸ਼ਾਹ ਅਬਦਾਲੀ ਅਤੇ ਮੀਰ ਮੰਨੂੰ ਦੀਆਂ ਫ਼ੌਜਾਂ ਵਿਚਾਲੇ ਲਾਹੌਰ ਦੇ ਨੇੜੇ ਬੜੀ ਘਮਸਾਨ ਦੀ ਲੜਾਈ ਹੋਈ । ਇਸ ਲੜਾਈ ਵਿੱਚ ਮੀਰ ਮੰਨੂੰ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਗਿਆ । ਇਸ ਤਰ੍ਹਾਂ ਅਹਿਮਦ ਸ਼ਾਹ ਅਬਦਾਲੀ ਨੇ 1752 ਈ. ਵਿੱਚ ਪੰਜਾਬ ਉੱਤੇ ਕਬਜ਼ਾ ਕਰ ਲਿਆ । ਅਹਿਮਦ ਸ਼ਾਹ ਅਬਦਾਲੀ ਨੇ ਮੀਰ ਮੰਨੂੰ ਨੂੰ ਹੀ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਨਿਯੁਕਤ ਕਰ ਦਿੱਤਾ ਅਤੇ ਉਸ ਨੂੰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਸਖ਼ਤ ਕਾਰਵਾਈ ਕਰਨ ਦਾ ਹੁਕਮ ਦਿੱਤਾ ।
7. ਸਿੱਖਾਂ ਉੱਤੇ ਮੁੜ ਅੱਤਿਆਚਾਰ (Renewal of the Sikh Persecution) – ਮੀਰ ਮੰਨੂੰ ਨੇ ਸਿੱਖਾਂ ਦਾ ਮਲੀਆਮੇਟ ਕਰਨ ਲਈ ਬੜੇ ਜ਼ੋਰਦਾਰ ਯਤਨ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੇ । ਸਿੱਖਾਂ ਦੇ ਸਿਰਾਂ ਦੇ ਮੁੱਲ ਨਿਯਤ ਕੀਤੇ ਗਏ । ਸਿੱਖਾਂ ਨੂੰ ਸ਼ਰਨ ਦੇਣ ਵਾਲਿਆਂ ਨੂੰ ਸਖ਼ਤ ਸਜ਼ਾਵਾਂ ਦਿੱਤੀਆਂ ਗਈਆਂ । ਮਾਰਚ, 1753 ਈ. ਵਿੱਚ ਜਦੋਂ ਸਿੱਖ ਹੋਲੇ ਮਹੱਲੇ ਦੇ ਮੌਕੇ ‘ਤੇ ਮਾਖੋਵਾਲ ਵਿਖੇ ਇਕੱਠੇ ਹੋਏ ਸਨ ਤਾਂ ਅਦੀਨਾ ਬੇਗ਼ ਨੇ ਅਚਾਨਕ ਹਮਲਾ ਕਰਕੇ ਬਹੁਤ ਸਾਰੇ ਸਿੱਖਾਂ ਨੂੰ ਕਤਲ ਕਰ ਦਿੱਤਾ । ਸਿੱਖ ਇਸਤਰੀਆਂ ਅਤੇ ਬੱਚਿਆਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਕੇ ਲਾਹੌਰ ਲੈ ਆਂਦਾ ਗਿਆ । ਇਨ੍ਹਾਂ ਇਸਤਰੀਆਂ ਅਤੇ ਬੱਚਿਆਂ ਉੱਤੇ ਜੋ ਜ਼ੁਲਮ ਅਤੇ ਜਬਰ ਢਾਹੇ ਗਏ, ਉਨ੍ਹਾਂ ਦਾ ਸ਼ਬਦਾਂ ਵਿੱਚ ਵਰਣਨ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਦਾ । ਹਰੇਕ ਇਸਤਰੀ ਨੂੰ ਸਵਾ-ਸਵਾ ਮਣ ਰੋਜ਼ਾਨਾ ਅਨਾਜ ਪੀਸਣ ਨੂੰ ਦਿੱਤਾ ਜਾਂਦਾ । ਛੋਟੇ ਬੱਚਿਆਂ ਨੂੰ ਉਨ੍ਹਾਂ ਦੀਆਂ ਮਾਂਵਾਂ ਤੋਂ ਖੋਹ ਕੇ ਉਨ੍ਹਾਂ ਦੇ ਸਾਹਮਣੇ ਕਤਲ ਕੀਤਾ ਗਿਆ । ਇਨ੍ਹਾਂ ਘੋਰ ਤਸੀਹਿਆਂ ਦੇ ਬਾਵਜੂਦ ਸਿੱਖਾਂ ਦੀ ਗਿਣਤੀ ਘਟਣ ਦੀ ਬਜਾਏ ਵਧਦੀ ਚਲੀ ਗਈ । ਉਸ ਸਮੇਂ ਇਹ ਅਖਾਣ ਬੜਾ ਪ੍ਰਚਲਿਤ ਸੀ,
“ਨੂੰ ਅਸਾਡੀ ਦਾਤਰੀ, ਅਸੀਂ ਮੰਨੂੰ ਦੇ ਸੋਏ ।
ਜਿਉਂ-ਜਿਉਂ ਸਾਨੂੰ ਵੱਢਦਾ, ਅਸੀਂ ਦੂਣ ਸਵਾਏ ਹੋਏ ।”
8. ਮੀਰ ਮੰਨੂੰ ਦੀ ਮੌਤ (Death of Mir Mannu) – 3 ਨਵੰਬਰ, 1753 ਈ. ਨੂੰ ਮੀਰ ਮੰਨੂੰ ਨੂੰ ਇਹ ਸੂਚਨਾ ਮਿਲੀ ਕਿ ਕੁਝ ਸਿੱਖ ਤਿਲਕਪੁਰ ਵਿਖੇ ਇੱਕ ਗੰਨੇ ਦੇ ਖੇਤ ਵਿੱਚ ਲੁਕੇ ਹੋਏ ਹਨ । ਉਹ ਫੌਰਨ ਸਿੱਖਾਂ ਦਾ ਅੰਤ ਕਰਨ ਲਈ ਆਪਣੇ ਘੋੜੇ ‘ਤੇ ਸਵਾਰ ਹੋ ਕੇ ਉੱਥੇ ਪਹੁੰਚ ਗਿਆ । ਉੱਥੇ ਸਿੱਖਾਂ ਵੱਲੋਂ ਚਲਾਈਆਂ ਗਈਆਂ ਗੋਲੀਆਂ ਕਾਰਨ ਉਸ ਦਾ ਘੋੜਾ ਘਬਰਾ ਗਿਆ ਤੇ ਉਸ ਨੇ ਮੀਰ ਮੰਨੂੰ ਨੂੰ ਹੇਠਾਂ ਸੁੱਟ ਦਿੱਤਾ, ਪਰ ਉਸ ਦਾ ਇੱਕ ਪੈਰ ਘੋੜੇ ਦੀ ਰਕਾਬ ਵਿੱਚ ਫਸ ਗਿਆ | ਘੋੜਾ ਉਸੇ ਤਰ੍ਹਾਂ ਮੀਰ ਮੰਨੂੰ ਨੂੰ ਘਸੀਟਦਾ ਗਿਆ, ਜਿਸ ਕਾਰਨ ਉਸ ਦੀ ਮੌਤ ਹੋ ਗਈ । ਇਸ ਤਰ੍ਹਾਂ ਕੁਦਰਤ ਨੇ ਮੀਰ ਮੰਨੂੰ ਤੋਂ ਉਸ ਦੇ ਜ਼ੁਲਮਾਂ ਦਾ ਬਦਲਾ ਲੈ ਲਿਆ । ਪ੍ਰਸਿੱਧ ਇਤਿਹਾਸਕਾਰ ਡਾਕਟਰ ਐੱਨ. ਕੇ. ਸਿਨਹਾ ਨੇ ਠੀਕ ਲਿਖਿਆ ਹੈ,
‘‘ਅਪ੍ਰਤੱਖ ਰੂਪ ਨਾਲ ਮੀਰ ਮੰਨੂੰ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਵਧਾਉਣ ਲਈ ਜ਼ਿੰਮੇਵਾਰ ਸੀ ।” –
ਨੋਟ-ਮੀਰ ਮੰਨੂੰ ਦੀ ਅਸਫ਼ਲਤਾ ਦੇ ਕਾਰਨਾਂ ਲਈ ਵਿਦਿਆਰਥੀ ਕਿਰਪਾ ਕਰਕੇ ਪ੍ਰਸ਼ਨ ਨੰ: 8 ਦਾ ਉੱਤਰ ਵੇਖਣ ।
ਮੀਰ ਮੰਨੂੰ ਦੀ ਅਸਫਲਤਾ ਦੇ ਕਾਰਨ (Causes of the Failure of Mir Mannu)
ਪ੍ਰਸ਼ਨ 8.
ਮੀਰ ਮੰਨੂੰ ਦੀ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਅਸਫਲਤਾ ਦੇ ਕੀ ਕਾਰਨ ਸਨ ? (What were the main reasons of the failure of Mir Mannu against the Sikhs ?)
ਜਾਂ
ਮੀਰ ਮੰਨੂੰ ਸਿੱਖਾਂ ਨੂੰ ਦਬਾਉਣ ਵਿੱਚ ਕਿਉਂ ਅਸਫਲ ਰਿਹਾ ? (Why did Mir Mannu fail to crush the Sikhs ?)
ਜਾਂ
ਮੀਰ ਮੰਨੂੰ ਦੀ ਅਸਫਲਤਾ ਦੇ ਕਾਰਨਾਂ ਦੀ ਵਿਆਖਿਆ ਕਰੋ । (Explain the causes of failure of Mir Mannu.)
ਉੱਤਰ-
ਮੀਰ ਮੰਨੂੰ ਨੇ ਸਿੱਖਾਂ ਦਾ ਮਲੀਆਮੇਟ ਕਰਨ ਲਈ ਅਣਥੱਕ ਯਤਨ ਕੀਤੇ, ਪਰ ਉਹ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ । ਉਸ ਦੀ ਅਸਫਲਤਾ ਲਈ ਹੇਠ ਲਿਖੇ ਮੁੱਖ ਕਾਰਨ ਜ਼ਿੰਮੇਵਾਰ ਸਨ-
1. ਦਲ ਖ਼ਾਲਸਾ ਦੀ ਜੱਥੇਬੰਦੀ (Organisation of the Dal Khalsa) – ਮੀਰ ਮੰਨੂੰ ਦੀ ਅਸਫਲਤਾ ਦਾ ਇੱਕ ਪ੍ਰਮੁੱਖ ਕਾਰਨ ਦਲ ਖ਼ਾਲਸਾ ਦੀ ਜੱਥੇਬੰਦੀ ਸੀ । ਸਿੱਖਾਂ ਨੇ ਮੀਰ ਮੰਨੂੰ ਦੇ ਅੱਤਿਆਚਾਰਾਂ ਦਾ ਡਟ ਕੇ ਮੁਕਾਬਲਾ ਕਰਨ ਲਈ ਖ਼ੁਦ ਨੂੰ 12 ਜੱਥਿਆਂ ਵਿੱਚ ਸੰਗਠਿਤ ਕਰ ਲਿਆ ਸੀ । ਸਿੱਖ ਦਲ ਖ਼ਾਲਸਾ ਦਾ ਦਿਲੋਂ ਸਤਿਕਾਰ ਕਰਦੇ ਸਨ ਅਤੇ ਇਸ ਦੇ ਹੁਕਮ ‘ਤੇ ਹਰ ਕੁਰਬਾਨੀ ਦੇਣ ਲਈ ਤਿਆਰ ਰਹਿੰਦੇ ਸਨ । ਸਿੱਟੇ ਵਜੋਂ ਮੀਰ ਮੰਨੂੰ ਲਈ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣਾ ਔਖਾ ਹੋ ਗਿਆ ।
2. ਸਿੱਖਾਂ ਦੇ ਅਸਾਧਾਰਨ ਗੁਣ (Uncommon qualities of the Sikhs) – ਸਿੱਖਾਂ ਵਿੱਚ ਆਪਣੇ ਪੰਥ ਲਈ ਦ੍ਰਿੜ੍ਹ ਨਿਸ਼ਚਾ, ਅਥਾਹ ਜੋਸ਼, ਦਲੇਰੀ ਅਤੇ ਕੁਰਬਾਨੀ ਦੀਆਂ ਭਾਵਨਾਵਾਂ ਸਨ । ਉਹ ਭਾਰੀ ਔਕੜਾਂ ਦੇ ਬਾਵਜੂਦ ਆਪਣਾ ਹੌਸਲਾ ਕਦੇ ਨਹੀਂ ਸਨ ਛੱਡਦੇ । ਮੀਰ ਮੰਨੂੰ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਅਣਗਿਣਤ ਤਸੀਹੇ ਦਿੱਤੇ ਪਰ ਉਹ ਸਿੱਖਾਂ ਨੂੰ ਵਿਚਲਿਤ ਕਰਨ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ ।
3. ਸਿੱਖਾਂ ਦੀ ਗੁਰੀਲਾ ਯੁੱਧ ਨੀਤੀ (Guerilla tactics of the Sikhs) – ਸਿੱਖਾਂ ਨੇ ਮੁਗ਼ਲ ਸੈਨਾ ਦੇ ਵਿਰੁੱਧ ਗੁਰੀਲਾ ਯੁੱਧ ਨੀਤੀ ਅਪਣਾਈ । ਇਸ ਨੀਤੀ ਅਨੁਸਾਰ ਸਿੱਖਾਂ ਨੂੰ ਜਦ ਮੌਕਾ ਮਿਲਦਾ ਉਹ ਮੁਗ਼ਲ ਫ਼ੌਜਾਂ ‘ਤੇ ਹਮਲਾ ਕਰਦੇ ਅਤੇ ਲੁੱਟਮਾਰ ਕਰਨ ਮਗਰੋਂ ਮੁੜ ਜੰਗਲਾਂ ਵਿੱਚ ਜਾ ਸ਼ਰਨ ਲੈਂਦੇ । ਇਸ ਤਰ੍ਹਾਂ ਆਹਮਣੇ-ਸਾਹਮਣੇ ਦੀ ਟੱਕਰ ਨਾ ਹੋਣ ਕਾਰਨ ਮੀਰ ਮੰਨੂੰ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ ।
4. ਦੀਵਾਨ ਕੌੜਾ ਮਲ ਦਾ ਸਿੱਖਾਂ ਨਾਲ ਸਹਿਯੋਗ (Cooperation of Diwan Kaura Mal with the Sikhs) – ਦੀਵਾਨ ਕੌੜਾ ਮਲ ਮੀਰ ਮੰਨੂੰ ਦਾ ਸਲਾਹਕਾਰ ਸੀ । ਸਹਿਜਧਾਰੀ ਸਿੱਖ ਹੋਣ ਕਾਰਨ ਉਹ ਸਿੱਖਾਂ ਨਾਲ ਹਮਦਰਦੀ ਰੱਖਦਾ ਸੀ । ਮੀਰ ਮੰਨੂੰ ਉਸ ਦੀ ਸਲਾਹ ਤੋਂ ਬਿਨਾਂ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕੋਈ ਕਾਰਵਾਈ ਨਹੀਂ ਕਰਦਾ ਸੀ । ਜਦੋਂ ਵੀ ਕਦੇ ਮੀਰ ਮੰਨੂੰ ਨੇ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕੋਈ ਸਖ਼ਤ ਕਦਮ ਚੁੱਕਣ ਦਾ ਨਿਰਣਾ ਕੀਤਾ ਤਾਂ ਕੌੜਾ ਮਲ ਉਸ ਨੂੰ ਸਿੱਖਾਂ ਨਾਲ ਸਮਝੌਤਾ ਕਰਨ ਲਈ ਮਨਾ ਲੈਂਦਾ ਸੀ । ਇਸ ਤਰ੍ਹਾਂ ਦੀਵਾਨ ਕੌੜਾ ਮਲ ਦਾ ਸਹਿਯੋਗ ਵੀ ਸਿੱਖ ਸ਼ਕਤੀ ਨੂੰ ਬਚਾਈ ਰੱਖਣ ਵਿੱਚ ਬੜਾ ਲਾਹੇਵੰਦ ਸਿੱਧ ਹੋਇਆ ।
5. ਅਦੀਨਾ ਬੇਗ਼ ਦੀ ਦੋਰੰਗੀ ਨੀਤੀ (Dual Policy of Adina Beg) – ਅਦੀਨਾ ਬੇਗ਼ ਜਲੰਧਰ ਦੁਆਬ ਦਾ ਫ਼ੌਜਦਾਰ ਸੀ । ਉਹ ਮੀਰ ਮੰਨੂੰ ਤੋਂ ਬਾਅਦ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਬਣਨਾ ਚਾਹੁੰਦਾ ਸੀ । ਮੀਰ ਮੰਨੂੰ ਨੇ ਜਦ ਵੀ ਉਸ ਨੂੰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਸਖ਼ਤ ਕਾਰਵਾਈ ਕਰਨ ਦਾ ਹੁਕਮ ਦਿੱਤਾ ਤਾਂ ਉਸ ਨੇ ਇਸ ਦਾ ਪੂਰੀ ਤਰ੍ਹਾਂ ਪਾਲਨ ਨਹੀਂ ਕੀਤਾ । ਉਹ ਪੰਜਾਬ ਵਿੱਚ ਅਸ਼ਾਂਤੀ ਦੇ ਮਾਹੌਲ ਨੂੰ ਬਣਾਈ ਰੱਖਣਾ ਚਾਹੁੰਦਾ ਸੀ । ਇਸ ਤਰ੍ਹਾਂ ਅਦੀਨਾ ਬੇਗ ਦੀ ਦੋਰੰਗੀ ਨੀਤੀ ਵੀ ਮੀਰ ਮੰਨੂੰ ਦੀ ਅਸਫਲਤਾ ਦਾ ਕਾਰਨ ਬਣੀ ।
6. ਮੀਰ ਮੰਨੂੰ ਦੀਆਂ ਸਮੱਸਿਆਵਾਂ (Problems of Mir Mannu) – ਆਪਣੇ ਸ਼ਾਸਨ ਕਾਲ ਦੇ ਦੌਰਾਨ ਕਈ ਸਮੱਸਿਆਵਾਂ ਵਿੱਚ ਘਿਰਿਆ ਰਹਿਣ ਦੇ ਕਾਰਨ ਵੀ ਮੀਰ ਮੰਨੂੰ ਸਿੱਖਾਂ ਨੂੰ ਪੂਰੀ ਤਰ੍ਹਾਂ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ ।ਉਸ ਦੀ ਪਹਿਲੀ ਵੱਡੀ ਸਮੱਸਿਆ ਅਹਿਮਦ ਸ਼ਾਹ ਅਬਦਾਲੀ ਦੇ ਹਮਲੇ ਸਨ । ਇਨ੍ਹਾਂ ਹਮਲਿਆਂ ਕਾਰਨ ਉਸ ਨੂੰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਆਪਣੀ ਕਾਰਵਾਈ ਸਥਗਿਤ ਕਰਨੀ ਪੈਂਦੀ ਸੀ ।ਦੂਜਾ, ਦਿੱਲੀ ਦਾ ਵਜ਼ੀਰ ਸਫ਼ਦਰਜੰਗ ਵੀ ਉਸ ਨੂੰ ਅਹੁਦੇ ਤੋਂ ਹਟਾਉਣ ਲਈ ਸਾਜ਼ਸ਼ਾਂ ਕਰਦਾ ਰਹਿੰਦਾ ਸੀ । ਉਸ ਦੇ ਉਕਸਾਉਣ ‘ਤੇ ਹੀ ਨਾਸਿਰ ਖ਼ਾਂ ਅਤੇ ਸ਼ਾਹਨਵਾਜ਼ ਖਾਂ ਨੇ ਮੀਰ ਮੰਨੂੰ ਵਿਰੁੱਧ ਵਿਦਰੋਹ ਕਰ ਦਿੱਤਾ ਸੀ । ਸਿੱਟੇ ਵਜੋਂ ਮੀਰ ਮੰਨੂੰ ਇਨ੍ਹਾਂ ਸਮੱਸਿਆਵਾਂ ਵਿੱਚ ਹੀ ਰੁੱਝਿਆ ਰਿਹਾ ।
![]()
ਸੰਖੇਪ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Short Answer Type Questions)
ਪ੍ਰਸ਼ਨ 1.
ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ‘ਤੇ ਇੱਕ ਨੋਟ ਲਿਖੋ । (Write a short note on Abdus Samad Khan.)
ਜਾਂ
ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਅਧੀਨ ਸਿੱਖਾਂ ‘ਤੇ ਕੀਤੇ ਗਏ ਅੱਤਿਆਚਾਰਾਂ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Briefly explain the repressions done on the Sikhs by Abdus Samad Khan.)
ਉੱਤਰ-
ਅਬਦੁਸ ਸਮਦ ਖਾਂ 1713-1726 ਈ. ਤਕ ਪੰਜਾਬ ਦਾ ਗਵਰਨਰ ਰਿਹਾ | ਅਬਦੁਸ ਸਮਦ ਖਾਂ 1715 ਈ. ਵਿੱਚ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਅਤੇ ਉਸ ਦੇ ਹੋਰ ਸਾਥੀਆਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਨ ਵਿੱਚ ਸਫਲ ਹੋਇਆ । ਇਸ ਤੋਂ ਬਾਅਦ ਸਿੱਖਾਂ ‘ਤੇ ਅੱਤਿਆਚਾਰਾਂ ਦਾ ਦੌਰ ਸ਼ੁਰੂ ਹੋ ਗਿਆ | ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਦੀ ਇਸ ਦਮਨਕਾਰੀ ਨੀਤੀ ਤੋਂ ਖ਼ੁਸ਼ ਹੋ ਕੇ ਮੁਗ਼ਲ ਬਾਦਸ਼ਾਹ ਫ਼ਰੁੱਖਸੀਅਰ ਨੇ ਉਸ ਨੂੰ ‘ਰਾਜੇ ਦੀ ਤਲਵਾਰ’ ਦੇ ਖਿਤਾਬ ਨਾਲ ਸਨਮਾਨਿਤ ਕੀਤਾ । ਅਬਦੁਸ ਸਮਦ ਮਾਂ ਆਪਣੇ ਪੂਰੇ ਯਤਨਾਂ ਦੇ ਬਾਵਜੂਦ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ । ਸਿੱਟੇ ਵਜੋਂ 1726 ਈ. ਵਿੱਚ ਉਸ ਨੂੰ ਉਸ ਦੇ ਅਹੁਦੇ ਤੋਂ ਹਟਾ ਦਿੱਤਾ ਗਿਆ ।
ਪ੍ਰਸ਼ਨ 2.
ਬੰਦਈ ਖ਼ਾਲਸਾ ਅਤੇ ਤੱਤ ਖ਼ਾਲਸਾ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? ਉਨ੍ਹਾਂ ਵਿਚਾਲੇ ਮਤਭੇਦ ਕਿਵੇਂ ਖ਼ਤਮ ਹੋਏ ?(What do you mean by Bandai Khalsa and Tat Khalsa ? How were their differences resolved ?)
ਜਾਂ
ਬੰਦਈ ਖ਼ਾਲਸਾ ਅਤੇ ਤੱਤ ਖ਼ਾਲਸਾ ਵਿਚ ਮਤਭੇਦ ਕਿਵੇਂ ਸਮਾਪਤ ਹੋਏ ?(How were the differences between Bandai Khalsa and Tat Khalsa finished ?)
ਜਾਂ
ਤੱਤ ਖ਼ਾਲਸਾ ਅਤੇ ਬੰਦਈ ਖ਼ਾਲਸਾ ਵਿੱਚ ਕੀ ਮਤਭੇਦ ਸਨ ? ਇਨ੍ਹਾਂ ਵਿੱਚ ਸਮਝੌਤਾ ਕਿਸ ਨੇ ਕਰਵਾਇਆ ? (What was the difference between Tat Khalsa and Bandai Khalsa ? Who compromised them ?)
ਜਾਂ
ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੀ ਸ਼ਹੀਦੀ ਤੋਂ ਬਾਅਦ ਸਿੱਖਾਂ ਦੀ ਕੀ ਸਥਿਤੀ ਸੀ ? (What was the position of the Sikhs after the martyrdom of Banda Singh Bahadur ?)
ਉੱਤਰ-
1716 ਈ. ਵਿੱਚ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੀ ਸ਼ਹੀਦੀ ਤੋਂ ਬਾਅਦ ਸਿੱਖ ਬੰਦਈ ਖ਼ਾਲਸਾ ਅਤੇ ਤੱਤ ਖ਼ਾਲਸਾ ਨਾਂ ਦੇ ਦੋ ਦਲਾਂ ਵਿੱਚ ਵੰਡੇ ਗਏ ਸਨ । ਉਹ ਸਿੱਖ ਜੋ ਗੁਰੂ ਗੋਬਿੰਦ ਸਿੰਘ ਜੀ ਦੇ ਸਿਧਾਂਤਾਂ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ, ਤੱਤ ਖ਼ਾਲਸਾ ਅਤੇ ਜੋ ਬੰਦਾ ਬਹਾਦਰ ਦੇ ਸਿਧਾਂਤਾਂ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ, ਬੰਦਈ ਖ਼ਾਲਸਾ ਅਖਵਾਏ । ਬੰਦਈ ਖ਼ਾਲਸਾ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਨੂੰ ਆਪਣਾ ਗੁਰੂ ਮੰਨਦੇ ਸਨ ਜਦਕਿ ਤੱਤ ਖ਼ਾਲਸਾ ਗੁਰੂ ਗ੍ਰੰਥ ਸਾਹਿਬ ਨੂੰ ਆਪਣਾ ਗੁਰੂ ਮੰਨਦੇ ਸਨ | 1721 ਈ. ਵਿੱਚ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਦੇ ਮੁੱਖ ਗ੍ਰੰਥੀ ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੇ ਇਨ੍ਹਾਂ ਦੋਹਾਂ ਦਲਾਂ ਵਿਚਾਲੇ ਸਮਝੌਤਾ ਕਰਵਾ ਦਿੱਤਾ । ਇਸ ਨਾਲ ਸਿੱਖ ਸੰਗਠਨ ਦੀ ਸ਼ਕਤੀ ਵਿੱਚ ਵਾਧਾ ਹੋਇਆ ।
ਪ੍ਰਸ਼ਨ 3.
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਨਾਲ ਨਜਿੱਠਣ ਦੀ ਕਿਸ ਤਰ੍ਹਾਂ ਕੋਸ਼ਿਸ਼ ਕੀਤੀ ? (How did Zakariya Khan try to deal with the Sikhs ?)
ਜਾਂ
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੇ ਅਧੀਨ ਸਿੱਖਾਂ ਉੱਪਰ ਜ਼ੁਲਮ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Discuss briefly the persecution of the Sikhs under Zakariya Khan.)
ਜਾਂ
ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਕੁਚਲਣ ਲਈ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਕੀ ਕਦਮ ਚੁੱਕੇ ? (What measures were adopted by Zakariya Khan to crush the power of the Sikhs ?)
ਜਾਂ
ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਕੁਚਲਣ ਲਈ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਕੀ ਕਦਮ ਚੁੱਕੇ ? ਉਸ ਨੂੰ ਆਪਣੇ ਯਤਨਾਂ ਵਿੱਚ ਕਿੱਥੋਂ ਤਕ ਸਫਲਤਾ ਮਿਲੀ ? (What measures were adopted by Zakariya Khan to crush the power of Sikhs ? How far did he succeed in his efforts ?) .
ਉੱਤਰ-
ਜ਼ਕਰੀਆ ਖ਼ਾਂ 1726 ਈ. ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਨਿਯੁਕਤ ਹੋਇਆ ਸੀ । ਉਸ ਨੇ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਲਈ ਸਖ਼ਤ ਨੀਤੀ ਅਪਣਾਈ । ਵੱਡੀ ਗਿਣਤੀ ਵਿੱਚ ਸਿੱਖਾਂ ਨੂੰ ਫੜ ਕੇ ਉਨ੍ਹਾਂ ਦਾ ਕਤਲੇਆਮ ਕੀਤਾ ਗਿਆ । ਪਰ ਜਦ ਉਹ ਸਿੱਖਾਂ ਨੂੰ ਪੂਰੀ ਤਰ੍ਹਾਂ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ ਤਾਂ ਉਸ ਨੇ 1733 ਈ. ਵਿੱਚ ਸਿੱਖਾਂ ਨਾਲ ਸਮਝੌਤਾ ਕਰ ਲਿਆ । ਕੁਝ ਸਮੇਂ ਦੇ ਬਾਅਦ ਸਿੱਖਾਂ ਨੇ ਮੁਗ਼ਲਾਂ ਨੂੰ ਫਿਰ ਲੁੱਟਣਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ । ਇਸ ਕਾਰਨ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੂੰ ਸਿੱਖਾਂ ਪ੍ਰਤੀ ਆਪਣੀ ਨੀਤੀ ਬਦਲਣੀ ਪਈ ।ਉਸ ਨੇ ਸਿੱਖਾਂ ਦਾ ਕਤਲੇਆਮ ਮੁੜ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ । ਆਪਣੇ ਸਾਰੇ ਯਤਨਾਂ ਦੇ ਬਾਵਜੂਦ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਆਪਣੀ ਮੌਤ ਤਕ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ ।
ਪ੍ਰਸ਼ਨ 4.
ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਵਾਂ ਕੌਣ ਸੀ ? ਉਸ ਦੀ ਸ਼ਹੀਦੀ ਦੀ ਸਿੱਖ ਇਤਿਹਾਸ ਵਿੱਚ ਕੀ ਮਹੱਤਤਾ ਹੈ ?(Who was Bhai Tara Singh ji Van ? What is the importance of his martyrdom in the Sikh History ?)
ਜਾਂ
ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਵਾਂ ‘ਤੇ ਸੰਖੇਪ ਨੋਟ ਲਿਖੋ । (Write a short note on Bhai Tara Singh ji Van.)
ਉੱਤਰ-
ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਵੀ ਆਪਣੀ ਪੰਥ ਸੇਵਾ ਅਤੇ ਬਹਾਦਰੀ ਕਾਰਨ ਸਿੱਖਾਂ ਵਿੱਚ ਬੜਾ ਹਰਮਨ-ਪਿਆਰਾ ਸੀ । ਨੌਸ਼ਹਿਰੇ ਦਾ ਚੌਧਰੀ ਸਾਹਿਬ ਰਾਏ ਜਾਣ ਬੁਝ ਕੇ ਸਿੱਖਾਂ ਦੇ ਖੇਤਾਂ ਵਿੱਚ ਆਪਣੇ ਘੋੜੇ ਛੱਡ ਦਿੰਦਾ ਸੀ । ਇੱਕ ਦਿਨ ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਵਾਂ ਨੇ ਸਾਹਿਬ ਰਾਏ ਦੀ ਇੱਕ ਘੋੜੀ ਨੂੰ ਫੜ ਕੇ ਵੇਚ ਦਿੱਤਾ ਅਤੇ ਉਨ੍ਹਾਂ ਪੈਸਿਆਂ ਨੂੰ ਲੰਗਰ ਲਈ ਦੇ ਦਿੱਤਾ । ਸਿੱਟੇ ਵਜੋਂ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਆਪਣੇ 2200 ਘੋੜਸਵਾਰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕਾਰਵਾਈ ਕਰਨ ਲਈ ਭੇਜੇ । ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਵਾਂ ਅਤੇ ਉਸ ਦੇ 22 ਸਾਥੀ ਬਹਾਦਰੀ ਨਾਲ ਮੁਗਲਾਂ ਦਾ ਮੁਕਾਬਲਾ ਕਰਦੇ ਹੋਏ 1726 ਈ. ਵਿੱਚ ਸ਼ਹੀਦ ਹੋ ਗਏ । ਇਸ ਸ਼ਹੀਦੀ ਦਾ ਬਦਲਾ ਲੈਣ ਲਈ ਸਿੱਖਾਂ ਨੇ ਆਪਣਾ ਸੰਘਰਸ਼ ਹੋਰ ਤੇਜ਼ ਕਰ ਦਿੱਤਾ ।
ਪ੍ਰਸ਼ਨ 5.
ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਕੌਣ ਸਨ ? ਉਨ੍ਹਾਂ ਦੀ ਸ਼ਹੀਦੀ ਦਾ ਸਿੱਖ ਇਤਿਹਾਸ ‘ਤੇ ਕੀ ਪ੍ਰਭਾਵ ਪਿਆ ? (Who was Bhai Mani Singh Ji ? What was the impact of his martyrdom ?)
ਜਾਂ
ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਕੌਣ ਸਨ ? ਉਨ੍ਹਾਂ ਦੀ ਸ਼ਹੀਦੀ ਕਿਉਂ ਹੋਈ ? (Who was Bhai Mani Singh Ji ? What were the causes of his martyrdom ?)
ਜਾਂ ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀ ਸ਼ਹੀਦੀ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ? (What do you know about Bhai Mani Singh Ji and his martyrdom ?)
ਜਾਂ
ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਦੀ ਸ਼ਹੀਦੀ ਦੇ ਕੋਈ ਤਿੰਨ ਕਾਰਨ ਦੱਸੋ । (Write any three causes of the martyrdom of Bhai Mani Singh Ji.)
ਜਾਂ
ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ‘ਤੇ ਇੱਕ ਸੰਖੇਪ ਨੋਟ ਲਿਖੋ । (Write a short note on Bhai Mani Singh Ji.) ਉੱਤਰ-ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਦਰਬਾਰ ਸਾਹਿਬ, ਅੰਮ੍ਰਿਤਸਰ ਵਿੱਚ ਮੁੱਖ ਗ੍ਰੰਥੀ ਸਨ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਉੱਤੇ ਦਰਬਾਰ ਸਾਹਿਬ ਜਾਣ ‘ਤੇ ਪਾਬੰਦੀ ਲਗਾ ਦਿੱਤੀ ਸੀ । ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੇ ਦੀਵਾਲੀ ਦੇ ਮੌਕੇ ‘ਤੇ ਸਿੱਖਾਂ ਨੂੰ ਦਰਬਾਰ ਸਾਹਿਬ ਵਿੱਚ ਇਕੱਠੇ ਹੋਣ ਦੀ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਤੋਂ ਇਜਾਜ਼ਤ ਲੈ ਲਈ । ਇਸ ਦੇ ਬਦਲੇ ਉਨ੍ਹਾਂ ਨੇ 5,000 ਰੁਪਏ ਜ਼ਕਰੀਆ ਮਾਂ ਨੂੰ ਦੇਣ ਦਾ ਵਾਅਦਾ ਕੀਤਾ | ਪਰ ਦੀਵਾਲੀ ਤੋਂ ਇੱਕ ਦਿਨ ਪਹਿਲਾਂ ਹੀ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਅੰਮ੍ਰਿਤਸਰ ’ਤੇ ਹਮਲਾ ਕਰ ਦਿੱਤਾ । ਇਸ ਕਾਰਨ ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੂੰ 5000 ਰੁਪਏ ਨਾ ਦੇ ਸਕੇ । ਸਿੱਟੇ ਵਜੋਂ ਭਾਈ ਸਾਹਿਬ ਜੀ ਨੂੰ 1738 ਈ. ਵਿੱਚ ਲਾਹੌਰ ਵਿਖੇ ਬੜੀ ਬੇਰਹਿਮੀ ਨਾਲ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ਗਿਆ । ਇਸ ਸ਼ਹੀਦੀ ਕਾਰਨ ਸਿੱਖ ਭੜਕ ਉੱਠੇ ।
![]()
ਪ੍ਰਸ਼ਨ 6.
ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਕੌਣ ਸਨ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀ ਸ਼ਹੀਦੀ ਦੀ ਸਿੱਖ ਇਤਿਹਾਸ ਵਿੱਚ ਕੀ ਮਹਤੱਤਾ ਹੈ ? (Who was Bhai Taru Singh Ji ? What is the significance of his martyrdom in the Sikh History ?)
ਜਾਂ
ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਦੀ ਸ਼ਹੀਦੀ ‘ਤੇ ਇੱਕ ਸੰਖੇਪ ਨੋਟ ਲਿਖੋ । (Write a short note on Martyrdom of Bhai Taru Singh Ji.)
ਉੱਤਰ-
ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਮਾਝੇ ਦੇ ਇਲਾਕੇ ਦੇ ਪਿੰਡ ਪੂਹਲਾ ਦੇ ਰਹਿਣ ਵਾਲੇ ਸਨ । ਉਹ ਖੇਤੀਬਾੜੀ ਦਾ ਧੰਦਾ ਕਰਦੇ ਸਨ ਅਤੇ ਆਪਣੀ ਹੋਣ ਵਾਲੀ ਆਮਦਨ ਤੋਂ ਸਿੱਖਾਂ ਦੀ ਸਹਾਇਤਾ ਕਰਦੇ ਸਨ । ਸਰਕਾਰ ਦੀਆਂ ਨਜ਼ਰਾਂ ਵਿੱਚ ਇਹ ਇੱਕ ਘੋਰ ਅਪਰਾਧ ਸੀ । ਸਿੱਟੇ ਵਜੋਂ ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਗਿਆ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਨੂੰ ਇਸਲਾਮ ਧਰਮ ਗ੍ਰਹਿਣ ਕਰਨ ਲਈ ਕਿਹਾ । ਭਾਈ ਸਾਹਿਬ ਜੀ ਨੇ ਇਨ੍ਹਾਂ ਦੋਹਾਂ ਗੱਲਾਂ ਤੋਂ ਇਨਕਾਰ ਕਰ ਦਿੱਤਾ । ਇਸ ’ਤੇ ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਦੀ ਖੋਪੜੀ ਨੂੰ ਉਤਾਰ ਕੇ 1 ਜੁਲਾਈ, 1745 ਈ. ਨੂੰ ਸ਼ਹੀਦ ਕੀਤਾ ਗਿਆ ।
ਪ੍ਰਸ਼ਨ 7.
ਨਾਦਰ ਸ਼ਾਹ ਕੌਣ ਸੀ ? ਉਸ ਨੇ ਭਾਰਤ ‘ਤੇ ਕਦੋਂ ਹਮਲਾ ਕੀਤਾ ? ਉਸ ਦੇ ਇਸ ਹਮਲੇ ਦਾ ਪੰਜਾਬ ‘ਤੇ ਕੀ ਪ੍ਰਭਾਵ ਪਿਆ ? (Who was Nadir Shah ? When did he invade India ? What was the effect of his invasion on the Punjab ?)
ਨਾਦਰ ਸ਼ਾਹ ਦੇ ਪੰਜਾਬ ਹਮਲੇ ਅਤੇ ਇਸ ਦੇ ਪ੍ਰਭਾਵਾਂ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Give a brief account of Nadir Shah’s invasion on the Punjab and its impact.)
ਉੱਤਰ-
ਨਾਦਰ ਸ਼ਾਹ ਈਰਾਨ ਦਾ ਬਾਦਸ਼ਾਹ ਸੀ ।ਉਸ ਨੇ 1739 ਈ. ਵਿੱਚ ਭਾਰਤ ‘ਤੇ ਹਮਲਾ ਕੀਤਾ । ਇਸ ਹਮਲੇ ਦੌਰਾਨ ਉਸ ਨੇ ਭਾਰੀ ਲੁੱਟਮਾਰ ਮਚਾਈ । ਇਸ ਕਾਰਨ ਭਾਰਤ ਅਤੇ ਖ਼ਾਸ ਤੌਰ ‘ਤੇ ਪੰਜਾਬ ਵਿੱਚ ਭਾਰੀ ਬਦਅਮਨੀ ਫੈਲ ਗਈ । ਈਰਾਨ ਪਰਤਦੇ ਸਮੇਂ ਜਦੋਂ ਉਹ ਪੰਜਾਬ ਵਿਚੋਂ ਲੰਘ ਰਿਹਾ ਸੀ ਤਾਂ ਸਿੱਖਾਂ ਨੇ ਉਸ ਦਾ ਬਹੁਤ ਸਾਰਾ ਖ਼ਜ਼ਾਨਾ ਲੁੱਟ ਲਿਆ ਸੀ । ਇਸ ਕਾਰਨ ਨਾਦਰ ਸ਼ਾਹ ਹੈਰਾਨ ਰਹਿ ਗਿਆ । ਨਾਦਰ ਸ਼ਾਹ ਨੇ ਜ਼ਕਰੀਆ ਖਾਂ ਨੂੰ ਚੇਤਾਵਨੀ ਦਿੱਤੀ ਕਿ ਜੇਕਰ ਉਸ ਨੇ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਸਖ਼ਤ ਕਦਮ ਨਾ ਚੁੱਕੇ ਤਾਂ ਛੇਤੀ ਹੀ ਸਿੱਖ ਪੰਜਾਬ ‘ਤੇ ਆਪਣਾ ਕਬਜ਼ਾ ਕਰ ਲੈਣਗੇ । ਸਿੱਟੇ ਵਜੋਂ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਉੱਤੇ ਵਧੇਰੇ ਅੱਤਿਆਚਾਰ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੇ ।
ਪ੍ਰਸ਼ਨ 8.
ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ‘ਤੇ ਇੱਕ ਸੰਖੇਪ ਨੋਟ ਲਿਖੋ । (Write a brief note on Buddha Dal and Taruna Dal.)
ਜਾਂ
ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ਦਾ ਗਠਨ ਕਦੋਂ ਕੀਤਾ ਗਿਆ ? ਸਿੱਖ ਇਤਿਹਾਸ ਵਿੱਚ ਇਨ੍ਹਾਂ ਦਾ ਕੀ ਮਹੱਤਵ ਹੈ ? (When were Buddha Dal and Taruna Dal organised ? What is, their importance in the Sikh History ?) ।
ਜਾਂ
ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? ਸੰਖੇਪ ਵਿੱਚ ਵਰਣਨ ਕਰੋ । (What do you mean by ‘Buddha Dal and ‘Taruna Dal’ ? Explain briefly.)
ਜਾਂ
ਤਰੁਣਾ ਦਲ ‘ਤੇ ਇੱਕ ਸੰਖੇਪ ਨੋਟ ਲਿਖੋ । (Write a brief note on Taruna Dal.)
ਉੱਤਰ-
1734 ਈ. ਵਿੱਚ ਨਵਾਬ ਕਪੂਰ ਸਿੰਘ ਨੇ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਮਜ਼ਬੂਤ ਕਰਨ ਦੇ ਉਦੇਸ਼ ਨਾਲ ਉਨ੍ਹਾਂ ਨੂੰ ਦੋ ਜੱਥਿਆਂ ਵਿੱਚ ਸੰਗਠਿਤ ਕਰ ਦਿੱਤਾ । ਇਹ ਜੱਥੇ ਸਨ-ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ । ਬੁੱਢਾ ਦਲ ਵਿੱਚ 40 ਸਾਲਾਂ ਤੋਂ ਵਡੇਰੀ ਉਮਰ ਦੇ ਸਿੱਖਾਂ ਨੂੰ ਸ਼ਾਮਲ ਕੀਤਾ ਗਿਆ ।ਤਰੁਣਾ ਦਲ ਵਿੱਚ ਚਾਲੀ ਸਾਲ ਤੋਂ ਘੱਟ ਉਮਰ ਵਾਲੇ ਭਾਵ ਨੌਜਵਾਨ ਸਿੱਖਾਂ ਨੂੰ ਭਰਤੀ ਕੀਤਾ ਗਿਆ । ਤਰੁਣਾ ਦਲ ਨੂੰ ਅੱਗੇ ਪੰਜ ਜੱਥਿਆਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ ਸੀ । ਬੁੱਢਾ ਦਲ ਧਾਰਮਿਕ ਸਥਾਨਾਂ ਦੀ ਦੇਖ-ਭਾਲ ਕਰਦਾ ਸੀ ਜਦ ਕਿ ਤਰੁਣਾ ਦਲ ਦੁਸ਼ਮਣਾਂ ਦਾ ਮੁਕਾਬਲਾ ਕਰਦਾ ਸੀ ।
ਪ੍ਰਸ਼ਨ 9.
ਯਾਹੀਆ ਖਾਂ ਕੌਣ ਸੀ ? ਉਸ ਦੇ ਸ਼ਾਸਨ ਕਾਲ ਸੰਬੰਧੀ ਜਾਣਕਾਰੀ ਦਿਓ । (Who was Yahiya Khan ? Give a brief information of his rule.)
ਉੱਤਰ-
ਯਾਹੀਆ ਖ਼ਾਂ 1746 ਈ. ਤੋਂ 1747 ਈ. ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਰਿਹਾ। ਉਸ ਨੇ ਸਿੱਖਾਂ ਪ੍ਰਤੀ ਦਮਨਕਾਰੀ ਨੀਤੀ ਜਾਰੀ ਰੱਖੀ । 1746 ਈ. ਵਿੱਚ ਸਿੱਖਾਂ ਨਾਲ ਹੋਈ ਇੱਕ ਲੜਾਈ ਵਿੱਚ ਲਾਹੌਰ ਦੇ ਦੀਵਾਨ ਲਖਪਤ ਰਾਏ ਦਾ ਭਰਾ ਜਸਪਤ ਰਾਏ ਮਾਰਿਆ ਗਿਆ ਸੀ । ਇਸ ਦਾ ਬਦਲਾ ਲੈਣ ਲਈ ਲਖਪਤ ਰਾਏ ਨੇ ਯਾਹੀਆ ਖ਼ਾਂ ਨਾਲ ਮਿਲ ਕੇ ਕਾਹਨੂੰਵਾਨ (ਗੁਰਦਾਸਪੁਰ ਵਿਖੇ ਸਿੱਖਾਂ ‘ਤੇ ਅਚਾਨਕ ਹਮਲਾ ਕਰ ਦਿੱਤਾ । ਸਿੱਟੇ ਵਜੋਂ 7,000 ਸਿੱਖ ਮਾਰੇ ਗਏ ਸਿੱਖ ਇਤਿਹਾਸ ਵਿੱਚ ਇਸ ਖ਼ੂਨੀ ਘਟਨਾ ਨੂੰ ਛੋਟਾ ਘੱਲੂਘਾਰਾ ਦੇ ਨਾਂ ਨਾਲ ਯਾਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । 1747 ਈ. ਵਿੱਚ ਯਾਹੀਆ ਖਾਂ ਦਾ ਤਖ਼ਤਾ ਪਲਟ ਦਿੱਤਾ ਗਿਆ ਸੀ ।
ਪ੍ਰਸ਼ਨ 10.
ਪਹਿਲੇ ਜਾਂ ਛੋਟੇ ਘੱਲੂਘਾਰੇ (1746 ਈ. ) ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ? (What do you know about the First Holocaust (1746) or Chhota Ghallughara ?)
ਜਾਂ
ਪਹਿਲੇ ਘੱਲੂਘਾਰੇ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ? (What do you know about First Holocaust ?)
ਜਾਂ
‘ਛੋਟਾ ਘੱਲੂਘਾਰਾ’ ’ਤੇ ਇੱਕ ਸੰਖੇਪ ਨੋਟ ਲਿਖੋ । (Write a short note on ‘Chhota Ghallughara’.)
ਜਾਂ
ਛੋਟੇ ਘੱਲੂਘਾਰੇ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ? (What do you know about the Chhota Ghallughara ?)
ਉੱਤਰ-
ਯਾਹੀਆ ਖ਼ਾਂ ਤੇ ਲਖਪਤ ਰਾਏ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਕੁਚਲਣ ਲਈ ਇੱਕ ਵੱਡੀ ਸੈਨਾ ਤਿਆਰ ਕੀਤੀ । ਇਸ ਸੈਨਾ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਅਚਾਨਕ ਕਾਹਨੂੰਵਾਨ ਵਿਖੇ ਘੇਰ ਲਿਆ। ਇਸ ਹਮਲੇ ਵਿੱਚ 7,000 ਸਿੱਖ ਸ਼ਹੀਦ ਹੋ ਗਏ ਅਤੇ 3,000 ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਗਿਆ ! ਸਿੱਖਾਂ ਨੂੰ ਪਹਿਲੀ ਵਾਰ ਇੰਨਾ ਭਾਰੀ ਜਾਨ-ਮਾਲ ਦਾ ਨੁਕਸਾਨ ਸਹਿਣਾ ਪਿਆ । ਇਸ ਕਾਰਨ ਇਸ ਘਟਨਾ ਨੂੰ ਇਤਿਹਾਸ ਵਿੱਚ ਪਹਿਲਾ ਜਾਂ ਛੋਟਾ ਘੱਲੂਘਾਰਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਹ ਘੱਲੂਘਾਰਾ ਮਈ, 1746 ਈ. ਨੂੰ ਵਾਪਰਿਆ । ਇਸ ਘੱਲੂਘਾਰੇ ਦੇ ਬਾਵਜੂਦ ਸਿੱਖਾਂ ਦੇ ਹੌਸਲੇ ਬੁਲੰਦ ਰਹੇ ।
![]()
ਪ੍ਰਸ਼ਨ 11.
ਮੀਰ ਮੰਨੂੰ ਕੌਣ ਸੀ ? ਉਸ ਨੇ ਆਪਣੇ ਸ਼ਾਸਨ ਕਾਲ ਵਿੱਚ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕੀ ਕਾਰਵਾਈ ਕੀਤੀ ? (Who was Mir Mannu ? What steps did he take against the Sikhs during his rule)
ਜਾਂ
ਮੀਰ ਮੰਨੂੰ ਵਲੋਂ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕੀਤੀਆਂ ਗਈਆਂ ਕਾਰਵਾਈਆਂ ਦਾ ਸੰਖੇਪ ਵੇਰਵਾ ਦਿਓ । (Describe briefly the Sikh persecution under Mir Mannu.)
ਜਾਂ
ਮੀਰ ਮੰਨੂੰ ਦੁਆਰਾ ਸਿੱਖਾਂ ਦੇ ਦਮਨ ਦਾ ਅਧਿਐਨ ਕਰੋ । (Study the persecution of the Sikhs by Mir Mannu.)
ਜਾਂ
ਮੀਰ ਮੰਨੂੰ ਦੇ ਸਿੱਖਾਂ ਨਾਲ ਸੰਬੰਧਾਂ ਦਾ ਸੰਖੇਪ ਹਾਲ ਲਿਖੋ । (Write briefly the relations of Mir Mannu with the Sikhs.)
ਉੱਤਰ-
ਮੀਰ ਮੰਨੂੰ 1748 ਈ. ਤੋਂ 1753 ਈ. ਤਕ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਰਿਹਾ। ਉਸ ਨੇ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਲਈ ਹਰ ਸੰਭਵ ਯਤਨ ਕੀਤੇ । ਸਿੱਖਾਂ ਨੂੰ ਰੋਜ਼ਾਨਾ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਕੇ ਲਾਹੌਰ ਵਿਖੇ ਸ਼ਹੀਦ ਕੀਤਾ ਜਾਣ ਲੱਗਾ । ਮੀਰ ਮੰਨੂੰ ਦੇ ਇਨ੍ਹਾਂ ਅੱਤਿਆਚਾਰਾਂ ਤੋਂ ਬਚਣ ਲਈ ਸਿੱਖਾਂ ਨੇ ਜੰਗਲਾਂ ਅਤੇ ਪਹਾੜਾਂ ਵਿੱਚ ਜਾ ਸ਼ਰਨ ਲਈ । ਸਿੱਖਾਂ ਦੇ ਹੱਥ ਨਾ ਆਉਣ ਕਾਰਨ ਮੀਰ ਮੰਨੂੰ ਦੇ ਸੈਨਿਕਾਂ ਨੇ ਸਿੱਖ ਇਸਤਰੀਆਂ ਅਤੇ ਬੱਚਿਆਂ ਨੂੰ ਗਿਫ਼ਤਾਰ ਕਰਨਾ ਸ਼ਰ ਕਰ ਦਿੱਤਾ । ਉਨ੍ਹਾਂ ਉੱਤੇ ਬਹੁਤ ਜ਼ੁਲਮ ਅਤੇ ਜਬਰ ਢਾਏ ਗਏ । ਇਨ੍ਹਾਂ ਘੋਰ ਅੱਤਿਆਚਾਰਾਂ ਦੇ ਬਾਵਜੂਦ ਮੀਰ ਮੰਨੂੰ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਅਸਫਲ ਰਿਹਾ ।
ਪ੍ਰਸ਼ਨ 12.
ਮੀਰ ਮੰਨੂੰ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਕਿਉਂ ਅਸਫਲ ਰਿਹਾ ? (Why did Mir Mannu fail to crush the Sikh power ?)
ਜਾਂ
ਮੀਰ ਮੰਨੂੰ ਦੀ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਅਸਫਲਤਾ ਦੇ ਕੀ ਕਾਰਨ ਸਨ ? (What were the causes of the failure of Mir Mannu against the Sikhs ?)
ਜਾਂ
ਮੀਰ ਮੰਨੂੰ ਦੀ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਅਸਫਲਤਾ ਦੇ ਕੋਈ ਪੰਜ ਕਾਰਨ ਲਿਖੋ । (Write any five causes of the failure of Mir Mannu against the Sikhs.)
ਉੱਤਰ-
- ਮੀਰ ਮੰਨੂੰ ਦੀ ਅਸਫਲਤਾ ਦਾ ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ ਕਾਰਨ ਇਹ ਸੀ ਕਿ ਸਿੱਖ ਭਾਰੀ ਔਕੜਾਂ ਦੇ ਬਾਵਜੂਦ ਆਪਣਾ ਹੌਸਲਾ ਕਦੇ ਨਹੀਂ ਛੱਡਦੇ ਸਨ ।
- ਸਿੱਖਾਂ ਦੀ ਛਾਪਾਮਾਰ ਯੁੱਧ ਨੀਤੀ ਨੇ ਮੀਰ ਮੰਨੂੰ ਦੀਆਂ ਯੋਜਨਾਵਾਂ ਨੂੰ ਅਸਫਲ ਬਣਾਉਣ ਵਿੱਚ ਮੁੱਖ ਭੂਮਿਕਾ ਨਿਭਾਈ ।
- ਮੀਰ ਮੰਨੂੰ ਦਾ ਦੀਵਾਨ ਕੌੜਾ ਮਲ ਸਿੱਖਾਂ ਨਾਲ ਹਮਦਰਦੀ ਰੱਖਦਾ ਸੀ ।
- ਜਲੰਧਰ ਦੁਆਬ ਦੇ ਫ਼ੌਜਦਾਰ ਅਦੀਨਾ ਬੇਗ਼ ਦੀ ਦੋ ਰੰਗੀ ਨੀਤੀ ਕਾਰਨ ਵੀ ਮੀਰ ਮੰਨੂੰ ਅਸਫਲ ਰਿਹਾ ।
- ਮੀਰ ਮੰਨੂੰ ਨੂੰ ਆਪਣੇ ਸ਼ਾਸਨ ਕਾਲ ਵਿੱਚ ਬਹੁਤ ਸਾਰੀਆਂ ਸਮੱਸਿਆਵਾਂ ਦਾ ਸਾਹਮਣਾ ਵੀ ਕਰਨਾ ਪਿਆ ਸੀ । ਸਿੱਟੇ ਵਜੋਂ ਉਹ ਸਿੱਖਾਂ ਨੂੰ ਕੁਚਲਣ ਵਿੱਚ ਸਫਲ ਨਾ ਹੋ ਸਕਿਆ ।
ਵਸਤੂਨਿਸ਼ਠ ਪ੍ਰਸ਼ਨ (Objective Type Questions)
ਇੱਕ ਸ਼ਬਦ ਤੋਂ ਇੱਕ ਵਾਕ ਵਿੱਚ ਉੱਤਰ (Answer in one Word to one Sentence)
ਪ੍ਰਸ਼ਨ 1.
1716 ਈ. ਤੋਂ 1752 ਈ. ਤਕ ਲਾਹੌਰ ਦੇ ਕਿਸੇ ਇੱਕ ਮੁਗ਼ਲ ਸੂਬੇਦਾਰ ਦਾ ਨਾਂ ਦੱਸੋ ।
ਜਾਂ
ਪੰਜਾਬ ਦੇ ਕਿਸੇ ਇੱਕ ਗਵਰਨਰ ਦਾ ਨਾਂ ਲਿਖੋ ਜਿਸ ਨੇ ਸਿੱਖਾਂ ‘ਤੇ ਜ਼ੁਲਮ ਕੀਤੇ ।
ਉੱਤਰ-
ਅਬਦੁਸ ਸਮਦ ਖਾਂ ।
ਪ੍ਰਸ਼ਨ 2.
ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਲਾਹੌਰ ਦੇ ਸੂਬੇਦਾਰ ਕਦੋਂ ਨਿਯੁਕਤ ਹੋਇਆ ?
ਉੱਤਰ-
1713 ਈ. ।
ਪ੍ਰਸ਼ਨ 3.
ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਦੀ ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ ਸਫਲਤਾ ਕਿਹੜੀ ਸੀ ?
ਉੱਤਰ-
ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਨਾ ।
ਪ੍ਰਸ਼ਨ 4.
ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਨੂੰ ਮੁਗ਼ਲ ਬਾਦਸ਼ਾਹ ਫ਼ਰੁਖਸੀਅਰ ਨੇ ਕਿਹੜੀ ਉਪਾਧੀ ਦਿੱਤੀ ?
ਉੱਤਰ-
ਰਾਜ ਦੀ ਤਲਵਾਰ ।
ਪ੍ਰਸ਼ਨ 5.
ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੀ ਮੌਤ ਤੋਂ ਬਾਅਦ ਸਿੱਖਾਂ ਦੇ ਜਿਹੜੇ ਦੋ ਸੰਪ੍ਰਦਾਇ ਬਣ ਗਏ ਸਨ, ਉਨ੍ਹਾਂ ਦੇ ਕੀ ਨਾਂ ਸਨ ?
ਜਾਂ
ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੀ ਸ਼ਹੀਦੀ ਤੋਂ ਬਾਅਦ ਸਿੱਖ ਕਿਹੜੇ ਦੋ ਦਲਾਂ ਵਿੱਚ ਵੰਡੇ ਗਏ ?
ਉੱਤਰ-
ਬੰਦਈ ਖ਼ਾਲਸਾ ਅਤੇ ਤੱਤ ਖ਼ਾਲਸਾ ।
![]()
ਪ੍ਰਸ਼ਨ 6.
ਤੱਤ ਖ਼ਾਲਸਾ ਅਤੇ ਬੰਦਈ ਖ਼ਾਲਸਾ ਵਿੱਚ ਕੀ ਅੰਤਰ ਹੈ ?
ਜਾਂ
ਤੱਤ ਖ਼ਾਲਸਾ ਤੋਂ ਤੁਹਾਡਾ ਕੀ ਭਾਵ ਹੈ ?
ਜਾਂ
ਬੰਦਈ ਖ਼ਾਲਸਾ ਤੋਂ ਤੁਹਾਡਾ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਤੱਤ ਖ਼ਾਲਸਾ ਗੁਰੂ ਗੋਬਿੰਦ ਸਿੰਘ ਜੀ ਦੇ ਅਸੂਲਾਂ ਵਿੱਚ ਜਦਕਿ ਬੰਦਈ ਖ਼ਾਲਸਾ ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੇ ਅਸੂਲਾਂ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ ।
ਪ੍ਰਸ਼ਨ 7.
ਬੰਦਈ ਖ਼ਾਲਸਾ ਅਤੇ ਤੱਤ ਖ਼ਾਲਸਾ ਵਿਚਾਲੇ ਝਗੜਾ ਕਦੋਂ ਖ਼ਤਮ ਹੋਇਆ ?
ਉੱਤਰ-
1721 ਈ. ਜਾਂ
ਪ੍ਰਸ਼ਨ 8.
ਬੰਦਈ ਖ਼ਾਲਸਾ ਅਤੇ ਤੱਤ ਖ਼ਾਲਸਾ ਵਿਚਕਾਰ ਮਤਭੇਦ ਕਿਸ ਨੇ ਖ਼ਤਮ ਕਰਵਾਏ ।
ਉੱਤਰ-
ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੇ ।
ਪ੍ਰਸ਼ਨ 9.
ਸਹਿਜਧਾਰੀ ਸਿੱਖ ਕਿਸ ਨੂੰ ਕਿਹਾ ਜਾਂਦਾ ਸੀ ?
ਉੱਤਰ-
ਇਹ ਉਹ ਗੈਰ-ਸਿੱਖ ਸਨ ਜੋ ਸਿੱਖ ਪੰਥ ਦੇ ਸਿਧਾਂਤਾਂ ਵਿੱਚ ਤਾਂ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ ਪਰ ਇਸ ਵਿੱਚ ਸ਼ਾਮਲ ਨਹੀਂ ਹੋਏ ਸਨ ।
ਪ੍ਰਸ਼ਨ 10.
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ।
ਪ੍ਰਸ਼ਨ 11.
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਕਦੋਂ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਬਣਿਆ ?
ਜਾਂ
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਕਦੋਂ ਬਣਿਆ ?
ਉੱਤਰ-
1726 ਈ. ।
![]()
ਪ੍ਰਸ਼ਨ 12.
ਜ਼ਕਰੀਆ ਖਾਂ ਦੇ ਸ਼ਾਸਨ ਕਾਲ ਵਿੱਚ ਸ਼ਹੀਦ ਕੀਤੇ ਜਾਣ ਵਾਲੇ ਕਿਸੇ ਇੱਕ ਪ੍ਰਸਿੱਧ ਸਿੱਖ ਦਾ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ।
ਪ੍ਰਸ਼ਨ 13.
ਜ਼ਕਰੀਆ ਖਾਂ ਨੇ ਸਿੱਖਾਂ ਨਾਲ ਸਮਝੌਤਾ ਕਦੋਂ ਕੀਤਾ ?
ਉੱਤਰ-
1733 ਈ. ।
ਪ੍ਰਸ਼ਨ 14.
ਸਿੱਖਾਂ ਦੇ ਉਸ ਨੇਤਾ ਦਾ ਨਾਂ ਦੱਸੋ ਜਿਸ ਨੂੰ 1733 ਈ. ਦੇ ਸਮਝੌਤੇ ਅਨੁਸਾਰ ਨਵਾਬ ਦੇ ਖ਼ਿਤਾਬ ਨਾਲ ਸਨਮਾਨਿਆ ਗਿਆ ਸੀ ?
ਉੱਤਰ-
ਸਰਦਾਰ ਕਪੂਰ ਸਿੰਘ ।
ਪ੍ਰਸ਼ਨ 15.
ਸਿੱਖਾਂ ਦੇ ਦੋ ਦਲਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ।
ਪ੍ਰਸ਼ਨ 16.
ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ਦੀ ਸਥਾਪਨਾ ਕਦੋਂ ਕੀਤੀ ਗਈ ਸੀ ?
ਉੱਤਰ-
1734 ਈ. ।
![]()
ਪ੍ਰਸ਼ਨ 17.
ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ਦੀ ਸਥਾਪਨਾ ਕਿੱਥੇ ਕੀਤੀ ਗਈ ਸੀ ?
ਉੱਤਰ-
ਅੰਮ੍ਰਿਤਸਰ ।
ਪ੍ਰਸ਼ਨ 18.
ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ਦਾ ਮੋਢੀ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਨਵਾਬ ਕਪੂਰ ਸਿੰਘ ।
ਪ੍ਰਸ਼ਨ 19.
ਬੁੱਢਾ ਦਲ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਬੁੱਢਾ ਦਲ ਵਿੱਚ 40 ਸਾਲ ਤੋਂ ਵਡੇਰੀ ਉਮਰ ਦੇ ਸਿੱਖ ਸ਼ਾਮਲ ਸਨ ।
ਪ੍ਰਸ਼ਨ 20.
ਤਰੁਣਾ ਦਲ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਤਰੁਣਾ ਦਲ ਸਿੱਖ ਨੌਜਵਾਨਾਂ ਦਾ ਦਲ ਸੀ ।
ਪਸ਼ਨ 21.
ਹੈਦਰੀ ਝੰਡੇ ਦੀ ਘਟਨਾ ਕਿਸਦੇ ਸ਼ਾਸਨ ਕਾਲ ਵਿੱਚ ਹੋਈ ?
ਉੱਤਰ-
ਜ਼ਕਰੀਆ ਖਾਂ ।
ਪ੍ਰਸ਼ਨ 22.
ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਵਾਂ ਕਦੋਂ ਸ਼ਹੀਦ ਹੋਏ ?
ਉੱਤਰ-
1726 ਈ. ।
![]()
ਪ੍ਰਸ਼ਨ 23.
ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਕੌਣ ਸਨ ?
ਉੱਤਰ-
ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਅੰਮ੍ਰਿਤਸਰ ਦੇ ਮੁੱਖ ਗ੍ਰੰਥੀ ।
ਪ੍ਰਸ਼ਨ 24.
ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੂੰ ਕਦੋਂ ਸ਼ਹੀਦ ਕੀਤਾ ਗਿਆ ਸੀ ?
ਉੱਤਰ-
1738 ਈ. ।
ਪ੍ਰਸ਼ਨ 25.
ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੂੰ ਕਿਸਨੇ ਸ਼ਹੀਦ ਕਰਵਾਇਆ ਸੀ ?
ਉੱਤਰ-
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ।
ਪ੍ਰਸ਼ਨ 26.
ਨਾਦਰ ਸ਼ਾਹ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਈਰਾਨ ਦਾ ਸ਼ਾਸਕ ।
ਪ੍ਰਸ਼ਨ 27.
ਨਾਦਰ ਸ਼ਾਹ ਨੇ ਭਾਰਤ ‘ਤੇ ਕਦੋਂ ਹਮਲਾ ਕੀਤਾ ?
ਉੱਤਰ-
1739 ਈ. ।
ਪ੍ਰਸ਼ਨ 28.
ਨਾਦਰ ਸ਼ਾਹ ਦੇ ਭਾਰਤ ਹਮਲੇ ਦਾ ਕੋਈ ਇੱਕ ਕਾਰਨ ਦੱਸੋ ।
ਉੱਤਰ-
ਉਹ ਭਾਰਤ ‘ਤੇ ਜਿੱਤ ਪ੍ਰਾਪਤ ਕਰਕੇ ਇੱਕ ਮਹਾਨ ਜੇਤੂ ਬਣਨਾ ਚਾਹੁੰਦਾ ਸੀ ।
![]()
ਪ੍ਰਸ਼ਨ 29.
ਮੱਸਾ ਰੰਗੜ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਅੰਮ੍ਰਿਤਸਰ ਜ਼ਿਲ੍ਹੇ ਦੇ ਮੰਡਿਆਲਾ ਪਿੰਡ ਦਾ ਚੌਧਰੀ ।
ਪ੍ਰਸ਼ਨ 30.
ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਜੀ ਨੂੰ ਕਦੋਂ ਸ਼ਹੀਦ ਕੀਤਾ ਗਿਆ ਸੀ ?
ਉੱਤਰ-
1742 ਈ. ਨੂੰ
ਪ੍ਰਸ਼ਨ 31.
ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਜੀ ਦੀ ਸ਼ਹੀਦੀ ਦਾ ਕੀ ਕਾਰਨ ਸੀ ?
ਉੱਤਰ-
ਕਿਉਂਕਿ ਉਨ੍ਹਾਂ ਨੇ ਬੀਬੀ ਫ਼ਾਤਮਾ ਬਾਰੇ ਕੁੱਝ ਅਪਮਾਨਜਨਕ ਸ਼ਬਦ ਕਹੇ ਸਨ ।
ਪ੍ਰਸ਼ਨ 32.
ਜ਼ਕਰੀਆ ਖਾਂ ਦੀ ਮੌਤ ਕਦੋਂ ਹੋਈ ?
ਉੱਤਰ-
1745 ਈ. ਨੂੰ
ਪ੍ਰਸ਼ਨ 33.
ਯਾਹੀਆ ਖਾਂ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਕਦੋਂ ਬਣਿਆ ?
ਉੱਤਰ-
1746 ਈ. ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 34.
ਛੋਟਾ ਜਾਂ ਪਹਿਲਾ ਘੱਲੂਘਾਰਾ ਕਦੋਂ ਹੋਇਆ ?
ਉੱਤਰ-
1746 ਈ. ।
ਪ੍ਰਸ਼ਨ 35.
ਛੋਟਾ ਘੱਲੂਘਾਰਾ ਕਿੱਥੇ ਹੋਇਆ ?
ਉੱਤਰ-
ਕਾਹਨੂੰਵਾਨ ।
ਪ੍ਰਸ਼ਨ 36.
ਮੀਰ ਮੰਨੂੰ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਕਦੋਂ ਬਣਿਆ ?
ਉੱਤਰ-
1748 ਈ. ਵਿੱਚ ।
![]()
ਪ੍ਰਸ਼ਨ 37.
ਮੁਈਨ-ਉਲ-ਮੁਲਕ ਕਿਸ ਨਾਂ ਨਾਲ ਪ੍ਰਸਿੱਧ ਹੋਇਆ ?
ਉੱਤਰ-
ਮੀਰ ਮੰਨੂੰ ।
ਪ੍ਰਸ਼ਨ 38.
ਪੰਜਾਬ ਵਿੱਚ ਮੁਗ਼ਲ ਸ਼ਾਸਨ ਦਾ ਅੰਤ ਕਦੋਂ ਹੋਇਆ ?
ਉੱਤਰ-
1752 ਈ. ।
ਪ੍ਰਸ਼ਨ 39.
ਪੰਜਾਬ ਵਿੱਚ ਮੁਗ਼ਲਾਂ ਦਾ ਆਖ਼ਰੀ ਸੂਬੇਦਾਰ ਕੌਣ ਸੀ ?
ਜਾਂ
ਪੰਜਾਬ ਵਿੱਚ ਅਫ਼ਗਾਨਾਂ ਦਾ ਪਹਿਲਾ ਸੂਬੇਦਾਰ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਮੀਰ ਮੰਨੂੰ ।
ਪ੍ਰਸ਼ਨ 40.
ਮੀਰ ਮੰਨੂੰ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਮੀਰ ਮੰਨੂੰ ਦਿੱਲੀ ਦੇ ਵਜ਼ੀਰ ਕਮਰਉੱਦੀਨ ਦਾ ਪੁੱਤਰ ਸੀ ।
ਪ੍ਰਸ਼ਨ 41.
ਮੀਰ ਮੰਨੂੰ ਸਿੱਖਾਂ ਦਾ ਵਿਰੋਧੀ ਕਿਉਂ ਸੀ ?
ਉੱਤਰ-
ਕਿਉਂਕਿ ਉਹ ਪੰਜਾਬ ਵਿੱਚ ਸਿੱਖਾਂ ਦਾ ਵੱਧਦਾ ਹੋਇਆ ਪ੍ਰਭਾਵ ਸਹਿਣ ਕਰਨ ਨੂੰ ਤਿਆਰ ਨਹੀਂ ਸੀ ।
ਪ੍ਰਸ਼ਨ 42.
ਮੁਗਲਾਂ ਦੇ ਵਿਰੁੱਧ ਸਿੱਖਾਂ ਦੀ ਸਫਲਤਾ ਦਾ ਕੋਈ ਇੱਕ ਕਾਰਨ ਦੱਸੋ ।
ਉੱਤਰ-
ਸਿੱਖਾਂ ਨੇ ਗੁਰੀਲਾ ਯੁੱਧ ਨੀਤੀ ਨੂੰ ਅਪਣਾਇਆ ।
ਪ੍ਰਸ਼ਨ 43.
ਕੌੜਾ ਮਲ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਮੀਰ ਮੰਨੂੰ ਦਾ ਦੀਵਾਨ ।
![]()
ਪ੍ਰਸ਼ਨ 44.
ਸਿੱਖ ਕੌੜਾ ਮਲ ਨੂੰ ਮਿੱਠਾ ਮਲ ਕਿਉਂ ਕਹਿੰਦੇ ਸਨ ?
ਉੱਤਰ-
ਸਿੱਖ ਕੌੜਾ ਮਲ ਨੂੰ ਸਿੱਖਾਂ ਪ੍ਰਤੀ ਹਮਦਰਦੀ ਕਰਕੇ ਮਿੱਠਾ ਮਲ ਕਹਿੰਦੇ ਸਨ ।
ਪਸ਼ਨ 45.
ਅਦੀਨਾ ਬੇਗ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਮੀਰ ਮੰਨੂੰ ਦੇ ਸਮੇਂ ਜਲੰਧਰ ਦੁਆਬ ਦਾ ਫ਼ੌਜਦਾਰ ।
ਪ੍ਰਸ਼ਨ 46.
ਮੀਰ ਮੰਨੂੰ ਸਿੱਖਾਂ ਦੀ ਤਾਕਤ ਨੂੰ ਖ਼ਤਮ ਕਰਨ ਵਿੱਚ ਕਿਉਂ ਅਸਫਲ ਰਿਹਾ ? ਇੱਕ ਕਾਰਨ ਲਿਖੋ ।
ਜਾਂ
ਮੀਰ ਮੰਨੂੰ ਦੀ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਅਸਫਲਤਾ ਦਾ ਕੋਈ ਇੱਕ ਕਾਰਨ ਦੱਸੋ ।
ਉੱਤਰ-
ਸਿੱਖਾਂ ਦੀ ਗੁਰੀਲਾ ਯੁੱਧ ਨੀਤੀ ਕਾਰਨ ।
ਪ੍ਰਸ਼ਨ 47.
ਮੀਰ ਮੰਨੂੰ ਦੀ ਮੌਤ ਕਦੋਂ ਹੋਈ ਸੀ ? ਉੱਤਰ-1753 ਈ. ।
ਪ੍ਰਸ਼ਨ 48.
ਮੁਗਲਾਨੀ ਬੇਗ਼ਮ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਪੰਜਾਬ ਦੇ ਸੂਬੇਦਾਰ ਮੀਰ ਮੰਨੂੰ ਦੀ ਵਿਧਵਾ ।
ਪ੍ਰਸ਼ਨ 49.
ਮੀਰ ਮੰਨੂੰ ਦੀ ਵਿਧਵਾ ਦਾ ਕੀ ਨਾਂ ਸੀ ?
ਉੱਤਰ-
ਮੁਗ਼ਲਾਨੀ ਬੇਗ਼ਮ ।
ਪ੍ਰਸ਼ਨ 50.
ਮੁਗਲਾਨੀ ਬੇਗ਼ਮ ਪੰਜਾਬ ਦੀ ਸੂਬੇਦਾਰ ਕਦੋਂ ਬਣੀ ਸੀ ?
ਉੱਤਰ-
1753 ਈ. ।
![]()
ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ (Fill in the Blanks)
ਨੋਟ :–ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ-
1. ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਨੂੰ ………………………… ਵਿੱਚ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਨਿਯੁਕਤ ਕੀਤਾ ਗਿਆ ।
ਉੱਤਰ-
(1713 ਈ.)
2. ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਨੂੰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਦਮਨ ਦੀ ਨੀਤੀ ਲਈ ਉਸ ਨੂੰ ……………………….. ਦੀ ਉਪਾਧੀ ਨਾਲ ਸਨਮਾਨਿਤ ਕੀਤਾ ਗਿਆ ।
ਉੱਤਰ-
(ਰਾਜ ਦੀ ਤਲਵਾਰ)
3. ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੀ ਸ਼ਹੀਦੀ ਤੋਂ ਬਾਅਦ ਸਿੱਖ ………………………. ਅਤੇ ……………………. ਨਾਂ ਦੀਆਂ ਦੋ ਸੰਪਰਦਾਵਾਂ ਵਿੱਚ ਵੰਡੇ ਗਏ ।
ਉੱਤਰ-
(ਤੱਤ ਖ਼ਾਲਸਾ, ਬੰਦਈ ਖ਼ਾਲਸਾ).
4. 1721 ਈ. ਵਿੱਚ ……………………. ਨੇ ਤੱਤ ਖ਼ਾਲਸਾ ਅਤੇ ਬੰਦਈ ਖ਼ਾਲਸਾ ਵਿਚਾਲੇ ਸਮਝੌਤਾ ਕਰਵਾਇਆ ।
ਉੱਤਰ-
(ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ)
5. ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਤੋਂ ਪਹਿਲਾਂ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ …………………. ਸੀ ।
ਉੱਤਰ-
(ਅਬਦੁਸ ਸਮਦ ਖਾਂ)
6. ਜ਼ਕਰੀਆ ਖ਼ਾਂ …………………………. ਵਿੱਚ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਨਿਯੁਕਤ ਹੋਇਆ ।
ਉੱਤਰ-
(1726 ਈ.)
![]()
7. ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ………………………. ਵਿੱਚ ਸਿੱਖਾਂ ਨਾਲ ਸਮਝੌਤਾ ਕੀਤਾ ।
ਉੱਤਰ-
(1733 ਈ.)
8. 1733 ਈ. ਦੇ ਸਮਝੌਤੇ ਅਨੁਸਾਰ ਨਵਾਬ ਦਾ ਖਿਤਾਬ ………………………… ਨੂੰ ਦਿੱਤਾ ਗਿਆ ।
ਉੱਤਰ-
ਸਰਦਾਰ ਕਪੂਰ ਸਿੰਘ)
9. ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ਦਾ ਗਠਨ ………………………….. ਵਿੱਚ ਕੀਤਾ ਗਿਆ ।
ਉੱਤਰ-
(1734 ਈ. )
10. ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੂੰ …………………………… ਵਿੱਚ ਸ਼ਹੀਦ ਕੀਤਾ ਗਿਆ ।
ਉੱਤਰ-
(1738 ਈ.)
11. ਅੰਮ੍ਰਿਤਸਰ ਜ਼ਿਲ੍ਹੇ ਦੇ ਮੰਡਿਆਲਾ ਪਿੰਡ ਦੇ ਚੌਧਰੀ ………………. ਨੇ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਦੀ ਪਵਿੱਤਰਤਾ ਨੂੰ ਭੰਗ ਕੀਤਾ ਸੀ ।
ਉੱਤਰ-
(ਮੱਸਾ ਰੰਗੜ)
12. ਮੱਸਾ ਰੰਗੜ ………………… ਪਿੰਡ ਦਾ ਚੌਧਰੀ ਸੀ ।
ਉੱਤਰ-
(ਮੰਡਿਆਲਾ)
![]()
13. ………………………….. ਵਿੱਚ ਨਾਦਰ ਸ਼ਾਹ ਨੇ ਭਾਰਤ ‘ਤੇ ਹਮਲਾ ਕੀਤਾ |
ਉੱਤਰ-
(1739 ਈ. )
14. ਨਾਦਰ ਸ਼ਾਹ …………………………. ਦਾ ਸ਼ਾਸਕ ਸੀ ।
ਉੱਤਰ-
(ਈਰਾਨ)
15. ਪਹਿਲਾ ਜਾਂ ਛੋਟਾ ਘੱਲੂਘਾਰਾ …………………………… ਵਿੱਚ ਵਾਪਰਿਆ ।
ਉੱਤਰ-
(1746 ਈ.)
16. ਪਹਿਲੇ ਘੱਲੂਘਾਰੇ ਦੇ ਸਮੇਂ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ……………….. ਸੀ ।
ਉੱਤਰ-
(ਯਾਹੀਆ ਖ਼ਾ)
17. ਮੀਰ ਮੰਨੂੰ ਨੂੰ ………………………. ਦੇ ਨਾਂ ਨਾਲ ਵੀ ਜਾਣਿਆ ਜਾਂਦਾ ਸੀ ।
ਉੱਤਰ-
ਮੁਈਨਉਲ-ਮੁਲਕ
18. ਮੀਰ ਮੰਨੂੰ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ……………………… ਵਿੱਚ ਨਿਯੁਕਤ ਹੋਇਆ ।
ਉੱਤਰ-
(1748 ਈ. )
![]()
19. ਮੀਰ ਮੰਨੂੰ ਨੇ ………………………. ਨੂੰ ਜਲੰਧਰ ਦੁਆਬ ਦਾ ਫ਼ੌਜਦਾਰ ਨਿਯੁਕਤ ਕੀਤਾ ।
ਉੱਤਰ-
(ਅਦੀਨਾ ਬੇਗ)
20. ਮੀਰ ਮੰਨੂੰ ਦੀ ਮੌਤ ……………….. ਵਿੱਚ ਹੋਈ ।
ਉੱਤਰ-
(1753 ਈ.)
ਠੀਕ ਜਾਂ ਗ਼ਲਤ (True or False)
ਨੋਟ :-ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਠੀਕ ਜਾਂ ਗ਼ਲਤ ਦੀ ਚੋਣ ਕਰੋ-
1. ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ 1716 ਈ. ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਬਣਿਆ ।
ਉੱਤਰ-
ਗਲਤ
2. ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਨੂੰ ਮੁਗ਼ਲ ਬਾਦਸ਼ਾਹ ਫ਼ਰੁਖ਼ਸੀਅਰ ਨੇ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਨਿਯੁਕਤ ਕੀਤਾ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
3. ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਨੂੰ ਰਾਜ ਦੀ ਤਲਵਾਰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਉੱਤਰ-
ਠੀਕ
4. ਬੰਦਾ ਸਿੰਘ ਬਹਾਦਰ ਦੀ ਸ਼ਹੀਦੀ ਤੋਂ ਬਾਅਦ ਪੰਜਾਬ ਦੇ ਸਿੱਖ ਤੱਤ ਖ਼ਾਲਸਾ ਅਤੇ ਬੰਦਈ ਖ਼ਾਲਸਾ ਨਾਂ ਦੇ ਦੋ ਸੰਪਰਦਾਵਾਂ ਵਿੱਚ ਵੰਡੇ ਗਏ ਸਨ ।
ਉੱਤਰ-
ਠੀਕ
![]()
5. ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੇ ਤੱਤ ਖ਼ਾਲਸਾ ਅਤੇ ਬੰਦਈ ਖ਼ਾਲਸਾ ਵਿੱਚ ਆਪਸੀ ਸਮਝੌਤਾ ਕਰਵਾਇਆ ।
ਉੱਤਰ-
ਠੀਕ
6. ਤੱਤ ਖ਼ਾਲਸਾ ਅਤੇ ਬੰਦਈ ਖ਼ਾਲਸਾ ਵਿਚਾਲੇ ਸਮਝੌਤਾ 1721 ਈ. ਵਿੱਚ ਹੋਇਆ ।
ਉੱਤਰ-
ਠੀਕ
7. ਜ਼ਕਰੀਆ ਖ਼ਾਂ 1720 ਈ. ਵਿੱਚ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਨਿਯੁਕਤ ਹੋਇਆ ।
ਉੱਤਰ-
ਗ਼ਲਤ
8. 1726 ਈ. ਵਿੱਚ ਭਾਈ ਤਾਰਾ ਸਿੰਘ ਜੀ ਵਾਂ ਨੂੰ ਸ਼ਹੀਦ ਕੀਤਾ ਗਿਆ ।
ਉੱਤਰ-
ਠੀਕ
9. ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ਨਾਲ 1733 ਈ. ਵਿੱਚ ਸਮਝੌਤਾ ਕੀਤਾ।
ਉੱਤਰ-
ਠੀਕ
10. ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ਦਾ ਗਠਨ ਸਰਦਾਰ ਜੱਸਾ ਸਿੰਘ ਰਾਮਗੜ੍ਹੀਆ ਨੇ ਕੀਤਾ ।
ਉੱਤਰ-
ਗ਼ਲਤ
![]()
11. ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ਦੀ ਸਥਾਪਨਾ 1734 ਈ. ਵਿੱਚ ਹੋਈ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
12. ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ 1738 ਈ. ਵਿੱਚ ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੂੰ ਸ਼ਹੀਦ ਕੀਤਾ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
13. ਨਾਦਰ ਸ਼ਾਹ ਨੇ 1739 ਈ. ਵਿੱਚ ਭਾਰਤ ‘ਤੇ ਹਮਲਾ ਕੀਤਾ ।
ਉੱਤਰ-
ਠੀਕ
14. ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਜੀ ਨੂੰ ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਦੇ ਸਮੇਂ ਸ਼ਹੀਦ ਕੀਤਾ ਗਿਆ ਸੀ ।
ਉੱਤਰ-
ਗ਼ਲਤ
15. ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਨੂੰ 1745 ਈ. ਵਿੱਚ ਸ਼ਹੀਦ ਕੀਤਾ ਗਿਆ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
16. ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ 1745 ਈ. ਵਿੱਚ ਹੋਈ ।
ਉੱਤਰ-
ਠੀਕ
![]()
17. ਪਹਿਲਾ ਜਾਂ ਛੋਟਾ ਘੱਲੂਘਾਰਾ 1746 ਈ. ਵਿੱਚ ਵਾਪਰਿਆ ।
ਉੱਤਰ-
ਠੀਕ
18. ਮੀਰ ਮੰਨੂੰ 1748 ਈ. ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਨਵਾਂ ਸੂਬੇਦਾਰ ਬਣਿਆ ।
ਉੱਤਰ-
ਠੀਕ
19. ਅਹਿਮਦ ਸ਼ਾਹ ਅਬਦਾਲੀ ਨੇ 1752 ਈ. ਵਿੱਚ ਪੰਜਾਬ ‘ਤੇ ਕਬਜ਼ਾ ਕਰ ਲਿਆ ।
ਉੱਤਰ-
ਠੀਕ
20. ਮੀਰ ਮੰਨੂੰ ਦੀ ਮੌਤ 1754 ਈ. ਵਿੱਚ ਹੋਈ ।
ਉੱਤਰ-
ਗਲਤ
21. ਮੀਰ ਮੰਨੂੰ ਦੇ ਸਮੇਂ ਅਦੀਨਾ ਬੇਗ ਜਲੰਧਰ ਦੁਆਬ ਦਾ ਫ਼ੌਜਦਾਰ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
![]()
ਬਹੁਪੱਖੀ ਪ੍ਰਸ਼ਨ (Multiple Choice Questions)
ਨੋਟ :-ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਠੀਕ ਉੱਤਰ ਦੀ ਚੋਣ ਕਰੋ-
ਪ੍ਰਸ਼ਨ 1.
1716 ਈ. ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਕੌਣ ਸੀ ?
(i) ਅਬਦੁਸ ਸਮਦ ਖਾਂ
(ii) ਅਹਿਮਦ ਸ਼ਾਹ ਅਬਦਾਲੀ
(iii) ਮੀਰ ਮੰਨੂੰ
(iv) ਜ਼ਕਰੀਆ ਖਾਂ ।
ਉੱਤਰ-
(i) ਅਬਦੁਸ ਸਮਦ ਖਾਂ ।
ਪ੍ਰਸ਼ਨ 2.
ਫ਼ਰੁਖ਼ਸੀਅਰ ਨੇ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਨੂੰ ਕਿਸ ਖ਼ਿਤਾਬ ਨਾਲ ਨਿਵਾਜਿਆ ਸੀ ?
(i) ਖ਼ਾਨ ਬਹਾਦਰ
(ii) ਰਾਜ ਦੀ ਤਲਵਾਰ
(iii) ਨਾਸਿਰ ਖ਼ਾਨ
(iv) ਮਿੱਠਾ ਮੱਲ ।
ਉੱਤਰ-
(ii) ਰਾਜ ਦੀ ਤਲਵਾਰ ।
ਪ੍ਰਸ਼ਨ 3.
ਬੰਦਈ ਖ਼ਾਲਸਾ ਅਤੇ ਤੱਤ ਖ਼ਾਲਸਾ ਵਿਚਾਲੇ ਸਮਝੌਤਾ ਕਦੋਂ ਹੋਇਆ ?
(i) 1711 ਈ. ਵਿੱਚ
(ii) 1716 ਈ. ਵਿੱਚ
(iii) 1721 ਈ. ਵਿੱਚ
(iv) 1726 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(iii) 1721 ਈ. ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 4.
ਬੰਦਈ ਖ਼ਾਲਸਾ ਅਤੇ ਤੱਤ ਖ਼ਾਲਸਾ ਵਿਚਾਲੇ ਸਮਝੌਤਾ ਕਿਸ ਨੇ ਕਰਵਾਇਆ ਸੀ ?
(i) ਬਾਬਾ ਦੀਪ ਸਿੰਘ ਜੀ ਨੇ
(i) ਨਵਾਬ ਕਪੂਰ ਸਿੰਘ ਨੇ
(iii) ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੇ
(iv) ਭਾਈ ਤਾਰੂ ਸਿੰਘ ਜੀ ਨੇ ।
ਉੱਤਰ-
(iii) ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੇ ।
ਪ੍ਰਸ਼ਨ 5.
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਕਦੋਂ ਬਣਿਆ ?
(i) 1716 ਈ. ਵਿੱਚ
(ii) 1717 ਈ. ਵਿੱਚ
(iii) 1726 ਈ. ਵਿੱਚ
(iv) 1728 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(iii) 1726 ਈ. ਵਿੱਚ ।
![]()
ਪ੍ਰਸ਼ਨ 6.
ਹੈਦਰੀ ਝੰਡੇ ਦੀ ਘਟਨਾ ਕਿਸ ਦੇ ਸ਼ਾਸਨ ਕਾਲ ਵਿੱਚ ਹੋਈ ਸੀ ?
(i) ਅਬਦੁਸ ਸਮਦ ਖਾਂ
(ii) ਯਾਹੀਆ ਖ਼ਾਂ
(iii) ਅਹਿਮਦ ਸ਼ਾਹ ਅਬਦਾਲੀ
(iv) ਜ਼ਕਰੀਆ ਖਾਂ ।
ਉੱਤਰ-
(iv) ਜ਼ਕਰੀਆ ਖਾਂ ।
ਪ੍ਰਸ਼ਨ 7.
ਸਿੱਖਾਂ ਅਤੇ ਮੁਗਲਾਂ ਵਿਚਾਲੇ ਸਮਝੌਤਾ ਕਦੋਂ ਹੋਇਆ ਸੀ ?
(i) 1721 ਈ. ਵਿੱਚ .
(ii) 1724 ਈ. ਵਿੱਚ
(iii) 1733 ਈ. ਵਿੱਚ
(iv) 1734 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(iii) 1733 ਈ. ਵਿੱਚ
ਪ੍ਰਸ਼ਨ 8.
ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ਦਾ ਗਠਨ ਕਦੋਂ ਕੀਤਾ ਗਿਆ ਸੀ ?
(i) 1724 ਈ. ਵਿੱਚ
(ii) 1725 ਈ. ਵਿੱਚ
(iii) 1733 ਈ. ਵਿੱਚ
(iv) 1734 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(iv) 1734 ਈ. ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 9.
ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ਦਾ ਗਠਨ ਕਿਸਨੇ ਕੀਤਾ ਸੀ ?
(i) ਨਵਾਬ ਕਪੂਰ ਸਿੰਘ ਨੇ
(ii) ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੇ
(iii) ਬਾਬਾ ਦੀਪ ਸਿੰਘ ਜੀ ਨੇ
(iv) ਭਾਈ ਮਹਿਤਾਬ ਸਿੰਘ ਜੀ ਨੇ
ਉੱਤਰ-
(i) ਨਵਾਬ ਕਪੂਰ ਸਿੰਘ ਨੇ
ਪ੍ਰਸ਼ਨ 10.
ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੂੰ ਕਦੋਂ ਸ਼ਹੀਦ ਕੀਤਾ ਗਿਆ ਸੀ ?
(i) 1721 ਈ. ਵਿੱਚ
(ii) 1733 ਈ. ਵਿੱਚ
(ii) 1734 ਈ. ਵਿੱਚ
(iv) 1738 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(iv) 1738 ਈ. ਵਿੱਚ ।
![]()
ਪ੍ਰਸ਼ਨ 11.
ਨਾਦਰ ਸ਼ਾਹ ਨੇ ਭਾਰਤ ‘ਤੇ ਕਦੋਂ ਹਮਲਾ ਕੀਤਾ ਸੀ ?
(i) 1736 ਈ. ਵਿੱਚ
(ii) 1737 ਈ. ਵਿੱਚ
(iii) 1738 ਈ. ਵਿੱਚ
(iv) 1739 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(iv) 1739 ਈ. ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 12.
ਨਾਦਰ ਸ਼ਾਹ ਕਿੱਥੋਂ ਦਾ ਸ਼ਾਸਕ ਸੀ ?
(i) ਅਫ਼ਗਾਨਿਸਤਾਨ
(ii) ਈਰਾਕ
(iii) ਬਲੋਚਿਸਤਾਨ
(iv) ਈਰਾਨ ।
ਉੱਤਰ-
(iv) ਈਰਾਨ ।
ਪ੍ਰਸ਼ਨ 13.
ਮੱਸਾ ਰੰਗੜ ਕੌਣ ਸੀ ?
(i) ਪਿੰਡ ਮੰਡਿਆਲਾ ਦਾ ਚੌਧਰੀ
(ii) ਪਿੰਡ ਵਾਂ ਦਾ ਚੌਧਰੀ
(iii) ਜਲੰਧਰ ਦਾ ਫ਼ੌਜਦਾਰ
(iv) ਸਰਹਿੰਦ ਦਾ ਫ਼ੌਜਦਾਰ ।
ਉੱਤਰ-
(i) ਪਿੰਡ ਮੰਡਿਆਲਾ ਦਾ ਚੌਧਰੀ
ਪ੍ਰਸ਼ਨ 14.
ਬਾਲ ਹਕੀਕਤ ਰਾਏ ਜੀ ਨੂੰ ਕਦੋਂ ਸ਼ਹੀਦ ਕੀਤਾ ਗਿਆ ਸੀ ?
(i) 1739 ਈ. ਵਿੱਚ
(ii) 1740 ਈ. ਵਿੱਚ ।
(iii) 1741 ਈ. ਵਿੱਚ
(iv) 1742 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(iv) 1742 ਈ. ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 15.
ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੀ ਮੌਤ ਕਦੋਂ ਹੋਈ ਸੀ ?
(i) 1742 ਈ. ਵਿੱਚ
(ii) 1743 ਈ. ਵਿੱਚ
(iii) 1744 ਈ. ਵਿੱਚ
(iv) 1745 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(iv) 1745 ਈ. ਵਿੱਚ ।
![]()
ਪ੍ਰਸ਼ਨ 16.
ਪਹਿਲਾ ਘੱਲੂਘਾਰਾ ਜਾਂ ਛੋਟਾ ਘੱਲੂਘਾਰਾ ਕਿੱਥੇ ਹੋਇਆ ਸੀ ?
(i) ਕਾਹਨੂੰਵਾਨ
(ii) ਭੂਪ
(iii) ਸਰਹਿੰਦ
(iv) ਮੰਡਿਆਲਾ ।
ਉੱਤਰ-
(i) ਕਾਹਨੂੰਵਾਨ
ਪ੍ਰਸ਼ਨ 17.
ਪਹਿਲਾ ਜਾਂ ਛੋਟਾ ਘੱਲੂਘਾਰਾ ਕਦੋਂ ਵਾਪਰਿਆ ਸੀ ?
(i) 1733 ਈ. ਵਿੱਚ
(ii) 1734 ਈ. ਵਿੱਚ
(iii) 1739 ਈ. ਵਿੱਚ
(iv) 1746 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(iv) 1746 ਈ. ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 18.
ਮੀਰ ਮੰਨੂੰ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਕਦੋਂ ਬਣਿਆ ?
(i) 1748 ਈ. ਵਿੱਚ
(ii) 1749 ਈ. ਵਿੱਚ
(iii) 1752 ਈ. ਵਿੱਚ
(iv) 1753 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(i) 1748 ਈ. ਵਿੱਚ
ਪ੍ਰਸ਼ਨ 19.
ਅਦੀਨਾ ਬੇਗ ਕੌਣ ਸੀ ?
(i) ਮੀਰ ਮੰਨੂੰ ਦਾ ਸਲਾਹਕਾਰ
(ii) ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦਾ ਦੀਵਾਨ
(iii) ਜਲੰਧਰ ਦੁਆਬ ਦਾ ਫ਼ੌਜਦਾਰ
(iv) ਪਿੰਡ ਮੰਡਿਆਲਾ ਦਾ ਚੌਧਰੀ 1
ਉੱਤਰ-
(iii) ਜਲੰਧਰ ਦੁਆਬ ਦਾ ਫ਼ੌਜਦਾਰ
ਪ੍ਰਸ਼ਨ 20.
ਮੀਰ ਮੰਨੂੰ ਦੀ ਮੌਤ ਕਦੋਂ ਹੋਈ ਸੀ ?
(i) 1750 ਈ. ਵਿੱਚ
(ii) 1751 ਈ. ਵਿੱਚ
(iii) 1752 ਈ. ਵਿੱਚ
(iv) 1753 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(iv) 1753 ਈ. ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 21.
ਮੀਰ ਮੰਨੂੰ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਕਿਉਂ ਅਸਫਲ ਰਿਹਾ ?
(i) ਅਦੀਨਾ ਬੇਗ਼ ਦੀ ਦੋ ਰੰਗੀ ਨੀਤੀ ਕਾਰਨ
(ii) ਸਿੱਖਾਂ ਦੀ ਗੁਰੀਲਾ ਯੁੱਧ ਨੀਤੀ ਕਾਰਨ
(iii) ਮੀਰ ਮੰਨੂੰ ਦੇ ਅੱਤਿਆਚਾਰ ਕਾਰਨ
(iv) ਉੱਪਰ ਲਿਖੇ ਸਾਰੇ ।
ਉੱਤਰ-
(iv) ਉੱਪਰ ਲਿਖੇ ਸਾਰੇ ।
![]()
ਪ੍ਰਸ਼ਨ 22.
ਮੁਗਲਾਨੀ ਬੇਗ਼ਮ ਪੰਜਾਬ ਦੀ ਸੂਬੇਦਾਰ ਕਦੋਂ ਬਣੀ ਸੀ ?
(i) 1751 ਈ. ਵਿੱਚ
(ii) 1752 ਈ. ਵਿੱਚ
(iii) 1753 ਈ. ਵਿੱਚ
(iv) 1754 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(iii) 1753 ਈ. ਵਿੱਚ ।
Source Based Questions
ਨੋਟ-ਹੇਠ ਲਿਖੇ ਪੈਰਿਆਂ ਨੂੰ ਧਿਆਨ ਨਾਲ ਪੜੋ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਅੰਤ ਵਿੱਚ ਦਿੱਤੇ ਗਏ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਦਿਓ-
1. ਸ਼ਾਹੀ ਫ਼ਰਮਾਨ ਦੇ ਜਾਰੀ ਹੋਣ ਤੋਂ ਬਾਅਦ ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਨੇ ਸਿੱਖਾਂ ‘ਤੇ ਘੋਰ ਅੱਤਿਆਚਾਰ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੇ । ਸੈਂਕੜੇ ਨਿਰਦੋਸ਼ ਸਿੱਖਾਂ ਨੂੰ ਰੋਜ਼ਾਨਾ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਕੇ ਲਾਹੌਰ ਲਿਆਂਦਾ ਜਾਂਦਾ । ਉਨ੍ਹਾਂ ਨੂੰ ਇਸਲਾਮ ਧਰਮ ਵਿੱਚ ਸ਼ਾਮਲ ਹੋਣ ‘ਤੇ ਜਾਨ ਬਖ਼ਸ਼ੀ ਦਾ ਲਾਲਚ ਦਿੱਤਾ ਜਾਂਦਾ ਪਰ ਗੁਰੂ ਦੇ ਸਿੱਖ ਅਜਿਹੀ ਜ਼ਿੰਦਗੀ ਤੋਂ ਸ਼ਹੀਦ ਹੋਣਾ ਜ਼ਿਆਦਾ ਚੰਗਾ ਸਮਝਦੇ ਸਨ । ਜੱਲਾਦ ਇਨ੍ਹਾਂ ਸਿੱਖਾਂ ਨੂੰ ਭਾਰੀ ਤਸੀਹੇ ਦੇਣ ਮਗਰੋਂ ਸ਼ਹੀਦ ਕਰ ਦਿੰਦੇ । ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਦੀ ਇਸ ਸਖ਼ਤ ਨੀਤੀ ਤੋਂ ਬਚਣ ਲਈ ਬਹੁਤ ਸਾਰੇ ਸਿੱਖਾਂ ਨੇ ਲੱਖੀ ਜੰਗਲ ਅਤੇ ਸ਼ਿਵਾਲਿਕ ਪਹਾੜਾਂ ਵਿੱਚ ਜਾ ਸ਼ਰਨ ਲਈ । ਇੱਥੇ ਉਨ੍ਹਾਂ ਨੂੰ ਭਾਰੀ ਔਕੜਾਂ ਦਾ ਸਾਹਮਣਾ ਕਰਨਾ ਪਿਆ ।
ਉਨ੍ਹਾਂ ਨੂੰ ਕਈ-ਕਈ ਦਿਨਾਂ ਤਕ ਭੁੱਖਿਆਂ ਰਹਿਣਾ ਪੈਂਦਾ ਸੀ ਜਾਂ ਉਹ ਰੁੱਖਾਂ ਦੇ ਪੱਤੇ ਤੇ ਛਿੱਲੜਾਂ ਖਾ ਕੇ ਆਪਣੀ ਭੁੱਖ ਮਿਟਾਉਂਦੇ ਸਨ । ਮੁਗ਼ਲ ਅਧਿਕਾਰੀਆਂ ਨੇ ਪਿੱਛੇ ਰਹਿ ਗਈਆਂ ਸਿੱਖ ਇਸਤਰੀਆਂ ਅਤੇ ਬੱਚਿਆਂ ‘ਤੇ ਆਪਣਾ ਕਹਿਰ ਢਾਹੁਣਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ । ਇਸ ਤਰ੍ਹਾਂ ਆਪਣੇ ਸ਼ਾਸਨ ਕਾਲ ਦੇ ਸ਼ੁਰੂ ਦੇ ਕੁਝ ਵਰਿਆਂ ਤਕ ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਦੀ ਸਿੱਖਾਂ ਵਿਰੁੱਧ ਦਮਨ ਨੀਤੀ ਬਹੁਤ ਸਫਲ ਰਹੀ । ਇਸ ਤੋਂ ਖੁਸ਼ ਹੋ ਕੇ ਫ਼ਰੁਖਸੀਅਰ ਨੇ ਉਸ ਨੂੰ “ਰਾਜ ਦੀ ਤਲਵਾਰ ਦੀ ਉਪਾਧੀ ਨਾਲ ਸਨਮਾਨਿਆ ।
1. ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਕੌਣ ਸੀ ?
2. ਸ਼ਾਹੀ ਫ਼ਰਮਾਨ ਦੇ ਜਾਰੀ ਹੋਣ ਤੋਂ ਬਾਅਦ ………………….. ਨੇ ਸਿੱਖਾਂ ‘ਤੇ ਘੋਰ ਅੱਤਿਆਚਾਰ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੇ ।
3. ਸਿੱਖਾਂ ਨੂੰ ਰੋਜ਼ਾਨਾ ਕਿੱਥੇ ਸ਼ਹੀਦ ਕੀਤਾ ਜਾਂਦਾ ਸੀ ?
4. ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਦੇ ਜੁਲਮਾਂ ਤੋਂ ਬਚਣ ਲਈ ਸਿੱਖਾਂ ਨੇ ਕੀ ਕੀਤਾ ?
5. ਫ਼ਰੁਖ਼ਸੀਅਰ ਨੇ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਨੂੰ ਕਿਹੜੀ ਉਪਾਧੀ ਨਾਲ ਸਨਮਾਨਿਤ ਕੀਤਾ ਸੀ ?
ਉੱਤਰ-
1. ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਸੀ ।
2. ਅਬਦੁਸ ਸਮਦ ਖਾਂ ।
3. ਸਿੱਖਾਂ ਨੂੰ ਰੋਜ਼ਾਨਾ ਲਾਹੌਰ ਵਿਖੇ ਸ਼ਹੀਦ ਕੀਤਾ ਜਾਂਦਾ ਸੀ ।
4. ਅਬਦੁਸ ਸਮਦ ਖ਼ਾਂ ਦੇ ਜ਼ੁਲਮਾਂ ਤੋਂ ਬਚਣ ਲਈ ਸਿੱਖਾਂ ਨੇ ਲੱਖੀ ਜੰਗਲ ਅਤੇ ਸ਼ਿਵਾਲਿਕ ਪਹਾੜਾਂ ਵਿੱਚ ਜਾ ਕੇ ਸ਼ਰਨ ਲਈ ।
5. ਫ਼ਰੁਖ਼ਸੀਅਰ ਨੇ ਅਬਦੁਸ ਸਮਦ ਖਾਂ ਨੂੰ ‘ਰਾਜ ਦੀ ਤਲਵਾਰ’ ਦੀ ਉਪਾਧੀ ਨਾਲ ਸਨਮਾਨਿਤ ਕੀਤਾ ਸੀ ।
2. ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਸਿੱਖਾਂ ਦੀਆਂ ਦਿਨੋ-ਦਿਨ ਵੱਧ ਰਹੀਆਂ ਕਾਰਵਾਈਆਂ ਤੋਂ ਬੜਾ ਪ੍ਰੇਸ਼ਾਨ ਸੀ । ਉਸ ਨੇ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਕੁਚਲਣ ਲਈ ਜ਼ਿਹਾਦ ਦਾ ਨਾਅਰਾ ਲਗਾਇਆ । ਸਿੱਟੇ ਵਜੋਂ ਹਜ਼ਾਰਾਂ ਦੀ ਗਿਣਤੀ ਵਿੱਚ ਮੁਸਲਮਾਨ ਉਸ ਦੇ ਝੰਡੇ ਅਧੀਨ ਆਣ ਇਕੱਠੇ ਹੋਏ । ਇਸ ਸੈਨਾ ਦੀ ਕਮਾਨ ਮੀਰ ਇਨਾਇਤਉੱਲਾ ਖਾਂ ਨੂੰ ਸੌਂਪੀ ਗਈ । ਉਨ੍ਹਾਂ ਨੂੰ ਈਦ ਦੇ ਮੁਬਾਰਕ ਦਿਨ ਇੱਕ ਹੈਦਰੀ ਝੰਡਾ ਦਿੱਤਾ ਗਿਆ ਅਤੇ ਇਹ ਐਲਾਨ ਕੀਤਾ ਗਿਆ ਕਿ ਇਸ ਝੰਡੇ ਅਧੀਨ ਲੜਨ ਵਾਲਿਆਂ ਨੂੰ ਅੱਲ੍ਹਾ ਜ਼ਰੂਰ ਫ਼ਤਹਿ ਦੇਵੇਗਾ । ਜਦੋਂ ਸਿੱਖਾਂ ਨੂੰ ਇਸ ਸੰਬੰਧੀ ਪਤਾ ਚਲਿਆ ਤਾਂ ਉਨ੍ਹਾਂ ਨੇ ਮੁੜ ਜੰਗਲਾਂ ਅਤੇ ਪਹਾੜਾਂ ਵਿੱਚ ਜਾ ਸ਼ਰਨ ਲਈ । ਇੱਕ ਦਿਨ ਲਗਭਗ 7 ਹਜ਼ਾਰ ਸਿੱਖਾਂ ਨੇ ਇਨ੍ਹਾਂ ਗਾਜ਼ੀਆਂ ਉੱਤੇ ਅਚਾਨਕ ਹਮਲਾ ਕਰਕੇ ਉਨ੍ਹਾਂ ਵਿੱਚ ਭਾਰੀ ਤਬਾਹੀ ਮਚਾ ਦਿੱਤੀ । ਹਜ਼ਾਰਾਂ ਗਾਜ਼ੀਆਂ ਨੂੰ ਕਤਲ ਕਰ ਦਿੱਤਾ ਗਿਆ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਸਿੱਖ ਉਨ੍ਹਾਂ ਦਾ ਸਾਮਾਨ ਵੀ ਲੁੱਟ ਕੇ ਲੈ ਗਏ ।ਇਸ ਘਟਨਾ ਨਾਲ ਜਿੱਥੇ ਸਰਕਾਰ ਦੇ ਗੌਰਵ ਨੂੰ ਭਾਰੀ ਸੱਟ ਵੱਜੀ ਉੱਥੇ ਇਸ ਅਦੁੱਤੀ ਸਫਲਤਾ ਦੇ ਕਾਰਨ ਸਿੱਖਾਂ ਦਾ ਹੌਸਲਾ ਬੁਲੰਦ ਹੋ ਗਿਆ ।
1. ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਕੌਣ ਸੀ ?
2. ਜਿਹਾਦ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
3. ਹੈਦਰੀ ਝੰਡੇ ਦੀ ਕਮਾਨ ਕਿਸ ਨੂੰ ਸੌਂਪੀ ਗਈ ਸੀ ?
4. ਹੈਦਰੀ ਝੰਡੇ ਦੀ ਘਟਨਾ ਸਮੇਂ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਕੌਣ ਸੀ ?
(i) ਅਬਦੁਸ ਸਮਦ ਖਾਂ
(ii) ਜ਼ਕਰੀਆ ਖ਼ਾਂ
(ii) ਮੀਰ ਮੰਨੂੰ
(iv) ਅਹਿਮਦ ਸ਼ਾਹ ਅਬਦਾਲੀ ।
5. ਸਿੱਖਾਂ ਨੇ ਜਿੱਥੇ ਸ਼ਰਨ ਲਈ ਸੀ ?
ਉੱਤਰ-
1. ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਸੀ ।
2. ਜ਼ਿਹਾਦ ਤੋਂ ਭਾਵ ਹੈ ਧਾਰਮਿਕ ਲੜਾਈ ।
3. ਹੈਦਰੀ ਝੰਡੇ ਦੀ ਕਮਾਨ ਮੀਰ ਇਨਾਇਤਉੱਲਾ ਖ਼ਾਂ ਨੂੰ ਸੌਂਪੀ ਗਈ ਸੀ ।
4. ਜ਼ਕਰੀਆ ਖਾਂ ।
5. ਸਿੱਖਾਂ ਨੇ ਜੰਗਲਾਂ ਅਤੇ ਪਹਾੜਾਂ ਵਿੱਚ ਜਾ ਸ਼ਰਨ ਲਈ ।
3. ਮੁਗ਼ਲਾਂ ਨਾਲ ਸਮਝੌਤਾ ਹੋ ਜਾਣ ਨਾਲ ਸਿੱਖਾਂ ਨੂੰ ਆਪਣੀ ਸ਼ਕਤੀ ਨੂੰ ਸੰਗਠਿਤ ਕਰਨ ਦਾ ਸੁਨਹਿਰੀ ਮੌਕਾ ਮਿਲਿਆ । ਨਵਾਬ ਕਪੂਰ ਸਿੰਘ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਇਹ ਸੁਨੇਹਾ ਭੇਜਿਆ ਕਿ ਉਹ ਜੰਗਲਾਂ ਅਤੇ ਪਹਾੜਾਂ ਨੂੰ ਛੱਡ ਕੇ ਮੁੜ ਆਪਣੇ ਘਰਾਂ ਵਿੱਚ ਆ ਜਾਣ । ਇਸ ਤਰ੍ਹਾਂ ਪਿਛਲੇ ਦੋ ਦਹਾਕਿਆਂ ਤੋਂ ਮੁਗਲਾਂ ਅਤੇ ਸਿੱਖਾਂ ਵਿਚਾਲੇ ਚਲੇ ਆ ਰਹੇ ਸੰਘਰਸ਼ ਦਾ ਅੰਤ ਹੋਇਆ ਤੇ ਸਿੱਖਾਂ ਨੂੰ ਕੁਝ ਸੁੱਖ ਦਾ ਸਾਹ ਮਿਲਿਆ 1734 ਈ. ਵਿੱਚ ਨਵਾਬ ਕਪੂਰ ਸਿੰਘ ਨੇ ਸਿੱਖਾਂ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਮਜ਼ਬੂਤ ਕਰਨ ਦੇ ਉਦੇਸ਼ ਨਾਲ ਉਨ੍ਹਾਂ ਨੂੰ ਦੋ ਜੱਥਿਆਂ ਵਿੱਚ ਸੰਗਠਿਤ ਕਰ ਦਿੱਤਾ । ਇਹ ਜੱਥੇ ਸਨ-ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ । ਬੁੱਢਾ ਦਲ ਵਿੱਚ 40 ਸਾਲਾਂ ਤੋਂ ਵਡੇਰੀ ਉਮਰ ਦੇ ਸਿੱਖਾਂ ਨੂੰ ਸ਼ਾਮਲ ਕੀਤਾ ਗਿਆ ਅਤੇ ਉਸ ਤੋਂ ਘੱਟ ਦੀ ਉਮਰ ਵਾਲੇ ਸਿੱਖਾਂ ਨੂੰ ਤਰੁਣਾ ਦਲ ਵਿੱਚ । ਤਰੁਣਾ ਦਲ ਨੂੰ ਅੱਗੇ ਪੰਜ ਜੱਥਿਆਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ ਸੀ । ਹਰੇਕ ਜੱਥੇ ਵਿੱਚ 1300 ਤੋਂ ਲੈ ਕੇ 2000 ਸਿੱਖ ਸਨ ਅਤੇ ਹਰੇਕ ਜੱਥੇ ਦਾ ਆਪਣਾ ਇੱਕ ਵੱਖਰਾ ਨੇਤਾ ਅਤੇ ਝੰਡਾ ਸੀ । ਬੁੱਢਾ ਦਲ ਧਾਰਮਿਕ ਸਥਾਨਾਂ ਦੀ ਦੇਖ-ਭਾਲ ਕਰਦਾ ਜਦਕਿ ਤਰੁਣਾ ਦਲ ਦੁਸ਼ਮਣਾਂ ਦਾ ਮੁਕਾਬਲਾ ਕਰਦਾ ਸੀ । ਇਨ੍ਹਾਂ ਦਲਾਂ ਨੇ ਭਵਿੱਖ ਦੇ ਸਿੱਖ ਇਤਿਹਾਸ ਵਿੱਚ ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਨਿਭਾਈ ।
1. ਮੁਗ਼ਲਾਂ ਅਤੇ ਸਿੱਖਾਂ ਵਿਚਾਲੇ ਸਮਝੌਤਾ ਕਦੋਂ ਹੋਇਆ ?
2. ਮੁਗ਼ਲਾਂ ਅਤੇ ਸਿੱਖਾਂ ਵਿਚਾਲੇ ਸਮਝੌਤੇ ਸਮੇਂ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਕੌਣ ਸੀ ?
(i) ਅਹਿਮਦ ਸ਼ਾਹ ਅਬਦਾਲੀ
(ii) ਮੀਰ ਮੰਨੂੰ
(iii) ਜ਼ਕਰੀਆ ਖ਼ਾਂ
(iv) ਇਨ੍ਹਾਂ ਵਿੱਚੋਂ ਕੋਈ ਨਹੀਂ ।
3. ਨਵਾਬ ਕਪੂਰ ਸਿੰਘ ਕੌਣ ਸੀ ?
4. ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ਦਾ ਗਠਨ ਕਦੋਂ ਕੀਤਾ ਗਿਆ ਸੀ ?
5. ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ਵਿੱਚ ਕੌਣ ਸ਼ਾਮਲ ਸਨ ?
ਉੱਤਰ-
1. ਮੁਗ਼ਲਾਂ ਅਤੇ ਸਿੱਖਾਂ ਵਿਚਾਲੇ ਸਮਝੌਤਾ 1733 ਈ. ਵਿੱਚ ਹੋਇਆ ਸੀ ।
2. ਜ਼ਕਰੀਆ ਖਾਂ ।
3. ਨਵਾਬ ਕਪੂਰ ਸਿੰਘ 18ਵੀਂ ਸਦੀ ਵਿੱਚ ਸਿੱਖਾਂ ਦਾ ਇੱਕ ਪ੍ਰਸਿੱਧ ਨੇਤਾ ਸੀ ।
4. ਬੁੱਢਾ ਦਲ ਅਤੇ ਤਰੁਣਾ ਦਲ ਦਾ ਗਠਨ 1734 ਈ. ਵਿੱਚ ਕੀਤਾ ਗਿਆ ਸੀ ।
5. ਬੁੱਢਾ ਦਲ ਵਿੱਚ 40 ਵਰੇ ਤੋਂ ਵਡੇਰੀ ਉਮਰ ਦੇ ਸਿੱਖ ਅਤੇ ਤਰੁਣਾ ਦਲ ਵਿਚ ਨੌਜਵਾਨਾਂ ਨੂੰ ਸ਼ਾਮਲ ਕੀਤਾ ਗਿਆ ਸੀ ।
![]()
4. ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਦੀ ਸ਼ਹਾਦਤ ਨੂੰ ਸਿੱਖ ਇਤਿਹਾਸ ਵਿੱਚ ਬਹੁਤ ਮਹੱਤਵਪੂਰਨ ਸਥਾਨ ਪ੍ਰਾਪਤ ਹੈ । ਸਿੱਖ ਪੰਥ ਦੀ ਅਦੁੱਤੀ ਸੇਵਾ ਕਾਰਨ ਉਨ੍ਹਾਂ ਦਾ ਸਿੱਖਾਂ ਵਿੱਚ ਬਹੁਤ ਸਤਿਕਾਰ ਸੀ । ਉਹ 1721 ਈ. ਤੋਂ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਦੇ ਮੁੱਖ ਗੰਥੀ ਚਲੇ ਆ ਰਹੇ ਸਨ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਦੇ ਸੈਨਿਕਾਂ ਦੁਆਰਾ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਦੇ ਕਬਜ਼ੇ ਅਤੇ ਉੱਥੇ ਸਿੱਖਾਂ ਨੂੰ ਨਾ ਜਾਣ ਦੇਣ ਲਈ ਸਥਾਪਿਤ ਕੀਤੀਆਂ ਗਈਆਂ ਸੈਨਿਕ ਚੌਕੀਆਂ ਕਾਰਨ ਉਹ ਬਹੁਤ ਨਿਰਾਸ਼ ਹੋਏ । 1738 ਈ. ਵਿੱਚ ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੇ ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੂੰ ਇਹ ਬੇਨਤੀ ਕੀਤੀ ਕਿ ਜੇਕਰ ਉਹ ਸਿੱਖਾਂ ਨੂੰ ਦੀਵਾਲੀ ਦੇ ਮੌਕੇ ‘ਤੇ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਆਉਣ ਦੀ ਇਜਾਜ਼ਤ ਦੇਵੇ ਤਾਂ ਉਹ 5,000 ਰੁਪਏ ਉਸ ਨੂੰ ਭੇਟ ਕਰਨਗੇ । ਜ਼ਕਰੀਆ ਖ਼ਾਂ ਨੇ ਇਹ ਪੇਸ਼ਕਸ਼ ਫੌਰਨ ਸਵੀਕਾਰ ਕਰ ਲਈ | ਅਸਲ ਵਿੱਚ ਉਸ ਦੇ ਦਿਮਾਗ਼ ਵਿੱਚ ਇੱਕ ਯੋਜਨਾ ਆਈ । ਇਸ ਯੋਜਨਾ ਅਨੁਸਾਰ ਉਹ ਅੰਮ੍ਰਿਤਸਰ ਵਿੱਚ ਦੀਵਾਲੀ ਦੇ ਮੌਕੇ ‘ਤੇ ਇਕੱਠੇ ਹੋਣ ਵਾਲੇ ਸਿੱਖਾਂ ‘ਤੇ ਅਚਾਨਕ ਹਮਲਾ ਕਰਕੇ ਉਨ੍ਹਾਂ ਦਾ ਮਲੀਆਮੇਟ ਕਰਨਾ ਚਾਹੁੰਦਾ ਸੀ ।
1. ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਕੌਣ ਸਨ ?
2. ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੇ ਕਿਸ ਨੂੰ ਬੇਨਤੀ ਕੀਤੀ ਕਿ ਸਿੱਖਾਂ ਨੂੰ ਅੰਮ੍ਰਿਤਸਰ ਵਿਚ ਦੀਵਾਲੀ ਦੇ ਮੌਕੇ ਇਕੱਠੇ ਹੋਣ ਦੀ ਆਗਿਆ ਦਿੱਤੀ ਜਾਵੇ ?
3. ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੇ ਸਿੱਖਾਂ ਨੂੰ ਅੰਮ੍ਰਿਤਸਰ ਆਉਣ ਦੇ ਲਈ ਜ਼ਕਰੀਆਂ ਖਾਂ ਨੂੰ ਕਿੰਨੇ ਰੁਪਏ ਦੇਣ ਦੀ ਪੇਸ਼ਕਸ਼ ਕੀਤੀ ?
(i) 2000 ਰੁਪਏ
(ii) 3000 ਰੁਪਏ
(iii) 4000 ਰੁਪਏ
(iv) 5000 ਰੁਪਏ ।
4. ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੂੰ ਕਦੋਂ ਸ਼ਹੀਦ ਕੀਤਾ ਗਿਆ ਸੀ ?
5. ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਦੀ ਸ਼ਹੀਦੀ ਦਾ ਕੀ ਸਿੱਟਾ ਨਿਕਲਿਆ ?
ਉੱਤਰ-
1. ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ 1721 ਈ. ਤੋਂ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਦੇ ਮੁੱਖ ਗ੍ਰੰਥੀ ਸਨ ।
2. ਲਾਹੌਰ ਦੇ ਸੂਬੇਦਾਰ ਜ਼ਕਰੀਆ ਖਾਂ ਨੂੰ ।
3. 5000 ਰੁਪਏ ।
4. ਭਾਈ ਮਨੀ ਸਿੰਘ ਜੀ ਨੂੰ 1738 ਈ. ਵਿੱਚ ਸ਼ਹੀਦ ਕੀਤਾ ਗਿਆ ਸੀ ।
5. ਇਸ ਕਾਰਨ ਸਿੱਖਾਂ ਵਿੱਚ ਇੱਕ ਨਵਾਂ ਜੋਸ਼ ਪੈਦਾ ਹੋਇਆ ।
5. ਸਿੱਖਾਂ ਦਾ ਮਲੀਆਮੇਟ ਕਰਨ ਲਈ ਯਾਹੀਆ ਖ਼ਾਂ ਤੇ ਲਖਪਤ ਰਾਏ ਨੇ ਇੱਕ ਭਾਰੀ ਸੈਨਾ ਤਿਆਰ ਕੀਤੀ । ਉਨ੍ਹਾਂ ਦੇ ਅਧੀਨ ਮੁਗ਼ਲ ਸੈਨਾ ਨੇ ਲਗਭਗ 15,000 ਸਿੱਖਾਂ ਨੂੰ ਅਚਾਨਕ ਕਾਹਨੂੰਵਾਨ ਵਿਖੇ ਘੇਰ ਲਿਆ । ਸਿੱਖ ਉੱਥੋਂ ਬਚ ਕੇ ਬਸੌਲੀ ਦੀਆਂ ਪਹਾੜੀਆਂ ਵੱਲ ਚਲੇ ਗਏ । ਮੁਗ਼ਲ ਸੈਨਿਕਾਂ ਨੇ ਉਨ੍ਹਾਂ ਦਾ ਬੜੀ ਤੇਜ਼ੀ ਨਾਲ ਪਿੱਛਾ ਕੀਤਾ । ਇੱਥੇ ਸਿੱਖ ਬੜੀ ਮੁਸ਼ਕਿਲ ਵਿੱਚ ਫਸ ਗਏ । ਇੱਕ ਪਾਸੇ ਉੱਚੀਆਂ ਪਹਾੜੀਆਂ ਸਨ ਅਤੇ ਦੂਜੇ ਪਾਸੇ ਦਰਿਆ ਰਾਵੀ ਵਿੱਚ ਬੜਾ ਹੜ੍ਹ ਆਇਆ ਹੋਇਆ ਸੀ । ਪਿਛਲੇ ਪਾਸੇ ਮੁਗ਼ਲ ਸੈਨਿਕ ਉਨ੍ਹਾਂ ਦਾ ਪਿੱਛਾ ਕਰ ਰਹੇ ਸਨ ਅਤੇ ਅੱਗੇ ਪਹਾੜੀ ਰਾਜੇ ਅਤੇ ਲੋਕ ਵੀ ਉਨ੍ਹਾਂ ਦੇ ਕੱਟੜ ਦੁਸ਼ਮਣ ਸਨ । ਸਿੱਖਾਂ ਕੋਲ ਰਸਦ ਤਾਂ ਬਿਲਕੁਲ ਹੀ ਨਹੀਂ ਸੀ । ਚਾਰੇ ਦੀ ਘਾਟ ਕਾਰਨ ਘੋੜਿਆਂ ਦਾ ਵੀ ਭੁੱਖ ਨਾਲ ਬੁਰਾ ਹਾਲ ਸੀ । ਇਸ ਹਮਲੇ ਵਿੱਚ 7,000 ਸਿੱਖ ਸ਼ਹੀਦ ਹੋ ਗਏ ਅਤੇ ਮੁਗ਼ਲਾਂ ਨੇ 3,000 ਸਿੱਖਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ । ਇਨ੍ਹਾਂ ਸਿੱਖਾਂ ਨੂੰ ਲਾਹੌਰ ਵਿਖੇ ਸ਼ਹੀਦ ਕਰ ਦਿੱਤਾ ਗਿਆ । ਸਿੱਖਾਂ ਦੇ ਇਤਿਹਾਸ ਵਿੱਚ ਇਹ ਪਹਿਲੀ ਵਾਰ ਸੀ ਜਦੋਂ ਸਿੱਖਾਂ ਦਾ ਇਕੋ ਵਾਰੀ ਇੰਨਾ ਭਾਰੀ ਜਾਨੀ ਨੁਕਸਾਨ ਹੋਇਆ ।
1. ਪਹਿਲਾ ਘੱਲੂਘਾਰਾ ਕਦੋਂ ਵਾਪਰਿਆ ?
2. ਪਹਿਲੇ ਘੱਲੂਘਾਰਾ ਸਮੇਂ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਕੌਣ ਸੀ ?
3. ਪਹਿਲੇ ਘੱਲੂਘਾਰੇ ਵਿੱਚ ਕਿੰਨੇ ਸਿੱਖਾਂ ਨੇ ਸ਼ਹੀਦੀ ਪ੍ਰਾਪਤ ਕੀਤੀ ਸੀ ?
4. ਪਹਿਲੇ ਘੱਲੂਘਾਰੇ ਵਿੱਚ ਮੁਗ਼ਲਾਂ ਨੇ …………………. ਸਿੱਖਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ।
5. ਪਹਿਲੇ ਘੱਲੂਘਾਰੇ ਨੂੰ ਹੋਰ ਕਿਸ ਨਾਂ ਨਾਲ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
1. ਪਹਿਲਾ ਘੱਲੂਘਾਰਾ ਮਈ 1746 ਈ. ਵਿੱਚ ਵਾਪਰਿਆ ।
2. ਪਹਿਲੇ ਘੱਲੂਘਾਰਾ ਸਮੇਂ ਲਾਹੌਰ ਦਾ ਸੂਬੇਦਾਰ ਯਾਹੀਆਂ ਖਾਂ ਸੀ ।
3. ਪਹਿਲੇ ਘੱਲੂਘਾਰੇ ਵਿੱਚ 7000 ਸਿੱਖਾਂ ਨੇ ਸ਼ਹੀਦੀ ਪ੍ਰਾਪਤ ਕੀਤੀ ਸੀ ।
4. 3,000.
5. ਪਹਿਲੇ ਘੱਲੂਘਾਰੇ ਨੂੰ ਛੋਟਾ ਘੱਲੂਘਾਰਾ ਦੇ ਨਾਂ ਨਾਲ ਵੀ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ ।