Class 6

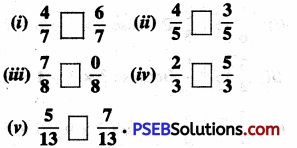
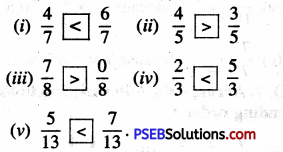
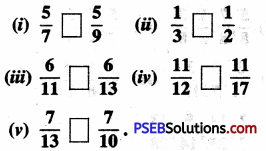
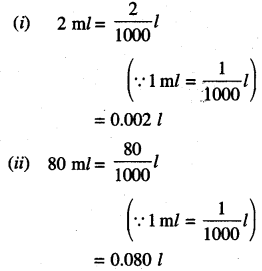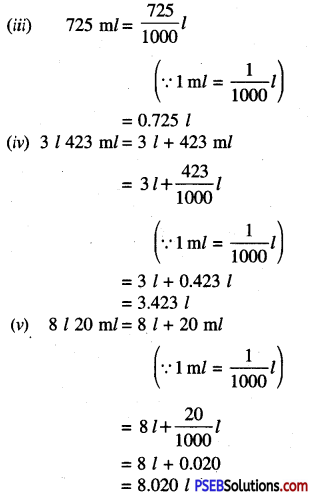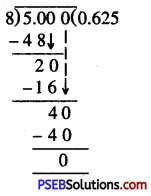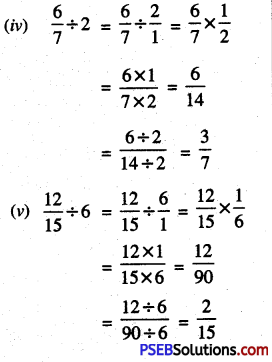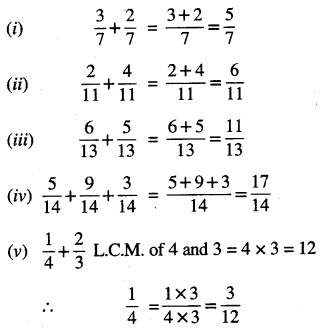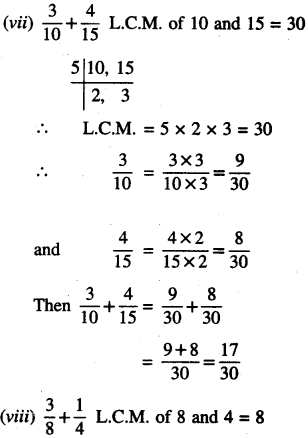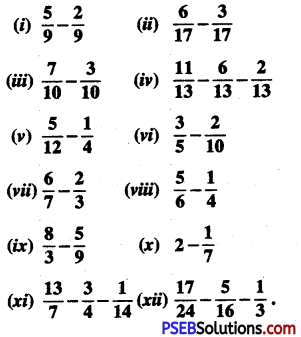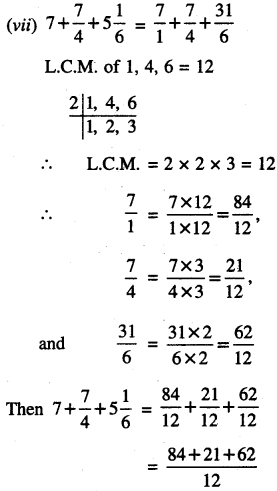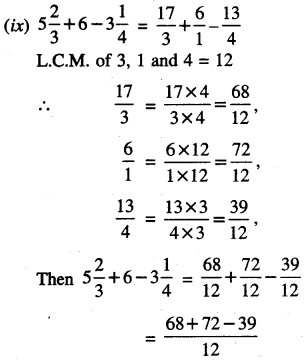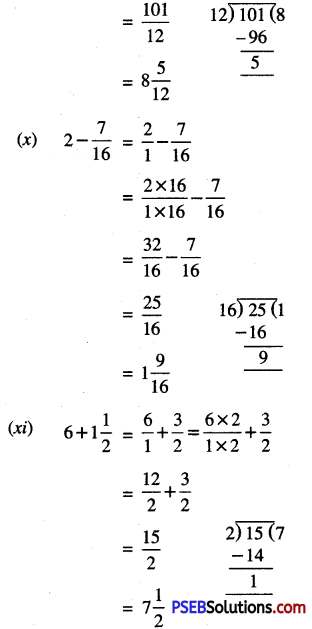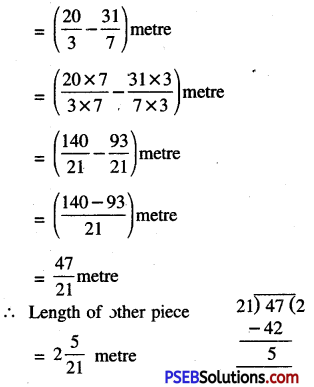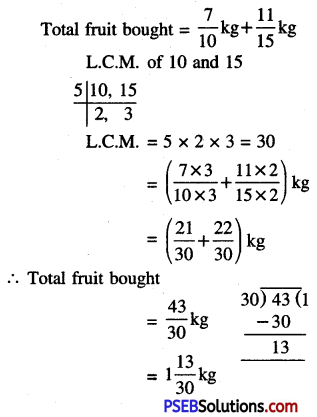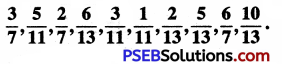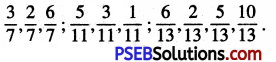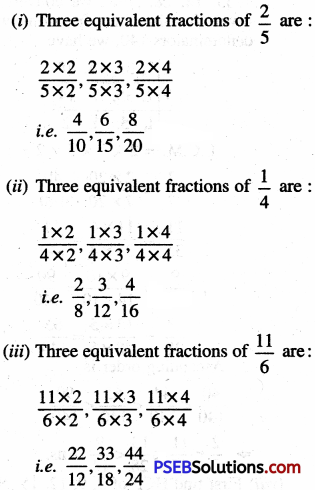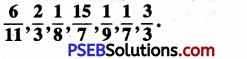Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 6 Decimals Ex 6.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 6 Decimals Ex 6.3

1. Express as rupee using decimals:

Question (i)
35 paise
Solution:
35 paise = ₹ \(\frac {35}{100}\)
= ₹ 0.35
(∵ 1 paise = ₹ \(\frac {1}{100}\))

Question (ii)
4 paise
Solution:
4 paise = ₹ \(\frac {4}{100}\)
= ₹ 0.04
(∵ 1 paise = ₹ \(\frac {1}{100}\))

Question (iii)
240 paise
Solution:
240 paise = ₹ \(\frac {240}{100}\)
= ₹ 2.40
(∵ 1 paise = ₹ \(\frac {1}{100}\))

Question (iv)
12 rupees 25 paise
Solution:
= (12 rupees) + 25 paise
= ₹ 12 + ₹ \(\frac {25}{100}\)
(∵ 1 paise = ₹ \(\frac {1}{100}\))
= ₹ 12 + ₹ 0.25
= ₹ 12.25

Question (v)
24 rupees 5 paise.
Solution:
(24 rupees) + (5 paise)
= ₹ 24 + ₹ \(\frac {5}{100}\)
(∵ 1 paise = ₹ \(\frac {1}{100}\))
= ₹ 24 + ₹ 0.05
= ₹ 24.05

2. Express as metre using decimals

Question (i)
5 cm
Solution:
5 cm = \(\frac {5}{100}\) m
= 0.05 m
(∵ 1cm =\(\frac {1}{100}\)m)

Question (ii)
62 cm
Solution:
62 cm = \(\frac {62}{100}\) m
= 0.62 m
(∵ 1cm =\(\frac {1}{100}\)m)

Question (iii)
135 cm
Solution:
135 cm = \(\frac {135}{100}\) m
= 1.35 m
(∵ 1cm =\(\frac {1}{100}\)m)

Question (iv)
5 m 20 cm
Solution:
= 5 m + 20 cm
(∵ 1cm = \(\frac {1}{100}\)m)
= 5m + 0.20m
= 5.20m

Question (v)
12 m 8 cm
Solution:
= 12 m + 8 cm
= 12 m + \(\frac {8}{100}\)m
(∵ 1cm = \(\frac {1}{100}\)m)
12 cm + 0.08 m
= 12.08 m

3. Express as centimetre using decimals:

Question (i)
2 mm
Solution:
2 mm = \(\frac {2}{10}\) cm
(∵ 1mm = \(\frac {1}{10}\)m)
= 0.2 cm

Question (ii)
28 mm
Solution:
28mm = \(\frac {28}{10}\)cm
(∵ 1mm = \(\frac {1}{10}\)m)

Question (iii)
8 cm 4 mm.
Solution:
8 cm 4 mm = 8 cm + 4 mm
= 8cm + \(\frac {4}{10}\)
= 8 cm + 0.4 cm
= 8.4 cm

4. Express as kilometre using decimals:

Question (i)
7 m
Solution:
= \(\frac {7}{1000}\)
= (∵ 1m = \(\frac {1}{1000}\) km)
= 0.007 km

Question (ii)
50 m
Solution:
= \(\frac {50}{1000}\)
= (∵ 1m = \(\frac {1}{1000}\) km)
= 0.050 km

Question (iii)
425 m
Solution:
= \(\frac {425}{1000}\)
= (∵ 1m = \(\frac {1}{1000}\) km)
= 0.425 km

Question (iv)
2475 m
Solution:
= \(\frac {2475}{1000}\) km
= (∵ 1m = \(\frac {1}{1000}\) km)
= 2.475 km

Question (v)
3 km 225 m.
Solution:
= 3 km + 225 m
= 3 km + \(\frac {225}{1000}\)
= (∵ 1m = \(\frac {1}{1000}\) km)
= 3.225 km

5. Express as kilogram using decimals:

Question (i)
5g
Solution:
5g = \(\frac {5}{1000}\)
= (∵ 1g = \(\frac {1}{1000}\) km)
= 0.005 kg

Question (ii)
75g
Solution:
75g = \(\frac {75}{1000}\)
= (∵ 1g = \(\frac {1}{1000}\) km)
= 0.075 kg

Question (iii)
423 g
Solution:
423 g = \(\frac {423}{1000}\)
= (∵ 1g = \(\frac {1}{1000}\) km)
= 0.423 kg

Question (iv)
1265 g
Solution:
1265 g = \(\frac {1265}{1000}\)
(∵ 1g = \(\frac {1}{1000}\) km)
= 1.265 kg

Question (v)
5 kg 418 g.
Solution:
= 5 kg + 418 g.
= 5 kg + \(\frac {418}{1000}\)
(∵ 1g = \(\frac {1}{1000}\) km)
= 5 kg + 0.418 kg
= 5.418 kg.

6. Express as litre using decimals:

(i) 2 ml
(ii) 80 ml
(iii) 725 ml
(iv) 3l 423 ml
(v) 8l 20 ml.
Solution:

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 6 Decimals Ex 6.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 6 Decimals Ex 6.1

1. Write each of the following in figures:

Question (i)
Seventy-two point one four.
Solution:
Seventy-two point one four = 72.14

Question (ii)
Two hundred fifty-seven point zero eight
Solution:
Two hundred fifty-seven point zero eight = 257.08

Question (iii)
Eight point two five-six.
Solution:
Eight point two five six = 8.256

Question (iv)
Forty-five and twenty-three hundredths.
Solution:
Forty five and twenty three hundredths
= 45 + \(\frac {23}{100}\)
= 45.23

Question (v)
Six hundred twenty-one and two hundred fifty-three thousandths
Solution:
Six hundred twenty-one and two hundred fifty-three thousandths
= 621 + \(\frac {253}{1000}\)
= 621.253

Question (vi)
Twelve and eight thousandths.
Solution:
Twelve and eight thousandths
= 12 + \(\frac {8}{1000}\)
= 12.008

2. Write the following decimal numbers in words:

Question (i)
12.52
Solution:
12.52 = Twelve point five two or twelve and fifty-two hundredths.

Question (ii)
7.148
Solution:
7.148 = Seven point one four eight or seven and one hundred forty-eight thousandths.

Question (iii)
0.24
Solution:
0.24 = Zero Point two four or twenty-four hundredths.

Question (iv)
5.018
Solution:
5.018 = Five-point zero one eight or five and eighteen thousandths.

Question (v)
.009.
Solution:
.009 = Point zero zero nine or nine thousandths.

3. Write the following decimals in the place value table:

Question (i)
(i) 21.569
(ii) 0.64
(iii) 3.51
(iv) 14.087
(v) 3.002.
Solution:

Number	Thousands	Hundreds	Tens	Ones	Tenths	Hundredths	Thousandths
1. 21.569	–	–	2	1	5	6	9
2. 0.64	–	–	–	0	6	4	–
3. 3.51	–	–	–	3	5	1	–
4. 14.087	–	–	1	4	0	8	7
5. 3.002	–	–	–	3	0	0	2

4. Write the following as decimals:

Question (i)
40 + \(\frac {2}{10}\)
Solution:
40 + \(\frac {2}{10}\) = 40.2

Question (ii)
700 + 5 + \(\frac {3}{10}\) + \(\frac {4}{100}\)
Solution:
700 + 5 + \(\frac {3}{10}\) + \(\frac {4}{100}\) = 705.34

Question (iii)
100 + \(\frac {5}{100}\) + \(\frac {3}{1000}\)
Solution:
100 + \(\frac {5}{100}\) + \(\frac {3}{1000}\) = 10.053

Question (iv)
100 + \(\frac {7}{10}\) + \(\frac {4}{1000}\)
Solution:
100 + \(\frac {7}{10}\) + \(\frac {4}{1000}\) = 0.704

Question (v)
\(\frac {5}{1000}\)
Solution:
\(\frac {5}{1000}\) = 0.005

5. Write the decimals shown in the following place value table:

Question (i)

Thousands	Hundreds	Tens	Ones	Tenth	Hundredths	Thousandths
–	5	2	4	1	2	–
2	0	3	4	2	1	–
–	–	6	1	0	2	3
–	–	–	4	0	0	1
–	1	0	0	0	3

Solution:
(i) 524.12
(ii) 2034.21
(iii) 61.023
(iv) 4.001
(v) 100.03

6. Expand the following decimals.

Question (i)
2.5
Solution:
2.5 = 2 + 0.5
= 2 + \(\frac {5}{10}\)

Question (ii)
18.43
Solution:
18.43 = 10 + 8 + 0.4 + 0.03
= 10 + 8 + \(\frac {4}{10}\) + \(\frac {3}{100}\)

Question (iii)
4.05
Solution:
4.05 = 4 + 0.05
= 4 + \(\frac {5}{100}\)

Question (iv)
13.123
Solution:
13.123 = 10 + 3 + 0.1 + 0.02 + 0.003
= 10 + 3 + \(\frac {1}{10}\) + \(\frac {2}{100}\) + \(\frac {3}{1000}\)

Question (v)
245.456
Solution:
245.456 = 200 + 40 + 5 + 0.4 + 0.05 + 0.006
= 200 + 40 + 5 + \(\frac {4}{10}\) + \(\frac {5}{100}\) + \(\frac {6}{1000}\)

Question (vi)
20.057
Solution:
20.057 = 20 + 0.05 + 0.007
= 20 + \(\frac {5}{100}\) + \(\frac {7}{1000}\)

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 6 Decimals Ex 6.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 6 Decimals Ex 6.2

1. Convert the following decimal numbers into fractions and reduce it to lowest form.

Question (i)
1.4
Solution:
1.4 = \(\frac{14}{10}=\frac{14 \div 2}{10 \div 2}\)
(H.C.F. of 14 and 10 is 2)
= \(\frac {7}{5}\)

Question (ii)
2.25
Solution:
2.25 = \(\frac{225}{100}=\frac{225 \div 25}{100 \div 25}\)
(H.C.F. of 225 and 100 is 25)
= \(\frac {9}{4}\)

Question (iii)
18.6
Solution:
18.6 = \(\frac{186}{10}=\frac{186 \div 2}{10 \div 2}\)
(H.C.F. of 186 and 10 is 2)
= \(\frac {93}{5}\)

Question (iv)
4.04
Solution:
4.04 = \(\frac{404}{100}=\frac{404 \div 4}{100 \div 4}\)
(H.C.F. of 404 and 100 is 4)
= \(\frac {101}{25}\)

Question (v)
21.6
Solution:
21.6 = \(\frac{216}{10}=\frac{216 \div 2}{10 \div 2}\)
(H.C.F. of 216 and 10 is 2)
= \(\frac {108}{5}\)

2. Convert the following fractions into decimal numbers:

Question (i)
\(\frac {7}{100}\)
Solution:
\(\frac {7}{100}\) = 0.07
(Here denominator is 100)

Question (ii)
\(\frac {12}{10}\)
Solution:
\(\frac {12}{10}\) = 1.2
(Here denominator is 10)

Question (iii)
\(\frac {215}{100}\)
Solution:
\(\frac {215}{100}\) = 2.15
(Here denominator is 100)

Question (iv)
\(\frac {18}{1000}\)
Solution:
\(\frac {18}{1000}\) = 0.018
(Here denominator is 1000)

Question (v)
\(\frac {245}{10}\)
Solution:
\(\frac {245}{10}\) = 24.5
(Here denominator is 10)

3. Convert the following fractions into decimal numbers by equivalent fraction method:

Question (i)
\(\frac {5}{2}\)
Solution:
Here denominator is 2.
Convert into equivalent fraction with denominator 10 by multiplying it by 5.
∴ \(\frac{5}{2}=\frac{5 \times 5}{2 \times 5}=\frac{25}{10}\) = 2.5

Question (ii)
\(\frac {3}{4}\)
Solution:
Here denominator is 4.
Convert into equivalent fraction with denominator 100 by multiplying it by 25.
∴ \(\frac{3}{4}=\frac{3 \times 25}{4 \times 25}=\frac{75}{100}\) = 0.75

Question (iii)
\(\frac {28}{5}\)
Solution:
Here denominator is 5.
Convert into equivalent fraction with denominator 10 by multiplying it by 2.
∴ \(\frac{28}{5}=\frac{28 \times 2}{5 \times 2}=\frac{56}{10}\) = 5.6

Question (iv)
\(\frac {135}{20}\)
Solution:
Here denominator is 20.
Convert into equivalent fraction with denominator 100 by multiplying it by 5.
∴ \(\frac{135}{20}=\frac{135 \times 5}{20 \times 5}=\frac{675}{100}\)
= 6.75

Question (v)
\(\frac {17}{4}\)
Here denominator is 4.
Convert into equivalent fraction with denominator 100 by multiplying it by 25.
∴ \(\frac{17}{4}=\frac{17 \times 25}{4 \times 25}=\frac{425}{100}\)
= 4.25

4. Convert the following fractions into decimals by long division method:

Question (i)
\(\frac {17}{2}\)
Solution:

= 8.5

Question (ii)
\(\frac {33}{4}\)
Solution:

= 8.25

Question (iii)
\(\frac {76}{5}\)
Solution:

= 15.2

Question (iv)
\(\frac {24}{25}\)
Solution:

= 0.96

Question (v)
\(\frac {5}{8}\)
Solution:

= 0.625

5. Represent the following decimals on number line:

Question (i)
(i) 0.7
(ii) 1.6
(iii) 3.7
(iv) 6.3
(v) 5.4
Solution:

6. Write three decimal numbers between:

Question (i)
1.2 and 1.6
Solution:
Three decimal numbers between 1.2 and 1.6 are:
1.3, 1.4, 1.5

Question (ii)
2.8 and 3.2
Solution:
Three decimal numbers between 2.8 and 3.2 are:
2.9, 3, 3.1

Question (iii)
5 and 5.5.
Solution:
Three decimal numbers between 5 and 5.5 are:
5.1, 5.2, 5.3, 5.4.

7. Which number is greater:

Question (i)
0.4 or 0.7
Solution:

Since, 7 > 4
So, 0.7 > 0.4

Question (ii)
2.6 or 2.5
Solution:

Since, 6 > 5
So, 2.6 > 2.5

Question (iii)
1.23 or 1.32
Solution:

Since, 3 > 2
So, 1.32 > 1.23

Question (iv)
12.3 or 12.4
Solution:

Since, 4 > 3
So, 12.4 > 12.3

Question (v)
18.35 or 18.3
Solution:

Since, 5 > 0
So, 18.35 > 18.30

Question (vi)
12 or 1.2
Solution:

Since, 12 > 1
So, 12 > 1.2

Question (vii)
5.06 or 5.061
Solution:

Since, 1 > 0
So, 5.061 > 5.060

Question (viii)
2.34 or 23.3
Solution:

Since, 23 > 2
So, 23.3 > 2.34

Question (ix)
13.08 or 13.078
Solution:

Since, 8 > 7
So, 13.08 > 13.078

Question (x)
2.3 or 2.03.
Solution:

Since, 3 > 0
So, 2.3 > 2.03

8. Arrange the decimal numbers in ascending order:

Question (i)
2.5, 2, 1.8, 1.9
Solution:
Ascending order is :
1.8, 1.9, 2, 2.5

Question (ii)
3.4, 4.3, 3.1, 1.3
Solution:
Ascending order is :
1.3, 3.1, 3.4, 4.3

Question (iii)
1.24, 1.2, 1.42, 1.8.
Solution:
Ascending order is :
1.2, 1.24, 1.42, 1.8.

9. Arrange the decimal numbers in descending order:

Question (i)
4.1, 4.01, 4.12, 4.2
Solution:
Descending order is :
4.2, 4.12, 4.1, 4.01

Question (ii)
1.3, 1.03, 1.003, 13
Solution:
Descending order is :
13, 1.3, 1.03, 1.003

Question (iii)
8.02, 8.2, 8.1, 8.002.
Solution:
Descending order is :
8.2, 8.1, 8.02, 8.002.

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 9 Understanding Elementary Shapes Ex 9.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 9 Understanding Elementary Shapes Ex 9.5

1. Which of the following are polygons and there is no polygon. Give the reason:

Solution:
(i) It is not a closed figure. Therefore it is not a polygon.
(ii) It is made up of lines segment. Therefore it is polygon.
(iii) It is not a polygon, because it is not made of line segments.
(iv) It is not closed by line segment. Therefore, it is not a polygon.
(v) It is not polygon because line segments are intersecting each other.
(vi) It is made up of line segments, therefore it is a polygon.

2. Classify the following as concave or convex polygons:

Solution:
(i) Concave Polygon
(ii) Convex Polygon
(iii) Concave Polygon
(iv) Concave Polygon
(v) Convex Polygon
(vi) Convex Polygon.

3. Tick in the boxes, if the property holds true for a particular quadrilateral otherwise eroes out ‘x’:

Quadrilateral Properties	Rectangle	Parallelogram	Rhombus	Trapezium	Square
All sides are equal
Only opposite sides are equal
Diagonals are equal
Diagonals bisect each other
Diagonals are perpendicular to each other
Each angle is 90°

Solution:

Quadrilateral Properties	Rectangle	Parallelogram	Rhombus	Trapezium	Square
All sides are equal	×	×	√	×	√
Only opposite sides are equal	√	√	×	×	×
Diagonals are equal	√	×	×	×	√
Diagonals bisect each other	√	√	√	×	√
Diagonals are perpendicular to each other	×	×	√	×	√
Each angle is 90°	√	×	X	×	√

4. Fill in the blanks:

Question (i)
…………… is a quadrilateral with only one pair of opposite sides parallel.
Solution:
Trapezium

Question (ii)
…………….. is a quadrilateral with all sides equal and diagonals of equal length.
Solution:
Square

Question (iii)
A polygon with atleast one angle is reflex is called ……………….. .
Solution:
Concave polygon

Question (iv)
………….. is a regular quadrilateral.
Solution:
Square

Question (v)
…………… is a quadrilateral with opposite sides equal and diagonals of unequal length.
Solution:
Parallelogram.

5. State True or False:

Question (i)
A rectangle is always a rhombus.
Solution:
False

Question (ii)
The diagonals of a rectangle are perpendicular to each other.
Solution:
False

Question (iii)
A square is a parallelogram.
Solution:
True

Question (iv)
A trapezium is a parallelogram.
Solution:
False

Question (v)
Opposite sides of a parallelogram are parallel.
Solution:
True.

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 9 Understanding Elementary Shapes Ex 9.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 9 Understanding Elementary Shapes Ex 9.4

1. Classify each of the following triangles as scalene, isosceles or equilateral:

Solution:
(i) Here, two sides of triangle are equal in length.
∴ It is an isosceles triangle.
(ii) Here, all the three sides of the triangle are equal in length.
∴ It is an equilateral triangle.
(iii) Here, no two sides are equal in length.
∴ It is scalene triangle.
(iv) Here, two sides of triangle are equal in length.
∴ It is an isosceles triangle.
(v) Here, no two sides are equal in length.
∴ It is scalene triangle.
(vi) Here, all the three sides of the triangle are equal in length.
∴ It is equilateral triangle.

2. Classify each of the following triangles as acute, obtuse or right triangle:

Solution:
(i) Here, one angle is 120°, which is obtuse angle.
∴ It is an obtuse-angled triangle.
(ii) Here, one angle is 90°, which is right angle.
∴ It is an right-angled triangle.
(iii) Here, each angle is acute angle.
∴ It is an acute-angled triangle.
(iv) Here, one angle is 90°, which is right angle.
∴ It is an right-angled triangle.
(v) Here, one angle is 120°, which is obtuse angle.
∴ It is an obtuse-angled triangle.
(vi) Here, each angle is 60°, which is actute angle.
∴ It is an actute angled triangle.

3. Which of the following triangles are possible with the given angles?

Question (i)
60°, 60°, 60°
Solution:
In a triangle sum of the three angles of a triangle is equal to 180°.
Here, sum of the three angles of triangle is:
60° + 60° + 60° = 180°
∴ This triangle is possible.

Question (ii)
110°, 50°, 30°
Solution:
Here, sum of the three angles of triangle is:
110° + 50° + 30°= 190° ≠ 180°
∴ This triangle is not possible.

Question (iii)
65°, 55°, 60°
Solution:
Here, sum of the three angles of triangle is:
65°+ 55°+ 60°= 180°
∴ This triangle is possible.

Question (iv)
90°, 40°, 50°
Solution:
Here, sum of the three angles of triangle is:
90°+ 40°+ 50°= 180°
∴ This triangle is possible.

Question (v)
48°, 62°, 50°
Solution:
Here, sum of the three angles of triangle is:
48°+ 62°+ 50°= 160° ≠ 180°
∴ This triangle is not possible.

Question (vi)
90°, 95°, 30°.
Solution:
Here, sum of the three angles of triangle is:
90°+ 95°+ 30° =215° ≠ 180°
∴ This triangle is not possible.

4. Classify each of the following triangles as scalene, isosceles or equilateral triangle:

Question (i)
4 cm, 5 cm, 6 cm
Solution:
The sides of triangle are 4 cm, 5 cm, 6 cm
No, two sides of this triangle are equal.
∴ This is a scalene triangle.

Question (ii)
5 cm, 7 cm, 5 cm
Solution:
The sides of triangle are 5 cm, 7 cm, 5 cm
Here, two sides are equal each of 5 cm in length.
∴ This is an isosceles triangle.

Question (iii)
4.2 m, S3 m, 6.1 m
Solution:
The sides of triangle are 4.2 m, 5.3 m, 6.1 m
Here, all sides are of different length.
∴ This is a scalene triangle.

Question (iv)
3.5 cm, 3.5 cm, 33 cm
Solution:
The sides of triangle are 3.5 cm, 3.5 cm, 3.5 cm
All the sides of triangle are of equal length.
∴ This is an equilateal triangle.

Question (v)
8 cm, 4.2 cm, 4.2 cm
Solution:
The sides of triangle are 8 cm, 4.2 cm, 4.2 cm
Here, two sides of the triangle are of equal length.
∴ This is an isosceles triangle.

Question (vi)
2 cm, 3 cm, 4 cm.
Solution:
The sides of triangle are 2 cm, 3 cm, 4 cm
All the sides of the triangle are of different lengths
∴ This is a scalene triangle.

5. Name the following triangles in both ways: (Based on sides and angles)

Solution:
(i) Based on sides: In this triangle, no two sides of the triangle are equal.
∴ This is a scalene triangle.
Based on angles: All the three angles of the triangle are acute.
∴ This is an acute-angled triangle.

(ii) Based on sides: In this triangle, two sides are of equal length each is 4 cm.
∴ This is an isosceles triangle.
Based on angles: In this triangle, one angle is of 90° which is a right angle.
∴ This is a right-angled triangle.

(iii) Based on sides: In this triangle, two sides are of equal length.
∴ This is an isosceles triangle.
Based on angles: In this triangle one angle is of 110°, which is obtuse angle.
∴ This is an obtuse-angled triangle.

(iv) Based on sides: In this triangle, all the sides are of equal length i.e. each = 4 cm.
∴ This is an equilateral triangle.
Based on angles: In this triangle, all the angles are acute angles.
∴ This is an acute-angled triangle.

(v) Based on sides: In this triangle, all the three sides are of different lengths.
∴ This is a scalene triangle.
Based on angles: In this triangle, one angle is 105°, which is obtuse angle.
∴ This is an obtuse-angled triangle.

6. Fill in the blanks:

Question (i)
A triangle has …………. sides.
Solution:
3

Question (ii)
A triangle has …………. vertices.
Solution:
3

Question (iii)
A triangle has …………. angles.
Solution:
3

Question (iv)
A triangle has …………. parts.
Solution:
6

Question (v)
A triangle whose all sides are different is known as ………………. .
Solution:
Scalene triangle

Question (vi)
A triangle whose all angles are acute is known as ……………….. .
Solution:
Acute angled triangle

Question (vii)
A triangle whose two sides are equal is known as ……………….. .
Solution:
Isosceles triangle

Question (viii)
A triangle whose one angle is obtuse is known as ……………….. .
Solution:
obtuse-angled triangle

Question (ix)
A triangle whose all sides are equal is known as ……………….. .
Solution:
Equilateral triangle

Question (x)
A triangle whose one angle is right angle is known as ……………….. .
Solution:
Right-angled triangle

7. State True or False:

Question (i)
Each equilateral triangle is an isosceles triangle.
Solution:
True

Question (ii)
Each acute-angled triangle is a scalene triangle.
Solution:
False

Question (iii)
Each isosceles triangle is an equilateral triangle.
Solution:
False

Question (iv)
There are two obtuse angles in an obtuse triangle.
Solution:
False

Question (v)
In right triangle, there is only one right angle.
Solution:
True

Question (vi)
Right triangle can never be isosceles.
Solution:
False.

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 5 Fractions MCQ Questions with Answers.

PSEB 6th Class Maths Chapter 5 Fractions MCQ Questions

Multiple Choice Questions

Question 1.
Which of the following does not represent any fraction?

Answer:

Question 2.
Which of the following is a proper fraction?
(a) \(\frac {5}{5}\)
(b) \(\frac {12}{11}\)
(c) \(\frac {7}{9}\)
(d) 7
Answer:
(c) \(\frac {7}{9}\)

Question 3.
Which of the following is an improper fraction?
(a) \(\frac {5}{8}\)
(b) \(2\frac {3}{4}\)
(c) \(\frac {7}{11}\)
(d) \(\frac {15}{16 }\)
Answer:
(b) \(2\frac {3}{4}\)

Question 4.
The fractions having las numerator are called …………. fractions.
(a) Like
(b) Unlike
(c) Unit
(d) Proper.
Answer:
(c) Unit

Question 5.
The fractions having same denominators are called …………. fractions.
(a) Proper
(b) Unit
(c) Improper
(d) Like.
Answer:
(d) Like.

Question 6.
The fraction having different denominators are called ……………. fractions.
(a) Unlike
(b) Like
(c) Improper
(d) Unit.
Answer:
(a) Unlike

Question 7.
Express 8 hours as a fraction of 1 day.
(a) \(\frac {2}{3}\)
(b) \(\frac {1}{3}\)
(c) \(\frac {8}{1}\)
(d) \(\frac {1}{8}\)
Answer:
(b) \(\frac {1}{3}\)

Question 8.
Find : \(\frac {2}{5}\) of ₹ 20.
(a) ₹ 8
(b) ₹ 10
(c) ₹ 12
(d) ₹ 40.
Answer:
(a) ₹ 8

Question 9.
Write \(\frac {19}{4}\) as mixed fraction.
(a) \(3\frac {4}{5}\)
(b) \(4\frac {4}{3}\)
(c) \(4\frac {3}{4}\)
(d) \(5\frac {1}{4}\)
Answer:
(c) \(4\frac {3}{4}\)

Question 10.
\(7\frac {2}{3}\) = ……………….
(a) \(\frac {17}{3}\)
(b) \(\frac {23}{3}\)
(c) \(\frac {13}{3}\)
(d) \(\frac {42}{3}\)
Answer:
(b) \(\frac {23}{3}\)

Question 11.
Which of the following represents an improper fraction?

Answer:

Question 12.
Which of the following is an equivalent of \(\frac {5}{7}\)?
(a) \(\frac {25}{49}\)
(b) \(\frac {20}{35}\)
(c) \(\frac {35}{49}\)
(d) \(\frac {35}{28}\)
Answer:
(c) \(\frac {35}{49}\)

Question 13.

(a) 32
(b) 24
(c) 40
(d) 16
Answer:
(a) 32

Question 14.
Which of the following are in ascending order?
(a) \(\frac{2}{3}, \frac{2}{7}, \frac{2}{5}\)
(b) \(\frac{2}{3}, \frac{2}{5}, \frac{2}{7}\)
(c) \(\frac{2}{7}, \frac{2}{3}, \frac{2}{5}\)
(d) \(\frac{2}{7}, \frac{2}{5}, \frac{2}{3}\)
Answer:
(d) \(\frac{2}{7}, \frac{2}{5}, \frac{2}{3}\)

Question 15.
Which of the following are in descending order?
(a) \(\frac{1}{8}, \frac{1}{3}, \frac{1}{9}\)
(b) \(\frac{1}{3}, \frac{1}{8}, \frac{1}{9}\)
(c) \(\frac{1}{8}, \frac{1}{9}, \frac{1}{3}\)
(d) \(\frac{1}{3}, \frac{1}{9}, \frac{1}{8}\)
Answer:
(b) \(\frac{1}{3}, \frac{1}{8}, \frac{1}{9}\)

Question 16.
\(\frac{4}{6}+\frac{3}{6}\) = …………. .
(a) \(\frac {7}{12}\)
(b) \(\frac {7}{8}\)
(c) \(1\frac {1}{6}\)
(d) \(1\frac {1}{12}\)
Answer:
(c) \(1\frac {1}{6}\)

Question 17.
\(\frac{4}{9}+\frac{5}{9}-\frac{2}{9}\) = ……………. .
(a) \(\frac {7}{9}\)
(b) \(\frac {7}{18}\)
(c) \(\frac {11}{9}\)
(d) \(\frac {5}{9}\)
Answer:
(a) \(\frac {7}{9}\)

Question 18.
\(\frac{2}{3}+\frac{1}{6}\) = ………………
(a) \(\frac {3}{9}\)
(b) \(\frac {5}{6}\)
(c) \(\frac {7}{6}\)
(d) \(\frac {5}{9}\)
Answer:
(b) \(\frac {5}{6}\)

Question 19.
4 – \(\frac {1}{3}\) = …………….
(a) \(4\frac {1}{3}\)
(b) \(3\frac {1}{3}\)
(c) \(4\frac {2}{3}\)
(d) \(3\frac {2}{3}\)
Answer:
(d) \(3\frac {2}{3}\)

Question 20.
Divide \(\frac {1}{6}\) by 2
(a) \(\frac {1}{3}\)
(b) \(\frac {1}{12}\)
(c) \(\frac {1}{18}\)
(d) 12
Answer:
(b) \(\frac {1}{12}\)

Question 21.
Which fraction is represented by point P on the adjoining number line?

(a) \(\frac {4}{5}\)
(b) \(\frac {5}{6}\)
(c) \(\frac {3}{4}\)
(d) \(\frac {3}{5}\)
Answer:
(a) \(\frac {4}{5}\)

Question 22.
Which fraction is represented by point P on the adjoining number line?

(a) \(\frac {1}{2}\)
(b) \(\frac {3}{5}\)
(c) \(\frac {4}{5}\)
(d) \(\frac {2}{5}\)
Answer:
(d) \(\frac {2}{5}\)

Question 23.
Which of the following fractions are in ascending order?
(a) \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}\)
(b) \(\frac{5}{10}, \frac{5}{11}, \frac{5}{12}\)
(c) \(\frac{1}{10}, \frac{1}{100}, \frac{1}{1000}\)
(d) \(\frac{3}{10}, \frac{4}{10}, \frac{7}{10}\)
Answer:
(d) \(\frac{3}{10}, \frac{4}{10}, \frac{7}{10}\)

Question 24.
Which of the following fractions are in descending order?
(a) \(\frac{1}{3}, \frac{1}{4}, \frac{1}{5}\)
(b) \(\frac{4}{11}, \frac{4}{12}, \frac{4}{13}\)
(c) \(\frac{1}{10}, \frac{1}{100}, \frac{1}{1000}\)
(d) \(\frac{7}{10}, \frac{9}{10}, \frac{11}{10}\)
Answer:
(a) \(\frac{1}{3}, \frac{1}{4}, \frac{1}{5}\)

Question 25.
Which of the following fraction is shown in the shaded portion of the figure?

(a) \(\frac {1}{3}\)
(b) \(\frac {2}{4}\)
(c) \(\frac {3}{4}\)
(d) \(\frac {2}{5}\)
Answer:
(b) \(\frac {2}{4}\)

Fill in the blanks:

Question (i)
The fraction shown in the shaded portion of the figure is ……………..,

Answer:
\(\frac {1}{4}\)

Question (ii)
The fraction of the shaded portion shown by the following figure is …………. .

Answer:
\(\frac {1}{8}\)

Question (iii)
The fraction of the shaded portion shown by the given figure is …………… .

Answer:
\(\frac {3}{7}\)

Question (iv)
The upper part of the fraction is called ……………. .
Answer:
numerator

Question (v)
The lower part of the fraction is called ……………. .
Answer:
denominator

Write True/False:

Question (i)
The fraction \(\frac {3}{5}\) is read as three fifth. (True/False)
Answer:
True

Question (ii)
The fraction whose numerator is less than the denominator is called the proper fraction. (True/False)
Answer:
True

Question (iii)
\(\frac {7}{8}\) is an improper fraction. (True/False)
Answer:
False

Question (iv)
Mixed fraction is a combination of a whole number and a proper fraction. (True/False)
Answer:
True

Question (v)
Fraction with the same denominator are called unlike fractions. (True/False)
Answer:
False

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 5 Fractions Ex 5.6 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 5 Fractions Ex 5.6

1. Multiply:

Question (i)
(i) \(\frac {1}{5}\) × 4
(ii) \(\frac {2}{7}\) × 3
(iii) \(\frac {5}{8}\) × 2
(iv) \(\frac {7}{12}\) × 4
(iv) 10 × \(\frac {4}{5}\)
Solution:

2. Divide:

Question (ii)
(i) \(\frac {1}{4}\) ÷ 5
(ii) \(\frac {3}{5}\) ÷ 3
(iii) \(\frac {5}{8}\) ÷ 3
(iv) \(\frac {6}{7}\) ÷ 2
(iv) \(\frac {12}{15}\) ÷ 6.
Solution:

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 5 Fractions Ex 5.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 5 Fractions Ex 5.5

1. Add the following:

Question (i)

Solution:

2. Subtract the following:

Question (i)

Solution:

3. Simplify the following:

Question (i)

Solution:

4. An iron pipe of length \(6 \frac{2}{3}\) metres long was cut into two pieces. One piece is \(4 \frac{3}{7}\) metre long. What is the length of other pieces?
Solution:
Total length of an iron pipe
= \(6 \frac{2}{3}\) m = \(\frac{20}{3}\) metre
Length of one piece
= \(4 \frac{3}{7}\) metre = \(\frac{31}{7}\) metre
∴ Length of other piece

5. Ashok bought \(\frac{7}{10}\)kg of mangoes and Taran \(\frac{11}{15}\)kg of apples. How much fruit did he buy in all?
Solution:

6. Avi did \(\frac{3}{5}\) of his homework on Saturday and \(\frac{1}{10}\) of the same homework on Sunday. How much of the homework did he do over the weekend?
Solution:
Homework he did weekend
\(\frac{3}{5}+\frac{1}{10}=\frac{3 \times 2}{5 \times 2}+\frac{1}{10}=\frac{6}{10}+\frac{1}{10}\)
∴ Home work done in weekend
\(\frac{6+1}{10}=\frac{7}{10}\)

7. Charan spent \(\frac {1}{4}\) of his pocket money on a movie and \(\frac {3}{8}\) on a new pen and \(\frac {1}{8}\) on a pencil. What fraction of his pocket money did he spend?
Solution:
Total money he spent
= \(\frac{1}{4}+\frac{3}{8}+\frac{1}{8}=\frac{1}{4} \times \frac{2}{2}+\frac{3}{8}+\frac{1}{8}\)
= \(\frac{2}{8}+\frac{3}{8}+\frac{1}{8}=\frac{2+3+1}{8}\)
= \(\frac{6}{8}=\frac{3}{4}\)
So, pocket money spent = \(\frac {3}{4}\)

8. Simar lives at a distance of 4 km from the school. Prabhjot lives at a distance of \(\frac {2}{3}\) km less than Simar’s distance from the school. How far does Prabhjot live from the school?
Solution:
Distance of Simar from school = 4 km Distance of Prabhjot from school

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 5 Fractions Ex 5.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 5 Fractions Ex 5.4

1. Find the different set of like fractions:

Solution:

2. Write any three like fractions of:

Question (i)
(i) \(\frac {2}{5}\)
(ii) \(\frac {1}{4}\)
(iii) \(\frac {11}{6}\)
Solution:

3. Encircle unit fractions:

Solution:
\(\frac{1}{8}, \frac{1}{9}, \frac{1}{7}\)

4. Fill in the boxes with >, < or =

Question (i)

Solution:

5. Compare using >, < or =

Question (i)

Solution:

6. Compare using >, < or =

Question (i)

Solution:

7. Arrange the following fractions in ascending order:

Question (i)

Solution:
We know that in fractions having the same denominator the greater the numerator, the greater the value of the fractional numbers. Therefore the given fractions in:
(i) Ascending order is : \(\frac{3}{10}, \frac{5}{10}, \frac{7}{10}\)
(ii) Ascending order is : \(\frac{1}{7}, \frac{4}{7}, \frac{6}{7}\)
(iii) Ascending order is : \(\frac{1}{8}, \frac{3}{8}, \frac{5}{8}, \frac{7}{8}\)
We know that in fractions having the same numerator, the fractions with smaller denominator is greater:
(iv) Ascending order is : \(\frac{5}{9}, \frac{5}{7}, \frac{5}{3}\)
(v) Ascending order is : \(\frac{3}{13}, \frac{3}{11}, \frac{3}{7}\)
(vi) First find L.C.M. of denominators 4, 6, 12. Now, we convert the given fractions into fractions with denominator 12, we have:

(vii) First find L.C.M. of denominators 7, 35, 14, 28. Now, we convert the given fraction into fractions with denominators 140, we have

(viii) First find HCF of 3, 9, 12, 15. Now we convert the given fractions into fractions with denominator 180, we have:

8. Arrange the following fractions in descending order:

Question (i)
\(\frac{5}{9}, \frac{7}{9}, \frac{1}{9}\)
Solution:
If two or more fractions having the same denominator then fraction with greater numerator is greater fraction:
(i) Descending order is : \(\frac{7}{9}, \frac{5}{9}, \frac{1}{9}\)

Question (ii)
\(\frac{3}{11}, \frac{5}{11}, \frac{2}{11}, \frac{7}{11}\)
Solution:
Descending order is : \(\frac{7}{11}, \frac{5}{11}, \frac{3}{11}, \frac{2}{11}\)
If two or more fractions having the same numerator then the fraction with a small denominator is greater.

Question (iii)
\(\frac{2}{7}, \frac{2}{13}, \frac{2}{9}\)
Solution:
Descending order is : \(\frac{2}{7}, \frac{2}{9}, \frac{2}{13}\)

Question (iv)
\(\frac{1}{5}, \frac{1}{3}, \frac{1}{8}, \frac{1}{2}\)
Solution:
Descending order is : \(\frac{1}{2}, \frac{1}{3}, \frac{1}{5}, \frac{1}{8}\)

Question (v)
\(\frac{1}{6}, \frac{5}{12}, \frac{5}{18}, \frac{2}{3}\)
Solution:
First find L.C.M. of denominators 6, 12, 18, 3.
Now, we convert the given fractions into a fraction with denominator 36, we have:

Question (vi)
\(\frac{3}{4}, \frac{9}{20}, \frac{11}{15}, \frac{17}{30}\)
Solution:
First find L.C.M. of denominator 4, 20,15, 30. Now, we convert the given fractions into a fraction with denominator 60, we have:

9. Kasvi covered \(\frac {1}{3}\) of her journey by car, \(\frac {1}{5}\) by rickshaw and \(\frac {2}{15}\) on foot. Find by which means, she covered the major part of her journey.
Solution:
Journey covered by car = \(\frac {1}{3}\)
Journey covered by Rickshaw = \(\frac {1}{5}\)
Journey covered on foot = \(\frac {2}{15}\)

We observe that \(\frac {5}{15}\) i.e. \(\frac {1}{3}\) is the greatest.
Hence the major part of journey was covered by car.

10. Father distributed his property among his three sons. The eldest one got \(\frac {3}{10}\), the middle got \(\frac {1}{6}\) and the youngest got \(\frac {1}{5}\) part of the property. State how the property was distributed in ascending order.
Solution:
Property eldest son got = \(\frac {3}{10}\) part
Property middle son got = \(\frac {1}{6}\) part
and Property youngest son got = \(\frac {1}{5}\) part

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 4 Integers MCQ Questions with Answers.

PSEB 6th Class Maths Chapter 4 Integers MCQ Questions

Multiple Choice Questions

Question 1.
How many integers are between -3 to 3?
(a) 5
(b) 6
(c) 4
(d) 3.
Answer:
(a) 5

Question 2.
Which of the following integer is greater than -3?
(a) -5
(b) -4
(c) 0
(d) -10.
Answer:
(c) 0

Question 3.
Which of the following integers are in ascending order?
(a) -5, -9, -7, -8
(b) -9, -8, -7, -5
(c) -5, -7, -8, -8, -9
(d) -8, -5, -9, -7.
Answer:
(b) -9, -8, -7, -5

Question 4.
Which of the following integers are in descending order?
(a) 3, 0, -2, -5
(b) -5, -2, 0, 3
(c) -5, 3,-2, 0
(d) -2, 0, -5, 3.
Answer:
(a) 3, 0, -2, -5

Question 5.
The given number line represents:

(a) 5 + 1
(b) 1 + 5
(c) 1 + 1 + 1 + 1 + 1
(d) 5 + 5 + 5 + 5 + 5.
Answer:
(c) 1 + 1 + 1 + 1 + 1

Question 6.
3 less than -2 =
(a) -5
(b) -6
(c) 5
(d) 6.
Answer:
(a) -5

Question 7.
(-2) + 8 =
(a) -6
(b) -10
(c) 10
(d) 6.
Answer:
(d) 6.

Question 8.
Which of the following statements is true about the given number line:

(a) Value of A is greater than value of B.
(b) Value of A is greater than value of C.
(c) Value of B is less than value of C.
(d) Value of C is less than value of B.
Answer:
(c) Value of B is less than value of C.

Question 9.
(-7) + (-12) + 11 =
(a) -19
(b) 30
(c) -23
(d) -8.
Answer:
(d) -8.

Question 10.
15 – (-12) + (-27) =
(a) 0
(b) -54
(c) -24
(d) 54.
Answers :
(a) 0

Question 11.
What is the number of integers between -4 and -1?
(a) 3
(b) 4
(c) 5
(d) 6.
Answer:
(b) 4

Question 12.
What is the number of integers between -8 and -2?
(a) 3
(b) 4
(c) 5
(d) 6.
Answer:
(c) 5

Question 13.
Which is the largest integers among -7, -6, -5, -4 and -3?
(a) -6
(b) -5
(c) -4
(d) -3.
Answer:
(d) -3.

Question 14.
Which is the smallest integer among -3, -2, 0 and 1?
(a) -3
(b) -2
(c) 0
(d) 1.
Answer:
(a) -3

Question 15.
The value of (-7) + (-9) + 4 + 16 is:
(a) 36
(b) 22
(c) 4
(d) 27.
Answer:
(c) 4

Fill in the blanks:

Question (i)
The sum of (-9) + (+4) + (-6) + (+3) is …………. .
Answer:
– 8

Question (ii)
The successor of -5 is ……………. .
Answer:
– 4

Question (iii)
-19 + …………. = 0.
Answer:
19

Question (iv)
100 + …………. = 0.
Answer:
– 100

Question (v)
50 + (-50) = ……………. .
Answer:
0

Write True/False:

Question (i)
-8 is to the right of -10 on number line. (True/False)
Answer:
True

Question (ii)
-100 is to the right of -50 on number line. (True/False)
Answer:
False

Question (iii)
Smallest negative integer is -1. (True/False)
Answer:
False

Question (iv)
-26 is larger than -25. (True/False)
Answer:
False

Question (v)
The sum of two integers is always an integer. (True/False)
Answer:
True