Punjab State Board PSEB 7th Class Agriculture Book Solutions Chapter 6 ਫਸਲਾਂ ਦੇ ਕੀੜੇ ਅਤੇ ਬੀਮਾਰੀਆਂ Textbook Exercise Questions, and Answers.
PSEB Solutions for Class 7 Agriculture Chapter 6 ਫਸਲਾਂ ਦੇ ਕੀੜੇ ਅਤੇ ਬੀਮਾਰੀਆਂ
Agriculture Guide for Class 7 PSEB ਫਸਲਾਂ ਦੇ ਕੀੜੇ ਅਤੇ ਬੀਮਾਰੀਆਂ Textbook Questions and Answers
ਪਾਠ-ਪੁਸਤਕ ਦੇ ਪ੍ਰਸ਼ਨ :
(ੳ) ਇੱਕ-ਦੋ ਸ਼ਬਦਾਂ ਵਿੱਚ ਉੱਤਰ ਦਿਓ
ਪ੍ਰਸ਼ਨ 1.
ਝੋਨੇ ਦੀ ਫ਼ਸਲ ਦੀ ਕਿਸ ਬੀਮਾਰੀ ਨਾਲ ਬੰਗਾਲ ਵਿੱਚ ਅਕਾਲ ਪਿਆ ?
ਉੱਤਰ-
ਭੂਰੇ ਧੱਬਿਆਂ ਦੀ ਬੀਮਾਰੀ ।
ਪ੍ਰਸ਼ਨ 2.
ਪੰਜਾਬ ਵਿੱਚ ਨਰਮੇ ਦੀ ਫ਼ਸਲ ਦਾ 1996-2002 ਤੱਕ ਕਿਸ ਕੀੜੇ ਨੇ ਸਭ ਤੋਂ ਵੱਧ ਨੁਕਸਾਨ ਕੀਤਾ ?
ਉੱਤਰ-
ਅਮਰੀਕਨ ਸੁੰਡੀ ।
ਪ੍ਰਸ਼ਨ 3.
ਉਨ੍ਹਾਂ ਫ਼ਸਲਾਂ ਨੂੰ ਕੀ ਕਹਿੰਦੇ ਹਨ, ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਕਿਸੇ ਹੋਰ ਜੀਵ-ਜੰਤੂ ਦੇ ਜੀਨ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਟਰਾਂਸਜੀਨਕ ।
ਪ੍ਰਸ਼ਨ 4.
ਕੀ ਰਸਾਇਣਿਕ ਦਵਾਈਆਂ ਮਨੁੱਖ ਲਈ ਹਾਨੀਕਾਰਕ ਹਨ ?
ਉੱਤਰ-
ਰਸਾਇਣਿਕ ਦਵਾਈਆਂ ਮਨੁੱਖਾਂ ਲਈ ਹਾਨੀਕਾਰਕ ਹਨ ਕਿਉਂਕਿ ਇਹ ਜ਼ਹਿਰ ਹੁੰਦੀ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 5.
ਕਿਸੇ ਇਕ ਫ਼ਸਲ ਦੇ ਜੀਵਾਣੂ ਰੋਗ ਦਾ ਨਾਮ ਦੱਸੋ ।
ਉੱਤਰ-
ਤਣੇ ਦਾ ਗਲਣਾ ।
ਪ੍ਰਸ਼ਨ 6.
ਕਿਸੇ ਇਕ ਫ਼ਸਲ ਦੇ ਵਿਸ਼ਾਣੂ ਰੋਗ ਦਾ ਨਾਮ ਦੱਸੋ ।
ਉੱਤਰ-
ਨੂਠੀ ਰੋਗ ।
ਪ੍ਰਸ਼ਨ 7.
ਕੋਈ ਦੋ ਰਸ ਚੂਸਣ ਵਾਲੇ ਕੀੜਿਆਂ ਦੇ ਨਾਮ ਦੱਸੋ ।
ਉੱਤਰ-
ਤੇਲਾ, ਚੇਪਾ ।
ਪ੍ਰਸ਼ਨ 8.
ਕੋਈ ਦੋ ਫ਼ਲਾਂ ਅਤੇ ਤਣਾ ਛੇਦਕ ਕੀੜਿਆਂ ਦਾ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਕਮਾਦ ਦਾ ਗੜੂਆਂ, ਚਿੱਤਕਬਰੀ ਸੁੰਡੀ, ਬੈਂਗਣਾਂ ਦੀ ਸੁੰਡੀ, ਮੱਕੀ ਦੀ ਸ਼ਾਖ ਦੀ ਮੱਖੀ ।
ਪ੍ਰਸ਼ਨ 9.
ਪੌਦਿਆਂ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਦਾ ਫੈਲਾਉ ਕਿਵੇਂ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਬੀਮਾਰੀ ਵਾਲੇ ਬੀਜਾਂ, ਬੀਮਾਰੀ ਵਾਲੇ ਖੇਤਾਂ, ਮੀਂਹ ਅਤੇ ਤੇਜ਼ ਹਵਾ ਕਾਰਨ ।
ਪ੍ਰਸ਼ਨ 10.
ਕੀ ਇੱਕ ਕੀੜਾ ਕਈ ਫ਼ਸਲਾਂ ਤੇ ਨੁਕਸਾਨ ਕਰ ਸਕਦਾ ਹੈ ? ਉਦਾਹਰਨ ਦਿਉ ।
ਉੱਤਰ-
ਹਾਂ, ਕਰ ਸਕਦਾ ਹੈ; ਜਿਵੇਂ ਤੇਲਾ, ਨਰਮਾ, ਮੱਕੀ, ਝੋਨਾ ਆਦਿ ਨੂੰ ਨੁਕਸਾਨ ਕਰਦਾ ਹੈ ।
(ਅ) ਇਕ-ਦੋ ਵਾਕਾਂ ਵਿੱਚ ਉੱਤਰ ਦਿਓ
ਪ੍ਰਸ਼ਨ 1.
ਪੌਦ ਸੁਰੱਖਿਆ ਦੇ ਕਿਹੜੇ-ਕਿਹੜੇ ਢੰਗ ਹਨ ?
ਉੱਤਰ-
ਪੌਦ ਸੁਰੱਖਿਆ ਦੇ ਢੰਗ ਹਨ-ਰਸਾਇਣਿਕ ਦਵਾਈਆਂ, ਰੋਗ ਸਹਿਣ ਕਰਨ ਫ਼ਸਲਾਂ ਦੇ ਕੀੜੇ ਅਤੇ ਬਿਮਾਰੀਆਂ ਵਾਲੀਆਂ ਕਿਸਮਾਂ, ਮਿੱਤਰ ਕੀੜਿਆਂ ਦੀ ਵਰਤੋਂ, ਫ਼ਸਲ ਕਾਸ਼ਤ ਸੰਬੰਧੀ ਸੁਚੱਜੇ ਤਰੀਕੇ ਜਿਵੇਂ ਬੀਜਾਈ ਦਾ ਸਮਾਂ, ਸਿੰਚਾਈ ਅਤੇ ਖਾਦ ਪ੍ਰਬੰਧ ਅਤੇ ਕਈ ਮਕੈਨੀਕਲ ਤਰੀਕੇ ।
ਪ੍ਰਸ਼ਨ 2.
ਟਰਾਂਸਜੀਨਕ ਵਿਧੀ ਕੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਪੌਦ ਸੁਰੱਖਿਆ ਦਾ ਸਭ ਤੋਂ ਆਧੁਨਿਕ ਢੰਗ ਹੈ । ਇਸ ਵਿਧੀ ਵਿੱਚ ਕਿਸੇ ਵੀ ਜੀਵ-ਜੰਤੂ ਤੋਂ ਲੋੜੀਂਦੇ ਜੀਨ ਫ਼ਸਲਾਂ ਵਿੱਚ ਪਾ ਕੇ ਪੌਦ ਸੁਰੱਖਿਆ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 3.
ਪੌਦ ਸੁਰੱਖਿਆ ਦੇ ਫੇਲ੍ਹ ਹੋਣ ਨਾਲ ਕਿਹੋ ਜਿਹੀ ਸਥਿਤੀ ਪੈਦਾ ਹੋ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਪੌਦ ਸੁਰੱਖਿਆ ਦੇ ਫੇਲ੍ਹ ਹੋਣ ਨਾਲ ਕਾਲ ਵਰਗੀ ਸਥਿਤੀ ਪੈਦਾ ਹੋ ਜਾਂਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 4.
ਵੱਖ-ਵੱਖ ਫ਼ਸਲਾਂ ਦੇ ਰਸ ਚੂਸਣ ਵਾਲੇ ਕੀੜੇ ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ:
| ਲੜੀ ਨੰ: | ਰਸ ਚੂਸਣ ਵਾਲਾ ਕੀੜਾ | ਫ਼ਸਲ ਦਾ ਨਾਂ |
| 1. | ਤੇਲਾ | ਨਰਮਾ, ਭਿੰਡੀ, ਅੰਬ ਆਦਿ |
| 2. | ਚੇਪਾ | ਤੇਲ ਬੀਜ, ਕਣਕ, ਆੜੂ ਆਦਿ |
| 3. | ਚਿੱਟੀ ਮੱਖੀ | ਨਰਮਾ, ਟਮਾਟਰ, ਪਪੀਤਾ ਆਦਿ |
| 4. | ਮਿੱਲੀ ਬੱਗ | ਨਰਮਾ, ਅੰਬ, ਨਿੰਬੂ ਜਾਤੀ ਦੇ ਫ਼ਲ ਆਦਿ । |
ਪ੍ਰਸ਼ਨ 5.
ਵਿਸ਼ਾਣੂ ਰੋਗ ਦਾ ਫੈਲਾਓ ਕਿਵੇਂ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਸ ਦੀ ਕੀ ਰੋਕਥਾਮ ਹੈ ?
ਉੱਤਰ-
ਪੌਦਿਆਂ ਵਿੱਚ ਕੀੜਿਆਂ-ਮਕੌੜਿਆਂ ਦੁਆਰਾ ਵਿਸ਼ਾਣੂ ਰੋਗ ਫੈਲਦਾ ਹੈ ਇਹਨਾਂ ਦੀ ਅਸਰਦਾਰ ਰੋਕਥਾਮ ਬਹੁਤ ਮੁਸ਼ਕਿਲ ਹੁੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 6.
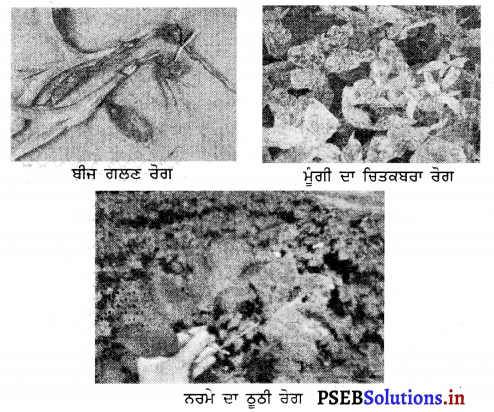
ਉੱਲੀ ਨਾਲ ਹੋਣ ਵਾਲੀਆਂ ਫ਼ਸਲਾਂ ਦੀਆਂ ਮੁੱਖ ਬੀਮਾਰੀਆਂ ਕਿਹੜੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਉੱਲੀ ਨਾਲ ਹੋਣ ਵਾਲੀਆਂ ਬੀਮਾਰੀਆਂ ਹਨ-ਝੁਲਸ ਰੋਗ, ਬੀਜ ਗਲਣ ਰੋਗ, ਕਾਂਗਿਆਰੀ, ਚਿੱਟੇ ਰੋਗ ॥
ਪ੍ਰਸ਼ਨ 7.
ਕੀੜੇ ਮਕੌੜਿਆਂ ਦੀਆਂ ਕਿਹੜੀਆਂ ਮੁੱਖ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਹਨ ਜਿਨ੍ਹਾਂ ਕਰਕੇ ਉਹ ਧਰਤੀ ਉੱਪਰ ਵਧੇਰੇ ਗਿਣਤੀ ਵਿੱਚ ਮੌਜੂਦ ਹਨ ?
ਉੱਤਰ-
ਸਰੀਰਕ ਬਣਤਰ, ਵਧਣ-ਫੁੱਲਣ ਦਾ ਢੰਗ, ਵੱਖੋ-ਵੱਖਰੇ ਭੋਜਨ ਪਦਾਰਥਾਂ ਨੂੰ ਖਾਣ ਦੀ ਸਮਰੱਥਾ, ਫੁਰਤੀਲਾਪਨ ਆਦਿ ਅਜਿਹੇ ਗੁਣ ਹਨ ।
ਪ੍ਰਸ਼ਨ 8.
ਤਣਾ ਛੇਦਕ ਅਤੇ ਫ਼ਲ ਛੇਦਕ ਕੀੜੇ ਫ਼ਸਲ ਦਾ ਕਿਵੇਂ ਨੁਕਸਾਨ ਕਰਦੇ ਹਨ ?
ਉੱਤਰ-
ਇਹ ਕੀੜੇ ਪੌਦੇ ਦੇ ਵੱਖ-ਵੱਖ ਹਿੱਸਿਆਂ ਦੇ ਅੰਦਰ ਵੜ ਕੇ ਨੁਕਸਾਨ ਕਰਦੇ ਹਨ, ਜਿਵੇਂ-ਤਣੇ ਵਿੱਚ ਛੇਕ ਕਰਦੇ ਹਨ, ਸਬਜ਼ੀਆਂ ਤੇ ਫ਼ਲਾਂ ਦੇ ਅੰਦਰ ਵੜ ਜਾਂਦੇ ਹਨ।
![]()
ਪ੍ਰਸ਼ਨ 9.
ਪੱਤਿਆਂ ਤੇ ਖਾਣ ਵਾਲੇ ਕੀੜੇ ਫ਼ਸਲ ਦਾ ਕਿਵੇਂ ਨੁਕਸਾਨ ਕਰਦੇ ਹਨ ?
ਉੱਤਰ-
ਇਹ ਕੀੜੇ ਪੱਤਿਆਂ ਨੂੰ ਖਾ ਕੇ ਪੌਦੇ ਦੀ ਪ੍ਰਕਾਸ਼ ਸੰਸ਼ਲੇਸ਼ਣ ਦੀ ਸਮਰੱਥਾ ਨੂੰ ਘੱਟ ਕਰ ਦਿੰਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 10.
ਰਸਾਇਣਿਕ ਦਵਾਈਆਂ ਦੀ ਵਰਤੋਂ ਲਈ ਕਿਹੜੀਆਂ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਰੱਖਣਾ ਜ਼ਰੂਰੀ ਹੈ ?
ਉੱਤਰ-
ਰਸਾਇਣਿਕ ਦਵਾਈਆਂ ਨੂੰ ਬੱਚਿਆਂ ਦੀ ਪਹੁੰਚ ਤੋਂ ਦੂਰ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ, ਵਰਤੋਂ ਸਮੇਂ ਪੂਰੀ ਸਾਵਧਾਨੀ ਵਰਤਣੀ ਚਾਹੀਦੀ ਹੈ, ਜੇ ਇਹਨਾਂ ਦੀ ਜ਼ਹਿਰ ਚੜ੍ਹ ਜਾਵੇ ਤਾਂ ਤੁਰੰਤ ਡਾਕਟਰ ਨੂੰ ਬੁਲਾ ਲੈਣਾ ਚਾਹੀਦਾ ਹੈ ।
(ੲ) ਪੰਜ-ਛੇ ਵਾਕਾਂ ਵਿੱਚ ਉੱਤਰ ਦਿਉ –
ਪ੍ਰਸ਼ਨ 1.
ਹਾਨੀਕਾਰਕ ਕੀੜੇ ਫ਼ਸਲਾਂ ਨੂੰ ਕਿਹੜੇ-ਕਿਹੜੇ ਢੰਗ ਨਾਲ ਨੁਕਸਾਨ ਪਹੁੰਚਾਉਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਹਾਨੀਕਾਰਕ ਕੀੜੇ ਫ਼ਸਲਾਂ ਨੂੰ ਵੱਖ-ਵੱਖ ਢੰਗਾਂ ਨਾਲ ਨੁਕਸਾਨ ਪਹੁੰਚਾਉਂਦੇ ਹਨ –
1. ਕਈ ਕੀੜੇ ਜਿਵੇਂ ਤੇਲਾ, ਚੇਪਾ, ਚਿੱਟੀ ਮੱਖੀ, ਮਿੱਲੀ ਬਗ ਆਦਿ ਪੱਤਿਆਂ ਵਿਚੋਂ ਰਸ ਚੂਸ ਕੇ ਇਹਨਾਂ ਵਿਚੋਂ ਹਰਾ ਮਾਦਾ ਅਤੇ ਖਣਿਜ ਪਦਾਰਥਾਂ ਦੀ ਕਮੀ ਕਰ ਦਿੰਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਪੱਤੇ ਪੀਲੇ ਪੈ ਜਾਂਦੇ ਹਨ ’ਤੇ ਪੌਦੇ ਦਾ ਵਾਧਾ ਰੁੱਕ ਜਾਂਦਾ ਹੈ ।
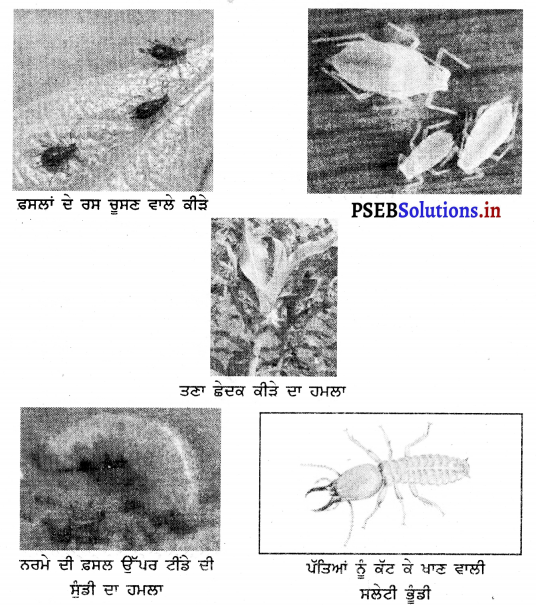
2. ਕੁੱਝ ਕੀੜੇ ਪੌਦਿਆਂ ਦੇ ਫਲਾਂ ਅਤੇ ਤਣਿਆਂ ਆਦਿ ਵਿਚ ਵੜ ਕੇ ਨੁਕਸਾਨ ਕਰਦੇ ਹਨ, ਜਿਵੇਂ ਕਮਾਦ ਦਾ ਗੜੁਆਂ, ਮੱਕੀ ਦੀ ਫ਼ਸਲ ਵਿੱਚ ਸ਼ਾਖ ਦੀ ਮੱਖੀ, ਨਰਮੇ ਦੀ ਅਮਰੀਕਨ ਸੁੰਡੀ ਆਦਿ ।
3. ਕੁੱਝ ਕੀੜੇ ਪੱਤਿਆਂ ਨੂੰ ਖਾ ਕੇ ਪ੍ਰਕਾਸ਼ ਸੰਸ਼ਲੇਸ਼ਣ ਦੀ ਸਮਰੱਥਾ ਘਟਾ ਦਿੰਦੇ ਹਨ । ਇਹ ਜਾਂ ਤਾਂ ਪੱਤਿਆਂ ਨੂੰ ਕਿਨਾਰਿਆਂ ਤੋਂ ਮੁੱਖ ਨਾੜੀ ਵੱਲ ਖਾਂਦੇ ਹਨ ਜਾਂ ਪੱਤਿਆਂ ਦਾ ਹਰਾ ਮਾਦਾ ਖਾ ਜਾਂਦੇ ਹਨ ਤੇ ਪੱਤੇ ਨੂੰ ਛਾਣਨੀ ਵਰਗਾ ਕਰ ਦਿੰਦੇ ਹਨ । ਇਹ ਹਨ-ਟਿੱਡੇ, ਸੈਨਿਕ ਸੁੰਡੀ, ਭੱਬੂ ਕੁੱਤਾ, ਹੱਡਾ ਭੰਡੀ ਆਦਿ ।
4. ਕੁੱਝ ਕੀੜੇ ਜਿਵੇਂ ਸਿਉਂਕ, ਚਿੱਟਾ ਸੁੰਡ ਜ਼ਮੀਨ ਹੇਠਲੇ ਹਿੱਸੇ ਜੜ੍ਹ, ਤਣਾ ਆਦਿ ਨੂੰ ਖਾ ਜਾਂਦੇ ਹਨ ਤੇ ਪੌਦਾ ਮਰ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਫ਼ਸਲਾਂ ਦੀਆਂ ਬੀਮਾਰੀਆਂ ਦੇ ਮੁੱਖ ਤੌਰ ‘ਤੇ ਕੀ ਕਾਰਨ ਹਨ ?
ਉੱਤਰ-
ਫ਼ਸਲਾਂ ਨੂੰ ਵੱਖ-ਵੱਖ ਅਵਸਥਾ ਵਿੱਚ ਉੱਲੀ, ਜੀਵਾਣੁ, ਵਿਸ਼ਾਣ ਆਦਿ ਤੋਂ ਕਈ ਕਿਸਮ ਦੀਆਂ ਬੀਮਾਰੀਆਂ ਲੱਗ ਜਾਂਦੀਆਂ ਹਨ । ਪੌਦਿਆਂ ਦੀਆਂ ਬੀਮਾਰੀਆਂ ਮੁੱਖ ਤੌਰ ‘ਤੇ ਬੀਮਾਰੀ ਵਾਲੇ ਬੀਜਾਂ, ਬੀਮਾਰੀ ਵਾਲੇ ਖੇਤਾਂ ਅਤੇ ਮੀਂਹ ਅਤੇ ਤੇਜ਼ ਹਵਾ ਕਾਰਨ ਇੱਕ ਖੇਤ ਤੋਂ ਦੁਸਰੇ ਖੇਤ ਵਿਚ ਫੈਲਦੀਆਂ ਹਨ । ਉੱਲੀ ਨਾਲ ਹੋਣ ਵਾਲੀਆਂ ਬੀਮਾਰੀਆਂ-ਉੱਲੀ ਨਾਲ ਹੋਣ ਵਾਲੀਆਂ ਬੀਮਾਰੀਆਂ ਹਨਝੁਲਸ ਰੋਗ, ਬੀਜ ਗਲਣ ਰੋਗ, ਕਾਂਗਿਆਰੀ, ਚਿੱਟੂ ਰੋਗ । ਜੀਵਾਣੂਆਂ ਤੋਂ ਹੋਣ ਵਾਲੀਆਂ ਬੀਮਾਰੀਆਂ-ਤਣੇ ਦਾ ਗਲਣਾ, ਪੱਤਿਆਂ ਦਾ ਧੱਬਾ ਰੋਗ ਆਦਿ । ਵਿਸ਼ਾਣੂਆਂ ਨਾਲ ਹੋਣ ਵਾਲੇ ਰੋਗ-ਜਿਵੇਂ ਠੁਠੀ ਰੋਗ, ਚਿਤਕਬਰਾ ਰੋਗ ।
ਪ੍ਰਸ਼ਨ 3.
ਫ਼ਸਲ ਸੁਰੱਖਿਆ ਦੀ ਕੀ ਮਹੱਤਤਾ ਹੈ ?
ਉੱਤਰ-
ਖੇਤੀ ਦੇ ਖੇਤਰ ਵਿਚ ਬਹੁਤ ਤਰੱਕੀ ਹੋ ਰਹੀ ਹੈ । ਬਹੁਤ ਉੱਨਤ ਕਿਸਮਾਂ ਤੇ ਨਵੀਆਂ ਤਕਨੀਕਾਂ ਇਜ਼ਾਦ ਕੀਤੀਆਂ ਜਾ ਰਹੀਆਂ ਹਨ । ਇਸ ਨਾਲ ਪੈਦਾਵਾਰ ਵਿਚ ਵੀ ਬਹੁਤ ਵਾਧਾ ਹੋਇਆ ਹੈ । ਪਰ ਵਧੇਰੇ ਝਾੜ ਲੈਣ ਲਈ ਕੀੜਿਆਂ ਅਤੇ ਬੀਮਾਰੀਆਂ ਤੋਂ ਫ਼ਸਲ ਦਾ ਬਚਾਉ ਕਰਨਾ ਵੀ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ । ਹਰ ਸਾਲ ਕੀੜਿਆਂ ਅਤੇ ਰੋਗਾਂ ਕਾਰਨ ਇੱਕ ਤਿਹਾਈ ਪੈਦਾਵਾਰ ਦਾ ਨੁਕਸਾਨ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਹ ਬਚਾਅ ਹੀ ਪੌਦ ਸੁਰੱਖਿਆ ਹੈ ਜਾਂ ਫ਼ਸਲ ਸੁਰੱਖਿਆ ਹੈ । ਜੇ ਫ਼ਸਲ ਦੀ ਰੋਗਾਂ ਤੇ ਕੀੜਿਆਂ ਦੇ ਹਮਲੇ ਤੋਂ ਸੁਰੱਖਿਆ ਨਹੀਂ ਕੀਤੀ ਜਾਵੇਗੀ ਤਾਂ ਅਕਾਲ ਪੈ ਸਕਦਾ ਹੈ, ਜਿਵੇਂ ਕਿ 1943 ਵਿੱਚ ਬੰਗਾਲ ਵਿਚ ਝੋਨੇ ਨੂੰ ਭੂਰੇ ਧੱਬਿਆਂ ਦੇ ਰੋਗ ਕਾਰਨ ਹੋਇਆ ਸੀ ਅਤੇ 1996-2002 ਦੌਰਾਨ ਪੰਜਾਬ ਵਿਚ ਨਰਮੇ ਤੇ ਅਮਰੀਕਨ ਸੁੰਡੀ ਦੇ ਹਮਲੇ ਕਾਰਨ ਸਾਰੀ ਫ਼ਸਲ ਹੀ ਖ਼ਤਮ ਹੋਣ ਦੀ ਹੱਦ ਤੱਕ ਪੁੱਜ ਗਈ ਸੀ । ਇਸ ਲਈ ਫ਼ਸਲ ਨੂੰ ਸੁਰੱਖਿਅਤ ਰੱਖ ਕੇ ਹੀ ਵਧੇਰੇ ਝਾੜ ਤੇ ਵਧੇਰੇ ਮੁਨਾਫ਼ਾ ਲਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 4.
ਬੀਮਾਰੀ ਜਾਂ ਕੀੜੇ ਦੇ ਹਮਲੇ ਤੋਂ ਪਹਿਲਾਂ ਪੌਦ ਸੁਰੱਖਿਆ ਲਈ ਕਿਹੜੇ ਢੰਗ ਅਪਣਾਉਣੇ ਚਾਹੀਦੇ ਹਨ ?
ਉੱਤਰ-
ਬੀਮਾਰੀ ਜਾਂ ਕੀੜੇ ਦੇ ਹਮਲੇ ਤੋਂ ਪਹਿਲਾਂ ਵਰਤੇ ਜਾਣ ਵਾਲੇ ਢੰਗ ਤਰੀਕੇ ਇਸ ਤਰ੍ਹਾਂ ਹਨ
- ਅਜਿਹੀਆਂ ਕਿਸਮਾਂ ਦੀ ਚੋਣ ਕਰੋ ਜੋ ਰੋਗ ਸਹਿਣ ਦੀ ਸਮਰੱਥਾ ਰੱਖਦੀਆਂ ਹੋਣ ।
- ਬੀਜਾਂ ਨੂੰ ਸੋਧ ਕੇ ਬੀਜਾਈ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ।
- ਕੁੱਝ ਬੀਮਾਰੀਆਂ ਅਤੇ ਕੀੜਿਆਂ ਤੋਂ ਬਚਾਅ ਕਰਨ ਲਈ ਖੇਤਾਂ ਨੂੰ ਧੁੱਪ ਵਿੱਚ ਖੁੱਲ੍ਹਾ ਰੱਖ ਕੇ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।
- ਸਿੰਚਾਈ, ਖਾਦਾਂ ਅਤੇ ਦਵਾਈਆਂ ਦੀ ਵਰਤੋਂ ਸਹੀ ਮਾਤਰਾ ਤੇ ਮਿਕਦਾਰ ਵਿਚ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ, ਬੇਲੋੜੀ ਨਹੀਂ ।
- ਖੇਤਾਂ ਦੇ ਆਲੇ-ਦੁਆਲੇ ਤੇ ਵੱਟਾਂ ਉੱਤੇ ਨਦੀਨਾਂ ਨੂੰ ਖ਼ਤਮ ਕਰਨ ਨਾਲ ਬੀਮਾਰੀਆਂ ਤੇ ਕੀੜਿਆਂ ਦਾ ਹਮਲਾ ਘੱਟ ਹੁੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 5.
ਬੀਮਾਰੀ ਜਾਂ ਕੀੜੇ ਦੇ ਹਮਲੇ ਤੋਂ ਬਾਅਦ ਪੌਦ ਸੁਰੱਖਿਆ ਲਈ ਕਿਹੜੇ ਢੰਗ ਅਤੇ ਸਾਵਧਾਨੀਆਂ ਵਰਤਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਬੀਮਾਰੀ ਜਾਂ ਕੀੜੇ ਦਾ ਹਮਲਾ ਹੋਣ ਤੋਂ ਬਾਅਦ ਵਰਤੇ ਜਾਣ ਵਾਲੇ ਤਰੀਕੇ ਇਸ ਤਰ੍ਹਾਂ ਹਨ –
- ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਬੀਮਾਰੀ ਕਿਹੜੀ ਹੈ ਤੇ ਇਸ ਦਾ ਕੀ ਕਾਰਨ ਹੈ ਪਤਾ ਲਗਾਓ । ਇਸੇ ਤਰ੍ਹਾਂ ਕੀੜੇ ਦੀ ਪਹਿਚਾਣ ਕਰਨੀ ਵੀ ਜ਼ਰੂਰੀ ਹੈ । ਇਸ ਤੋਂ ਬਾਅਦ ਹੀ ਇਹਨਾਂ ਦੀ ਰੋਕਥਾਮ ਦੀ ਵਿਉਂਤ ਤਿਆਰ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ । ਜਿਵੇਂ ਵਿਸ਼ਾਣੂ ਰੋਗ ਵਿਚ ਇਸ ਨੂੰ ਫੈਲਾਉਣ ਵਾਲੇ ਕੀੜੇ ਦੀ ਰੋਕਥਾਮ ਕਰਨੀ ਜ਼ਰੂਰੀ ਹੈ ।
- ਸ਼ੁਰੂ ਵਿੱਚ ਹੀ ਜਦੋਂ ਬੀਮਾਰੀ ਜਾਂ ਕੀੜਿਆਂ ਦਾ ਹਮਲਾ ਘੱਟ ਹੁੰਦਾ ਹੈ ਅਜਿਹੇ ਬਟਿਆਂ ਨੂੰ ਪੁੱਟ ਕੇ ਨਸ਼ਟ ਕਰ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ ।
- ਕੀੜੇ ਜਾਂ ਬੀਮਾਰੀ ਕਾਰਨ ਹੋਏ ਨੁਕਸਾਨ ਲਈ ਦਿੱਤੇ ਗਏ ਚੇਤਾਵਨੀ ਵਾਲੇ ਪੱਧਰ ਤੇ ਹੀ ਰਸਾਇਣਿਕ ਕੀਟਨਾਸ਼ਕਾਂ/ਉੱਲੀਨਾਸ਼ਕਾਂ ਦੀ ਵਰਤੋਂ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ।
- ਰਸਾਇਣਿਕ ਦਵਾਈਆਂ ਦੀ ਚੋਣ ਕੀੜੇ ਦੇ ਸੁਭਾਅ, ਹਮਲੇ ਦੀਆਂ ਨਿਸ਼ਾਨੀਆਂ ਅਤੇ ਬੀਮਾਰੀ ਦੇ ਕਾਰਨ ਮੁਤਾਬਿਕ ਹੀ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ।
- ਰਸਾਇਣਿਕ ਦਵਾਈਆਂ ਦੀ ਸਹੀ ਮਾਤਰਾ ਅਤੇ ਸਹੀ ਸਮੇਂ ਦਾ ਧਿਆਨ ਰੱਖ ਕੇ ਹੀ ਵਰਤੋਂ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ।
- ਮਿੱਤਰ ਕੀੜੇ ਤੇ ਹੋਰ ਸੂਖ਼ਮ ਜੀਵਾਂ ਦੀ ਵਰਤੋਂ ਕਰਕੇ ਵੀ ਕੀੜਿਆਂ ਤੇ ਬੀਮਾਰੀਆਂ ਦੀ ਰੋਕਥਾਮ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ।
PSEB 7th Class Agriculture Guide ਫਸਲਾਂ ਦੇ ਕੀੜੇ ਅਤੇ ਬੀਮਾਰੀਆਂ Important Questions and Answers
ਕੁੱਝ ਹੋਰ ਮਹੱਤਵਪੂਰਨ ਪ੍ਰਸ਼ਨ
ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਤੇਲਾ ਕਿਹੜੀਆਂ ਫ਼ਸਲਾਂ ਨੂੰ ਹਾਨੀ ਪਹੁੰਚਾਉਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਨਰਮਾ, ਭਿੰਡੀ, ਮੱਕੀ, ਅੰਬ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 2.
ਚੇਪਾ ਕਿਹੜੀਆਂ ਫ਼ਸਲਾਂ ਦਾ ਨੁਕਸਾਨ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ-
ਕਣਕ, ਤੇਲ ਬੀਜ, ਗਾਜਰੀ ਬੂਟੇ, ਆਤੂ ॥
ਪ੍ਰਸ਼ਨ 3.
ਚਿੱਟੀ ਮੱਖੀ ਕਿਹੜੀਆਂ ਫ਼ਸਲਾਂ ਦਾ ਨੁਕਸਾਨ ਕਰਦੀ ਹੈ ?
ਉੱਤਰ-
ਨਰਮਾਂ, ਦਾਲਾਂ, ਟਮਾਟਰ, ਪਪੀਤਾ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 4.
ਮਿੱਲੀ ਬੱਗ ਕਿਹੜੀਆਂ ਫ਼ਸਲਾਂ ਨੂੰ ਨੁਕਸਾਨ ਪਹੁੰਚਾਉਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਨਰਮਾ, ਅੰਬ, ਨਿੰਬੂ ਜਾਤੀ ਦੇ ਫ਼ਲ, ਪਪੀਤਾ ।
ਪ੍ਰਸ਼ਨ 5.
ਕਿਸੇ ਤਣਾ ਛੇਦਕ ਕੀੜੇ ਦਾ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਮੱਕੀ ਦੀ ਫ਼ਸਲ ਵਿੱਚ ਸ਼ਾਖ ਦੀ ਮੱਖੀ, ਕਮਾਦ ਦਾ ਗੜੁਆਂ ।
![]()
ਪ੍ਰਸ਼ਨ 6.
ਫਲ ਛੇਦਕ ਕੀੜੇ ਦੀ ਪਹਿਚਾਣ ਕਿਵੇਂ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਕੀੜੇ ਦੇ ਛੱਡੇ ਹੋਏ ਮਲਮੂਤਰ ਤੋਂ ।
ਪ੍ਰਸ਼ਨ 7.
ਫ਼ਲ ਛੇਦਕ ਕੀੜੇ ਦੀ ਉਦਾਹਰਨ ਦਿਉ ।
ਉੱਤਰ-
ਅਮਰੀਕਨ ਸੁੰਡੀ, ਬੈਂਗਣਾਂ ਦੀ ਸੁੰਡੀ ।
ਪ੍ਰਸ਼ਨ 8.
ਪੱਤਿਆਂ ਨੂੰ ਕੱਟ ਕੇ ਖਾਣ ਵਾਲੇ ਕੀੜੇ ਪੱਤੇ ਨੂੰ ਕਿਵੇਂ ਖਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਇਹ ਪੱਤਿਆਂ ਨੂੰ ਕਿਨਾਰਿਆਂ ਤੋਂ ਮੁੱਖ ਨਾੜੀ ਵੱਲ ਖਾਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 9.
ਪੱਤਿਆਂ ਨੂੰ ਕੱਟ ਕੇ ਖਾਣ ਵਾਲੇ ਕੀੜਿਆਂ ਦੇ ਉਦਾਹਰਨ ਦਿਓ ।
ਉੱਤਰ-
ਟਿੱਡੇ, ਸੈਨਿਕ ਸੁੰਡੀ, ਸਲੇਟੀ ਸੁੰਡੀ, ਲਾਲ ਭੂੰਡੀ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 10.
ਪੱਤਿਆਂ ਦੀ ਛਾਨਣੀ ਬਣਾਉਣ ਵਾਲੇ ਕੀੜੇ ਪੱਤਿਆਂ ਦਾ ਕਿਵੇਂ ਨੁਕਸਾਨ ਕਰਦੇ ਹਨ ?
ਉੱਤਰ-
ਇਹ ਪੱਤਿਆਂ ਦਾ ਹਰਾ ਮਾਦਾ ਖਾ ਜਾਂਦੇ ਹਨ ਪਰ ਪੱਤਿਆਂ ਦੀਆਂ ਨਾੜੀਆਂ ਨੂੰ ਨੁਕਸਾਨ ਨਹੀਂ ਕਰਦੇ ਜਿਸ ਕਾਰਨ ਪੱਤੇ ਛਾਨਣੀ ਵਰਗੇ ਹੋ ਜਾਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 11.
ਪੱਤਿਆਂ ਨੂੰ ਛਾਨਣੀ ਵਰਗਾ ਬਣਾਉਣ ਵਾਲੇ ਕੀੜਿਆਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਪੱਡਾ ਭੰਡੀ, ਭੱਬੂ ਕੁੱਤਾ, ਗੋਭੀ ਦੀ ਤਿੱਤਲੀ ।
ਪ੍ਰਸ਼ਨ 12.
ਜੜ੍ਹਾਂ ਨੂੰ ਨੁਕਸਾਨ ਪਹੁੰਚਾਉਣ ਵਾਲੇ ਕੀੜਿਆਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਸਿਉਂਕ, ਚਿੱਟਾ ਲੰਡ ।
ਪ੍ਰਸ਼ਨ 13.
ਝੁਲਸ ਰੋਗ ਦੇ ਲੱਛਣ ਦੱਸੋ ।
ਉੱਤਰ-
ਪਾਣੀ ਸਿੰਮਦੇ ਧੱਬੇ ਪੱਤਿਆਂ ਤੇ ਤਣੇ ਉੱਪਰ ਬਣੇ ਹੋਏ ਦਿਖਾਈ ਦਿੰਦੇ ਹਨ । ਚਿੱਟੀ ਉੱਲੀ ਪੱਤਿਆਂ ਦੇ ਹੇਠਲੇ ਪਾਸੇ ਦਿਖਾਈ ਦਿੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 14.
ਬੀਜ ਗਲਣ ਰੋਗ ਦੇ ਲੱਛਣ ਦੱਸੋ ।
ਉੱਤਰ-
ਜ਼ਮੀਨ ਅੰਦਰ ਹੀ ਬੀਜ ਗਲ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 15.
ਕਾਂਗਿਆਰੀ ਦੇ ਲੱਛਣ ਦੱਸੋ ।
ਉੱਤਰ-
ਇਸ ਵਿੱਚ ਦਾਣਿਆਂ ਦੀ ਬਜਾਏ ਕਾਲਾ ਧੂੜਾ ਬਣ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 16.
ਚਿੱਟੋਂ ਰੋਗ ਕਿਹੜੀ ਫ਼ਸਲ ਨੂੰ ਲੱਗਦੇ ਹਨ ?
ਉੱਤਰ-
ਬੇਰ, ਮਟਰ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 17.
ਵਿਸ਼ਾਣੂ ਰੋਗ ਕਿਵੇਂ ਫੈਲਦੇ ਹਨ ? ਉੱਤਰ-ਵਿਸ਼ਾਣੂ ਰੋਗ ਕੀੜੇ ਮਕੌੜਿਆਂ ਦੁਆਰਾ ਫੈਲਦੇ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 18.
ਨਰਮੇ ਵਿੱਚ ਚਿੱਟੀ ਮੱਖੀ ਕਿਹੜਾ ਰੋਗ ਫੈਲਾਉਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਝੂਠੀ ਰੋਗ ।
ਪ੍ਰਸ਼ਨ 19.
ਕੀ ਵਿਸ਼ਾਣੂ ਰੋਗਾਂ ਦੀ ਰੋਕਥਾਮ ਸੌਖਿਆਂ ਹੋ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਨਹੀਂ, ਇਹਨਾਂ ਦੀ ਰੋਕਥਾਮ ਬਹੁਤ ਮੁਸ਼ਕਿਲ ਹੈ ।
ਪ੍ਰਸ਼ਨ 20.
ਝੂਠੀ ਰੋਗ ਦੇ ਲੱਛਣ ਦੱਸੋ ।
ਉੱਤਰ-
ਪੱਤੇ ਸਿਰਿਆਂ ਤੋਂ ਅੰਦਰ ਨੂੰ ਮੁੜ ਜਾਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 21.
ਚਿਤਕਬਰਾ ਰੋਗ ਦੇ ਲੱਛਣ ਦੱਸੋ ।
ਉੱਤਰ-
ਪੱਤਿਆਂ ਤੇ ਬੇਤਰਤੀਬੇ ਪੀਲੇ ਅਤੇ ਹਰੇ ਚਟਾਕ ਪੈ ਜਾਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 22.
ਪਪੀਤੇ ਨੂੰ ਲੱਗਣ ਵਾਲਾ ਇਕ ਵਿਸ਼ਾਣੂ ਰੋਗ ਦੱਸੋ ।
ਉੱਤਰ-
ਝੂਠੀ ਰੋਗ ॥
ਪ੍ਰਸ਼ਨ 23.
ਮੂੰਗੀ ਨੂੰ ਲੱਗਣ ਵਾਲਾ ਇੱਕ ਵਿਸ਼ਾਣੂ ਰੋਗ ਦੱਸੋ ।
ਉੱਤਰ-
ਚਿਤਕਬਰਾ ਰੋਗ |
ਪ੍ਰਸ਼ਨ 24.
ਕੀੜਿਆਂ ਅਤੇ ਬੀਮਾਰੀਆਂ ਦੀ ਸੁਚੱਜੀ ਰੋਕਥਾਮ ਨੂੰ ਕਿੰਨੇ ਹਿੱਸਿਆਂ ਵਿੱਚ ਵੰਡ ਸਕਦੇ ਹਾਂ ?
ਉੱਤਰ-
ਦੋ ਹਿੱਸਿਆਂ ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 25.
ਕੀੜੇ ਜਾਂ ਬੀਮਾਰੀਆਂ ਨੂੰ ਖ਼ਤਮ ਕਰਨ ਲਈ ਰਸਾਇਣਾਂ ਦੀ ਚੋਣ ਕਿਸ ਅਨੁਸਾਰ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
ਕੀੜੇ ਦੇ ਸੁਭਾਅ, ਹਮਲੇ ਦੀਆਂ ਨਿਸ਼ਾਨੀਆਂ ਅਤੇ ਬੀਮਾਰੀ ਦੇ ਕਾਰਨ ਅਨੁਸਾਰ ॥
ਪ੍ਰਸ਼ਨ 26.
ਜੇ ਕਿਸੇ ਨੂੰ ਜ਼ਹਿਰ ਚੜ੍ਹ ਜਾਵੇ ਤਾਂ ਕੀ ਪਿਲਾ ਕੇ ਉਲਟੀ ਕਰਵਾਈ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਲੂਣ ਵਾਲਾ ਪਾਣੀ ਪਿਲਾ ਕੇ ।
ਪ੍ਰਸ਼ਨ 27.
ਉਲਟੀ ਕਿਸ ਹਾਲਤ ਵਿਚ ਨਹੀਂ ਕਰਵਾਉਣੀ ਚਾਹੀਦੀ ?
ਉੱਤਰ-
ਜਦੋਂ ਮਰੀਜ਼ ਬੇਹੋਸ਼ ਹੋ ਜਾਵੇ ।
ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਜੇਕਰ ਕੀਟਨਾਸ਼ਕ ਦਵਾਈ ਕਿਸੇ ਦੀ ਅੱਖ ਵਿਚ ਪੈ ਜਾਵੇ ਤਾਂ ਕੀ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਅੱਖਾਂ ਦੀਆਂ ਪਲਕਾਂ ਖੁੱਲ੍ਹੀਆਂ ਰੱਖੋ ਤੇ ਡਾਕਟਰ ਦੇ ਆਉਣ ਤੱਕ ਸਹਿਜੇ-ਸਹਿਜੇ ਪਾਣੀ ਨਾਲ ਧੋਦੇ ਰਹੋ ਤੇ ਡਾਕਟਰ ਦੇ ਦੱਸੇ ਬਗੈਰ ਕੋਈ ਦਵਾਈ ਅੱਖਾਂ ਵਿਚ ਨਾ ਪਾਉ ।
ਪ੍ਰਸ਼ਨ 2.
ਕੀੜੀਆਂ ਦਾ ਫ਼ਸਲਾਂ ਦੇ ਵਿਕਾਸ ਨਾਲ ਕੀ ਸੰਬੰਧ ਹੈ ?
ਉੱਤਰ-
ਕਈ ਕੀੜੇ ਫ਼ਸਲਾਂ ਨੂੰ ਨੁਕਸਾਨ ਪਹੁੰਚਾਉਂਦੇ ਹਨ ਤੇ ਝਾੜ ਘੱਟ ਜਾਂਦਾ ਹੈ ਤੇ ਕੁੱਝ ਕੀੜੇ ਲਾਭਕਾਰੀ ਵੀ ਹੁੰਦੇ ਹਨ, ਜਿਵੇਂ ਮਧੂ ਮੱਖੀਆਂ ਜੋ ਪਰਾਗਣ ਕਿਰਿਆ ਦੁਆਰਾ ਫ਼ਸਲਾਂ ਦਾ ਝਾੜ ਵਧਾਉਣ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦੀਆਂ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 3.
ਕੀਟਨਾਸ਼ਕ ਦਵਾਈਆਂ ਦੀਆਂ ਖ਼ਾਲੀ ਸ਼ੀਸ਼ੀਆਂ ਅਤੇ ਡੱਬਿਆਂ ਨੂੰ ਕੀ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਖ਼ਾਲੀ ਸ਼ੀਸ਼ੀਆਂ ਅਤੇ ਡੱਬਿਆਂ ਨੂੰ ਸਾੜਨ ਦੀ ਬਜਾਏ ਜ਼ਮੀਨ ਵਿਚ ਦੱਬ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 4.
ਜ਼ਹਿਰਾਂ ਦੇ ਛਿੜਕਾਅ ਕਰਨ ਵਾਲੇ ਦੇ ਖਾਣ-ਪੀਣ ਬਾਰੇ ਦੱਸੋ ।
ਉੱਤਰ-
ਭੁੱਖੇ ਪੇਟ ਛਿੜਕਾਅ ਨਾ ਕਰੋ ਅਤੇ ਛਿੜਕਾਅ ਦੌਰਾਨ ਕੁੱਝ ਵੀ ਖਾਣਾ ਪੀਣਾ ਨਹੀਂ ਚਾਹੀਦਾ ਪਹਿਲਾਂ ਹੀ ਪੇਟ ਭਰ ਕੇ ਖਾਣਾ ਖਾ ਕੇ ਛਿੜਕਾਅ ਕਰੋ ।
ਪ੍ਰਸ਼ਨ 5.
ਸਾਹ ਰਾਹੀਂ ਅੰਦਰ ਗਏ ਜ਼ਹਿਰ ਤੋਂ ਬਚਾਓ ਬਾਰੇ ਦੱਸੋ ।
ਉੱਤਰ-
ਮਰੀਜ਼ ਨੂੰ ਜਿੰਨੀ ਜਲਦੀ ਹੋਵੇ ਚੁੱਕ ਕੇ ਖੁੱਲ੍ਹੀ ਹਵਾ ਵਿਚ ਲੈ ਜਾਓ ਅਤੇ ਬੰਦ ਕਮਰੇ ਦੇ ਸਾਰੇ ਦਰਵਾਜ਼ੇ ਤੇ ਖਿੜਕੀਆਂ ਖੋਲ੍ਹ ਦਿਓ ਮਰੀਜ਼ ਦੇ ਪਾਏ ਹੋਏ ਤੰਗ ਕੱਪੜਿਆਂ ਨੂੰ ਢਿੱਲੇ ਕਰੋ । ਜੇ ਸਾਹ ਬੰਦ ਹੁੰਦਾ ਹੋਵੇ ਜਾਂ ਚਾਲ ਵਿਚ ਤਬਦੀਲੀ ਆਉਂਦੀ ਨਜ਼ਰ ਆਵੇ ਤਾਂ ਬਨਾਉਟੀ ਸਾਹ ਦਿਉ ਪਰ ਛਾਤੀ ਤੇ ਭਾਰ ਨਾ ਪਾਉ ।ਮਰੀਜ਼ ਨੂੰ ਠੰਡ ਨਾ ਲੱਗਣ ਦਿਉ ਅਤੇ ਉਸ ਉੱਤੇ ਕੰਬਲ ਆਦਿ ਦੇ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ । ਮਰੀਜ਼ ਨੂੰ ਬੋਲਣ ਨਾ ਦਿਉ । ਜੇ ਮਰੀਜ਼ ਨੂੰ ਕੜਵੱਲ ਪੈਣ ਤਾਂ ਉਸਨੂੰ ਹਨੇਰੇ ਕਮਰੇ ਵਿੱਚ ਬਿਸਤਰ ਵਿੱਚ ਰੱਖੋ । ਉੱਥੇ ਰੌਲਾ ਰੱਪਾ ਨਾ ਪਾਉ ।
ਪ੍ਰਸ਼ਨ 6.
ਮੁਸਾਮਾਂ ਰਾਹੀਂ ਅੰਦਰ ਗਏ ਜ਼ਹਿਰ ਤੋਂ ਬਚਾਓ ਬਾਰੇ ਦੱਸੋ ।
ਉੱਤਰ-
ਪਾਣੀ ਨਾਲ ਸਰੀਰ ਨੂੰ ਗਿੱਲਾ ਕਰੋ ਅਤੇ ਮਰੀਜ਼ ਦੇ ਕੱਪੜੇ ਉਤਾਰ ਕੇ ਸਰੀਰ ਤੇ ਲਗਾਤਾਰ ਪਾਣੀ ਪਾਉਂਦੇ ਜਾਓ । ਸਰੀਰ ਨੂੰ ਪਾਣੀ ਨਾਲ ਚੰਗੀ ਤਰ੍ਹਾਂ ਸਾਫ਼ ਕਰੋ। ਸਰੀਰ ਨੂੰ ਛੇਤੀ ਧੋ ਲਉ, ਕਿਉਂਕਿ ਇਸ ਨਾਲ ਕਾਫ਼ੀ ਫ਼ਰਕ ਪੈ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 7.
ਜ਼ਹਿਰੀਲੀ ਦਵਾਈ ਅੱਖਾਂ ਵਿਚ ਪੈ ਜਾਣ ਤੇ ਕੀ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਅਜਿਹੀ ਹਾਲਤ ਵਿਚ ਹੇਠ ਲਿਖੀਆਂ ਹਦਾਇਤਾਂ ਤੇ ਅਮਲ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।
- ਅੱਖਾਂ ਦੀਆਂ ਪਲਕਾਂ ਨੂੰ ਖੋਲ੍ਹ ਕੇ ਰੱਖੋ ।
- ਚੱਲਦੇ ਪਾਣੀ ਨਾਲ ਜਿੰਨੀ ਜਲਦੀ ਹੋਵੇ ਅੱਖਾਂ ਨੂੰ ਸਹਿਜੇ-ਸਹਿਜੇ ਧੋਵੋ ।
- ਡਾਕਟਰ ਦੇ ਆਉਣ ਤੱਕ ਅੱਖਾਂ ਨੂੰ ਧੋਂਦੇ ਰਹੋ !
- ਕਿਸੇ ਵੀ ਦਵਾਈ ਦੀ ਵਰਤੋਂ ਡਾਕਟਰ ਦੀ ਸਲਾਹ ਤੋਂ ਬਗੈਰ ਨਾ ਕਰੋ ਗ਼ਲਤ ਦਵਾਈ ਹਾਨੀਕਾਰਕ ਵੀ ਹੋ ਸਕਦੀ ਹੈ ।
ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਖੇਤੀ ਜ਼ਹਿਰਾਂ ਤੋਂ ਬਚਾਉ ਦੇ ਆਮ ਸਾਧਨ ਦੱਸੋ ।
ਉੱਤਰ-
ਮਰੀਜ਼ ਨੂੰ ਠੰਡ ਤੋਂ ਬਚਾਉਣ ਲਈ ਹਲਕੇ ਜਿਹੇ ਕੰਬਲ ਨਾਲ ਢੱਕ ਦਿਉ । ਇਸ ਕੰਮ ਲਈ ਗਰਮ ਪਾਣੀ ਵਾਲੀ ਬੋਤਲ ਦੀ ਵਰਤੋਂ ਨਾ ਕਰੋ | ਮਰੀਜ਼ ਦਾ ਬਿਸਤਰ ਪੈਰਾਂ ਵੱਲੋਂ ਉੱਚਾ ਰੱਖੋ ਅਤੇ ਲੱਤਾਂ ਅਤੇ ਬਾਹਾਂ ਨੂੰ ਫੀਤਿਆਂ ਨਾਲ ਬੰਨ੍ਹ ਦਿਓ | ਮਰੀਜ਼ ਨੂੰ ਚੁਸਤੀ ਵਾਸਤੇ ਹਾਈਪੋਡਰਮਿਕ ਟੀਕੇ ਜਿਵੇਂ-ਕੈਫੀਨ ਅਤੇ ਏਪਾਈਨਾਫਰਿਨ ਲਗਾਓ । ਡੈਕਸਟਰੋਜ 5% ਦਾ ਘੋਲ ਨਾੜੀ ਵਿਚ ਦੀ ਸਰੀਰ ਵਿਚ ਭੇਜੋ | ਮਰੀਜ਼ ਨੂੰ ਲਹੂ ਜਾਂ ਪਲਾਜਮਾ ਵੀ ਦਿਓ | ਮਰੀਜ਼ ਨੂੰ ਤੇਜ਼ ਅਤੇ ਵਧੇਰੇ ਦਵਾਈਆਂ ਦੇ ਕੇ ਨਾ ਥਕਾਓ ।
ਪ੍ਰਸ਼ਨ 2.
ਖੇਤੀ-ਜ਼ਹਿਰਾਂ ਦੀ ਉੱਚਿਤ ਵਰਤੋਂ ਦਾ ਕੀ ਮਹੱਤਵ ਹੈ ?
ਉੱਤਰ-
ਖੇਤੀ ਜ਼ਹਿਰਾਂ ਦੀ ਉੱਚਿਤ ਵਰਤੋਂ ਸੰਬੰਧੀ ਕੁੱਝ ਗੱਲਾਂ ਦਾ ਖ਼ਿਆਲ ਰੱਖਣਾ ਅਤਿ ਜ਼ਰੂਰੀ ਹੈ ਜੋ ਕਿ ਇਸ ਤਰ੍ਹਾਂ ਹਨ –
- ਪਹਿਲਾਂ ਕੀੜੇ, ਬਿਮਾਰੀ ਅਤੇ ਨਦੀਨਾਂ ਦੀ ਪਛਾਣ ਕਰ ਕੇ ਹੀ ਸਿਫ਼ਾਰਸ਼ ਕੀਤੇ ਜ਼ਹਿਰ ਦੀ ਸਿਫਾਰਸ਼ ਕੀਤੀ ਮਾਤਰਾ ਦੀ ਵਰਤੋਂ ਕਰੋ । ਹਰ ਕੀੜੇ, ਬਿਮਾਰੀ ਅਤੇ ਨਦੀਨ ਦੇ ਖ਼ਾਤਮੇ ਲਈ ਵੱਖ-ਵੱਖ ਜ਼ਹਿਰਾਂ ਦੀ ਸਿਫ਼ਾਰਸ਼ ਵੱਖ-ਵੱਖ ਮਾਤਰਾ ਵਿੱਚ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।
- ਦੁਕਾਨਦਾਰਾਂ ਦੀ ਗਲਤ ਸਲਾਹ ਨਾ ਮੰਨੋ, ਸਗੋਂ ਖੇਤੀ ਮਾਹਿਰਾਂ ਨਾਲ ਵਿਚਾਰ ਵਟਾਂਦਰਾ ਜ਼ਰੂਰ ਕਰੋ ।
- ਕਦੇ ਵੀ ਕੀਟਨਾਸ਼ਕਾਂ ਅਤੇ ਨਦੀਨਨਾਸ਼ਕਾਂ ਨੂੰ ਖੇਤੀ ਮਾਹਿਰਾਂ ਨਾਲ ਵਿਚਾਰ ਵਟਾਂਦਰਾ ਕੀਤੇ ਬਗੈਰ ਮਿਲਾ ਕੇ ਨਾ ਛਿੜਕੋ ।
- ਖੇਤੀ ਜ਼ਹਿਰਾਂ ਦਾ ਛਿੜਕਾਅ ਜਿਸ ਦਿਨ ਹਵਾ ਨਾ ਚਲਦੀ ਹੋਵੇ ਜਾਂ ਘੱਟ ਤੋਂ ਘੱਟ ਹਵਾ ਵਾਲੇ ਦਿਨ ਹੀ ਕਰੋ । ਛਿੜਕਾਅ ਕਰਨ ਵਾਲੇ ਵਿਅਕਤੀ ਦਾ ਮੂੰਹ ਹਵਾ ਦੀ ਦਿਸ਼ਾ ਤੋਂ ਉਲਟ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
- ਜੇ ਛਿੜਕਾਅ ਕਰਨ ਤੋਂ 24 ਘੰਟੇ ਦੇ ਅੰਦਰ ਮੀਂਹ ਪੈ ਜਾਵੇ ਤਾਂ ਮੁੜ ਤੋਂ ਛਿੜਕਾਅ ਕਰੋ ।
ਪ੍ਰਸ਼ਨ 3.
ਖੇਤੀ ਜ਼ਹਿਰਾਂ ਦੀ ਸੁਚੱਜੀ ਵਰਤੋਂ ਲਈ ਚਾਰ ਨੁਕਤੇ ਸੁਝਾਉ ।
ਉੱਤਰ-
ਇਨ੍ਹਾਂ ਦੀ ਸੁਰੱਖਿਅਤ ਵਰਤੋਂ ਲਈ ਹੇਠ ਲਿਖੀਆਂ ਗੱਲਾਂ ਦਾ ਖਿਆਲ ਰੱਖੋ
- ਘਰਾਂ ਵਿਚ ਇਨ੍ਹਾਂ ਕੀਟਨਾਸ਼ਕਾਂ ਨੂੰ ਖਾਣ-ਪੀਣ ਦੀਆਂ ਵਸਤਾਂ ਅਤੇ ਹੋਰ ਦਵਾਈਆਂ ਦੇ ਨੇੜੇ ਨਾ ਰੱਖੋ ।
- ਖੇਤੀ ਜ਼ਹਿਰ ਦੀ ਸ਼ੀਸ਼ੀ ਜਾਂ ਡੱਬੇ ਉੱਪਰ ਲਿਖੀਆਂ ਹਦਾਇਤਾਂ ਨੂੰ ਧਿਆਨ ਨਾਲ ਪੜੋ ਤੇ ਉਸੇ ਅਨੁਸਾਰ ਅਮਲ ਵਿਚ ਲਿਆਉ ।
- ਕੀਟਨਾਸ਼ਕ ਦਵਾਈਆਂ ਵਾਲੀਆਂ ਸ਼ੀਸ਼ੀਆਂ ਅਤੇ ਡੱਬਿਆਂ ਦੀ ਮੁੜ ਵਰਤੋਂ ਨਹੀਂ ਕਰਨੀ ਚਾਹੀਦੀ ।
- ਖੇਤੀ ਜ਼ਹਿਰਾਂ ਨੂੰ ਘਰ ਵਿਚ ਹਮੇਸ਼ਾਂ ਬੱਚਿਆਂ ਦੀ ਪਹੁੰਚ ਤੋਂ ਦੂਰ ਰੱਖੋ ।
- ਜੇ ਸਪਰੇਅ ਕਰਦੇ ਸਮੇਂ ਨੋਜ਼ਲ ਬੰਦ ਹੋ ਜਾਵੇ ਤਾਂ ਕਦੇ ਵੀ ਮੂੰਹ ਨਾਲ ਫੂਕ ਮਾਰ ਕੇ ਇਸ ਨੂੰ ਖੋਲ੍ਹਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਨਾ ਕਰੋ ।
- ਛਿੜਕਾਅ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਹੀ ਰੱਜ ਕੇ ਖਾਣਾ ਖਾ ਲਉ ਕਦੇ ਵੀ ਖ਼ਾਲੀ ਪੇਟ ਛਿੜਕਾਅ ਨਾ ਕਰੋ ਅਤੇ ਇਸ ਦੌਰਾਨ ਕੁੱਝ ਵੀ ਨਾ ਖਾਉ ਪੀਉ | ਖਾਣ-ਪੀਣ ਤੋਂ ਪਹਿਲਾਂ ਚੰਗੀ ਤਰ੍ਹਾਂ ਸਾਬਣ ਨਾਲ ਹੱਥ ਧੋ ਲਉ ।
- ਛਿੜਕਾਅ ਕਰਨ ਵਾਲੇ ਵਿਅਕਤੀ ਨੂੰ ਦਿਹਾੜੀ ਵਿਚ 8 ਘੰਟੇ ਤੋਂ ਵੱਧ ਕੰਮ ਨਹੀਂ ਕਰਨਾ ਚਾਹੀਦਾ ।
- ਕੀਟਨਾਸ਼ਕ ਦਵਾਈਆਂ ਨੂੰ ਪਾਣੀ ਵਿਚ ਘੋਲਣ ਸਮੇਂ ਕੋਈ ਛਿੱਟਾ ਆਦਿ ਨਹੀਂ ਪੈਣ ਦੇਣਾ ਚਾਹੀਦਾ ।
- ਤੇਜ਼ ਚੱਲਦੀ ਹਵਾ ਵਾਲੇ ਦਿਨ ਸਪਰੇਅ ਨਾ ਕਰੋ ।
- ਛਿੜਕਾਅ ਦਾ ਕੰਮ ਖ਼ਤਮ ਕਰਕੇ ਇਕਦਮ ਮਗਰੋਂ ਪਹਿਲਾਂ ਪਹਿਨੇ ਹੋਏ ਕੱਪੜਿਆਂ ਨੂੰ ਬਦਲ ਕੇ ਸਾਬਣ ਨਾਲ ਚੰਗੀ ਤਰ੍ਹਾਂ ਧੋ ਲਵੋ ।
- ਦਵਾਈ ਵਾਲੇ ਖ਼ਾਲੀ ਡੱਬਿਆਂ ਨੂੰ ਨਾ ਸਾੜੋ, ਸਗੋਂ ਇਹਨਾਂ ਨੂੰ ਜ਼ਮੀਨ ਵਿਚ ਦੱਬ ਦਿਉ ।
ਪ੍ਰਸ਼ਨ 4.
ਨਿਗਲੀ ਹੋਈ ਕੀਟਨਾਸ਼ਕ ਦਵਾਈ ਤੋਂ ਬਚਾਅ ਲਈ ਕੀ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਜੇ ਖੇਤੀ ਜ਼ਹਿਰ ਨਿਗਲ ਲਿਆ ਗਿਆ ਹੋਵੇ ਤਾਂ ਉਲਟੀ ਕਰਵਾਉਣੀ ਚਾਹੀਦੀ ਹੈ । ਇਸ ਲਈ ਇਕ ਚਮਚ ਨਮਕ ਨੂੰ ਗਰਮ ਪਾਣੀ ਦੇ ਗਲਾਸ ਵਿਚ ਘੋਲ ਕੇ ਮਰੀਜ਼ ਨੂੰ ਦਿਓ ਅਤੇ ਉਦੋਂ ਤਕ ਦਿਉ ਜਦੋਂ ਤਕ ਕਿ ਉਲਟੀ ਨਾ ਹੋ ਜਾਵੇ । ਗਲੇ ਨੂੰ ਉਂਗਲੀ ਨਾਲ ਹੌਲੀ-ਹੌਲੀ ਟੋਹਣ ਜਾਂ ਚਮਚੇ ਦਾ ਖੁੰਢਾ ਪਾਸਾ ਗਲ ਉੱਤੇ ਰੱਖਣ ਨਾਲ ਜਦੋਂ ਪੇਟ ਨਮਕੀਨ ਪਾਣੀ ਨਾਲ ਭਰਿਆ ਹੋਵੇ ਤਾਂ ਉਲਟੀ ਆਸਾਨੀ ਨਾਲ ਹੋ ਜਾਵੇਗੀ । ਜੇ ਮਰੀਜ਼ ਪਹਿਲਾਂ ਹੀ ਉਲਟੀ ਕਰ ਦੇਵੇ ਤਾਂ ਉਸਨੂੰ ਨਮਕ ਤੋਂ ਬਗੈਰ ਗਰਮ ਪਾਣੀ ਬਹੁਤੀ ਮਾਤਰਾ ਵਿਚ ਦਿਓ ਅਤੇ ਫਿਰ ਦੱਸੀਆਂ ਹਦਾਇਤਾਂ ਅਨੁਸਾਰ ਅਮਲ ਕਰੋ । ਜੇ ਮਰੀਜ਼ ਬੇਸੁਰਤ ਹੋਵੇ ਤਾਂ ਉਸਨੂੰ ਉਲਟੀਆਂ ਦੀ ਦਵਾਈ ਨਾ ਦਿਉ ।
![]()
ਫਸਲਾਂ ਦੇ ਕੀੜੇ ਅਤੇ ਬੀਮਾਰੀਆਂ PSEB 7th Class Agriculture Notes
ਪਾਠ ਇੱਕ ਨਜ਼ਰ ਵਿਚ-
- ਫ਼ਸਲਾਂ ਦੀ ਵਧੇਰੇ ਪੈਦਾਵਾਰ ਲਈ ਫ਼ਸਲਾਂ ਦੀ ਕੀੜਿਆਂ ਅਤੇ ਬੀਮਾਰੀਆਂ ਤੋਂ ਸੁਰੱਖਿਆ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ ।
- ਹਰ ਸਾਲ ਬੀਮਾਰੀਆਂ ਅਤੇ ਕੀੜਿਆਂ ਕਾਰਨ ਇੱਕ ਤਿਹਾਈ ਪੈਦਾਵਾਰ ਦਾ ਨੁਕਸਾਨ ਹੋ ਜਾਂਦਾ ਹੈ ।
- ਬੰਗਾਲ ਵਿਚ 1943 ਵਿਚ ਝੋਨੇ ਦੇ ਭੂਰੇ ਧੱਬਿਆਂ ਦੇ ਰੋਗ ਕਾਰਨ ਅਕਾਲ ਪੈ ਗਿਆ ਸੀ ।
- ਪੰਜਾਬ ਵਿਚ 1996 ਤੋਂ 2002 ਵਿੱਚ ਅਮਰੀਕਨ ਸੁੰਡੀ ਦੇ ਹਮਲੇ ਕਾਰਨ ਨਰਮੇ ਦੀ ਫ਼ਸਲ ਤਬਾਹ ਹੋ ਗਈ ਸੀ ।
- ਕੀੜੇ-ਮਕੌੜਿਆਂ ਦੀਆਂ ਜਾਤੀਆਂ ਬਾਕੀ ਹੋਰ ਪਾਣੀਆਂ ਨਾਲੋਂ ਵੱਧ ਹਨ । ਇਹ ਆਪਣੇ ਆਪ ਨੂੰ ਹਰ ਤਰ੍ਹਾਂ ਦੇ ਵਾਤਾਵਰਨ ਵਿੱਚ ਢਾਲ ਲੈਂਦੇ ਹਨ ।
- ਫ਼ਸਲ ਨੂੰ ਮੁੱਖ ਰੂਪ ਵਿੱਚ ਚਾਰ ਕਿਸਮ ਦੇ ਕੀੜੇ ਨੁਕਸਾਨ ਕਰਦੇ ਹਨ ।
- ਰਸ ਚੂਸਣ ਵਾਲੇ ਕੀੜੇ ਹਨ- ਤੇਲਾ, ਚੇਪਾ, ਚਿੱਟੀ ਮੱਖੀ ਆਦਿ ।
- ਫ਼ਲ ਅਤੇ ਤਣਾ ਛੇਦਕ ਕੀੜੇ ਹਨ-ਕਮਾਦ ਦਾ ਗੜੂਆ, ਗੁਲਾਬੀ ਸੁੰਡੀ, ਸ਼ਾਖ ਦੀ ਮੱਖੀ, ਅਮਰੀਕਨ ਤੇ ਚਿਤਕਬਰੀ ਸੁੰਡੀ, ਬੈਂਗਣਾਂ ਦੀ ਸੁੰਡੀ ਆਦਿ ।
- ਪੱਤੇ ਖਾਣ ਵਾਲੇ ਕੀੜੇ ਹਨ-ਟਿੱਡੇ, ਸੈਨਿਕ ਸੁੰਡੀ, ਲਾਲ ਭੂੰਡੀ, ਸਲੇਟੀ ਕੁੰਡੀ ਆਦਿ ।
- ਪੱਤਿਆਂ ਦੀ ਛਾਣਨੀ ਬਣਾਉਣ ਵਾਲੇ ਕੀੜੇ ਹਨ-ਹੱਡਾ ਲੂੰਡੀ, ਭੱਬੂ ਕੁੱਤਾ, ਗੋਭੀ ਦੀ ਤਿੱਤਲੀ ਆਦਿ ।
- ਜੜ੍ਹਾਂ ਨੂੰ ਨੁਕਸਾਨ ਪਹੁੰਚਾਉਣ ਵਾਲੇ ਕੀੜੇ ਹਨ। ਸਿਉਂਕ, ਚਿੱਟਾ ਸੁੰਡ ਆਦਿ ।
- ਫ਼ਸਲਾਂ ਨੂੰ ਬੀਮਾਰੀਆਂ ਜੀਵਾਣੂਆਂ, ਵਿਸ਼ਾਣੂਆਂ, ਉੱਲੀ ਆਦਿ ਕਾਰਨ ਲਗਦੀਆਂ ਹਨ ।
- ਉੱਲੀ ਨਾਲ ਹੋਣ ਵਾਲੀਆਂ ਬੀਮਾਰੀਆਂ ਹਨ-ਲਸ ਰੋਗ, ਬੀਜ ਗਲਣ ਰੋਗ, ਕਾਂਗਿਆਰੀ, ਚਿੱਟੂ ਰੋਗ !
- ਵਿਸ਼ਾਣੂਆਂ ਨਾਲ ਹੋਣ ਵਾਲੇ ਰੋਗ ਹਨ-ਠੂਠੀ ਰੋਗ, ਚਿਤਕਬਰਾ ਰੋਗ ।