Class 7

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 10 Practical Geometry MCQ Questions with Answers.

PSEB 7th Class Maths Chapter 10 Practical Geometry MCQ Questions

Multiple Choice Questions :

Question 1.
Number of parallel lines that can be drawn passing through a point not lying on the given line is :
(a) 0
(b) 1
(c) 2
(d) 3.
Answer:
(b) 1

Question 2.
The sum of three angles of a Δ is :
(a) 90°
(b) 180°
(c) 360°
(d) None
Answer:
(b) 180°

Question 3.
A triangle can be constructed by taking its sides of these :
(a) 3 cm, 5 cm, 7 cm
(b) 4 cm, 5 cm, 9 cm
(c) 4 cm, 3 cm, 8 cm
(d) 3 cm, 2 cm, 5 cm.
Answer:
(a) 3 cm, 5 cm, 7 cm

Question 4.
Two angles of a triangle are 40° and 50°. Third angle is :
(a) 40°
(b) 50°
(c) 90°
(d) 60°
Answer:
(c) 90°

Question 5.
The angles of a triangle are 30° and 50°, third angle is :
(a) 100°
(b) 60°
(c) 80°
(d) 50°.
Answer:
(a) 100°

Fill in the blanks :

Question 1.
Sum of lengths of any two sides of a triangle is …………….
Answer:
greater than third side

Question 2.
In right angled triangle.
(Hypotenuse)² = (…………….)² + (…………….)²
Answer:
Base, Perpendicular

Question 3.
SAS stands for …………….
Answer:
Side, angle, Side

Question 4.
RHS stands for …………….
Answer:
Right angle hypotenuse side

Question 5.
ASA stands for …………….
Answer:
Angle, side, angle.

Write True or False

Question 1.
Exterior angle of a triangle is equal to the sum of opposite interior angles. (True/False)
Answer:
True

Question 2.
The lengths of three sides can be used to construct a triangle. (True/False)
Answer:
True

Question 3.
The sum of the three angles of a triangle is 160°. (True/False)
Answer:
False

Question 4.
Construction of a triangle is possible when some of too angle is 180°. (True/False)
Answer:
True

Question 5.
Each angle of equilateral triangle is 60°. (True/False)
Answer:
True

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 10 Practical Geometry Ex 10.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 10 Practical Geometry Ex 10.5

1. Construct a right angled triangle ABC with ∠C = 90°, AB = 5 cm and BC = 3 cm.
Solution:
Given : Two sides of ΔABC as
AB = 5 cm,
BC = 3 cm
and ∠C = 90°.
To construct : A triangle with these two sides and one right angle.
Steps of Construction :
Step 1. We first draw a rough sketch of the triangle ABC and indicate the measure of these two sides and mark the right angle.

Step 2. Draw BC of length 3 cm.

Step 3. At C, draw CX ⊥ BC. (A should be somewhere on this perpendicular).

Step 4. With B as centre, draw an arc of radius 5 cm. (A must be on this arc since it is at a distance of 5 cm from B).

Step 5. A has to be on the perpendicular line CX as well as on the arc drawn with centre C.
∴ A is the meeting point of these two.
ΔABC is now obtained.

2. Construct an isosceles right angled triangle DEF where ∠E = 90° and EF = 6 cm.
Solution:
Given : An isoscele right angled ΔDEF where ∠E = 90° and EF = 6 cm.
To Construct: A right angled triangle with one side.
Steps of Construction:
Steps 1. Draw a rough sketch of given measures.

Step 2. Draw a line segment EF = 6 cm.

Step 3. With the help of compass taking E as centre, draw a ray EX making an angle of 90° with EF.

Step 4. With E as centre and radius 6 cm (= DE) draw an arc intersecting EX at D.

Step 5. Join D and F. Therefore ΔDEF is required isosceles right triangle.

3. Construct a right-angled triangle PQR in which :
∠Q= 90°, PQ = 3.6 cm and PR = 8.5 cm
Solution:
Given : Right triangle be PQR; right-angled at Q
i. e. ∠Q = 90°
and PQ = 3.6 cm,
PR = 8.5 cm
To construct : A triangle with these two sides and one right angle.
Steps of Construction :
Step 1. We first draw a rough sketch of the triangle PQR and indicate the measure of these two sides and mark the right angle.

Step 2. Draw PQ of length 3.6 cm.

Step 3. At Q, draw QX ⊥ PQ.
(R should be somewhere on this perpendicular).

Step 4. With P as centre, draw arc of radius
(R must be on this arc, since it is at a distance of 8.5 cm from P).

Step 5. R has to be on the perpendicular line QX as well as on the arc drawn with centre P.
∴ R is the meeting point of these two.
ΔPQR is now obtained.

4. Question (i).
Which of the following is a pythagorian triplet ?
(a) 1, 2, 3
(b) 2, 3, 4
(c) 4, 5, 6
(d) 12, 13, 5
Answer:
(d) 12, 13, 5

Question (ii).
Construction of unique triangle is not possible when :
(a) Three sides are given.
(b) Two sides and an included angle are given.
(c) Three angles are given.
(d) Two angles & included side are given.
Answer:
(c) Three angles are given.

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 11 Perimeter and Area Ex 11.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.2

1. Estimate the area of the following figures by counting unit squares.

Question (i).

Solution:
In the given figure, number of squares covered completely = 135
Area of a square = 1 sq. unit
Area of (135 square) figure = 135 sq. units, (approx.)

Question (ii).

Solution:
In the given figure number of square covered completely = 114
Area of one square = 1 unit
∴ Area of 114 squares = 114 sq units approx
Thus area of given figure = 114 sq units approx.

2. In the following figures find the area of 

Question (i).
ΔABC

Solution:
Given length of rectangle = 15 cm
Breadth of rectangle = 8 cm
The diagonal AC divides the rectangle into two triangles ΔABC and ΔADC
So, area of ΔABC = \(\frac {1}{2}\) × Area of rectangle ABCD
= \(\frac {1}{2}\) × length × breadth
= \(\frac {1}{2}\) × 15 × 8
= 60 cm²

Question (ii).
ΔCOD

Solution:
Given side of square = 6 cm
The diagonals AC and BD divides the square into four equal posses (triangles)
So, area of ΔCOD = \(\frac {1}{4}\) × Area of square
= \(\frac {1}{4}\) × 6 × 6
= 9 cm²

3. Find the area of following parallelograms.

Question (i).

Solution:
Given base of parallelogram = 9 cm
Height of parallelogram = 6 cm
Area of parallelogram = Base × height
= 9 × 6
= 54 cm²

Question (ii).

Solution:
Given base of parallelogram = 6.5 cm
Height of parallelogram= 8.4 cm
Area of parallelogram = Base × height
= 6.5 × 8.4
= 54.6 cm²

4. Find the value of x in the following parallelograms.

Question (i).

Solution:
Given base (AD) of parallelogram = 5.6 cm
Corresponding height of parallelogram = 9 cm
Area of parallelogram = 5.6 × 9 cm² ….(1)
Also in the paralleogram, base (AB) = x
Corresponding height of parallelogram = 7 cm
Area of parallelogram will be = x × 7 ….(2)
From (1) and (2), we get
x × 7 = 5.6 × 9
x = \(\frac{5.6 \times 9}{7}\)
= 7.2

Question (ii).

Solution:
Given base (AB) of parallelogram = 15 cm
Corresponding height = 6 cm
Area of parallelogram =15 × 6 cm² ….(1)
Also Base (AD || BC) of parallelogram = 9 cm
Corresponding height = x
So area of parallelogram = 9 × x ….(2)
From (1) and (2)
9 × x = 15 × 6
x = \(\frac{15 \times 6}{9}\)
= 10 cm.

5. The adjacent sides of a parallelogram are 28 cm and 45 cm and the altitude on longer side is 18 cm. Find the area of parallelogram.
Solution:
Given base of the parallelogram = 45 cm
Corresponding height = 18 cm
Area of parallelogram = Base × Height
= 45 × 18
= 810 cm2

6. ABCD is a parallelogram given in figure. DN and DM are the altitudes on side AB and CB respectively. If area of the parallelogram is 1225 cm², AB = 35 cm and CB = 25 cm, find DN and DM.

Solution:
In the given parallelogram ABCD
Base (AB) = 35 cm
Let height (DN) = x cm
So area of parallelogram = 35 × x cm²
But given area of parallelogram (ABCD) = 1225 cm²
Therefore 35x = 1225
x = \(\frac {1225}{35}\)
= 35 cm
Similarly, for base (BC) and height (DM)
1225 = BC × DM
\(\frac{1225}{\mathrm{BC}}\) = DM
or DM = \(\frac {1225}{25}\)
= 49 cm.

7. Find the area of the following triangles.

Question (i).

Solution:
Given base of triangle = 7 cm
Height of triangle = 4.8 cm
Area of triangle = \(\frac {1}{2}\) × Base × Height
= \(\frac {1}{2}\) × 7 × 4.8
= 16.8 cm².

Question (ii).

Solution:
Given base of triangle =6 cm
Height of triangle = 9 cm
Area of triangle = \(\frac {1}{2}\) × Base × Height
= \(\frac {1}{2}\) × 6 × 9
= 27 cm²

8. Find the value of x in the following triangles.

Question (i).

Solution:
In ΔABC, BC = 8 cm, AC = 15 cm
Area of triangle ABC = \(\frac {1}{2}\) × Base × height
= \(\frac {1}{2}\) × BC × AC
= \(\frac {1}{2}\) × 8 × 15
= 60 cm² …(1)
Also, in ΔABC, AB = 20 cm
height = x
Area of triangle ABC = \(\frac {1}{2}\) × Base × Height
= \(\frac {1}{2}\) × 20 × x ….(2)
From (1) and (2)
\(\frac {1}{2}\) × 20 × x = 60
x = \(\frac{60 \times 2}{20}\)
x = 6 cm.

Question (ii).

Solution:
In ΔABC, base (AC) = 25 cm
height = 14 cm
Area of triangle ABC = \(\frac {1}{2}\) × Base × height
\(\frac {1}{2}\) × 14 × 25 ….(1)
Also, in ΔABC, base AB = x cm
height = 20 cm
So, area of ΔABC = \(\frac {1}{2}\) × Base × Height
= \(\frac {1}{2}\) × x × 20 ….(2)
From (1) and (2) we get
\(\frac {1}{2}\) × x × 20 = \(\frac {1}{2}\) × 14 × 25
x = 17.5 cm

9. ABCD is a square, M is a point on AB such that AM = 9 cm and area of ΔDAM is 171 cm². What is the area of the square ?

Solution:
Given area of ΔDAM = 171 cm²
Base of triangle = 9 cm
As, area of triangle ΔDAM = \(\frac {1}{2}\) × base × height
171 = \(\frac {1}{2}\) × 9 × (DA)
Hence height (DA) = \(\frac{171 \times 2}{9}\)
= 18 cm
Hence side of square (DA) = 18 cm
Therefore area of square = (side)²
= (18)²
= 324 cm²

10. ΔABC is right angled at A as shown in figure. AD is perpendicular to BC, if AB = 9 cm, BC = 15 cm and AC = 12 cm. Find the area of ΔABC, also find file length of AD.

Solution:
Given AB = 9 cm
BC = 15 cm
AC = 12 cm
Let AD = x cm
Area of triangle = \(\frac {1}{2}\) × Base × height
= \(\frac {1}{2}\) × 12 × 9 cm².
= 54 cm² ….(1)
Since, AD is perpendicular to BC
So, area of triangle = \(\frac {1}{2}\) × BC × AD
= \(\frac {1}{2}\) × 15 × AD ….(2)
From (1) and (2) we get
\(\frac {1}{2}\) × 15 × AD = 54
AD = \(\frac{54 \times 2}{15}\)
AD = 7.2 cm

11. ΔABC is isosceles with AB = AC = 9 cm, BC = 12 cm and the height AD from A to BC is 4.5 cm. Find the area of ΔABC. What will be the height from B to AC i.e. BN ?

Solution:
In triangle ABC, Base (BC) = 12 cm
AD = 4.5 cm
AD is perpendicular to BC
So, Area of ΔABC = \(\frac {1}{2}\) × base × height
= \(\frac {1}{2}\) × 12 × 4.5 cm
= 27 cm ….(1)
Also, in ΔABC, Base (AC) = 9 cm
Let corresponding height (BN) = x
So area of ΔABC = \(\frac {1}{2}\) × base × height
= \(\frac {1}{2}\) × 9 × BN ….(2)
From (1) and (2)
\(\frac {1}{2}\) × 9 × BN = 27
BN = \(\frac{27 \times 2}{9}\)
= 6 cm.

12. Multiple choice questions :

Question (i).
Find the height of a parallelogram whose area is 246 cm² and base is 20 cm.
(a) 1.23 cm²
(b) 13.2 cm²
(c) 12.3 cm²
(d) 1.32 cm²
Answer:
(c) 12.3 cm²

Question (ii).
One of the side and the corresponding height of a parallelogram are 7 cm and 3.5 cm respectively. Find the area of the parallelogram.
(a) 21 cm²
(b) 24.5 cm²
(c) 21.5 cm²
(d) 24 cm²
Answer:
(b) 24.5 cm²

Question (iii).
The height of a triangle whose base is 13 cm and area is 65 cm² is :
(a) 12 cm
(b) 15 cm
(c) 10 cm
(d) 20 cm
Answer:
(c) 10 cm

Question (iv).
Find the area of an isosceles right angled triangle, whose equal sides are of length 40 cm each.
(a) 400 cm²
(b) 200 cm²
(c) 600 cm²
(d) 800 cm²
Answer:
(d) 800 cm²

Question (v).
If the sides of a parallelogram are increased to twice of its original length, how much will be the perimeter of the new parallelogram ?
(a) 1.5 times
(b) 2 times
(c) 3 times
(d) 4 times
Answer:
(b) 2 times

Question (vi).
In a right angled triangle one leg is double the other and area is 64 cm² find the smaller leg.
(a) 8 cm
(b) 16 cm
(c) 24 cm
(d) 32 cm.
Answer:
(a) 8 cm

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 11 Perimeter and Area Ex 11.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.1

1. Find the perimeter and the area of a rectangle having :
(i) Length = 28 cm, Breadth = 15 cm
(ii) Length = 9.4 cm Breadth = 2.5 cm
Solution:
(i) Given length of rectangle = 28 cm
Breadth of rectangle = 15 cm
Perimeter of rectangle = 2 [length + Breadth]
= 2 [28 + 15]
= 2 × 43
= 86 cm

Area of rectangle = length × Breadth
= 28 × 15
= 420 cm²

(ii) Perimeter of rectangle = 2 [9.4 + 2.5]
= 2 × 11.9
= 23.8 cm
Area of rectangle = 9.4 × 2.5
= 23.5 cm²

2. Find the perimeter and the area of a square whose side measures
(i) 29 cm
(ii) 8.3 cm
Solution:
(i) Given side of square = 29 cm
Perimeter of square = 4 × side
= 4 × 29
= 116 cm
Area of square = (side)²
= (29)²
= 841 cm²

(ii) Perimeter of square = 4 × 8.3
= 33.2 cm
Area of square = 8.3 × 8.3
= 68.89 cm²

3. The perimeter of a square park is 148 m. Find its area.
Solution:
Given the perimeter of square park = 148 m
Side of the square park = \(\frac{perimeter}{4}\)
= \(\frac {148}{4}\)
Area of the square park = (side)²
= (37)²
= 1369 m²

4. The area of a rectangle is 580 cm². Its length is 29 cm. Find its breadth and also, the perimeter.
Solution:
Given area of rectangle = 580 cm²
Length of the rectangle = 29 cm
Let breadth of the rectangle = b cm
Area of the rectangle = length × breadth
580 = 29 × b
\(\frac {580}{29}\) = b
b = 20 cm
Perimeter of rectangle = 2 [length + breadth]
= 2 [29 + 20]
= 2 × 49
= 98 cm

5. A wire is in the shape of a rectangle. Its length is 48 cm and breadth is 32 cm. If the same wire is rebent into the shape of a square, what will be the measure of each side. Also, find which shape encloses more area and by how much ?
Solution:
Given length of the rectangle = 48 cm
Breadth of the rectangle = 32 cm
Perimeter of the rectangle = 2 [length + breadth]
= 2 [48 + 32]
= 2 × 80
= 160 cm
Let side of square = a cm
Perimeter of the square = 4 × a
Since wire is rebent into the shape of a square
Perimeter of square = Perimeter of rectangle
4 a = 160
Therefore, a = \(\frac {160}{4}\)
= 40 cm
Area of square = (side)²
= 40 × 40
= 1600 cm²
Area of rectangle = length × breadth
= 48 × 32
= 1536 cm²
∴ Square encloses more area by 64 cm²

6. The area of a square park is the same as that of a rectangular park. If the side of the square park is 75 m and the length of the rectangular park is 125 m, find the breadth of the rectangular park. Also, find the perimeter of rectangular park.
Solution:
Given side of square park = 75 m
Area of square park = (75)²
= 75 × 75
= 5625 m²
Length of rectangular park = 125 m
Let breadth of rectangular park = b m
Area of rectangular park = length × breadth
= 125 × b m²
Given that
Area of rectangular park = Area of square park
125 × b = 5625
= 45 m
Perimeter of rectangular park = 2 [length + breadth]
= 2 [125 + 45]
= 2 × 170
= 340 m

7. A door of length 2.5 m and breadth 1.5 m is fitted in a wall. The length of wall, is 9 m and breadth is 6 m. Find the cost of painting the wall, if the rate of painting the wall is ₹ 30 per m².

Solution:
Length of door = 2.5 m
Breadth of door = 1.5 m
Area of door = length × breadth
= 2.5 × 1.5
= 3.75 m²
Area of wall = 9 × 6
= 54 m²
Area of wall painting = Area of wall including door – Area of door
= 54 – 3.75
= 50.25 m²
Cost of painting 1 m² of wall = ₹ 30
Cost of painting 50.25 m² of wall = ₹ 50.25 × 30
= ₹ 1507.50

8. A door of dimensions 3 m × 2 m and a window of dimensions 2.5 m × 1.5 m is fitted in a wall. The length of the wall is 7.8 m and breadth is 3.9 m. Find the cost of painting the wall, if the rate of painting the wall is ₹ 25 per m².
Solution:
Area of door = 3 × 2 = 6 m²
Area of window = 2.5 m × 1.5 m
= 3.75 m²
Area of wall = 7.8 m × 3.9 m
= 30.42 m²
Area of painting the wall = Area of wall – Area of door – Area of window
= 30.42 – 6 – 3.75
= 20.67 m²
Cost of painting the wall = ₹ 25 × 20.67
= ₹ 516.75

9. Find the area and the perimeter of the following figures.

Solution:
(i) Perimeter of the given figure
= AB + BC + CD + DE + EF + FG + GH + HA
= 2 + 3.5 + 3 + 2 + 5 + 3.5 + 10 + 9
= 38 cm²
Area of the figure = Area of rectangle ABCJ + Area of rectangle JDEI + Area of rectangle IFGH
= 2 × 3.5 + 5 × 2 + 10 × 3.5
= 7 + 10 + 35
= 52 cm²

(ii) Perimeter of the given figure
= 8cm + 5 cm + 1.5 cm + 2.5 cm + 2.5 cm + 1.5 cm + 1.5 cm + 1.5 cm + 2.5 cm + 1.5 cm
= 29 cm
Area of the given figure = Area of rectangle I + Area of rectangle II + Area of rectangle III
= 8 cm × 1.5 cm + 3.5 cm × 1.5 cm + 1.5 cm × 1.5 cm
= 12 cm² + 5.25 cm² + 2.25 cm
= 19.5 cm²

10. Multiple Choice Questions :

Question (i).
What is the area of a rectangle of dimensions 12 cm × 10 cm ?
(a) 44 cm²
(b) 120 cm²
(c) 1200 cm²
(d) 1440 cm²
Answer:
(b) 120 cm²

Question (ii).
Find the breadth of a rectangle whose length is 12 cm and perimeter is 36 cm.
(a) 6 cm
(b) 3 cm
(c) 9 cm
(d) 12 cm
Answer:
(a) 6 cm

Question (iii).
If each side of a square is 1 m then its area is ?
(a) 10 cm²
(b) 100 cm²
(c) 1000 cm²
(d) 10000 cm²
Answer:
(d) 10000 cm²

Question (iv).
Find the area of a square whose perimeter is 96 cm.
(a) 576 cm²
(b) 626 cm²
(c) 726 cm²
(d) 748 cm².
Answer:
(a) 576 cm²

Question (v).
The area of a rectangular sheet is 500 cm². If the length of the sheet is 25 cm, what is its breadth ?
(a) 30 cm
(b) 40 cm
(c) 20 cm
(d) 25 cm.
Answer:
(c) 20 cm

Question (vi).
What happens to the area of a square, if its side is doubled ?
(a) The area becomes 4 times, the area of original square.
(b) The area becomes \(\frac {1}{4}\) times, the area of original square.
(c) The area becomes 16 times, the area of original square.
(d) The area becomes \(\frac {1}{6}\) times, 6 the area of original square.
Answer:
(a) The area becomes 4 times, the area of original square.

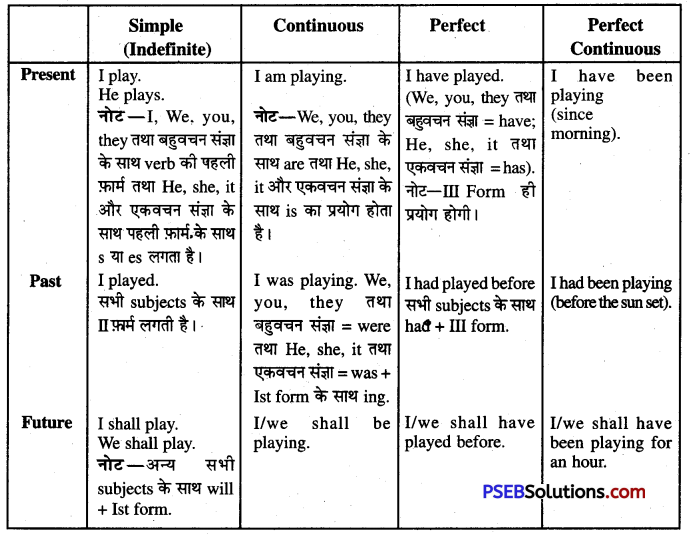
Punjab State Board PSEB 7th Class English Book Solutions English Reading Comprehension Conversation / Dialogue Based Exercise Questions and Answers, Notes.

PSEB 7th Class English Reading Comprehension Conversation / Dialogue Based

Read the following conversation carefully and answer the questions that follow:

1. Akbar : Birbal make me a painting. Use your imagination in it.
Birbal : I am not an artist, how can I paint ?
Akbar : If I don’t get a good painting, you shall be punished.
Birbal : (Next day) I am here with the painting.
Akbar : I am happy to see that you obeyed me. Please show me the painting.
Birbal : Huzoor, have a look. I am opening the covered frame.
Akbar : This painting is nothing but only ground and sky. There is a little grass on the ground. What is this?
Birbal : A cow eating grass, Huzoor!
Akbar : Where is the cow and grass ?
Birbal : I used my imagination. The cow ate the grass and returned to its shed.

Question 1.
The given conversation is between ……………
(a) Birbal and Begum
(b) Birbal and his Son
(c) Akbar and his Son
(d) Akbar and Birbal.
Answer:
(d) Akbar and Birbal.

Question 2.
What did Akbar want Birbal to make for him?
(a) a cake
(b) a painting
(c) a dish
(d) all of the above.
Answer:
(b) a painting.

Question 3.
Who ate the grass ?
(a) cow
(b) cat
(c) camel
(d) goat.
Answer:
(a) cow.

Question 4.
What was in the painting ?
(a) ground and sky
(b) boy and sky
(c) girl and kite
(d) cat and dog.
Answer:
(a) ground and sky.

Question 5.
Birbal carried a ……………. with him.
(a) covered glass
(b) covered frame
(c) covered bowl
(d) covered box.
Answer:
(b) covered frame.

2. Sadab : Good afternoon.
Ritu : Good afternoon.
Sadab : So, where are you going now?
Ritu : I am going to meet my friend Garima in Kolkata Market.
Sadab : Oh, so nice, I have to buy a new school uniform.
Ritu : Will you accompany me ?
Sadab : Yes, it will be great fun for me.
Ritu : So, can we move now so that we can reach on time.
Sadab : Sure.

Question 1.
This conversation is between ………..
(a) Sadab and Garima
(b) Ritu and Garima
(c) Ritu and Sadab
(d) Garima and Kolkata Market.
Answer:
(c) Ritu and Sadab.

Question 2.
Where is Ritu going ?
(a) to meet her sister Garima
(b) to meet her friend Garima
(c) to meet her teacher
(d) to buy a school uniform.
Answer:
(b) to meet her friend Garima.

Question 3.
Garima will be found ……………
(a) in Kolkata market
(b) in Bombay market
(c) in Kolkata street
(d) in Sadab market.
Answer:
(a) in Kolkata market.

Question 4.
What does Sadab want to buy ?
(a) some new books
(b) a new mobile phone
(c) a new school uniform
(d) new shoes.
Answer:
(c) a new school uniform.

Question 5.
What was the time of conversation ?
(a) early morning
(b) afternoon
(c) late evening
(d) night.
Answer:
(b) afternoon.

3. Headman Ant asked, “What happened ? Why are you running ?” Rabbit said, “We’re running for our lives. I heard the news of Tsunami, very high sea waves.”

Headman Ant asked everyone to stay calm and explained that they were just testing the warning system. It didn’t happen for real. Let us all be prepared to deal with disasters.

Next day at the village meeting, everyone gave their ideas.

Elephant : “We should always follow news carefully.”
Butterfly : “I have already put my valuable things away in a safe place.”
Rats : “I have prepared survival bag which will always be close to me. I have kept a bottle of water, medicines, dried food, some beans, the radio for news and a family photo.”
Mother Frog : “My kids will not go out to play by themselves in hazardous places.”
Mother Goat : “We must run to higher grounds or to the safe areas. I shall make a map of the village.
Headman Ant : “Why didn’t you run like asked Grandpa others ?
OX : ……..
Grandpa OX : “We are too old. We don’t want to be a burden to anyone.”
Headman Ant : (said politely) “No one is a burden. What would your grandchildren do without you ??

Question 1.
Rabbit was running for life because he had heard the news of ……………
(a) Earthquake
(b) Tsunami
(c) Flash flood
(d) Land slide.
Answer:
(b) Tsunami.

Question 2.
What did the Headman Ant tell the animals about the news ?
(a) It was real
(b) It was to create panic only
(c) It was not real
(d) It was to entertain the old people.
Answer:
(c) It was not real.

Question 3.
Who is most careful about news ?
(a) Grandpa Ox
(6) Rabbit
(c) Elephant
(d) Frog.
Answer:
(c) Elephant.

Question 4.
Which one of the following is not true according to the conversation ?
(a) The elephant was not present at the meeting
(6) Grandpa Ox does not want to be a burden to anyone
(c) Mother Goat wants to run to the higher places
(d) Rats have prepared survival bags.
Answer:
(a) The elephant was not present at the meeting.

Question 5.
Tsunami is a ……………..
(a) safe place from high sea wave
(b) very high sea wave
(c) cool breeze coming from sea
(d) dry wind blowing towards sea.
Answer:
(b) very high sea wave.

4. Ali : Hello ! I’m Ali. What’s your name?
Ravi : Hello ! My name’s Ravi. I’m ten years old.
Ali . : I’m ten, too. Do you play cricket ?
Ravi : Not very well. I’m fond of football.
Ali : Oh, good ! Will you help me with my homework?
Ravi : Of course, I will. Come to me during the break.
Ali : Thanks. I’ll help you play cricket.
Ravi : That will be great. Thank you !
Ali : : Where do you live ?
Ravi : I live near the school and Ali, where do you live?
Ali : I live in the school hostel.

Question 1.
What is common between Ali and Ravi ?
(a) both are ten years old
(b) both play cricket very well
(c) both live in the school hostel
(d) both are fond of playing football.
Answer:
(a) both are ten years old.

Question 2.
Where does Ali live ?
(a) near the school
(b) in the school hostel
(c) near the football club
(d) near the cricket club.
Answer:
(b) in the school hostel.

Question 3.
Ali will help Ravi ……………
(a) play football
(b) do his homework
(c) play cricket
(d) all the above.
Answer:
(c) play cricket.

Question 4.
Ravi will help Ali ………
(a) play cricket
(b) play football
(c) do his homework
(d) none of these.
Answer:
(c) do his homework.

Question 5.
When will Ravi help Ali with his homework?
(a) after playing cricket
(b) after playing football
(c) when the school starts
(d) during the break.
Answer:
(d) during the break.

5. Ravi : Do you know what time it is now, please ?
Aman : No, I’m really very sorry, I don’t have a watch.
Rama : Could you tell me the time, please ?
Radha : It’s about eleven-thirty.
Rama : Thanks a lot.
Radha : At what time do you come to school ?
Rama : At 8:30 in the morning.
Radha : At what time does the school get over ?
Rama : At 3 o’clock in the afternoon.
Ajay : What time is the next bus, please ?
Anil : It leaves at 5:30 p.m.
Ajay : Is there any bus after 10 p.m. ?
Anil : The last bus leaves at 10:30 p.m.
Ajay : Thanks a lot for the information.

Question 1.
The main point in this conversation is …………… .
(a) bus
(b) time
(c) watch
(d) school.
Answer:
(b) time.

Question 2.
Aman is unable to tell Ravi time because …………….
(a) he is in a hurry
(b) he is very sorry
(c) he has no watch
(d) he has no clock.
Answer:
(c) he has no watch.

Question 3.
When does Rama go to school ?
(a) at 8:30
(b) at 3 o’clock
(c) at 11:30
(d) at 10 o’clock.
Answer:
(a) at 8:30.

Question 4.
What does Ajay want to know ?
(a) times about school
(b) times about buses
(c) time by Aman’s watch
(d) none of these.
Answer:
(b) times about buses.

Question 5.
Who tells Ajay time for last bus ?
(a) Rama
(b) Anil
(c) Radha
(d) Aman.
Ans.
(b) Anil.

6. Raj : Could you help me, please ?
Shopkeeper : Certainly.
Raj : Thank you.
Shopkeeper : What can I get you ?
Raj : A black shoe polish.
Rani : Excuse me please, where are the pens ?
Shopkeeper : They are in the second row. Let me help you.
Rani : How much do the two pens cost ?
Shopkeeper : The price is written on them. They cost Rs. 10 each.
Rani : Thank you.

Question 1.
Whose help does Raj ask for ?
(a) Rani’s
(b) shopkeeper’s
(c) nobody’s
(d) his own.
Answer:
(b) shopkeeper’s.

Question 2.
Raj wants to buy a ……………..
(a) brown shoe polish
(b) black shoe polish
(c) some pens and a polish
(d) none of these.
Answer:
(b) black shoe polish.

Question 3.
The pens are lying
(a) in a box
(b) in the first row
(c) in the second row
(d) on the upmost shelf.
Answer:
(c) in the second row.

Question 4.
How many pens does Rani want to buy ?
(a) two
(b) three
(c) one.
(d) four.
Answer:
(a) two.

Question 5.
How much do the two pens cost ?
(a) Rs. 20
(6) Rs. 10
(c) Rs. 30
(d) Rs. 15.
Answer:
(a) Rs. 20.

7. Aryan : Why are you wearing this funny dress, Praveen ?
Praveen : Aryan, what is funny about it?
Aryan : Look at your clothes ! They look so tight, and your shoes have wheels. And what’s that you have on your head ?
Praveen : (laughs) Oh, are you talking about this dress ? I’m going for my skating class and this is my helmet to save me from injuries.
Aryan : Skating ?
Praveen : Yes, skating. That’s why I’m wearing these roller skating shoes.
Aryan : Where are you going for your skating class ?
Praveen : I’m going to the ‘Roller Mall’. It has a skating rink.
Aryan : Could I come with you to see what you do there?
Praveen : Sure, come along. (They reach the skating rink.) Aryan (amazed) Oh, so many people moving on the wheels !
Praveen : They’re all skaters moving on roller skates.
Aryan : Look ! How they all are gliding on the floor. I wish I could do the same. Will you teach me how to skate ?
Praveen : Oh yes, whenever you are ready.
Aryan : Thanks.

Question 1.
Praveen’s dress looks funny to Aryan. Why?
(a) It is very tight.
(b) His shoes have wheels.
(c) There is a, helmet on his head.
(d) all these.
Answer:
(d) all these.

Question 2.
Praveen is going to …………
(a) his school to take part in a drama
(b) a park for a picnic
(c) perform a magic show
(d) his skating class.
Answer:
(d) his skating class.

Question 3.
A helmet saves us from …………
(a) foot injuries
(b) severe cold on ice
(c) head injuries
(d) all the above.
Answer:
(c) head injuries.

Question 4.
What does Aryan want to learn ?
(a) skating
(b) use of wheeled shoes
(c) using a helmet
(d) wearing a tight dress.
Answer:
(a) skating.

Question 5.
Who will teach Aryan how to skate ?
(a) skating teacher
(b) his elder brother
(c) Praveen
(d) class teacher.
Answer:
(c) Praveen.

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 10 Practical Geometry Ex 10.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 10 Practical Geometry Ex 10.2

1. Construct ΔABC in which AB = 3.5 cm, BC = 5 cm and CA = 7 cm.
Solution:
Given : Three sides of a triangle as AB = 3.5 cm, BC = 5 cm and CA = 7 cm.
To construct : A triangle with these three sides.
Step 1. We first draw a rough sketch of the triangle ABC and indicate the lengths of the three sides.

Step 2. Draw a line segment BC = 5 cm.

Step 3 : From B; point A is at a distance 3.5 cm. So, with B as centre, draw an arc of radius
3.5 cm (Now point A will be some where on this arc. Our job is to find where exactly A is.)

Step 4. From C, point A is at a distance of 7 cm. So, with C as centre; draw an arc of radius 7 cm. (A will be some where on this arc. We have to fix it).

Step 5. A has to be on both the arcs drawn. So it is the point of intersection of arcs.
Mark the point of intersection of arcs as A. Join AB and AC.
Thus we obtain ΔABC.

2. Construct a triangle ABC in which AB = BC = 6.5 cm and CA = 4 cm. Also name the kind of triangle drawn.
Solution:
Given : Three sides of triangle as AB = BC = 6.5 cm. and CA = 4 cm.
To construct : A triangle with these three sides.
Steps of Construction :
Step 1. We first draw a rough sketch of the triangle ABC and indicate the lengths of the three sides.

Step 2. Draw a line segment AC = 4 cm.

Step 3. From A; point B is at a distance of 6.5 cm. So, with A as centre, draw an arc of radius 6.5 cm. (Now point B will be somewhere on this arc. Our job is to find where exactly A is.)

Step 4. From C; point B is at a distance of 6.5 cm. So; with C as centre; draw an arc of radius 6.5 cm. (B will be some where on this arc. We have to fix it.)

Step 5. B has to be on both the arcs drawn. So it is the point of intersection of arcs. Mark the point of intersection of arcs as B. Join AB and BC.

We observe that AB = BC = 6.5 cm.
Since two sides are of equal length. Thus we obtain an isosceles ΔABC.

3. Construct a triangle XYZ such that length of each side is 5 cm. Also name the kind of triangle drawn.
Solution:
Given : A triangle XYZ in which XY = YZ = ZX = 5 cm..
To Construct. A triangle XYZ with each side 5 cm.
Steps of Construction :
Step 1. We first draw a rough sketch of the triangle XYZ and indicate the lengths of the three sides.

Step 2. Draw a line segment YZ = 5 cm.

Step 3. From Y; point X is at a distance of 5 cm. So, with Y as centre, draw an arc of radius 5 cm. (Now point X will be somewhere on this arc. Our job is to find where exactly X is.)

Step 4. From Z, point X is at a distance of 5 cm. So, with Z as centre, draw an arc of radius 5 cm. (X will be somewhere oh this arc. We have to fix it.)

Step 5. Point X has to be on both the arcs drawn. So, it is the point of intersection of arcs.
Mark the point of intersection of arcs as X. Join XY and XZ.

Thus we obtain an equilateral ΔXYZ each of whose side is 5 cm.

4. Construct a triangle PQR such that PQ = 2.5 cm, QR = 6 cm and RP = 6.5 cm. Measure ∠PQR and also name the kind of triangle drawn.
Solution:
Given. Three sides of triangle as PQ = 2.5 cm, QR = 6 cm and RP = 6.5 cm.
To construct. A triangle with these three sides.
Steps of Construction :
Step 1. We first draw a rough sketch of the triangle PQR and indicate the lengths of the three sides.

Step 2. Draw a line segment QR of length 6 cm.

Step 3. From Q; point P is at a distance of 2.5 cm. So, with Q as centre, draw an arc of radius 2.5 cm. (Now point P will be some where on this arc. Our job is to find where exactly P is.)

Step 4. From R; point P is at a distance of 6.5 cm. So; with R as centre; draw an arc of radius 6.5 cm. (P will be somewhere on this arc. We have to fix it.)

Step 5. Point P has to be on both the arcs drawn. So, it is the point of intersection of arcs. Mark a point of intersection of arcs as P. Join PQ and PR.

Thus we obtain ΔPQR; on measuring ∠PQR, we observe that ∠PQR = 90° so it is a right angled triangle.

5. Construct a triangle ABC, in which AB = 6 cm, BC = 2 cm, CA = 3 cm. (If possible). If not possible give the reason.
Solution:
Since AB = 6 cm, BC = 2 cm, CA = 3 cm
Here BC + CA = 2 cm + 3 cm
= 5 cm < 6 cm < AB
Which is not possible because the sum of two sides of a triangle is always greater than third side of the triangle.

6. Question (i).
Which of the following can be used to construct a triangle ?
(a) The lengths of the three sides
(b) The perimeter of the triangle
(c) The measures of three angles
(d) The name of three vertices
Answer:
(a) The lengths of the three sides

Question (ii).
A triangle can be constructed by taking its sides as :
(a) 1.8 cm, 2.6 cm, 4.4 cm
(b) 3 cm, 4 cm, 8 cm
(c) 4 cm, 7 cm, 2 cm
(d) 5 cm, 4 cm, 4 cm.
Answer:
(d) 5 cm, 4 cm, 4 cm.

Punjab State Board PSEB 7th Class English Book Solutions English Notice Writing Exercise Questions and Answers, Notes.

PSEB 7th Class English Notice Writing

Notice लोगों को किसी घटना की जानकारी देने का संदेश अथवा समाचार होता है। उदाहरण के लिए किसी स्कूल के Notice-board पर विद्यार्थियों को स्कूल की विभिन्न गतिविधियों की जानकारी दी जा सकती है। Notice लिखते समय अग्रलिखित बातों का उल्लेख अवश्य करें:

1. शीर्षक-इसमें स्पष्ट किया जाना चाहिए कि Notice किसके लिए है।
2. Notice लिखे जाने की तिथि
3. संबंधित घटना का दिन, समय तथा स्थान
4. Notice के नीचे लिखने वाले का नाम, पद, पता आदि।
5. शब्द-सीमा लगभग 30 शब्दों तक।

1. You are the PTI of your school. Write a notice asking the students to enrol for free yoga classes.

Free Yoga Classes

Attention!

20 March 20 ……

All students interested in attending free yoga classes from 10th April every. morning from 6 a.m. to 7 a.m. should contact the undersigned before 7th April.

Sd/
B.S. Bedi
PTI

2. You are the librarian of your school. Write a notice asking the students to return borrowed books before the school closes down.

Attention!

10 March 20…….

The school is going to be closed down for the summer vacation next week. All students who have borrowed any book from the library must return it before the school closes down.

Raman Kumar
Librarian

3. You are Anupam, the editor of the school magazine, and want to hold an interclass competiton to collect poems and cartoons for the magazine before Sept. 9. Draft a notice for the students ‘Notice-board inviting entires.

Interesting Contest, Amazing Prizes

We are going to hold an inter-class compition to collet poems and cartoons for the school magazine. Entries for the same are invited to reach the under signed befors 9th September. The result of the contest will be declared on 15th. The best poem and cartoon shall win a free school blazer. There will be some consolation prizes to.

4. You are Sangeets, the secretary of the school quiz club. You want to hold an inter-class competition to decide on entires for an inter-school competition 2 weeks from now. Draft a notice for the students notice-board inviting participants.

Prizes Through Quizzes

An inter-school quiz-competition is going to be held two weeks from now. In order to decide entreis for the same, we have decided to hold on inter-class competition on Monday, the 15th. All those who desire to participets schould give their name to the undersigned by tomorrow. The three best participants shall be awarded free school blazers Sangeeta.

(Secretary, School Quiz Club.)

5. You are Kulbir Singh of Class VII. You have lost your new water bottle. Write the notice that you would like to put up on the school notice-board.

Lost ! Lost ! Lost !

12 March 20……..

I have lost my new water bottle somewhere in the school garden. The bottle is of Eagle make with blue colour. The finder is requested to return it to me or deposit it with the school office.

Kulbir Singh
Roll No. 2
VII B.

6. You are the Sarpanch of your village. Write a notice inviting adults to donate blood at the blood donation camp to be held at the community centre.

Blood Donation Camp

8 March 20 ………

The village Panchayat is going to organise a blood donation camp in the community centre on 8th April from 9 a.m. to 11 a.m. All the adults of the village should come forward and donate blood to save lives of many.

Balwan Singh
Village Sarpanch.

7. You have misplaced a library book ‘Panchtantra Tales’. Write a notice that you would like to put up in the classroom.

Book Misplaced

10 March 20 …….

I have misplaced my book “Panchtantra Tales’ somewhere in the classroom. I borrowed it from the library yesterday. The finder is requested to return it to me or deposit it with the class teacher.

Rajni
Roll No. 5
VII A.

8. You are the sports captain of your school. Write a notice to all participants to submit their names and event in which they are taking part.

Attention ! Sports Participants

02 May 20 …….

All the participants in the school sports are requested to submit their names with the undersigned before Sunday, the 6th May. They must mention the event they are taking part in.

Geeta Sharma
Sports Captain
Khalsa Girls High School, Moga.

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 10 Practical Geometry Ex 10.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 10 Practical Geometry Ex 10.4

1. Construct ΔABC, given AB = 6 cm, ∠A = 30° and ∠B = 75°.
Solution:
Given. One side of ΔABC as AB = 6 cm, m∠A = 30° and m∠B = 75°.
To construct: A triangle with one side and these two angles.
Steps of Construction :
Step 1. We first draw a rough sketch of ΔABC and indicate the measures of side and two angles.

Step 2. Draw a ray AB of length 6 cm.

Step 3. At A; draw a ray AX making an angle 30° with AB.

Step 4. With the help of compass. At B; draw a ray BY making an angle of 75° with AB.

Step 5. Both rays AX and BY intersect, at a point. So the point of intersection of the two rays is C Then. ΔABC is now obtained.

2. Construct an isosceles ΔABC such that AB = 5.3 cm and each base angle = 45°.
Solution:
Given : Isosceles ΔABC with AB = 5.3 cm each base angle = 45°.
To Construct: A triangle with one side and two base angles.
Steps of construction :
Step 1. Draw a rough sketch of ΔABC with given measures

Step 2. Draw a line segment AB = 5.3 cm.

Step 3. Taking A as centre with the help of compass. Draw a ray AX making an angle 45° with AB.

Step 4. With the help of compass and taking B as a centre. Draw a ray BY making an angle 45° with the line segment AB.

Step 5. Rays AX and BY intersect, at a point say C, then ABC is the required triangle.

3. Construct ΔXYZ if XY = 4 cm, ∠X = 45° and ∠Z = 60°.
[Hint : ∠Y = 180° – 45° – 60° = 75°]
Solution:
One side of ΔXYZ as
XY = 4 cm,
∠X = 45°
and ∠Z = 60°.
As we know that by angle-sum property of a triangle; sum of all three angles of a triangle is equal to 180°.
∴ ∠X + ∠Y + ∠Z = 180°
⇒ 45° + ∠Y + 60° = 180°
⇒ 105° + ∠Y = 180°
⇒ ∠Y = 75°.
Now it will be easy to construct triangle with side
XY = 4 cm,
∠X = 45°
and ∠Y = 75°.
Steps of Construction :
Step 1. We first draw a rough sketch of ΔXYZ and indicate the measure of side and two angles.

Step 2. Draw a ray XY of length 4 cm.

Step 3. At X draw a ray XA making an angle of 45° with XY.

Step 4. At Y; draw a ray YB making an angle of 75° with XY.

Step 5. Z has to lie on both rays XA and YB. So, the point of intersection of two rays is Z.
ΔXYZ is now obtained.

4. Examine whether you can construct ΔPQR such that ∠P = 100°, ∠Q = 90° and PQ = 4.3 cm If not possible given reason.
Solution:
No, we cannot construct given ΔPQR.
Reason :
As we know that by angle sum property of a triangle; sum of all three angles a triangle is equal to 180°. But in given question sum of two angles;
m∠P + m∠Q
= 100° + 90°
= 190°
The sum of these two angles should be less than 180°. So triangle with given measures cannot be constructed as it violates the angle sum property of a triangle.

5. Question (i).
In which of the following cases a unique triangle can be drawn ?
(a) BC = 5 cm, ∠B = 90° and ∠C = 100°
(b) AB = 4 cm, BC = 7 cm and CA = 2 cm
(c) XY = 5 cm, ∠X = 45°, ∠Y = 60°
(d) An isosceles triangle with length of each equal side equal to 5 cm.
Answer:
(c) XY = 5 cm, ∠X = 45°, ∠Y = 60°

Question (ii).
A triangle can be constructed by taking two of its angles as.
(a) 110°, 40°
(b) 70°, 115°
(c) 135°, 45°
(d) 90°, 90°
Answer:
(a) 110°, 40°

Punjab State Board PSEB 7th Class English Book Solutions English Grammar Tense Exercise Questions and Answers, Notes.

PSEB 7th Class English Grammar Tense

Study the Chart

Exercise 1

I. Fill in the blanks with the right tense form of the verb given in the brackets:

1. Our school ……………………… (begin) with a prayer everyday.
2. Ahmed ……………………… (keep awake) till midnight these days.
3. What…………….(make) you do so ?
4. This box ………………….. (contain) a gift for him.
5. This road is closed. They …………………….. (repair) it.
6. The clerk ……………. (type) the letter still, he never …………… (finish) the work in time.
7. Don’t make a noise. An important meeting ……………………. (go on) here. 8. She
8. ………… (say) a prayer to God regularly before going to bed.
9. The peon ……………….. (ring) the bell now.
10. We ……………. (feel) uneasy on a very hot day.
Hints:
1. begins
2. keeps awake
3. makes
4. contains
5. are repairing
6. is typing, finishes
7. is going on
8. says
9. is ringing
10. feel.

Exercise 2

Fill in the blanks with the right tense form of the verb given in the brackets: (Use Present Perfect Tense)

1. The water level …………………… (go up) because of rains.
2. The doctor ……………………. (examine) the patient. He is improving now.
3. I ……………………… (finish) my work. I am going home now.
4. They ………………….. (leave) the place.
5. Sheela …………………. (learn) her lesson.
6. Father ………………………. (not come) home for lunch yet.
7. ………………… you ………………. (finish) your work ? Can you come with me now?
8. I ……………………. (study) the problem. It is easy to solve.
9. ………….. he ………. (take charge) of his new assignment ?
10. The train …………………………… (leave) the station. The platform looks deserted.
Hints:
1. has gone up
2. has examined
3. have finished
4. have left
5. has learnt
6. has not come
7. Have, finished
8. have studied
9. Has, taken charge
10. has left.

Exercise 3

Fill in the blanks with the right tense form (Past Continuous or Simple Past) of the verbs given in brackets:

1. She ………………… (look) for a book shop, when I ………………….. (meet) her.
2. The policeman …………………… (arrest) the thief, when I …………………… (see) him.
3. I……………………………… (go) to the cattle-shed, when I …………………….. (hear) someone quarrelling.
4. The sarpanch ………… (take) the horse out of the stable, when I ……. (call) him.
5. Yesterday as I …………. (walk) along the street. I ……………………… (meet) my friend.
6. In January 1948 Gandhiji ……………………… (stay) in Delhi. He was shot while he ……………. (come out) of the prayer meeting.
7. While I …………………. (watch) the T.V., the lights ………….. (go off).
Hints:
1. was looking, met
2. was arresting, saw
3. was going, heard
4. was taking, called
5. was walking, met
6. was staying, was coming out
7. was watching, went off.

Exercise 4

Fill in the blanks using the verbs in the brackets according to the tense form indicated:

1. A group of officials ……….. (go) to Delhi tomorrow. (Simple Future)
2. We …………………… (visit) Kashmir next January. (Future Continuous)
3. What …………………….. you ……………(do) tomorrow evening ? (Future Continuous)
4. I …….. (go) with my brother. I am sure I ……………… (have) a very nice time on this (Simple Future)
5. I want to give this book to Jaspreet …………………… you ……………………… (go) to give this book to her ? (Simple Future)
Hints:
1. will go
2. shall be visiting
3. will, be doing
4. shall go, will have
5. will, go.

Exercise 5

Fill in the blanks to express Future Perfect aspects of the verbs given in the brackets.

1. The police …………………… (arrest) the thief by tomorrow.
2. Davinder. ………………… (tell) me all before you talk to him.
3. He ………………….. (return) before you arrive.
4. Gobind ……………………. (write) the story before you return.
5. We …………………… (enjoy) our holidays for about a month before he arrives.
Hints:
1. will have arrested
2. will have told
3. will have returned
4. will have written
5. shall have enjoyed.

Exercise 6
(Miscellaneous)

I. Underline the verb and write in the space given whether the sentence is in the Present, Past or Future Perfect tense. One has been done for you.

1. The rain had stopped before I arrived. (Past Perfect Tense)
2. I have lived in Bhatinda since childhood. (Present Perfect Tense)
3. We shall have reached home before they arrive. (Future Perfect Tense)
4. The children shall have eaten something by the time I reach home, (Future Perfect Tense)
5. She has not finished writing the book. (Present Perfect Tense)
6. The watchman had run away before the owner reached. (Past Perfect Tense)
7. The children have learnt the song. (Present Perfect Tense)
8. Naaz has posted the letter. (Present Perfect Tense)
9. My uncle has given me a room in the new house. (Present Perfect Tense)
10. They will have left for Patiala by night. (Future Perfect Tense)

II. Complete the following letter by using the verb in the bracket in present perfect/ past tense. One has been done for you:

Dear sir
I wrote (write) to you some time ago-asking about conditions of entry to your competition. You replied (reply) enclosing an entry form which I filled up (fill up) and sent (send) without delay. I have heard (hear) nothing from you and am beginning to wonder if my application has gone (go) astray. Please check if you have received (receive) it or not. In case you have not got (not get) it. Kindly inform me.

Thanking you
Yours faithfully
Amarjit Singh

III. You have planned to undertake a railway journey in your summer holidays. In about ten sentences describe your forth coming trip using simple future tense.

I will go to Amritsar during summer holidays. I will go by train. I will catch the train from Ludhiana. I will go to the railway station. I will buy a ticket and go to the platform to board the train. The train will reach Amritsar within three hours. There, I will stay in a hotel. I will visit Sri Harmandar Sahib. I will have a holy dip in the tank there. I will also visit the Durgiana Mandir. I will not miss to see the Jallianwala Bagh before I come back.

IV. Your house is flooded due to heavy rains. You saved yourself by sitting on the roof top for almost three days and nights. Using simple and continuous past tense, write your experience.

I found water all around me. It was rising continually. I, with my family, took shelter on the roof of my house. We took with us all the eatables available in home. There was a large carpet at the roof. At night we slept on it. But the rain did not stop for three days. All our eatables were consumed. We grew weaker and weaker. We prayed to God for help. Then one day, it stopped raining. We came down, took buckets and threw the water out of the house. We thanked God for saving our lives.

V. Supply for the blanks the future perfect tense of the verb given in the brackets:

1. Our maid will have broken all the cups (break).
2. He …………..by that time. (return)
3. The sun …………… when we reach home. (set)
4. We …………. all the cakes by evening. (eat)
5. She ……………for the family by night. (cook)
6. He …………. his pledge. (keep)
7. Each child …………… a new pull over. (bought)
8. The shoeshine …………… my shoes. (polish)
9. The commander ………….. the army to march. (order)
10. I……………. the job by sunset. (complete)
11. She …………. to speak English by the year end. (learn)
12. You ………….. tea before we reach there. (drink)
13. Meeta ………….. the beauty contest. (win)
14. Mini …………… to India by early September. (fly)
Hints:
2. will have returned
3. will have set
4. shall have eaten
5. will have cooked
6. will have kept
7. will have bought
8. will have polished
9. will have ordered
10. shall have completed
11. will have learnt
12. will have drunk
13. will have won
14. will have flown.

VI. Given below is a complaint letter. Fill in the blanks with the correct form of the verb given in the brackets. One has been done.

The Secretary
DIV/4901
Vasant Kunj
New Delhi.
Dear Sir

I regret to bring (bring/brought) to your notice that Bihari Lal, the sweeper is not doing (is not doing / has not done) his duty well. He sweeps (sweeps / sweep) the road only once a day. He leaves (leave /leaves) the garbage on the road or throws (threw / throws) them all around. As a result the area is filthy. I have requested (am requesting /have requested) him many times but he refused (refuses / refused) to obey. It seems (seem / seems) he does not care (do not care/does not care).

Yours sincerely
Anil Sharma

VII. Rewrite the following sentences after changing the verbs into the present or past continuous tense:

1. Sudha lies on the bed.
2. Raja plays with his brother.
3. The servant rang the bell.
4. The children scream.
5. The sun sets in the west.
6. They go out for a picnic.
7. She likes the game.
8. I eat my food.
Answer:
1. Sudha is lying on the bed.
2. Raja is playing with his brother.
3. The servant was ringing the bell.
4. The children are screaming.
5. The sun is setting in the west.
6. They are going out for a picnic.
7. She is liking the game.
8. I am eating my food.

VIII. Fill in the blanks with the past perfect tense of the verb given in brackets:

1. He …………. a tiger before I reached the forest. (kill)
2. She ………….. a sweater before I bought a new one. (knit)
3. I ……………. money from my friend before I received my salary. (borrow)
4. The river ……………. its bank before the dam was built. (overflow)
5. She ……………. my book before I could check her. (steal)
6. The train …………….. before I could reach the station. (arrive)
7. I ………….. a funny story before the sad one. (hear)
8. The thief ………….. from the jail before the police arrived. (escape)
Answer:
1. He had killed a tiger before I reached the forest. (kill)
2. She had knitted a sweater before I bought a new one. (knit)
3. I had borrowed money from my friend before I received my salary. (borrow)
4. The river had overflown its bank before the dam was built. (overflow)
5. She had stolen my book before I could check her. (steal)
6. The train had arrived before I could reach the station. (arrive)
7. I had heard a funny story before the sad one. (hear)
8. The thief had escaped from the jail before the police arrived. (escape)

Punjab State Board PSEB 7th Class English Book Solutions English Vocabulary Arrange in Alphabetical Order Exercise Questions and Answers, Notes.

PSEB 7th Class English Vocabulary Arrange in Alphabetical Order

Question 1.
Monkey, picture, bury, dengue, donkey, village, heart, tomb, women, develop.
Answer:
Bury, dengue, develop, donkey, heart, monkey, picture, tomb, village, women.

Question 2.
Able, Wednesday, frozen, return, extremely, disappointed, shivering, wisest, realise, looking.
Answer:
Able, disappointed, extremely, frozen, looking, realise, return, shivering, Wednesday, wisest.

Question 3.
Quick, fine, nice, ancient, bold, clever, deep, mountain, heavy, happy.
Answer:
Ancient, bold, clever, deep, fine, happy, heavy, mountain, nice, quick.

Question 4.
Astronaut, truth, resident, clown, scratch, journey, assigned, disbelief, humble, mission.
Answer:
Assigned, astronaut, clown, disbelief, humble, journey, mission, resident, scratch, truth.

Question 5.
Sheep, bull, horse, bowl, goal, crow, parrot, frog, donkey, duck.
Answer:
Bowl, bull, crow, donkey, duck, frog, goal, horse, parrot, sheep.

Question 6.
Belt, girl, chalk, wife, picture, sister, error, host, duke, actor.
Answer:
Actor, belt, chalk, duke, error, girl, host, picture, sister, wife.

Question 7.
Active, helpful, careful, brother, popular, faithful, famous, difficult, intelligent, polite.
Answer:
Active, brother, careful, difficult, faithful, famous, helpful, intelligent, polite, popular.

Question 8.
Parent, child, sky, plate, madam, doctor, witch, televisiori, bulb, niece.
Answer:
Bulb, child, doctor, madam, niece, parent, plate, sky, television, witch.

Question 9.
Wash, dance, cook, pray, dust, jump, table, father, laugh, help.
Answer:
Cook, dance, dust, father, help, jump, laugh, pray, table, wash.