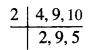Class 8

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 6 ਵਰਗ ਅਤੇ ਵਰਗਮੂਲ Ex 6.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 6 ਵਰਗ ਅਤੇ ਵਰਗਮੂਲ Exercise 6.4

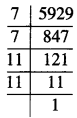
1. ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਦਾ ਵਰਗਮੂਲ, ਵੰਡ ਵਿਧੀ ਦੁਆਰਾ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
2304
ਹੱਲ:
\(\sqrt {2304}\)
∴ \(\sqrt {2304}\) = 48.

ਪ੍ਰਸ਼ਨ (ii).
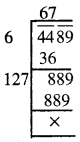
4489
ਹੱਲ:
\(\sqrt {4489}\)
∴ \(\sqrt {4489}\) = 67.

ਪ੍ਰਸ਼ਨ (iii).
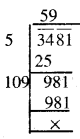
3481
ਹੱਲ:
\(\sqrt {3481}\)
∴ \(\sqrt {3481}\) = 59.

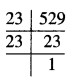
ਪ੍ਰਸ਼ਨ (iv).
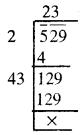
529
ਹੱਲ:
\(\sqrt {529}\)
∴ \(\sqrt {529}\) = 23.

ਪ੍ਰਸ਼ਨ (v).
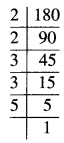
3249
ਹੱਲ:
\(\sqrt {3249}\)
∴ \(\sqrt {3249}\) = 57.

ਪ੍ਰਸ਼ਨ (vi).
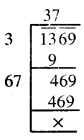
1369.
ਹੱਲ:
\(\sqrt {1369}\)
∴ \(\sqrt {1369}\) = 37.

ਪ੍ਰਸ਼ਨ (vii).
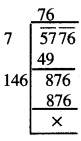
5776
ਹੱਲ:
\(\sqrt {5776}\)
∴ \(\sqrt {5776}\) = 76.

ਪ੍ਰਸ਼ਨ (viii).
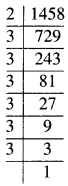
7921
ਹੱਲ:
\(\sqrt {7921}\)
∴ \(\sqrt {7921}\) = 89.

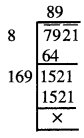
ਪ੍ਰਸ਼ਨ (ix).
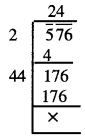
576
ਹੱਲ:
\(\sqrt {576}\)
∴ \(\sqrt {576}\) = 24.

ਪ੍ਰਸ਼ਨ (x).
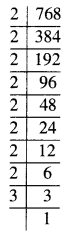
1024
ਹੱਲ:
\(\sqrt {1024}\)
∴ \(\sqrt {1024}\) = 32.

ਪ੍ਰਸ਼ਨ (xi).
3136
ਹੱਲ:
\(\sqrt {3136}\)
∴ \(\sqrt {3136}\) = 56.

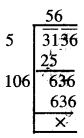
ਪ੍ਰਸ਼ਨ (xii).
900.
ਹੱਲ:
\(\sqrt {900}\)
∴ \(\sqrt {900}\) = 30.

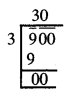
ਪ੍ਰਸ਼ਨ 2.
ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਵਿਚੋਂ ਹਰੇਕ ਦੇ ਵਰਗਮੂਲ ਵਿੱਚ ਅੰਕਾਂ ਦੀ ਸੰਖਿਆ ਪਤਾ ਕਰੋ : (ਬਿਨਾਂ ਗਣਨਾ ਕੀਤੇ :
(i) 64
(ii)14
(iii) 489
(iv) 27225
(v) 390625.
ਹੱਲ:
ਜਿਵੇਂ ਕਿ ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ 2 ਅੰਕਾਂ ਵਾਲੀ ਸੰਖਿਆ ਦਾ ਵਰਗਮੂਲ ਇਕ ਅੰਕ ਵਾਲੀ ਸੰਖਿਆ ਤਿੰਨ ਜਾਂ ਚਾਰ ਅੰਕਾਂ ਵਾਲੀ ਸੰਖਿਆ ਦਾ ਵਰਗਮੂਲ ਦੋ ਅੰਕਾਂ ਵਾਲੀ | ਸੰਖਿਆ, ਪੰਜ ਜਾਂ ਛੇ ਅੰਕਾਂ ਵਾਲੀ ਸੰਖਿਆ ਦਾ ਵਰਗਮੂਲ ਤਿੰਨ | ਅੰਕਾਂ ਵਾਲੀ ਸੰਖਿਆ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਸ ਤਰ੍ਹਾਂ ਹੀ ਅੱਗੇ ਵੀ ………….
(i) 64
64 ਇਕ ਦੋ-ਅੰਕਾਂ ਵਾਲੀ ਸੰਖਿਆ ਹੈ । ਇਸ ਲਈ ਇਸਦੇ ਵਰਗਮੂਲ ਦੇ ਅੰਕਾਂ ਦੀ ਸੰਖਿਆ 1 ਹੈ ।
(ii) 144
144 ਇਕ ਤਿੰਨ-ਅੰਕਾਂ ਵਾਲੀ ਸੰਖਿਆ ਹੈ । ਇਸ ਲਈ ਇਸਦੇ ਵਰਗਮੂਲ ਦੇ ਅੰਕਾਂ ਦੀ ਸੰਖਿਆ 2 ਹੈ ।
(iii) 4489
4489 ਚਾਰ ਅੰਕ ਵਾਲੀ ਸੰਖਿਆ ਹੈ । ਇਸ ਲਈ ਇਸਦੇ ਵਰਗਮੂਲ ਵਿਚ ਅੰਕਾਂ ਦੀ ਸੰਖਿਆ 2 ਹੈ ।
(iv) 27225
27225 ਪੰਜ ਅੰਕਾਂ ਵਾਲੀ ਸੰਖਿਆ ਹੈ । ਇਸ ਲਈ | ਇਸਦੇ ਵਰਗਮੂਲ ਵਿਚ ਅੰਕਾਂ ਦੀ ਸੰਖਿਆ 3 ਹੈ ।
(v) 390625
390625 ਇਕ ਛੇ ਅੰਕਾਂ ਵਾਲੀ ਸੰਖਿਆ ਹੈ । ਇਸ ਲਈ ਇਸਦੇ ਵਰਗਮੂਲ ਵਿਚ ਅੰਕਾਂ ਦੀ ਸਿਖਿਆ ਤੇ ਹੈ ।

3. ਹੇਠਾਂ ਲਿਖੀਆਂ ਦਸ਼ਮਲਵ ਸੰਖਿਆਵਾਂ ਦਾ ਵਰਗਮੂਲ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
2.56
ਹੱਲ:
\(\sqrt {2.56}\)
∴ \(\sqrt {2.56}\) = 1.6

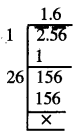
ਪ੍ਰਸ਼ਨ (ii).
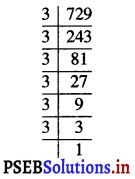
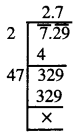
7.29
ਹੱਲ:
\(\sqrt {7.29}\)
∴ \(\sqrt {7.29}\) = 2.7

ਪ੍ਰਸ਼ਨ (iii).
51.84
ਹੱਲ:
\(\sqrt {51.84}\)
∴ \(\sqrt {51.84}\) = 7.2

ਪ੍ਰਸ਼ਨ (iv).
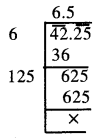
42.25
ਹੱਲ:
\(\sqrt {42.25}\)
∴ \(\sqrt {42.25}\) = 6.5

ਪ੍ਰਸ਼ਨ (v).
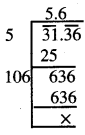
31.36.
ਹੱਲ:
\(\sqrt {31.36}\)
∴ \(\sqrt {31.36}\) = 5.6

4. ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਵਿਚੋਂ ਕਿਹੜੀ ਛੋਟੀ ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ ਘਟਾਈ ਜਾਵੇ ਕਿ ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਹੋ ਜਾਵੇ । ਇਸ ਤਰ੍ਹਾਂ ਪ੍ਰਾਪਤ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆਵਾਂ ਦਾ ਵਰਗਮੂਲ ਵੀ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
402
ਹੱਲ:
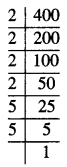
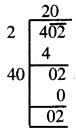
402
ਜੇਕਰ ਅਸੀਂ 402 ਵਿਚੋਂ 02 ਘਟਾਵਾਂਗੇ ਤਾਂ ਅਸੀਂ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਅਰਥਾਤ 402 – 02 = 400, ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ । ਜਿਸਦਾ ਵਰਗਮੂਲ 20 ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
1989
ਹੱਲ:
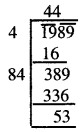
1989
ਇਸ ਲਈ, ਜੇਕਰ ਅਸੀਂ 1989 ਵਿਚੋਂ 53 ਘਟਾਵਾਂਗੇ ਤਾਂ ਅਸੀਂ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਅਰਥਾਤ 1989 – 53 = 1936 ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ । ਜਿਸਦਾ ਵਰਗਮੂਲ 44 ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
3250
ਹੱਲ:
3250
ਇਸ ਲਈ, ਜੇਕਰ ਅਸੀਂ 3250 ਵਿਚੋਂ 1 ਘਟਾਵਾਂਗੇ ਤਾਂ ਅਸੀਂ ਪੂਰਨੇ ਵਰਗ ਸੰਖਿਆ ਅਰਥਾਤ 3250 – 1 = 3249 ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ । ਜਿਸਦਾ ਵਰਗਮੂਲ 57 ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv).
825
ਹੱਲ:
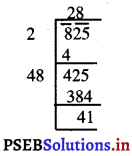
825
ਇਸ ਲਈ, ਜੇਕਰ ਅਸੀਂ 825 ਵਿਚੋਂ 41 ਘਟਾਵਾਂਗੇ ਤਾਂ ਅਸੀਂ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਅਰਥਾਤ 825 – 41 = 784 ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ । ਜਿਸਦਾ ਵਰਗਮੂਲ 28 ਹੈ ।

ਪ੍ਰਸ਼ਨ (v).
4000.
ਹੱਲ:
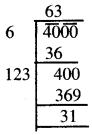
4000
ਇਸ ਲਈ, ਜੇਕਰ ਅਸੀਂ 4000 ਵਿਚੋਂ 31 ਘਟਾਵਾਂਗੇ ਤਾਂ ਅਸੀਂ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਅਰਥਾਤ 4000 – 31 = 3969 ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ । ਜਿਸਦਾ ਵਰਗਮੂਲ 63 ਹੈ ।

5. ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਵਿਚੋਂ ਹਰੇਕ ਵਿਚ | ਛੋਟੀ ਤੋਂ ਛੋਟੀ ਕਿਹੜੀ ਸੰਖਿਆ ਜੋੜੀ ਜਾਵੇ ਤਾਂਕਿ ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਹੋ ਜਾਵੇ। ਇਸ ਤਰ੍ਹਾਂ ਪ੍ਰਾਪਤ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆਵਾਂ ਦਾ ਵਰਗਮੂਲ ਵੀ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
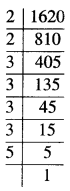
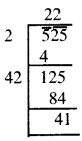
525
ਹੱਲ:
525
ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ 525, 22² ਤੋਂ ਵੱਡੀ ਹੈ । ਅਗਲੀ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ।
= 23² = 529.
ਇਸ ਲਈ, ਜੋੜੀ ਜਾਣ ਵਾਲੀ ਸੰਖਿਆ = 529 – 525 = 4.

ਪ੍ਰਸ਼ਨ (ii).
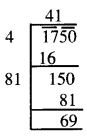
1750
ਹੱਲ:
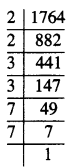
1750
ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ 1750, 41² ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ ਹੈ । ਅਗਲੀ ਪੂਰਨ ਵਰਗੇ ਸੰਖਿਆ
= 42² = 174.
ਇਸ ਲਈ, ਜੋੜੀ ਜਾਣ ਵਾਲੀ ਸੰਖਿਆ = 1764 – 1750 = 14.

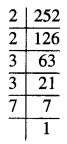
ਪ੍ਰਸ਼ਨ (iii).
252
ਹੱਲ:
252
ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ 252, 15² ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ ਹੈ । ਅਗਲੀ ਪੁਰਨ ਵਰਗ ਸੰਖਿਆ = 16² = 256.
ਇਸ ਲਈ, ਜੋੜੀ ਜਾਣ ਵਾਲੀ ਸੰਖਿਆ = 256 – 252 = 4.

ਪ੍ਰਸ਼ਨ (iv).
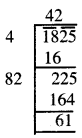
1825
ਹੱਲ:
1825
ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ 1825, 42² ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ ਹੈ । ਅਗਲੀ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ = 43² = 1849.
ਇਸ ਲਈ, ਜੋੜੀ ਜਾਣ ਵਾਲੀ ਸੰਖਿਆ = 1849 – 1825 = 24.

ਪ੍ਰਸ਼ਨ (v).
6412.
ਹੱਲ:
6412
ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ 6412, 80². ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ ਹੈ । ਅਗਲੀ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ 81² = 6561.
ਇਸ ਲਈ, ਜੋੜੀ ਜਾਣ ਵਾਲੀ ਸੰਖਿਆ = 6561 – 6412 = 149.

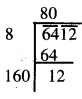
ਪ੍ਰਸ਼ਨ 6.
ਕਿਸੇ ਵਰਗ ਦੀ ਭੁਜਾ ਦੀ ਲੰਬਾਈ ਪਤਾ ਕਰੋ ਜਿਸਦਾ ਖੇਤਰਫਲ 441 m² ਹੈ ?
ਹੱਲ:
ਮੰਨ ਲਉ ਵਰਗ ਦੀ ਭੁਜਾ = x ਮੀਟਰ
∴ ਵਰਗ ਦਾ ਖੇਤਰਫਲ = ਭੁਜਾ × ਭੁਜਾ
= x × x = x² ਮੀਟਰ²
ਪਰੰਤੂ ਵਰਗ ਦਾ ਖੇਤਰਫਲ 441 m² ਹੈ ।
x² = 441
⇒ x = \(\sqrt {442}\)
= \(\sqrt {3×3×7×7}\)
= 3 × 7
⇒ x = 21 m.

ਪ੍ਰਸ਼ਨ 7.
ਕਿਸੇ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ABC ਵਿਚ, ∠B = 90°.
(a) ਜੇ AB = 6 cm, BC = 8 cm, ਹੈ ਤਾਂ AC ਪਤਾ ਕਰੋ ।
(b) ਜੇ AC = 13 cm, BC = 5 cm, ਹੈ ਤਾਂ AB ਪਤਾ ਕਰੋ ।
ਹੱਲ:
(a) ਸਮਕੋਣ ਤਿਭੁਜ ABC ਵਿਚੋਂ, ∠B = 90°
AB = 6 cm, BC = 8 cm
∴ ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦੇ ਅਨੁਸਾਰ,

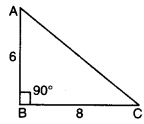
AC² = AB² + BC²
⇒ AC² = (6)² + (8)²
AC² = 36 + 64
⇒AC² = 100
⇒ AC = \(\sqrt {100}\) = 10 cm.

(b) ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ABC ਵਿਚ ; ∠B = 90°
AC = 13 cm, BC = 5 cm
∴ ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦੇ ਅਨੁਸਾਰ,

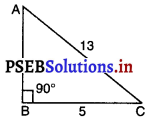
AC² = AB² + BC²
⇒ (13)² = AB² + (5)²
⇒ 169 = (AB)² + 25
⇒ 169 – 25 = (AB)²
⇒ 144 = (AB)² ⇒ AB = \(\sqrt {144}\)
= 12 cm.

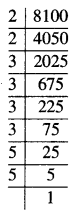
ਪ੍ਰਸ਼ਨ 8.
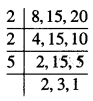
ਇਕ ਮਾਲੀ ਦੇ ਕੋਲ 1000 ਪੌਦੇ ਹਨ । ਇਹਨਾਂ ਪੌਦਿਆਂ ਨੂੰ ਉਹ ਇਸ ਤਰ੍ਹਾਂ ਲਗਾਉਣਾ ਚਾਹੁੰਦਾ ਹੈ ਕਿ ਕਤਾਰਾਂ ਦੀ ਸੰਖਿਆ ਅਤੇ ਹਰੇਕ ਕਤਾਰ ਵਿੱਚ ਪੌਦਿਆਂ ਦੀ ਸੰਖਿਆ ਬਰਾਬਰ ਹੋਵੇ । ਇਸਦੇ ਲਈ ਘੱਟ ਤੋਂ ਘੱਟ ਪੌਦਿਆਂ ਦੀ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ਜਿਸਦੀ ਉਸ ਨੂੰ ਜ਼ਰੂਰਤ ਹੈ ।
ਹੱਲ:
ਪੌਦਿਆਂ ਦੀ ਕੁੱਲ ਸੰਖਿਆ = 1000.

∴ ਘੱਟ ਤੋਂ ਘੱਟ
ਪੌਦਿਆਂ ਦੀ ਸੰਖਿਆ ਜਿਸ ਦੀ ਮਾਲੀ ਨੂੰ ਜ਼ਰੂਰਤ ਹੈ ।
124 = 124 – 100
= 24 ਪੌਦੇ
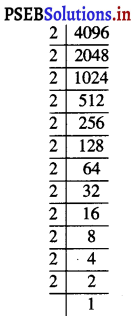
ਇਸ ਲਈ, ਪੌਦਿਆ ਦੀ ਕੁੱਲ ਸੰਖਿਆ = 1000 + 24 = 1024
∴ ਲਾਈਨ ਵਿਚ ਅਤੇ ਕਾਲਮ ਵਿਚ ਪੌਦਿਆਂ ਦੀ ਸੰਖਿਆ
= \(\sqrt {1024}\)
= 32.

ਪ੍ਰਸ਼ਨ 9.
ਇਕ ਸਕੂਲ ਵਿਚ 500 ਵਿਦਿਆਰਥੀ ਹਨ । ਪੀ.ਟੀ. ਦੇ ਅਭਿਆਸ ਦੇ ਲਈ ਇਹ ਇਸ ਤਰ੍ਹਾਂ ਖੜੇ ਕੀਤੇ ਗਏ ਹਨ ਕਿ ਕਤਾਰਾਂ ਦੀ ਸੰਖਿਆ, ਹਰੇਕ ਕਤਾਰ ਵਿੱਚ ਵਿੱਦਿਆਰਥੀਆਂ ਦੀ ਸੰਖਿਆ ਦੇ ਬਰਾਬਰ ਹੋਵੇ । ਇਸ ਤਰ੍ਹਾਂ ਕਰਨ ਲਈ ਕਿੰਨੇ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਬਾਹਰ ਜਾਣਾ ਹੋਵੇਗਾ ?
ਹੱਲ:
ਸਕੂਲ ਵਿਚ ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਸੰਖਿਆ = 500
∴ ਇਸੇ ਵਿਵਸਥਾ ਨੂੰ ਬਣਾਉਣ ਵਿਚ ਜਿੰਨੇ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਬਾਹਰ ਜਾਣਾ ਹੋਵੇਗਾ = 16

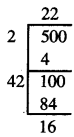
ਹੁਣ ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਸੰਖਿਆ = 500 – 16 = 484
∴ ਹਰੇਕ ਲਾਈਨ ਵਿਚ ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਸੰਖਿਆ
= \(\sqrt {484}\) = 22.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 6 ਵਰਗ ਅਤੇ ਵਰਗਮੂਲ Ex 6.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 6 ਵਰਗ ਅਤੇ ਵਰਗਮੂਲ Exercise 6.3

ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਦੇ ਵਰਗਮੂਲ ਵਿਚ ਇਕਾਈ ਅੰਕ ਕੀ ਆ ਸਕਦਾ ਹੈ ?
(i) 9801
(ii) 99856
(iii) 998001
(iv) 651666025.
ਹੱਲ:
(i) 9801
ਇੱਥੇ 9801 ਦਾ ਇਕਾਈ ਦਾ ਅੰਕ = 1
∴ \(\sqrt {9801}\) ਦਾ ਇਕਾਈ ਦਾ ਅੰਕ = 9.

(ii) 99856
ਇੱਥੇ 99856 ਦਾ ਇਕਾਈ ਦਾ ਅੰਕ = 6.
∴ \(\sqrt {99856}\) ਦਾ ਇਕਾਈ ਦਾ ਅੰਕ = 6.

(iii) 998001
ਇੱਥੇ 998001 ਦਾ ਇਕਾਈ ਦਾ ਅੰਕ = 1.
∴ \(\sqrt {998001}\) ਦਾ ਇਕਾਈ ਦਾ ਅੰਕ = 9.

(iv) 657666025
ਇੱਥੇ 657666025 ਦਾ ਇਕਾਈ ਦਾ ਅੰਕ = 5.
∴ \(\sqrt {657666025}\) ਦਾ ਇਕਾਈ ਦਾ ਅੰਕ = 5.

ਪ੍ਰਸ਼ਨ 2.
ਬਿਨ੍ਹਾਂ ਗਣਨਾ ਕੀਤੇ ਉਹ ਸੰਖਿਆ ਦੱਸੋ ਜੋ ਕਿ | ਪੂਰਨ ਵਰਗ ਨਹੀਂ ਹੋ ਸਕਦੀਆਂ ।
(i) 153
(ii) 257
(iii) 408
(iv) 441
ਹੱਲ:
(i) 153
ਕਿਉਂਕਿ ਅੰਕਾਂ 2, 3, 7 ਜਾਂ 8 ਤੋਂ ਖ਼ਤਮ ਹੋਣ ਵਾਲੀ ਸੰਖਿਆ ਕਦੇ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਨਹੀਂ ਹੋ ਸਕਦੀ ।
∴ 153 ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਨਹੀਂ ਹੈ ।

(ii) 257
ਕਿਉਂਕਿ ਅੰਕਾਂ 2, 3, 7 ਜਾਂ 8 ਤੋਂ ਖ਼ਤਮ ਹੋਣ ਵਾਲੀ ਸੰਖਿਆ ਕਦੇ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਨਹੀਂ ਹੋ ਸਕਦੀ ।
∴ 257 ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਨਹੀਂ ਹੈ ।

(iii) 408
ਕਿਉਂਕਿ ਅੰਕਾਂ 2, 3, 7 ਜਾਂ 8 ਤੋਂ ਖ਼ਤਮ ਹੋਣ ਵਾਲੀ ਸੰਖਿਆ ਕਦੇ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਨਹੀਂ ਹੋ ਸਕਦੀ ।
∴ 408 ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਨਹੀਂ ਹੈ ।

(iv) 441.
441 ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਘਟਾਉ ਵਿਧੀ ਨਾਲ 100 ਅਤੇ 169 ਦਾ ਵਰਗਮੂਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
(a) 100
(i) 100 – 1 = 99
(ii) 99 – 3 = 96
(iii) 96 – 5 = 91
(iv) 91 – 7= 84
(v) 84 – 9 = 75
(vi) 75 – 11 = 64
(vii) 64 – 13 = 51
(viii) 51 – 15 = 36
(ix) 36 – 17 = 19
(x) 19 – 19 = 0.
ਇੱਥੇ, ਅਸੀਂ 10ਵਾਂ ਪਦ, 0 ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ।
∴ \(\sqrt {100}\) = 10.

(b) 169
(i) 169 – 1 = 168
(ii) 168 – 3 = 165
(iii) 165 – 5 = 160
(iv) 160 – 7 = 153
(v) 153 – 9 = 144
(vi) 144 – 11 = 133
(vii) 133 – 13 = 120
(viii) 120 – 15 = 105
(ix) 105 – 17 = 88
(x) 88 – 19 = 69
(xi) 69 – 21 = 48
(xii) 48 – 23 = 25
(xiii) 25 – 25 = 0
ਇੱਥੇ, ਅਸੀਂ 13ਵਾਂ ਪਦ, 0 ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ।
∴ \(\sqrt {169}\) = 13.

4. ਅਭਾਜ ਗੁਣਨਖੰਡ ਵਿਧੀ ਨਾਲ ਹੇਠ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਦਾ ਵਰਗਮੂਲ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
729
ਹੱਲ:
729
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
729 = \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\)
∴ \(\sqrt {729}\) = 3 × 3 × 3 = 27

ਪ੍ਰਸ਼ਨ (ii).
400
ਹੱਲ:
400
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
400 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{5 \times 5}\)
∴ \(\sqrt {400}\) = 2 × 2 × 5 = 20.

ਪ੍ਰਸ਼ਨ (iii).
1764
ਹੱਲ:
1764
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
1764 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{7 \times 7}\)
∴ \(\sqrt {1764}\) = 2 × 3 × 7 = 42.

ਪ੍ਰਸ਼ਨ (iv).
4096
ਹੱਲ:
4096
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
4096 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\)
∴ \(\sqrt {4096}\) = 2 × 2 × 2 × 2 × 2 × 2
= 64.

ਪ੍ਰਸ਼ਨ (v).
7744
ਹੱਲ:
7744
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
7744 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{11 \times 11}\)
∴ \(\sqrt {7744}\) = 2 × 2 × 2 × 11
= 88

ਪ੍ਰਸ਼ਨ (vi).
9604
ਹੱਲ:
9604
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ 2 4802 ਕਰਦੇ ਹਾਂ :
9604 = \(\underline{2 \times 2}\) × \(\underline{7 \times 7}\) × \(\underline{7 \times 7}\)
∴ \(\sqrt {9604}\) = 2 × 7 × 7 = 98

ਪ੍ਰਸ਼ਨ (vii).
5929
ਹੱਲ:
5929
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
5929 = \(\underline{7 \times 7}\) × \(\underline{11 \times 11}\)
∴ \(\sqrt {5929}\) = 7 × 11 = 77

ਪ੍ਰਸ਼ਨ (viii).
9216
ਹੱਲ:
9216
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰ ਕਰਦੇ ਹਾਂ :
9216 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\)
∴ \(\sqrt {9216}\) = 2 × 2 × 2 × 2 × 2 × 3
= 96

ਪ੍ਰਸ਼ਨ (ix).
529
ਹੱਲ:
529
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
529 = \(\underline{23 \times 23}\)
∴ \(\sqrt {529}\) = 23

ਪ੍ਰਸ਼ਨ (x).
8100.
ਹੱਲ:
8100
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
8100 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\) × \(\underline{5 \times 5}\)
∴ \(\sqrt {8100}\) = 2 × 3 × 3 × 5
= 90

5. ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਵਿਚ ਹਰੇਕ ਦੇ ਲਈ | ਉਹ ਸਭ ਤੋਂ ਛੋਟੀ ਪੂਰਨ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ਜਿਸ ਨਾਲ ਇਸ | ਸੰਖਿਆ ਨੂੰ ਗੁਣਾ ਕਰਨ ਤੇ ਇਹ ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਬਣ ਜਾਵੇ । ਇਸ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਦਾ ਵਰਗਮੂਲ ਪਤਾ ਕਰੋ ।

ਪ੍ਰਸ਼ਨ (i).
252
ਹੱਲ:
252
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
252 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 7

ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ 3 ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਇਕ ਹੋਰ 7 ਦੀ ਜ਼ਰੂਰਤ ਹੈ। | ਇਸ ਲਈ ਦਿੱਤੀ ਗਈ ਸੰਖਿਆ ਨੂੰ 7 ਨਾਲ ਗੁਣਾ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ਤਾਂਕਿ ਗੁਣਨਫ਼ਲ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਬਣ ਜਾਵੇ ।
∴ 252 × 7 = 1764
∴ \(\sqrt {1764}\) = 2 × 3 × 7 = 42

ਪ੍ਰਸ਼ਨ (ii).
180
ਹੱਲ:
180
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
180 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 5

ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਪਾਪਤ ਕਰਨ ਦੇ ਲਈ ਇਕ ਹੋਰ 5 ਦੀ ਜ਼ਰੂਰਤ ਹੈ । ਇਸ ਲਈ ਦਿੱਤੀ ਗਈ ਸੰਖਿਆ ਨੂੰ ਨਾਲ ਗੁਣਾ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ਤਾਂਕਿ ਗੁਣਨਫਲ ਪੁਰਨੇ ਵਰਗ ਸੰਖਿਆ ਬਣ ਜਾਵੇ ।
∴ 180 × 5 = 900
∴ \(\sqrt {900}\) = 2 × 3 × 5 = 30

ਪ੍ਰਸ਼ਨ (iii).
1008
ਹੱਲ:
1008
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
1008 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 7

ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਪੁਰਨ ਵਰਗ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਲਈ ਇਕ ਹੋਰ 7 ਦੀ ਜ਼ਰੂਰਤ 2504 ਹੈ ।
ਇਸ ਲਈ ਦਿੱਤੀ ਗਈ ਸੰਖਿਆ ਨੂੰ 7 ਨਾਲ ਗੁਣਾ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ਤਾਂਕਿ ਗੁਣਨਫਲ ਪੁਰਨ ਵਰਗ ਸੰਖਿਆ ਬਣ ਜਾਵੇ ।
∴ 1008 × 7 = 7056
∴ \(\sqrt {7056}\) = 2 × 2 × 3 × 7 = 84

ਪ੍ਰਸ਼ਨ (iv).
2028
ਹੱਲ:
2028
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
2028 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × 2
ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਲਈ, 2 ਇਕ ਹੋਰ 2 ਦੀ ਜ਼ਰੂਰਤ ਹੈ ।

ਇਸ ਲਈ, ਦਿੱਤੀ ਗਈ ਸੰਖਿਆ ਨੂੰ 2 ਨਾਲ ਗੁਣਾ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ਤਾਂਕਿ ਗੁਣਨਫਲ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਬਣ ਜਾਵੇ ।
∴ 2028 × 2 = 4056
∴ \(\sqrt {4056}\) = 2 × 2 × 2 × 2 × 2 × 2 = 64

ਪ੍ਰਸ਼ਨ (v).
1458
ਹੱਲ:
1458
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
1458 = 2 × \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\)

ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਲਈ ਇਕ ਹੋਰ 2 ਦੀ ਜ਼ਰੂਰਤ ਹੈ ।
ਇਸ ਲਈ ਅਸੀਂ ਦਿੱਤੀ ਗਈ ਸੰਖਿਆ ਨੂੰ 2 ਨਾਲ ਗੁਣਾ ਕਰਦੇ ਹਾਂ।
ਤਾਂਕਿ ਗੁਣਨਫਲ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਬਣ ਜਾਵੇ ।
∴ 1458 × 2 = 2916
∴ \(\sqrt {2916}\) = 2 × 3 × 3 × 3 = 54

ਪ੍ਰਸ਼ਨ (vi).
768.
ਹੱਲ:
768
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
768 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × 3

ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਲਈ ਇਕ ਹੋਰ 3 ਦੀ ਜ਼ਰੂਰਤ ਹੈ।
ਇਸ ਲਈ, ਦਿੱਤੀ ਗਈ । ਸੰਖਿਆ ਨੂੰ 3 ਨਾਲ ਗੁਣਾ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ਤਾਂਕਿ ਗੁਣਨਫਲ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਬਣ ਜਾਵੇ ।
∴ 768 × 3 = 2304
∴ \(\sqrt {2304}\) = 2 × 2 × 2 × 2 × 3
= 48

6. ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਵਿਚ ਹਰੇਕ ਦੇ ਲਈ ਉਹ ਸਭ ਤੋਂ ਛੋਟੀ ਪੂਰਨ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ਜਿਸ ਨਾਲ ਇਸ ਸੰਖਿਆ ਨੂੰ ਵੰਡਣ ਤੇ ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਬਣ ਜਾਵੇ । ਇਸ ਤਰ੍ਹਾਂ ਨਾਲ ਪਤਾ ਕੀਤੀ ਗਈ ਸੰਖਿਆ ਦਾ ਵਰਗਮੂਲ ਪਤਾ ਕਰੋ ।

ਪ੍ਰਸ਼ਨ (i).
252
ਹੱਲ:
252
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
252 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 7

ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਇਕ ਪੂਰਨ ਵਰਗ | ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਲਈ ਇਸਨੂੰ ਨਾਲ ਵੰਡਦੇ ਹਾਂ ।
ਇਸ ਲਈ, ਦਿੱਤੀ ਗਈ ਸੰਖਿਆ ਨੂੰ 7 ਨਾਲ ਭਾਗ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂਕਿ ਭਾਗਫਲ ਇਕ ਤਨ ਵਰਗ ਸੰਖਿਆ ਬਣ ਜਾਵੇ ।
∴ 252 ÷ 7 = 36
∴ \(\sqrt {36}\) = 2 × 3 = 6

ਪ੍ਰਸ਼ਨ (ii).
2925
ਹੱਲ:
2925
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
2925 = \(\underline{3 \times 3}\) × \(\underline{5 \times 5}\) × 13
ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਲਈ ਇਸਨੂੰ 13 975 ਨਾਲ ਭਾਗ ਕਰਦੇ ਹਾਂ ।
ਇਸ ਲਈ, ਦਿੱਤੀ ਗਈ ਸੰਖਿਆ ਨੂੰ ਨਾਲ ਭਾਗ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂਕਿ ਭਾਗਫਲ ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਬਣ ਜਾਵੇ ।

∴ 2925 ÷ 13 = 225
∴ \(\sqrt {225}\) = 3 × 5 = 15

ਪ੍ਰਸ਼ਨ (iii).
396
ਹੱਲ:
396
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
396 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 11

ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਇਕ ਪੁਰਨ ਵਰਗ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਅਸੀਂ ਇਸਨੂੰ 11 ਨਾਲ ਭਾਗ ਕਰਦੇ ਹਾਂ ।
ਇਸ ਲਈ, ਦਿੱਤੀ ਗਈ ਸੰਖਿਆ ਨੂੰ 11 ਨਾਲ ਭਾਗ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂਕਿ ਭਾਗਫਲ ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਬਣ ਜਾਵੇ ।
∴ 396 ÷ 11 = 36
∴ \(\sqrt {36}\) = 2 × 3 = 6

ਪ੍ਰਸ਼ਨ (iv).
2645
ਹੱਲ:
2645
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
2645 = 5 × \(\underline{23 \times 23}\)
ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਲਈ ਇਸਨੂੰ 5 ਨਾਲ ਭਾਗ ਕਰਦੇ ਹਾਂ ।

ਇਸ ਲਈ, ਦਿੱਤੀ ਗਈ ਸੰਖਿਆ ਨੂੰ 5 ਨਾਲ ਭਾਗ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂਕਿ ਭਾਗਫਲ ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਬਣ ਜਾਵੇ ।
∴ 2645 ÷ 5 = 529
∴ \(\sqrt {529}\) = 23

ਪ੍ਰਸ਼ਨ (v).
2800
ਹੱਲ:
2800
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
2800 = \(\underline{2 \times 2}\) × \(\underline{2 \times 2}\) × \(\underline{5 \times 5}\) × 7
ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਲਈ ਇਸਨੂੰ ਨਾਲ ਭਾਗ ਕਰਦੇ ਹਾਂ ।

ਇਸ ਲਈ, ਦਿੱਤੀ ਗਈ ਸੰਖਿਆ ਨੂੰ 7 ਨਾਲ ਭਾਗ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂਕਿ ਭਾਗਫਲ ਪੁਰਨ ਵਰਗ ਸੰਖਿਆ ਬਣ ਜਾਵੇ ।
∴ 2800 ÷ 7 = 400
∴ \(\sqrt {400}\) = 2 × 2 × 5 = 20.

ਪ੍ਰਸ਼ਨ (vi).
1620.
ਹੱਲ:
1620
ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
1620 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\) × 5

ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਲਈ ਇਸਨੂੰ 5 ਨਾਲ ਭਾਗ ਕਰਦੇ ਹਾਂ ।
ਇਸ ਲਈ, ਦਿੱਤੀ ਗਈ ਸੰਖਿਆ ਨੂੰ 5 ਨਾਲ ਭਾਗ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂਕਿ ਭਾਗਫਲ ਇਕ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਬਣ ਜਾਵੇ ।
∴ 1620 ÷ 5 = 324
∴ \(\sqrt {324}\) = 2 × 3 × 3 = 18

ਪ੍ਰਸ਼ਨ 7.
ਇਕ ਸਕੂਲ ਵਿਚ ਜਮਾਤ VIII ਦੇ ਸਾਰੇ ਵਿਦਿਆਰਥੀਆਂ ਨੇ ਪ੍ਰਧਾਨ ਮੰਤਰੀ ਰਾਸ਼ਟਰੀ ਰਾਹਤ ਫੰਡ ਵਿਚ ₹ 2401 ਦਾਨ ਕੀਤੇ ਹਰੇਕ ਵਿਦਿਆਰਥੀ ਨੇ ਉੱਨੇ ਹੀ ₹ ਦਾਨ ਵਿਚ ਦਿੱਤੇ, ਜਿੰਨ੍ਹੇ ਜਮਾਤ ਵਿਚ ਵਿਦਿਆਰਥੀ ਸਨ । ਜਮਾਤ ‘ ਦੇ ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਜਮਾਤ VIII ਦੇ ਵਿਦਿਆਰਥੀਆਂ ਦੁਆਰਾ ਦਾਨ ਦਿੱਤੀ ਗਈ ਕੁੱਲ ਰਾਸ਼ੀ = ₹ 2401
∴ ਹਰੇਕ ਵਿਦਿਆਰਥੀ ਦੁਆਰਾ ਦਾਨ ਦਿੱਤੀ ਗਈ ਰਾਸ਼ੀ = \(\sqrt {2401}\)
∴ 2401 = \(\underline{7 \times 7}\) × \(\underline{7 \times 7}\)
∴ \(\sqrt {2401}\) = 7 × 7 = 49

∴ ਹਰੇਕ ਵਿਦਿਆਰਥੀ ਦੁਆਰਾ ਦਾਨ ਦਿੱਤੀ ਗਈ ਰਾਸ਼ੀ = ₹ 49

ਪ੍ਰਸ਼ਨ 8.
ਇਕ ਬਾਗ਼ ਵਿੱਚ 2025 ਪੌਦੇ ਇਸ ਤਰ੍ਹਾਂ ਲਗਾਏ ਗਏ ਹਨ ਕਿ ਹਰੇਕ ਲਾਈਨ ਵਿਚ ਉੱਨੇ ਹੀ ਪੈਂਦੇ ਹਨ, ਜਿੰਨੀਆਂ ਲਾਈਨਾਂ ਦੀ ਸੰਖਿਆ ਹੈ । ਲਾਈਨਾਂ ਦੀ ਸੰਖਿਆ ਅਤੇ ਹਰੇਕ ਲਾਈਨ ਵਿੱਚ ਪੌਦਿਆਂ ਦੀ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਪੌਦਿਆਂ ਦੀ ਕੁੱਲ ਸੰਖਿਆ = 2025
∴ ਹਰੇਕ ਲਾਈਨ ਵਿਚ ਪੌਦਿਆਂ ਦੀ ਸੰਖਿਆ = \(\sqrt {2025}\)
∴ 2025 = \(\underline{3 \times 3}\) × \(\underline{3 \times 3}\) × \(\underline{5 \times 5}\)
∴ \(\sqrt {2025}\) = 3 × 3 × 5 = 45
∴ ਹਰੇਕ ਲਾਈਨ ਵਿਚ ਪੌਦਿਆਂ ਦੀ ਸੰਖਿਆ ਅਤੇ ਲਾਈਨਾਂ ਦੀ ਸੰਖਿਆ = 45.

ਪ੍ਰਸ਼ਨ 9.
ਸਭ ਤੋਂ ਛੋਟੀ ਵਰਗ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ਜੋ ਕਿ 4, 9 ਅਤੇ 10 ਹਰੇਕ ਨਾਲ ਵੰਡੀ ਜਾਵੇ ।
ਹੱਲ:
4, 9 ਅਤੇ 10 ਨਾਲ ਵਿਭਾਜਿਤ ਹੋਣ ਵਾਲੀ ਸਭ ਤੋਂ ਰੋਟੀ ਵਰਗ ਸੰਖਿਆ ਇਸਦਾ ਲ.ਸ.ਵ. ਹੈ ।
ਹੁਣ 4, 9, 10 ਦਾ ਲ.ਸ.ਵ.
= 2 × 2 × 9 × 5
=180

∴ ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
180 = \(\underline{2 \times 2}\) × \(\underline{3 \times 3}\) × 5
ਇਸ ਨੂੰ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਬਣਾਉਣ ਦੇ ਲਈ ਇਸਨੂੰ 5 ਨਾਲ ਗੁਣਾ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।

∴ ਲੌੜੀਂਦੀ ਸੰਖਿਆ ਹੈ = 180 × 5
=900

ਪ੍ਰਸ਼ਨ 10.
ਸਭ ਤੋਂ ਛੋਟੀ ਵਰਗ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ਜੋ ਕਿ ਹਰੇਕ 8, 15 ਅਤੇ 20 ਨਾਲ ਵੰਡੀ ਜਾਵੇ ।
ਹੱਲ:
8, 15 ਅਤੇ 20 ਨਾਲ ਵੰਡੀ ਜਾਣ ਵਾਲੀ ਸਭ ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ ਇਸਦਾ ਲ.ਸ.ਵ. ਹੈ ।

ਹੁਣ, 8, 15, 20 ਦਾ ਲ.ਸ.ਵ. = (2 × 2 × 5 × 2 × 3)
= 120
∴ ਅਭਾਜ ਗੁਣਨਖੰਡ ਦੁਆਰਾ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
120 = \(\underline{2 \times 2}\) × 2 × 3 × 5
ਇਸਨੂੰ ਪੂਰਨ ਵਰਗ ਸੰਖਿਆ ਬਣਾਉਣ ਦੇ ਲਈ ਇਸਨੂੰ (2 × 3 × 5 = 30) ਨਾਲ ਗੁਣਾ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।

∴ ਲੋੜੀਂਦੀ ਸੰਖਿਆ = 120 × 30
= 3600

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 5 ਅੰਕੜਿਆਂ ਦਾ ਪ੍ਰਬੰਧਨ Ex 5.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 5 ਅੰਕੜਿਆਂ ਦਾ ਪ੍ਰਬੰਧਨ Exercise 5.1

ਪ੍ਰਸ਼ਨ 1.
ਹੇਠਾਂ ਲਿਖਿਆਂ ਵਿਚੋਂ ਕਿਹੜੇ ਅੰਕੜਿਆਂ ਨੂੰ ਦਰਸਾਉਣ ਦੇ ਲਈ ਤੁਸੀਂ ਇਕ ਆਇਤਕਾਰ ਚਿੱਤਰ ਦੀ ਵਰਤੋਂ ਕਰੋਗੇ ?
(a) ਇਕ ਡਾਕੀਏ ਦੇ ਥੈਲੇ ਵਿਚ ਵੱਖ-ਵੱਖ ਖੇਤਰਾਂ ਦੀਆਂ ਚਿੱਠੀਆਂ ਦੀ ਗਿਣਤੀ ।
(b) ਕਿਸੇ ਖੇਡ ਮੁਕਾਬਲੇ ਵਿਚ ਹਿੱਸਾ ਲੈਣ ਵਾਲੇ ਖਿਡਾਰੀਆਂ ਦੀਆਂ ਉੱਚਾਈਆਂ ।
(c) 5 ਕੰਪਨੀਆਂ ਦੁਆਰਾ ਬਣਾਈਆਂ ਕੈਸਟਾਂ ਦੀ ਗਿਣਤੀ ।
(d) ਕਿਸੇ ਸਟੇਸ਼ਨ ਤੇ ਸਵੇਰੇ 7 ਵਜੇ ਤੋਂ ਸ਼ਾਮ 7 ਵਜੇ ਤਕ ਰੇਲ ਗੱਡੀਆਂ ਵਿਚ ਜਾਣ ਵਾਲੇ ਯਾਤਰੀਆਂ ਦੀ ਗਿਣਤੀ ।
ਹਰੇਕ ਦੇ ਲਈ, ਕਾਰਨ ਵੀ ਦੱਸੋ ।
ਹੱਲ:
(b), (d) ਇਹਨਾਂ ਸਥਿਤੀਆਂ ਵਿਚੋਂ, ਅੰਕੜਿਆਂ ਨੂੰ ਵਰਗ ਅੰਤਰਾਲ ਵਿਚ ਵਿਭਾਜਿਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਕਿਉਂਕਿ (a) ਅਤੇ (c) ਦੀ ਸਥਿਤੀ ਵਿਚ ਸਾਨੂੰ ਵਿਭਿੰਨ ਖੇਤਰਾਂ ਅਤੇ ਕੰਪਨੀਆਂ ਦੇ ਨਾਂ ਦਿੱਤੇ ਗਏ ਹਨ, ਇਸ ਲਈ ਇਨ੍ਹਾਂ ਸਥਿਤੀਆਂ ਵਿਚ ਅੰਕੜਿਆਂ ਨੂੰ ਵਰਗੀਕਰਨ ਕਰਨ ਦੀ ਜ਼ਰੂਰਤ ਨਹੀਂ ਹੈ । ,

ਪ੍ਰਸ਼ਨ 2.
ਕਿਸੇ ਡਿਪਾਰਟਮੈਂਟਲ ਸਟੋਰ ਤੇ ਖਰੀਦਦਾਰੀ ਕਰਨ ਆਏ ਵਿਅਕਤੀਆਂ ਨੂੰ ਇਸ ਪ੍ਰਕਾਰ ਅੰਕਿਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ : ਪੁਰਸ਼ (M), ਔਰਤ (W), ਲੜਕਾ (B) ਜਾਂ ਲੜਕੀਆਂ (G) । ਹੇਠਾਂ ਲਿਖੀ ਸੂਚੀ ਉਹਨਾਂ ਖਰੀਦਦਾਰਾਂ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ ਜੋ ਕਿ ਸਵੇਰ ਦੇ ਪਹਿਲੇ ਘੰਟੇ ਵਿਚ ਆਏ ਹਨ :
W W W G B W W M G G M M W W W W G B M W B G G M W W M M W W W M W B W G M W W W W G W M M W W M W G W M G W M M B G G W
ਮਿਲਾਨ ਚਿੰਨ੍ਹਾਂ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋਏ ਇਕ ਬਾਰੰਬਾਰਤਾ ਵੰਡ ਸਾਰਣੀ ਬਣਾਉ । ਇਸ ਨੂੰ ਦਰਸਾਉਣ ਲਈ ਇਕ ਛੜ ਗਰਾਫ ਖਿੱਚੋ ।
ਹੱਲ:
ਮਿਲਾਨ ਚਿੰਨ੍ਹਾਂ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋਏ ਬਣਾਈ ਗਈ ਬਾਰੰਬਾਰਤਾ ਵੰਡ ਸਾਰਣੀ ਅੱਗੇ ਦਿੱਤੀ ਗਈ ਹੈ :

ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਦਾ ਛੜ ਗਰਾਫ ਇਸ ਤਰ੍ਹਾਂ ਦਿੱਤਾ ਗਿਆ ਹੈ :

ਪ੍ਰਸ਼ਨ 3.
ਕਿਸੇ ਫੈਕਟਰੀ ਦੇ 30 ਮਜ਼ਦੂਰਾਂ ਦੀ ਹਫ਼ਤੇ ਦੀ ਆਮਦਨ ਰੁਪਏ ਵਿਚ ਹੇਠਾਂ ਲਿਖੀ ਹੈ :
830, 835, 80, 810, 835, 836, 869, 845, 898, 890, 820, 86, 832, 833, 855, 845, 04, 808, 81, 80, 885, 835, 835, 86, 878, 840, 868, 80, 86, 840.
ਮਿਲਾਣ ਚਿੰਨ੍ਹਾਂ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋਏ, ਅੰਤਰਾਲਾਂ 800810, 810-820 ਆਦਿ ਵਾਲੀ ਇਕ ਬਾਰੰਬਾਰਤਾ ਸਾਰਣੀ ਬਣਾਉ ॥
ਹੱਲ:

ਪ੍ਰਸ਼ਨ 4.
ਪ੍ਰਸ਼ਨ 3 ਵਿਚ ਦਿੱਤੇ ਅੰਕੜਿਆਂ ਤੋਂ ਪ੍ਰਾਪਤ ਸਾਰਣੀ ਦੇ ਲਈ ਇਕ ਆਇਤ ਚਿੱਤਰ ਬਣਾਉ ਅੜੇ ਹੇਠਾਂ ਲਿਖੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਦਿਓ :
(i) ਕਿਸ ਗੁੱਟ ਵਿਚ ਮਜ਼ਦੂਰਾਂ ਦੀ ਗਿਣਤੀ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਹੈ ?
(ii) ਕਿੰਨੇ ਮਜ਼ਦੂਰ ਤੋਂ 850 ਜਾਂ ਉਸ ਤੋਂ ਵੱਧ ਕਮਾਉਂਦੇ ਹਨ ?
(iii) ਕਿੰਨੇ ਮਜ਼ਦੂਰ ਤੋਂ 850 ਤੋਂ ਘੱਟ ਕਮਾਉਂਦੇ ਹਨ ?
ਹੱਲ:
ਉਪਰ ਲਿਖੇ ਅੰਕੜਿਆਂ ਦਾ ਆਇਤ ਚਿੱਤਰ ਹੇਠਾਂ ਆਕ੍ਰਿਤੀ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ ।
(i) 830—840. ਇਸ ਵਰਗ ਵਿਚ ਮਜ਼ਦੂਰਾਂ ਦੀ ਗਿਣਤੀ 9 ਹੈ ।
(ii) 10
(iii) 20

ਪ੍ਰਸ਼ਨ 5.
ਛੁੱਟੀਆਂ ਦੇ ਦਿਨਾਂ ਵਿਚ ਇਕ ਖ਼ਾਸ ਜਮਾਤ ਦੇ ਵਿਦਿਆਰਥੀਆਂ ਦੁਆਰਾ ਪ੍ਰਤੀ ਦਿਨ ਟੈਲੀਵਿਜ਼ਨ (ਟੀ. ਵੀ.). ਦੇਖਣ ਦੇ ਸਮੇਂ (ਘੰਟਿਆਂ ਵਿਚ ਦਿੱਤੇ ਗਏ ਗਰਾਫ਼ ਰਾਹੀਂ ਦਰਸਾਇਆ ਗਿਆ ਹੈ ; ਹੇਠਾਂ ਲਿਖੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਦਿਓ :
(i) ਸਭ ਤੋਂ ਵੱਧ ਵਿਦਿਆਰਥੀਆਂ ਨੇ ਕਿੰਨੇ ਘੰਟੇ ਤੱਕ ਟੀ. ਵੀ. ਦੇਖਿਆ ?
(ii) 4 ਘੰਟਿਆਂ ਤੋਂ ਘੱਟ ਸਮੇਂ ਤੱਕ ਕਿੰਨੇ ਵਿਦਿਆਰਥੀਆਂ ਨੇ ਟੀ.ਵੀ. ਦੇਖਿਆ ?
(iii) ਕਿੰਨੇ ਵਿਦਿਆਰਥੀਆਂ ਨੇ ਟੀ. ਵੀ. ਦੇਖਣ ਵਿਚ 5 ਘੰਟੇ ਤੋਂ ਜ਼ਿਆਦਾ ਸਮਾਂ ਬਿਤਾਇਆ ?

ਹੱਲ:
(i) 4—5 ਘੰਟੇ ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਗਿਣਤੀ 32
(ii) 34
(iii) 14.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 4 ਪ੍ਰਯੋਗਿਕ ਜਿਆਮਿਤੀ Ex 4.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 4 ਪ੍ਰਯੋਗਿਕ ਜਿਆਮਿਤੀ Exercise 4.5

ਹੇਠਾਂ ਲਿਖਿਆਂ ਦੀ ਰਚਨਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ 1.
ਇਕ ਵਰਗ READ ਜਿਸ ਵਿਚ RE = 5.1 cm ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ: ਵਰਗ READ ਦੀ ਇਕ ਭੁਜਾ RE = 5.1 cm ਹੈ ।
ਰਚਨਾ ਦੇ ਪਗ :
(i) ਇਕ ਰੇਖਾਖੰਡ RE = 5.1 cm ਲਉ ।

(ii) ਹਰੇਕ ਬਿੰਦੂ R ਅਤੇ E ਉੱਤੇ 90° ਦਾ ਕੋਣ ਚੋ ।
(iii) ਹੁਣ, Rਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਤੇ ਅਰਧ ਵਿਆਸ 5.1 cm ਲੈ ਕੇ ਇਕ ਚਾਪ ਖਿੱਚੋ ਜੋ 90° ਦੇ ਕੋਣ ਨੂੰ D ਉੱਤੇ ਕੱਟਦੀ ਹੈ ।
(iv) ਇਸ ਤਰ੍ਹਾਂ E ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਤੇ ਅਰਧ ਵਿਆਸ 5.1 cm ਲੈ ਕੇ ਇਕ ਚਾਪ ਖਿੱਚੋ ਜੋ 90° ਦੇ ਕੋਣ ਨੂੰ A ਉੱਤੇ ਕੱਟਦੀ ਹੈ ।
(v) AD ਨੂੰ ਮਿਲਾਉ ।
∴ READ ਲੋੜੀਂਦਾ ਵਰਗ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਇਕ ਸਮਚਤੁਰਭੁਜ ਜਿਸਦੇ ਵਿਕਰਨਾਂ ਦੀ ਲੰਬਾਈ 5.2 cm ਅਤੇ 6.4 cm ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਸਮਚਤਰਭੁਜ ਦੇ ਦੋ ਵਿਕਰਣ 5.2 cm ਅਤੇ 6.4 cm ਦਿੱਤੇ ਹਨ ।
ਰਚਨਾ ਦੇ ਪਗ :
(i) ਇਕ ਰੇਖਾਖੰਡ AC = 6.4 cm ਖਿੱਚੋ |

(ii) ਰੇਖਾਖੰਡ AC ਦੇ ਲੰਬ ਸਮਦੋਭਾਜਕ ਦੀ ਚਰਨਾ ਕਰੋ ਜੋ AC ਨੂੰ O ਉੱਤੇ ਕੱਟਦਾ ਹੈ ।
(iii) ਲੰਬ ਸਮਦੋਭਾਜਕ ਨੂੰ ਬਿੰਦੂ O ਤੋਂ ਦੋਨੋਂ ਪਾਸੇ ਨੇ \(\frac{1}{2}\) × 5.2 cm = 2.6 cm ਲੰਬਾਈ ਦੇ ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਦੋ ਚਾਪ ਖਿੱਚੋ ਜੋ ਲੰਬ ਸਮਦੋਭਾਜਕ ਨੂੰ ਬਿੰਦੂ B ਅਤੇ ਬਿੰਦੂ D ਉੱਤੇ ਕੱਟਦੇ ਹਨ ।
(iv) AB, BC, CD ਅਤੇ DA ਨੂੰ ਮਿਲਾਉ ।
∴ ABCD ਲੋੜੀਂਦੀ ਸਮ ਚਤੁਰਭੁਜ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਇਕ ਆਇਤ ਜਿਸਦੀਆਂ ਲਾਗਵੀਆਂ ਭੁਜਾਵਾਂ ਦੀ ਲੰਬਾਈ 5 cm ਅਤੇ 4 cm ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਇਕ ਆਇਤ ਜਿਸਦੀਆਂ ਲਾਹਵੀਆਂ ਭੁਜਾਵਾਂ 5 cm ਅਤੇ 4 cm ਹਨ ।
ਅਰਥਾਤ AB = 5 cm ਅਤੇ BC = 4 cm.
ਰਚਨਾ ਦੇ ਪਗ :
(i) ਇਕ ਰੇਖਾਖੰਡ AB = 5 cm ਖਿੱਚੋ ।
(ii) ਬਿੰਦੂ A ਅਤੇ B ਹਰੇਕ ਉੱਤੇ 90° ਦਾ ਕੋਣ ਖਿੱਚੋ !
(iii) ਹੁਣ, A ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਤੇ ਅਰਧ ਵਿਆਸ 4 | cm ਲੈ ਕੇ ਇਕ ਚਾਪ ਖਿੱਚੇ ਜੋ AX ਨੂੰ D ਉੱਤੇ ਕੱਟਦੀ ਹੈ ।
(iv) ਇਸੇ ਤਰ੍ਹਾਂ, B ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਤੇ ਅਰਧ ਵਿਆਸ ਤੋਂ 4 cm ਲੈ ਕੇ ਇਕ ਚਾਪ ਖਿੱਚੋ ਜੋ BY ਨੂੰ C ਉੱਤੇ ਕੱਟਦੀ ਹੈ ।
(v) CD ਨੂੰ ਮਿਲਾਉ ॥

∴ ABCD ਲੋੜੀਂਦੀ ਆਇਤ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ OKAY ਜਿੱਥੇ OK = 5.5 cm ਅਤੇ KA =42 cm ਹੈ । ਕੀ ਇਹ ਵਿਲੱਖਣ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ OKAY ਦੀਆਂ ਭੁਜਾਵਾਂ OK = 5.5 cm ਅਤੇ KA = 4.2 cm ਹਨ ।
ਕੇਵਲ ਦੋ ਭੁਜਾਵਾਂ ਨਾਲ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੀ ਰਚਨਾ | ਸੰਭਵ ਨਹੀਂ ਹੈ । ਇੱਥੇ ਸਾਨੂੰ ਇਕ ਹੋਰ ਮਾਪ ਦੀ ਜਰੂਰਤ ਹੋਵੇਗੀ । ਜੋ ਦੋ ਭੁਜਾਵਾਂ ਦੇ ਵਿਚਕਾਰ ਦਾ ਕੋਣ ਜਾਂ ਵਿਕਰਨ ਹੋ ਸਕਦਾ ਹੈ ।

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 4 ਪ੍ਰਯੋਗਿਕ ਜਿਆਮਿਤੀ Ex 4.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 4 ਪ੍ਰਯੋਗਿਕ ਜਿਆਮਿਤੀ Exercise 4.4

1. ਹੇਠਾਂ ਲਿਖੇ ਚਤੁਰਭੁਜਾਂ ਦੀ ਰਚਨਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
ਚਤੁਰਭੁਜ DEAR ਜਿਸ ਵਿਚ
DE = 4 cm
EA = 5 cm
AR = 4.5 cm
∠E = 60°
ਅਤੇ ∠A = 90° ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਚਤੁਰਭੁਜ DEAR ਦੀਆਂ ਤਿੰਨ ਭੁਜਾਵਾਂ ਅਤੇ ਦੋ ਵਿਚਕਾਰ ਦੇ ਕੋਣ ਦਿੱਤੇ ਹਨ ।
ਅਰਥਾਤ DE = 4 cm, EA = 5 cm, AR = 4.5 cm, ∠E = 60°, ∠A = 90°
ਰਚਨਾ ਦੇ ਪਗ :
(i) ਇਕ ਰੇਖਾਖੰਡ DE = 4 cm ਖਿੱਚੋ ।

(ii) ਬਿੰਦੂ E, ਉੱਤੇ ਕੋਣ ∠DEX = 60° ਖਿੱਚੋ ਅਤੇ EX ਵਿਚੋਂ 5cm ਲੰਬਾਈ ਦੀ ਇਕ ਚਾਪ ਖਿੱਚੋ ਜੋ EX ਨੂੰ A ਉੱਤੇ ਕੱਟਦੀ ਹੈ ।
(iii) ਬਿੰਦੂ A, ਉੱਤੇ ਕੋਣ ∠EAY = 90°, ਖਿੱਚੋ ਅਤੇ AY ਵਿਚੋਂ 4.5 cm ਲੰਬਾਈ ਦੀ ਇਕ ਚਾਪ ਖਿੱਚੋ ਜੋ AY ਨੂੰ R ਉੱਤੇ ਕੱਟਦੀ ਹੈ ।
(iv) DR ਨੂੰ ਮਿਲਾਉ ।
∴ DEAR ਲੋੜੀਂਦੀ ਚਤੁਰਭੁਜ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
ਚਤੁਰਭੁਜ TRUE ਜਿਸ ਵਿਚ
TR = 3.5 cm
RU = 3 cm
UE = 4 cm
∠R = 750
ਅਤੇ ∠U = 120° ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : TRUE ਦੀਆਂ ਤਿੰਨ ਭੁਜਾਵਾਂ ਅਤੇ ਵਿਚਕਾਰ ਦੇ ਦੋ ਕੋਣ ਦਿੱਤੇ ਗਏ ਹਨ
ਅਰਥਾਤ TR = 3.5 cm, RU = 3 cm, UE = 4 cm,
∠R = 75° ਅਤੇ ∠U = 120°.
ਰਚਨਾ ਦੇ ਪ੍ਰਗ :
(i) ਰੇਖਾਖੰਡ RU = 3 cm ਖਿੱਚੋ !
(ii) ਬਿੰਦੁ R, ਉੱਤੇ ∠XRU = 75 ਖਿੱਚੋ ਅਤੇ Rx ਵਿਚੋਂ 3.5 cm ਦੀ ਚਾਪ ਕੱਟੋ ਜੋ RX ਨੂੰ T ਉੱਤੇ ਕੱਟਦੀ ਹੈ ।

(iii) ਬਿੰਦੁ U ਉੱਤੇ ਕੋਣ ∠RUY = 120° ਖਿੱਚੋ ਅਤੇ | UY ਵਿਚੋਂ 4 cm ਦੀ ਲੰਬਾਈ ਦਾ ਚਾਪ ਕੱਟੋ ਜੋ UY ਨੂੰ E ਉੱਤੇ ਕੱਟਦੀ ਹੈ ।
(iv) TE ਮਿਲਾਉ ।
∴ TRUE ਲੋੜੀਂਦੀ ਚਤੁਰਭੁਜ ਹੈ ।

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 4 ਪ੍ਰਯੋਗਿਕ ਜਿਆਮਿਤੀ Ex 4.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 4 ਪ੍ਰਯੋਗਿਕ ਜਿਆਮਿਤੀ Exercise 4.3

1. ਹੇਠਾਂ ਲਿਖੇ ਚਤੁਰਭੁਜਾਂ ਦੀ ਰਚਨਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
ਚਤੁਰਭੁਜ MORE ਜਿਸ ਵਿਚ
MO = 6 cm OR = 4.5 cm
∠M = 60°
∠O = 105°
∠R = 105° ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਚਤੁਰਭੁਜ MORE ਦੀਆਂ ਦੋ ਸੰਗਤ ਭੁਜਾਵਾਂ ਅਤੇ ਤਿੰਨ ਕੋਣ
ਅਰਥਾਤ MO = 6 cm, OR = 4.5 cm,
∠M = 60°, ∠O = 105°, ∠R = 105°
ਰਚਨਾ ਦੇ ਪਗ :
(i) MO = 6 cm ਖਿੱਚੋ !
(ii) O ਤੇ ; ∠XOM = 105: ਖਿੱਚੋ ।
(iii) ਕਿਰਣ OX, ਵਿਚੋਂ OR = 4.5 cm ਕੱਟੋ !
(iv) R; ਉੱਤੇ ਕੋਣ ∠YRO = 105° ਖਿੱਚੋ |
(v) M, ਉੱਤੇ ਕੋਣ ∠ZMO = 60° ਖਿੱਚੋ ਅਤੇ ਕਿਰਣ RY ਅਤੇ MZ ਨੂੰ ਇਕ ਦੂਜੇ ਤੋਂ E ਉੱਤੇ ਕੱਟਣ ਦਿਉ ।

∴ MORE ਲੋੜੀਂਦੀ ਚੁਤਰਭੁਜ ਹੈ !

ਪ੍ਰਸ਼ਨ (ii).
ਚਤੁਰਭੁਜ PLAN ਜਿਸ ਵਿਚ
PL = 4 cm
LA = 6.5 cm
∠P = 90°
∠A = 110°
∠N = 85° ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : PLAN ਦੀਆਂ ਦੋ ਲਾਗਵੀਆਂ ਭੁਜਾਵਾਂ ਅਤੇ ਤਿੰਨ ਕੋਣ
ਅਰਥਾਤ PL = 4 cm, LA = 6.5 cm, ∠P = 90°, ∠A = 110°, ∠N = 85°.
ਰਚਨਾ ਦੇ ਪਗ :
(i) LA = 6.5 cm ਖਿੱਚੋ ।
(ii) A ਉੱਤੇ ਕੋਣ ∠XAL = 110° ਖਿੱਚੋ ।

(iii) L ਉੱਤੇ ਕੋਣ ∠YLA = 750 ਖਿੱਚੋ ।
[∵ ਕੋਣ-ਯੋਗ ਗੁਣਧਰਮ ਤੋਂ]
∠P + ∠L + ∠A + ∠N
= 360°
90° + ∠L + 110° + 85° = 360°
∠L + 285° = 360°
⇒ ∠L = 360° – 285° = 75°
(iv) ਕਿਰਣ LY ਵਿਚੋਂ LP = 4 cm ਕੱਟੋ ।
(v) Pਉੱਤੇ 90° ਦਾ ਕੋਣ ਖਿੱਚੋ ਜੋ ਕਿਰਣ AX ਨੂੰ N ਉੱਤੇ ਕੱਟਦਾ ਹੈ ।
∴ PLAN ਲੋੜੀਂਦੀ ਚਤੁਰਭੁਜ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ HEAR ਜਿਸ ਵਿਚ
HE = 5 cm
EA = 6 cm
ਅਤੇ ∠R = 85° ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੀਆਂ ਦੋ ਲਾਗਵੀਆਂ ਭੁਜਾਵਾਂ ਅਤੇ ਇਕ ਕੋਣ
ਅਰਥਾਤ HE = 5 cm,
EA = 6 cm ਅਤੇ ∠R = 85°
ਰਚਨਾ ਦੇ ਪਗ :
(i) EA = 6 cm ਖਿੱਚੋ ।
(ii) A ਉੱਤੇ ਕੋਣ ∠XAE = 95° ਖਿੱਚੋ । ਕਿਰਣ AX ਵਿਚੋਂ AR = 5 cm ਕੋਣ [∵ ∠A + ∠R = 180° ⇒ ∠A + 85° = 180° ⇒ ∠A = 180° – 85° = 95°]
(iii) E ਉੱਤੇ ਕੋਣ ∠YEA = 85° ਖਿੱਚੋ । ਕਿਰਣ EY ਵਿਚੋਂ HE = 5 cm ਕੋਣ [∵ ∠E = ∠R ਸਮਾਂਤਰ ਜਤੁਰਭੁਜ ਦੇ ਸਨਮੁਖ ਕੋਣ । ]
(iv) HR ਨੂੰ ਮਿਲਾਉ ॥
∴ HEAR ਲੋੜੀਂਦੀ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv).
ਆਇਤ OKAY ਜਿਸ ਵਿਚ
OK = 7 cm
KA = 5 cm ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਆਇਤ OKAY ਦੀਆਂ ਲਾਗਵੀਆਂ ਭੁਜਾਵਾਂ
ਅਰਥਾਤ OK = 7 cm और KA = 5 cm.
ਕਿਉਂਕਿ ਆਇਤ ਦਾ ਹਰੇਕ ਕੋਣ 90° ਹੈ ।
ਰਚਨਾ ਦੇ ਪਗ :
(i) ਇਕ ਰੇਖਾਖੰਡ OK = 7 cm ਖਿੱਚੋ ।

(ii) ਬਿੰਦੂਆਂ O ਅਤੇ K ਹਰੇਕ ਉੱਤੇ 90° ਦਾ ਕੋਣ ਅਰਥਾਤ ∠XKO ਅਤੇ ∠POK ਖਿੱਚੋ !
(iii) XK ਵਿਚੋਂ AK = 5 cm ਕੱਟੋ ॥
(iv) PO ਵਿਚੋਂ OY = 5 cm ਕੱਟੋ ।
(v) AY ਨੂੰ ਮਿਲਾਉ ॥
∴ OKAY ਲੋੜੀਂਦੀ ਆਇਤ ਹੈ ।

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 4 ਪ੍ਰਯੋਗਿਕ ਜਿਆਮਿਤੀ Ex 4.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 4 ਪ੍ਰਯੋਗਿਕ ਜਿਆਮਿਤੀ Exercise 4.2

1. ਹੇਠਾਂ ਲਿਖੇ ਚਤੁਰਭੁਜਾਂ ਦੀ ਰਚਨਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
ਚਤੁਰਭੁਜ LIFT ਜਿਸ ਵਿਚ
LI = 4 cm
IF = 3 cm
TL = 2.5 cm
LF = 4.5 cm
IT = 4 cm ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਚਤੁਰਭੁਜ LIFT ਦੀਆਂ ਤਿੰਨ ਭੁਜਾਵਾਂ ਅਤੇ ਦੋ ਵਿਕਰਣ ਇਸ ਤਰ੍ਹਾਂ ਹਨ :
ਅਰਥਾਤ LI = 4 cm, IF = 3 cm, TL= 2.5 cm, LF = 4.5 cm, IT = 4 cm.
ਰਚਨਾ ਦੇ ਪਰੀ :
(i) ਇਕ ਰੇਖਾ ਖੰਡ LI = 4 cm ਖਿੱਚੋ !
(ii) I ਨੂੰ ਕੇਂਦਰ ਜੀ ਅਤੇ ਅਰਧ ਵਿਆਸ 3 cm. ਲੈ ਕੇ ਇਕ ਚਾਪ ਖਿੱਚੋ ।

(iii) L ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ 4.5 cm ਲੈ ਕੇ ਇਕ ਦੂਸਰੀ ਚਾਪ ਚੋ ਜੋ ਪਹਿਲੀ ਚਾਪ ਨੂੰ Fਉੱਤੇ ਕੱਟੇ ।
(iv) LF ਅਤੇ IF ਨੂੰ ਮਿਲਾਉ ।
(v) Lਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ 2.5 cm, ਲੈ ਕੇ ਇਕ ਚਾਪ ਖਿੱਚੋ |
(vi) I ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ 4 cm, ਲੈ ਕੇ ਇੱਕ ਹੋਰ ਚਾਪ ਖਿੱਚੋ ਜੋ ਪਹਿਲੀ ਚਾਪ ਨੂੰ 1 ਬਿੰਦੂ ਤੇ ਕੱਟੇ ।
(vii) LI, IT ਅਤੇ FT ਨੂੰ ਮਿਲਾਉ ॥
∴ LIFT ਲੋੜੀਂਦੀ ਚਤੁਰਭੁਜ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
ਚਤੁਰਭੁਜ GOLD ਜਿਸ ਵਿਚ
OL = 7.5 cm
GL = 6 cm
GD = 6 cm
LD = 5 cm
OD = 10 cm ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਚਤੁਰਭੁਜ GOLD ਦੀਆਂ ਤਿੰਨ ਭੁਜਾਵਾਂ ਅਤੇ ਦੋ ਵਿਕਣ ਦਿੱਤੇ ਗਏ ਹਨ :
ਅਰਥਾਤ OL = 7.5 cm, GL = 6 cm, GD = 6 cm, LD = 5 cm, OD = 10 cm.

ਰਚਨਾ ਦੇ ਪਗ :
(i) ਇਕ ਰੇਖਾਖੰਡ OL = 7.5 cm ਲਉ !
(ii) O ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ 10 cm, ਲੈ ਕੇ ਇਕ ਚਾਪ ਖਿੱਚੋ ।
(iii) L ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ 5 cm ਲੈ ਕੇ ਇਕ । ਦੂਸਰੀ ਚਾਪ ਖਿੱਚੋ ਜੋ ਪਹਿਲੀ ਚਾਪ ਨੂੰ D ਉੱਤੇ ਕੱਟੇ ।
(iv) OD ਅਤੇ LD ਨੂੰ ਮਿਲਾਉ !
(v) D ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ 6 cm ਲੈ ਕੇ ਇਕ ਚਾਪ ਖਿੱਚੋ ।
(vi) L ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ 6 cm ਲੈ ਕੇ ਇਕ ਦੂਸਰੀ ਚਾਪ ਖਿੱਚੋ ਜੋ ਪਹਿਲੀ ਚਾਪ ਨੂੰ G ਉੱਤੇ ਕੱਟੇ ।
(vii) GL, GD ਅਤੇ OG ਨੂੰ ਮਿਲਾਉ ।
∴ GOLD ਲੋੜੀਂਦੀ ਚਤੁਰਭੁਜ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
ਸਮਲੰਬ ਚਤੁਰਭੁਜ BEND ਜਿਸ ਵਿਚ
BN = 5.6 cm
DE : 6.5 cm ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਸਮਚਤੁਰਭੁਜ BEND ਦੇ ਦੋ ਵਿਕਰਣ ਅਰਥਾਤ BN = 5.6 cm, DE = 6.5 cm.

ਰਚਨਾ ਦੇ ਪਰੀ :
(i) ਇਕ ਰੇਖਾਖੰਡ DE = 6.5 cm ਲਉ ।
(ii) ਰੇਖਾਖੰਡ DE ਨੂੰ ਸਮਦੋਭਾਜਿਤ ਕਰੋ ।
(iii) O ਨੂੰ ਕੇਂਦਰ ਲੈ ਕੇ ਲੰਬਾਈ \(\frac{5.6}{2}\) = 2.8 cm ਦੇ ਦੋ ਚਾਪ, ਰੇਖਾ DE ਦੇ ਉੱਤੇ ਅਤੇ ਥੱਲੇ ਖਿੱਚ ਜੋ ਕਿ ਸਮਦੋਭਾਜਿਤ ਨੂੰ ਕ੍ਰਮਵਾਰ ਬਿੰਦੂ N ਅਤੇ B ਉੱਤੇ ਕੱਟਦੇ ਹਨ ।
(iv) BE, EN, ND ਅਤੇ BD ਨੂੰ ਮਿਲਾਉ ।
∴ BEND ਲੋੜੀਂਦੀ ਸਮਚਤੁਰਭੁਜ ਹੈ ।

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 4 ਪ੍ਰਯੋਗਿਕ ਜਿਆਮਿਤੀ Ex 4.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 4 ਪ੍ਰਯੋਗਿਕ ਜਿਆਮਿਤੀ Exercise 4.1

1. ਹੇਠਾਂ ਲਿਖੇ ਚਤੁਰਭੁਜਾਂ ਦੀ ਰਚਨਾ ਕਰੋਂ :

ਪ੍ਰਸ਼ਨ (i).
ਚਤੁਰਭੁਜABCD ਜਿਸ ਵਿਚ
AB = 4.5 cm
BC = 5.5 cm
CD = 4 cm
AD = 6 cm
AC = 7 cm ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਚਤੁਰਭੁਜ ਦੀਆਂ ਚਾਰ ਭੁਜਾਵਾਂ ਅਤੇ ਇਕ ਵਿਕਰਣ ਜਿਵੇਂ ਕਿ ਹੇਠਾਂ ਦਿੱਤਾ ਗਿਆ ਹੈ :
AB = 4.5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm, AC = 7 cm.
ਪਹਿਲਾ ਅਸੀਂ ਦਿੱਤੇ ਗਏ ਮਾਪਾਂ ਨੂੰ ਨਿਰੂਪਿਤ ਕਰਨ ਦੇ ਲਈ ਇਕ ਕੱਚੀ ਆਕ੍ਰਿਤੀ ਬਣਾਉਂਦੇ ਹਾਂ ।

ਰਚਨਾ ਦੇ ਪਗ :
(i) ਇਕ ਰੇਖਾਖੰਡ AC = 7 cm ਖਿੱਚੋ ।
(ii) A ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ AD = 6 cm ਲੈ ਕੇ ਇਕ ਚਾਪ ਖਿੱਚੋ ।
(iii) c ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ CD = 4 cm ਲੈ ਕੇ ਇਕ ਦੂਸਰੀ ਚਾਪ ਖਿੱਚੋ ਅ ਜੋ ਪਹਿਲੀ ਚਾਪ ਨੂੰ D ਬਿੰਦੂ ਉੱਤੇ ਕੱਟੇ ।

(iv) AD ਅਤੇ CD ਨੂੰ ਮਿਲਾਉ ।
(y) A ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ AB = 4.5 cm, ਲੈ ਕੇ ਇਕ ਚਾਪ ਖਿੱਚੋ ।
(vi C ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ BC = 5.5 cm, ਲੈ ਕੇ ਇਕ ਦੁਸਰੀ ਚਾਪ ਖਿੱਚੋ ਜੋ ਪਹਿਲੀ ਚਾਪ ਨੂੰ B ਉੱਤੇ ਕੱਟੇ ।
(vii) AB ਅਤੇ BC ਨੂੰ ਮਿਲਾਉ ॥
ਤਾਂ, ABCD ਲੋੜੀਦੀ ਚਤੁਰਭੁਜੇ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
ਚਤੁਰਭੁਜ JUMP ਜਿਸ ਵਿਚ
JU = 3.5 cm
UM = 4 cm
MP = 5 cm
PJ = 45 cm
PU = 6.5 cm ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਚਤੁਰਭੁਜ ਦੀਆਂ ਚਾਰ ਭੁਜਾਵਾਂ ਅਤੇ ਇਕ ਵਿਕਰਣ ਇਸ ਤਰ੍ਹਾਂ ਦਿੱਤਾ ਗਿਆ ਹੈ :
JU = 3.5 cm, UM = 4 cm, MP = 5 cm, PJ = 4.5 cm, PU = 6.5 cm.
ਪਹਿਲਾਂ ਅਸੀਂ, ਦਿੱਤੇ ਗਏ ਅੰਕੜਿਆਂ ਨੂੰ ਨਿਰੂਪਿਤ ਕਰਨ ਲਈ ਇਕ ਕੱਚੀ ਆਕ੍ਰਿਤੀ ਬਣਾਉਂਦੇ ਹਾਂ ।

ਰਚਨਾ ਦੇ ਪਗ :
(i) ਇਕ ਰੇਖਾਖੰਡ PU = 6.5 cm ਲਉ ।
(ii) P ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ P] =4.5 cm, ਲੈ ਕੇ ਇਕ ਚਾਪ ਖਿੱਚੋ ।
(iii) U ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ UJ = 3.5 cm, | ਲੈ ਕੇ ਇਕ ਦੂਸਰੀ ਚਾਪ ਖਿੱਚੋ ਜੋ ਪਹਿਲੀ ਚਾਪ ਨੂੰ J ‘ਤੇ ਕੱਟੇ ।

(iv) PJ ਅਤੇ JU ਨੂੰ ਮਿਲਾਉ ॥
(v) P ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ PM = 5 cm, ਲੈ ਕੇ ਇਕ ਚਾਪ ਖਿੱਚੋ ।
(vi) U ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ UM = 4 cm ਲੈ ਕੇ ਇਕ ਦੁਸਰੀ ਚਾਪ ਖਿੱਚੋ । ਜੋ ਪਹਿਲੀ ਚਾਪ ਨੂੰ M ਉਤੇ ਕੱਟੇ ।
(vii) PM ਅਤੇ UM ਨੂੰ ਮਿਲਾਉ,
ਤਾਂ JUMP ਲੋੜੀਂਦੀ ਚਤੁਰਭੁਜ, ਹੈ |

ਪ੍ਰਸ਼ਨ (iii).
ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ MORE ਜਿਸ ਵਿਚ
OR = 6 cm
RE = 4.5 cm
EO : 7.5 cm ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਅਤੇ ਇਕ ਵਿਕਰਣ ਇਸ ਤਰ੍ਹਾਂ ਹੈ ।
OR = 6 cm, RE = 4.5 cm ਅਤੇ EO = 7.5 cm.
ਰਚਨਾ ਦੇ ਪਗ :
(i) ਇਕ ਰੇਖਾਖੰਡ OE = 7.5 cm ਲਉ ।
(ii) O ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ OR = 6 cm ਲੈ ਕੇ ਇਕ ਚਾਪ ਖਿੱਚੋ ।

(iii) E ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ ER =4.5 cm ਲੈ ਕੇ ਇਕ ਦੂਸਰੀ ਚਾਪ ਖਿੱਚੋ ਜੋ ਪਹਿਲੀ ਚਾਪ ਨੂੰ Rਉੱਤੇ ਕੱਟੇ ।
(iv) OR ਅਤੇ ER ਨੂੰ ਮਿਲਾਉ ॥
(v) O ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ OM = 4.5 cm, ਲੈ ਕੇ ਇਕ ਚਾਪ ਖਿੱਚੋ ।
(vi) E ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ EM = 6 cm ਲੈ ਕੇ ਇਕ ਦੁਸਰੀ ਚਾਪ ਖਿੱਚੋ ਜੋ ਪਹਿਲੀ ਚਾਪ ਨੂੰ M ਉੱਤੇ ਕੱਟੇ ।
(vii) OM ਅਤੇ EM ਨੂੰ ਮਿਲਾਉ ।
ਤਾਂ, MORE ਲੋੜੀਂਦੀ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv).
ਸਮ ਚਤੁਰਭੁਜ BEST ਜਿਸ ਵਿਚ
BE = 4.5 cm ਅਤੇ
ET : 6 cm ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਮੰਨ ਲਉ ਕਿ ਬਣਾਈ ਜਾਣ ਵਾਲੀ ਸਮ ਚਤੁਰਭੁਜ BEST ਵਿਚ, BE = ES = ST = TB = 4.5 cm ਅਤੇ ਵਿਕਰਣ ET = 6 cm ਹੈ !

ਪਹਿਲਾਂ ਅਸੀਂ ਦਿੱਤੇ ਗਏ ਮਾਪ ਨਾਲ ਕੱਚੀ ਆਕ੍ਰਿਤੀ ਬਣਾਉਂਦੇ ਹਾਂ ।
ਰਚਨਾ ਦੇ ਪਗ :
(i) ਇਕ ਰੇਖਾ ਖੰਡ ET = 6 cm ਲਉ ।
(ii) E ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ ES = EB = 4.5 cm, ਲੈ ਕੇ ਭੁਜਾ ET ਦੇ ਉੱਪਰ ਅਤੇ ਹੇਠਾਂ ਦੋ ਚਾਪਾਂ ਖਿੱਚੋ ।

(iii) T ਨੂੰ ਕੇਂਦਰ ਅਤੇ ਅਰਧ ਵਿਆਸ TS = TB =4.5 cm, ਲੈ ਕੇ ਚਾਪ ਖਿੱਚੋ ਜੋ ਪਗ (ii) ਦੀਆਂ ਚਾਪਾਂ ਨੂੰ ਕ੍ਰਮਵਾਰ S ਅਤੇ B ਉੱਤੇ ਕੱਟੇ । (iv) ES, ST, BE ਅਤੇ BT ਨੂੰ ਮਿਲਾਉ ।
ਤਾਂ, BEST ਲੋੜੀਂਦੀ ਸਮਚਤੁਰਭੁਜ ਹੈ ।

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 3 ਚਤੁਰਭੁਜਾਵਾਂ ਨੂੰ ਸਮਝਣਾ InText Questions and Answers.

PSEB 8th Class Maths Solutions Chapter 3 ਚਤੁਰਭੁਜਾਵਾਂ ਨੂੰ ਸਮਝਣਾ InText Questions

ਕੋਸ਼ਿਸ਼ ਕਰੋ :

ਪ੍ਰਸ਼ਨ 1.
ਇਕ ਸਮ ਛੇਭੁਜ ਲਵੋ (ਚਿੱਤਰ ਦੇਖੋ)।

(i) ਬਾਹਰੀ ਕੋਣ x, y, z, p, q ਅਤੇ r ਦੇ ਮਾਪਾਂ ਦਾ ਜੋੜ ਕੀ ਹੈ ?
(ii) ਕੀ x = y = z = p = q = r ਹੈ ? ਕਿਉਂ ?
(iii) ਹਰ ਇੱਕ ਦਾ ਮਾਪ ਕੀ ਹੈ ?
(i) ਬਾਹਰੀ ਕੋਣ
(ii) ਅੰਦਰਲਾ ਕੋਣ
(iv) ਇਸ ਕਿਰਿਆ ਨੂੰ ਹੇਠਾਂ ਲਿਖਿਆਂ ਦੇ ਲਈ ਦੁਹਰਾਉ :
(i) ਇਕ ਸਮ ਅੱਠਭੁਜ
(ii) ਇਕ ਸਮ 20 ਕੁਜ ।
ਹੱਲ:
(i) ਮੰਨ ਲਉ ABCDEF ਇਕ ਸਮ ਛੇਭੁਜ ਹੈ ਜਿਸ ਦੀ ਹਰੇਕ ਭੁਜਾ ਬਰਾਬਰ ਹੈ ।
ਕਿਉਂਕਿ ਕਿਸੇ ਚਤੁਰਭੁਜ ਦੇ ਬਾਹਰੋਂ ਕੋਣਾਂ ਦੀਆਂ ਮਾਪਾਂ ਦਾ ਜੋੜ 360° ਹੁੰਦਾ ਹੈ ।
∴ x + y + z + p + q + r = 360°
ਹਾਂ, x = y = z = p = q = r, ਕਿਉਂਕਿ ਛੇਭੁਜ ਸਮਭੁਜ
ਹਰੇਕ ਬਾਹਰੀ ਕੋਣ ਦਾ ਮਾਪ 1 ਦੁਆਰਾ ਦਿੱਤਾ ਗਿਆ ਹੈ ।
x + x + x + x + x + x = 360°
⇒ 6x = 360°
⇒ x = 60°
∴ ਹਰੇਕ ਅੰਦਰਲੇ ਕੋਣ ਦਾ ਮਾਪ = 180° – 60°
= 120°

(i) ਬਹੁਭੁਜ ਦੀਆਂ ਭੁਜਾਵਾਂ ਦੀ ਸੰਖਿਆ = 8
ਕਿਉਂਕਿ ਬਹੁਭੁਜ ਸਮਭੁਜ ਹੈ
ਇਸ ਲਈ ਇਸਦੇ ਸਾਰੇ ਬਾਹਰੀ ਕੋਣ ਬਰਾਬਰ ਹਨ ।
ਮੰਨ ਲਉ ਹਰੇਕ ਬਾਹਰੀ ਕੋਣ ਦਾ ਮਾਪ x ਹੈ ।
8x = 360°
x = \(\frac{360^{\circ}}{8}\) = 45°
x = ਹਰੇਕ ਬਾਹਰੋਂ ਕੋਣ ਦਾ ਮਾਪ = 45°
ਹਰੇਕ ਅੰਦਰਲੇ ਕੋਣ ਦਾ ਮਾਪ = 180° – 45°
= 135°

(ii) ਬਹੁਭੁਜ ਦੀਆਂ ਭੁਜਾਵਾਂ ਦੀ ਸੰਖਿਆ = 20
ਕਿਉਂਕਿ ਬਹੁਭੁਜ ਸਮ ਬਹੁਭੁਜ ਹੈ, ਇਸ ਲਈ ਇਸਦੇ ਸਾਰੇ ਬਾਹਰੀ ਕੋਣ ਬਰਾਬਰ ਮਾਪ ਦੇ ਹਨ ।
ਮੰਨ ਲਉ ਹਰੇਕ ਬਾਹਰੀ ਕੋਣ ਦਾ ਮਾਪ ਹੈ ।
20x = 360°
x = \(\frac{360^{\circ}}{20}\) = 18°
ਹਰੇਕ ਬਾਹਰੀ ਕੋਣ ਦਾ ਮਾਪ = 18°
ਹਰੇਕ ਅੰਦਰਲੇ ਕੋਣ ਦਾ ਮਾਪ = 180° – 18°
= 162°

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 3 ਚਤੁਰਭੁਜਾਵਾਂ ਨੂੰ ਸਮਝਣਾ Ex 3.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 3 ਚਤੁਰਭੁਜਾਵਾਂ ਨੂੰ ਸਮਝਣਾ Exercise 3.4

ਪ੍ਰਸ਼ਨ 1.
ਦੱਸੋ, ਕਥਨ ਸੱਚ ਹੈ ਜਾਂ ਨਹੀਂ :
(a) ਸਾਰੇ ਆਇਤ ਵਰਗ ਹੁੰਦੇ ਹਨ ।
(b) ਸਾਰੇ ਸਮਚਤੁਰਭੁਜ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੁੰਦੇ ਹਨ ।
(c) ਸਾਰੇ ਵਰਗ ਸਮਚਤੁਰਭੁਜ ਅਤੇ ਆਇਤ ਵੀ ਹੁੰਦੇ ਹਨ ।
(d) ਸਾਰੇ ਵਰਗ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਨਹੀਂ ਹੁੰਦੇ ।
(e) ਸਾਰੀਆਂ ਪੰਗਾਂ ਸਮਚਤੁਰਭੁਜ ਹੁੰਦੀਆਂ ਹਨ ।
(f) ਸਾਰੇ ਸਮਚਤੁਰਭੁਜ ਪਤੰਗ ਹੁੰਦੇ ਹਨ ।
(g) ਸਾਰੇ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਸਮਲੰਬ ਹੁੰਦੇ ਹਨ ।
(h) ਸਾਰੇ ਵਰਗ ਸਮਲੰਬ ਹੁੰਦੇ ਹਨ ।
ਹੱਲ:
(a) ਗਲਤ
(b) ਸਹੀ
(c) ਸਹੀ
(d) ਗ਼ਲਤ
(e) ਗ਼ਲਤ
(f) ਸਹੀ
(g) ਸਹੀ
(h) ਸਹੀ

ਪ੍ਰਸ਼ਨ 2.
ਉਹ ਸਾਰੇ ਚਤੁਰਭੁਜਾਂ ਦੀ ਪਹਿਚਾਣ ਕਰੋ ਜਿਸ ਵਿਚ
(a) ਚਾਰ ਭੁਜਾਵਾਂ ਬਰਾਬਰ ਲੰਬਾਈ ਦੀਆਂ ਹੋਣ ।
(b) ਚਾਰ ਸਮਕੋਣ ਹੋਣ ।
ਹੱਲ:
(a) ਵਰਗ ਅਤੇ ਸਮਚਤੁਰਭੁਜ
(b) ਵਰਗ ਅਤੇ ਆਇਤ ।

ਪ੍ਰਸ਼ਨ 3.
ਦੱਸੋ ਕਿਸ ਤਰ੍ਹਾਂ ਇਕ ਵਰਗ
(i) ਇਕ ਚਤੁਰਭੁਜ
(ii) ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ
(iii) ਇਕ ਸਮਚਤੁਰਭੁਜ
(iv) ਇਕ ਆਇਤ ਹੈ ।
ਹੱਲ:
(i) ਕੋਈ ਵੀ ਚਾਰ ਭੁਜਾਵਾਂ ਵਾਲੀ ਆਕ੍ਰਿਤੀ ਇਕ ਚਤੁਰਭੁਜ ਕਹਾਉਂਦੀ ਹੈ ਅਤੇ ਇਸ ਲਈ ਇਕ ਵਰਗ ਇਕ ਚਤੁਰਭੁਜ ਹੈ ।
(ii) ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੀਆਂ ਸਨਮੁਖ ਭੁਜਾਵਾਂ ਬਰਾਬਰ ਅਤੇ ਸਮਾਂਤਰ ਹੁੰਦੀਆਂ ਹਨ, ਇਸ ਲਈ ਵਰਗ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ।
(iii) ਸਮਚਤੁਰਭੁਜ ਦੀਆਂ ਸਾਰੀਆਂ ਚਾਰ ਭੁਜਾਵਾਂ ਬਰਾਬਰ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਵਰਗ ਵਿਚ ਵੀ ਇਸ ਤਰ੍ਹਾਂ ਹੀ ਹੈ ।
(iv) ਆਇਤ ਦੇ ਸਾਰੇ ਚਾਰੇ ਕੋਣ ਸਮਕੋਣ ਅਤੇ ਸਨਮੁਖ ਭੁਜਾਵਾਂ ਸਮਾਨ ਹੁੰਦੀਆਂ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਹੀ ਵਰਗ ਵਿਚ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਇਕ ਚਤੁਰਭੁਜ ਦਾ ਨਾਮ ਦੱਸੋ ਜਿਸਦੇ ਵਿਕਰਨ
(i) ਇਕ ਦੂਸਰੇ ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦੇ ਹਨ ।
(ii) ਇਕ ਦੂਸਰੇ ’ਤੇ ਲੰਬ ਸਮਭਾਜਕ ਹੋਣ ।
(iii) ਬਰਾਬਰ ਹੋਣ ।
ਹੱਲ:
(i) ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ, ਸਮਚਤੁਰਭੁਜ ਵਰਗਾ, ਆਇਤ
(ii) ਸਮਚਤੁਰਭੁਜ, ਵਰਗ
(iii) ਆਇਤ, ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ।

ਪ੍ਰਸ਼ਨ 5.
ਦੱਸੋ ਇਕ ਆਇਤ ਉੱਤਲ ਚਤੁਰਭੁਜ ਕਿਸ ਤਰ੍ਹਾਂ ਹਨ ?
ਹੱਲ:
ਇਕ ਆਇਤ ਉਤ ਚਤੁਰਭੁਜ ਹੁੰਦੀ ਹੈ ਕਿਉਂਕਿ ਇਸਦੇ ਦੋਨੋਂ ਵਿਕਰਣ ਆਇਤ ਵਿਚ ਸਥਿਤ ਹੁੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ABC ਇਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ਅਤੇ ‘O’ ਸਮਕੋਣ ਦੀ ਸਨਮੁੱਖ ਭੁਜਾ ਦਾ ਮੱਧ ਬਿੰਦੁ ਹੈ । ਦੱਸੋ ਕਿਸ ਤਰ੍ਹਾਂ ‘O’ ਬਿੰਦੂ A, B ਅਤੇ Cਤੋਂ ਸਮਾਨ ਦੂਰੀ ‘ਤੇ ਸਥਿਤ ਹੈ । (ਬਿੰਦੂਆਂ ਨਾਲ ਬਣਾਈਆਂ ਭੁਜਾਵਾਂ ਤੁਹਾਡੀ ਸਹਾਇਤਾ ਦੇ ਲਈ ਖਿੱਚੀਆਂ ਗਈਆਂ ਹਨ ?)

ਹੱਲ:
ਕਿਉਂਕਿ △ABC ਇਕ ਸਮਕੋਣ ਤਿਭੁਜ ਹੈ ਜੋ B ਤੇ ਸਮਕੋਣ ਹੈ ਅਤੇ O, AC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ।
ਆਇਤ ABCD ਨੂੰ ਨਾਲ ਦਿੱਤੀ ਆਕ੍ਰਿਤੀ ਵਿਚੋਂ ਦਰਸਾਏ ਅਨੁਸਾਰ ਪੂਰਾ ਕਰੋ ।
ਕਿਉਂਕਿ ਆਇਤ ਦੇ ਵਿਕਰਣ ਬਰਾਬਰ ਹਨ ।
ਅਤੇ ਸਾਰੇ ਆਇਤ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੁੰਦੇ ਹਨ ।
ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੇ ਵਿਕਰਣ ਇਕ ਦੂਸਰੇ ਨੂੰ ਸਮਦੋਭਾਜਿਤ ਕਰਦੇ ਹਨ ।
∴ O, AC ਅਤੇ BD ਦੋਨਾਂ ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ।
∴ O, A, B, C ਅਤੇ D ਸਮਾਨ ਦੂਰੀ ਤੇ ਹਨ ।