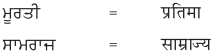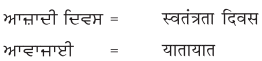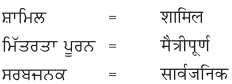Punjab State Board PSEB 8th Class Hindi Book Solutions Chapter 18 अंतरिक्ष परी : कल्पना चावला Textbook Exercise Questions and Answers.
PSEB Solutions for Class 8 Hindi Chapter 18 अंतरिक्ष परी : कल्पना चावला (2nd Language)
Hindi Guide for Class 8 PSEB अंतरिक्ष परी : कल्पना चावला Textbook Questions and Answers
अंतरिक्ष परी : कल्पना चावला अभ्यास
1. नीचे गुरुमुखी और देवनागरी लिपि में दिये गये शब्दों को पढ़ें और हिंदी शब्दों को लिखने का अभ्यास करें :


उत्तर :
छात्र अध्यापक की सहायता से स्वयं करें।
![]()
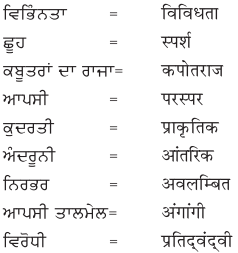
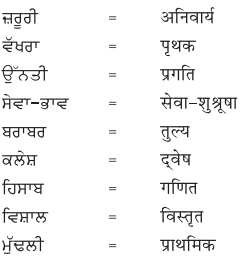
2. नीचे एक ही अर्थ के लिए पंजाबी और हिंदी भाषा में शब्द दिये गये हैं। इन्हें ध्यान से पढ़ें और हिंदी शब्दों को लिखें :
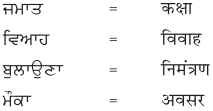

उत्तर :
विद्यार्थी अपने अध्यापक/अध्यापिका की सहायता से स्वयं करें।
3. शब्दार्थ :
- स्नातक = विश्वविद्यालय की उपाधि
- स्नातकोत्तर = स्नातक की डिग्री के ऊपर की उपाधि
- प्रवृत्ति = मन का झुकाव
- बरबस = जबरदस्ती
- इंजीनियरिंग = इंजीनियर की पढ़ाई
- अंतरिक्ष = आकाश
- उपाध्यक्ष = संस्था, समिति में अध्यक्ष का सहायक
- अदम्य = प्रबल, प्रचंड, जो दबाया न जा सके
उत्तर :
विद्यार्थी स्वयं करें।
4. इन प्रश्नों के उत्तर एक या दो वाक्यों में लिखें:
(क) सपने कैसे पूरे होते हैं?
उत्तर :
सपने कठिन परिश्रम, दृढ़ निश्चय, आत्मविश्वास एवं एकाग्रता से पूरे होते हैं।
![]()
(ख) बचपन से ही कल्पना चावला का क्या सपना था?
उत्तर :
बचपन से ही कल्पना चावला का सपना आसमान की सैर करने का था।
(ग) कल्पना चावला का जन्म कब और कहाँ हुआ?
उत्तर :
कल्पना चावला का जन्म 1 जुलाई, सन् 1961 ई० को हरियाणा राज्य के करनाल नगर में हुआ था।
(घ) कल्पना का विवाह कब और किससे हुआ?
उत्तर :
कल्पना का विवाह सन् 1983 ई० में जीन पियरे हैरिसन से हुआ।
(ङ) कल्पना की प्रारंभिक शिक्षा कहाँ पूरी हुई?
उत्तर :
कल्पना की प्रारम्भिक शिक्षा करनाल के टैगोर बाल निकेतन स्कूल में पूरी हुई।
5. इन प्रश्नों के उत्तर चार या पाँच वाक्यों में लिखें :
(क) कल्पना चावला का सपना कब और कैसे पूरा हुआ?
उत्तर :
कल्पना चावला का सपना 19 नवम्बर, सन् 1997 ई० को पूरा हुआ जब उसने एस० टी० एस० 87 अन्तरिक्ष यान द्वारा दोपहर 2.37 बजे अपनी पहली उड़ान भरी। यह मिशन अन्तरिक्ष में 17 दिन 16 घंटे 32 मिनट रहकर धरती पर लौट आया।
(ख) कल्पना की दूसरी अंतरिक्ष यात्रा उसकी जीवन की अंतिम यात्रा बनी? स्पष्ट करें।
उत्तर :
कल्पना चावला ने दूसरी अन्तरिक्ष उड़ान 16 जनवरी, सन् 2003 को अन्तरिक्षयान कोलंबिया से शुरू की। इस मिशन में अन्तरिक्ष में 80 परीक्षण एवं प्रयोग किए। यह विमान 16 दिनों बाद अन्तरिक्ष से 1 फरवरी, सन् 2003 को लौट रहा था। यह लौटते समय पृथ्वी से 63 कि० मी० की ऊँचाई पर एक बड़े धमाके के साथ टूटकर बिखर गया। इसमें कल्पना सहित सभी छ: यात्री अन्तरिक्ष में विलीन हो गए। इस तरह कल्पना की दूसरी उड़ान उनकी जीवन की अन्तिम यात्रा बनी।
![]()
(ग) कल्पना चावला के जीवन से आप क्या प्रेरणा लेते हैं?
उत्तर :
कल्पना चावला के जीवन से हमें यह प्रेरणा मिलती है कि सपने केवल सोचने से सच नहीं होते बल्कि उन्हें पूरा करने के लिए कठिन परिश्रम, दृढ़ निश्चय, आत्मविश्वास एवं एकाग्रता से आगे बढ़ना चाहिए। उन्हें पूरा करने में कठोर मेहनत करनी चाहिए।
6. निम्नलिखित साल कल्पना चावला के जीवन में क्यों महत्वपूर्ण थे?
साल – महत्वपूर्ण क्यों?
- 1978 _________________
- 1982 _________________
- 1984 _________________
- 1988 _________________
- 1994 _________________
- 1997 _________________
उत्तर :
साल – महत्त्वपूर्ण क्यों
- 1978 – इस वर्ष कल्पना ने प्री इंजीनियरिंग की परीक्षा पास की।
- 1982 – पंजाब इंजीनियरिंग कॉलेज चण्डीगढ से ऐरोनॉटिकल इंजीनियरिंग में स्नातक की डिग्री ली।
- 1984 – टैक्सास विश्वविद्यालय से ऐरोस्पेस इंजीनियरिंग में स्नातकोत्तर डिग्री प्राप्त की।
- 1988 – कोलोरोडो विश्वविद्यालयं से ऐरोस्पेस इंजीनियरिंग में पीएच० डी० की डिग्री ग्रहण की।
- 1994 – नासा के अन्तरिक्ष यात्री के रूप में चुना गया।
- 1997 – अन्तरिक्ष यान एस० टी० एस० 87 द्वारा अन्तरिक्ष की प्रथम उड़ान भरी।
7. निम्नलिखित शब्दों के वाक्य इस तरह बनायें ताकि अर्थ स्पष्ट हो जायें :
शब्द – वाक्य
- अनुसरण = …………………………..
- एकाग्रता = …………………………..
- आकर्षित = …………………………..
- आकांक्षा = …………………………..
- नियंत्रित = …………………………..
- नियुक्ति = …………………………..
- परीक्षण = …………………………..
- परिसर = …………………………..
उत्तर :
शब्द – वाक्य
- अनुसरण हमें अपने सपनों को साकार करने के लिए कल्पना का अनुसरण करना चाहिए।
- एकाग्रता मनुष्य को पूरी एकाग्रता से परिश्रम करना चाहिए।
- आकर्षित – संसार कल्पना चावला की उड़ान की तरफ आकर्षित था।
- आकांक्षा जीवन में आकांक्षा रखना बहुत ज़रूरी है।
- नियंत्रित हमें अपने मन को नियंत्रित रखना चाहिए।
- नियुक्ति रवि की अध्यक्ष पद पर नियुक्ति हुई।
- परीक्षण भारतीय सेना ने दूरमारक यंत्रों का सफल परीक्षण किया।
- परिसर विश्वविद्यालय का परिसर बहुत सुन्दर है।
![]()
8. इन मुहावरे/लोकोक्तियों के अर्थ लिखकर उन्हें वाक्यों में प्रयोग करें :
- जहाँ चाह वहाँ राह _________________
- दु:ख के सागर में डूब जाना _________________
- दिलों पर राज करना _________________
- खुशी का ठिकाना न रहना _________________
- दिल दहला देना _________________
उत्तर :
- जहाँ चाह वहाँ राह–इच्छा से ही रास्ता निकलता है-कल्पना ने बचपन में अन्तरिक्ष में उड़ने का सपना देखा और पूरा कर लिया। इसे कहते हैं जहाँ चाह वहाँ राह।
- दुःख के सागर में डूब जाना-बहुत दुखी होना-कल्पना चावला की मृत्यु से संसार दुःख के सागर में डूब गया।
- दिलों पर राज करना-सबको अच्छा लगने वाला-कल्पना चावला सबके दिलों पर राज करती है।
- खुशी का ठिकाना न रहना-बहुत खुश होना-निधि राज्य में प्रथम आई तो उसकी खुशी का ठिकाना न रहा।
- दिल दहला देना-भयभीत करना- जापान की सुनामी ने सब का दिल दहला दिया था।
9. इन वाक्यों में क्रिया अकर्मक है अथवा सकर्मक :
(क) स्कूल में वह सभी अध्यापकों की चहेती थी।
उत्तर :
सकर्मक।
(ख) आसमान में विमानों को उड़ता देखकर वह उनकी ओर आकर्षित हो जाती थी।
उत्तर :
अकर्मक।
(ग) वह स्नातकोत्तर की डिग्री लेने के लिए अमेरिका पहुँच गयी।
उत्तर :
सकर्मक।
(घ) कल्पना ने 19 नवम्बर 1997 को अंतरिक्ष में अपनी पहली उड़ान भरी।
उत्तर :
सकर्मक।
(ङ) प्रत्येक मनुष्य सपने देखता है।
उत्तर :
अकर्मक।
![]()
(च) बड़े होने पर कल्पना ने अपने सपने को साकार कर दिखाया।
उत्तर :
सकर्मक।
(छ) नासा ने उसे एक बार फिर अंतरिक्ष यात्रा के लिए चुना।
उत्तर :
सकर्मक।
10. निम्नलिखित पंजाबी वाक्यों का हिंदी में अनुवाद करें :
(क) ਇਹ ਉਸਦਾ ਮਨਪਸੰਦ ਵਿਸ਼ਾ ਸੀ।
उत्तर :
यह उसका मनपसद विषय था।
(ख) ਉਹ ਆਪਣੇ ਪਰਿਵਾਰ ਵਿੱਚ ਸਭ ਤੋਂ ਛੋਟੀ ਸੀ।
उत्तर :
वह अपने परिवार में सब से छोटी थी।
(ग) ਕਲਪਨਾ ਚਾਵਲਾ ਨੂੰ ਸੰਗੀਤ ਬੇਹਦ ਪਸੰਦ ਸੀ।
उत्तर :
कल्पना चावला को संगीत बहुत पसन्द था।
(ਬ) ਉਹ ਜਹਾਜ਼ਾਂ ਨੂੰ ਉਡਾਉਣ ਵਿੱਚ ਪਹਿਲਾਂ ਤੋਂ ਹੀ ਮਾਹਿਰ ਸੀ।
उत्तर :
वह जहाजों को उड़ाने में पहले से ही माहिर थी।
(ङ) ਅੱਜ ਵੀ ਉਹ ਸਾਰਿਆਂ ਦੇ ਦਿਲਾਂ ਤੇ ਰਾਜ ਕਰਦੀ ਹੈ।
उत्तर :
आज भी वह सभी के दिलों पर राज करती है।
![]()
रचनात्मक अभिव्यक्ति :
(क) मौखिक अभिव्यक्ति – ‘जहाँ चाह वहाँ राह’ विषय पर अपने विचार कक्षा में प्रस्तुत करें।
उत्तर :
विद्यार्थी अपने अध्यापक/अध्यापिका की सहायता से कक्षा में करें।
(ख) लिखित अभिव्यक्ति
(i) आपका क्या सपना है ? लिखें
(ii) कल्पना चावला के बाद सुनीता विलियम्स ने भी अंतरिक्ष की यात्रा की है। उनके बारे में अध्यापक/अभिभावक से जानकारी लेकर पाँच वाक्य लिखें।
(iii) भारत में सबसे पहले कौन-सा वैज्ञानिक अंतरिक्ष पर गया? पता करें और लिखें।
उत्तर :
विद्यार्थी अपने अध्यापक/अध्यापिका की सहायता से स्वयं करें।
परीक्षोपयोगी अन्य प्रश्नोत्तर
प्रश्न 1.
सपने किनके सच होते हैं ?
उत्तर :
सपने उनके सच होते हैं जो दृढ़ निश्चय, आत्मविश्वास एवं एकाग्रता से कठिन परिश्रम करते हैं, जो बाधाओं से घबराते नहीं बल्कि उनका साहसपूर्वक सामना करते हैं।
प्रश्न 2.
सपनों के बारे में कल्पना चावला के क्या विचार थे ?
उत्तर :
कल्पना चावला का विचार था कि सपनों से सफलता की ओर जाने की राह मौजूद होती है। व्यक्ति में उसे खोजने की दृष्टि, उस पर चलने का साहस तथा उसका अनुसरण करने की इच्छा शक्ति होनी चाहिए।
प्रश्न 3.
कल्पना चावला के चरित्र की विशेषताएँ लिखिए।
उत्तर :
कल्पना चावला के चरित्र की निम्नलिखित विशेषताएँ हैं
- जिज्ञासु – कल्पना चावला बचपन से ही जिज्ञासु प्रवृत्ति की थी। वह आसमान में विमानों को उड़ता देखकर अचानक ही उनकी ओर आकर्षित हो जाती थी। वह भी सपनों के पंख लगा गगन की सैर करना चाहती थी।
- साहसी – कल्पना चावला बहुत साहसी थी। वह अपना प्रत्येक कार्य साहसपूर्वक ढंग से करती थी। कठिनाइयों से घबराती नहीं थी। इसी कारण उसने अन्तरिक्ष की सैर की।
- परिश्रमी – कल्पना चावला कठोर परिश्रमी थी। वह बचपन से काम को पूरी एकाग्रता से करती थी।
![]()
प्रश्न 4.
कल्पना चावला ने इंजीनियर बनने का इरादा कब कर लिया था ?
उत्तर :
आठवीं कक्षा में।
प्रश्न 5.
कल्पना चावला की अन्तरिक्ष यात्रा का वर्णन कीजिए।
उत्तर :
कल्पना चावला ने अन्तरिक्ष यान एस० टी० एस० 87 द्वारा 19 नवम्बर, सन् 1997 ई० को पहली उड़ान भरी। यह मिशन अन्तरिक्ष में 17 दिन 16 घंटे 32 मिनट तक रहा और फिर धरती पर लौट आया। 16 जनवरी, सन् 2003 को अन्तरिक्ष यान कोलंबिया द्वारा शुरू की। किन्तु दुर्भाग्यवश 16 दिनों के अन्तरिक्ष अभियान से लौटते हुए विमान दुर्घटनाग्रस्त हो गया।
प्रश्न 6.
कल्पना चावला संगीतप्रिय महिला थी। कैसे ?
उत्तर :
कल्पना चावला को संगीत से बहुत लगाव था। वह भरतनाट्यम् भी जानती थी। वह अपनी दूसरी अन्तरिक्ष यात्रा पर अपने साथ हरीप्रसाद चौरसिया का बासुरी वादन, रविशंकर के सितार, नुसरत फतेह अली खाँ के सूफ़ी कलाम आदि की एलबम सी०डी० ले गई थीं। इससे पता चलता है कि कल्पना चावला संगीतप्रिय महिला थी।
बहुविकल्पीय प्रश्न
निम्नलिखित प्रश्नों के उत्तर सही विकल्प चुनकर लिखें :
प्रश्न 1.
कल्पना चावला का जन्म कब हुआ था ?
(क) 1 – 7 – 1961
(ख) 1 – 7 – 1962
(ग) 1 – 7 – 1963
(घ) 1 – 7 – 1964
उत्तर :
(क) 1 – 7 – 1961
प्रश्न 2.
कल्पना चावला का जन्म कहाँ हुआ था ?
(क) अंबाला
(ख) करनाल
(ग) पानीपत
(घ) रोहतक।
उत्तर :
(ख) करनाल
![]()
प्रश्न 3.
पंजाब इंजीनियरिंग कॉलेज से कल्पना चावला ने किस विषय में डिग्री प्राप्त की ?
(क) ऐरोनाटिकल
(ख) कैमीकल
(ग) मकैनिकल
(घ) कंप्यूटर।
उत्तर :
(क) ऐरोनाटिकल
प्रश्न 4.
कल्पना चावला ने ऐरोस्पेस इंजीनियरिंग में पी एच० डी० डिग्री किस विश्वविद्यालय से प्राप्त की ?
(क) कोलोराडो
(ख) टैक्सास
(ग) फ्लोरिडा
(घ) मैक्सिको।
उत्तर :
(क) कोलोराडो
प्रश्न 5.
कल्पना चावला को नासा ने अंतरिक्ष यात्री के रूप में कब चुना ?
(क) 1992
(ख) 1993
(ग) 1994
(घ) 1995
उत्तर :
(ग) 1994
![]()
प्रश्न 6.
कल्पना चावला ने अंतरिक्ष में पहली उड़ान कब भरी थी ?
(क) 19 – 11 – 1997
(ख) 19 – 10 – 1997
(ग) 19 – 9 – 1997
(घ) 19 – 8 – 1997
उत्तर :
(क) 19 – 11 – 1997
प्रश्न 7.
कल्पना चावला ने अंतरिक्ष में दूसरी उड़ान कब भरी?
(क) 16 – 1 – 2003
(ख) 16 – 2 – 2003
(ग) 16 – 3 – 2003
(घ) 16 – 4 – 2003
उत्तर :
(क) 16 – 1 – 2003
प्रश्न 8.
कल्पना चावला का अंतरिक्ष विमान में धमाके के बाद कब निधन हुआ?
(क) 1 – 2 – 2003
(ख) 1 – 3 – 2003
(ग) 1 – 4 – 2003
(घ) 1 – 5 – 2003
उत्तर :
(क) 1 – 2 – 2003
अंतरिक्ष परी : कल्पना चावला Summary in Hindi
अंतरिक्ष परी : कल्पना चावला पाठ का सार
‘अन्तरिक्ष परी : कल्पना चावला’ शीर्षक पाठ डॉ. सुनील बहल द्वारा रचित है। इसमें लेखक ने अन्तरिक्ष परी कल्पना चावला के बारे में बताया है। प्रत्येक मनुष्य सपने देखता है किन्तु सपने पूरे करने के लिए अनथक परिश्रम, दृढ़ निश्चय, आत्मविश्वास एवं एकाग्रता की अत्यंत आवश्यकता पड़ती है। इन्हीं गुणों से कल्पना चावला ने अपने सपनों को पूरा किया। उनका मानना था कि सपनों में सफलता की ओर जाने की राह होती है।

इनका जन्म 1 जुलाई, सन् 1961 ई० में हरियाणा राज्य के करनाल के एक मध्यमवर्गीय परिवार में हुआ था। इनकी माँ का नाम श्रीमती संज्योति तथा पिता का नाम श्री बनारसी लाल चावला है। कल्पना चावला अपने परिवार में चार भाई-बहनों में सबसे छोटी थी। घर में उसे प्यार से मोंटू कह कर बुलाते थे। उनकी प्रारम्भिक शिक्षा टैगोर बाल निकेतन स्कूल में हुई। वह बचपन से ही जिज्ञासु प्रवृत्ति की थी। उनका बचपन से आसमान में उड़ने का सपना था।
![]()
उन्होंने आठवीं कक्षा में ही अपने माता-पिता से इंजीनियर बनने की इच्छा जाहिर की। सन् 1978 ई० में कल्पना ने प्री इंजीनियरिंग पास की। सन् 1982 ई० में पंजाब इंजीनियरिंग कॉलेज चण्डीगढ़ से ऐरोनॉटिकल इंजीनियरिंग में स्नातक की डिग्री प्राप्त की। इसके बाद उन्होंने अमेरिका जाकर स्नातकोत्तर की डिग्री टैक्सास विश्वविद्यालय से प्राप्त की। वहीं जीन पियरे हैरिसन उसके मित्र बन गए जो फ्लाइंग क्लब का छात्र थे।
कल्पना भी उसके साथ फ्लाइंग क्लब में जाने लगी। सन् 1983 ई० में कल्पना तथा हैरिसन का विवाह हो गया। सन् 1988 ई० में कल्पना ने कोलोराडो विश्वविद्यालय से ऐरोस्पेस इंजीनियरिंग में पीएच०डी० की डिग्री प्राप्त की। सन् 1993 ई० में अमेरिका में कैलिफोर्निया की कम्पनी मेथडस इन्कॉर्पोरेशन में उपाध्यक्ष पर कार्य किया। सन् 1994 में नासा में उन्हें अन्तरिक्ष यात्री के रूप में चुना गया। इससे कल्पना को बहुत खुशी हुई।
इससे उनका आत्मविश्वास और अधिक बढ़ गया। 16 मार्च, सन् 1995 ई० को कल्पना चावला ने एक वर्ष तक प्रशिक्षण शुरू किया। इसके बाद उनकी नियुक्ति अंतरिक्ष यात्री के प्रतिनिधि के रूप में हुई। 19 नवम्बर, सन् 1997 ई० को भारतीय समयानुसार दोपहर 2:37 बजे कल्पना ने अपने दल के साथ एस० टी० एस० 87 अन्तरिक्ष यान द्वारा अपनी पहली उड़ान भरी। यह मिशन 17 दिन, 16 घंटे, 32 मिनट अन्तरिक्ष में रहकर पृथ्वी पर लौट आया।
इसमें अन्तरिक्ष में 161 भारहीनता से भौतिक क्रियाओं को प्रभावित करने वाले परीक्षणों पर जोर दिया गया। कल्पना ने दूसरी उडान 16 जनवरी, सन 2003 को अन्तरिक्ष यान कोलम्बिया से शुरू की। इस मिशन में अन्तरिक्ष में 80 परीक्षण एवं प्रयोग किए गए। यह अन्तरिक्ष यान 16 दिनों के बाद लौट रहा था कि अचानक 1 फरवरी, सन् 2003 को पृथ्वी से 63 किलोमीटर की ऊँचाई पर बड़े धमाके के साथ टूटकर बिखर गया जिसमें कल्पना सहित छ: अन्य अन्तरिक्ष यात्री अन्तरिक्ष में विलीन हो गए। इस घटना ने सारे विश्व को झकझोर कर रख दिया।
![]()
सारा संसार दुःख के सागर में डूब गया। कल्पना के परिवार के सदस्य भी उनके स्वागत के लिए अमेरिका पहुँच चुके थे। वे उनके इंतज़ार में थे किन्तु कल्पना सभी को रोता छोड़कर कल्पनाओं में खो गई। वास्तव में कल्पना युवाओं की प्रेरणा स्रोत रहेगी।
अंतरिक्ष परी : कल्पना चावला शब्दार्थ :
- अंतरिक्ष = आसमान।
- लक्ष्य = उद्देश्य।
- अनथक = बिना थके।
- दृढ़ = मज़बूत।
- एकाग्रता = एक मन से।
- चाह = इच्छा।
- राह = रास्ता।
- साकार = आकार रूप में।
- दृष्टि = नज़र।
- जिज्ञासु = जानने की प्रवृत्ति।
- बखूबी = पूरी तरह।
- फ्लाइंग जहाज़ उड़ना।
- निरन्तर लगातार।
- अदम्य = प्रबल।
- विश्व = संसार।
- नमन = नमस्कार। अभिवादन।
अंतरिक्ष परी : कल्पना चावला सप्रसंग व्याख्या
1. प्रत्येक मनुष्य सपने देखता है। सपने ही किसी लक्ष्य की नींव होते हैं। किन्तु यह भी सच है कि सपने केवल सोचने से ही सच नहीं हो जाते। उनको पूरा करने के लिए अनथक परिश्रम, दृढ़ निश्चय, आत्मविश्वास व एकाग्रता की अत्यन्त आवश्यकता होती है। कहा भी गया है- जहां चाह वहां राह। अत: जो अपने सपनों को साकार करने के लिए जी-तोड़ मेहनत करता है, उसको सफलता निश्चित रूप से मिलती ही है। वह कितना सौभाग्यशाली होता है जो अपने सपनों को साकार होते देखता है।
प्रसंग-यह गद्यांश डॉ० सुनील बहल द्वारा लिखित ‘अन्तरिक्ष परी : कल्पना चावला’ शीर्षक पाठ से लिया गया है। मनुष्य के सपने मेहनत से ही पूरे होते हैं-इसी का वर्णन किया है।
व्याख्या-लेखक कहता है कि इस संसार में प्रत्येक मनुष्य सपने देखता है। सपने ही किसी उद्देश्य की नींव या आधारशिला होते हैं। किन्तु यह बात बिल्कुल सच है कि सपने केवल सोचने से ही सच नहीं होते बल्कि उन्हें पूरा करने के लिए कठोर परिश्रम, दृढ़ निश्चय, आत्मविश्वास, एकाग्रता की बहुत आवश्यकता होती है। कहा भी गया है कि जहाँ इच्छा होती है वहाँ रास्ता अपने आप ही बन जाता है। यदि मनुष्य इच्छा रखे तो आगे बढ़ने का रास्ता तो बन ही जाता है। इसलिए जो व्यक्ति सपनों को पूरा करने के लिए कठोर परिश्रम करता है। उसे सफलता अवश्य ही मिलती है। वह व्यक्ति बहुत सौभाग्यशाली होता है जो अपने सपने को पूरा करते हुए देखता है।
भावार्थ-सपनों को साकार करने के लिए कठोर परिश्रम करने की प्रेरणा दी है।
![]()
2. बच्चो ! ऐसे ही बचपन में उड़ते हुए विमानों को देखकर आसमान की सैर करने का सपना कल्पना चावला ने देखा और बड़े होने पर उस सपने को साकार कर दिखाया। कल्पना चावला का भी मानना था कि सपनों से सफलता की ओर जाने की राह मौजूद होती है। व्यक्ति में उसे खोजने की दृष्टि, उस पर चलने का साहस और उसका अनुसरण करने की इच्छा शक्ति होनी चाहिए।
प्रसंग-ये पंक्तियाँ डॉ. सुनील बहल द्वारा रचित ‘अन्तरिक्ष-परी : कल्पना चावला’ शीर्षक पाठ से ली गई हैं। इनमें लेखक ने सपनों को साकार करने के लिए साहस एवं इच्छा शक्ति रखने की प्रेरणा दी है।
व्याख्या- लेखक बच्चों को सम्बोधित करते हुए कहता है कि हे बच्चो ! इसी तरह से कल्पना चावला ने अपने बचपन में उड़ते हुए विमानों को देखकर आसमान की सैर करने का सपना देखा था। उन्होंने बड़े होकर उन सपनों को पूरा करके भी दिखाया। कल्पना चावला का मानना था कि सपनों से सफलता की ओर जाने का रास्ता मौजूद होता है। बस व्यक्ति में उसे खोजने की दृष्टि, उस पर चलने का साहस और उसका अनुसरण करने की इच्छा शक्ति होनी चाहिए। कहने का भाव है कि यदि यह सब व्यक्ति में है तो वह अपने सपने पूरे कर सकता है। भावार्थ-लेखक ने सपनों को पूरा करने के लिए साहस एवं इच्छा शक्ति से परिश्रम करने की प्रेरणा दी है।
3. यह बात पूर्णतः सत्य है कि सच्ची लगन, जी-तोड़ मेहनत व सतत अभ्यास कभी निष्फल नहीं जाता। वह देर-सवेर ज़रूर फलीभूत होता है। एक दिन दिसम्बर 1994 में नासा (नेशनल एयरोनॉटिकल एण्ड स्पेस एडमिनिस्ट्रेशन) के एक अधिकारी ने टेलीफ़ोन पर कल्पना को बताया कि उन्होंने उसे अन्तरिक्ष यात्री के रूप में चुना है। उन्होंने उसे अन्तरिक्ष यात्रियों के लिए आयोजित की जाने वाली कार्यशाला में भाग लेने का निमंत्रण भी दिया। यह सब सुनकर कल्पना की खुशी का ठिकाना न रहा। आज उसके कानों में वह बात सुनी जिसका उसे वर्षों से इन्तज़ार था। यह एक ऐसा अवसर था जिसके लिए दुनिया के बड़े-बड़े वैज्ञानिक तरसते हैं।
प्रसंग-यह गद्यांश ‘डॉ० सुनील बहल’ द्वारा लिखित ‘अन्तरिक्ष-परी : कल्पना चावला’ शीर्षक से लिया गया है। इसमें लेखक ने सच्ची लगन, कठोर परिश्रम एवं अभ्यास करने
की प्रेरणा दी है।
व्याख्या-लेखक कहता है कि यह बात बिल्कुल सच है कि सच्ची लगन, कठोर परिश्रम एवं निरन्तर अभ्यास कभी भी बेकार नहीं जाती। वह देर-सवेर अवश्य परा होता है। एक दिन दिसम्बर 1994 ई० में नासा अर्थात नेशनल एयरोनॉटिकल एण्ड स्पेस एडमिनिस्ट्रेशन के एक अधिकारी ने टेलीफ़ोन पर कल्पना को बताया कि उन्होंने उसे अन्तरिक्ष यात्री के रूप में चुना है। उन्होंने उसे अन्तरिक्ष यात्रियों के लिए आयोजित की जाने वाली कार्यशाला में भाग लेने का निमन्त्रण दिया। यह सब सुनकर कल्पना बहुत खुश हुई।
![]()
आज उसके कानों ने वह बात सुनी जिसका उसे अनेक वर्षों से इन्तजार था। उनके लिए वह एक ऐसा अवसर था जिसके लिए दुनिया के बड़े-बड़े वैज्ञानिक तरसते हैं।
भावार्थ-कल्पना के सपनों को साकार करते हुए दिखाया है।
4. अन्तरिक्ष यात्री के रूप में चुने जाने के बाद उसका आत्मविश्वास और भी बढ़ गया। वह जहाजों को उड़ाने में तो पहले ही कुशल थी किन्तु अन्तरिक्ष में उड़ने के अवसर को लेकर वह बहुत ही उत्साहित थी। 16 मार्च, सन् 1995 को कल्पना ने एक साल का प्रशिक्षण शुरू किया। प्रशिक्षण के बाद कल्पना की अन्तरिक्ष यात्री के प्रतिनिधि के रूप में तकनीकी क्षेत्रों में नियुक्ति की गयी। यहाँ पर रोबोटिक उपकरणों का विकास और अन्तरिक्ष यान को नियन्त्रित करने वाले साफ्ट वेयर की शटल एवियोनिक्स प्रयोगशाला में परीक्षण करना इसके मुख्य काम थे।
प्रसंग-यह गद्यांश हिन्दी की पाठ्य-पुस्तक में संकलित ‘अन्तरिक्ष-परी : कल्पना चावला’ शीर्षक से लिया गया है। यह ‘डॉ० सुनील बहल’ द्वारा रचित है। इसमें कल्पना को अन्तरिक्ष यात्री के रूप में चुने जाने को दर्शाया है।
व्याख्या-लेखक कहता है कि जब कल्पना चावला को अन्तरिक्ष यात्री के रूप में चुन लिया गया तो उसके बाद उसका आत्मविश्वास और ज्यादा बढ़ गया। वह जहाजों को उड़ाने में तो पहले ही कुशल थी किन्तु अन्तरिक्ष में उड़ने के अवसर को लेकर वह बहुत ही उत्साहित हुई थी। 16 मार्च, सन् 1995 ई० को कल्पना ने एक वर्ष का प्रशिक्षण शुरू किया। प्रशिक्षण के बाद कल्पना की अन्तरिक्ष यात्री के प्रतिनिधि के रूप में तकनीकी क्षेत्रों में नियुक्ति की गई। यहाँ पर रोबोटिक उपकरणों का विकास तथा अन्तरिक्ष यान को नियन्त्रित करने वाले साफ़्टवेयर की शटल एवियोनिक्स प्रयोगशाला में परीक्षण करने इनके मुख्य कार्य थे।
भावार्थ-कल्पना चावला के आत्मविश्वास एवं कठिन परिश्रम के बारे में बताया है।
5. सारे विश्व के लिए यह एक दिल दहला देने वाली घटना थी। जहाँ सभी अन्तरिक्ष यात्रियों के लौटने का इन्तज़ार कर रहे थे वहीं एक दम से सभी दुःख के सागर में डूब गये। अमेरिका के मानव अन्तरिक्ष उड़ान के इतिहास में यह पहला अवसर था जब कोई अन्तरिक्ष यान अपने मिशन को सफलतापूर्वक सम्पन्न करने के बाद पृथ्वी पर लौटते समय दुर्घटनाग्रस्त हो गया था। कल्पना के परिवार के सदस्य उसके स्वागत के लिए तो पहले से ही अमेरिका पहुँच गये थे। वे उसकी वापसी की प्रतीक्षा में थे किन्त कमबख्त वक्त ने ऐसा होने न दिया। भारत की होनहार कल्पना सभी को उस दिन बिलखता छोड़कर कहीं कल्पनाओं में खो गयी किन्तु आज भी वह सभी के दिलों पर राज करती है। युवाओं के लिए तो यह निस्संदेह प्रेरणा स्त्रोत रही है और रहेगी। पूरा विश्व उसे नमन करता है।
प्रसंग-ये पंक्तियाँ डॉ. सुनील बहल द्वारा रचित ‘अन्तरिक्ष-परी-कल्पना चावला’ शीर्षक से ली गई हैं। इसमें सारे विश्व को दहला देने वाली घटना कल्पना चावला की मृत्यु का वर्णन है।
![]()
व्याख्या- लेखक कहता है कि कल्पना चावला अपने यात्रियों सहित अन्तरिक्ष में गुम हो गई। यह घटना सारे संसार के लिए दिल को दहला देने वाली घटना थी। जहाँ सभी अन्तरिक्ष यात्रियों के लौटने की प्रतीक्षा कर रहे थे। उसी समय सभी लोग दुःख के सागर में डूब गए। अमेरिका के मानव अन्तरिक्ष उड़ान के इतिहास में यह पहला अवसर था जब कोई अन्तरिक्ष वायुयान अपने मिशन को सफलतापूर्वक पूरा करने के बाद पृथ्वी पर लौटते समय दुर्घटनाग्रस्त हो गया था। कल्पना के परिवार के सदस्य उसके स्वागत के लिए तो पहले से ही अमेरिका पहुँच गए थे।
वे सभी उसकी वापसी आने की प्रतीक्षा कर रहे थे किन्तु दुष्ट समय ने ऐसा नहीं होने दिया। भारत की मेधावी कल्पना सारे संसार को उस दिन रोता हुआ छोड़कर कल्पनाओं में खो गई। किन्तु आज भी वह सभी के दिलों पर राज करती है। युवाओं के लिए तो वह वास्तव में एक प्रेरणा स्रोत रही है और भविष्य में भी रहेगी। सारा संसार उसे नमन करता है।
भावार्थ-कल्पना चावला की मृत्यु से विश्व में फैले मातम करुण का चित्रण है।