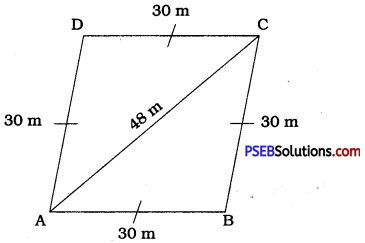
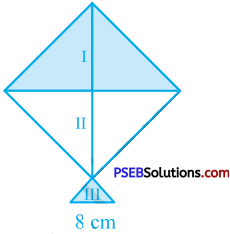
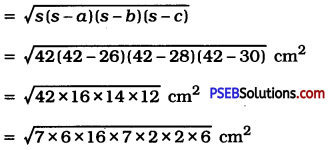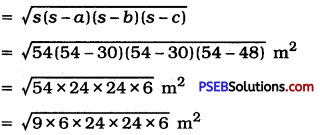Punjab State Board PSEB 9th Class English Book Solutions English Paragraph Writing Exercise Questions and Answers, Notes.
PSEB 9th Class English Paragraph Writing
1. My Father
My father is an able person. He is a farmer. He is not well-educated. But he knows his work well. He is very hard-working. He is truthful and honest. So people respect him. They greet him respectfully. My father has an open mind. He tries to settle the quarrels among the people of the village. He is the wisest man of the village. He leads a simple and clean life. He does not lose temper with anybody. He is respected by one and all. I am proud of my father.
2. My Mother
Shrimati Asha is my mother. She is 40 years old. She is a kind and noble lady. She is active and smart. She is an M.A. She is a very simple lady. She has good habits. She gets up early in the morning. Then she cleans the house. She takes a bath and prays to God. She goes to temple daily. She prepares food for us. She looks after us all. She helps me in my studies. At night, she tells us stories. She loves me very much. I am proud of my mother. May she live long !

3. My Younger Brother
Surinder is my younger brother. He is twelve years old. He is strong and healthy. He is tall for his age. He is very intelligent. He is honest. He never tells a lie. He is hard-working and obedient. He reads in the 6th class. He is the monitor of his class. He stands first in his class. He does his homework daily. He does not mix with bad boys. All the teachers love him. He is very fond of cricket. He is a member of the school cricket team. He is a good singer also. He is fond of reading storybooks. We are proud of him.
4. The Person I Dislike Most
Mr. Chaudhry, our next-door neighbour, is the person I dislike most. He has made our life miserable. Whenever he sees that we are studying, he switches on his TV at full volume. He has a big dog. He keeps it unchained. Many a time the dog bites people going through the street. Mr. Chaudhry’s wife is a very quarrelsome lady. She quarrels over trifles. She has six children. They make mischiefs all the day. Their mother never scolds them. These children are very rude. They know no manners. They write dirty words on the walls. But nobody dares complain against them to their parents. It is really a curse to have such a neighbour.
5. My School
I read in Arya High School, Ludhiana. It is a very big school. It has one huge gate. It has two storeys. There are fifty rooms. The rooms are airy. Each room has two electric fans. The hall of our school is very big. The school has two big playgrounds. It has a beautiful garden also. There are ten classes in our school.

Each class has four sections. Each section has about sixty students. Our Headmaster is very able. He is very kind to the students. He is very hardworking. The teachers of our school are also able and hard-working. They love the students and the students respect them. Our school shows very good results every year. I love my school. I am proud of it. May it propser day and night!
6. Our Headmaster
Sh. Sohan Lal is the headmaster of our school. He is forty years old. He is tall and strong. He is active and smart. He is an M.A., B.Ed. Our headmaster is true to his duty. He is very punctual. He comes to school in time. He sits in his office. He works very hard. He plans his work well. He is very intelligent. He watches the working of the school. All the teachers and students respect him. He is a good teacher. He is a good speaker. He is a good writer also. He has written many books. He is a good player. He plays games in the evening. He is all in all in our school. We are proud of him. May he live long !
7. The Prize Distribution Function
The prize distribution function of our school was held on the seventh of March this year. The Education Minister presided over the function. The Minister took his seat and the function began. The Headmaster spoke a few words to welcome the guests and the Minister. Then the Headmaster requested the Minister to give away the prizes. The Minister shook hands with the prize-winners. All the prize-winners were loudly cheered. After giving away the prizes, the Minister made a short speech. He congratulated the prize-winners. He congratulated the Headmaster and the staff on their excellent work. In the end, the Headmaster thanked the Minister and the function was over. Tea was served to the guests and the prize-winners.
8. Our School Peon
Ramu is our school peon. He is twenty-five years old. He is tall and strong. He wears a khaki uniform. He is obedient and honest. He is true to his duty. He respects the teachers. He always speaks the truth. He knows his job well. Ramu lives in the school. He gets up early in the morning. He sweeps the school. He dusts the office. He rings the bell at the right time. He is busy the whole day. He is loyal to the school. He looks after the school property. His duty is hard, but his pay is small. I pity his lot.
9. A Postman
The postman is a very useful public servant. His duty is very hard. He has to do his duty in sun and rain. He goes to the Head Post Office in the morning. There he gets the dak. He arranges the letters. He puts them in a bag. Then he goes on his beat. He goes from door to door. He is eagerly waited for. He brings good as well as bad news. He helps to bring the world closer. A postman has to work hard. But his pay is small. He can hardly make both ends meet. I pity his lot.

10. A Rickshaw-Puller
The life of a rickshaw-puller is very hard. He lives by the sweat of his brow. He pulls heavy loads. He pulls men, women and children. It is very painful to look at him. A rickshaw-puller hardly gets as much as he deserves. People try to give him as little as possible. He has to work in sun and rain from morning till evening. Even then, he gets very little to eat. He is in rags. It is unlucky that even in this age of science men have to work like beasts of burden to earn their bread.
11. The Diwali Festival
Diwali is an important Indian festival. It falls in the month of October or November. It comes twenty days after Dussehra. Shri Ram came back to Ayodhya on this day. Shri Guru Hargobind was set free by the Mughal Emperor on this day. This festival is celebrated in every village and town. Houses and shops are painted in new colours. People light their homes with candles and electric lights. They buy sweets and toys. They distribute gifts among friends and relatives. Children enjoy fireworks at night. On this day, people worship goddess Lakshmi Some people gamble on this day. It is evil. It should be ended.
12. The Dussehra Festival
Dussehra is an important Hindu festival. It comes off in October. Rama defeated Ravar on this day. It marks the victory of good over evil. The festival lasts for ten days. Ram Lila staged at night. Many people come to see this Lila. On the last day, a fair is held. Many people come to see the fair. Everyone looks happy. Effigies of Ravana, Meghnada and Kumbhakarn are set up. Rama shoots arrows at the effigies. At about sunset, Hanumana sets them on fire After this people come back to their homes. They feel happy.
13. The Independence Day
India became a free country on August 15, 1947. So, August 15 is called the Independence Day of India. The British rule came to an end on this day. It is a red-letter day in the history of the country. It is celebrated all over the country with great enthusiasm. On this day, all schools, colleges and offices remain closed. It is a national holiday. Public meetings are held in all towns and cities. A big function is held in Delhi. The Prime Minister unfurls the national flag at the Red Fort. Our freedom is a hard-won freedom. We should protect it.
14. The Republic Day
India became a Republic on January 26, 1950. The Constitution of the country came into force on this day. India became a secular democratic country. The power of government passed into the hands of the common people. All castes, creeds and religions are to be equal in the eyes of the law. It is a red-letter day in the history of the country. It is celebrated all over the country with great enthusiasm. The national flag is unfurled at all the public buildings. A big function is held in Delhi. The President of the country presides over this function. It is worth seeing. This day is a national holiday.
15. Mahatma Gandhi
Mahatma Gandhi was born on October 2, 1869. He was unlike other boys. He was very gentle. He loved truth. He respected his teachers. After doing law he started practice in India. He did not take up false cases. He went to Africa to fight a case. There he saw the poor Indians. The English treated them badly. Gandhiji fought for their rights for ten years. Then he came back to India. He fought for the freedom of India. He gave us a new way of fighting. It was ‘ahimsa’. It was more powerful than violence. He was able to free India in 1947. He was a real Mahatma. He led a very simple life. He is called the Father of our Nation. A mad person shot him dead on January 30, 1948. Gandhiji’s name will always be remembered.
16. An Ideal Student
An ideal student is a knowledge-seeker in the real sense. He obeys his teachers. He has full confidence in them. He is regular and punctual. He works hard at studies. But he takes part in games also. He does not read cheap and dirty literature. He reads only good and useful books. An ideal student believes in simple living and high thinking. He knows the value of discipline. He does not waste the hard-earned money of his parents. An ideal student is a true patriot. In short, he has all the qualities of head and heart.

17. The Recess Period
The recess is the period of enjoyment. In this period, the students feel happy. They enjoy freedom for some time. As soon as the recess period begins, students rush out of their classrooms. Some of them run to the vendors. They buy things to eat. Others go to the taps to drink water. There is great rush in the playground. Some love to play there while others like to sit under the shady trees. They talk about their friends and teachers. Soon the bell goes. Students run back to their classes. The students feel fresh and start their studies once again.
18. A One-Day Cricket Match
Last Sunday, a one-day cricket match was played between our school and Arya High School. Each team played 40 overs. The match started at 10 a.m. We won the toss. We decided to bat first. Mohan and Gopal were our openers. Mohan made 30 runs and was out. Now Raja came in to bat. He did not play well. He was out for a duck. The next four players made 60 runs. Our team was out at 120 runs. Now it was the turn of Arya High School. They had good openers. They made 60 runs. Their third batsman was a hitter. He made 30 runs. But the other players were soon out. Their team could make only one hundred runs. We won the match by 20 runs. It was really a very interesting match.
19. A Football Match
Last Monday, a football match was played between our school and Khalsa School. It was played on our school grounds. Sh. Jaswant Singh was the referee. He blew the whistle. There was a toss. We won the toss. We chose our side. The match began. At first, the game was slow, but soon it became brisk. All the players played well. Our defence was very strong. There was no goal. The referee blew the whistle for interval. In the second half, Vinod passed the ball on to me. I ran with it into the Then I kicked it hard. It went through the poles. It was a goal. There were loud cheers. The referee blew the whistle. The game was over. We won the march by one goal.
20. A Kabaddi Match
I saw a kabaddi match last Sunday. It was played between our school and New High School. Sh. Mohan Lal was the referee. Many people came to see the match. There was a toss. We won the toss. We chose our side. Then the match began. First of all, our captain went running to the other side. He shouted, “Kabaddi, Kabaddi.” He came back. There was no point. Now it was the turn of New High School.

One of their players came to our side. He was caught. He could not go back. We scored a point. There were loud cheers. We scored more points. New High School team got only 8 points. We had gained 20 points. The referee blew a long whistle. The match came to an end. We won the match by 12 points. It was an interesting match.
21. Morning Walk
Morning walk is the best form of exercise. It costs nothing. It is very useful for our health. It refreshes our mind. It strengthens our body. It saves us from many diseases. Morning walk keeps us fresh for the whole day. It develops in us the habit of rising early. It brings pure thoughts in our mind. The dew drops, the fresh flowers, the chirping birds and the rustling leaves charm our mind. We start loving these objects of natural beauty. Thus, morning walk is useful not only for our body but for our mind also.
22. A Journey by Bus
Last Sunday, I went to Delhi by bus. I went to the bus stand and bought a ticket. A bus bound for Delhi was standing there. I got in and took the front seat. The conductor gave a whistle and the bus started. ‘We were soon out of the city. The driver drove very fast. But he was very good at his job. We felt quite safe. He left many buses behind. I saw farmers working in their fields. Here and there, I saw carts going on the road. The conductor was a jolly fellow. He made the journey pleasant by his witty talk. The bus reached Delhi at 6 p.m. It was a very pleasant journey.
23. A Journey by Train
Last year, I went to Delhi by train. I packed my luggage. I hired a rickshaw. I reached the station. I bought a ticket. I went to the platform. Soon the train arrived. I got into it. There was a great rush. But I was lucky. I got a seat near the window. The train started. I saw many things on the way. Farmers were ploughing the fields. Children were playing. A ticket-checker came. He checked our tickets. A young man was without ticket. He was fined. The train stopped at many stations. I bought a newspaper, I read it. It was 10 a.m. The train reached Delhi. It was a happy journey.
24. A Visit to a Zoo
There is a zoo in our city. I visited it last Sunday. I went with my parents. We bought tickets and went in. First of all, we saw birds. There were many beautiful and rare kinds of birds. We saw parrots, canaries, swallows, peacocks, ducks, cranes, herons, gulls and geese. Then we saw some wild beasts. A lioness and her cub were basking in the sun. They roared now and then. We also saw wolves, tigers, elephants and rhinos. When we were coming back, we saw a muddy pond. There were many big snakes in it. It was fearful to look at them. We stayed in the zoo for about three hours. Then we came back home.
25. A Visit to a Fair
I went to see a fair last Tuesday. This fair is held every year in our town. It is held in the memory of a pious faqir. Many people go to see this fair. They include men of all religions and faiths. This year I went to see the fair with my parents. We offered flowers at the faqir’s tomb.

Then we went round the fair. There was a temporary bazaar. Stalls were arranged on either side. There was a great hustle and bustle. Sweets were in great demand. Children were enjoying rides in merry-go-rounds. A big shamiana was set up on one side of the fair. Qawalis were being sung there. We sat there for some time. Then we came back home.
26. A Visit to a Circus
A circus came to our town last month. I went to see it with my parents. We bought tickets and went in. We took our seats in the front row. First of all, a young girl came in. She had an umbrella in her hand. She walked on a rope. Then some more girls joined her. They showed various feats in gymnastics. They looked like rubber dolls. One of the girls jumped through a fire ring. Then there were animal shows. An elephant drank water from a bottle. A lion and a goat played with each other. A monkey drove a mini-cycle. The show came to an end at 7 p.m. I liked it very much.
27. A Visit to a Historical Place
During the last spring holidays, I went to Agra. There I visited the Taj. It is built outside the city on the bank of the Yamuna. A large gateway of red stone provides the entrance. The Taj is a large and beautiful building. It stands on a raised platform. In the middle of the platform, there is a splendid white dome. At its four corners, there are four stately towers. Underneath the white dome are the marble tombs of Mumtaz Mahal and Shah Jahan. The whole building is surrounded by a garden on three sides. On the fourth side, the river Yamuna grazes it. No words can describe the beauty of the Taj.
28. A Scene at the Railway Station
Last Sunday, my father went to Delhi. I went to the station to see him off. I bought a ticket and a platform ticket. We went to the platform. There was great hustle and bustle. Some men were buying books at the bookstall. The hawkers were going up and down the platform. The coolies were busy. People were waiting for the train. Soon the train arrived. There was a great rush in it. Some passengers got down. Others got in and took their seats. I got a seat for my father. The engine gave a whistle. The guard waved a green flag. The train again whistled and steamed off. Now there was all quiet on the platform. I came back home.
29. A Scene at the Bus Stand
Last Monday, I went to the bus stand to see off my uncle. The bus stand was humming with life. There were separate parking stands for different routes. A bus was parked at each stand. Men behind the counter were issuing tickets. The conductors were shouting to attract passengers for their respective buses. As soon as a bus was full, the conductor blew his whistle and the bus moved out of the stand. Another one immediately took its place. This activity was going on endlessly. I bought a ticket for my uncle, got him a good seat and then came back home.
30. A House on Fire
It was Sunday. I was sitting in my room with my friend, Atul. Suddenly, we saw clouds of smoke rising in the sky. There was a big fire in the next street. People were running to the site of fire. Children were shouting for help. People brought buckets of water. We also joined them. We threw sand and water on the flames. The fire was put out after half an hour. It was the house of a carpenter. The poor man suffered a big loss. All his wood, grain and money were gone. The house was reduced to ashes. He was very sad at his loss. People felt sorry for him. They gave him food, clothes and some money. The poor carpenter thanked them with folded hands.

31. A Bus Accident
Last Monday, I was travelling from Panipat to Delhi by bus. We had hardly gone twenty kilometres when a dreadful accident took place. All of a sudden a scooterist, coming from a side-road, came in front of the bus. The driver at once applied the brakes, and also turned the bus to one side. All the passengers were thrown off their seats. In no time, the bus went off the road and fell into a ditch. There were loud cries. Many passengers were badly wounded. I, too, got a deep cut on my forehead. Many people gathered there. They helped us to get out of the bus. Luckily there was no death. The scooterist had sped away. I reached home with a bandaged head.
32. A Street Quarrel
Last evening, I was sitting near the window of my room. I saw two children playing in the street. Suddenly, they fell out. Other boys of the street gathered there. None tried to separate them. They kept looking on. Soon, the mothers of both the children reached there. They started abusing each other. They used very dirty words for each other. From hot words, they came to blows. They pulled each other’s hair. Luckily, an elderly woman came there. She separated the fighting ladies. She spoke to them very wisely. The two women realised their mistake. They went back to their homes. Both the children started playing together once again.
33. A Rainy Day
It was the month of July last year. One day, it was very hot. Men and animals were panting. All were perspiring. We longed for a shower of rain. In the afternoon, some clouds appeared in the east. Soon the whole sky was overcast with dark clouds. It started raining heavily. Streets and bazaars were flooded with water. Little children came out and played in the rain. They splashed water over one another. The rain stopped after two hours. It became very cool and pleasant. Streets and bazaars were washed clean. The city gave a fresh look.
34. Life in a Village
The three words that can amply describe the life in a village are — Simple, Pure and Fresh. The villagers are very simple-hearted people. They know no cunning. They are pure in their thoughts and actions. They are very hospitable. They live simply and happily. They have no anxiety. Life in a village is very calm and peaceful. It is free from the noise and din of cities. The air is fresh and health-giving. Says Leo Tolstoy in one of his stories, “A villager’s life is not a fat one, but it is a long one.” He may never grow rich, but he has always enough to eat. In short, we can say that life in a village is worth living.
35. How I Celebrated My Birthday
I gave a party on my birthday. I invited all my friends. The party was held at my house. The party began at 6 p.m. A big cake was placed on a table. All my friends stood round the table. I cut the cake with a knife. My friends and parents chanted three times : ‘Happy Birthday To You.’ Then everybody set to eating. The cake was served to all. It was very tasty. There were many things to eat. Everybody ate to their heart’s content. There was singing and dancing also. Everyone enjoyed the party. It was over by 8 p.m. My friends congratulated me once again and went back to their homes.
36. A Drowning Tragedy
One day, I was picnicking with some of my friends on the riverbank. A boy named Kamal fell into the river. He didn’t know how to swim. I saw him struggling with water. It was a painful sight. I at once jumped into the river. I swam to him and brought him out with great difficulty. He had swallowed a lot of water. He was unconscious. We, at once called a doctor. Someone ran to inform Kamal’s parents. The doctor pressed out the water from Kamal’s belly. Kamal opened his eyes. We felt great relief. After some time Kamal’s parents reached the place. They thanked me and the doctor again and again.

37. The Golden Temple
Amritsar is also called Guru-ki-nagri. It is famous for the Golden Temple. The Temple is situated in the city. It is surrounded by many narrow lanes. The golden shrine built in the middle of the sarover shines at sunrise and sunset. It was built by Guru Arjun Dev Ji. It is a unique experience when Granth Sahib is brought out from the Akal Takhat Sahib amidst chanting of hymns and blowing of bugles.
The Akal Takhat Sahib, facing the Harmandir Sahib, was built by Guru Hargobind Ji. It was used for holding courts. The complex has a museum of rare paintings, books, shashtras, etc. The lives of the Gurus are described through them. There is a big bazaar near Darshani Deori. Gutakas, karas and other articles related to the Sikh religion are sold there. Home-made papad-varian, chura-bangles, dry fruit are also sold in many shops. There are number of hotels and guest houses near the Temple for tourists to stay. There is a sarai also for pilgrims in the Temple. The Golden Temple is indeed a worth-visiting place.
38. Canada
Canada is one of the largest country of the world. Its area is 9,976,139 sq. km. and population is about 32 million. The capital city of Canada is Ottawa. The currency of the country is Canadian dollar. English and French are the official languages of Canada. In winter, the climate of Canada is bitterly cold. In some regions, the mercury may dip to -65°C. The average temperature in Ottawa is from -15°C to -6°C in January.
In July, the average temperature is 15°C to 26°C. The main products of Canada are fruit, vegetables, livestock, tobacco, copper, zinc, iron, salt, oil and natural gas. And major industries of the country are agriculture, forestry, food processing, transport, chemicals, oil and gas refining and cement. Vehicles, machinery, food stuffs, natural gas, meat, coal and timber are exported to other countries. Canada is one of the most developed nations of the world.
39. Aruna Asif Ali
Aruna Asif Ali is known as the Grand Old Lady of India. She took active part in the Independence movement. She was born in an orthodox Hindu Bengali family in 1909 at Kalka. She married a Muslim, Mr. Asif Ali, thus breaking all conventions regarding marriage. Her husband, Mr. Asif Ali, was also involved in the freedom struggle. Aruna Asif Ali took part in Salt Satyagrah under the leadership of Gandhiji.
She addressed many public meetings and led processions for the cause of India’s independence from the British rule. As a result, she was sentenced to one-year imprisonment. But she didn’t give up the cause for which she was fighting against the British rule. She was again sentenced to jail.
She became the editor of the newspaper ‘Inquilab’. After Independence, she became a social worker. She fought for the rights of women. In 1992 she received Nehru Award for International Understanding. She passed away in July 1996. She was honoured with Bharat Ratna posthumously.
40. The Tribals of Odisha
There are many tribal groups in Odisha. They live in remote places. One such group lives in the forests of Kalahandi. These people are one of most backward tribes in the world. They have dark skin and black hair. The women wear bright-coloured saris while the men wear nothing but loincloth.
They still believe that India is ruled by kings. These people are illiterate as they do not have any facility of schooling, means of transportation and proper motorable roads. As a result, they are cut off from the rest of the world. They do not have any idea of currency notes. They still use barter system.

They usually live in groups and each group has common property. They cure diseases with herbs and set bones by rubbing oils. The government should launch schemes to educate them and bring them to the mainstream of the nation.
41. An Incident of Burglary
Mr. Ramanathan is an affluent businessman of our town. One day, he with his family went out of the town to attend a wedding. There was nobody at home and the house was locked from outside. A thief broke into the house at night. He decamped with the jewellery, valuables and money.
But the neighbours had seen the lights on and they informed the police about it. The police came along with a dog. They found the thief’s glove. The dog sniffed the scent of the thief. It took the policemen to the thief’s place. Thus the thief was arrested and the case was solved. The policemen were rewarded by the department for their efficiency.
42. Floods in Mumbai
On July 26, 2005, I was busy shopping in a famous crowded market, although it was raining. Gradually, it started raining heavily. Now, it was impossible to go from there. Therefore, I took shelter in a shop. Soon, the place got flooded and water started entering the shops. The articles in the shops started floating in the water and the shopkeeper tried to retrieve valuable articles. The entire area was submerged in the flood water.
Many vehicles couldn’t move in the flood water. The people had to stay in them. Some other people took shelter in shops and houses. Suddenly, it started raining like hell. Now water in the shops and houses rose up to 6-7 feet. The people had to move to first floor. In no time the army swung into action. The volunteers of many NGO’s started helping the affected people with food and water. All this went on for more than 24 hours. It was really a horrifying experience which I can never forget.
43. The Lohri Festival
Lohri is a festival of fun and frolic. It is generally celebrated on 13th of January every year. This festival is related to the folklore of Dulla Bhatti. At sunset, people light up bonfires in the open in front of their houses. Lohri is celebrated with more enthusiasm in the families where there is a newborn son or a newly married person.
Giddha or Bhangra is performed to the beats of the drums. On the day of Lohri, children go singing from house to house asking for money and sweets. Lohri is a busy festival. People meet their friends and relatives and exchange greetings and gifts.
44. How to Make Papier-mache -Toys
In order to make toys with papier-mache, old newspaper sheets are taken. They are torn into small pieces. These pieces are soaked in water overnight. Next day, the mixture is boiled for half an hour. After that, the mixture is whipped till it becomes soft and pulpy.

The water is squeezed out from the mixture and two tablespoons of white gum are added into it. The mixture is stirred well and then the toys are made from it. These toys are left to dry overnight or more. Then they are painted with water-based colour. To make these toys waterproof, two or three coats of lacquer are given on them. Masks can also be made in the same manner.
45. How to Make Gajrela
It is very easy to make gajrela at home. Take three kilograms of large carrots and wash them properly. Then grate the carrots. Mix 242 litres milk with the carrots. After that put the mixture in a pan and boil it till the mixture becomes very thick. Add 3/4 cup of sugar and 250 gm of khoya in the mixture.
Stir the mixture till it becomes thick. Stir it continuously as the mixture should not stick to the pan. Now remove the pan from the fire. Add nuts to it. Your gajrela is ready. Let it cool before serving. It can also be served hot.
![]()
![]()
![]()
![]()
![]()