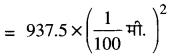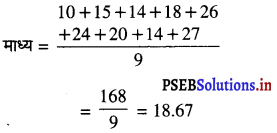Class 9

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5

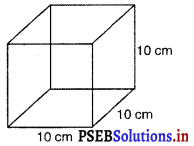
प्रश्न 1.
माचिस की डिब्बी के माप 4 cm × 2.5 cm × 1.5 cm हैं। ऐसी 12 डिब्बियों के एक पैकेट का आयतन क्या होगा ?
हल :
मान लीजिए माचिस की डिब्बी के माप लंबाई l = 4 cm, चौड़ाई ; b = 2.5 cm और ऊँचाई ; h = 1.5 cm

माचिस की डिब्बी का आयतन = l × b × h
= (4 × 2.5 × 1.5) cm³
= 15cm³
अब, हमें प्राप्त है, माचिस की डिब्बी का आयतन
= 15 cm³
∴ ऐसे माचिस की ऐसी 12 डिब्बियों का आयतन
= (12 × 15) cm
= 180 cm³

प्रश्न 2.
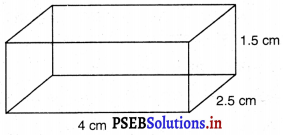
एक घनाभाकार पानी की टंकी 6 m लंबी, 5 m चौड़ी और 4.5 m गहरी है। इसमें कितने लीटर पानी आ सकता है ? (1 m³ = 1000 l)
हल :
घनाभाकार टंकी में पानी का आयतन = 6 m × 5 m × 4.5 m
[∵ घनाभ का आयतन = लंबाई × चौड़ाई × ऊँचाई]

= 135 m³
= 135 × 1000 लीटर
[∵ 1 m³ = 1000 लीटर]
= 1,35,000 लीटर
अतः, टंकी में 1,35000 लीटर पानी आ सकता है।

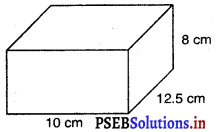
प्रश्न 3.
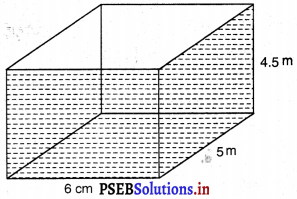
एक घनाभाकार बर्तन 10 m लंबा और 8 m चौड़ा है। इसको कितना ऊँचा बनाया जाए कि इसमें 380 घन मीटर द्रव आ सके ?
हल :
मान लीजिए घनाभाकार बर्तन की ऊँचाई = h
घनाभाकार बर्तन में द्रव का आयतन = 380 घन मीटर
अतः, लंबाई × चौड़ाई × ऊँचाई = 380 घन मीटर
⇒ 10 m × 8 m × h = 380
⇒ h = \(\frac{380}{10 \times 8}\) m
⇒ h = 4.75 m
अतः, घनाभाकार बर्तन की ऊँचाई 4.75 m है।

प्रश्न 4.
8 m लंबा, 6 m चौड़ा और 3 m गहरा एक घनाभाकार गढ्ढा खुदवाने में 30 रुपए प्रति m³ की दर से होने वाला व्यय ज्ञात कीजिए।
हल :

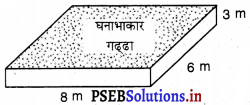
घनाभाकार गढ्ढे का आयतन = 8 m × 6 m × 3 m
= 144 m³
1 m³ गढ्डा खुदवाने का व्यय = 30 रु
144 m³ गढ्डा खुदवाने का व्यय = (30 × 144) रु
= 4320 रु.

प्रश्न 5.
एक घनाभाकार टंकी की धारिता 50000 लीटर पानी की है। यदि इस टंकी की लंबाई और गहराई क्रमश: 2.5 m और 10 m हैं, तो इसकी चौड़ाई ज्ञात कीजिए।
हल :
मान लीजिए घनाभाकार टंकी की चौड़ाई b m है।
घनाभाकार टंकी की धारिता = 50000 लीटर
⇒ लंबाई × चौड़ाई × ऊँचाई = 50000 लीटर
⇒ 2.5 m × b × 10 m = \(\frac{50000}{1000}\) m³
[∵ 1000 l = 1 m³]
⇒ 25b = 50
⇒ b = 25
⇒ b = 2 m
अतः, घनाभाकार टंकी की चौड़ाई 2 m है।

प्रश्न 6.
एक गाँव जिसकी जनसंख्या 4000 है, को प्रतिदिन प्रति व्यक्ति 150 लीटर पानी की आवश्यकता है। इस गाँव में 20 m × 15 m × 6 m मापों वाली एक टंकी बनी हुई है। इस टंकी का पानी वहाँ कितने दिन के लिए पर्याप्त होगा ?
हल :
घनाभाकार टंकी की धारिता = लंबाई × चौड़ाई × ऊंचाई
= 20 m × 15 m × 6 m
= 1800 m³
= 1800 × 1000 लीटर
[∵ 1 m³ = 1000 लीटर]
= 1800000 लीटर
प्रति व्यक्ति प्रतिदिन पानी की आवश्यकता = 150 लीटर
प्रतिदिन 4000 व्यक्तियों के लिए पानी की आवश्यकता = (150 × 4000) लीटर
= 600000 लीटर
जितने दिनों के लिए पानी पर्याप्त होगा

= \(\frac{1800000}{600000}\)
= 3
अतः, टंकी का पानी 3 दिन के लिए पर्याप्त होगा।

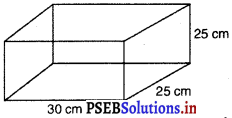
प्रश्न 7.
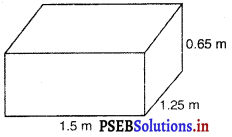
किसी गोदाम का माप 40 m × 25 m × 10 m हैं। इस गोदाम में 1.5 m × 1.25 m × 0.5 m की माप वाले लकड़ी के कितने अधिकतम क्रेट (crate) रखे जा सकते हैं ?
हल :
घनाभाकार गोदाम की धारिता (आयतन) = 40 m × 25 m × 15 m
[∵ गोदाम की धारिता = l × b × h]
= 15000 m³
लकड़ी के क्रेट की धारिता (आयतन) = 1.5 m × 1.25 m × 0.5 m
= 0.9375 m³
गोदाम में रखे जा सकने वाले लकड़ी के अधिकतम क्रेटों की संख्या

अतः, गोदाम में रखे जा सकने वाले क्रेटों की अधिकतम संख्या 16000 है।

प्रश्न 8.
12 cm भुजा वाले एक ठोस घन को बराबर आयतन वाले 8 घनों में काटा जाता है। नए घन की क्या भुजा होगी ? साथ ही, इन दोनों घनों के पृष्ठीय क्षेत्रफलों का अनुपात भी ज्ञात कीजिए।
हल :
ठोस घन का आयतन = (भुजा)³
= (12 cm)³
= 1728 cm³
दिया है कि ठोस घन को बराबर आयतन वाले 8 घनों में काटा गया है।
∴ प्रत्येक नए घन का आयतन = \(\frac{1}{8}\) = (मूल घन का आयतन)

अब, मूल ठोस घन का पृष्ठीय क्षेत्रफल
= 6(भुजा)²
= 6(12)²
= 6 × 12 × 12 cm²
= 864 cm²
नये घन का पृष्ठीय क्षेत्रफल = 6 (भुजा)²
= 6 (6 cm)
= 6 × 6 × 6 cm²
= 216 cm²
अब प्रश्नानुसार,

अतः मूलधन और नये घन के पृष्ठीय क्षेत्रफलों का अनुपात 4 : 1 है।

प्रश्न 9.
3 m गहरी और 40 m चौड़ी एक नदी 2 किमी. प्रति घंटा की चाल से बहकर समुद्र में गिरती है। एक मिनट में समुद्र में कितना पानी गिरेगा ?
हल :

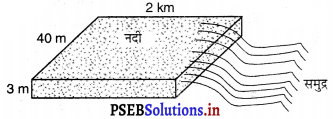
क्योंकि पानी 2 किमी. प्रति घंटा की चाल से बहता है। 2 किमी. नदी से पानी 1 घंटे में समुद्र में गिरता है। इसलिए, एक घंटे में समुद्र में गिर रहे पानी का आयतन = घनाभ का आयतन
= l × b × h
= 2000 m × 40 m × 3 m
[∵ 1 किमी. = 1000 किमी.]
= 240000 m³
अब,
∴ 1 घंटे अर्थात् 60 मिनट में समुद्र में गिर रहे पानी का आयतन = 240000 किमी.³
1 मिनट में समुद्र में गिर रहे पानी का आयतन = \(\frac{240000}{60}\)
= 4000 m³

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 7 त्रिभुज Ex 7.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.4

प्रश्न 1.
दर्शाइए कि समकोण त्रिभुज में कर्ण सबसे लंबी भुजा होती है।
हल :
मान लीजिए ABC एक समकोण त्रिभुज है जिसमें B पर समकोण है।
हमने सिद्ध करना है कि कर्णAC, सबसे लंबी भुजा होती है।

समकोण ΔABC में,
⇒ ∠A + ∠B + ∠C = 180°
∠A + 90°+ ∠C = 180° [∵ ∠B = 90°]
⇒ ∠A + ∠C = 180° – 90° = 90°
अब ∠A + ∠C = 90°
और ∠B = 90°
⇒ ∠B > ∠C और ∠B > ∠A
जैसा कि हम जानते हैं कि बड़े कोण के सम्मुख भुजा बड़ी होती है।
AC > AB और AC > BC
दूसरे शब्दों में, ∠B सबसे बड़ा होने के कारण इसकी सम्मुख भुजा AC अर्थात् कर्ण बड़ा होता है।

प्रश्न 2.
आकृति में, ΔABC की भुजाओं AB और AC को क्रमशः बिंदुओं P और Q तक बढ़ाया गया है। साथ ही, ∠PBC < ∠QCB है। दर्शाइए कि AC > AB है।
हल:
∠ABC + ∠PBC = 180° …..(i) (रैखिक युग्म)

∠ACB + ∠QCB = 180° ………(ii)
(रैखिक युग्म अभिगृहीत)
(i) और (ii), से हमें प्राप्त होता है ।
∠ABC + ∠PBC = ∠ACB + ∠QCB ….(iii)
परंतु ∠PBC ∠ ∠QCB (दिया है) …(iv)
∴ (iv) को (iii) में, प्रयोग करने पर
∠ABC > ∠ACB
अब ΔABC में,
∠ABC > ∠ACB
[ऊपर (iv) में सिद्ध किया है।
∴ AC > AB [∵ बड़े कोण के सम्मुख भुजा बड़ी होती है]

प्रश्न 3.
आकृति में, ∠B < ∠A और ∠C < ∠D है। दर्शाइए कि AD < BC है।

हल :
ΔAOB में,
∠B < ∠A (दिया है) या, ∠A > ∠B
इसलिए, OB > OA ……..(i) [∵ बड़े कोण के सम्मुख भुजा बड़ी होती है]
ΔCOD में,
∠C < ∠D (दिया है) या, ∠D > ∠C
∴ OC > OD ………..(ii)
[∵ बड़े कोण के सम्मुख भुजा बड़ी होती है]
(i) और (ii), को जोड़ने पर हमें प्राप्त होता है :
OB + OC > OA + OD
⇒ BC > AD
या, AD < BC (सिद्ध किया है)

प्रश्न 4.
AB और CD क्रमशः एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजाएँ हैं ( देखिए आकृति)। दर्शाइए कि ∠A > ∠C और ∠B > ∠D
हल :
दिया है : ABCD एक चतुर्भुज है। AB सबसे छोटी भुजा और CD सबसे बड़ी भुजा है।
सिद्ध करना है : ∠A > ∠C और ∠B > ∠D.
रचना : A और C तथा B और D को मिलाइए।
उपपत्ति : ΔABC में AB सबसे छोटी भुजा है
∴ BC > AB
⇒ ∠1 > ∠2 …………(i)
[ बड़ी भुजा के सम्मुख कोण बड़ा होता है।]

ΔADC में, CD सबसे बड़ी भुजा है।
∴ CD > AD
⇒ ∠3 > ∠4 …………(ii)
(i) और (ii), को जोड़ने पर
∠1 + ∠3 > ∠2 + ∠4
⇒ ∠A > ∠C
[इति सिद्धम् भाग (1)]
अब ΔADB में, AB सब से छोटी भुजा है।
∴ AD > AB
⇒ ∠5 > ∠6 ……..(iii)
और ΔBCD में, CD सबसे बड़ी भुजा है।
∴ CD > BC
⇒ ∠7 > ∠8 ……..(iv)
(iii) और (iv), को जोड़ने पर
∠5 + ∠7 > ∠6 + ∠8
∠B > ∠D [इति सिद्धम् (2)]
अतः, ∠A > ∠C और ∠B > ∠D(इति सिद्धम्)

प्रश्न 5.
आकृति में PR > PQ है और PS कोण QPR को समद्विभाजित करता है। सिद्ध कीजिए कि ∠PSR > ∠PSQ है।
हल:

ΔPQR में,
PR > PQ (दिया है)
∴ ∠PQR > ∠PRQ (बड़ी भुजा के सम्मुख कोण बड़ा होता है) …….(1)
पुनः ∠1 = ∠2
[∵ PS, ∠P का समद्विभाजक है] …(2)
∴ ∠PQR + ∠1 > ∠PRQ + ∠2 …(3)
परंतु ∠PQS + ∠1 + ∠PSQ = ∠PRS + ∠2 + ∠PSR = 180°
[त्रिभुज के कोणों का योगफल 180° होता है।]
⇒ ∠PQR + ∠1 + ∠PSQ = ∠PRQ + ∠2 + ∠PSR …(4) [∵ ∠PRS = ∠PRQ और ∠PQS = ∠PQR]
(3) और (4), से हमें प्राप्त होता है
∠PSQ < ∠PSR या, ∠PSR > ∠PSQ

प्रश्न 6.
दर्शाइए कि एक रेखा पर एक दिए हुए बिंदु से, जो उस रेखा पर स्थित नहीं है, जितने रेखाखंड खींचे जा सकते हैं उनमें लंब रेखाखंड सबसे छोटा होता है।
हल :
दिया है : l एक रेखा है और P एक बिंदु है जो l पर स्थित नहीं है। PM ⊥ l है।
M से भिन्न कोई बिंदु N; रेखा l पर है।
(आकृति देखिए)

सिद्ध करना है : PM < PN उपपत्ति : ΔPMN में, ∠M एक समकोण है। N एक न्यूनकोण है। (त्रिभुज का कोण गुणधर्म) ∴ ∠M > N
∴ PN > PM
(बड़े कोण की सम्मुख भुजा)
या, PM < PN.
अतः, एक रेखाखंड पर एक दिए बिंदु से जो उस रेखा पर नहीं है, खींचे गए सभी रेखा खंडों में लंब रेखा खंड सबसे छोटा होता है।

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.4

जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) लीजिए।

प्रश्न 1.
निम्न त्रिज्या वाले गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए :
(i) 10.5 cm
(ii) 5.6 cm
(iii) 14 cm
हल :
गोले की त्रिज्या = 105 cm
∴ गोले का पृष्ठीय क्षेत्रफल = 4πR²
= 4 × \(\frac{22}{7}\) × 10.5 × 10.5 cm²
= 4 × \(\frac{22}{7} \times \frac{56}{10} \times \frac{56}{10}\) cm²
= 1386 cm²

(ii) गोले की त्रिज्या = 5.6 cm
गोले का पृष्ठीय क्षेत्रफल
= 4πR² = 4 × \(\frac{22}{7}\) × 5.6 × 5.6
= 4 × \(\frac{22}{7} \times \frac{56}{10} \times \frac{56}{10}\)
= 394.24 cm²

(iii) गोले की त्रिज्या = 14 cm
गोले का पृष्ठीय क्षेत्रफल
= 4πR² = 4 × \(\frac{22}{7}\) × 14 × 14 cm²
= 2464 cm²

प्रश्न 2.
निम्न व्यास वाले गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए :
(i) 14 cm
(ii) 21 cm
(iii) 3.5 m
हल :
(i) गोले का व्यास = 14 cm
गोले की त्रिज्या, R = \(\frac{14}{2}\) = 7 cm
गोले का पृष्ठीय = 4πR²
= 4 × \(\frac{22}{7}\) × 7 × 7 = 616 cm²

(ii) गोले का व्यास = 21 cm
गोले की त्रिज्या, R = \(\frac{21}{2}\) cm
गोले का पृष्ठीय क्षेत्रफल
= 4πR² = 4 × \(\frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}\)
= 1386 cm²

(iii) गोले का व्यास = 3.5 cm
गोले की त्रिज्या, R = \(\frac{3.5}{2}\) = 1.75 cm
गोले का पृष्ठीय क्षेत्रफल = 4πR²
= 4 × \(\frac{22}{7}\) × 1.75 × 1.75 cm²
= 4 × \(\frac{22}{7} \times \frac{175}{100} \times \frac{175}{100}\) cm²
= 4 × \(\frac{22}{7} \times \frac{7}{4} \times \frac{7}{4}\) m²
= 38.5 m²

प्रश्न 3.
10 cm त्रिज्या वाले एक अर्ध गोले का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए)
हल:
मान लीजिए अर्ध गोले की त्रिज्या = r cm
∴ r = 10 cm

अर्ध गोले का कुल पृष्ठीय क्षेत्रफल = वक्र पृष्ठीय क्षेत्रफल + ऊपरी वृत्ताकार भाग का क्षेत्रफल
= 2πr + πr²
= 3πr²
= 3 × 3.14 × (10)² cm
= 3 × \(\frac{314}{100}\) × 100 cm²
= 3 × 314 cm²
= 942 cm²
अतः, अर्धगोले का कुल पृष्ठीय क्षेत्रफल 942 cm² है।

प्रश्न 4.
एक गोलाकार गुब्बारे में हवा भरने पर, उसकी त्रिज्या 7 cm से 14 cm हो जाती है। इन दोनों स्थितियों में, गुब्बारे के पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :
पहली स्थिति में
गुब्बारे की त्रिज्या ; r = 7 cm
∴ गुब्बारे का पृष्ठीय क्षेत्रफल = 4πr²
= 4π × 7 × 7 cm² (I)

दूसरी स्थिति में
गुब्बारे की त्रिज्या ; R = 14 cm
∴ गुब्बारे का पृष्ठीय क्षेत्रफल = 4πr²
= 4π × 14 × 14 cm² (II)
अब, पृष्ठीय क्षेत्रफलों में अनुपात

अतः, वांछित अनुपात = 1 : 4

प्रश्न 5.
पीतल से बने एक अर्धगोलाकार कटोरे का आंतरिक व्यास 10.5 cm है। 16 रुपए प्रति 100 cm² की दर से इसके आंतरिक पृष्ठ पर कलई कराने का व्यय ज्ञात कीजिए।
हल :
कटोरे का आंतरिक व्यास = 10.5 cm
कटोरे की आंतरिक त्रिज्या
r = \(\frac{10.5}{2}\) = 5.25 cm

∵ कटोरा अर्धगोलाकार है
∴ कटोरे का आंतरिक पृष्ठीय क्षेत्रफल = 2πr²

100 cm² पृष्ठ पर कलई कराने का व्यय = 16 रु
1 cm² पृष्ठ पर कलई कराने का व्यय = \(\frac{16}{100}\) रु
\(\frac{693}{4}\) cm² पृष्ठ पर कलाई कराने का व्यय
= \(\frac{16}{100} \times \frac{693}{4}\) = 27.72 रु०

प्रश्न 6.
उसे गोले की त्रिज्या ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 154 cm² है।
हल :
गोले का पृष्ठीय क्षेत्रफल = 154 m²
मान लीजिए गोले की त्रिज्या = R
∴ 4πR² = 15
या 4 × \(\frac{22}{7}\) × R² = 154
या R² = 154 × \(\frac{7}{22} \times \frac{1}{4}=\frac{7 \times 7}{4}=\frac{49}{4}\)
या, R = \(\sqrt{\frac{49}{4}}\) = \(\frac{7}{2}\) = 3.5 cm

प्रश्न 7.
चन्द्रमा का व्यास पृथ्वी के व्यास का लगभग एक चौथाई है। इन दोनों के पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :
मान लीजिए पृथ्वी का व्यास = x

∴ पृथ्वी की त्रिज्या ; R = \(\frac{x}{2}\)
∵ क्योंकि पृथ्वी को गोलाकार माना गया है
∴ पृथ्वी का पृष्ठीय क्षेत्रफल = 4πR²
= 4π × \(\frac{x}{2} \times \frac{x}{2}\)
= π × x ……(i)
अब चंद्रमा का व्यास
= पृथ्वी के व्यास का \(\frac{1}{4}\) भाग
∴ चंद्रमा की त्रिज्या कह लीजिए,
= \(\frac{1}{4}\) × x = \(\frac{x}{4}\)
चंदरमा की त्रिज्या ; r = \(\frac{x}{4 \times 2}=\frac{x}{8}\)
∵ चंद्रमा भी गोलाकार है
∴ चंद्रमा का पृष्ठीय क्षेत्रफल
= 4πr² = 4 × π × \(\frac{x}{8} \times \frac{x}{8}\)
= \(\frac{\pi \times x^2}{16}\) ….(ii)

वांछित अनुपात = 1 : 16

प्रश्न 8.
एक अर्धगोलाकार कटोरा 0.25 cm मोटी स्टील से बना है। इस कटोरे की आंतरिक त्रिज्या 5 cm है। कटोरे का बाहरी वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :
कटोरे की आंतरिक त्रिज्या ; r = 5 cm
स्टील की मोटाई ; t = 0.25 cm
कटोरे की बाहरी त्रिज्या ; R = r + t
= 5 + 0.25 = 5.25 cm
कटोरे का बाहरी पृष्ठीय क्षेत्रफल = 2πR²

प्रश्न 9.
एक लंब वृत्तीय बेलन त्रिज्या वाले एक गोले को पूर्णतया घेरे हुए है (देखिए आकृति) ज्ञात कीजिए :
(i) गोले का पृष्ठीय क्षेत्रफल
(ii) बेलन का वक्र पृष्ठीय क्षेत्रफल
(iii) ऊपर (i) और (ii) में प्राप्त क्षेत्रफल का अनुपात

हल :
(i) गोले की त्रिज्या = r
∴ गोले का पृष्ठीय क्षेत्रफल = 4π²
(ii) ∵ गोला बेलन के अंतर्गत है।
∴ बेलन की ऊँचाई गोले के व्यास तथा बेलन की त्रिज्या गोले की त्रिज्या के बराबर होगी।
अब बेलन की त्रिज्या = r
बेलन की ऊँचाई h = 2r
∴ बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2πr × 2r [∵ h = 2r]
= 4πr²

∴ वांछित अनुपात = 1 : 1

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 7 त्रिभुज Ex 7.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.3

प्रश्न 1.
ΔABC और ΔDBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए आकृति)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि,
(i) ΔABD ≅ ΔACD
(ii) ΔABP ≅ ΔACP
(iii) AP कोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP रेखाखंड BC का लंब समद्विभाजक है।
हल:

ΔABC एक समद्विबाहु त्रिभुज है।
∴ AB = AC
ΔDBC एक समद्विबाहु त्रिभुज है।
∴ BD = CD
अब, ΔABD और ΔACD में,
AB = AC (दिया है)
BD = CD (दिया है)
AD = AD (उभयनिष्ठ)
∴ ΔABD ≅ ΔACD
(SSS सर्वांगसमता नियम से)
भाग (i) सिद्ध हुआ
⇒ ∠BAD = ∠CAD …………. (a)
[सर्वांगसम त्रिभुज के संगत भाग]

(ii) अब, ΔABP और ΔACP में,
AB = AC (दिया है)
∠BAD = ∠CAD
[(a) का प्रयोग करने पर]
AP = AP (उभयनिष्ठ)
∴ ΔABP ≅ ΔACP
(SAS सर्वांगसमता नियम से)

(iii) दूसरे भाग में हमने सिद्ध किया है कि
ΔABP ≅ ΔACP
इसलिए, ∠BAP= ∠CAP
(सर्वांगसम त्रिभुजों के संगत भांग)
⇒ AP, ∠A को समद्विभाजित करता है।
भाग (i) में हमने सिद्ध किया है कि
ΔABD ≅ ΔACD
इसलिए, ∠ADB = ∠ADC ………….(b)
(सर्वांगसम त्रिभुजों के संगत भाग)
∠ADB + ∠BDP = 180°
(रैखिक युग्म) …… (c)
∠ADC + ∠CDP = 180° …………..(d) (रैखिक युग्म)
(c) और (d), से हमें प्राप्त होता है।
∠ADB + ∠BDP = ∠ADC + ∠CDP
या ∠ADB + ∠BDP = ∠ADB + ∠CDP
[(b) के प्रयोग करने पर]
⇒ ∠BDP = ∠CDP
⇒ DP, ∠D को समद्विभाजित करता है।
अर्थात् हम कह सकते हैं कि AP, ∠D को समद्विभाजित करता है।

(iv) भाग (ii) में हमने सिद्ध किया है कि
ΔABP ≅ ΔACP
∴ BP = PC ….(e)
(सर्वांगसम त्रिभुजों के संगत भाग)
और ∠APB = ∠APC …………(f)
(सर्वांगसम त्रिभुजों के संगत भाग)
अब, ∠APB + ∠APC = 180° (रैखिक युग्म)
⇒∠APB + ∠APB = 180°
[(f) का प्रयोग करने पर]
⇒ 2∠APB = 180°
⇒ ∠APB = \(\frac {180°}{2}\)
⇒ ∠APB = 90°
⇒ AP ⊥ BC … (g)
(e) से हम प्राप्त करते हैं BP = PC और (g),से हमने सिद्ध किया है कि AP ⊥ BC । दोनों को इकट्ठा लेने पर हम कह सकते हैं कि AP, BC का लंब समद्विभाजक है।

प्रश्न 2.
AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलंब है, जिसमें AB = AC है। दर्शाइए कि
(i) AD रेखा खंड BC को समद्विभाजित करता है।
(ii) AD कोण A को समद्विभाजित करता है।

हल :
ΔABD और ΔACD में,
AB = AC (दिया है)
∠ADB = ∠ADC (प्रत्येक = 90°)
[∵ AD ⊥ BC (दिया है)]
AD = AD (उभयनिष्ठ)
∴ ΔABD ≅ ΔACD
(RHS सर्वांगसमता नियम से)
इसलिए, BD = DC
(सर्वांगसम त्रिभुजों के संगत भाग)
⇒ AD; BC, को समद्विभाजित करती है।
(भाग (i) सिद्ध हुआ है)
साथ ही, ∠BAD = ∠CAD (सर्वांगसम त्रिभुजों के संगत भाग)
⇒ AD, ∠A को समद्विभाजित करती है।

प्रश्न 3.
एक त्रिभुज ABC की दो भुजाएँ AB और BC तथा माध्यिका AM क्रमशः एक-दूसरे त्रिभुज की भुजाओं PQ और QR तथा माध्यिका PN के बराबर है (देखिए आकृति)। दर्शाइए कि
(i) ΔABM ≅ ΔPQN
(ii) ΔABC ≅ ΔPQR

हल :
AM, ΔABC की माध्यिका है।
∴ BM = MC = \(\frac {1}{2}\) BC ……….(a)
PN, ΔPQR की माध्यिका है।
∴ QN = NR = \(\frac {1}{2}\) OR ……. (b)
अब, BC = QR (दिया है)
⇒ \(\frac {1}{2}\)BC = \(\frac {1}{2}\)QR
इसलिए, BM = QN ……. (c)
[(a) और (b) का प्रयोग करने पर]
(i) अब, ΔABM और ΔPQN में,
AB = PQ (दिया है)
AM = PN (दिया है)
BM = QN
[भाग (c) में सिद्ध किया है]
∴ ΔΑΒΜ ≅ ΔΡQN
(sss सर्वांगसमता नियम से)
इसलिए, ∠B = ∠Q ……….(d)
(सर्वांगसम त्रिभुजों के संगत भाग)

(ii) ΔABC और ΔPQR में,
AB = PQ (दिया है)
∠B = ∠Q
[भाग (d) प्रयोग करने पर]
BC = QR (दिया है)
∴ ΔABC ≅ ΔPQR ,
(SAS सर्वांगसमता नियम से)

प्रश्न 4.
BE और CF एक त्रिभुज ABC के दो बराबर शीर्षलंब हैं| RHS सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है।

हल :
ΔBEC और ΔCFB में,
∠BEC = ∠CFB (प्रत्येक = 90°)
[∵ BE ⊥ AC और CF ⊥ AB]
BC = BC (उभयनिष्ठ)
BE = CF (दिया है)
∴ ΔBEC ≅ ΔCFB
(RHS सर्वांगसमता नियम से)
इसलिए, EC = FB …………(i)
(सर्वांगसम त्रिभुजों के संगत भाग)
अब ΔAEB और ΔAFC में,
∠A = ∠A (उभयनिष्ठ)
∠AEB = ∠AFC
(प्रत्येक = 90°) [दिया है।
EB = FC (दिया है)
∴ ΔAEB ≅ ΔAFC
(AAS सर्वांगसमता नियम से)
इसलिए, AE = AF …………..(ii)
(सर्वांगसम त्रिभुजों के संगत भाग)
(i) और (ii), को जोड़ने पर हमें प्राप्त होता है।
EC + AE = FB + AF
⇒ AC = AB
अब ΔABC में, हमें प्राप्त है
AB = AC
⇒ ΔABC एक समद्विबाहु त्रिभुज है।

प्रश्न 5.
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP ⊥ BC खींच कर दर्शाइए कि ∠B = ∠C है।

हल :
दिया है : ABC एक समद्विबाहु त्रिभुज है जिसमें
AB = AC
सिद्ध करना है : ∠B = ∠C
रचना : AP ⊥ BC खींचिए।
उपपत्ति : ΔABP और ΔACP में
∠APB = ∠APC
(प्रत्येक = 90°) [रचना से]
AB = AC (दिया है)
AP = AP (उभयनिष्ठ)
∴ ΔABP ≅ ΔACP
(RHS सर्वांगसमता नियम से)
इसलिए, ∠B = ∠C
(सर्वांगसम त्रिभुजों के संगत भाग)

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.3

जब तक अन्यथा न कहा जाए π = \(\frac{22}{7}\) लीजिए।

प्रश्न 1.
एक शंकु के आधार पर व्यास 10.5 cm है और इसकी तिर्यक ऊँचाई 10 cm है। इसका वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :
मान लीजिए कि वृत्ताकार आधार की त्रिज्या = r cm
∴ व्यास ; 2r = 10.5 cm
⇒ r = \(\frac{10.5}{2}\)
⇒ r = \(\frac{105}{20}\)
⇒ r = \(\frac{21}{4}\)

शंकु की तिर्यक ऊँचाई = l = 10 cm
इसलिए, शंकु का वक्र पृष्ठीय क्षेत्रफल = πrl
= \(\frac{22}{7}\) × \(\frac{21}{4}\) × 10
= 165 cm²

प्रश्न 2.
एक शंकु का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए, जिसकी तिर्यक ऊँचाई 21 m है और आधार का व्यास 24 m है।
हल :
शंकु की तिर्यक ऊँचाई l = 21 m
शंकु का व्यास = 24 m
शंकु की त्रिज्या, r = \(\frac{24}{2}\) = 12 m
शंकु का कुल पृष्ठीय क्षेत्रफल = πrl + πr²
= πr (l + r)
= \(\frac{22}{7}\) × 12 (21 + 12) m²

= \(\frac{264}{7}\) × 33 = 1244.57 m²

प्रश्न 3.
एक शंकु का वक्र पृष्ठीय क्षेत्रफल 380 cm² है और इसकी तिर्यक ऊँचाई 14 cm है। ज्ञात कीजिए :
(i) आधार की त्रिज्या
(ii) शंकु का कुल पृष्ठीय क्षेत्रफल
हल :
(i) मान लीजिए शंकु के वृत्तीकार आधार की त्रिज्या = r
तिर्यक ऊँचाई ; l = 14 cm
शंकु का वक्र पृष्ठीय क्षेत्रफल = 308 cm² (दिया है)
⇒ πrl = 308
⇒ \(\frac{22}{7}\) × r × 14 = 308
⇒ r = 308 × \(\frac{7}{22}\) × \(\frac{1}{14}\)
⇒ r = 7 cm

(ii) शंकु का कुल पृष्ठीय क्षेत्रफल = शंकु का वक्र पृष्ठीय क्षेत्रफल + शंकु के वृत्तीय आधार का क्षेत्रफल
= 308 + πr²
= 308 + \(\frac{22}{7}\) × 72
= 308 + 22 × 7
= 308 + 154
= 462 cm²

प्रश्न 4.
शंकु के आकार का एक तंबू 10 m ऊँचा है उसके आधार की त्रिज्या 24 m है। ज्ञात कीजिए:
(i) तंबू की तिर्यक ऊँचाई
(ii) तंबू में लगे केनवास (canvas) की लागत, यदि 1 m² केनवास की लागत 70 रुपए है।
हल :
शंक्वाकार तंबू की ऊँचाई h = 10 m
शंक्वाकार तंबू की त्रिज्या ; r = 24 m
(i) तंबू की तिर्यक ऊँचाई ; l = \(\sqrt{r^2+h^2}\)
= \(\sqrt{(24)^2+(10)^2}\)
= \(\sqrt{576+100}\)
= \(\sqrt{676}\)
= 26 m
भाग (ii) के लिए, तंबू को बनाने में लगा केनवास = तंबू का वक्र पृष्ठीय क्षेत्रफल
= πrl
= \(\frac{22}{7}\) × 24 × 26 = \(\frac{13728}{7}\) m²
\(\frac{13728}{7}\) m² केनवास का मूल्य
= 70 × \(\frac{13728}{7}\) रु
= 137280 रु

प्रश्न 5.
8 m ऊँचाई और आधार की त्रिज्या 6 m वाले एक शंकु के आकार का तंबू बनाने में 3 m चौड़े तिरपाल की कितनी लंबाई लगेगी? यह मान कर चलिए कि इसकी सिलाई और कटाई में 20 cm तिरपाल अतिरिक्त लगेगा। (π = 3.14 का प्रयोग कीजिए)
हल :
तंबू की ऊँचाई ; h = 8 m
तंबू की त्रिज्या ; r = 6 m
तंबू की तिर्यक ऊँचाई ; l = \(\sqrt{r^2+h^2}\)
= \(\sqrt{(6)^2+(8)^2}\)
= \(\sqrt{36+64}\)
= \(\sqrt{100}\)
= 10 m
तिरपाल का क्षेत्रफल = तंबू का वृक्र पृष्ठीय क्षेत्रफल
= πrl = 3.14 × 6 × 10 = 188.4 m²
तिरपाल की चौड़ाई = 3 m
मान लीजिए तिरपाल की लंबाई = L
तिरपाल का क्षेत्रफल = लंबाई × चौड़ाई
= L × 3 = 3L
3L = 188.4 [∵ क्षेत्रफल = 188.4 m²]
L = \(\frac{188.4}{3}\) = 62.8 m
सिलाई और कटाई में लगी तिरपाल की अतिरिक्त लंबाई 20 cm है।
अर्थात् 0.2 m [∵ 1 cm = \(\frac{1}{100}\) m]
इसलिए तंबू बनाने में लगी तिरपाल की कुल लंबाई (62.8 + 0.2) m = 63 m

प्रश्न 6.
शंकु के आधार की एक गुंबज की तिर्यक ऊँचाई और आधार व्यास क्रमशः 25 m और 14 m हैं। इसकी वक्र पृष्ठ पर 210 रुपए प्रति 100 m² की दर से सफेदी कराने का व्यय ज्ञात कीजिए।
हल :
शंक्वाकार गुंबज की तिर्यक ऊँचाई l = 25 m
शंक्वाकार गुंबज के आधार का व्यास = 14 m
शंक्वाकार गुंबज की त्रिज्या r = \(\frac{14}{2}\) = 7m
गुंबज का वक्र पृष्ठीय क्षेत्रफल = πrl
= \(\frac{22}{7}\) × 7 × 25 = 550 m²
100 m² पर सफेदी कराने का व्यय = 210 रु
1 m² पर सफेदी कराने का व्यय = \(\frac{210}{100}\) रु
550 m² पर सफेदी कराने का व्यय = \(\frac{210}{100}\) × 550 रु
= 1155 रु

प्रश्न 7.
एक जोकर की टोपी एक शंकु के आकार की है, जिसके आधार की त्रिज्या 7 cm और ऊँचाई 24 cm है। इसी प्रकार की 10 टोपियाँ बनाने के लिए आवश्यक गत्ते का क्षेत्रफल ज्ञात कीजिए।
हल :
टोपी के आधार की त्रिज्या r = 7 cm
टोपी की ऊँचाई ; h = 24 cm
टोपी शंकु के आकार की है।

तिर्यक ऊँचाई ; l = \(\sqrt{r^2+h^2}\)
= \(\sqrt{(7)^2+(24)^2}\)
= \(\sqrt{49+576}\) = \(\sqrt{625}\) = 25 cm
एक टोपी बनाने में लगे गत्ते का क्षेत्रफल = शंकु का वक्र पृष्ठीय क्षेत्रफल
= πrl
= \(\frac{22}{7}\) × 7 × 25 = 550 cm²
∴ 10 टोपियाँ बनाने में लगे गत्ते का क्षेत्रफल = 10 × 550 = 5500 cm²

प्रश्न 8.
किसी बस स्टाप को पुराने गत्ते से बने 50 खोखले शंकुओं द्वारा सड़क से अलग किया हुआ है। प्रत्येक शंकु के आधार का व्यास 40 cm है और ऊँचाई 1 m है। यदि इन शंकुओं की बाहरी पृष्ठों को पेंट करवाना है और पेट की दर 12 रुपए प्रति m² है, तो इनको पेंट कराने में कितनी लागत आएगी ?
(π = 3.14, और \(\sqrt{1.04}\) = 1.02 का प्रयोग कीजिए)
हल :
मान लीजिए वृत्तीकार आधार की त्रिज्या = r
∴ व्यास ; 2r = 40
⇒ r = \(\frac{40}{2}\)
⇒ r = 20 m
⇒ r = \(\frac{20}{100}\) m

शंकु की ऊँचाई, h = 1 m
तिर्यक ऊँचाई, l = \(\sqrt{r^2+h^2}\)
= \(\sqrt{(0.2)^2+(1)^2}\)
l = \(\sqrt{0.04+1}\)
l = \(\sqrt{1.04}\)
शंकु का वक्र पृष्ठीय क्षेत्रफल = πrl
= 3.14 × 0.2 × \(\sqrt{1.04}\)
= 3.14 × 0.2 × 1.02
= 0.64056 m²
1m2 शंकु को पेंट कराने की लागत = 12 रु
0.64056 m² शंकु को पेंट कराने की लागत = (12 × 0.64056) रु
= 7.68672 रु
एक शंकू को पेंट कराने की लागत = 7.68672 रु
ऐसे 50 शंकु को पेंट कराने की लागत = 50 × 7.68672 रु
= 384.34 रु (लगभग)

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 7 त्रिभुज Ex 7.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.2

प्रश्न 1.
एक समद्विबाहु त्रिभुज ABC में जिसमें AB = AC है, ∠B और ∠C के समद्विभाजक परस्पर बिंदु O पर प्रतिच्छेद करते हैं। A और O को जोड़िए। दर्शाइए कि :
(i) OB = OC
(ii) AO कोण A को समद्विभाजित करता है।
हल :
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC
∴ ∠C = ∠B (त्रिभुज में समान भुजाओं के सम्मुख कोण समान होते हैं।)

⇒ ∠OCA + ∠OCB = ∠OBA + ∠OBC
⇒ ∠OCB + ∠OCB = ∠OBC + ∠OBC
∵ OB, ∠B को समद्विभाजित करता है।
∴ ∠OBA = ∠OBC
और OC, ∠C को समद्विभाजित करता है।
∴ ∠OCA = ∠OCB
⇒ 2∠OCB = 2∠OBC
⇒ ∠OCB = ∠OBC
अब, ΔOBC में,
∠OCB = ∠OBC(ऊपर सिद्ध किया है)
∴ OB = OC
(समान कोणों की सम्मुख भुजाएँ)

(ii) अब ΔAOB और ΔAOC में,
AB = AC. (दिया है)
∠OBA = ∠OCA
∵ ∠B = ∠C
BO, ∠B और CO, ∠C को समद्विभाजित करता है
∴ \(\frac {1}{2}\)∠B = \(\frac {1}{2}\)∠C
⇒ ∠OBA = ∠OCA
OB = OC [(i) में सिद्ध किया है]
∴ ΔAOB = ΔAOC
(SAS सर्वांगसमता नियम से)
⇒ ∠OAB = ∠OAC
(सर्वामसम त्रिभुजों के संगत भाग)
अतः, AO; ∠A को समद्विभाजित करता है।

प्रश्न 2.
ΔABC में AD भुजा BC का लंब समद्विभाजक है (देखिए आकृति) दर्शाइए ΔABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है।

हल:
ΔABD और ΔACD में,
BD = CD [∵ AD, BC को समद्विभाजित करते हैं
(दिया है)] ∠ADB = ∠ADC = प्रत्येक 90°
[∵ AD ⊥ BC (दिया है)]
AD = AD (उभयनिष्ठ)
∴ ΔABD ≅ ΔACD
(SAS सर्वांगसम नियम से)
⇒ AB = AC
(सर्वांगसम त्रिभुजों के संगत भाग)
इसलिए, ABC एक समद्विबाहु त्रिभुज है।

प्रश्न 3.
ABC एक समद्विबाहु त्रिभुज है, जिसमें बराबर भुजाओं AC और AB पर क्रमशः शीर्षलंब BE और CF खींचे गए हैं। (देखिए आकृति)। दर्शाइए कि ये शीर्षलंब बराबर हैं।

हल :
ΔABE और ΔACF में,
∠A = ∠A (उभयनिष्ठ)
∠AEB = ∠AFC
(प्रत्येक = 90°) [दिया है]
AB = AC (दिया है)
∴ ΔABE ≅ ΔACF
(AAS सर्वांगसमता नियम से)
इसलिए BE = CF
(सर्वांगसम त्रिभुजों के संगत भाग)
दूसरे शब्दों में समान भुजाओं पर खींचे गए शीर्षलंब समान होते हैं।

प्रश्न 4.
ABC एक त्रिभुज है जिसमें AC और AB पर खींचे गए शीर्ष लंब BE और CF बराबर हैं ( देखिए आकृति)। दर्शाइए कि
(i) ΔABE ≅ ΔACF
(ii) AB = AC, अर्थात् ΔABC एक समद्विबाहु त्रिभुज है।

हल :
ΔABE और ΔACF में,
∠A = ∠A (उभयनिष्ठ)
∠AEB = ∠AEC (प्रत्येक = 90°) [∵ BE ⊥ AC और CF ⊥ AB (दिया है)]
BE = CF (दिया है)
(i) ∴ ΔABE ≅ ΔACF
[AAS सर्वांगसमता नियम से]

(ii) इसलिए, AB = AC
सर्वांगसम त्रिभुजों के संगत भाग]
अर्थात्, ΔABC एक समद्विबाहु त्रिभुज है।

प्रश्न 5.
ARC और DBC समान आधार BC पर स्थित दो समद्विबाहु त्रिभुज हैं (देखिए आकृति)। दर्शाइए कि ∠ABD = ∠ACD है।

हल :
समद्विबाहु ΔABC में,
AB = AC (दिया है)
∴ ∠ACB = ∠ABC ………… (i)
(समान भुजाओं के सम्मुख कोण)
साथ ही, समद्विबाहु ΔBCD में,
BD = DC
∴ ∠BCD = ∠CBD ………… (ii)
(समान भुजाओं के सम्मुख कोण)
(i) और (ii) के संगत पक्षों को जोड़ने पर
∠ACB + ∠BCD = ∠ABC + ∠CBD
⇒ ∠ACD = ∠ABD
या ∠ABD = ∠ACD (इति सिद्धम)

प्रश्न 6.
ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है। भुजा BA बिंदु D तक इस प्रकार बढ़ाई गई है कि AD = AB है ( देखिए आकृति)। दर्शाइए कि ∠BCD एक समकोण है।
हल :

समद्विबाहु त्रिभुज ABC में,
AB = AC
∴ ∠ACB = ∠ABC …. (i)
(समान भुजाओं के सम्मुख कोण)
अब
AD = AB (रचना से)
AB = AC (दिया है)
∴ AD = AB = AC
⇒ AD = AC
अब ΔADC में,
AD = AC
⇒ ∠ADC = ∠ACD …………..(ii)
[ΔADC में समान भुजाओं के सम्मुख कोण] आकृति से हमें प्राप्त होता है :
∠BAC + ∠CAD = 180° … (iii)
(रैखिक युग्म)
जैसा कि हम जानते हैं कि त्रिभुज का बहिष्कोण अंतः सम्मुख कोणों के योगफल के बराबर होता है।
∴ ΔABC
∠CAD = ∠ABC + ∠ACB
= ∠ACB + ∠ACB
[(i) के प्रयोग से]
⇒ ∠CAD = 2∠ACB … (iv)
इसी प्रकार, ΔADC के लिए
∠BAC =∠ACD + ∠ADC [जैसा कि हम जानते हैं कि त्रिभुज का बहिष्कोण अंतः सम्मुख कोणों के योगफल के बराबर होता है।]
= ∠ACD + ∠ACD
[(ii) के प्रयोग से]
⇒ ∠BAC = 2 ∠ACD … (v)
(iii), (iv) और (v), से हमें प्राप्त होता है।
2∠ACB + 2∠ACD = 180°
या, 2(∠ACB + ∠ACD) = 180°
या, ∠ACB + ∠ACD = \(\frac {180°}{2}\)
⇒ ∠BCD =90°
अतः ∠BCD एक समकोण है।

प्रश्न 7.
ABC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C ज्ञात कीजिए।

हल:
ABC एक समकोण त्रिभुज है, जिसमें
∠A = 90°
और AB = AC
ΔABC में,
AB = AC
∠C = ∠B ………..(i)
(समान भुजाओं के सम्मुख कोण)
अब, ΔABC में,
∠A + ∠B + ∠C = 180°
(कोण योगफल गुण)
⇒ 90° + ∠B + ∠B = 180° [∵ ∠A = 90° (दिया है) और ∠B = ∠C (i) से]
⇒ 2∠B = 180° – 90°
⇒ 2∠B = 90°
⇒ ∠B = \(\frac {90°}{2}\)
⇒ ∠B = 45°
साथ ही, ∠C = ∠B
⇒ ∠C= 45°

प्रश्न 8.
दर्शाइए कि किसी समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।
हल :
माल लीजिए ABC एक समबाहु त्रिभुज है
∴ AB = BC = AC
AB = BC

⇒ ∠C = ∠A …………(i)
(समान भुजाओं के सम्मुख कोण)
इसलिए,
AB = AC
⇒ ∠C = ∠B …… (ii)
(समान भुजाओं के सम्मुख कोण)
(i) और (ii) से हमें प्राप्त होता है
∠A = ∠B = ∠C …… (iii)
अब ΔABC में;
∠A + ∠B + ∠C = 180° ……. (iv)
[कोण योगफल गुण]
⇒ ∠A + ∠A + ∠A = 180°
⇒ 3∠A = 180
⇒ ∠A = \(\frac {180°}{3}\)
⇒ ∠A = 60°
(iii) से ; ∠A = ∠B = ∠C
⇒ ∠A = ∠B = ∠C = 60°
अतः, समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.2

जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) लीजिए।

प्रश्न 1.
ऊँचाई 14 cm वाले एक लंब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 88 cm² है। बेलन के आधार का व्यास ज्ञात कीजिए।
हल :
मान लीजिए लंब वृत्तीय बेलन के आधार की त्रिज्या = r cm
बेलन की ऊँचाई = h = 14 cm
बेलन का वक्र पृष्ठीय क्षेत्रफल = 88 cm²
⇒ 2πrh = 88
⇒ 2× \(\frac{22}{7}\) × r × 14 = 88

⇒ r = 88 × \(\frac{7}{22}\) × \(\frac{1}{14}\) × \(\frac{1}{2}\)
⇒ r = 1 cm
बेलन के आधार का व्यास = 2r
= 2 × 1
= 2 cm

प्रश्न 2.
धातु की चादर से 1 m ऊँची और 140 cm व्यास के आधार वाली एक बंद बेलनाकार टंकी बनाई जानी है। इस कार्य के लिए कितने वर्ग मीटर चादर की आवश्यकता होगी ?

हल :
मान लीजिए बेलनाकार टंकी के आधार की त्रिज्या = r cm
∴ व्यास = 2r = 140 cm
⇒ r = \(\frac{140}{2}\) cm
⇒ r = 70 cm
⇒ r = \(\frac{70}{100}\)
⇒ r = 0.7 m
बेलन की ऊँचाई = h = 1m
बेलन का कुल पृष्ठीय क्षेत्रफल = 2πr (r + h)
= 2 × \(\frac{22}{7}\) × 0.7(0.7+1)
= 2 × 22 × 0.1 × 1.7
= 7.48 m²
अतः, बंद बेलनकारार टंकी बनाने के लिए 7.48 m² चादर की आवश्यकता है।

प्रश्न 3.
धातु का एक पाइप 77 cm लंबा है। इसके एक अनुप्रस्थकाट का आंतरिक व्यास 4 cm है और बाहरी व्यास 4.4 cm है ( देखिए आकृति)।
(i) आंतरिक वक्र पृष्ठीय क्षेत्रफल
(ii) बाहरी वक्र पृष्ठीय क्षेत्रफल
(iii) कुल पृष्ठीय क्षेत्रफल

हल :

पाइप की लंबाई = 77 cm
(i) अनुप्रस्थ काट का आंतरिक व्यास = 4 cm
∴ अनुप्रस्थ काट की आंतरिक त्रिज्या r = \(\frac{4}{2}\)
= 2 cm
क्योंकि पाइप बेलनाकार है,
∴ आंतरिक वक्र पृष्ठीय क्षेत्रफल = 2πrh
[∵ पइप की लंबाई = ऊँचाई]
= 2 × \(\frac{22}{7}\) × 2 × 77
= 2 × 22 × 2 × 11
= 968 cm²

(ii) पाइप की लंबाई = 77 cm
पाइप का बाहरी व्यास = 4.4 cm
पाइप की बाहरी त्रिज्या R = \(\frac{4.4}{2}\) = 2.2 cm
∴ बेलन का बाहरी वक्र पृष्ठीय क्षेत्रफल
= 2πrh
= 2 × \(\frac{22}{7}\) × 2.2 × 77
= \(\frac{44}{7}\) × \(\frac{22}{10}\) × 77
= 44 × \(\frac{22}{10}\) × 11
= 1064.8 cm²

(iii) अब पाइप के दोनों अंत सिरों में प्रत्येक सिरे पर 2 cm और 2.2 cm त्रिज्याओं के वृत्त हैं,
∴ पाइप के दोनों सिरों का क्षेत्रफल = 2
(बाहरी वृत्त का क्षेत्रफल – आंतरिक वृत्त का क्षेत्रफल)
= 2 (πR² – πr²)
= 2π(R² – r²)
= 2 × 2 [(2.2)² – (2)²]
= \(\frac{44}{7}\) [4.84 – 4]
= \(\frac{44}{7}\) × 0.84
= 5.28 cm²
∴ पाइप का कुल पृष्ठीय क्षेत्रफल = आंतरिक वक्र पृष्टीय क्षेत्रफल + बाहरी वक्र पृष्ठीय क्षेत्रफल + दो वृत्तीय सिरों का क्षेत्रफल
= 968 cm² + 1064.8 cm² + 5.28 cm²
= 2038.08 cm²

प्रश्न 4.
एक रोलर (roller) का व्यास 84 cm है और लंबाई 120 cm है। एक खेल के मैदान को एक बार समतल करने के लिए 500 चक्कर लगाने पड़ते हैं। खेल के मैदान का m² में क्षेत्रफल ज्ञात कीजिए।
हल :
रोलर का व्यास = 84 cm

रोलर की त्रिज्या r = \(\frac{84}{2}\) = 42 cm
रोलर की लंबाई l = 120 cm
∵ रोलर बेलन के आकार का है
∴ रोलर का वक्र पृष्ठीय क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल
= 2π rh (l = h)
= 2 × \(\frac{22}{7}\)42 × 120
= 31680 cm²
\(\frac{31680}{100 \times 100} \mathrm{~m}^2\) = 3.1680 m²
अब रोलर द्वारा एक चक्कर में समतल किया गया क्षेत्रफल = 3.1680 m²
∴ रोलर द्वारा 500 चक्करों में समतल किया गया क्षेत्रफल = 500 × 3.1680
= 1584.0000
= 1584 m²
खेल के मैदान का क्षेत्रफल = रोलर द्वारा 500 चक्करों में समतल किया गया क्षेत्रफल
= 1584 m²

प्रश्न 5.
किसी बेलनाकार स्तंभ का व्यास 50 cm है और ऊँचाई 3.5 cm है। 12.50 रुपए प्रति m² की दर से इस स्तंभ के वक्र पृष्ठ पर पेंट कराने का व्यय ज्ञात कीजिए।
हल :
स्तंभ का व्यास = 50 cm
∴ स्तंभ की त्रिज्या = \(\frac{50}{2}\) = 25 cm = \(\frac{25}{100}\)
= \(\frac{1}{4}\) m
स्तंभ की ऊँचाई = 3.5 m
स्तंभ का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 × \(\frac{22}{7}\) × \(\frac{1}{4}\) × 3.5
= 2 × \(\frac{22}{7}\) × \(\frac{1}{4}\) × \(\frac{35}{10}\) = \(\frac{11}{2}\) m²
1 m² पेंट कराने का व्यय = 12.50 रु

प्रश्न 6.
एक लंब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 4.4 m² है। यदि बेलन के आधार की त्रिज्या 0.7 m है, तो उसकी ऊँचाई ज्ञात कीजिए।
हल :
बेलन का वक्र पृष्ठीय क्षेत्रफल = 4.4 m²
बेलन की त्रिज्या r = 0.7 m
मान लीजिए बेलन की ऊँचाई = h
∴ 2πrh = 4.4
या, 2 × \(\frac{22}{7}\) × 0.7 × h = 4.4
या, 44 × 0.1 × h = 4.4
या, 44 × \(\frac{1}{210}\) × h = \(\frac{44}{10}\)
या, h = \(\frac{44}{10} \times \frac{10}{1} \times \frac{1}{44}\) = 1 m

प्रश्न 7.
किसी वृत्ताकार कुएँ का आंतरिक व्यास 3.5 m है और यह 10 m गहरा है। ज्ञात कीजिए:
(i) आंतरिक वक्र पृष्ठीय क्षेत्रफल
(ii) 40 रुपए प्रति m² की दर से इसके वक्र पृष्ठ पर प्लास्टर कराने का व्यय।
हल :
वृत्ताकार कुएँ का आंतरिक व्यास = 3.5 m
वृत्ताकार कुएँ की त्रिज्या = \(\frac{3.5}{2}\) = 1.75 m
कुएँ की गहराई = 10 m
कुएँ का आकार बेलनाकार है।
भाग (i) के लिए, ∴ कुएँ की आंतरिक वक्र पृष्ठीय
= 2πrh [यहाँ गहराई = कुएँ की ऊँचाई]

= 2× \(\frac{22}{7}\) × 1.75 × 10 m²
= 2 × \(\frac{22}{7}\) × \(\frac{175}{100}\) × 10 m²
= 110 m²
भाग (ii), के लिए 1m² पर प्लास्टर कराने का व्यय = 40 रु०
100 m² पर प्लस्टर कराने का व्यय
40 × 110 रु० = 4400 रु०

प्रश्न 8.
गरम पानी द्वारा गरम रखने वाले एक संयंत्र में 28 m लंबाई और 5 cm व्यास वाला एक बेलनाकार पाइप है। इस संयत्र में गर्मी देने वाला कुल कितना पृष्ठ है ?
हल :
मान लीजिए बेलनकार पाइप की लंबाई (अर्थात् ऊँचाई) = h
∴ h = 28 m
और बेलनाकार पाइप की त्रिज्या = r ,
∴ 2r = 5 cm
⇒ r = \(\frac{5}{2}\) cm
गर्मी देने वाला बेलनाकार
∴ पाइप का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 × \(\frac{22}{7}\) × \(\frac{5}{2}\) × 2800
= 44000 cm²
= \(\frac{44000}{10000}\) m²
[∵ 1 cm = \(\frac{1}{100}\) m
∴ 1 cm² = \(\frac{1}{10000}\) m²]
= 4.4 m²

प्रश्न 9.
ज्ञात कीजिए :
(i) एक बेलनाकार पेट्रोल की बंद टंकी का पाव या वक्र पृष्ठीय क्षेत्रफल, जिसका व्यास 4.2 m है और ऊँचाई 4.5 m है।
(ii) इस टंकी को बनाने में कुल कितना इस्पात (steel) लगा होगा, यदि कुल इस्पात का \(\frac{1}{2}\) भाग बनाने में नष्ट हो गया है ?
हल :
(i) मान लीजिए बेलनाकार पेट्रोल की टंकी की त्रिज्या = r
∴ व्यास; 2r = 4.2 m
⇒ r = 2.1 m
टंकी की ऊँचाई, h = 4.5 m
पेट्रोल की टंकी का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 × \(\frac{22}{7}\) × 2.1 × 1.45 m²
= 59.4 m²

(ii) मान लीजिए टंकी बनाने में प्रयुक्त हुआ इस्पात का वास्तविक क्षेत्रफल x m² है।
क्योंकि कुल इस्पात का \(\frac{1}{12}\) भाग बनाने में नष्ट हुआ, टंकी को बनाने में लगे इस्पात का क्षेत्रफल
= x – \(\frac{1}{12}\)x
= \(\frac{11}{12}\)x
\(\frac{11}{12}\)x = 59.4 m²
⇒ x = 59.4 × \(\frac{12}{11}\)
⇒ x = 64.8 m²
अतः, टंकी को बनाने में लगा स्टील 64.8 m² है।

प्रश्न 10.
आकृति में, आप एक लैंपशेड का फ्रेम देख रहे हैं। इसे एक सजावटी कपड़े से ढका जाना है। इस फ्रेम के आधार का व्यास 20 cm है और ऊँचाई 30 cm है। फ्रेम के ऊपर और नीचे मोड़ने के लिए दोनों ओर 2.5 cm अतिरिक्त कपड़ा भी छोड़ा जाना है। ज्ञात कीजिए कि लैंपशेड को ढकने के लिए कुल कितने कपड़े की आवश्यकता होगी।

हल :

फ्रेम की ऊँचाई, H = 30 सेमी
ऊपर और नीचे मोड़ने वाले प्रत्येक कपड़े की ऊँचाई
h = 2.5 सेमी
मान लीजिए प्रत्येक भाग की त्रिज्या = r
व्यास, 2r = 20 cm
⇒ r = \(\frac{20}{2}\) cm
लैंपशेड ढकने के लिए आवश्यक कंपड़ा = बेलन I के वक्र पृष्ठ का क्षे० + बेलन II के वक्र पृष्ठ का क्षे० + बेलन III के वक्र पृष्ठ का क्षे०
= 2πrh + 2πrH + 2πrh
= 2πr (h + H + h)
= 2πr (H + 2h)
= 2 × \(\frac{22}{7}\) × 10 (30 + 2 × 2.5) सेमी²
= \(\frac{440}{7}\) × 35
= 440 × 5
= 2200 सेमी²

प्रश्न 11.
किसी विदयालय के विदयार्थियों से एक आधार वाले बेलनाकार कलमदानों को गत्ते से बनाने और सजाने की प्रतियोगिता में भाग लेने के लिए कहा गया। प्रत्येक कलमदान को 3 cm त्रिज्या और 10.5 cm ऊँचाई का होना था। विद्यालय को इसके लिए प्रतिभागियों को गत्ता देना था। यदि इसमें 35 प्रतिभागी थे, तो विद्यालय को कितना गत्ता खरीदना पड़ा होगा ?
हल :
मान लीजिए बेलनकार कलमदान की त्रिज्या = r
∴ r = 3 cm
और बेलनाकार कलमदान की ऊँचाई = h एक कलमदान के लिए वांछित गत्ता
∴ h = 10.5 cm
कलमदान का वक्र पृष्ठीय क्षेत्रफल + वृत्ताकार आधार का क्षेत्रफल
= 2πrh + πr²
= πr (2h + r)
= \(\frac{22}{7}\) × 3 (2 × 10.5 + 3)
= \(\frac{22}{7}\) × 3 (21 + 3)
= \(\frac{22}{7}\) × 3 × 24
= 226.28 cm²
अब, एक कलमदान बनाने के के लिए वांछित गत्ता = 226.28 cm²
∴ 35 कलमदान बनाने के लिए वांछित गत्ता
= (226.28 × 35) cm²
= 7919.8 cm²
= 7620 cm² (लगभग)

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.1

प्रश्न 1.
1.5 m लंबा, 1.25 m चौड़ा और 65 cm गहरा प्लास्टिक का एक डिब्बा बनाया जाना है। इसे ऊपर से खुला रखना है। प्लास्टिक शीट की मोटाई को नगण्य मानते हुए, निर्धारित कीजिए :
(i) डिब्बा बनाने के लिए आवश्यक प्लास्टिक शीट का क्षेत्रफल।
(ii) इस शीट का मूल्य, यदि 1 m² शीट का मूल्य 20 रुपए है।
हल :
(i) मान लीजिए प्लास्टिक शीट की लंबाई (l) = 1.5 m
चौड़ाई (b) = 1.25 m
और गहराई (h) = 65 m

= \(\frac{65}{100}\) m
= 0.65 cm
ऊपर से खुला बॉक्स बनाने के लिए वांछित शीट का क्षेत्रफल
= 2(bh + hl) + lb
= 2 \(\left(1.25 \times \frac{65}{100}+\frac{65}{100} \times 1.5\right)\) + 1.5 × 1.25
= 2 (0.8125 + 0.975) + 1.875
= 2 (1.7875) + 1.875
= 3.575 + 1.875
= 5.45 m²

(ii) 1 m² शीट का मूल्य = 20 रु.
5.45 m² शीट का मूल्य = (20 × 5.45) रु.
= 109 रु.

प्रश्न 2.
एक कमरे की लंबाई, चौड़ाई और ऊँचाई क्रमशः 5m, 4m और 3m हैं। 7.50 रुपए प्रति m² की दर से इस कमरे की दीवारों और छत पर सफेदी कराने का व्यय ज्ञात कीजिए।
हल :
मान लीजिए कमरे की लंबाई (l) = 5 m
चौड़ाई (b) = 4 m
और ऊँचाई (h) = 3 m
कमरे की चार दीवारों का क्षेत्रफल = पार्श्व पृष्ठीय क्षेत्रफल
= 2 (bh + hl)
= 2 (b + l) h
= 2 (4 + 5)3
= 2 × 9 × 3
= 54 m²
छत का क्षेत्रफल = l × b
= (5 × 4) m²
= 20 m²
अतः, दीवारों और छत का कुल क्षेत्रफल
= 54 m² + 20 m²
= 74 m²
1 m² सफेदी करवाने का व्यय = 7.50 रु
74 m² सफेदी करवाने का व्यय
= (7.50 × 74) रु
= 555 रु

प्रश्न 3.
किसी आयताकार हॉल के फर्श का परिमाप 250 m है। यदि 10 रुपए प्रति m² की दर से चारों दीवारों पर पेंट कराने की लागत 15000 रुपए है, तो इस हॉल की ऊँचाई ज्ञात कीजिए।
हल :
मान लीजिए आयताकार हाल की लंबाई = l m
चौड़ाई = b m
∴ आयताकार हाल का परिमाप = 2 (l + b)
= 250 m …… (i)
अब कमरे की चार दीवारों का क्षेत्रफल

मान लीजिए मीटरों में आयताकार हाल की ऊँचाई = h
चार दीवारों का क्षेत्रफल (पार्श्व पृष्ठीय क्षेत्रफल) = 2 (l + b) h = 1500 m²
[(ii) का प्रयोग करने से]
⇒ 250 × h = 1500 [(ii) का प्रयोग करने से]
⇒ h = \(\frac{1500}{250}\)
⇒ h = 6 m
अतः, हाल की वांछित ऊँचाई 6 m है।

प्रश्न 4.
किसी डिब्बे में भरा हआ पेंट 9.375 m² के क्षेत्रफल पर पेंट करने के लिए पर्याप्त है। इस डिब्बे के पेंट से 22.5 cm × 10 cm × 7.5 cm विमाओं वाली कितनी ईंटें पेंट की जा सकती हैं ?
हल :
मान लीजिए ईंट की लंबाई = l = 22.5 cm
चौड़ाई = b = 10 cm
और ऊँचाई = h = 7.5 cm
ईंट का क्षेत्रफल = 2 (lb + bh + hl)
= 2 (22.5 × 10 + 10 × 7.5 + 7.5 × 22.5)
= 2 (225 + 75 + 468.75)
= 2 × 468.75
= 937.5 सेमी²
= 937.5 × \(\frac{1}{2}\)


अत:, डिब्बे में उपलब्ध पेंट से 100 ईंटें पेंट की जा सकती हैं।

प्रश्न 5.
एक घनाकार डिब्बे का किनारा 10 cm लंबाई का है तथा एक अन्य घनाभाकार डिब्बे की लंबाई, चौड़ाई और ऊँचाई क्रमशः 12.5 cm, 10 cm और 8 cm हैं।
(i) किस डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल अधिक है और कितना अधिक है ?
(ii) किस डिब्बे का कुल पृष्ठीय क्षेत्रफल कम है और कितना कम है?
हल :
मान लीजिए घनाकार डिब्बे का किनारा = l
∴ l = 10 cm
(i) घनाकार डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल = इसकी चार दीवारों का क्षेत्रफल

= दीवार के क्षेत्रफल का 4 गुना
= 4l²
= 4 (10)²
= 4 (10 × 10)
= 4 × 100
= 400 cm² …. (a)
मान लीजिए घनाभाकार की लंबाई = l cm
∴ l = 12.5 cm
चौड़ाई; b = 10 cm
और ऊँचाई; h = 8 cm
घनाभाकार डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल = चार दीवारों का क्षेत्रफल

= 2(l + b) h
= 2 (12.5 + 10) 8
= 2 (22.5) 8
= 2 × 22.5 × 8
= 360 cm² ……. (b)
(a) और (b) हम देखते हैं कि घनाकार डिब्बे का पृष्ठीय क्षेत्रफल घनाभाकार डिब्बे से (400 – 360) cm² अर्थात् 40 cm² बड़ा है।
(ii) घनाकार डिब्बे का कुल पृष्ठीय क्षेत्रफल = 6 l²
= 6 (10)²
= 6 × 10 × 10 = 600 cm² … (c)
घनाभाकार डिब्बे का कुल पृष्ठीय क्षेत्रफल
= 2 (lb + bh + hl)
= 2 (10 × 12.5 + 12.5 × 8 × 10)
= 2 (125 + 100 + 80)
= 2 (305)
= 2 × 305
= 610 cm² … (d)
(c) और (d) से हम देखते हैं कि घनाकार डिब्बे का पृष्ठीय क्षेत्रफल घनाभकार डिब्बे से (610 – 600) cm² अर्थात् 10 cm² कम है।

प्रश्न 6.
एक छोटा पौधा घर (green house) सम्पूर्ण रूप से शीशे की पट्टियों से (आधार भी सम्मिलित है) घर के अंदर ही बनाया गया है और शीशे की पट्टियों को टेप द्वारा चिपका कर रोका गया है। यह पौधा घर 30 cm लंबा, 25 cm चौड़ा और 25 cm ऊँचा है।
(i) इसमें प्रयुक्त शीशे की पट्टियों का क्षेत्रफल क्या है ?
(ii) सभी 12 किनारों के लिए कितने टेप की आवश्यकता है ?
हल :
(i) मान लीजिए पौधा घर की लंबाई = l
∴ l = 30 cm
चौड़ाई ; b = 25 cm
और ऊँचाई ; h = 25 cm

शीशे का कुल पृष्ठीय क्षेत्रफल
= 2 (lb + bh + hl)
= 2 (30 × 25 + 25 × 25 + 25 × 30)
= 2 (750 + 625 + 750)
= 2 × 2125
= 4250 cm²
अत:, 4250 cm² शीशे की आवश्यकता है।

(ii) 12 किनारों पर टेप प्रयुक्त की गई है
अर्थात् 4 लंबाइयाँ, 4 चौड़ाइयाँ 4 ऊँचाइयाँ
टेप की कुल लंबाई = 4 (l + b + h)
= 4 (30 + 25 + 25) cm
= 4 (80) cm
= 320 cm
अतः, सभी 12 किनारों के लिए 320 cm टेप की आवश्यकता है।

प्रश्न 7.
शांति स्वीट स्टाल अपनी मिठाइयों को पैक करने के लिए गत्ते के डिब्बे बनाने का ऑर्डर दे रहा था। दो मापों के डिब्बों की आवश्यकता थी। बड़े डिब्बों की माप 25 cm × 20 cm × 5 cm और छोटे डिब्बे की माप 15 cm × 2 cm × 5 cm थीं। सभी प्रकार की अतिव्यापिकता (over laps) के लिए कुल पृष्ठीय क्षेत्रफल के 5% के बराबर अतिरिक्त गत्ता लगेगा। यदि गत्ते की लागत 4 रुपए प्रति 1000 cm² है, तो प्रत्येक प्रकार के 250 डिब्बे बनवाने की कितनी लागत आएगी ?
हल :
मान लीजिए बड़े डिब्बे की लंबाई = L cm
∴ L = 25 cm
चौड़ाई B = 20 cm
और ऊँचाई H = 5 cm

बड़े डिब्बे का कुल पृष्ठीय क्षेत्रफल
= 2(LB + BH + HL)
= 2 (25 × 20 + 20 × 5 + 5 × 25) cm²
= 2 (500 + 100 + 125) cm²
= 2 (725) cm²
= 1450 cm²
सभी प्रकार की अतिव्यापिकता के लिए कुल पृष्ठीय क्षेत्रफल के 5% के बराबर वांछित गत्ते का क्षेत्रफल
∴ 1450 cm² का 5%
= \(\frac{5}{100}\) × 1450
= 72.5 cm²
अब अतिरिक्त अतिव्यापिकता के साथ एक बड़े डिब्बे का कुल पृष्ठीय क्षेत्रफल
= (1450 + 72.5) cm²
= 1522.5 cm²
ऐसे 250 डिब्बों का कुल पृष्ठीय क्षेत्रफल (अतिरिक्त अतिव्यापिकता के साथ)
= (1522.5 × 250) cm²
= 380625 cm²
1000 cm² गत्ते की लागत = 4 रु
1 cm² गत्ते की लागत = \(\frac{4}{1000}\) रु
380625 cm² गत्ते की लागत = (\(\frac{4}{1000}\) × 380625) र
= 1522.50 रु
अब, मान लीजिए छोटे डिब्बे की लम्बाई = l cm
∴ l = 15 cm
चौड़ाई ; b = 12 cm
और ऊँचाई ; h = 5 cm

छोटे डिब्बे का कुल पृष्ठीय क्षेत्रफल
= 2 (lb + bh + hl)
= 2 (15 × 12 + 12 × 5 + 5 × 15) cm²
= 2 (180 + 60 + 75) cm²
= 2 (315) cm²
= 630 cm²
सभी प्रकार की अतिव्यापिकता के लिए कुल पृष्ठीय क्षेत्रफल के लिए अतिरिक्त 5% गत्ता
∴ 630 cm² का 5%
= \(\frac{5}{100}\) × 630
= 31.5 cm²
अब अतिरिक्त अतिव्यापिकता के साथ छोटे डिब्बे का कुल पृष्ठीय क्षेत्रफल
= (630 + 31.5) cm
= 661.5 cm²
ऐसे 250 छोटे डिब्बों का (अतिरिक्त कुल पृष्ठीय क्षेत्रफल)
= (661.5 × 250) cm²
= 165375 cm
1000 cm² के लिए गत्ते की लागत = 4 रु
1 cm² के लिए गत्ते की लागत = (\(\frac{4}{1000}\)) रु
165375 cm² के लिए गत्ते की लागत
= (\(\frac{4}{1000}\) × 165375) र
= 661.5 रु
प्रत्येक प्रकार के 250 गत्ते के डिब्बों की कुल लागत
= बड़े डिब्बों की लागत + छोटे डिब्बों की लागत
= 1522.5 रु + 661.5 रु
= 2184 रु

प्रश्न 8.
परवीन अपनी कार खड़ी करने के लिए, एक संदूक के प्रकार के ढाँचे जैसा एक अस्थाई स्थान तिरपाल की सहायता से बनाना चाहती है, जो कार को चारों ओर से और ऊपर से ढक ले (सामने वाला फलक लटका हुआ होगा जिसे घुमाकर ऊपर किया जा सकता है)। यह मानते हुए कि सिलाई के समय लगा तिरपाल का अतिरिक्त कपड़ा नगण्य होगा, आधार विमाओं 4 मीटर × 3 मीटर और ऊँचाई 2.5 मीटर वाले इस ढांचे को बनाने के लिए कितने तिरपाल की आवश्यकता होगी ?
हल :
मान लीजिए आधार की लंबाई = l
∴ l = 4 m
और आधार की चौड़ाई = b
∴ b = 3 m
ढांचे की ऊँचाई = h
∴ h = 2.5 m
आवश्य तिरपाल = चार दीवारों का क्षेत्रफल + छत का क्षेत्रफल
= 2 (l + b) h + lb
= 2 (4 + 3) 2.5 + 4 × 3
= 2 × 3 × 2.5 + 12
= 35 + 12
= 47 m²
अतः, ढाँचे के लिए 47 m² तिरपाल की आवश्यकता है।

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 14 सांख्यिकी MCQ Questions with Answers.

PSEB 9th Class Maths Chapter 14 सांख्यिकी MCQ Questions

बहुविकल्पीय प्रश्न:

दिये गए चार विकल्पों में से सही उत्तर का चयन करें।

प्रश्न 1.
वर्ग 150 – 160 का वर्ग चिन्ह है :
(A) 145
(B) 310
(C) 10
(D) 155
उत्तर:
(D) 155

प्रश्न 2.
अंकों 10, 8, 9, 7, 8 का माध्य है :
(A) 8.4
(B) 7.4
(C) 4.8
(D) 8.2
उत्तर:
(A) 8.4

प्रश्न 3.
पहली 10 प्राकृत संख्याओं की औसत है :
(A) 6.5
(B) 5.5
(C) 7.5
(D) 8.5
उत्तर:
(B) 5.5

प्रश्न 4.
किसी कक्षा में 9 विद्यार्थियों की ऊँचाई (सेमी० में) दी गई है :
155, 160, 145, 149, 150, 147, 152, 144, 148.
इन आंकड़ों का माध्य है :
(A) 150
(B) 147
(C) 149
(D) 148
उत्तर:
(C) 149

प्रश्न 5.
किसी कक्षा के 20 विद्यार्थियों के अंक (10 में से) निम्नलिखित है :
9, 6, 5, 9, 3, 2, 7, 7, 6, 5, 4, 9, 10, 10, 3, 4, 7, 6, 9, 9.
बहुलक अंक क्या है :
(A) 7
(B) 9
(C) 3
(D) 10.
उत्तर:
(B) 9

प्रश्न 6.
किसी बारंबारता बंटन में पाँच सतत वर्गों में से प्रत्येक की चौड़ाई 5 है तथा सबसे छोटे वर्ग की निम्न सीमा 10 है। सबसे बड़े वर्ग की उपरि सीमा है-
(A) 15
(B) 25
(C) 35
(D) 40
उत्तर:
(C) 35

प्रश्न 7.
मान लीजिए कि एक सतत बारंबारता बंटन में एक वर्ग का मध्य-बिंदु m है और उपरि वर्ग सीमा 1 है। इस वर्ग की निम्न वर्ग सीमा है-
(A) 2m + l
(B) 2m – l
(C) m – l
(D) m – 2l.
उत्तर:
(B) 2m – l

प्रश्न 8.
एक बारंबारता बंटन के वर्ग चिन्ह 15, 20, 25, ………….. हैं। वर्ग चिन्ह 20 के संगत वर्ग हैं-
(A) 12.5 – 17.5
(B) 17.5 – 22.5
(C) 18.5 – 21.5
(D) 19.5 – 20.5.
उत्तर:
(B) 17.5 – 22.5

प्रश्न 9.
वर्ग अंतराल 10-20, 20-30, में संख्या 20 निम्नलिखित में सम्मिलित है-
(A) 10-20
(B) 20-30
(C) दोनों अंतरालों में
(D) इनमें से किसी में भी नहीं।
उत्तर:
(B) 20-30

प्रश्न 10.
निम्नलिखित आँकड़ों के लिए, एक अंतराल 250-270 (270 सम्मिलित नहीं) लेते हुए बराबर मापों के वर्ग अंतरालों वाली एक वर्गीकृत बारंबारता सारणी की रचना की जाती है-
268, 220, 368, 258, 242, 310, 272, 342, 310, 290, 300, 320, 319, 304, 402, 318, 406, 292, 354, 278, 210, 240, 330, 316, 406, 215, 258, 236.
वर्ग अंतराल 310-330 की बारंबारता है :
(A) 4
(B) 5
(C) 6
(D) 7
उत्तर:
(C) 6

प्रश्न 11.
निम्नलिखित आँकड़ों के लिए एक वर्ग 63-72 (72 सम्मिलित है) लेते हुए बराबर मापों के वर्ग वाली एक वर्गीकृत बारंबारता सारणी की रचना की जाती है-
30, 32, 45, 54, 74, 78, 108, 112, 66, 76, 88, 40, 14, 20, 15, 35, 44, 66, 75, 84, 95, 96, 102, 110, 88, 74, 112, 14, 34, 44.
(A) 9
(B) 10
(C) 11
(D) 12.
उत्तर:
(B) 10

प्रश्न 12.
बारंबारता बंटन

का एक आयतचित्र खींचने के लिए, वर्ग 25-45 की समायोजित बारंबारता है :
(A) 6
(B) 5
(C) 3
(D) 2
उत्तर:
(D) 2

प्रश्न 13.
पाँच संख्याओं का माध्य 30 है। यदि इनमें से एक संख्या को हटा दिया जाए, तो उनका माध्य 28 हो जाता है। हटाई गई संख्या है-
(A) 28
(B) 30
(C) 35
(D) 38.
उत्तर:
(D) 38.

प्रश्न 14.
यदि x, x + 3, x + 5, x + 7 प्रेक्षणों और x + 10 के माध्य 9 है, तो अंतिम तीन प्रेक्षणों का माध्य है-
(A) 10\(\frac{1}{3}\)
(B) 10\(\frac{2}{3}\)
(C) 11\(\frac{1}{3}\)
(D) 11\(\frac{2}{3}\)
उत्तर:
(C) 11\(\frac{1}{3}\)

प्रश्न 15.
यदि n प्रेक्षण x₁, x₂, ……. x_n के माध्य को \(\bar{x}\) से निरूपित किया जाता है, तो \({ }_{i=1}^n\left(x_1-\bar{x}\right)\) का मान है-
(A) -1
(B) 0
(C) 1
(D) n – 1.
उत्तर:
(B) 0

प्रश्न 16.
यदि आँकड़ों के प्रत्येक प्रेक्षण में 5 की वृद्धि की जाती है तो उनका माध्य
(A) वही रहता है
(B) प्रारंभिक माध्य का पांच गुना हो जाता है
(C) 5 कम हो जाता है
(D) 5 बढ़ जाता है।
उत्तर:
(D) 5 बढ़ जाता है।

प्रश्न 17.
यदि x₁, x₂, ….., x_n का माध्य \(\bar{x}\) है, y₁, y₂, ……. y_n का माध्य \(\bar{y}\) है तथा x₁, x₂, ….., x_n, y₁, y₂, ….. y_n का माध्य \(\bar{z}\) बराबर है-
(A) \(\bar{x}\) + \(\bar{x}\)
(B) \(\frac{\bar{x}+\bar{y}}{2}\)
(C) \(\frac{\bar{x}+\bar{y}}{n}\)
(D) \(\frac{\bar{x}+\bar{y}}{2 n}\)
उत्तर:
(B) \(\frac{\bar{x}+\bar{y}}{2}\)

प्रश्न 18.
यदि x₁, x₂, …… x_n का माध्य \(\bar{x}\) है, a ≠ 0, के लिए ax₁, ax₂, …… ax_n, \(\frac{x_1}{a}, \frac{x_2}{a}, \ldots \ldots, \frac{x_n}{a}\) का माध्य ज्ञात कीजिए।
(A) \(\left(a+\frac{1}{a}\right) \bar{x}\)
(B) \(\left(a+\frac{1}{a}\right) \frac{\bar{x}}{2}\)
(C) \(\left(a+\frac{1}{a}\right) \frac{\bar{x}}{n}\)
(D) \(\frac{\left(a+\frac{1}{a}\right) \bar{x}}{2 n}\)
उत्तर:
(B) \(\left(a+\frac{1}{a}\right) \frac{\bar{x}}{2}\)

प्रश्न 19.
यदि \(\bar{x}_1, \bar{x}_2, \bar{x}_3, \ldots, \bar{x}_n\) क्रमशः प्रेक्षणों की संख्या n₁, n₂, ….., n_n, वाले n समूहों के माध्य हैं, तो सभी समूहों को मिलाकर लेने पर उनका माध्य \(\bar{x}\) निम्नलिखित से प्राप्त होता है-
(A) \(\sum_{i=1}^n n_i \bar{x}_i\)
(B) \(\frac{\sum_{i=1}^n n_i \bar{x}_i}{n^2}\)
(C) \(\frac{\sum_{i=1}^n n_i \bar{x}_i}{\sum_{i=1}^n n_1}\)
(D) \(\frac{\sum_{i=1}^n n_i x_i}{2 n}\)
उत्तर:
(C) \(\frac{\sum_{i=1}^n n_i \bar{x}_i}{\sum_{i=1}^n n_1}\)

प्रश्न 20.
100 प्रेक्षणों का माध्य 50 है। यदि इनमें से एक प्रेक्षण 50 को 150 से प्रतिस्थापित कर दिया जाए तो परिणामी माध्य हो जाएगा-
(A) 50.5
(B) 51
(C) 51.5
(D) 52
उत्तर:
(B) 51

प्रश्न 21.
50 संख्याएँ दी हुई हैं। इनमें से प्रत्येक संख्या को 53 में से घटाया जाता है तथा इस प्रकार प्राप्त संख्याओं का माध्य -3.5 ज्ञात किया जाता है। दी हुई संख्याओं का माध्य है-
(A) 46.5
(B) 49.5
(C) 53.5
(D) 56.5.
उत्तर:
(D) 56.5.

प्रश्न 22.
25 प्रेक्षणों का माध्य 36 है। इन प्रेक्षणों में से यदि प्रथम 13 प्रेक्षणों का माध्य 32 है तथा अंतिम 13 का माध्य 40 है तो 13वाँ प्रेक्षण है-
(A) 23
(B) 36
(C) 38
(D) 40
उत्तर:
(B) 36

प्रश्न 23.
78, 56, 22, 34, 45, 54, 39, 68, 54, 84 आँकड़ों का माध्यक है-
(A) 45
(B) 49.5
(C) 54
(D) 56.
उत्तर:
(C) 54

प्रश्न 24.
एक सतत् बारंबारता बंटन का बारंबारता बहुभुज खींचने के लिए, हम उन बिंदुओं को आलेखित करते हैं जिनकी कोटियाँ क्रमश: वर्गों की बारंबारताएँ होती हैं तथा भुज क्रमशः होते हैं-
(A) वर्गों की उपरि सीमाएँ
(B) वर्गों की निम्न सीमाएँ
(C) वर्गों के वर्ग चिन्ह
(D) पिछले वर्गों की उपरि सीमाएँ।
उत्तर:
(C) वर्गों के वर्ग चिन्ह

प्रश्न 25.
4, 4, 5, 7, 6, 7, 7, 12, 3 संख्याओं का माध्यक है-
(A) 4
(B) 5
(C) 6
(D) 7
उत्तर:
(C) 6

प्रश्न 26.
15, 14, 19, 20, 14, 15, 16, 14, 15, 18, 14, 19, 15, 17, 15 आँकड़ों का बहुलक है-
(A) 14
(B) 15
(C) 16
(D) 17.
उत्तर:
(B) 15

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 14 सांख्यिकी Ex 14.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 14 सांख्यिकी Ex 14.4

प्रश्न 1.
एक टीम ने फुटबाल के 10 मैचों में निम्नलिखित गोल किए:
2, 3, 4, 5, 0, 1, 3,3,4,3
इन गोलों के माध्य, माध्यक और बहुलक ज्ञात कीजिए।
हल :
जैसा कि हमें ज्ञात है कि

माध्यक के लिए :
दिए गए आंकड़ों को आरोही क्रम में लिखने पर हमें प्राप्त होता है।
0, 1, 2, 3, 3, 3, 3, 4, 4, 5
यहां n = 10, एक सम संख्या है।
∴ माध्यक = \(\frac{n}{2}\) वे और \(\left(\frac{n}{2}+1\right)\) वें प्रेक्षणों का माध्य या 5वें और 6वें प्रेक्षण का माध्य
∴ माध्यक = \(\frac{3+3}{2}=\frac{6}{2}\) = 3

बहुलक के लिए :
दिए गए प्रेक्षणों के लिए बारंबारता सारणी बनाने पर हमें प्राप्त होता है :

गोल	0	1	2	3	4	5
बारंबारता	1	1	1	4	2	1

यहां पर प्रेक्षण अर्थात् गोलों की अधिकतम बारंबारता 4 है। इसलिए बहुलक = 3.

प्रश्न 2.
णित की परीक्षा में 15 विद्यार्थियों ने (100 में से) निम्नलिखित अंक प्राप्त किए :-
41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 40, 42, 52, 60
इन आँकड़ों के माध्य, माध्यक और बहुलक ज्ञात कीजिए।
हल :
जैसा कि हमें ज्ञात है कि

माध्यक के लिए:
दिए गए आँकड़ों को आरोही क्रम में लिखने पर हमें प्राप्त होता है :
39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62, 96, 98
यहां n = 15, एक विषय संख्या है।
∴ माध्यक = \(\left(\frac{n+1}{2}\right)\) वाँ प्रेक्षण
= \(\left(\frac{15+1}{2}\right)\) वाँ प्रेक्षण = 8वाँ प्रेक्षण।
= 52
अतः, माध्यक = 52

बहुलक के लिए
दिए गए प्रेक्षणों के लिए बारंबारता सारणी बनाने पर हमें प्राप्त होता है :

यहाँ अंक 52 की अधिकतम बारंबारता 3 है।
इसलिए, बहुलक = 52.

प्रश्न 3.
निम्नलिखित प्रेक्षणों को आरोही क्रम में व्यवस्थित किया गया है। यदि आँकड़ों का माध्यक 63 हो,तो x का मान ज्ञात कीजिए:
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
हल:
दिए गए आँकड़े आरोही क्रम में हैं और यहाँ n = 10 एक सम संख्या है।
∴ माध्यक = \(\left(\frac{n}{2}\right)\) वें और \(\left(\frac{n}{2}+1\right)\) वें प्रेक्षणों का माध्य अर्थात् 5वें और 6 प्रेक्षणों का माध्य
∴ माध्यक = \(\frac{x+(x+2)}{2}\)
⇒ 63 = x + 1
[∵ माध्यक = 63 दिया है]
⇒ x + 1 = 63
⇒ x = 62

प्रश्न 4.
आँकड़ों 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18 का बहुलक ज्ञात कीजिए।
हल :
हमें प्राप्त है :
(i) 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18
बारंबारता सारणी बनाने पर हम प्राप्त करते हैं :

यहां प्रेक्षण 14 की अधिकतम बारंबारता 4 है।
इसलिए बहुलक = 14

प्रश्न 5.
निम्न सारणी से एक फैक्टरी में काम कर रहे 60 कर्मचारियों का माध्य वेतन मान ज्ञात कीजिए।

वेतन (रुपयों में)	कर्मचारियों की संख्या
3000	16
4000	12
5000	10
6000	8
7000	6
8000	4
9000	3
10000	1
कुल योग	60

हल :

वेतमान (रु. में) xi	व्यक्तियों की संख्या fi	fixi
3000	16	48000
4000	12	48000
5000	10	50000
6000	8	48000
7000	6	42000
8000	4	32000
9000	3	27000
10000	1	10000
कुल योग	Σfi = N = 60	Σfixi = 305000

अतः, मध्य वेतन 5083.33 रु. है।

प्रश्न 6.
निम्न स्थिति पर आधारित एक उदाहरण दीजिए
(i) माध्य की केंद्रीय प्रवृत्ति का उपयुक्त माप है।
(ii) माध्य केंद्रीय प्रवृत्ति का उपयुक्त माप नहीं है, जबकि माध्यक एक उपयुक्त माप है।
हल :
(i) माध्य केंद्रीय प्रवृत्ति का उपयुक्त माप है क्योंकि इसके परिकलन में प्रत्येक पद लिया जाता है, यह हरेक मद द्वारा प्रभावित होता है। इसका उपयोग अधिकतर विभिन्न आँकड़ों के समूहों की तुलना करने के लिए किया जाता है।
उदाहरण के लिए 7 विद्यार्थियों द्वारा प्राप्त अंक है, 10, 15, 14, 18, 26, 24, 20, 14 और 27

परंतु 10, 14, 14, 15, 18, 20, 24, 26 और 27 का माध्य 18 है। और बहुलक 14 है।
उपरोक्त उदाहरण से हम इस निष्कर्ष पर पहुंचते हैं कि 18.67 9 विद्यार्थियों के प्रदर्शन को निरूपित करता है। पंरतु माध्यक और बहुलक नहीं।

(ii) (a) माध्य चरम मानों से प्रभावित होता है परंतु माध्यक चरम मानों से प्रभावित नहीं होते।
उदाहरण के लिए यदि 5 मान है :
4, 7, 12, 18, 19.
इस स्थिति में माध्य (\(\overline{\mathbf{X}}\)) 12 है और माध्यक भी 12 है।
यदि हम इसमें दो मान 450 और 1000 जोड़ दें तो नया माध्यम है :
= \(\frac{4+7+12+18+19+450+1000}{7}\)
= \(\frac{1510}{7}\)
= 215.7
यह पहले पाँच मानों के माध्य की तुलना एक महान् परिवर्तन है परंतु
4, 7, 12, 18, 19, 450, 1000
का नया माध्यक 18 है जिसमें पहले 5 की तुलना में अधिक परिवर्तन नहीं है।
अतः हम इस निष्कर्ष पर पहुंचते है कि माध्य चरम मानों से प्रभावित होता है।

(b) कई बार माध्य असंभव निष्कर्ष निकालता है उदाहरण के लिए यदि 3 कक्षाओं में यदि 60, 50 और 42 विद्यार्थी हो, तो विद्यार्थियों का माध्य \(\frac{60+50+42}{3}\) = 50.67, जोकि असंभव है क्योकि 3 विद्यार्थी भिन्नों में नहीं हो सकते।
परंतु 42, 50 और 60 का माध्यक 50 है।