PSEB 10th Class Maths Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.4

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.4 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 1 वास्तविक संख्याएँ 1.4

प्रश्न 1.
बिना लंबी विभाजन प्रक्रिया किए, बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत हैं या असांत आवर्ती हैं :
(i) \(\frac{13}{3125}\)

(ii) \(\frac{17}{8}\)

(iii) \(\frac{64}{455}\)

(iv) \(\frac{15}{1600}\)

(v) \(\frac{29}{343}\)

(vi) \(\frac{23}{2^{3} 5^{2}}\)

(vii) \(\frac{129}{2^{2} 5^{7} 7^{5}}\)

(viii) \(\frac{6}{15}\)

(ix) \(\frac{35}{50}\)

(x) \(\frac{77}{210}\)

हल :
(i) मान लीजिए x = \(\frac{13}{3125}\) ………………(1)
(1) की x = P से तुलना कीजिए,
यहाँ p = 13 और q = 3125
q के अभाज्य गुणनखंड = 3125 = 5 × 5 × 5 × 5
= 55 × 20
जोकि 2ⁿ × 5^m के रूप का है।
जहाँ n = 0, m = 5
जो ऋणोतर पूर्णांक हैं।
∴ x = \(\frac{13}{3125}\) का सांत दशमलव प्रसार है। उत्तर

(ii) मान लीजिए x = \(\frac{17}{8}\) ………….. (1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए
यहाँ p = 17 और q = 8
q के अभाज्य गुणनखंड = 8 = 2 × 2 × 2 = 23
= 23 × 50
जोकि 2ⁿ × 5^m के रूप का है।
जहाँ n = 3 m = 0 है।
और ये ऋणेतर पूर्णांक हैं।
∴ x = \(\frac{17}{8}\)
जिसका दशमलव प्रसार सांत है। उत्तर

(iii) मान लीजिए x = \(\frac{64}{455}\) ……………. (1)
(1) की x = ” से तुलना कीजिए।
यहाँ p = 64, q = 455
q के अभाज्य गुणनखंड = 455 = 5 × 7 × 13
जोकि 2ⁿ × 5^m के रूप का नहीं है।
∴ x = \(\frac{64}{455}\) का दशमलव प्रसार असांत आवर्ती है।। उत्तर

(iv) मान लीजिए x = \(\frac{15}{1600}\) ……………..(1)
(1) की x = = के साथ तुलना कीजिए।
यहाँ p = 15 और q = 1600
q के अभाज्य गुणनखंड = 600
= 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5
= 2⁶ × 5² .
जोकि 2ⁿ × 5^m, के रूप का है,
जहाँ n = 6, m = 2 और ये ऋणेतर पूर्णांक हैं।
∴ x = \(\frac{15}{1600}\) जिसका दशमलव प्रसार सांत है। उत्तर

(v) मान लीजिए x = \(\frac{29}{343}\) ……………(1)
(1) की x = \(\frac{p}{q}\) के साथ तुलना कीजिए।
यहाँ p = 29 और q = 343
q के अभाज्य गुणनखंड हैं = 343
= 7 × 7 × 7
= 7³
जोकि 2ⁿ × 5^m के रूप में नहीं है।
∴ x = \(\frac{29}{343}\) का दशमलव प्रसार असांत आवर्ती है। उत्तर

(vi) मान लीजिए x = \(\frac{23}{2^{3} 5^{2}}\) …………..(1)
(1) की x = 4 के साथ तुलना कीजिए।
यहाँ p = 23 और 4 = 2³5²
q के अभाज्य गुणनखंड = 2³5²
जोकि 2ⁿ × 5^m के रूप का है,
जहाँ n = 3, m = 2 और ये ऋणेतर पूर्णांक हैं।
∴ x = \(\frac{23}{2^{3} 5^{2}}\) का दशमलव प्रसार सांत है। उत्तर

(vii) मान लीजिए x = \(\frac{129}{2^{2} 5^{7} 7^{5}}\) ………………(1)
(1) की x = \(\frac{p}{q}\) के साथ तुलना कीजिए।
यहाँ p = 129 और q = 2² 5⁷ 7⁵
q के अभाज्य गुणनखंड = 2² 5⁷ 7⁵
जोकि 2ⁿ × 5^m के रूप में नहीं है।
∴ x = \(\frac{129}{2^{2} 5^{7} 7^{5}}\) का दशमलव प्रसार असांत आवर्ती है। उत्तर

(viii) मान लीजिए x = \(\frac{6}{15}=\frac{2}{5}\) ………….(1)
(1) की x = \(\frac{p}{q}\) के साथ से तुलना कीजिए।
यहाँ p = 2, q = 5
q के अभाज्य गुणनखंड हैं 5 = 2⁰ × 5¹
जोकि 2ⁿ × 5^m के रूप का है।
जहां n = 0, m = 1 और ये ऋणेतर पूर्णांक हैं।
∴ x = \(\frac{6}{15}\) का दशमलव प्रसार सांत है। उत्तर

(ix) मान लीजिए x = \(\frac{35}{50}=\frac{7}{10}\) ……………..(1)
(1) की x = \(\frac{p}{q}\) के साथ तुलना कीजिए।
यहाँ p = 7, q = 10
q के अभाज्य गुणनखंड हैं = 10 = 2 × 5 = 2¹ × 5¹
जहां 2ⁿ × 5^m के रूप का है,
जहाँ n = 1, m = 1 दोनों n और m ऋणेतर पूर्णांक हैं। .
∴ x = \(\frac{35}{50}\) का दशमलव प्रसार सांत है। उत्तर

(x) मान लीजिए x = \(\frac{77}{210}=\frac{11}{30}\)
(1) की. x = \(\frac{p}{q}\) के साथ तुलना कीजिए।
यहाँ p = 11, q = 30
q के अभाज्य गुणनखंड हैं = 30 = 2 × 3 × 5
जोकि 2ⁿ × 5^m के रूप में नहीं है।
∴ x = \(\frac{77}{210}\) का दशमलव प्रसार असांत आवर्ती है। उत्तर

प्रश्न 2.
ऊपर दिए गये प्रश्न में उन परिमेय संख्याओं के दशमलव प्रसारों को लिखिए जो सांत हैं।
हल :
(i) मान लीजिए x = \(\frac{13}{3125}\) ………….. (1)
(1) की x = \(\frac{p}{q}\) के साथ तुलना कीजिए
यहाँ p = 13, q = 3125
q के अभाज्य गुणनखंड = 3125 = 5 × 5 × 5 × 5 × 5
= 5⁵ × 2⁰
जोकि 2ⁿ × 5^m के रूप का है,
जहाँ n = 0, m = 5
∴ x = \(\frac{13}{3125}\) का दशमलव प्रसार सांत है। उत्तर

दशमलव के रूप में व्यक्त करना
x = \(\frac{13}{3125}=\frac{13}{5^{5} \times 2^{0}}\)

x = \(\frac{13 \times 2^{5}}{5^{5} \times 2^{5}}\)
[::: हम हर को 10 की कोई घात बनाने के लिए इसे 25 से गुणा और भाग करते हैं।] |

x = \(\frac{13 \times 32}{(2 \times 5)^{5}}\)

x = \(\frac{416}{(10)^{5}}=\frac{416}{100000}\)

x = 0.00416 उत्तर

(i) मान लीजिए x = \(\frac{17}{8}\)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए।
यहाँ p = 17, q = 8
q के अभाज्य गुणनखंड = 8 = 2 × 2 × 2
= 2³ × 5⁰
जोकि 2ⁿ × 5^m के रूप का है, जहाँ n = 3, m = 0 · और ये ऋणेतर पूर्णांक हैं।
∴ x = \(\frac{17}{8}\) को सांत दशमलव प्रसार के रूप में व्यक्त किया जा सकता है।

दशमलव के रूप में व्यक्त करना
x = \(\frac{17}{8}=\frac{17}{2^{3} \times 5^{0}}\)

x = \(\frac{17 \times 5^{3}}{2^{3} \times 5^{3}}\)
[हम हर को 10 की घात बनाने के लिए 53 से गुणा और भाग करते हैं।]

x = \(\frac{17 \times 125}{(2 \times 5)^{3}}\)

x = \(\frac{2125}{(10)^{3}}=\frac{2125}{1000}\)

x = 2.125
∴ \(\frac{17}{8}\) = 2.125 उत्तर .

(iii) मान लीजिए x = \(\frac{64}{455}\) ………….(1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए
यहाँ p = 64, q = 455
q के अभाज्य गुणनखंड = 455 = 5 × 7 × 13
जोकि 2ⁿ × 5^m के रूप में नहीं है
∴ x = \(\frac{64}{455}\) का दशमलव प्रसार असांत आवर्ती है। उत्तर

(iv) मान लीजिए x = \(\frac{15}{1600}\) …………(1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए।
यहाँ p = 15, q = 1600
q के अभाज्य गुणनखंड = 1600 = 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5
= 2⁶ × 5²
जोकि 2ⁿ × 5^m के रूप का है,
जहाँ n = 6, m = 2 और ये ऋणेतर पूर्णांक हैं
∴ x = \(\frac{15}{1600}\) का सांत दशमलव प्रसार है।

दशमलव के रूप में व्यक्त करना

(v) मान लीजिए x = \(\frac{29}{343}\) …………. (1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए
यहाँ p = 29 और q = 343 = 7 × 7 × 7 = 7³
जोकि 2ⁿ × 5^m के रूप में नहीं हैं।
∴ x = \(\frac{29}{343}\) का असांत आवर्ती दशमलव प्रसार होगा।

(vi) मान लीजिए x = \(\frac{23}{2^{3} 5^{2}}\) ………….. (1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए
यहाँ p = 23 और q = 2³5²
q के अभाज्य गुणनखंड = 2³5²
जोकि 2ⁿ × 5^m के रूप का है,
जहाँ n = 3 और m = 2 और ये ऋणेतर पूर्णांक हैं।
∴ x = \(\frac{23}{2^{3} 5^{2}}\) का सांत दशमलव प्रसार है।

दशमलव के रूप में व्यक्त करना

(vii) मान लीजिए x = \(\frac{129}{2^{2} 5^{7} 7^{5}}\) ……….. (1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए .
यहाँ p = 129 और 4 = 2² x 5⁷ x 7⁵
q के अभाज्य गुणनखंड = 2² x 5⁷ × 7⁵
जोकि 2ⁿ × 5^m के रूप में नहीं है।
∴ x = \(\frac{129}{2^{2} 5^{7} 7^{5}}\) का एक असांत आवर्ती दशमलव प्रसार है। उत्तर

(viii) मान लीजिए x = \(\frac{6}{15}=\frac{2}{5}\) ……………. (1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए ।
यहाँ p = 2, q = 5
q के अभाज्य गुणनखंड = 5 = 2⁰ × 5¹
जोकि 2ⁿ × 5^m के रूप का है,
जहाँ n = 0, m = 1 है।
∴ x = \(\frac{6}{15}[/layex] का एक सांत दशमलव प्रसार है।

दशमलव के रूप में व्यक्त करना
x = [latex]\frac{6}{15}=\frac{2}{5}\)

x = \(\frac{2 \times 2^{1}}{2^{1} \times 5^{1}}=\frac{4}{10}\) = 0.4

दशमलव के रूप में,
x = \(\frac{6}{15}\) = 0.4.

(x) मान लीजिए x = \(\frac{35}{50}=\frac{7}{10}\) ………….. (1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए।
यहाँ p = 7, q = 10
q के अभाज्य गुणनखंड = 10 = 2¹ × 5¹
जोकि 2ⁿ × 5^m के रूप का है,
जहाँ n = 1, m = 1
और n और m दोनों ऋणोतर पूर्णांक हैं।
∴ x = \(\frac{7}{10}\) का एक सांत दशमलव प्रसार है।

दशमलव के रूप में व्यक्त करना

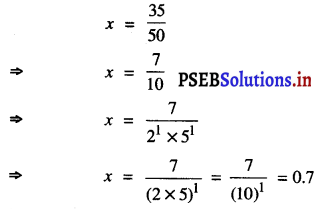
अत: दशमलव रूप में,
x = 0.7.

(x) मान लीजिए x = \(\frac{77}{210}=\frac{11}{30}\) ……………..(1)
(1) की x = \(\frac{p}{q}\) से तुलना कीजिए।
यहाँ p = 11, q = 30
q के अभाज्य गुणनखंड = 30 = 2 × 3 × 5
जोकि 2ⁿ × 5^m के रूप में नहीं है
∴ x = \(\frac{77}{210}\) का असांत आवर्ती दशमलव प्रसार है। उत्तर

प्रश्न 3.
कुछ वास्तविक संख्याओं के दशमलव प्रसार नीचे दर्शाए गये हैं। प्रत्येक स्थिति के लिए निर्धारित कीजिए कि यह संख्या परिमेय संख्या है या नहीं। यदि यह परिमेय संख्या है और \(\frac{p}{q}\) के.रूप की है, तो के अभाज्य गुणनखंडों के बारे में आप क्या कह सकते हैं ?
(i) 43.123456789
(ii) 0.120120012000120000
(iii) \(43 . \overline{123456789}\)
हल :
(i) मान लीजिए x = 43.123456789 ……………(1)
संख्या से स्पष्ट है कि x एक परिमेय संख्या है।
अब संख्या में से दशमलव को हटा दीजिए
∴ x = \(\frac{43123456789}{1000000000}\)

x = \(\frac{43123456789}{10^{9}}\) ……………….(2)

(2) से x \(\frac{p}{q}\) के रूप की एक परिमेय संख्या है
जब p = 43123456789 और q = 10⁹
अब q के अभाज्य गुणनखंड = 10⁹ = (2 × 5)⁹
⇒ q के अभाज्य गुणनखंड 2⁹ × 5⁹ हैं। उत्तर

(ii) मान लीजिए x = 0.120120012000120000
संख्या से स्पष्ट है कि यह एक अपरिमेय संख्या है।

(iii) मान लीजिए x = \(43 . \overline{123456789}\) …. (1)
यह स्पष्ट है कि दी गई संख्या एक परिमेय संख्या है क्योंकि यह असांत और आवर्ती दशमलव है।

यह दर्शाने के लिए कि (i) P के रूप का है
(1) के दोनों पक्षों को 10⁹ से गुणा कीजिए
10⁹ x = 43123456789.123456789… …. (2)
(1) को (2) से घटाने पर हम प्राप्त करते हैं :

अतः, q के अभाज्य गुणनखंड 32 (12345679) हैं।