PSEB 10th Class Maths Solutions Chapter 10 वृत्त Ex 10.2

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 10 वृत्त Ex 10.2 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 10 वृत्त Ex 10.2

प्रश्न सं. 1, 2, 3 में सही विकल्प चुनिए एवं उचित कारण दीजिए।

प्रश्न 1.
एक बिंदुए से एक वृत्त पर स्पर्श रेखा की लंबाई 24 cm तथा Q की केंद्र से दूरी 25 cm है। वृत्त की त्रिज्या है:
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
हल :
एक वृत्त जिसका केंद्र 0 है।
बाह्य बिंदु Q से स्पर्श रेखा PQ की लंबाई 24 cm तथा Q की केंद्र 0 से दूरी 25 cm है।

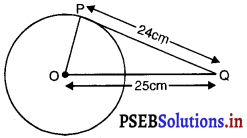
∴ ∠QPO = 90°
अब, समकोण ∆OPQ में,
OQ² = PQ² + OP²
(25)² = (24)² + OP²
या 625 = 576 + OP²
या OP² = 625 – 576
या OP² = 49 = (7)²
या OP = 7 cm
∴ विकल्प (A) सही है।

प्रश्न 2.
आकृति में, यदि TP, TQ केंद्र 0 वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠POQ = 110°, तो ∠PTQ बराबर है :
(A) 60°
(B) 70°
(C) 80°
(D) 90°.

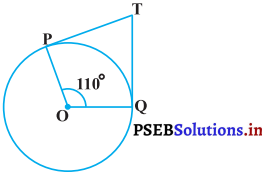
हल :
आकृति में OP त्रिज्या है और PT वृत्त पर स्पर्श रेखा है।
∠OPT = 90°
इसी तरह ∠OQT = 90° और ∠POQ = 110° (दिया है)
अब POQT एक चतुर्भुज है,
∴ ∠POQ + ∠OQT + ∠QTP + ∠TPO = 360°
110° + 90° + ∠QTP + 90° = 360°
∠QTP + 290° = 360°
या ∠QTP = 360° – 290°
या ∠QTP = 70°
∴ विकल्प (B) सही है।

प्रश्न 3.
यदि एक बिंदु P से 0 केंद्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर 80° के कोण पर झुकी हों, तो ZPOA बराबर है :
(A) 50°
(B) 60°
(C)70°
(D)80°
हल :
दी गई आकृति में OA त्रिज्या है और AP वृत्त पर स्पर्श रेखा है।

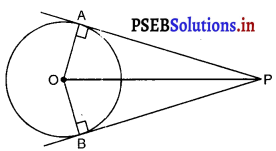
∴ ∠OAP = 90°
इसी प्रकार, ∠OBP = 90°
अब समकोण ∆PAO और ∆PBO में,
∠PAO = ∠PBO = 90°
OP = OP (उभयनिष्ठ भुजा)
OA = OB (एक ही वृत्त की त्रिज्याएँ)
∴ ∠PAO = ∆PBO [RHS सर्वांगसमता]
∴ ∠AOP = ∠BOP
∠AOP = ∠BOP = \(\frac{1}{2}\) ∠AOB ……………(1)
साथ ही, चतुर्भुज OAPB में,
∠OBP + ∠BPA + ∠PAO + ∠AOB = 360°
90° + 80° + 90° + ∠AOB = 360°
∠AOB = 360° – 260°
∠AOB = 100° …………..(2)
(1) और (2) से, हमें प्राप्त होता है
∠AOP = ∠BOP
= \(\frac{1}{2}\) × 100° = 50°
∴ विकल्प (A) सही है।

प्रश्न 4.
सिद्ध कीजिए किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समांतर होती हैं।
हल :
दिया है : एक वृत्त जिसका केंद्र 0 तथा व्यास AB है।
l और m बिंदु A और B पर स्पर्श रेखाएँ हैं।

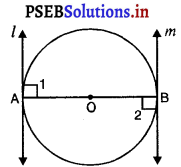
सिद्ध करना है : l || m
उपपत्ति ∴ OA त्रिज्या है और । वृत्त पर स्पर्श रेखा है।
∴ ∠1 = 90°
इसी प्रकार, ∠2 = 90°
अब, ∠1 = ∠2 = 90°
परंतु यह दो रेखाओं के एकांतर कोण हैं, जब एक तिर्यक रेखा उन्हें काटती है।
∴ l || m
अतः, किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ परस्पर समांतर होती हैं।

प्रश्न 5.
सिद्ध कीजिए कि स्पर्श बिंदु से स्पर्श रेखा पर खींचा गया लंब वृत्त के केंद्र से होकर जाता है।
हल :
दिया है : एक वृत्त जिसका केंद्र O है।
AB इसकी स्पर्श रेखा है जो वृत्त को P पर मिलती है।
अर्थात् बिंदु P वृत्त का स्पर्श बिंदु है

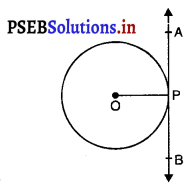
सिद्ध करना है : स्पर्श बिंदु से स्पर्श रेखा पर खींचा गया लंब वृत्त के केंद्र से होकर जाता है।
रचना : OP को मिलाइए।
उपपत्ति: क्योंकि OP वृत्त की त्रिज्या है और AB वृत्त पर स्पर्श रेखा है जिसमें बिंदु P स्पर्श बिंदु है।
∴ ∠OPA = ∠OPB = 90°
[∵ वृत्त के किसी बिंदु पर स्पर्श रेखा स्पर्श बिंदु से जाने वाली त्रिज्या पर लंब होती है।
या OP ⊥ AB
क्योंकि किसी वृत्त की त्रिज्या सदैव वृत्त के केंद्र से गुजरती है।
अतः, स्पर्श बिंदु से स्पर्श रेखा पर खींचा गया लंब वृत्त के केंद्र से होकर जाता है।

प्रश्न 6.
एक बिंदु A से, जो एक वृत्त के केंद्र से 5 cm दूरी पर है, वृत्त पर स्पर्श रेखा की लंबाई 4 cm है। वृत्त की त्रिज्या ज्ञात कीजिए।
हल :
एक वृत्त जिसका केंद्र ‘0’ है।
वृत्त के बाहर इसके केंद्र से 5 cm की दूरी पर कोई बिंदु A है।

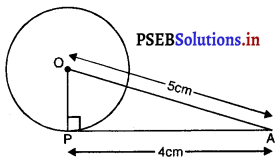
स्पर्श रेखा की लंबाई = PA = 4 cm
क्योंकि OP त्रिज्या है और PA वृत्त पर स्पर्श रेखा है।
∴ ∠OPA = 90°
अब, समकोण ∆OPA में, पाइथागोरस प्रमेय का प्रयोग करने पर
OA² = OP² + PA²
(5)² = OP² + (4)²
या OP² = 25 – 16
या OP² = 9 = (3)²
या OP = 3 cm.
अतः, वृत्त की त्रिज्या 3 cm है।

प्रश्न 7.
दो संकेंद्रीय वृत्तों की त्रिज्याएँ 5 cm तथा 3 cm हैं। बड़े वृत्त की उस जीवा की लंबाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती है।
हल :
दो संकेंद्रीय वृत्त जिनका एक ही केंद्र 0 तथा त्रिज्याएँ क्रमश: 5 cm और 3 cm हैं।
मान लीजिए PQ बड़े वृत्त की जीवा है परंतु छोटे वृत्त की स्पर्श रेखा है।

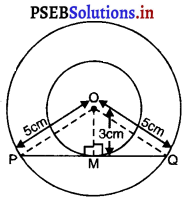
क्योंकि, OM छोटे वृत्त की त्रिज्या है और PMQ स्पर्श रेखा है।
∴ ∠OMP = ∠OMQ = 90°
समकोण त्रिभुजें OMP और OMQ लीजिए।
∠OMP = ∠OMQ = 90°
OP = OQ (एक ही वृत्त की त्रिज्याएँ]
OM = OM [उभयनिष्ठ भुजा]
∴ ∆OMP = OMQ [RHS सर्वांगसमता]
∴ PM = MQ [CPCT]
या PQ = 2 PM = 2 MQ
अब समकोण, ∆ OMQ में, पाइथागोरस प्रमेय से,
OQ² = OM² + MO²
(5)² = (3)² + (MQ)²
या MQ² = 25 – 9
या MQ² = 16 = (4)²
या MQ = 4 cm
∴ जीवा PQ की लंबाई = 2 MQ
= 2 (4) cm
= 8 cm
अतः, अभीष्ट जीवा की लंबाई 8 cm है।

प्रश्न 8.
एक वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है (देखिए आकृति)
सिद्ध कीजिए : AB + CD = AD + BC.

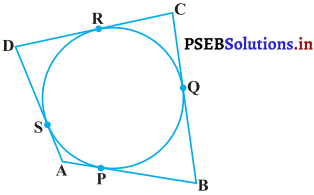
हल:
दिया है : वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है।
सिद्ध करना है : AB + CD = AD + BC
उपपत्ति : क्योंकि किसी बाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाओं की लंबाई बराबर होती है।
अब, B वृत्त के बाहर स्थित कोई बिंदु है और BP; BQ वृत्त पर स्पर्श रेखाएँ हैं।
∴ BP = BQ …………(1)
इसी प्रकार,
AP = AS …………….(2)
और CR = CQ …………..(3)
साथ ही, DR = DS …………..(4)
(1), (2), (3) और (4) को जोड़ने पर, हमें प्राप्त होता
(BP + AP) + (CR + DR) = (BQ + CQ) + (AR + DR)
AB + CD = BC + AD
अभीष्ट परिणाम है।

प्रश्न 9.
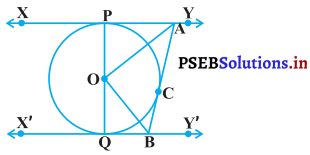
आकृति में , XY तथा X’Y’ केंद्र 0 वाले किसी AB वृत्त पर दो समांतर स्पर्श रेखाएं हैं और स्पर्श बिंदु C पर स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर प्रतिच्छेद करती है। सिद्ध कीजिए कि ∠AOB = 90° है।

हल :
दिया है : XY तथा X’Y’ केंद्र 0 वाले वृत्त पर दो समांतर स्पर्श रेखाएँ हैं और स्पर्श बिंदु C पर एक अन्य स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर प्रतिच्छेद करती है।
सिद्ध करना है : ∠AOB = 90°
रचना : OC, OA और OB को मिलाइए
उपपत्ति : क्योंकि बाह्य बिंदु से किसी वृत्त पर खींची गई दोनों स्पर्श रेखाओं की लंबाइयाँ समान होती हैं।
अब, A वृत्त के बाहर कोई बिंदु है जिसमें से दो स्पर्श रेखाएँ PA और AC वृत्त पर खींची गई हैं।
∴ PA = AC
साथ ही, ∆ POA और ∆ AOC में,
PA = AC (प्रमाणित)
OA = OA (उभयनिष्ठ भुजा)
OP = OC (एक ही वृत्त की त्रिज्याएँ)
∴ ∆POA = ∆AOC [SSS सर्वांगसमता]
और ∠PAO = ∠CAO [CPCT]
या ∠PAC = 2 ∠PAO = 2 ∠CAO ……….(1)
इसी प्रकार
∠QBC = 2 ∠OBC = 2 ∠OBQ ………….(2)
अब, ∠PAC + ∠QBC = 180°
[∵ किसी तिर्यक रेखा के एक ही ओर के अंत: कोणों का योगफल 180° होता है।
या 2 ∠CAO + 2 ∠OBC = 180°
[(1) और (2) का प्रयोग करने पर]
या ∠CAO + ∠OBC = \(\frac{180^{\circ}}{2}\) = 90° ………….(3)
अब, ∆OAB में,
∠CAO + ∠OBC + ∠AOB = 180°
90° + ∠AOB = 180°
[(3) का प्रयोग करने पर]
या ∠AOB = 180° – 90° = 90°
अतः, ∠AOB = 90°

प्रश्न 10.
सिद्ध कीजिए कि किसी बाह्य बिंदु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिंदुओं को मिलाने वाले रेखाखंड द्वारा केंद्र पर अंतरित कोण का संपूरक होता है।
हल :
दिया है : एक वृत्त जिसका केंद्र 0 है। P वृत्त के बाहर स्थित किसी बिंदु P से PQ और PR दिए गए वृत्त पर स्पर्श रेखाएँ हैं।

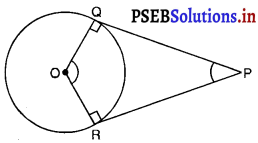
सिद्ध करना है : ∠ROQ + ∠QPR = 180°
उपपत्ति : 0Q त्रिज्या है और PQ बिंदु P से दिए गए वृत्त पर स्पर्श रेखा है।
∠OQP = 90° ………….(1)
[:: वृत्त के किसी बिंदु पर स्पर्श रेखा स्पर्श बिंदु से जाने वाली त्रिज्या पर लंब होती है।]
इसी प्रकार ∠ORP = 90° ……………(2)
अब, चतुर्भुज ROQP में,
∠ROQ + ∠PRO + ∠OQP + ∠QPR = 360°
या ∠ROQ + 90° + 90° + ∠QPR = 360°
[(1) और (2) का प्रयोग करने पर]
या ∠ROQ + ∠QPR + 180° = 360°
या ∠ROQ + ∠QPR = 360° – 180°
या ∠ROQ + ∠QPR = 180°
अतः, किसी बाह्य बिंदु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिंदुओं को मिलाने वाले रेखाखंड द्वारा केंद्र पर अंतरित कोण का संपूरक होता है।

प्रश्न 11.
सिद्ध कीजिए कि किसी वृत्त के परिगत समांतर चतुर्भुज समचतुर्भुज होता है।
हल :
दिया है : एक समांतर चतुर्भुज ABCD केंद्र 0 वाले वृत्त के परिगत है।

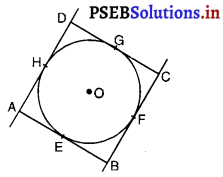
सिद्ध करना है : ABCD एक समचतुर्भुज है।
उपपत्ति : क्योंकि बाह्य बिंदु से किसी वृत्त पर खींची गई दोनों स्पर्श रेखाओं की लंबाइयाँ समान होती हैं।
अब, वृत्त के बाहर स्थित किसी बिंदु B से BE और BF वृत्त पर दो स्पर्श रेखाएँ हैं।
BE = BF …………(1)
इसी प्रकार
AE = AH ………….(2)
और CG = CF ………..(3)
साथ ही, DG = DH ………….(4)
(1), (2), (3) और (4) को जोड़ने पर हमें प्राप्त होता है
(BE + AE) + (CG + DG) = (BF + CF) + (AH + DH)
या AB + CD = BC + AD ……………(5)
अब, ABCD एक सामांतर चतुर्भुज है।
∴ AB = CD और BC = AD ………….(6)
(5) और (6) से हमें प्राप्त होता है।
AB + AB = BC + BC
या 2AB = 2BC
या AB = BC
अब, AB = BC = CD = AD
∴ ABCD समचतुर्भुज है।
अतः किसी वृत्त के परिगत समांतर चतुर्भुज समचतुर्भुज होता है।

प्रश्न 12.
4 cm त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींची गया है कि रेखाखण्ड BD और DC (जिनमें स्पर्श बिंदु D द्वारा BC विभाजित है) की लंबाइयाँ क्रमशः 8 cm और 6 cm हैं ( देखिए आकृति)। भुजाएं AB और AC ज्ञात कीजिए।

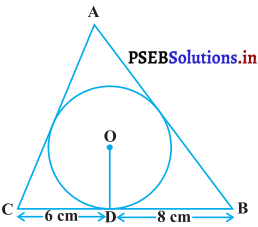
हल :
4 cm त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC खींचा गया है।
त्रिभुज की भुजाएं BC, CA, AB वृत्त को क्रमशः बिंदुओं D, E तथा F पर स्पर्श करती हैं।
क्योंकि किसी बाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाओं की लंबाइयाँ बराबर होती हैं।
∴ AE = AF = x cm (माना)
CE = CD = 6 cm
और BF = BD = 8 cm
क्योंकि वृत्त की स्पर्श रेखा स्पर्श बिंदु से जाने वाली त्रिज्या पर लंब होती है।

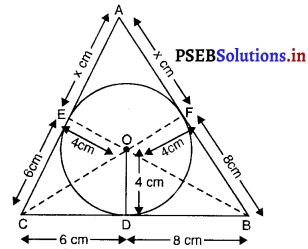
∴ OD ⊥ BC ; OE ⊥ AC और OF ⊥ AB.
साथ ही, OE = OD = OF = 4 cm.

उपपत्ति: क्योंकि बाह्य बिंदु से किसी वृत्त पर खींची गई दो स्पर्श रेखाएं केंद्र पर समान कोण अंतरित करती हैं।
∴ ∠2 = ∠3; ∠4 = ∠5 ; ∠6 = ∠7; ∠8 = ∠1 ………….(1)
क्योंकि एक बिंदु पर सभी कोणों का जोड़ 360° होता है। .
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
या ∠1 + ∠2 + ∠2 + ∠5 + ∠5 + ∠6 + ∠6 + ∠1 = 360°
या 2 (∠1 + ∠2 + ∠5 + ∠6) = 360°
या (∠1 + ∠2) + (∠5 + ∠6) = \(\frac{360^{\circ}}{2}\) = 180°
∠POQ +∠SOR = 180°
इसी प्रकार, ∠SOP + ∠ROQ = 180°
अतः वृत्त के परिगत बनी चतुर्भुज की आमने-सामने की भुजाएं केंद्र पर संपूरक कोण अंतरित करती हैं।