PSEB 10th Class Maths Solutions Chapter 10 ਚੱਕਰ Ex 10.2

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 10 ਚੱਕਰ Ex 10.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 10 ਚੱਕਰ Exercise 10.2

ਪ੍ਰਸ਼ਨ ਨੰ : 1, 2, 3 ਵਿੱਚੋਂ ਸਹੀ ਵਿਕਲਪ ਚੁਣੋ ਅਤੇ ਉੱਚਿਤ ਕਾਰਣ ਦਿਓ।

ਪ੍ਰਸ਼ਨ 1.
ਇੱਕ ਬਿੰਦੂ Q ਤੋਂ ਇੱਕ ਚੱਕਰ ‘ਤੇ ਸਪਰਸ਼ ਰੇਖਾ ਦੀ ਲੰਬਾਈ 24 cm ਅਤੇ 9 ਦੀ ਕੇਂਦਰ ਤੋਂ ਦੂਰੀ 25 cm ਹੈ । ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਹੈ :
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
ਹੱਲ:
ਇੱਕ ਚੱਕਰ ਜਿਸਦਾ ਕੇਂਦਰ ਹੈ । ਬਾਹਰੀ ਬਿੰਦੂ Q ਤੋਂ ਸਪਸ਼ ਰੇਖਾ PQ ਦੀ ਲੰਬਾਈ 24 cm ਅਤੇ Q ਦੀ ਕੇਂਦਰ O ਤੋਂ ਦੂਰੀ 25 cm ਹੈ ।

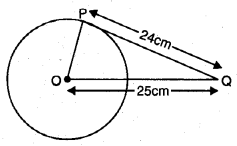
∵ ∠QPO = 90°
ਹੁਣ, ਸਮਕੋਣ △OPQ ਵਿਚ
OQ² = PQ² + Op²
(25)² = (24)² + OP²
625 = 576 + OP²
OP² = 625 – 576
OP² = 49 = (7)²
OP = 7 cm
∴ ਵਿਕਲਪ (A) ਸਹੀ ਹੈ। ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 2.
ਚਿੱਤਰ ਵਿਚ, ਜੇਕਰ TP, TQ ਕੇਂਦਰ O ਵਾਲੇ ਕਿਸੇ ਚੱਕਰ `ਤੇ ਦੋ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਇਸ ਤਰ੍ਹਾਂ ਹਨ ਕਿ ∠POQ = 110°, ਤਾਂ ∠PTQ ਬਰਾਬਰ ਹੈ : (A) 6o°
(B) 70°
(C) 80°
(D) 90°

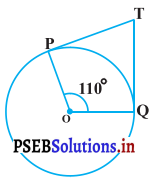
ਹੱਲ:
ਚਿੱਤਰ ਵਿੱਚ OP ਅਰਧ ਵਿਆਸ ਹੈ ਅਤੇ PT ਚੱਕਰ ‘ਤੇ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ
∴ ∠OPT = 90°
ਇਸੇ ਤਰ੍ਹਾਂ ∠OQT = 90°
ਅਤੇ ∠POQ = 110° ਦਿੱਤਾ ਹੈ
ਹੁਣ, POQT ਇੱਕ ਚਤੁਰਭੁਜ ਹੈ
∴ ∠POQ + ∠OQT + ∠QTP + ∠TPO = 360°
110° + 90° + ∠QTP + 90° = 360°
∠QTP + 290° = 360°
∠QTP = 360° – 290°
ਜਾਂ ∠QTP = 70°
∴ ਵਿਕਲਪ (B) ਸਹੀ ਹੈ।

ਪ੍ਰਸ਼ਨ 3.
ਜੇਕਰ ਇਕ ਬਿੰਦੂ P ਤੋਂ O ਕੇਂਦਰ ਵਾਲੇ ਕਿਸੇ ਚੱਕਰ ‘ਤੇ PA, PB ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਆਪਸ ਵਿੱਚ 80° ਦੇ ਕੋਣ ‘ਤੇ ਝੁਕੀਆਂ ਹੋਣ ਤਾਂ ∠POA ਬਰਾਬਰ ਹੈ :
(A) 50°
(B) 60°
(C) 70°
(D) 80°
ਹੱਲ:
ਦਿੱਤੇ ਹੋਏ ਚਿੱਤਰ ਵਿਚ OA ਅਰਧ ਵਿਆਸ ਹੈ ਅਤੇ AP ਚੱਕਰ ਦੀ ਸਪੱਰਸ਼ ਰੇਖਾ ਹੈ :
∴ ∠OAP = 90°

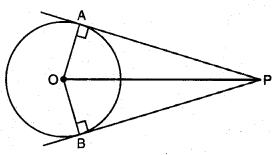
ਇਸੇ ਤਰ੍ਹਾਂ ∠OBP = 90°
ਹੁਣ, ਸਮਕੋਣ △PAO ਅਤੇ △PBO ਵਿੱਚ
∠PAO = ∠PBO = 90°
OP = OP (ਸਾਂਝੀ ਭੂਜਾ)
OA = OB (ਇੱਕ ਹੀ ਚੱਕਰ ਦੇ ਅਰਧ ਵਿਆਸ)
∴ ∠PAO ≅ △PBO
[RHS ਸਰਬੰਗਸਮਤਾ ਦੁਆਰਾ]
∴ ∠AOP = ∠BOP (CPCT)
ਜਾਂ ∠AOP = ∠BOP = \(\frac{1}{2}\)∠AOB …(1)
ਚਤੁਰਭੁਜ OAPB ਵਿਚ
∠OBP + ∠BPA + ∠PAO + ∠AOB = 360°
90° + 80° + 90° + ∠AOB = 360°
∠AOB = 360° – 260°
∠AOB = 100° …(2)
(1) ਅਤੇ (2) ਤੋਂ
∠AOP = ∠BOP = \(\frac{1}{2}\) × 100° = 50°
∴ ਵਿਕਲਪ (A) ਸਹੀ ਹੈ। ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 4.
ਸਿੱਧ ਕਰੋ ਕਿ ਕਿਸੇ ਚੱਕਰ ਦੇ ਕਿਸੇ ਵਿਆਸ ਦੇ ਸਿਰਿਆਂ ‘ਤੇ ਖਿੱਚੀਆਂ ਗਈਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਸਮਾਂਤਰ ਹੁੰਦੀਆਂ ਹਨ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਇਕ ਚੱਕਰ ਜਿਸਦਾ ਕੇਂਦਰ ਹੈ O ਅਤੇ ਵਿਆਸ AB ਹੈ ਅਤੇ m ਬਿੰਦੂਆਂ A ਅਤੇ B ‘ਤੇ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ।

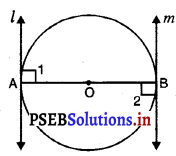
ਸਿੱਧ ਕਰਨਾ : l || m
ਸਬੂਤ : ∴ OA ਇੱਕ ਅਰਧ ਵਿਆਸ ਹੈ ਅਤੇ l ਇੱਕ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ।
∴ ∠1 = 90°
∠2 = 90°
ਹੁਣ, ∠1 = ∠2 = 90°
ਪਰ ਇਹ ਦੋ ਰੇਖਾਵਾਂ ਦੇ ਇਕਾਂਤਰ ਕੋਣ ਹਨ । ਜਦੋਂ ਇੱਕ ਕਾਟਵੀਂ ਰੇਖਾ ਇਨ੍ਹਾਂ ਨੂੰ ਕੱਟਦੀ ਹੈ ।
∴ l || m
ਕਿਸੇ ਵਿਆਸ ਦੇ ਸਿਰਿਆਂ ਤੇ ਖਿੱਚੀਆਂ ਗਈ ਸਪੱਰਸ਼ ਰੇਖਾਵਾਂ ਪਰਸਪਰ ਸਮਾਂਤਰ ਹੁੰਦੀਆਂ ਹਨ।

ਪ੍ਰਸ਼ਨ 5.
ਸਿੱਧ ਕਰੋ ਕਿ ਸਪਰਸ਼ ਬਿੰਦੂ ਤੋਂ ਸਪੱਰਸ਼ ਰੇਖਾ ‘ਤੇ ਖਿੱਚਿਆ ਗਿਆ ਲੰਬ ਚੱਕਰ ਦੇ ਕੇਂਦਰ ਤੋਂ ਹੋ ਕੇ ਜਾਂਦਾ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਇੱਕ ਚੱਕਰ ਜਿਸਦਾ ਕੇਂਦਰ O ਹੈ । AB ਇਸਦੀ ਇੱਕ ਸਪਰਸ਼ ਰੇਖਾ ਹੈਂ ਜੋ ਚੱਕਰ ਨੂੰ P ਉੱਤੇ ਮਿਲਦੀ ਹੈ ।
ਭਾਵ ਬਿੰਦੁ P ਚੱਕਰ ਦਾ ਸਪਰਸ਼ ਬਿੰਦੁ ਹੈ ।

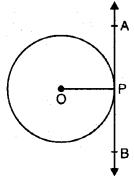
ਸਿੱਧ ਕਰਨਾ : ਸਪਰਸ਼ ਬਿੰਦੂ ਤੋਂ ਸਪਰਸ਼ ਰੇਖਾ ‘ਤੇ ਖਿੱਚਿਆ ਗਿਆ ਲੰਬ ਚੱਕਰ ਦੇ ਕੇਂਦਰ ਤੋਂ ਹੋ ਕੇ ਜਾਂਦਾ ਹੈ ।
ਰਚਨਾ : OP ਨੂੰ ਮਿਲਾਓ ।
ਸਬੂਤ : ਕਿਉਂਕਿ OP ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਹੈ ਅਤੇ AB ਚੱਕਰ ਉੱਤੇ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ਜਿਸ ਵਿੱਚ ਬਿੰਦੁ P ਸਪਰਸ਼ ਬਿੰਦੂ ਹੈ।
∴ ∠OPA = ∠OPB = 90°
[∵ ਚੱਕਰ ਦੇ ਕਿਸੇ ਬਿੰਦੂ ‘ਤੇ ਸਪਰਸ਼ ਰੇਖਾ ਸਪਰਸ਼ ਬਿੰਦੂ ਤੋਂ ਜਾਣ ਵਾਲੇ ਅਰਧ ਵਿਆਸ ਉੱਤੇ ਲੰਬ ਹੁੰਦੀ ਹੈ ॥]
ਜਾਂ OP ⊥ AB
ਕਿਉਂਕਿ ਕਿਸੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਹਮੇਸ਼ਾਂ ਚੱਕਰ ਦੇ ਕੇਂਦਰ ਵਿਚੋਂ ਲੰਘਦਾ ਹੈ ।
ਇਸ ਲਈ ਸਪਰਸ਼ ਬਿੰਦੂ ਤੋਂ ਸਪਸ਼ ਰੇਖਾ ਤੇ ਖਿੱਚਿਆ ਗਿਆ ਲੰਬ ਚੱਕਰ ਦੇ ਕੇਂਦਰ ਵਿਚੋਂ ਹੋ ਕੇ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਇੱਕ ਬਿੰਦੂ A ਤੋਂ, ਜੋ ਇੱਕ ਚੱਕਰ ਦੇ ਕੇਂਦਰ ਤੋਂ 5 cm | ਦੀ ਦੂਰੀ ‘ਤੇ ਹੈ, ਚੱਕਰ ‘ ਤੇ ਸਪਰਸ਼ ਰੇਖਾ ਦੀ ਲੰਬਾਈ 4cm ਹੈ । ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਚੱਕਰ ਦਾ ਕੇਂਦਰ ‘O’ ਹੈ । ਚੱਕਰ ਦੇ ਬਾਹਰ 5 cm ਦੀ ਦੂਰੀ ‘ਤੇ ਇੱਕ ਬਿੰਦੂ A ਹੈ ।

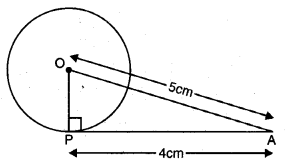
ਸਪਰਸ਼ ਰੇਖਾ ਦੀ ਲੰਬਾਈ = PA = 4 cm
ਕਿਉਂਕਿ OP ਇੱਕ ਅਰਧ ਵਿਆਸ ਹੈ ਅਤੇ PA ਚੱਕਰ | ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ
∴ ∠OPA = 90°
ਸਮਕੋਣ △OPA ਵਿੱਚ ਪਾਈਥਾਗੋਰਸ ਥਿਊਰਮ ਤੋਂ
OA² = OP² + PA²
(5)² = OP² + (4)²
OP² = 25 – 16
OP² = 9 = (3)²
OP = 3 cm.
∴ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ 3 cm ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਦੋ ਸਮਕੇਂਦਰੀ ਚੱਕਰਾਂ ਦੇ ਅਰਧ ਵਿਆਸ 5 cm ਤੇ 3 cm ਹਨ। ਵੱਡੇ ਚੱਕਰ ਦੀ ਉਸ ਜੀਵਾ ਦੀ ਲੰਬਾਈ ਪਤਾ ਕਰੋ ਜੋ ਛੋਟੇ ਚੱਕਰ ਨੂੰ ਸਪਰਸ਼ ਕਰਦੀ ਹੈ ।
ਹੱਲ:
ਦੋ ਸਮਕੇਂਦਰੀ ਚੱਕਰ ਜਿਨ੍ਹਾਂ ਦਾ ਕੇਂਦਰ O ਹੈ ਅਤੇ ਅਰਧ ਵਿਆਸ ਕ੍ਰਮਵਾਰ 5 cm ਅਤੇ 3 cm ਹਨ ।
ਮੰਨ ਲਉ PQ ਵੱਡੇ ਚੱਕਰ ਦੀ ਜੀਵਾ ਹੈ ਪਰ ਛੋਟੇ ਚੱਕਰ ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ।

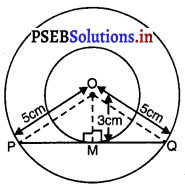
ਕਿਉਂਕਿ OM ਛੋਟੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਹੈ ਅਤੇ PMQ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ।
∴ ∠OMP = ∠OMQ = 90°
ਸਮਕੋਣ ਤ੍ਰਿਭੁਜਾਂ OMP ਅਤੇ OMQ ਵਿੱਚ,
∠OMP = ∠OMQ = 90°
OP = OQ [ਇੱਕ ਹੀ ਚੱਕਰ ਦੇ ਅਰਧ ਵਿਆਸ ਸਾਂਝੀ ਭੁਜਾ]
OM = OM
∴ △OMP ≅ OMO [RHS ਸਰਬੰਸਮਤਾ ਦੁਆਰਾ]
∴ PM = MQ
PQ = 2 PM = 2 MQ
ਹੁਣ, ਸਮਕੋਣ △ OMQ ਵਿਚ ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ
OQ² = OM² + MQsup>2
(5)² = (3)² + (MQ)²
MQ² = 25 – 9
MQ² = 16 = (4)²
MQ = 4 cm
∴ ਜੀਵਾਂ ਦੀ ਲੰਬਾਈ PQ = 2 MQ
= 2 (4) cm
= 8 cm
ਲੋੜੀਂਦੀ ਜੀਵਾਂ ਦੀ ਲੰਬਾਈ 8 cm ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਇੱਕ ਚੱਕਰ ਨੂੰ ਬਾਹਰਲੇ ਪਾਸੇ ਤੋਂ ਛੂੰਹਦਾ ਚਤੁਰਭੁਜ ABCD ਖਿੱਚਿਆ ਗਿਆ ਹੈ (ਦੇਖੋ ਚਿੱਤਰ) । ਸਿੱਧ ਕਰੋ ਕਿ :
AB + CD = AD + BC.

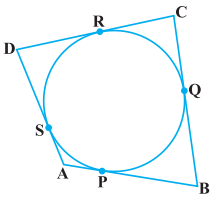
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਚੱਕਰ ਨੂੰ ਬਾਹਰਲੇ ਪਾਸੇ ਤੋਂ ਛੁੰਹਦਾ ਚਤੁਰਭੁਜ ABCD ਖਿੱਚਿਆ ਗਿਆ ਹੈ।
ਸਿੱਧ ਕਰਨਾ : AB + CD = AD + BC
ਸਬੂਤ : ਕਿਉਂਕਿ ਕਿਸੇ ਬਾਹਰੀ ਬਿੰਦੂ ਤੋਂ ਚੱਕਰ ਤੇ ਖਿੱਚੀਆਂ ਗਈਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਦੀ ਲੰਬਾਈ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ ।
ਹੁਣ, B ਚੱਕਰ ਦੇ ਬਾਹਰ ਸਥਿਤ ਕੋਈ ਬਿੰਦੂ ਹੈ ਅਤੇ | BP ; BQ ਚੱਕਰ ‘ਤੇ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ।
∴ BP = BQ ….(1)
ਇਸੇ ਤਰ੍ਹਾਂ AP = AS …(2)
CR = CQ …(3)
DR = DS ….(4)
(1), (2), (3), (4) ਨੂੰ ਜੋੜਣ ‘ਤੇ
(BP + AP) +(CR + DR) = (BQ + CQ) + (AS + DS)
AB + CD = BC+ AD ਲੋੜੀਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਚਿੱਤਰ ਵਿੱਚ, XY ਅਤੇ X’Y’, O ਕੇਂਦਰ ਵਾਲੇ ਕਿਸੇ ਚੱਕਰ ‘ਤੇ ਦੋ ਸਮਾਂਤਰ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ਅਤੇ ਸਪਰਸ਼ ਬਿੰਦੂ C ’ਤੇ ਸਪਰਸ਼ ਰੇਖਾ AB, XY ਨੂੰ A ਅਤੇ X’Y’, ਨੂੰ B ’ਤੇ ਕੱਟਦੀ ਹੈ । ਸਿੱਧ ਕਰੋ ∠AOB = 90° ਹੈ ।

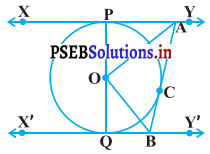
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : XY ਅਤੇ X’Y’ ਕੇਂਦਰ O ਵਾਲੇ ਚੱਕਰ ਉੱਤੇ ਦੋ ਸਮਾਂਤਰ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ਅਤੇ ਸਪਰਸ਼ ਬਿੰਦੁ cਉੱਤੇ ਇੱਕ ਹੋਰ ਸਪਰਸ਼ ਰੇਖਾ AB, XY ਨੂੰ A ਅਤੇ X’Y’ ਨੂੰ B ਉੱਤੇ ਕੱਟਦੀ ਹੈ ।
ਸਿੱਧ ਕਰਨਾ : ∠AOB = 90°
ਰਚਨਾ : OC, OA ਅਤੇ OB ਨੂੰ ਮਿਲਾਉ ।
ਸਬੂਤ : ਕਿਉਂਕਿ ਬਾਹਰੀ ਬਿੰਦੂ ਤੋਂ ਕਿਸੇ ਚੱਕਰ ਉੱਤੇ ਖਿੱਚੀਆਂ ਗਈਆਂ ਸਪੱਰਸ਼ ਰੇਖਾਵਾਂ ਦੀਆਂ ਲੰਬਾਈਆਂ ਬਰਾਬਰ ਹੁੰਦੀਆਂ ਹਨ ।
ਹੁਣ, A ਚੱਕਰ ਦੇ ਬਾਹਰ ਕੋਈ ਬਿੰਦੂ ਹੈ ਜਿਸ ਦੀਆਂ ਦੋ ਸਪੱਰਸ਼ ਰੇਖਾਵਾਂ PA ਅਤੇ PC ਹਨ ।
∴ PA = PC
ਨਾਲ ਹੀ, △POA ਅਤੇ △ AOC ਵਿਚ
PA = PC (ਸਿੱਧ ਕੀਤਾ)
OA = OA (ਸਾਂਝੀ ਭੁਜਾ)
OP = OC (ਇੱਕ ਹੀ ਚੱਕਰ ਦੇ ਅਰਧ ਵਿਆਸ)
∴ △POA ≅ △AOC [SSS]
∠PAO = ∠CAO [CPCT]
∠PAC = 2∠PAO = 2∠CAO …(1)
ਇਸੇ ਤਰ੍ਹਾਂ ∠QBC = 2∠OBC = 2∠OBQ …(2)
ਹੁਣ, ∠PAC + ∠QBC = 180° [∵ ਕਾਟਵੀਂ ਰੇਖਾ ਦੇ ਇੱਕੋ ਪਾਸੇ ਬਣੇ ਕੋਣਾਂ ਦਾ ਜੋੜ 180° ਹੁੰਦਾ ਹੈ |]
2∠CAO + 2∠OBC = 180° [(1) ਅਤੇ (2) ਤੋਂ।]
∠CAO + ∠OBC = \(\frac{180^{\circ}}{2}\) = 90° …(3)
ਹੁਣ, △OAB ਵਿਚ
∠CAO + ∠OBC + ∠AOB = 180°
90° + ∠AOB = 180° [(3) ਤੋਂ]
∠AOB = 180° – 90° = 90°
∴ ∠AOB = 90°

ਪ੍ਰਸ਼ਨ 10.
ਸਿੱਧ ਕਰੋ ਕਿ ਕਿਸੇ ਬਾਹਰੀ ਬਿੰਦੂ ਤੋਂ ਕਿਸੇ ਚੱਕਰ ਤੇ ਖਿੱਚੀਆਂ ਗਈਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਦਾ ਵਿਚਕਾਰਲਾ ਕੋਣ ਸਪਰਸ਼ ਬਿੰਦੂਆਂ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਦੁਆਰਾ ਕੇਂਦਰ ਤੇ ਬਣੇ ਕੋਣ ਦਾ ਸੰਪੂਰਕ ਹੁੰਦਾ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਇੱਕ ਚੱਕਰ ਜਿਸਦਾ ਕੇਂਦਰ ) ਹੈ । ਦੇ ਚੱਕਰ ਦੇ ਬਾਹਰ ਸਥਿਤ ਕਿਸੇ ਬਿੰਦੂ P ਤੋਂ PQ ਅਤੇ PR ਦਿੱਤੇ ਗਏ ਚੱਕਰ ਦੀਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ।

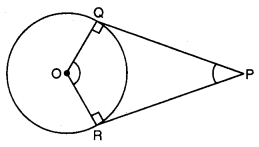
ਸਿੱਧ ਕਰਨਾ : ∠ROQ + ∠QPR = 180°
ਸਬੂਤ : OQ ਇਕ ਅਰਧ ਵਿਆਸ ਹੈ ਅਤੇ PQ ਬਿੰਦੂ P ਤੋਂ ਦਿੱਤੇ ਗਏ ਚੱਕਰ ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ।
∴ ∠OQP = 90° …(1)
[∵ ਚੱਕਰ ਦੇ ਕਿਸੇ ਬਿੰਦੂ ‘ਤੇ ਸਪਰਸ਼ ਰੇਖਾ, ਸਪਰਸ਼ ਚੌਦੂ ਵਿਚੋਂ ਲੰਘਣ ਵਾਲੇ ਅਰਧ ਵਿਆਸ ‘ਤੇ ਲੰਬ ਹੁੰਦੀ ਹੈ ॥]
ਇਸੇ ਤਰ੍ਹਾਂ ∠ORP = 90° ….(2)
ਚਤੁਰਭੁਜ ROQP ਵਿੱਚ
∠ROQ + ∠PRO + ∠OQP + ∠QPR = 360°
∠ROQ + 90° + 90° + ∠QPR = 360° [(1) ਅਤੇ (2) ਤੋਂ।]
ROQ + ∠QPR + 180° = 360°
∠ROQ + ∠QPR = 360° -180°
∠ROQ + ∠QPR = 180°
ਕਿਸੇ ਬਾਹਰੀ ਬਿੰਦੂ ਤੋਂ ਕਿਸੇ ਚੱਕਰ ‘ਤੇ ਖਿੱਚੀਆਂ ਗਈਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਦਾ ਵਿਚਕਾਰਲਾ ਕੋਣ ਸਪਰਸ਼ ਬਿੰਦੂਆਂ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਦੁਆਰਾ ਕੇਂਦਰ ‘ਤੇ ਬਣੇ ਅੰਦਰਲੇ ਕੋਣ ਦਾ ਸੰਪੂਰਕ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
ਸਿੱਧ ਕਰੋ ਕਿ ਕਿਸੇ ਚੱਕਰ ਦੇ ਬਾਹਰਲੇ ਪਾਸੇ ਛੂਹਦਾ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ, ਸਮਚਤੁਰਭੁਜ ਹੁੰਦਾ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਕੇਂਦਰ O ਵਾਲੇ ਚੱਕਰ ਦੇ ਬਾਹਰ ਹੈ ।

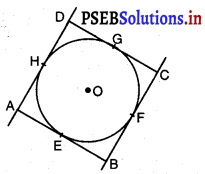
ਸਿੱਧ ਕਰਨਾ : ABCD ਇਕ ਸਮਚਤੁਰਭੁਜ ਹੈ
ਸਬੂਤ : ਕਿਉਂਕਿ ਬਾਹਰੀ ਬਿੰਦੂ ਤੋਂ ਕਿਸੇ ਚੱਕਰ ਉੱਤੇ ਖਿੱਚੀਆਂ ਗਈਆਂ ਦੋਵੇਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਦੀਆਂ ਲੰਬਾਈਆਂ ਸਮਾਨ ਹੁੰਦੀਆਂ ਹਨ।
ਹੁਣ, ਚੱਕਰ ਦੇ ਬਾਹਰ ਸਥਿਤ ਕਿਸੇ ਬਿੰਦੂ B ਤੋਂ BE ਅਤੇ BF ਚੱਕਰ ਉੱਤੇ ਦੋ ਸਪੱਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ।
∴ BE = BF ….(1)
ਇਸੇ ਤਰ੍ਹਾਂ AE = AH …(2)
CG = CF ….(3)
DG = DH ….(4)
(1), (2), (3), (4) ਨੂੰ ਜੋੜਣ ‘ਤੇ
(BE + AE) + (CG + DG) = (BF + CF) + (AH + DH)
AB + CD = BC + AD …(5)
ਹੁਣ, ABCD ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ।
∴ AB = CD ਅਤੇ BC= AD …(6)
(5) ਅਤੇ (6) ਤੋਂ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ
AB + AB = BC + BC
2AB = 2BC
AB = BC
ਹੁਣ, AB = BC = CD = AD
∴ ABCD ਇੱਕ ਸਮਚਤੁਰਭੁਜ ਹੈ ।
∴ ਕਿਸੇ ਚੱਕਰ ਦੇ ਬਾਹਰਲੇ ਪਾਸੇ ਛੂੰਹਦਾ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਸਮਚਤੁਰਭੁਜ ਹੁੰਦਾ ਹੈ।

ਪ੍ਰਸ਼ਨ 12.
4 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਇੱਕ ਚੱਕਰ ਦੇ ਬਾਹਰਲੇ ਪਾਸੇ ਛੂਹਦਾ ਇੱਕ ਤ੍ਰਿਭੁਜ ABCਇਸ ਤਰ੍ਹਾਂ ਖਿੱਚਿਆ ਗਿਆ ਹੈ ਕਿ ਰੇਖਾਖੰਡ BD ਅਤੇDC (ਜਿਸ ਵਿੱਚ ਸਪਰਸ਼ ਬਿੰਦੂD ਦੁਆਰਾ BC ਵਿਭਾਜਿਤ ਹੈ ਦੀਆਂ ਲੰਬਾਈਆਂ ਕ੍ਰਮਵਾਰ 8 cm ਅਤੇ 6 cm ਹੈ (ਦੇਖੋ ਚਿੱਤਰ । ਭੁਜਾਵਾਂ AB ਅਤੇ AC ਪਤਾ ਕਰੋ ।

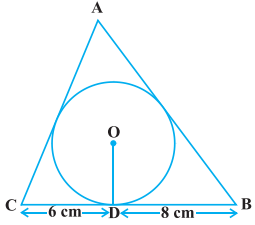
ਹੱਲ:
4 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਚੱਕਰ ਦੇ ਬਾਹਰਲੇ ਪਾਸੇ ਛੂੰਹਦਾ ਇੱਕ ਤਿਭੁਜ ABC ਖਿੱਚਿਆ ਗਿਆ ਹੈ ਤ੍ਰਿਭੁਜ ਦੀਆਂ ਭੁਜਾਵਾਂ BC, CA, AB ਚੱਕਰ ਨੂੰ ਕ੍ਰਮਵਾਰ ਬਿੰਦੂ D, E ਅਤੇ Fਉੱਤੇ ਸਪਰਸ਼ ਕਰਦੀਆਂ ਹਨ।
ਕਿਉਂਕਿ ਕਿਸੇ ਬਾਹਰੀ ਬਿੰਦੂ ਤੋਂ ਚੱਕਰ ‘ਤੇ ਖਿੱਚੀਆਂ ਗਈਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਦੀਆਂ ਲੰਬਾਈਆਂ ਬਰਾਬਰ ਹੁੰਦੀਆਂ ਹਨ।
∴ AE = AF = 1 cm (ਮੰਨ ਲਉ।)
CE = CD= 6 cm
BF = BD = 8 cm
ਕਿਉਂਕਿ ਚੱਕਰ ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਸਪੱਰਸ਼ ਬਿੰਦੂ ਤੋਂ ਜਾਣ ਵਾਲੇ ਅਰਧ ਵਿਆਸ ’ਤੇ ਲੰਬ ਹੁੰਦੀ ਹੈ ।

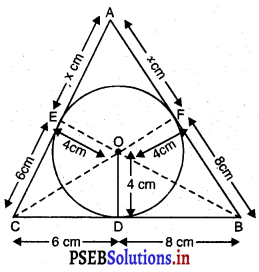
∴ OD ⊥ BC; OE ⊥ AC ਅਤੇ OF ⊥ AB.
ਨਾਲ ਹੀ, OE = OD = OF =4 cm.
△ ABC ਵਿਚ
a = AC = (x + 6) cm ;
b = CB = (6 + 8) cm = 14 cm
c = BA = (8 + x) cm

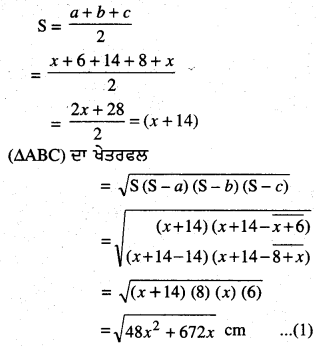
(△OBC) ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) × ਅਧਾਰ × ਸਿਖਰਲੰਬ
= \(\frac{1}{2}\) × 14 × 4 = 28 cm2 …(2)
(△BOA) ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) × ਅਧਾਰ × ਸਿਖਰਲੰਬ
= \(\frac{1}{2}\) × (8 + x) × 4
= (16 + 2x) cm2 …(3)
(△AOC) ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) × ਅਧਾਰ × ਸਿਖਰਲੰਬ
= \(\frac{1}{2}\) × (6 + x) × 4
= (12 + 21) cm2 …(4)
ਚਿੱਤਰ ਤੋਂ ਖੇਤਰਫਲ ਜੋੜਣ ਤੇ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ
ar (△ABC) = ar (△OBC) + ar (△BOA) + ar (△AOC)
\(\sqrt{48 x^{2}+672 x}\) = 28 + 16 + 2x + 12 + 2x
\(\sqrt{48 x^{2}+672 x}\) = 4x + 56
\(\sqrt{48 x^{2}+672 x}\) = 4[x + 14]
ਦੋਵੇਂ ਪਾਸੇ ਵਰਗ ਕਰਨ ਤੇ
48x² + 672x = 16 (x + 14)²
48x(x + 14) = 16(x + 14)²
48x = 16(x + 14)
3x = x + 14
2x = 14
x = 7
x = \( \frac{14}{2}\) = 7
∴ AC = (x + 6) cm
= (7 + 6) cm = 13 cm
AB = (x + 8) cm
= (7 + 8) cm = 15 cm
AB = 15 cm ਅਤੇ AC = 13 cm

ਪ੍ਰਸ਼ਨ 13.
ਸਿੱਧ ਕਰੋ ਕਿ ਚੱਕਰ ਦੇ ਬਾਹਰਲੇ ਪਾਸੇ ਛੂੰਹਦੀ ਹੋਈ ਚਤੁਰਭੁਜ ਦੀਆਂ ਆਹਮਣੇ-ਸਾਹਮਣੇ ਦੀਆਂ ਭੁਜਾਵਾਂ ਕੇਂਦਰ ‘ਤੇ ਸੰਪੁਰਕ ਕੋਣ ਬਣਾਉਂਦੀਆਂ ਹਨ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਕੇਂਦਰ O ਵਾਲੇ ਚੱਕਰ ਦੇ ਬਾਹਰ ਬਣੀ ਚਤੁਰਭੁਜ PORS ਜਿਸ ਦੀਆਂ ਭੁਜਾਵਾਂ PQ, QR, RS ਅਤੇ SP ਚੱਕਰ ਨੂੰ ਕ੍ਰਮਵਾਰ L, M, N ਅਤੇ 1 ਤੇ ਸਪਰਸ਼ ਕਰਦੀਆਂ ਹਨ।

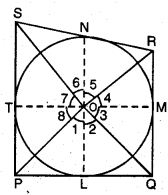
ਸਿੱਧ ਕਰਨਾ ਹੈ :
∠POQ + ∠SOR = 180°
ਅਤੇ ∠SOP + ∠ROQ = 180°
ਰਚਨਾ :
OP, OL, OQ, OM, OR, ON, OS ਅਤੇ OT ਨੂੰ ਮਿਲਾਉ ।
ਸਬੂਤ : ਕਿਉਂਕਿ ਬਾਹਰੀ ਬਿੰਦੂ ਤੋਂ ਕਿਸੇ ਚੱਕਰ ‘ਤੇ
ਖਿੱਚੀਆਂ ਗਈਆਂ ਦੋ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਕੇਂਦਰ ‘ਤੇ ਸਮਾਨ ਕੋਣ ਬਣਾਉਂਦੀਆਂ ਹਨ ।
∴ ∠2 = ∠3; ∠4 = ∠5 ; ∠6 = ∠7; ∠8 = ∠1 ….(1)
ਕਿਉਂਕਿ ਇਕ ਬਿੰਦੂ ਦੇ ਸਾਰੇ ਕੋਣਾਂ ਦਾ ਜੋੜ 360° ਹੁੰਦਾ ਹੈ ।
∴ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
∠1 + ∠2 + ∠2 + ∠5 + ∠5 + ∠6 + ∠6 + ∠1 = 360°
ਜਾਂ 2(∠1 + ∠2 + ∠5 + ∠6) = 360°
ਜਾਂ (∠1 + ∠2) + (∠5 + ∠6) = \(\frac{360^{\circ}}{2}\) = 180°
ਜਾਂ ∠POQ + ∠SOR = 180°
ਇਸੇ ਤਰ੍ਹਾਂ, ∠SOP + ∠ROQ = 180°
∴ ਚੱਕਰ ਦੇ ਬਾਹਰਲੇ ਪਾਸੇ ਛੂੰਹਦੀ ਹੋਈ ਚਤੁਰਭੁਜ ਦੀਆਂ ਆਹਮਣੇ-ਸਾਹਮਣੇ ਦੀਆਂ ਭੁਜਾਵਾਂ ਕੇਂਦਰ ’ਤੇ ਸੰਪੂਰਕ ਕੋਣ ਬਣਾਉਂਦੀਆਂ ਹਨ ।