PSEB 10th Class Maths Solutions Chapter 11 रचनाएँ Ex 11.2

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 11 रचनाएँ Ex 11.2 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 11 वृत्त Ex 11.2

निम्न में से प्रत्येक के लिए रचना का औचित्य भी दीजिए :

प्रश्न 1.
6 cm त्रिज्या का एक वृत्त खींचिए। केन्द्र से | 10 cm दूर स्थित एक बिंदु से वृत्त पर स्पर्श रेखा युग्म की रचना कीजिए और उनकी लंबाइयाँ मापिए।
हल :

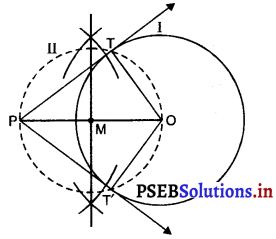
रचना के चरण :
1. एक वृत्त (I) त्रिज्या 6 cm का खींचिए।
2. केन्द्र से 10 cm की दूरी पर एक बिंदु 0 लीजिए। OP को मिलाइए।
3. OP का लंब समद्विभाजक खींचिए। मान लीजिए ‘M’, OP का मध्य बिंदु है।।
4. ‘M’ को केन्द्र मानकर तथा MO त्रिज्या लेकर एक वृत्त (II) खींचिए जो कि वृत्त (I) को T और T’ पर प्रतिच्छेद करता है।
5. तब PT और PT’ अभीष्ट दो स्पर्श रेखाएँ हैं।

रचना का औचित्य :
हम जानते हैं कि किसी बिंदु पर स्पर्श रेखा उस बिंदु पर त्रिज्या पर लंब होती है। हमने सिद्ध करना है कि
∠PTO = ∠PT’O = 90°.
OT को मिलाया गया है।
अब, PMO वृत्त (II) की व्यास है।

टिप्पणी :
यदि वृत्त का केन्द्र न दिया हो, तो आप और ∠PTO अर्धवृत्त में है। इसकी दो असमांतर जीवाएँ खींच कर और उनके लंब
∴ ∠PTO = 90° समद्विभाजक खींच कर उनका प्रतिच्छेद बिंदु ज्ञात करके
[अर्धवृत्त का कोण समकोण होता है।] वृत्त का केन्द्र अंकित कीजिए।
इसी प्रकार, ∠PT’O = 90°
∴ PT और PT’ वृत्त की T और T’ पर स्पर्श रेखाएँ हैं।
स्पर्श रेखाओं की लंबाई मापने पर दीजिए:
अर्थात्, PT = 8.1 cm
PT’ = 8.1 cm.

प्रश्न 2.
4 cm त्रिज्या के एक वृत्त पर 6 cm fervente के एक सकेंद्रीय वृत्त के किसी बिंदु से एक स्पर्श रेखा की रचना कीजिए और इसकी लंबाई मापिए। परिकलन से इस माप की जाँच भी कीजिए।
हल :
सकेंद्रीय वृत्त : दो या अधिक वृत्त जिनका एक ही केन्द्र हो परंतु भिन्न-भिन्न त्रिज्याएँ हों, संकेन्द्रीय वृत्त कहलाते हैं।
रचना के चरण :
1. एक वृत्त जिसका केन्द्र ‘O’ और त्रिज्या 4 cm हो खींचिए। इसे I अंकित कीजिए।

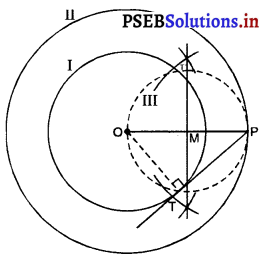
2. उसी केन्द्र ‘O’ से और त्रिज्या 6 cm का एक और वृत्त खींचिए इसे II अंकित कीजिए।
3. वृत्त II पर कोई बिंदु ‘P’ लीजिए।OP को मिलाइए।
4. OP का लंब समद्विभाजक खींचिए। मान लीजिए यह ‘OP’ को M पर प्रतिच्छेद करती है।
5. M को केन्द्र मानकर और त्रिज्या ‘MO’ या ‘MP’, लेकर एक वृत्त III खींचिए जो वृत्त I को T और T’ पर प्रतिच्छेद करे है।
6. PT को मिलाइए। PT अभीष्ट चतुर्भुज है।

रचना का औचित्य :
OT को मिलाइए।
अब OP वृत्त III का व्यास है।
∠OTP अर्धवृत्त में कोण है।
∴ ∠OTP = 90°
अब OT ⊥ PT [(1) का प्रयोग करने पर]
∵ एक रेखा जो, वृत्त में किसी बिंदु पर त्रिज्या के साथ 90° का कोण बनाए, वह वृत्त पर स्पर्श रेखा होती है।
∴ PT वृत्त ‘I’ की स्पर्श रेखा है।
अर्थात् PT, 4 cm त्रिज्या वाले वृत्त पर स्पर्श रेखा है।

स्पर्श रेखा की लंबाई का परिकलन :
∆OTP लीजिए।
∠OTP = 90°
(i) का प्रयोग करने पर]
∴ ∆OTP एक समकोण त्रिभुज है।
OT = 4 cm [वृत्त I की त्रिज्या (दिया है)] OP = 6 cm
[वृत्त II की त्रिज्या (दिया है)]
PT = ? [परिकलित करना है]
समकोण ∆OTP में, पाइथागोरस प्रमेय से
OP² = OT² + PT²
[(कर्ण)² = (आधार)² + (लंब)²]
या PT² = OP² – OT²
= 6² – 4²
= 36 – 16 = 20
PT = √20 cm = 2√5
= 2 × 2.24 = 4.48 cm.
इसलिए, परिकलन से स्पर्श रेखा की लंबाई = 4.48 cm = 4.5 cm
मापने पर स्पर्श रेखा की लंबाई = 4.5 cm
अत: स्पर्श रेखा ‘PT” की लंबाई सत्यापित है।

प्रश्न 3.
3 cm त्रिज्या का एक वृत्त खींचिए। इसके किसी बढ़ाए गए व्यास पर केन्द्र से 7 cm की दूरी पर स्थित दो बिंदु P और Q लीजिए। इन दोनों बिंदुओं से वृत्त पर स्पर्श रेखाएँ खींचिए।
हल :
रचना के चरण :
1. केन्द्र ‘O’ और त्रिज्या 3 cm का एक वृत्त खींचिए।
2. इसका व्यास ‘AB’ खींचिए और इसे दोनों दिशाओं में बढ़ाइए जैसे कि OX और OX’
3. ‘OX” दिशा पर बिंदु ‘P’ और ‘OX’ दिशा पर बिंदु Qसे इस प्रकार लीजिए कि ।
OP = OQ = 7 cm. .

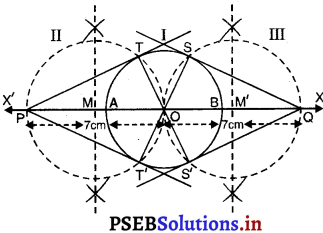
4. OP और OQ पर लंब समद्विभाजक खींचिए जो OP और OQ को क्रमश: ‘M’ और ‘M” पर प्रतिच्छेद करें।
5. ‘M’ को केन्द्र मानकर और त्रिज्या = ‘MO’ या MP लेकर एक वृत्त ‘II’ खींचिए जो वृत्त ‘I’ को T और T’ पर प्रतिच्छेद करे।
6. इसी प्रकार ‘M” को केन्द्र मानकर और वृत्त = M’O या MQ, लेकर वृत्त (III) खींचिए जो वृत्त ‘I’ को ‘S’ और ‘S” पर प्रतिच्छेद करे।
7. PT, PT’ और QS तथा QS’ को मिलाइए।

रचना का औचित्य :
‘OT’ और ‘OT” तथा ‘os’ और OS’ को मिलाइए।
PT और PT’ वृत्त की स्पर्श रेखाएँ हैं को सिद्ध करने के लिए हमें सिद्ध करना है कि
∠PTO = ∠PT’O = 90° है।
अब ‘OP’ वृत्त II’ का व्यास है और ∠OTP अर्धवृत्त में बना कोण है।
∴ ∠OTP = 90° …………(1)
[∵ अर्धवृत्त का कोण 90° का होता है।]
परंतु ‘OT’ वृत्त ‘I’ की त्रिज्या है और रेखा ‘PT’ वृत्त को ‘T’ पर स्पर्श करती है।
∵ एक रेखा जो वृत्त को किसी बिंदु पर स्पर्श करती है और उस बिंदु पर त्रिज्या के साथ 90° का कोण बनाती है, वृत्त की स्पर्श रेखा होती है।
∴ PT वृत्त I की बिंदु T पर बिंदु ‘P’ से स्पर्श रेखा है।
इसी तरह PT’, QS और Os’ वृत्त I पर स्पर्श रेखाएँ हैं।

प्रश्न 4.
5 cm त्रिज्या के एक वृत्त पर ऐसी दो स्पर्श रेखाएँ खींचिए, जो परस्पर 60° के कोण पर झुकी हों।
हल :
रचना के चरण :
1. अभीष्ट आकृति का कच्चा खाका खींचिए।

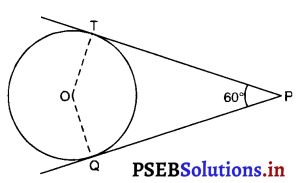
∵ स्पर्श रेखाएँ परस्पर 60° का कोण बनाती हैं।
∠OTP = ∠OQT = 90°
[स्पर्श रेखा वृत्त की त्रिज्या पर लंब है।]
त्रिज्याओं का परस्पर झुकाव ज्ञात करना कि
∠TOQ + ∠OTP + ∠OQT + ∠TPQ = 360° [चतुर्भुज के कोण योग गुण]
या ∠TOQ + 90° + 90° + 60 = 360°
या ∠TOQ = 360° – 90° – 90° – 60° = 120°
2. 5 cm त्रिज्या का एक वृत्त खींचिए।
3. इस वृत्त की दो त्रिज्याएँ खींचीए जो परस्पर 120° का कोण बनाएं।
4. त्रिज्याएं वृत्त को ‘A’ और ‘B’ पर प्रतिच्छेद करें।
5. A और B पर 90° का कोण बनाएं जो परस्पर ‘P’ पर प्रतिच्छेद करें।

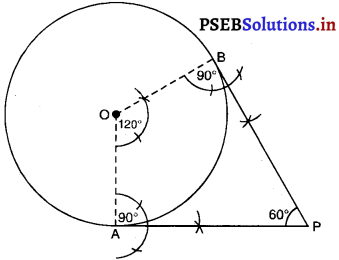
6. PA और PB अभीष्ट स्पर्श रेखाएँ हैं।

प्रश्न 5.
8 cm लंबा एक रेखाखंड AB खींचिए। ‘A’ को केन्द्र मान कर 4 cm त्रिज्या का एक वृत्त तथा ‘B’ को केन्द्र लेकर 3 cm त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केन्द्र से स्पर्श रेखाओं की रचना कीजिए।
हल:

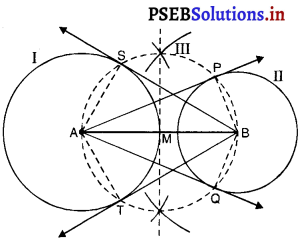
रचना के चरण :
1. एक रेखाखंड AB = 8 cm खींचिए।
2. ‘A’ को केन्द्र मानकर और त्रिज्या 4 cm लेकर वृत्त (I) खींचिए।
3. ‘B’ को केन्द्र मानकर और त्रिज्या 3 cm लेकर वृत्त II’ खींचिए।
4. रेखाखंड AB का लंब समद्विभाजक खींचिए जो _ ‘AB’ को ‘M’ पर प्रतिच्छेद करे।
5. ‘M’ को केन्द्र मानकर और त्रिज्या MA या MB लेकर वृत्त (III) खींचिए जो वृत्त (I) को ‘S’ और ‘T’ पर और वृत्त (II) को ‘P’ और ‘Q’ पर प्रतिच्छेद करे।
6. ‘AP’ और ‘AQ’ को मिलाइए। ये बिंदु ‘A’ से 3 cm त्रिज्या वाले वृत्त की अभीष्ट स्पर्श रेखाएँ हैं।
7. ‘BS’ और ‘BT’ को मिलाइए। ये बिंदु ‘B’ से 4 cm त्रिज्या वाले वृत्त की अभीष्ट स्पर्श रेखाएं हैं।

रचना का औचित्य :
वृत्त (III) में, AB व्यास है, तो ∠ASB और ZBPA अर्धवृत्त के कोण हैं।
∴ ∠ASB = 90° [अर्धवृत्त में कोण] ………………..(1)
और ∠BPA = 90° ……………..(2)
परंतु ∠ASB की त्रिज्या और रेखाखंड (BS’ के बीच का कोण है और ∠BPA की त्रिज्या और रेखाखंड वृत्त (II) ‘AP’ के बीच का कोण है।
∵ रेखाखंड जो वृत्त की त्रिज्या पर लंब है, उस बिंदु पर वृत्त की स्पर्श रेखा है।
∴ BS का वृत्त (I) की बिंदु ‘S’ पर स्पर्श रेखा है और AP वृत्त (II) की बिंदु ‘P’ पर स्पर्श रेखा है।
इसी प्रकार, AQ और BT क्रमशः वृत्त (II) और (I) की स्पर्श रेखाएं हैं।

प्रश्न 6.
माना ABC एक समकोण त्रिभुज है, जिसमें AB = 6 cm, BC = 8 cm तथा ∠B = 90° है। B से AC पर BD लंब है। बिंदुओं B, C, D से होकर जाने वाला एक वृत्त खींचा गया है। ‘A’ से इस वृत्त पर स्पर्श रेखा की रचना कीजिए।
हल :

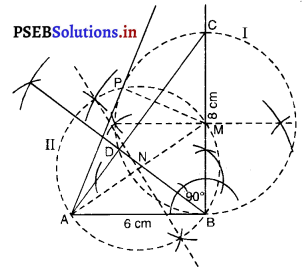
रचना के चरण:
1. समकोण त्रिभुज ABC की रचना दी गई शर्तों और माप के साथ कीजिए।
2. BD ⊥ AC खींचिए।
3. भुजा BC पर मध्य बिंदु ‘M’ लीजिए।
4. ‘M’ को केन्द्र और BC को व्यास मानकर, B, C, D में से अर्धवृत्त में बना कोण 90° (∠BDC = 90°) होता है। परकार का प्रयोग करके, एक वृत्त खींचिए। इसे वृत्त I लीजिए।
5. ‘A’ और ‘M’ को मिलाइए।
6. AM का लंब समद्विभाजक खींचिए जो AM को ‘N’ पर प्रतिच्छेद करे। ‘N’ को केन्द्र और ‘NA’ या ‘NM’ | त्रिज्या लेकर एक वृत्त (II) खींचिए जो वृत्त (I) को ‘B’ और ‘P’ पर प्रतिच्छेद करे।
7. AP को मिलाइए।
8. AP और AB अभीष्ट स्पर्श रेखाएँ हैं।

रचना का औचित्य :
रेखाखंड AM’ को व्यास लेकर वृत्त (II) खींचिए।
∠APM अर्धवृत्त है।
∵ ∠APM = 90° [अर्धवृत्त में कोण]
अर्थात् MP ⊥ AP परंतु ‘MP’ वृत्त (I) की त्रिज्या है।
∴ AP वृत्त (II) की स्पर्श रेखा है।
[∵ वृत्त के किसी बिंदु पर वृत्त की त्रिज्या के लंब कोई रेखा उस वृत्त की स्पर्श रेखा होती है।]
इसी प्रकार ‘AB’ वृत्त (I) की स्पर्श रेखा है।

प्रश्न 7.
किसी चूड़ी की सहायता से वृत्त खींचिए। वृत्त के बाहर एक बिंदु लीजिए। इस बिंदु से वृत्त पर स्पर्श रेखाओं की रचना कीजिए।
हल :
किसी चूड़ी की सहायता से वृत्त खींचने का अर्थ है कि वृत्त का केन्द्र अज्ञात है।
सर्वप्रथम हम केन्द्र ज्ञात करेंगे।

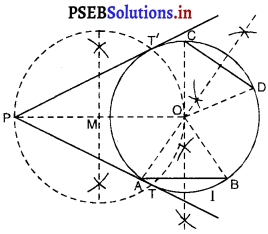
रचना के चरण :
1. चूड़ी की सहायता से वृत्त (I) खींचिए।
2. वृत्त पर कोई दो जीवाएँ AB और CD (समांतर नहीं) खींचिए।
3. जीवा AB और CD के लंब समद्विभाजक खींचिए जो परस्पर प्रतिच्छेद करें।
[∵ रेखाखंड के लंब समद्विभाजक पर स्थित कोई बिंदु इसके अंत बिंदुओं स समदूरस्थ होता है।]
[∵ ‘O’, AB और CD के लंब समद्विभाजक पर स्थित है।]
∴ OA = OB और OC = OD
∴ OA = OB = OC = OD (वृत्त की त्रिज्याएँ)
∴ ‘O’ वृत्त का केन्द्र है।
4. वृत्त के बाहर कोई बिंदु ‘P’ लीजिए।
5. OP को मिलाइए।
6. OP का लंब समद्विभाजक खींजिए। मान लीजिए ‘M’, OP का मध्य बिंदु है।
7. ‘M’ को केन्द्र और त्रिज्या ‘MP’ या ‘MO’ लेकर एक वृत्त II खींचिए जो वृत्त (I) को T और T’ पर प्रतिच्छेद करे।
8. PT और PT’ को मिलाइए जो कि अभीष्ट स्पर्श रेखाओं का युग्म है।

रचना का औचित्य :
त्रिज्या ; स्पर्श रेखा वाले बिन्दु से हमेशा समकोण बनाती है।
अब, हमने सिद्ध करना है कि ∠PTO = ∠PT’O = 90°. OT को मिलाइए।
अब ∠PTO अर्धवृत I में हैं।
∴ ∠PTO = 90° [समकोण में बना कोण समकोण होता है]
इसी तरह, ∠PTO = 90°
∴ PT और PT’ वृत पर बिन्दुओं T और T’ पर क्रमशः स्पर्श रेखाएं हैं।