Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 12 ਚੱਕਰ ਨਾਲ ਸੰਬੰਧਿਤ ਖੇਤਰਫਲ Ex 12.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 12 ਚੱਕਰ ਨਾਲ ਸੰਬੰਧਿਤ ਖੇਤਰਫਲ Exercise 12.1
ਜਦੋਂ ਤੱਕ ਹੋਰ ਕੁੱਝ ਨਾ ਕਿਹਾ ਜਾਵੇ, ਗ π = \(\frac{22}{7}\) ਪ੍ਰਯੋਗ ਕਰੋ !
ਪ੍ਰਸ਼ਨ 1.
ਦੋ ਚੱਕਰਾਂ ਦੇ ਅਰਧ ਵਿਆਸ ਕੁਮਵਾਰ 19cm ਅਤੇ 9cm ਹਨ । ਉਸ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਪਤਾ ਕਰੋ ਜਿਸ ਦਾ ਘੋਰਾ ਇਨ੍ਹਾਂ ਦੋਨਾਂ ਚੱਕਰਾਂ ਦੇ ਘੇਰਿਆਂ ਦੇ ਜੋੜ ਦੇ ਬਰਾਬਰ ਹੈ।
ਹੱਲ:
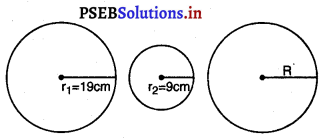
ਪਹਿਲੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (r1) = 19 cm
ਦੂਸਰੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (r2) = 9 cm
ਮੰਨ ਲਉ ਤੀਸਰੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ = R cm
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ,
ਪਹਿਲੇ ਚੱਕਰ ਦਾ ਘੇਰਾ + ਦੂਸਰੇ ਚੱਕਰ ਦਾ ਘੇਰਾ = ਤੀਸਰੇ ਚੱਕਰ ਦਾ ਘੇਰਾ
2πr1 + 2πr2 = 2πR
2π [r1 + r2] = 2π R
19 + 9 = R
∴ R = 28
∴ ਤੀਸਰੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ = 28 cm
ਪ੍ਰਸ਼ਨ 2.
ਦੋ ਚੱਕਰਾਂ ਦੇ ਅਰਧ ਵਿਆਸ ਕੁਮਵਾਰ 8 cm ਅਤੇ 6 cm ਹਨ । ਉਸ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਪਤਾ ਕਰੋ ਜਿਸ ਦਾ ਖੇਤਰਫਲ ਇਨ੍ਹਾਂ ਦੋਨਾਂ ਚੱਕਰਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦੇ ਜੋੜ ਦੇ ਬਰਾਬਰ ਹੈ ।
ਹੱਲ:
ਪਹਿਲੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (r1) = 8 cm
ਦੂਸਰੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (r2) = 6 cm
ਤੀਸਰੇ ਚੱਕਰ ਦਾ ਅਰਧਵਿਆਸ = R cm
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
ਤੀਸਰੇ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ = ਪਹਿਲੇ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ + ਦੂਸਰੇ ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ
πR2 = π\(r_{1}^{2}\) + π\(r_{2}^{2}\)
πR2 = π[\(r_{1}^{2}\) + π\(r_{2}^{2}\)]
R2 = (8)2 + (6)2
R = \(\sqrt {64+36}\) = \(\sqrt {100}\)
R= 10 cm
∴ ਲੋੜੀਂਦਾ ਅਰਧ ਵਿਆਸ (R) = 10 cm
![]()
ਪ੍ਰਸ਼ਨ 3.
ਦਿੱਤਾ ਹੋਇਆ ਚਿੱਤਰ ਇੱਕ ਤੀਰ ਅੰਦਾਜ਼ੀ ਨਿਸ਼ਾਨੇ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ, ਜਿਸ ਵਿੱਚ ਕੇਂਦਰ ਦੇ ਬਾਹਰ ਵੱਲ ਪੰਜ ਖੇਤਰ GOLD,RED, BLUE, BLACK ਅਤੇ WHITE ਨੂੰ ਦਰਸਾਉਂਦੇ ਹਨ, ਜਿਨ੍ਹਾਂ ‘ਤੇ ਅੰਕ ਪ੍ਰਾਪਤ ਕੀਤੇ ਜਾ ਸਕਦੇ ਹਨ । GOLਅੰਕ ਵਾਲੇ ਖੇਤਰ ਦਾ ਵਿਆਸ 21 cm ਹੈ ਅਤੇ ਹਰੇਕ ਹੋਰ ਪੱਟੀ 10.5 cm ਚੌੜੀ ਹੈ । ਅੰਕ ਪ੍ਰਾਪਤ ਕਰਾਉਣ ਵਾਲੇ ਇਨ੍ਹਾਂ ਪੰਜਾਂ ਖੇਤਰਾਂ ਵਿੱਚੋਂ ਹਰੇਕ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

ਹੱਲ:
Gold ਖੇਤਰ ਦਾ ਵਿਆਸ = 21 cm
Gold ਖੇਤਰ ਦਾ ਅਰਧ ਵਿਆਸ (R1).
= \(\frac{21}{2}\) cm = 10.5 cm
∴ Gold ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ
= π\(R_{1}^{2}\) = \(\frac{22}{7}\) × \(\frac{21}{2}\) × \(\frac{21}{2}\) = \(\frac{693}{2}\) cm2
= 346∙5 cm2
ਹਰੇਕ ਪੱਟੀ ਦੀ ਚੌੜਾਈ = 10.5 cm
∴ Red ਅਤੇ Gold ਖੇਤਰ ਦਾ ਅਰਧ ਵਿਆਸ (R2)
= (10.5 + 10.5) cm
= 21 cm
Blue, Red ਅਤੇ Gold ਖੇਤਰ ਦਾ ਸੰਯੁਕਤ ਅਰਧ ਵਿਆਸ (R3) = R2 + 10.5 cm
= 21 + 10.5 = 31.5 cm
Black, Blue, Red ਅਤੇ Gold ਖੇਤਰ ਦਾ ਸਾਂਝਾ ਅਰਧ ਵਿਆਸ (R4) = R3 + 10.5
= (31.5 + 10.5) cm
= 42 cm
Black ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ = Gold, Red, Blue ਅਤੇ Black ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ – Gold, Red ਅਤੇ Blue ਖੇਤਰ ਦਾ ਸਾਂਝਾ ਅਰਧ ਵਿਆਸ
= π\(r_{4}^{2}\) – π\(r_{3}^{2}\)
= π[(42)2 – (31.5)2] cm2
= \(\frac{22}{7}\) [1764 – 99225] cm2
= \(\frac{22}{7}\) [771.75] cm2 = 2425.5 cm2
White, black, blue, red, gold ਖੇਤਰ ਦਾ ਸਾਂਝਾ | ਅਰਧ ਵਿਆਸ (R5)
= R4 + 15
R5 = 42 + 10.5 = 52.5 cm
Black, blue, red ਅਤੇ gold ਖੇਤਰ ਦਾ ਅਰਧ | ਵਿਆਸ (R4) = 42 cm
White ਅੰਕ ਲੈਣ ਵਾਲੇ ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ = White, black, blue, red, gold ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ – Black blue, red, gold ਦਾ ਖੇਤਰਫਲ
= π\(R_{5}^{2}\) – π\(R_{4}^{2}\)
= π[\(R_{5}^{2}\) – \(R_{4}^{2}\)]
= \(\frac{22}{7}\)[(525)2 – (42)2] cm2
= \(\frac{22}{7}\)[2756.25 -1764] cm2
= \(\frac{22 \times 992.25}{7}\) = \(\frac{21829.5}{7}\) cm2
= 3118.5 cm2
∴ White ਅੰਕ ਵਾਲੇ ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ
= 3118.5 cm2
∴ Red ਅੰਕ ਵਾਲੇ ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ = Red or Gold ਦਾ ਖੇਤਰਫਲ – Gold ਦਾ ਖੇਤਰਫਲ
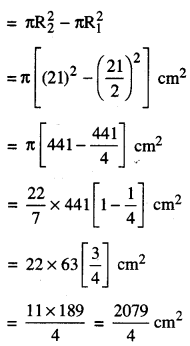
= 1039.5 cm2
∴ Red ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ = 1039.5 cm2
Gold, Red ਅਤੇ Blue ਦਾ ਸਾਂਝਾ ਅਰਧਵਿਆਸ R,
= (10.5 + 10.5 + 10.5) = 31.5 cm
Blue ਅੰਕ ਵਾਲੇ ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ
= Red, blue ਅਤੇ Gold ਦਾ ਖੇਤਰਫਲ – Gold ਅਤੇ Red ਦਾ ਖੇਤਰਫਲ
= π\(R_{3}^{2}\) – π\(R_{2}^{2}\)
= π[\(R_{3}^{2}\) – \(R_{2}^{2}\)]
= \(\frac{22}{7}\)[(31.52)2 – (21)2] cm2
= \(\frac{22}{7}\)[99225 – 441] cm 2
= \(\frac{22}{7}\) × 551.25 cm2 = \(\frac{12127.5}{7}\) cm2
= 1732.5 cm2 .
ਪ੍ਰਸ਼ਨ 4.
ਕਿਸੇ ਕਾਰ ਦੇ ਹਰੇਕ ਪਹੀਏ ਦਾ ਵਿਆਸ 80 cm ਹੈ । ਜੇਕਰ ਇਹ ਕਾਰ 66 km/h ਦੀ ਚਾਲ ਨਾਲ ਚਲ ਰਹੀ ਹੈ । ਤਾਂ 10 ਮਿੰਟ ਵਿੱਚ ਹਰੇਕ ਪਹੀਆ ਕਿੰਨੇ ਚੱਕਰ ਲਗਾਉਂਦਾ ਹੈ ।
ਹੱਲ:
ਪਹੀਏ ਦਾ ਵਿਆਸ = 80 cm
ਪਹੀਏ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 40 cm
= \(\frac{4}{100}\) m = 0.04 m
ਪਹੀਏ ਦਾ ਘੇਰਾ = 2πr
= 2 × \(\frac{22}{7}\) × 0.04 m
ਮੰਨ ਲਉ ਕਾਰ ਦਾ ਪਹੀਆ ॥ ਪੂਰੇ ਚੱਕਰ ਲਗਾਉਣ ਵਿਚ 10 ਮਿੰਟ ਦਾ ਸਮਾਂ ਲੈਂਦਾ ਹੈ ।
= n[0.08 × \(\frac{22}{7}\)] m
ਕਾਰ ਦੀ ਚਾਲ = 66 km/h
60 ਮਿੰਟਾਂ ਵਿਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ
= 66 km = 66 × 1000 m
10 ਮਿੰਟ ਵਿਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ
= \(\) 10 m
= 11000 m
∴ n[\(\frac{22}{7}\) × 0.08] = 1100
n = \(\frac{11000}{0.08}\) × \(\frac{7}{22}\)
n = 4375
∴ ਕਾਰ ਦੇ ਪਹੀਏ ਦੁਆਰਾ 10 ਮਿੰਟਾਂ ਵਿਚ ਲਗਾਏ ਗਏ ਚੱਕਰਾਂ ਦੀ ਗਿਣਤੀ 4375 ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 5.
ਹੇਠਾਂ ਲਿਖਿਆਂ ਵਿਚੋਂ ਸਹੀ ਉੱਤਰ ਚੁਣੋ ਅਤੇ ਆਪਣੇ ਉੱਤਰ ਦਾ ਸਪਸ਼ਟੀਕਰਨ ਦਿਓ :
ਜੇਕਰ ਇੱਕ ਚੱਕਰ ਦਾ ਪਰਿਮਾਪ ਅਤੇ ਖੇਤਰਫਲ ਸੰਖਿਆਤਮਕ ਰੂਪ ਵਿੱਚ ਬਰਾਬਰ ਹੈ, ਤਾਂ ਉਸ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਹੈ ।
(A) 2 ਇਕਾਈਆਂ
(B) π ਇਕਾਈਆਂ
(C) 4 ਇਕਾਈਆਂ
(D) 7 ਇਕਾਈਆਂ
ਹੱਲ:
ਚੱਕਰ ਦਾ ਪਰਿਮਾਪ = ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ
2πR = πR2
2R = R2
⇒ R = 2
∴ ਸਹੀ ਉੱਤਰ A ਹੈ (R) = 2 ਇਕਾਈਆਂ
