PSEB 10th Class Maths Solutions Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Ex 13.1

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Ex 13.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Exercise 13.1

ਜਦੋਂ ਤੱਕ ਨਾ ਕਿਹਾ ਜਾਵੇ, π = \(\frac{22}{7}\) ਲਓ ।

ਪ੍ਰਸ਼ਨ 1.
ਦੋ ਘਣ, ਜਿਨ੍ਹਾਂ ਵਿੱਚੋ ਹਰੇਕ ਦਾ ਆਇਤਨ 64 cm³ ਹੈ, ਦੇ ਸਮਾਨ ਫਲਕਾਂ ਨੂੰ ਮਿਲਾ ਕੇ ਇੱਕ ਠੋਸ ਬਣਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਨਾਲ ਪ੍ਰਾਪਤ ਘਣਾਵ ਦੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਹਰੇਕ ਘਣ ਦੀ ਭੁਜਾ = 1 cm
ਘਣ ਦਾ ਆਇਤਨ = 64 cm³
[ ਘਣ ਦਾ ਆਇਤਨ = (ਭੁਜਾ)³]

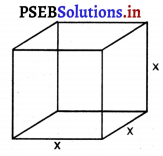
x³ = 64
x = \(\sqrt[3]{64}\)
= \(\sqrt[3]{4 \times 4 \times 4}\) cm
x = 4 cm
∴ ਘਣ ਦੀ ਭੁਜਾ = 4 cm
ਜਦੋਂ ਦੋ ਘਣਾਂ ਨੂੰ ਨਾਲ-ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਘਣਾਵ ਬਣ ਜਾਂਦਾ ਹੈ ।
ਜਿਸਦੀ ਲੰਬਾਈ (L) = 2x cm = 2(4) = 8 cm
ਚੌੜਾਈ (B) = x cm = 4 cm
ਉੱਚਾਈ (H) = x cm = 4 cm

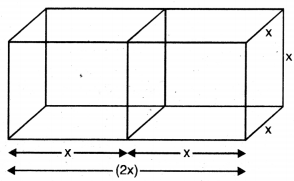
ਘਣਾਵ ਦੀ ਸੰਪੂਰਨ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 2[LB + BH + HL]
= 2 [8 × 4 + 4 × 4 + 4 × 8] cm²
= 2 [ 32 + 16 + 32] cm²
= 2 [30] cm²
= 160 cm²

ਪ੍ਰਸ਼ਨ 2.
ਕੋਈ ਬਰਤਨ ਇੱਕ ਖੋਖਲੇ ਅਰਧ ਗੋਲੇ ਦੇ ਆਕਾਰ ਦਾ ਹੈ ਜਿਸਦੇ ਉਪਰ ਇੱਕ ਖੋਖਲਾ ਬੋਲਣ ਲੱਗਿਆ ਹੈ । ਅਰਧ ਗੋਲੇ ਦਾ ਵਿਆਸ 14 cm ਹੈ ਅਤੇ ਇਸ ਬਰਤਨ ਦੀ ਕੁੱਲ ਉੱਚਾਈ 13 cm ਹੈ । ਇਸ ਬਰਤਨ ਦੀ ਅੰਦਰੂਨੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਅਰਧ ਗੋਲੇ ਦਾ ਵਿਆਸ = ਬੇਲਣ ਦਾ ਵਿਆਸ
= 14 cm
2R = 14 cm
ਅਰਧ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 7 cm

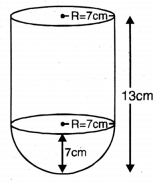
ਬਰਤਨ ਦੀ ਕੁੱਲ ਉੱਚਾਈ = 13 cm
∴ ਬੇਲਣ ਦੀ ਉਚਾਈ = (13 – 7) = 6 cm
ਬਰਤਨ ਦੀ ਅੰਦਰੂਨੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ = ਬੇਲਣ ਦਾ ਅੰਦਰੂਨੀ ਸੜਾ ਦਾ ਖੇਤਰਫਲ + ਅਰਧ ਗੋਲੇ ਅੰਦਰੂਨੀ ਸਤਾ ਦਾ ਖੇਤਰਫਲ
= 2πRH + 2πR²
= 2πR [H + R]
= 2 × \(\frac{22}{7}\) × 7 (6 + 7) cm²
= 44 × 13 cm²
= 572 cm²
∴ ਬਰਤਨ ਦੀ ਅੰਦਰੂਨੀ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 572 cm²

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਖਿਡੌਣਾ ਅਰਧ ਵਿਆਸ 3.5 cm ਵਾਲੇ ਇੱਕ ਸ਼ੰਕੁ ਆਕਾਰ ਦਾ ਹੈ ਜੋ ਉਸੇ ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਇੱਕ ਅਰਧ ਗੋਲੇ ‘ਤੇ ਟਿਕਿਆ ਹੈ । ਇਸ ਖਿਡੌਣੇ ਦੀ ਕੁੱਲ ਉੱਚਾਈ 15.5 cm ਹੈ । ਇਸ ਖਿਡੌਣੇ ਦੀ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਸ਼ੰਕੁ ਦਾ ਅਰਧ ਵਿਆਸ = ਅਰਧ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 3.5 cm
ਖਿਡੌਣੇ ਦੀ ਕੁੱਲ ਉੱਚਾਈ = 15.5 cm
∴ ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ (H) = (15.5 – 3.5) cm = 12 cm

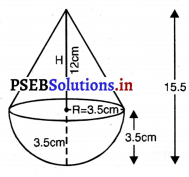
ਸ਼ੰਕੂ. ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ = \(\sqrt{\mathrm{R}^{2}+\mathrm{H}^{2}}\)
= \(\sqrt{(3.5)^{2}+(12)^{2}}\) cm
= \(\sqrt {1225+144}\) cm
= \(\sqrt {156.25}\) cm
ਸ਼ੰਕੂ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ (l) = 12.5 cm
ਖਿਡੌਣੇ ਦੀ ਕੁੱਲ ਸਤਾ ਦਾ ਖੇਤਰਫਲ
= ਸ਼ੰਕੁ ਦੀ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ + ਅਰਧ ਗੋਲੇ ਦੀ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ
= πRL + 2πR²
= πR [L + 2R]
= \(\frac{22}{7}\) × 35 [12.5 + 2 (3.5)] cm
= \(\frac{22}{7}\) × 35 [19.5] cm²
= \(\frac{1501.5}{7}\) cm²
= 214.5 cm²
∴ ਖਿਡੌਣੇ ਦੀ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 214.5 cm²

ਪ੍ਰਸ਼ਨ 4.
ਭੁਜਾ 7 cm ਵਾਲੇ ਇੱਕ ਘਣਾਕਾਰ ਬਲਾਕ ਦੇ ਉੱਪਰ ਇੱਕ ਅਰਧ ਗੋਲਾ ਰੱਖਿਆ ਹੋਇਆ ਹੈ । ਅਰਧ ਗੋਲੇ ਦਾ ਵੱਧ ਤੋਂ ਵੱਧ ਵਿਆਸ ਕੀ ਹੋ ਸਕਦਾ ਹੈ ? ਇਸ ਤਰ੍ਹਾਂ ਬਣੇ ਠੋਸ ਦੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਘਣਾਕਾਰ ਬਲਾਕ ਦੀ ਭੁਜਾ = 7 cm

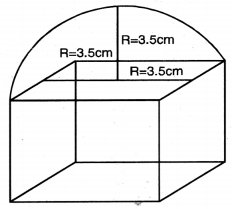
ਅਰਧ ਗੋਲੇ ਦਾ ਵਿਆਸ = ਘਣਾਕਾਰ ਬਲਾਕ ਦੀ ਭੁਜਾ = 7 cm
2R = 7
R = \(\frac{7}{2}\) cm = 3.5 cm
ਬਣੇ ਠੋਸ ਦੀ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ = ਘਣ ਦੀ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ + ਅਰਧ ਗੋਲੇ ਦੀ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 6(ਭੁਜਾ)² + 2R²
= 6l² + R²
= 6(7)² + 2 × \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) cm²
= 294 + 77 = 371 cm²
ਠੋਸ ਦੀ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ = (ਘਣ ਦੀ ਕੁੱਲ ਸਤਾ ਦਾ ਖੇਤਰਫਲ) – (ਅਰਧ ਗੋਲੇ ਦੇ ਆਧਾਰ ਦਾ ਖੇਤਰਫਲ) + (ਅਰਧ ਗੋਲੇ ਦੀ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ )
= 6l² – πR² + 2πR²
= 6l² + πR²
= [6(7)² + \(\frac{22}{7}\) × \(\left(\frac{7}{2}\right)^{2}\) ] cm²
= [6(49) + 11 × \(\frac{7}{2}\)] cm²
= 332.5 cm²

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਘਣਾਕਾਰ ਲੱਕੜ ਦੇ ਬਲਾਕ ਦੇ ਇੱਕ ਫਲਕ ਨੂੰ ਅੰਦਰ ਵੱਲ ਕੱਟ ਕੇ ਇੱਕ ਅਰਧ ਗੋਲਾਕਾਰ ਖੱਡਾ ਇਸ ਤਰ੍ਹਾਂ ਬਣਾਇਆ ਗਿਆ ਹੈ ਕਿ ਅਰਧ ਗੋਲੇ ਦਾ ਵਿਆਸ ਘਣ ਦੇ ਇੱਕ ਕਿਨਾਰੇ l ਦੇ ਬਰਾਬਰ ਹੈ । ਬਾਕੀ ਬਚੇ ਠੋਸ ਦੀ ਸਤਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਘਣ ਦੀ ਭੁਜਾ = a
∴ ਅਰਧ ਗੋਲੇ ਦਾ ਵਿਆਸ = ਘਣ ਦੀ ਭੁਜਾ = a
2R = a
R = \(\frac{a}{2}\)

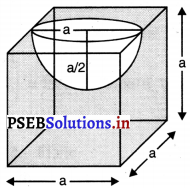
ਬਾਕੀ ਬਚੇ ਠੋਸ ਦੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ = ਘਣ ਦੀ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ – ਘਣ ਦੇ ਆਧਾਰ ਦਾ ਖੇਤਰਫਲ + ਅਰਧ ਗੋਲੇ ਦਾ ਅੰਦਰੂਨੀ ਵਕਰ ਸੜਾ ਦਾ
ਖੇਤਰਫਲ
= 6 (ਭੁਜਾ)² – πR² + 2πR²
= 6(a)² + πR²
= 6(a)² + π\(\left(\frac{a}{2}\right)^{2}\)
= 6a² + π\(\frac{a^{2}}{4}\)
= a²[6 + \(\frac{\pi}{4}\)]

ਪ੍ਰਸ਼ਨ 6.
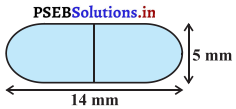
ਦਵਾਈ ਦਾ ਇੱਕ ਕੈਪਸੂਲ (capsule) ਇੱਕ ਬੇਲਣ ਦੇ ਆਕਾਰ ਦਾ ਹੈ ਜਿਸ ਦੇ ਦੋਨਾਂ ਸਿਰਿਆਂ ‘ਤੇ ਇੱਕ-ਇੱਕ | ਅਰਧ ਗੋਲਾ ਲੱਗਿਆ ਹੋਇਆ ਹੈ । ਦੇਖੋ ਚਿੱਤਰ) ਪੁਰੇ ਕੈਪਸੂਲ ਦੀ ਲੰਬਾਈ 14 mm ਹੈ ਅਤੇ ਉਸ ਦਾ ਵਿਆਸ 5 mm ਹੈ । ਇਸ਼ਦੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

ਹੱਲ:
ਕੈਪਸੁਲ ਦਾ ਵਿਆਸ = ਅਰਧ ਗੋਲੇ ਦਾ ਵਿਆਸ = ਬੇਲਣ ਦਾ ਵਿਆਸ = 5 mm
∴ 2R = 5 mm
R = \(\frac{5}{2}\) mm

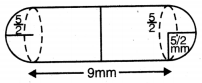
ਕੈਪਸੂਲ ਦੀ ਅੰਦਰੂਨੀ ਲੰਬਾਈ = 14 mm
ਬੇਲਣਾਕਾਰ ਭਾਗ ਦੀ ਉੱਚਾਈ = (14 – \(\frac{5}{2}\) – \(\frac{5}{2}\)) mm
= (14 – 5) mm
H = 9 mm
ਕੈਪਸੂਲ ਦੀ ਕੁੱਲ ਸਤਾ ਦਾ ਖੇਤਰਫਲ
= ਬੇਲਣ ਦੀ ਕੁੱਲ ਸਤਾ ਦਾ ਖੇਤਰਫਲ + 2 ਅਰਧ ਗੋਲੇ ਦਾ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ
= 2πRH + 2(2πR²)
= 2πRH + 4πR²
= 2πR [H + 2R]
= 2 × \(\frac{22}{7}\) × \(\frac{5}{2}\)[9 + 5 ] mm²
= \(\frac{22}{7}\) × 5 × 14 mm²
= 22 × 5 × 2 mm²
= 220 mm²

ਪ੍ਰਸ਼ਨ 7.
ਕੋਈ ਤੰਬੂ ਇੱਕ ਬੇਲਣ ਦੇ ਆਕਾਰ ਦਾ ਹੈ ਜਿਸ ‘ਤੇ ਇੱਕ ਸ਼ੰਕੂ ਬਣਿਆ ਹੋਇਆ ਹੈ । ਜੇਕਰ ਬੇਲਣਾਕਾਰ ਭਾਗ ਦੀ ਉੱਚਾਈ ਅਤੇ ਵਿਆਸ ਕੁਮਵਾਰ 2.1 m ਅਤੇ 4m ਹਨ ਅਤੇ ਸ਼ੰਭ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ 2.8 m ਹੈ, ਤਾਂ ਇਸ ਤੰਬੂ ਨੂੰ ਬਣਾਉਣ ਲਈ ਵਰਤੇ ਜਾਣ ਵਾਲੇ ਕੈਨਵਸ (canvas) ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ । ਨਾਲ ਹੀ ਤੋਂ 500 ਪ੍ਰਤੀ m² ਦੀ ਦਰ ਨਾਲ ਇਸ ਵਿੱਚ ਵਰਤੋਂ ਹੋਣ ਵਾਲੇ ਕੈਨਵਸ ਦੀ ਲਾਗਤ ਪਤਾ ਕਰੋ । (ਧਿਆਨ ਦਿਉ ਕਿ ਤੰਬੂ ਦੇ ਆਧਾਰ ਨੂੰ ਕੈਨਵਸ ਨਾਲ ਨਹੀਂ ਢੱਕਿਆ ਜਾਂਦਾ ॥
ਹੱਲ:
ਸ਼ੰਕੂ ਦਾ ਵਿਆਸ = ਬੇਲਣ ਦਾ ਵਿਆਸ
2R = 4 m
R = 2 m

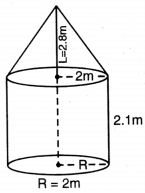
ਸ਼ੰਕੂ ਦਾ ਅਰਧ ਵਿਆਸ = ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ
ਬੇਲਣ ਦੀ ਉੱਚਾਈ (H) = 2.1 m
ਸ਼ੰਕੂ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ(L) = 2.8m
ਤੰਬੂ ਦੀ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ
= ਬੇਲਣ ਦੀ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ + ਸ਼ੰਕੂ ਦੀ ਵਕਰ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 2πRH + πRL
= πR [2H + L]
= \(\frac{22}{7}\) × 2[2(21) + 28]m²
= \(\frac{22}{7}\) × 2[42 + 2.8]m²
= \(\frac{22}{7}\) × 2 × 7 m²
= 44 m²
∴ ਤੰਬੂ ਦੀ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ = 44 m²
1m² ਕੈਨਵਸ ਦੀ ਲਾਗਤ = ₹ 500
44 m² ਕੈਨਵਸ ਦੀ ਲਾਗਤ = ₹ 44 × 500
= ₹ 22000
ਕੈਨਵਸ ਦੀ ਕੁਲ ਲਾਗਤ = ₹ 22000

ਪ੍ਰਸ਼ਨ 8.
ਉੱਚਾਈ 2.4 cm ਅਤੇ ਵਿਆਸ 1.4 cm ਵਾਲੇ ਇੱਕ ਠੋਸ ਬੇਲਣ ਵਿੱਚੋਂ ਇਸੇ ਉੱਚਾਈ ਅਤੇ ਇਸੇ ਵਿਆਸ ਵਾਲਾ ਇੱਕ ਸ਼ੰਕੂ ਆਕਾਰ ਦਾ ਖੋਲ (cavity) ਕੱਟ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਬਾਕੀ ਬਚੇ ਠੋਸ ਦਾ ਨੇੜੇ ਤੋਂ ਨੇੜੇ ਵਰਗ ਸੈਂਟੀਮੀਟਰ (cm²) ਤੱਕ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਬੇਲਣ ਦਾ ਵਿਆਸ (D) = 1.4 cm
= ਸ਼ੰਕੂ ਦਾ ਵਿਆਸ
∴ ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ =ਸ਼ੰਕੂ ਦਾ ਅਰਧ ਵਿਆਸ
(R) = 0.7 cm
ਬੇਲਣ ਦੀ ਉੱਚਾਈ (H) = 2.4 cm

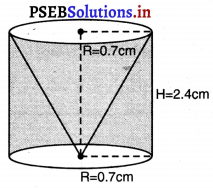
ਜਿਵੇਂ ਕਿ ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ L² = R² + H²
L = \(\sqrt{(0.7)^{2}+(2.4)^{2}}\)
= \(\sqrt {0.49+5.76}\)
= \(\sqrt {6.25}\) = 2∙5
L = 2.5 cm
ਬਾਕੀ ਬਚੇ ਠੋਸ ਦੀ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= ਬੇਲਣ ਦੀ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ + ਬੇਲਣ ਦੇ ਆਧਾਰ ਦਾ ਖੇਤਰਫਲ + ਸ਼ੰਕੂ ਦੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ
= 2πRH + πR² + πRL
= πR [2R + R + L]
= \(\frac{22}{7}\) × 0.7 [2(24) + 0.7 + 25]
= \(\frac{22}{7}\) × \(\frac{7}{10}\) [48 + 3.2] cm²
= \(\frac{22}{10}\) × [8] cm²
= \(\frac{176}{10}\) = 17.6 cm²
ਬਾਕੀ ਬਚੇ ਠੋਸ ਦਾ ਖੇਤਰਫਲ = 17.6 cm²

ਪ੍ਰਸ਼ਨ 9.
ਲੱਕੜੀ ਦੇ ਇੱਕ ਠੋਸ ਬੇਲਣ ਦੇ ਹਰੇਕ ਸਿਰੇ ‘ਤੇ ਇਕ ਅਰਧ ਗੋਲਾ ਖੋਦ ਕੇ ਕੱਢਦੇ ਹੋਏ, ਇੱਕ ਵਸਤੂ ਬਣਾਈ ਗਈ ਹੈ, ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ। ਜੇਕਰ ਬੇਲਣ ਦੀ ਉੱਚਾਈ 10 cm ਹੈ ਅਤੇ ਆਧਾਰ ਦਾ ਅਰਧ ਵਿਆਸ 3.5 cm ਹੈ ਤਾਂ ਇਸ ਵਸਤੂ ਦੀ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

ਹੱਲ:
ਬੇਲਣ ਦੀ ਉੱਚਾਈ (H) = 10 cm
ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ = ਅਰਧਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 3.5 cm

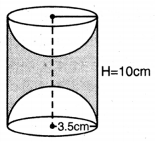
ਵਸਤੂ ਦੀ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ = ਬੇਲਣ ਦੀ ਵਕਰ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ + 2 (ਅਰਧ ਗੋਲੇ ਦੀ ਵਕਰ ਸੜਾ ਦਾ ਖੇਤਰਫਲ)
= 2πRH + 2(2πR²)
= 2πR[H + 2R]
= 2 × \(\frac{22}{7}\) × 35 [10 + (35)] cm²
= \(\frac{44}{7}\) × \(\frac{35}{10}\)[10 + 7]cm²
= 44 × \(\frac{5}{10}\) × 17 cm²
= 44 × \(\frac{1}{2}\) × 17 cm²
= 22 × 17 cm²
= 374 cm²
∴ ਵਸਤੂ ਦੀ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 374 cm²