PSEB 10th Class Maths Solutions Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Ex 13.2

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Ex 13.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Exercise 13.2

(ਜਦੋਂ ਤੱਕ ਨਾ ਕਿਹਾ ਜਾਵੇ, π = \(\frac{22}{7}\) ਲਓ )

ਪ੍ਰਸ਼ਨ 1.
ਇੱਕ ਠੋਸ ਇੱਕ ਅਰਧ ਗੋਲੇ ‘ਤੇ ਖੜ੍ਹੇ ਸ਼ੰਕੂ ਦੇ ਆਕਾਰ ਦਾ ਹੈ । ਦੋਹਾਂ ਦਾ ਅਰਧ ਵਿਆਸ 1 cm ਹੈ ਅਤੇ ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ ਉਸਦੇ ਅਰਧ ਵਿਆਸ ਦੇ ਬਰਾਬਰ ਹੈ । ਇਸ ਠੋਸ ਦਾ ਆਇਤਨ π ਦੇ ਪਦਾਂ ਵਿੱਚ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਸ਼ੰਕੁ ਦਾ ਅਰਧ ਵਿਆਸ = ਅਰਧਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ = 1 cm
R = 1 cm
∴ ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ (H) = 1 cm

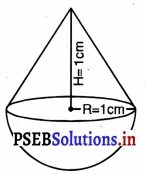
ਠੋਸ ਦਾ ਆਇਤਨ = ਸ਼ੰਕੂ ਦਾ ਆਇਤਨ + ਅਰਧਗੋਲੇ ਦਾ ਆਇਤਨ
= \(\frac{1}{3}\)πR²H + \(\frac{2}{3}\)πR³
= \(\frac{1}{3}\)πR²[H + 2R]
= \(\frac{1}{3}\)π × 1 × 1[1 + 2 × 1] cm²
= \(\frac{1}{3}\)π × 3 = \(\frac{3 \pi}{3}\) cm²
= π cm³
∴ ਠੋਸ ਦਾ ਆਇਤਨ = π cm³

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਇੰਜੀਨਿਅਰਿੰਗ ਦੇ ਵਿਦਿਆਰਥੀ ਮਨੋਹਰ ਨੂੰ ਇੱਕ ਪਤਲੀ ਐਲੂਮੀਨੀਅਮ ਦੀ ਸ਼ੀਟ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋਏ ਇੱਕ ਮਾਡਲ ਬਣਾਉਣ ਲਈ ਕਿਹਾ ਗਿਆ ਜੋ ਇੱਕ ਅਜਿਹੇ ਬੇਲਣ ਦੇ ਆਕਾਰ ਦਾ ਹੋਵੇ ਜਿਸਦੇ ਦੋਨੋਂ ਸਿਰਿਆਂ ‘ਤੇ ਦੋ ਸ਼ੰਕੂ ਜੁੜੇ ਹੋਏ ਹੋਣ ।ਇਸ ਮਾਡਲ ਦਾ ਵਿਆਸ 3 cm ਹੈ ਅਤੇ ਇਸ ਦੀ ਲੰਬਾਈ 12 cm ਹੈ । ਜੇਕਰ ਹਰੇਕ ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ 2 cm ਹੋਵੇ ਤਾਂ ਮਨੋਹਰ ਦੁਆਰਾ ਬਣਾਏ ਗਏ ਮਾਡਲ ਵਿੱਚ ਮੌਜੂਦ ਹਵਾ ਦਾ ਆਇਤਨ ਪਤਾ ਕਰੋ। (ਇਹ ਮੰਨ ਲਓ ਮਾਡਲ ਦੀਆਂ ਅੰਦਰੂਨੀ ਅਤੇ ਬਾਹਰੀ ਪਸਾਰਾਂ ਲਗਭਗ ਬਰਾਬਰ ਹਨ ।
ਹੱਲ:

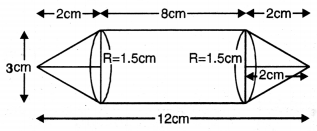
ਸ਼ੰਕੂ ਦਾ ਅਰਧ ਵਿਆਸ = ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ (R) = \(\frac{3}{2}\) cm
R = 5 cm
∴ R = 1.5 cm
ਹਰੇਕ ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ (h) = 2 cm
∴ ਬੇਲਣ ਦੀ ਉਚਾਈ = (12 -2 – 2) cm
= 8 cm
ਬੇਲਣ ਵਿਚ ਮੌਜੂਦ ਹਵਾ ਦਾ ਆਇਤਨ = ਬੇਲਣ ਦਾ ਆਇਤਨ + 2 (ਸ਼ੰਕੂ ਦਾ ਆਇਤਨ)

ਬੇਲਣ ਵਿਚ ਹਵਾ ਦਾ ਆਇਤਨ
= \(\frac{22}{7}\) × \(\frac{3}{2}\) × \(\frac{3}{2}\) × \(\frac{28}{3}\) cm³
= 22 × 3 cm³
= 66 cm³
= 66 cm³

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਗੁਲਾਬਜਾਮਣ ਵਿੱਚ ਉਸਦੇ ਆਇਤਨ ਦੀ ਲਗਭਗ 30% ਖੰਡ ਦੀ ਚਾਸ਼ਣੀ ਹੁੰਦੀ ਹੈ | 45 ਗੁਲਾਬ ਜਾਮਣਾਂ ਵਿਚ ਲਗਭਗ ਕਿੰਨੀ ਚਾਸ਼ਣੀ ਹੋਵੇਗੀ, ਜੇਕਰ ਹਰੇਕ ਗੁਲਾਬਜਾਮਣ ਇੱਕ ਬੇਲਣ ਦੇ ਆਕਾਰ ਦਾ ਹੈ, ਜਿਸਦੇ ਦੋਨੋਂ ਸਿਰੇ ਅਰਧਗੋਲਾਕਾਰ ਹਨ ਅਤੇ ਉਸ ਦੀ ਲੰਬਾਈ 5 cm ਅਤੇ ਵਿਆਸ 2.8 cm ਹੈ (ਦੇਖੋ ਚਿੱਤਰ) ।

ਹੱਲ:
ਗੁਲਾਬ ਜਾਮਣ ਬੇਲਣ ਦੇ ਆਕਾਰ ਦਾ ਹੈ, ਜਿਸਦੇ ਦੋਵੇਂ ਸਿਰੇ ਅਰਧਗੋਲਾਕਾਰ ਹਨ ।
ਵੇਲਣ ਦਾ ਵਿਆਸ = ਅਰਧ ਗੋਲੇ ਦਾ ਵਿਆਸ = 2.8 cm
ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ = ਅਰਧ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (R)
= \(\frac{2.8}{2}\) = 1.4 cm
R = 1.4 cm

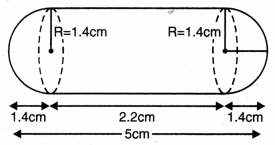
ਬੇਲਣਾਕਾਰ ਭਾਗ ਦੀ ਉੱਚਾਈ
= (5 – 14 – 1.4) cm
= (5 – 2.8) cm
= 2.2 cm
ਇੱਕ ਗੁਲਾਬ ਜਾਮਣ ਦਾ ਆਇਤਨ
= ਬੇਲਣ ਦਾ ਆਇਤਨ + 2 [ਅਰਧ ਗੋਲੇ ਦਾ ਆਇਤਨ]

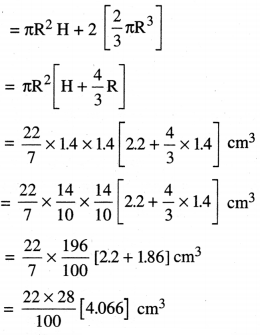
= 22∙05 cm³
ਇਕ ਗੁਲਾਬ ਜਾਮਣ ਦਾ ਆਇਤਨ
= 25.05 cm³
ਹੁਣ, 45 ਗੁਲਾਬ ਜਾਮਣਾਂ ਦਾ ਆਇਤਨ
= 45 × 25.05 cm³
= 1127.25 cm³
∴ ਖੰਡ ਦੀ ਚਾਸ਼ਣੀ ਦਾ ਆਇਤਨ
= 45 ਗੁਲਾਬ ਜਾਮਣਾਂ ਦੇ ਆਇਤਨ ਦਾ 30%
= \(\frac{30 \times 1127.25}{100}\) cm³
= 338.175 cm³
∴ ਖੰਡ ਦੀ ਚਾਸ਼ਣੀ ਦੀ ਮਾਤਰਾ = 338 cm³

ਪ੍ਰਸ਼ਨ 4.
ਇੱਕ ਕਲਮਦਾਨ ਘਣਾਵ ਆਕਾਰ ਦੀ ਇੱਕ ਲੱਕੜੀ ਨਾਲ ਦਾ ਬਣਿਆ ਹੈ ਜਿਸ ਵਿੱਚ ਕਲਮ ਰੱਖਣ ਦੇ ਲਈ ਚਾਰ ਸ਼ੰਕੁ ਆਕਾਰ ਖੱਡੇ ਬਣੇ ਹੋਏ ਹਨ | ਘਣਾਵ ਦੀਆਂ ਪਸਾਰਾਂ (dimensions) 15 cm × 10 cm × 3.5 cm ਹਨ । ਹਰੇਕ ਖੰਡੇ ਦਾ ਅਰਧ ਵਿਆਸ 0.5 cm ਹੈ ਅਤੇ ਗਹਿਰਾਈ 1.4 cm ਹੈ । ਪੁਰੇ ਕਲਮਦਾਨ ਵਿੱਚ ਲੱਕੜੀ ਦਾ ਆਇਤਨ ਪਤਾ ਕਰੋ । (ਦੇਖੋ ਚਿੱਤਰ)

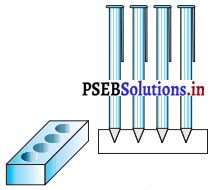
ਹੱਲ:
ਘਣਾਵ ਦੀ ਲੰਬਾਈ (L) = 15 cm
ਘਣਾਵ ਦੀ ਚੌੜਾਈ (B) = 10 cm
ਘਣਾਵ ਦੀ ਉੱਚਾਈ (H) = 3.5 cm
ਸ਼ੰਕੁ ਆਕਾਰ ਖੰਡੇ ਦਾ ਅਰਧ ਵਿਆਸ = 0.5 cm
ਸ਼ੰਕੂ ਆਕਾਰ ਖੱਡੇ ਦੀ ਉੱਚਾਈ h = 1.4 cm
ਕਲਮਦਾਨ ਵਿੱਚ ਲੱਕੜੀ ਦਾ ਆਇਤਨ
= ਘਣਾਵ ਦਾ ਆਇਤਨ – 4 [ਸ਼ੰਕੂ ਦਾ ਆਇਤਨ]

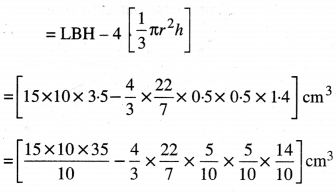
= (15 × 35 – \(\frac{22}{3×5}\) ) cm³
= (525 – 1.466) cm³
= 523.534 cm³.
ਕਲਮਦਾਨ ਵਿੱਚ ਲੱਕੜੀ ਦਾ ਆਇਤਨ
= 523.53 cm³

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਬਰਤਨ ਇੱਕ ਉਲਟੇ ਸ਼ੰਕੂ ਦੇ ਆਕਾਰ ਦਾ ਹੈ । ਇਸਦੀ ਉੱਚਾਈ 8 cm ਹੈ ਅਤੇ ਇਸਦੇ ਉੱਪਰੀ ਸਿਰੇ (ਜੋ ਖੁਲਿਆ ਹੋਇਆ ਹੈ) ਦਾ ਅਰਧ ਵਿਆਸ 5 cm ਹੈ । ਇਹ ਉੱਪਰ ਤੱਕ ਪਾਣੀ ਨਾਲ ਭਰਿਆ ਹੋਇਆ ਹੈ। ਜਦੋਂ ਇਸ ਬਰਤਨ ਵਿੱਚ ਸਿੱਕੇ ਦੀਆਂ ਕੁੱਝ ਗੋਲੀਆਂ ਜਿੰਨ੍ਹਾਂ ਵਿੱਚੋਂ ਹਰੇਕ 0:5 cm ਅਰਧ ਵਿਆਸ ਵਾਲਾ ਇੱਕ ਗੋਲਾ ਹੈ, ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ਤਾਂ ਇਸ ਵਿੱਚੋਂ ਭਰੇ ਹੋਏ ਪਾਣੀ ਦਾ ਇੱਕ ਚੌਥਾਈ ਭਾਗ ਬਾਹਰ ਨਿਕਲ ਜਾਂਦਾ ਹੈ | ਬਰਤਨ ਵਿਚ ਪਾਈਆਂ ਗਈਆਂ ਸਿੱਕੇ ਦੀਆਂ ਗੋਲੀਆਂ ਦੀ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ।
ਹੱਲ:

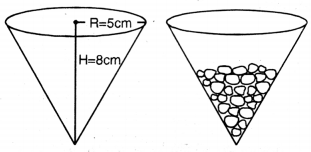
ਸ਼ੰਕੂ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 5 cm
ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ (H) = 8 cm
ਸਿੱਕੇ ਦੀ ਹਰੇਕ ਗੋਲੀ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 0.5 cm
ਮੰਨ ਲਉ ਗੋਲੀਆਂ ਦੀ ਸੰਖਿਆ = N
ਤਾਂ ਪਾਣੀ ਦਾ ਇੱਕ ਚੌਥਾਈ ਭਾਗ ਬਾਹਰ ਨਿਕਲ ਜਾਂਦਾ ਹੈ ।
N [ਗੋਲੀਆਂ ਦਾ ਆਇਤਨ = \(\frac{1}{4}\) ਸ਼ੰਕੂ ਵਿੱਚ ਪਾਣੀ ਦਾ ਆਇਤਨ


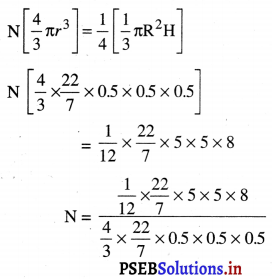
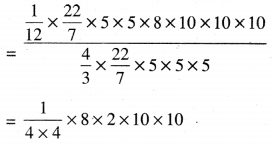
= 10 × 10 = 100
ਗੋਲੀਆਂ ਦੀ ਸੰਖਿਆ = 100

ਪ੍ਰਸ਼ਨ 6.
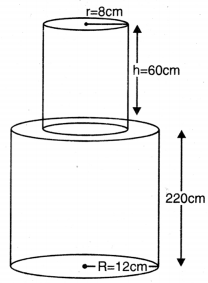
ਉੱਚਾਈ 220 cm ਅਤੇ ਆਧਾਰ ਵਿਆਸ 24 cm ਵਾਲੇ ਇੱਕ ਬੇਲਣ ਜਿਸ ਤੇ ਉੱਚਾਈ 60 cm ਅਤੇ ਅਰਧ ਵਿਆਸ 8 cm ਵਾਲਾ ਇੱਕ ਹੋਰ ਬੇਲਣ ਰੱਖਿਆ ਹੋਇਆ ਹੈ, ਨਾਲ ਲੋਹੇ ਦਾ ਇੱਕ ਖੰਬਾ ਬਣਾਇਆ ਗਿਆ ਹੈ । ਇਸ ਖੰਬੇ ਦਾ ਮਾਨ (ਭਾਰ) ਪਤਾ ਕਰੋ, ਜਦੋਂ ਕਿ ਦਿੱਤਾ ਹੈ 1 cm³ ਲੋਹੇ ਦਾ ਮਾਣ (ਭਾਰ) 8g ਹੁੰਦਾ ਹੈ (π = 3∙14 ਲਓ) ।
ਹੱਲ:
ਹੇਠਾਂ ਵਾਲੇ ਬੇਲਣ ਦਾ ਵਿਆਸ = 24 cm
ਹੇਠਾਂ ਵਾਲੇ ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 12 cm
ਹੇਠਾਂ ਵਾਲੇ ਬੇਲਣ ਦੀ ਉੱਚਾਈ (H) = 220 cm
ਉੱਪਰ ਵਾਲੇ ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 8 cm
ਉੱਪਰ ਵਾਲੇ ਬੇਲਣ ਦੀ ਉੱਚਾਈ (h) = 60 cm

ਖੰਬੇ ਦਾ ਆਇਤਨ = ਹੇਠਾਂ ਵਾਲੇ ਬੇਲਣ ਦਾ ਆਇਤਨ + | ਉੱਪਰ ਵਾਲੇ ਬੇਲਣ ਦਾ ਆਇਤਨ
= πR²H + πr²h
= [3.14 × 12 × 12 × 220 + 3.14 × 8 × 8 × 60] cm³
= [99475.2 + 12057.6] cm³
ਖੰਬੇ ਦਾ ਆਇਤਨ = 111532.8 cm³
1 cm³ ਦਾ ਦ੍ਰਵਸਾਨ = 8 gm
111532.8 cm³ ਦਾ ਦ੍ਰਵਸਾਨ = 8 × 111532. 8 gm
= 892262.4 gm
= \(\frac{892262.4}{1000}\) gm
= 892.2624 kg
= 892.2624 kg

ਪ੍ਰਸ਼ਨ 7.
ਇੱਕ ਠੋਸ ਵਿੱਚ, ਉੱਚਾਈ 120 cm ਅਤੇ ਅਰਧ ਵਿਆਸ 60 cm ਵਾਲਾ ਇੱਕ ਸ਼ੰਕੂ ਸ਼ਾਮਿਲ ਹੈ ਜੋ 60 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਇੱਕ ਅਰਧਗੋਲੇ ‘ਤੇ ਬਣਿਆ ਹੈ ਇਸ ਠੋਸ ਨੂੰ ਪਾਣੀ ਨਾਲ ਭਰੇ ਹੋਏ ਇੱਕ ਲੰਬ ਚੱਕਰੀ ਬੋਲਣ ਵਿੱਚ ਇਸ ਪ੍ਰਕਾਰ ਸਿੱਧਾ ਪਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਕਿ ਇਹ ਬੋਲਣ ਦੇ ਤਲ ਨੂੰ ਸਪਰਸ਼ ਕਰੇ । ਜੇਕਰ ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ 60 cm ਹੈ ਅਤੇ ਉੱਚਾਈ 180 cm ਹੈ ਤਾਂ ਬੇਲਣ ਵਿੱਚ ਬਾਕੀ ਬੱਚੇ ਪਾਣੀ ਦਾ ਆਇਤਨ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਸ਼ੰਕੂ ਦਾ ਅਰਧ ਵਿਆਸ = ਅਰਧ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ
= ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ
= 60 cm

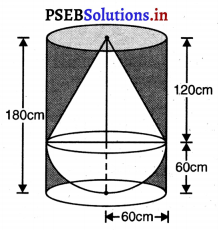
ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ (h) = 120 cm
ਬੇਲਣ ਦੀ ਉੱਚਾਈ (H) = 180 cm
ਬੇਲਣਾਕਾਰ ਬਰਤਨ ਦਾ ਆਇਤਨ = πR²H
= \(\frac{22}{7}\) × 60 × 60 × 180 cm³
= 2036571.4 cm³
ਬੇਲਣ ਵਿਚ ਪਾਏ ਗਏ ਠੋਸ ਦਾ ਆਇਤਨ = ਅਰਧ ਗੋਲੇ ਦਾ ਆਇਤਨ + ਸ਼ੰਕੂ ਦਾ ਆਇਤਨ
= \(\frac{2}{3}\)πR³ + \(\frac{1}{3}\)πR²h
= \(\frac{1}{3}\)πR²[2R + h]
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 60 × 60 [2 × 60 +120] cm³
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 3600 [120 + 120] cm³
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 3600 × 40 cm³
= 905142.86 cm³
ਬਾਹਰ ਨਿਕਲੇ ਪਾਣੀ ਦਾ ਆਇਤਨ
= 905142.86 cm³
∴ ਬੇਲਣ ਵਿਚ ਬਚੇ ਬਾਕੀ ਪਾਣੀ ਦਾ ਆਇਤਨ = ਬੇਲਣ ਦਾ ਆਇਤਨ – ਬਰਤਨ ਵਿਚ ਪਾਏ ਗਏ ਠੋਸ ਦਾ ਆਇਤਨ
= (2036571.4 – 905142.86) cm³
= 1131428.5 cm³
= \(\frac{1131428.5}{100 \times 100 \times 100}\) m³
= 1.131 m³
∴ ਬੇਲਣ ਵਿੱਚ ਬਾਕੀ ਬਚੇ ਪਾਣੀ ਦਾ ਆਇਤਨ
= 1.131 m³

ਪ੍ਰਸ਼ਨ 8.
ਇੱਕ ਗੋਲਾਕਾਰ ਕੱਚ ਦੇ ਬਰਤਨ ਦੀ ਇੱਕ ਬੇਲਣ ਦੇ ਆਕਾਰ ਦੀ ਗਰਦਨ ਹੈ ਜਿਸ ਦੀ ਲੰਬਾਈ 8 cm ਹੈ ਅਤੇ ਵਿਆਸ 2 cm ਹੈ ਜਦੋਂ ਕਿ ਗੋਲਾਕਾਰ ਭਾਗ ਦਾ ਵਿਆਸ 8.5 cm ਹੈ । ਇਸ ਵਿੱਚ ਭਰੇ ਜਾ ਸਕਣ ਵਾਲੇ ਪਾਣੀ ਦੀ ਮਾਤਰਾ ਮਾਪ ਕੇ, ਇੱਕ ਬੱਚੇ ਨੇ ਇਹ ਪਤਾ ਕੀਤਾ ਕਿ ਇਸ ਬਰਤਨ ਦਾ ਆਇਤਨ 345 cm³ ਹੈ । ਜਾਂਚ ਕਰੋ ਕਿ ਉਸ | ਬੱਚੇ ਦਾ ਉੱਤਰ ਸਹੀ ਹੈ ਜਾਂ ਨਹੀਂ, ਇਹ ਮੰਨਦੇ ਹੋਏ ਕਿ ਉਪਰੋਕਤ ਮਾਪਣ ਅੰਦਰੂਨੀ ਮਾਪਣ ਹੈ ਅਤੇ π = 3.14।
ਹੱਲ:
ਗਰਦਨ ਦਾ ਵਿਆਸ ਬਿਲਣਾਕਾਰ ਭਾਗ) = 2 cm

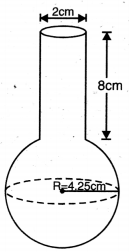
∴ ਗਰਦਨ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 1 cm
ਬੇਲਣਾਕਾਰ ਭਾਗ ਦੀ ਉੱਚਾਈ (H) = 8 cm
ਗੋਲਾਕਾਰ ਭਾਗ ਦਾ ਵਿਆਸ = 8.5 cm
ਗੋਲਾਕਾਰ ਭਾਗ ਦਾ ਅਰਧ ਵਿਆਸ (R) = \(\frac{8.5}{2}\) cm
= 4.25 cm
ਬਰਤਨ ਵਿਚ ਪਾਣੀ ਦਾ ਆਇਤਨ = ਗੋਲੇ ਦਾ ਆਇਤਨ + ਬੇਲਣ ਦਾ ਆਇਤਨ
= \(\frac{4}{3}\)πR³ + πr²h
= (\(\frac{4}{3}\) × 3.14 × 4.25 × 4.25 + 2.25 + 3.14 × 1 × 1 × 8) cm³
= (321.39 + 25.12) cm³
= 346.51 cm³
ਬਰਤਨ ਵਿਚ ਪਾਣੀ ਦਾ ਆਇਤਨ = 346.51 cm³ ਉਹ ਗਲਤ ਹੈ।