PSEB 10th Class Maths Solutions Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Ex 13.3

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Ex 13.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Exercise 13.3

ਜਦੋਂ ਤੱਕ ਕਿਹਾ ਨਾ ਜਾਵੇ, π = \(\frac{22}{7}\) ਲਓ।

ਪ੍ਰਸ਼ਨ 1.
ਅਰਧ ਵਿਆਸ 4.2 cm ਵਾਲੇ ਧਾਤੂ ਦੇ ਇੱਕ ਗੋਲੇ ਨੂੰ ਪਿਘਲਾ ਕੇ ਅਰਧ ਵਿਆਸ 6 cm ਵਾਲੇ ਇੱਕ ਬੇਲਣ ਦੇ ਰੂਪ ਵਿੱਚ ਢਾਲਿਆ ਜਾਂਦਾ ਹੈ । ਬੇਲਣ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:

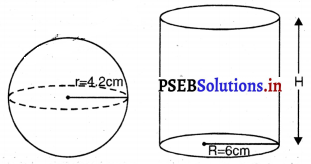
ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 4.2 cm
ਬੋਲਣ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 6 cm
ਮੰਨ ਲਉ ਬੇਲਣ ਦੀ ਉੱਚਾਈ = H cm
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ,
ਗੋਲੇ ਦਾ ਆਇਤਨ = ਬੇਲਣ ਦਾ ਆਇਤਨ
\(\frac{4}{3}\)πr³ = πR²H
\(\frac{4}{3}\) × \(\frac{22}{7}\) × 4.2 × 4.2 × 4.2
= \(\frac{22}{7}\) × 6 × 6 × H

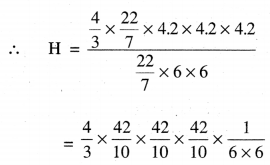
= \(\frac{2744}{1000}\) = 2.744 cm
ਬੇਲਣ ਦੀ ਉੱਚਾਈ (H) = 2744 cm

ਪ੍ਰਸ਼ਨ 2.
ਕ੍ਰਮਵਾਰ : 6 cm, 8 cm ਅਤੇ 10 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਧਾਤੂ ਦੇ ਤਿੰਨ ਠੋਸ ਗੋਲਿਆਂ ਨੂੰ ਪਿਘਲਾ ਕੇ ਇੱਕ ਵੱਡਾ ਠੋਸ ਗੋਲਾ ਬਣਾਇਆ ਜਾਂਦਾ ਹੈ ਇਸ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ ਪਤਾ ਕਰੋ ।
ਹੱਲ:

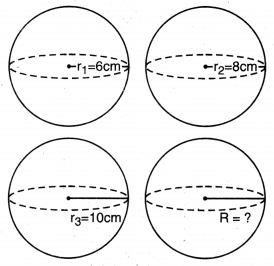
ਪਹਿਲੇ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (r₁) = 6 cm
ਦੂਸਰੇ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (r₂) = 8 cm
ਤੀਸਰੇ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (r₃) = 10 cm
ਮੰਨ ਲਉ ਨਵੇਂ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ = R cm
ਤਿੰਨਾਂ ਗੋਲਿਆਂ ਦਾ ਆਇਤਨ = ਵੱਡੇ ਗੋਲੇ ਦਾ ਆਇਤਨ

= 2 × 2 × 3 cm
R = 12 cm
∴ ਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ = 12 cm

ਪ੍ਰਸ਼ਨ 3.
ਵਿਆਸ 7 m ਵਾਲਾ ਇੱਕ ਖੁਹ 20 m ਡੂੰਘਾ ਪੁੱਟਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਪੁੱਟਣ ਨਾਲ ਨਿਕਲੀ ਹੋਈ ਮਿੱਟੀ ਨੂੰ ਇੱਕੋ ਜਿਹੇ | ਰੂਪ ਵਿੱਚ ਫੈਲਾ ਕੇ 22 m × 14 m ਵਾਲਾ ਇੱਕ ਚਬੂਤਰਾ | ਬਣਾਇਆ ਗਿਆ ਹੈ | ਚਬੂਤਰੇ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਖੂਹ ਦਾ ਵਿਆਸ = 7 m
ਖੂਹ (ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ) R = 6 m
ਖੂਹ ਦੀ ਉੱਚਾਈ (H) = 20 m
ਚਬੂਤਰੇ ਦੀ ਲੰਬਾਈ (L) = 22 m
ਦੇ ਚਬੂਤਰੇ ਦੀ ਚੌੜਾਈ (B) = 14 m
ਮੰਨ ਲਓ ਚਬੂਤਰੇ ਦਾ ਅਰਧ ਵਿਆਸ = H m

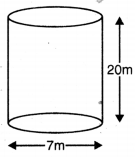
ਖੂਹ ਵਿਚੋਂ ਨਿਕਲੀ ਮਿੱਟੀ ਦਾ ਆਇਤਨ = ਬਣਾਏ ਗਏ ਚਬੂਤਰੇ ਦਾ ਆਇਤਨ

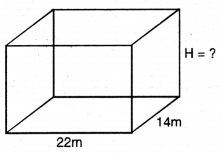
πR²H = L × B × H
\(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) × 20 = 22 × 14 × h
∴ H = \(\frac{\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 20}{22 \times 14}\)
H = 2.5 cm
∴ ਚਬੂਤਰੇ ਦੀ ਉੱਚਾਈ H = 2.5 cm.

ਪ੍ਰਸ਼ਨ 4.
3 m ਵਿਆਸ ਦਾ ਇੱਕ ਖੁਹ 14 m ਦੀ ਗਹਿਰਾਈ ਡੂੰਘਾਈ) ਤੱਕ ਪੁੱਟਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਵਿੱਚੋਂ ਨਿਕਲੀ ਹੋਈ ਮਿੱਟੀ ਨੂੰ ਖੂਹ ਦੇ ਚਾਰੇ ਪਾਸੇ 4m ਚੌੜੀ ਇੱਕ ਚੱਕਰਾਕਾਰ ਚਬੂਤਰਾ (ring) ਬਣਾਉਂਦੇ ਹੋਏ, ਸਮਾਨ ਰੂਪ ਨਾਲ ਫੈਲਾ ਕੇ ਇੱਕ ਪ੍ਰਕਾਰ ਦਾ ਬੰਨ ਬਣਾਇਆ ਜਾਂਦਾ ਹੈ। ਬੰਨ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਖੂਹ ਦੀ ਗਹਿਰਾਈ (h) = 14
ਖੂਹ ਦਾ ਅਰਧ ਵਿਆਸ (P) = \(\frac{3}{2}\) m

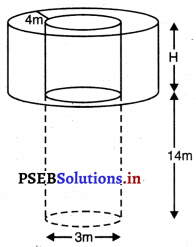
ਬੰਨ ਖੋਖਲੇ ਬੇਲਣ ਦੇ ਆਕਾਰ ਦਾ ਹੈ ਜਿਸਦਾ ਅੰਦਰੂਨੀ ਅਰਧ ਵਿਆਸ ਖੂਹ ਦੇ ਅਰਧ ਵਿਆਸ ਦੇ ਬਰਾਬਰ ਹੈ ਅਤੇ ਬੰਨ ਦੀ ਚੌੜਾਈ 4 m ਹੈ ।
ਬੰਨ ਦੇ ਅੰਦਰਲਾ ਅਰਧ ਵਿਆਸ (r)
= ਖੂਹ ਦਾ ਅਰਧ ਵਿਆਸ (r) = \(\frac{3}{2}\) m
ਬੰਨ ਦਾ ਬਾਹਰੀ ਅਰਧ ਵਿਆਸ (R)
= (\(\frac{3}{2}\) + 4) m
R = \(\frac{11}{2}\) m
= 5.5 m
ਨਿਕਲੀ ਹੋਈ ਮਿੱਟੀ ਦਾ ਆਇਤਨ
= ਬਣੇ ਹੋਏ ਬੰਨਦਾ ਆਇਤਨ
πr²h = ਬਾਹਰੀ ਬੇਲਣ ਦਾ ਆਇਤਨ – ਅੰਦਰੂਨੀ ਬੇਲਣ ਦਾ ਆਇਤਨ
= πR²H – πr²H
= πH[R² – r²]
\(\frac{22}{7}\) × \(\frac{3}{2}\) × \(\frac{3}{2}\) × 14
= \(\frac{22}{7}\) × H[(5.5)² – (1.5)²]
H = \(=\frac{\frac{22}{7} \times \frac{3}{2} \times \frac{3}{2} \times 14}{\frac{22}{7} \times(5.5-1.5)(5.5+1.5)}\) m
= \(\frac{1.5 \times 1.5 \times 14}{4 \times 7}\) m
= 1.125 m
∴ ਬੰਨ ਦੀ ਉੱਚਾਈ H = 1.125 m

ਪ੍ਰਸ਼ਨ 5.
12 cm ਵਿਆਸ ਅਤੇ 15 cm ਉੱਚਾਈ ਵਾਲੇ ਇੱਕ । ਲੰਬ ਚੱਕਰੀ ਬੇਲਣ ਦੇ ਆਕਾਰ ਦਾ ਬਰਤਨ ਆਇਸਕੀਮ ਨਾਲ ਪੂਰਾ ਭਰਿਆ ਹੋਇਆ ਹੈ । ਇਸ਼ ਆਇਸਕ੍ਰੀਮ ਦੀ ਉੱਚਾਈ 12 cm ਅਤੇ ਵਿਆਸ 6 cm ਵਾਲੇ ਸ਼ੰਕੂਆਂ ਵਿੱਚ ਭਰਿਆ ਜਾਣਾ ਹੈ, ਜਿਨ੍ਹਾਂ ਦਾ ਉੱਪਰੀ ਸਿਰਾ ਅਰਧ ਗੋਲਾਕਾਰ ਹੋਵੇਗਾ । ਉਨ੍ਹਾਂ ਸ਼ੰਕੂਆਂ ਦੀ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ਜੋ ਇਸ ਆਇਸਕੀਮ ਨਾਲ ਭਰੇ ਜਾ ਸਕਦੇ ਹਨ।
ਹੱਲ:

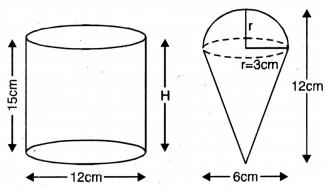
ਬੇਲਣ ਦਾ ਵਿਆਸ (D) = 12 cm
∴ ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 6 cm
ਬੇਲਣ ਦੀ ਉੱਚਾਈ (H) = 15 cm
ਸ਼ੰਕੂ ਦਾ ਵਿਆਸ = 6 cm
ਸ਼ੰਕੂ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 3 cm
ਅਰਧਗੋਲੇ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 3 cm
ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ (h) = 12 cm
ਮੰਨ ਲਉ ਸ਼ੰਕੂਆਂ ਦੀ ਸੰਖਿਆ = n
ਬਰਤਨ ਵਿਚ ਆਇਸਕ੍ਰਿਮ ਦਾ ਆਇਤਨ
= n [ਇੱਕ ਸ਼ੰਕੂ ਦਾ ਆਇਤਨ
πR²H = n
[ਸ਼ੰਕੂ ਦਾ ਆਇਤਨ + ਅਰਧਗੋਲੇ ਦਾ ਆਇਤਨ]

n = 10
ਸ਼ੰਕੂਆਂ ਦੀ ਸੰਖਿਆ = 10

ਪ੍ਰਸ਼ਨ 6.
5.5 cm × 10 cm × 3.5 cm ਪਸਾਰਾਂ ਵਾਲਾ ਇੱਕ ਘਣਾਵ ਬਣਾਉਣ ਦੇ ਲਈ 1.75 cm ਵਿਆਸ ਅਤੇ 2 mm ਮੋਟਾਈ ਵਾਲੇ ਕਿੰਨੇ ਚਾਂਦੀ ਦੇ ਸਿੱਕਿਆਂ (coins) ਨੂੰ ਪਿਘਲਾਉਣਾ ਪਏਗਾ ?
ਹੱਲ:
ਚਾਂਦੀ ਦਾ ਸਿੱਕਾ ਬੇਲਣ ਆਕਾਰ ਦਾ ਹੈ
ਚਾਂਦੀ ਦੇ ਸਿੱਕੇ ਦਾ ਵਿਆਸ = 1.75 cm
∴ ਚਾਂਦੀ ਦੇ ਸਿੱਕੇ ਦਾ ਅਰਧ ਵਿਆਸ (r) = \(\frac{1.75}{2}\) cm
ਚਾਂਦੀ ਦੇ ਸਿੱਕੇ ਦੀ ਮੋਟਾਈ
= ਬੇਲਣ ਦੀ ਉੱਚਾਈ (h) = 2 mm
ਅਰਥਾਤ h = \(\frac{2}{10}\) cm

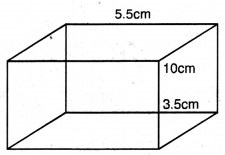
ਘਣਾਵ ਦੀ ਲੰਬਾਈ (L) = 5.5 cm
ਘਣਾਵ ਦੀ ਚੌੜਾਈ (B) = 10 cm
ਘਣਾਵ ਦੀ ਉਚਾਈ (H) = 3.5 cm

ਮੰਨ ਲਉ ਚਾਂਦੀ ਦੇ ਸਿੱਕਿਆਂ ਨੂੰ ਪਿਘਲਾ ਕੇ ਨਵਾਂ ਘਣਾਵ ਬਣਾਇਆ ਗਿਆ ਹੈ
ਘਣਾਵ ਦਾ ਆਇਤਨ = n[ਚਾਂਦੀ ਦੇ ਸਿੱਕੇ ਦਾ ਆਇਤਨ]
= n[πr²h]

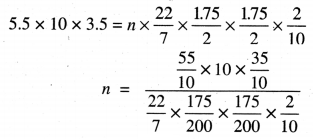
= 400
ਬਣੇ ਚਾਂਦੀ ਦੇ ਸਿੱਕਿਆਂ ਦੀ ਸੰਖਿਆ = 400

ਪ੍ਰਸ਼ਨ 7.
32 cm ਉੱਚੀ ਅਤੇ 18 cm ਆਧਾਰ ਦੇ ਅਰਧ ਵਿਆਸ ਵਾਲੀ ਇੱਕ ਬੇਲਣਾਕਾਰ ਬਾਲਟੀ ਰੇਤ ਨਾਲ ਭਰੀ ਹੋਈ ਹੈ । ਇਸ ਬਾਲਟੀ ਨੂੰ ਭੂਮੀ ‘ਤੇ ਖਾਲੀ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਸ ਰੇਤ ਦੀ ਇੱਕ ਸ਼ੰਕੂ ਆਕਾਰ ਢੇਰੀ ਬਣਾਈ ਜਾਂਦੀ ਹੈ । ਜੇਕਰ ਸ਼ੰਕੁ ਆਕਾਰ ਢੇਰੀ ਦੀ ਉੱਚਾਈ 24 cm ਹੈ, ਤਾਂ ਇਸ ਢੇਰੀ ਦਾ ਅਰਧ ਵਿਆਸ ਅਤੇ ਤਿਰਛੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:

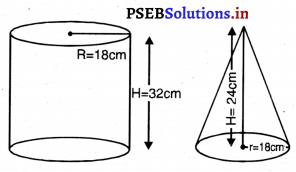
ਬੇਲਣਾਕਾਰ ਬਾਲਟੀ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 18 cm
ਬੇਲਣਾਕਾਰ ਬਾਲਟੀ ਦੀ ਉੱਚਾਈ (H) = 32 cm
ਸ਼ੰਕੂ ਦੀ ਉੱਚਾਈ (h) = 24 cm
ਮੰਨ ਲਉ ਸ਼ੰਕੂ ਦਾ ਅਰਧ ਵਿਆਸ ਅਤੇ ਢੇਰੀ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ ‘r’ cm ਅਤੇ ‘l’ cm ਹੈ ।
ਬਾਲਟੀ ਵਿਚ ਰੇਤ ਦਾ ਆਇਤਨ = ਸ਼ੰਕੂ ਵਿੱਚ ਰੇਤ ਦਾ ਆਇਤਨ

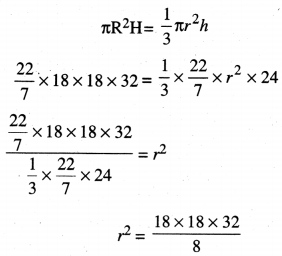
r² = 1296
r = \(\sqrt {1296}\) cm
r = 36 cm
∴ ਕੂ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 36 cm
ਜਿਵੇਂ ਕਿ ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ
(ਤਿਰਛੀ ਉੱਚਾਈ)² = (ਅਰਧਵਿਆਸ)² + (ਉੱਚਾਈ)²
l² = r² + h²
l = \(\sqrt{(36)^{2}+(24)^{2}}\)
= \(\sqrt {1296+576}\)
= \(\sqrt {1872}\)
= \(\sqrt {12×12×13}\)
l = 12\(\sqrt {13}\) cm
∴ ਸ਼ੰਕੂ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ (l) = 12\(\sqrt {13}\) cm

ਪ੍ਰਸ਼ਨ 8.
6 m ਚੌੜੀ ਅਤੇ 1.5 m ਗਹਿਰੀ (ਡੂੰਘੀ) ਇੱਕ ਨਹਿਰ ਵਿੱਚ ਪਾਣੀ 10 km/h ਦੀ ਚਾਲ ਨਾਲ ਵਹਿ (ਚੱਲ) ਰਿਹਾ ਹੈ ।30 ਮਿੰਟ ਵਿੱਚ, ਇਹ ਨਹਿਰ ਕਿੰਨੇ ਖੇਤਰਫਲ ਦੀ ਸਿੰਚਾਈ ਕਰ ਸਕੇਗੀ, ਜਦਕਿ ਸਿੰਚਾਈ ਦੇ ਲਈ 8 cm ਡੂੰਘੇ ਪਾਣੀ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ।
ਹੱਲ:
ਨਹਿਰ ਦੀ ਚੌੜਾਈ = 6 m
ਨਹਿਰ ਵਿੱਚ ਪਾਣੀ ਦੀ ਡੂੰਘਾਈ = 1.5 m
ਜਿਸ ਚਾਲ ਨਾਲ ਪਾਣੀ ਚਲ ਰਿਹਾ ਹੈ = 10 km/hr
ਇੱਕ ਘੰਟੇ ਵਿੱਚ ਨਿਕਲੇ ਪਾਣੀ ਦਾ ਆਇਤਨ = ਇਕ ਘੰਟੇ ਵਿੱਚ ਨਿਕਲੇ ਪਾਣੀ ਦੀ ਚਾਲ
= (6 × 1.5 m²) × 10 km
= 6 × 1.5 × 10 × 10 × 1000 m³.
∴ \(\frac{1}{2}\) ਘੰਟੇ ਵਿੱਚ ਨਿਕਲੇ ਪਾਣੀ ਦਾ ਆਇਤਨ
\(\frac{1}{2}\) × \(\frac{6×15}{10}\) × 100000
= 450000 m³
ਮੰਨ ਲਉ ਸਿੰਚਾਈ ਦਾ ਖੇਤਰਫਲ = (x) m²
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ ਖੇਤ ਵਿੱਚ 8 cm ਗਹਿਰੇ ਪਾਣੀ ਦੀ ਲੋੜ
∴ \(\frac{1}{2}\) ਘੰਟੇ ਵਿਚ ਨਿਕਲੇ ਪਾਣੀ ਦਾ ਆਇਤਨ ਹੈ
= ਖੇਤ ਵਿੱਚ ਪਾਣੀ ਦਾ ਆਇਤਨ
450000 m³ = (ਖੇਤ ਦਾ ਖੇਤਰਫਲ) × ਪਾਣੀ ਦੀ ਉੱਚਾਈ
450000 m³ = x × (m)
\(\frac{450000}{8}\) × 100 = x
x = 562500 m²
x = \(\frac{562500}{10000}\) ਹੈਕਟੇਅਰ
[1 m² = \(\frac{1}{10000}\) ਹੈਕਟੇਅਰ]
x = 56.25 ਹੈਕਟੇਅਰ
∴ ਖੇਤ ਦਾ ਖੇਤਰਫਲ = 56.25 ਹੈਕਟੇਅਰ

ਪ੍ਰਸ਼ਨ 9.
ਇੱਕ ਕਿਸਾਨ ਆਪਣੇ ਖੇਤ ਵਿਚ ਬਣੀ 10 m ਵਿਆਸ ਵਾਲੀ ਅਤੇ 2 m ਡੂੰਘੀ ਇੱਕ ਬੇਲਣਾਕਾਰ ਟੈਂਕੀ ਨੂੰ ਅੰਦਰੂਨੀ ਵਿਆਸ 20 cm ਵਾਲੇ ਇੱਕ ਪਾਇਪ ਦੁਆਰਾ ਇੱਕ ਨਹਿਰ ਨਾਲ ਜੋੜਦਾ ਹੈ। ਜੇਕਰ ਪਾਇਪ ਵਿੱਚ ਪਾਣੀ 3 km/h ਦੀ । ਚਾਲ ਨਾਲ ਚੱਲ (ਵਹਿ ਰਿਹਾ ਹੈ ਤਾਂ ਕਿੰਨੇ ਸਮੇਂ ਬਾਅਦ ਟੈਂਕੀ ਭਰ ਜਾਵੇਗੀ ?
ਹੱਲ:
ਪਾਣੀ ਦੀ ਚਾਲ = 3 km/hr
ਪਾਇਪ ਦਾ ਅੰਦਰੂਨੀ ਵਿਆਸ = 20 cm
∴ ਪਾਇਪ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 10 cm = \(\frac{10}{100}\) m
= \(\frac{1}{10}\) m
ਟੈਂਕੀ ਦਾ ਵਿਆਸ = 10 m
ਟੈਂਕੀ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 5 m
ਟੈਂਕੀ ਦੀ ਡੂੰਘਾਈ (H) = 2 m
ਮੰਨ ਲਉ ਪਾਇਪ n ਮਿੰਟਾਂ ਵਿਚ ਟੰਕੀ ਭਰਦੀ ਹੈ ਟੈਂਕੀ ਵਿਚ ਪਾਣੀ ਦਾ ਆਇਤਨ
= ਪਾਇਪ ਦੁਆਰਾ n ਮਿੰਟਾਂ ਵਿੱਚ ਚੱਕਿਆ ਪਾਣੀ
πR²H = n [ਅੰਦਰੂਨੀ ਕਾਟ ਦਾ ਖੇਤਰਫਲ × ਪਾਣੀ ਦੀ ਚਾਲੀ]
πR²H = n[(πr²) × 3 km/h]
\(\frac{22}{7}\) × (5)² × 2
= n[\(\frac{22}{7}\) × \(\frac{1}{10}\) × \(\frac{1}{10}\) × \(\frac{31000}{60}\)]
= 25 × 2
= n\(\frac{1}{10}\) × 50
⇒ n = 100 ਮਿੰਟ
∴ ਟੈਂਕੀ ਨੂੰ ਭਰਨ ਵਿਚ ਲੱਗਾ ਸਮਾਂ
= 100 ਮਿੰਟ