PSEB 10th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल और आयतन Ex 13.4

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल और आयतन Ex 13.4 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 13 पृष्ठीय क्षेत्रफल और आयतन Ex 13.4

(जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) लीजिए।)

प्रश्न 1.
पानी पीने वाला एक गिलास 14 cm ऊँचाई वाले एक शंकु के छिन्नक के आकार का है। दोनों वृत्ताकार सिरों के व्यास 4 cm और 2 cm हैं। इस गिलास की धारिता ज्ञात कीजिए। (Pb. 2015 Set B)
हल :

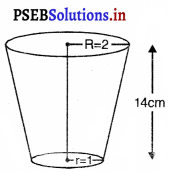
ऊपरी सिरे की त्रिज्या (R) = 2 cm
निचले सिरे की त्रिज्या (r) = 1 cm
गिलास की ऊँचाई (H) = 14 cm
गिलास छिन्नक के आकार का है
छिन्नक का आयतन = \(\frac{1}{3}\) π [R² + r² + Rr] H
= \(\frac{1}{3} \times \frac{22}{7}\) [(2)² + (1)² + 2 × 1] 14
= \(\frac{1}{3} \times \frac{22}{7}\) [4 + 1 + 2] 14
= \(\frac{1}{3} \times \frac{22}{7}\) 7 × 14
= \(\frac{22 \times 14}{3}\)
गिलास का आयतन = 102.67 cm³

प्रश्न 2.
एक शंकु के छिन्नक की तिर्यक ऊँचाई 4 cm है तथा इसके वृत्तीय सिरों के परिमाप ( परिधियां) 18 cm और 6 cm हैं। इस छिन्नक का वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :
छिन्नक की तिर्यक ऊँचाई = 4 cm

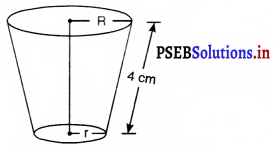
मान लीजिए ऊपरी सिरे और निचले सिरे की त्रिज्या R और r है।
ऊपरी सिरे की परिधि = 18 cm
2πR = 18
R = \(\frac{18}{2 \pi}=\frac{9}{\pi}\) cm
निचले सिरे की परिधि = 6 cm
2πr = 6 cm
r = \(\frac{6}{2 \pi}=\frac{3}{\pi}\) cm
छिन्नक का वक्र पृष्ठीय क्षेत्रफल = π [R + r]
= π \(\left[\frac{9}{\pi}+\frac{3}{\pi}\right]\) 4
= π \(\left[\frac{9+3}{\pi}\right]\)
= 12 × 4
= 48 cm²
छिन्नक का वक्र पृष्ठीय क्षेत्रफल = 48 cm².

प्रश्न 3.
एक तुर्की टोपी शंकु के एक छिन्नक के आकार की है ( देखिए आकृति)। यदि इसके खुले सिरे की त्रिज्या 10 cm है, ऊपरी सिरे की त्रिज्या 4 cm है और टोपी की तिर्यक ऊँचाई 15 cm है, तो इसके बनाने में प्रयुक्त पदार्थ का क्षेत्रफल ज्ञात कीजिए।

हल :

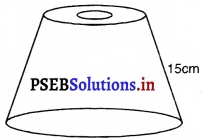
छिन्नक के निचले सिरे की त्रिज्या (R) = 10 cm
छिन्नक के ऊपरी सिरे की त्रिज्या (r) = 4 cm
छिन्नक की तिर्यक ऊँचाई (l) = 15 cm

छिन्नक का वक्र पृष्ठीय क्षेत्रफल = πl [R + r]
= \(\frac{22}{7}\) × 15 [10 + 4]
= \(\frac{22}{7}\) × 15 × 14
= 22 × 15 × 2
= 660 cm².
बंद सिरे का क्षेत्रफल = r = Fx (4)².
प्रयुक्त पदार्थ का कुल क्षेत्रफल = छिन्नक का वक्र पृष्ठीय क्षेत्रफल + बंद सिरे का क्षेत्रफल
= 660 + 50.28
= 710.28 cm².
अतः प्रयुक्त पदार्थ का कुल क्षेत्रफल = 710.28 cm².

प्रश्न 4.
धातु की चादर से बना और ऊपर से खुला एक बर्तन शंकु के एक छिन्नक के आकार का है, जिसकी ऊँचाई 16 cm है तथा निचले और ऊपरी सिरों की त्रिज्याएँ क्रमशः 8 cm और 20 cm हैं। ₹ 20 प्रति लीटर की दर से, इस बर्तन को पूरा भर सकने वाले दूध का मूल्य ज्ञात कीजिए। साथ ही, इस बर्तन को बनाने के लिए प्रयुक्त धातु की चादर का मूल्य ₹ 8 प्रति 100 cm- की दर से ज्ञात कीजिए। (= 3.14 लीजिए।)
हल :

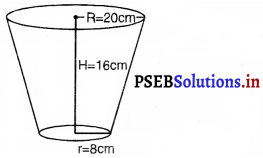
बर्तन के ऊपरी सिरे की त्रिज्या (R) = 20 cm
बर्तन के निचले सिरे की त्रिज्या (7) = 8 cm
बर्तन की ऊँचाई (H) = 16 cm
तिर्यक ऊँचाई (l) = \(\sqrt{\mathrm{H}^{2}+(\mathrm{R}-r)^{2}}\)
= \(\sqrt{(16)^{2}+(20-8)^{2}}\)
= \(\sqrt{256+144}\)
तिर्यक ऊँचाई (l) = \(\sqrt{400}=\sqrt{20 \times 20}\) = 20 cm
‘
बर्तन की धारिता = \(\frac{1}{3}\) πH [R² + r² + Rr]
= \(\frac{1}{3}\) × 3.14 × 16 [(20)² + (8)² + 20 × 8]
= \(\frac{3.14 \times 16}{3}\) [400 + 64 + 160]
= 3.14 × 16 × 624
= 10449.92 cm³
∴ बर्तन में दूध का आयतन = 10449.92 cm³
= \(\frac{10449.92}{1000}\) लिटर
∴ बर्तन में दूध का आयतन = 10.45 लिटर
1 लिटर का मूल्य = ₹ 20
∴ 10.45 लिटर का मूल्य = ₹ 20 × 10.45
दूध का मूल्य = ₹ 209
छिन्नक का वक्र पृष्ठीय क्षेत्रफल = πL [R + r]
= 3.14 × 20 [20 + 8)
= 3.14 × 20 × 28 cm²
= 1758.4 cm²
बर्तन के आधार का क्षेत्रफल = πr²
= 3.14 × (8)²
= 3.14 × 64
= 200.96 cm²
बर्तन बनाने के लिए प्रयुक्त धातु = छिन्नक का वक्र पृष्ठीय क्षेत्रफल + आधार का क्षेत्रफल
= (1758.4 + 200.96) cm²
= 1959.36 cm²
100 cm² धातु की चादर का मूल्य = ₹ 8
1 cm² धातु की चादर का मूल्य = ₹ \(\frac{8}{100}\)
1959.36 cm² धातु की चादर का मूल्य = ₹ \(\frac{8}{100}\) × 1959.36
= ₹156.748 = ₹ 156.75
अतः धातु की चादर का कुल मूल्य = ₹ 156.75
और दूध का कुल मूल्य ₹ 209 है।

प्रश्न 5.
20 cm ऊँचाई और शीर्ष कोण (vertical angle) 60° वाले एक शंकु की ऊँचाई के बीचो-बीच से होकर जाते हुए एक तल से दो भागों में काटा गया है, जबकि तल शंकु के आधार के समांतर है। यदि इस प्राप्त शंकु के छिन्नक को व्यास \(\frac{1}{16}\) cm वाले एक तार के रूप में बदल दिया जाता है तो तार की लंबाई ज्ञात कीजिए।
हल :
शंकु का शीर्ष कोण = 60°
शंक का शीर्षलम्ब शीर्ष कोण को द्विभाजित करता है।
∠EOF = 30°

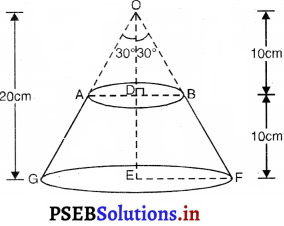
छिन्नक का आयतन = \(\frac{22}{7} \times 10 \times \frac{700}{9}\) cm³
= \(\frac{22}{7} \times \frac{7000}{9}\) cm³
छिन्नक की तार बनाई गई है जो कि बेलन के आकार की है जिसका व्यास \(\frac{1}{16}\) cm है।
∴ बेलनाकार तार की त्रिज्या (r₁) = \(\frac{1}{2} \times \frac{1}{16} \mathrm{~cm}=\frac{1}{32} \mathrm{~cm}\)
मान लीजिए इस प्रकार बने बेलन की ऊँचाई = H cm
रूप बदलने पर भी आयतन समान ही रहता है।
छिन्नक का आयतन = बेलनाकार तार का आयतन

H = 7964.44 m
अतः, बेलनाकार तार की लंबाई (H) = 7964.44 m