PSEB 10th Class Maths Solutions Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Ex 13.4

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Ex 13.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Exercise 13.4

(ਜਦੋਂ ਤੱਕ ਕਿਹਾ ਨਾ ਜਾਵੇ, π = \(\frac{22}{7}\) ਲਓ )

ਪ੍ਰਸ਼ਨ 1.
ਪਾਣੀ ਪੀਣ ਵਾਲਾ ਇੱਕ ਗਿਲਾਸ 14 cm ਉੱਚਾਈ | ਵਾਲੇ ਇੱਕ ਸ਼ੰਭੂ ਦੇ ਸ਼ੌਨਕ ਦੇ ਆਕਾਰ ਦਾ ਹੈ । ਦੋਨਾਂ ਚੱਕਰਾਕਾਰ ਸਿਰਿਆਂ ਦੇ ਵਿਆਸ 4 cm ਅਤੇ 2 cm ਹਨ । ਇਸ ਗਿਲਾਸ ਦੀ ਧਾਰਨ ਸਮਰੱਥਾ ਪਤਾ ਕਰੋ ।
ਹੱਲ:

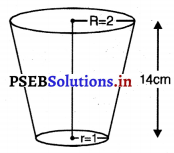
ਉੱਪਰੀ ਸਿਰੇ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 2 cm
ਹੇਠਲੇ ਸਿਰੇ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 1 cm
ਗਿਲਾਸ ਦੀ ਉੱਚਾਈ (H) = 14 cm
ਗਿਲਾਸ ਸ਼ੌਨਕ ਦੇ ਆਕਾਰ ਦਾ ਹੈ
ਸ਼ੌਨਕ ਦਾ ਆਇਤਨ
= \(\frac{1}{3}\)π[R² + r² + Rr]H
= \(\frac{1}{3}\) × \(\frac{22}{7}\)[(2)² + (1)² + 2 × 1]14 cm³
= \(\frac{1}{3}\) × \(\frac{22}{7}\)[4 + 1 + 2] 14 cm³
= \(\frac{1}{3}\) ×\(\frac{22}{7}\) × 7 × 14 cm³
= \(\frac{2214}{3}\) cm³ = 102.67 cm³
ਗਿਲਾਸ ਦੀ ਧਾਰਨ ਸਮਰੱਥਾ = 102.67 cm³

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਨਕ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ 4 cm ਹੈ ਅਤੇ ਇਸਦੇ ਚੱਕਰੀ ਸਿਰਿਆਂ ਦੇ ਪਰਿਮਾਪ (ਘੇਰਾ) 18 cm ਅਤੇ 6 cm ਹਨ ।ਇਸ ਛਿੰਕ ਦੀ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਛਿਨਕ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ (l) = 4 cm

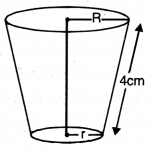
ਮੰਨ ਲਉ ਉੱਪਰੀ ਸਿਰੇ ਅਤੇ ਹੇਠਲੇ ਸਿਰੇ ਦਾ ਅਰਧ ਵਿਆਸ R ਅਤੇ r ਹੈ ।
ਉੱਪਰਲੇ ਸਿਰੇ ਦਾ ਪਰਿਮਾਪੁ = 18 cm
2πR = 18
R = \(\frac{18}{2 \pi}\) = \(\frac{9}{\pi}\) cm
ਹੇਠਲੇ ਸਿਰੇ ਦਾ ਪਰਿਮਾਪ = 6 cm
2πr = 6 cm
r = \(\frac{6}{2 \pi}\) = \(\frac{3}{\pi}\) cm
ਜ਼ਿੰਕ ਦੀ ਵਕਰ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= π[R + r]l
= π[\(\frac{9}{\pi}\) + \(\frac{3}{\pi}\)] 4 cm²
= 4[latex]\frac{9+3}{\pi}[/latex] 4 cm²
= 12 × 4 cm²
= 48 cm²
ਸ਼ੌਨਕ ਦੀ ਵਕਰ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ
= 48 cm²

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਤੁਰਕੀ ਟੋਪੀ ਸ਼ੰਕੁ ਦੇ ਇੱਕ ਛਿਨਕ ਦੇ ਆਕਾਰ ਦੀ ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ) ਜੇਕਰ ਇਸਦੇ ਖੁੱਲ੍ਹੇ ਸਿਰੇ ਦਾ ਅਰਧ ਵਿਆਸ 10 cm ਹੈ, ਉਪਰੀ ਸਿਰੇ ਦਾ ਅਰਧ ਵਿਆਸ 4 cm ਹੈ ਅਤੇ ਟੋਪੀ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ 15 cm ਹੈ, ਤਾਂ ਇਸ ਦੇ ਬਣਾਉਣ ਲਈ ਲੱਗੇ ਪਦਾਰਥ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

ਹੱਲ:

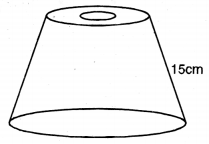
15cm
ਸ਼ੌਨਕ ਦੇ ਹੇਠਲੇ ਸਿਰੇ ਦਾ ਅਰਧਵਿਆਸ (R) = 10 cm
ਸ਼ੌਨਕ ਉੱਪਰਲੇ ਸਿਰੇ ਦਾ ਅਰਧਵਿਆਸ (r) =4 cm
ਛਿਨਕ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ (l) = 15 cm
ਛਿਨਕ ਦੀ ਵਕਰ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ
= πl[R + r]
=\(\frac{22}{7}\) × 15[10 + 4] cm²
= \(\frac{22}{7}\) × 15 × 14 cm²
= 22 × 15 × 2 cm²
= 660 cm²
ਬੰਦ ਸਿਰੇ ਦਾ ਖੇਤਰਫਲ = πr² = \(\frac{22}{7}\) × (4)² cm²
= \(\frac{22}{7}\) × 4 × 4cm² = \(\frac{352}{7}\) cm
ਲੋੜੀਂਦੇ ਪਦਾਰਥ ਦਾ ਕੁੱਲ ਖੇਤਰਫਲ
= ਛਿਨਕ ਦੀ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ + ਬੰਦ ਸਿਰੇ ਦਾ ਖੇਤਰਫਲ
= (660 + 50.28) cm²
= 710.28 cm²

ਪ੍ਰਸ਼ਨ 4.
ਧਾਤੂ ਦੀ ਚਾਦਰ ਨਾਲ ਬਣਿਆ ਅਤੇ ਉੱਪਰ ਤੋਂ ਖੁਲਿਆ ਇੱਕ ਬਰਤਨ ਸ਼ੰਕੂ ਦੇ ਇੱਕ ਛਿਨਕ ਦੇ ਆਕਾਰ ਦਾ ਹੈ, ਜਿਸਦੀ ਉੱਚਾਈ 16 cm ਹੈ ਅਤੇ ਹੇਠਲੇ ਅਤੇ ਉੱਪਰੀ ਸਿਰਿਆਂ ਦੇ ਅਰਧ ਵਿਆਸ ਕੁਮਵਾਰ 8 cm ਅਤੇ 20 cm ਹਨ । ₹ 20 ਪ੍ਰਤਿ ਲਿਟਰ ਦੀ ਦਰ ਨਾਲ, ਇਸ ਬਰਤਨ ਨੂੰ ਪੂਰਾ ਭਰ ਸਕਣ ਵਾਲੇ ਦੁੱਧ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ । ਨਾਲ ਹੀ, ਇਸ ਬਰਤਨ ਨੂੰ ਬਣਾਉਣ ਦੇ ਲਈ ਪ੍ਰਯੋਗ ਕੀਤੀ ਧਾਤੂ ਦੀ ਚਾਦਰ ਦਾ ਮੁੱਲ ₹ 8 ਤਿ 100 cm² ਦੀ ਦਰ ਨਾਲ ਪਤਾ ਕਰੋ । (π = 3.14 ਲਓ)
ਹੱਲ:

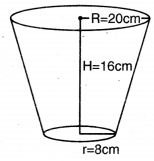
ਬਰਤਨ ਦੇ ਉੱਪਰੀ ਸਿਰੇ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 20 cm
ਹੇਠਲੇ ਸਿਰੇ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 8 cm
ਬਰਤਨ ਦੀ ਉੱਚਾਈ (H) = 16 cm
ਤਿਰਛੀ ਉੱਚਾਈ (l) =\(\sqrt{\mathrm{H}^{2}+(\mathrm{R}-r)^{2}}\)
= \(\sqrt{(16)^{2}+(20-8)^{2}}\)
= \(\sqrt {256+144}\)
(l) = \(\sqrt {400}\) = \(\sqrt {20×20}\) cm
= 20 cm
ਬਰਤਨ ਦੀ ਧਾਰਿਤਾ = \(\frac{1}{3}\) πH[R² + r² + Rr²]
= \(\frac{1}{3}\) × 3.14 × 16[(20)² + (8)² + 20 × 8]
= \(\frac{3.14×16}{3}\)[400 + 64 + 160] cm³
= 3.14 × 16 × 624 cm³
= 10449.92 cm³
∴ ਬਰਤਨ ਵਿਚ ਦੁੱਧ ਦਾ ਆਇਤਨ
= 10449.92 cm³
= \(\frac{10449.92}{1000}\) ਲਿਟਰ
∴ ਬਰਤਨ ਵਿਚ ਦੁੱਧ ਦਾ ਆਇਤਨ = 10.45 ਲਿਟਰ
1 ਲਿਟਰ ਦਾ ਮੁੱਲ = ₹ 20
∴ 10.45 ਲਿਟਰ ਦਾ ਮੁੱਲ = ₹ 20 × 10.45
ਦੁੱਧ ਦਾ ਮੁੱਲ = ₹ 209
ਸ਼ੌਨਕ ਦੀ ਵਿਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ
= πL [R + r]
= 3:14 × 20 [20 + 8]
= 3.14 × 20 × 28 cm²
= 1758.4 cm²
ਬਰਤਨ ਦੇ ਆਧਾਰ ਦਾ ਖੇਤਰਫਲ = πr²
= 3.14 × (8)²
= 3.14 × 64
= 200.96 cm²
ਬਰਤਨ ਬਣਾਉਣ ਲਈ ਪ੍ਰਯੋਗ ਕੀਤੀ ਧਾਤੂ ਦੀ ਚਾਦਰ ਦਾ ਖੇਤਰਫਲ = ਸ਼ੌਨਕ ਦੀ ਵਕਰ ਸੜਾ ਦਾ ਖੇਤਰਫਲ + ਆਧਾਰ ਦਾ ਖੇਤਰਫਲ :
= (1758. 4 + 200.96) cm²
= 1959.36 cm²
100 cm² ਧਾਤੂ ਦੀ ਚਾਦਰ ਦਾ ਮੁੱਲ = ₹ 8
1 cm² ਧਾਤੂ ਦੀ ਚਾਦਰ ਦਾ ਮੁੱਲ = ₹ \(\frac{8}{10}\)
1959.36 cm² ਧਾਤੂ ਦੀ ਚਾਦਰ ਦਾ ਮੁੱਲ
= ₹ \(\frac{8}{100}\) × 1959.36
= ₹ 156.748
= ₹ 15675
ਧਾਤੂ ਦੀ ਚਾਦਰ ਦਾ ਕੁੱਲ ਮੁੱਲ
= ₹ 156.75
ਦੁੱਧ ਤੇ ਕੁੱਲ ਲਾਗਤ ਤੋਂ 209

ਪ੍ਰਸ਼ਨ 5.
20 cm ਉੱਚਾਈ ਅਤੇ ਸਿਖ਼ਰ ਕੋਣ (Vertical angle) 60° ਵਾਲੇ ਇੱਕ ਸ਼ੰਕੂ ਨੂੰ ਉਸਦੀ ਉੱਚਾਈ ਦੇ ਵਿੱਚਕਾਰ ਤੋਂ ਹੋ ਕੇ ਜਾਂਦੇ ਇੱਕ ਤਲ ਨਾਲ ਦੋ ਭਾਗਾਂ ਵਿੱਚ ਕੱਟਿਆ ਗਿਆ ਹੈ, ਜਦੋਂ ਕਿ ਤਲ ਸ਼ੰਕੂ ਦੇ ਆਧਾਰ ਦੇ ਸਮਾਂਤਰ ਹੈ । ਜੇਕਰ ਇਸ ਪ੍ਰਾਪਤ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਕ ਨੂੰ ਵਿਆਸ \(\frac{1}{16}\) cm ਵਾਲੇ ਇੱਕ ਤਾਰ ਦੇ ਰੂਪ ਵਿੱਚ ਬਦਲ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਤਾਂ ਤਾਰ ਦੀ ਲੰਬਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਸ਼ੰਕੂ ਦੇ ਸਿਖਰ ਦਾ ਕੋਣ = 60°
ਸ਼ੰਕੂ ਦਾ ਸਿਖਰਲੰਬ ਸਿਖ਼ਰ ਕੋਣ ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦਾ ਹੈ
∠EOF = 30°

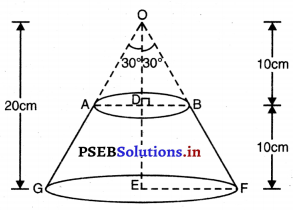
△ODB ਵਿਚ,
\(\frac{BD}{OD}\) = tan 30°
\(\frac{r}{10}\) = \(\frac{1}{\sqrt{3}}\)
r = \(\frac{1o}{\sqrt{3}}\) cm
△OEF ਵਿਚ,
\(\frac{EF}{OE}\) = tan 30°
\(\frac{R}{20}\) = \(\frac{1}{\sqrt{3}}\)
R = \(\frac{20}{\sqrt{3}}\) cm

ਛਿਨਕ ਦੀ ਤਾਰ ਬਣਾਈ ਗਈ ਹੈ ਜੋ ਬੇਲਣ ਆਕਾਰ ਦੀ ਹੈ ਜਿਸਦਾ ਵਿਆਸ \(\frac{1}{16}\) cm ਹੈ ।
∴ ਬੇਲਣਾਕਾਰ ਤਾਰ ਦਾ ਅਰਧ ਵਿਆਸ (r₁)
= \(\frac{1}{2}\) × \(\frac{1}{16}\) cm = \(\frac{1}{32}\) cm
ਮੰਨ ਲਉ ਇਸ ਤਰ੍ਹਾਂ ਬਣੇ ਬੇਲਣ ਦੀ ਉੱਚਾਈ = H cm
ਰੂਪ ਬਦਲਣ ‘ਤੇ ਆਇਤਨ ਬਰਾਬਰ ਰਹਿੰਦਾ ਹੈ
ਸ਼ੌਨਕ ਦਾ ਆਇਤਨ = ਬੇਲਣਾਕਾਰ ਤਾਰ ਦਾ ਆਇਤਨ
\(\frac{22}{7}\) × \(\frac{7000}{9}\) = πr₁²H
\(\frac{22}{7}\) × \(\frac{7000}{9}\) = \(\frac{22}{7}\) × \(\left(\frac{1}{32}\right)^{2}\) × H
H = \(\frac{\frac{22}{7} \times \frac{7000}{9}}{\frac{22}{7} \times \frac{1}{32} \times \frac{1}{32}}\) cm
= \(\frac{7000}{9}\) × 32 × 32 cm
H = \(\frac{796444.44}{100}\) m
H = 7964.44 m
∴ ਬੇਲਣਾਕਾਰ ਤਾਰ ਦੀ ਲੰਬਾਈ
H = 7964.44 m