PSEB 10th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल और आयतन Ex 13.5

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल और आयतन Ex 13.5 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 13 पृष्ठीय क्षेत्रफल और आयतन Ex 13.5

प्रश्न 1.
व्यास 3 mm वाले ताँबे के तार को 12 cm लंबे और 10 cm व्यास वाले एक बेलन पर इस प्रकार लपेटा जाता है कि वह बेलन के वक्र पृष्ठ को पूर्णतया ढक लेता है। तार की लंबाई और द्रव्यमान ज्ञात कीजिए, यह मानते हुए कि ताँबे का घनत्व 8.88 g प्रति cm है।
हल :
तार का व्यास (d) = 3 mm
∴ तार की त्रिज्या (r) = \(\frac{3}{2}\) mm = \(\frac{3}{20}\) mm

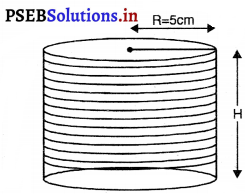
बेलन का व्यास = 10 cm
बेलन की त्रिज्या (R) = 5 cm
बेलन की ऊँचाई (H) = 12 cm
बेलन का परिमाप = एक लपेटे में प्रयुक्त तार की लंबाई
2πR = एक लपेटे में प्रयुक्त तार की लंबाई
2 × \(\frac{22}{7}\) × 5 = एक लपेटे में प्रयुक्त तार की लंबाई
\(\frac{220}{7}\) = एक लपेटे में प्रयुक्त तार की लंबाई
लपेटों की संख्या = बेलन की ऊँचाई / तार का व्यास
= \(\frac{12 \mathrm{~cm}}{3 \mathrm{~mm}}=\frac{12}{3} \times 10\)
= \(\frac{120}{3}\) = 40
∴ प्रयुक्त तार की लंबाई = लपेटों की संख्या × एक लपेटे में प्रयुक्त तार की लंबाई
H = 40 × \(\frac{220}{7}\) cm = 1257.14 cm
प्रयुक्त तार का आयतन = πr²H
= \(\frac{22}{7} \times \frac{3}{20} \times \frac{3}{20}\) × 1257.14
= 88.89 cm³
1 cm³ का द्रव्यमान = 8.88 gm
88.89 cm³ का द्रव्यमान = 8.88 x 88.89 = 789.41 gm

प्रश्न 2.
एक समकोण त्रिभुज, जिसकी भुजाएँ 3 cm और 4 cm हैं (कर्ण के अतिरिक्त), को उसके कर्ण के परितः घुमाया जाता है। इस प्रकार प्राप्त द्वि-शंकु (double cone) के आयतन और पृष्ठीय क्षेत्रफल ज्ञात कीजिए। ( का मान जो भी उपयुक्त लगे, प्रयोग कीजिए।)
हल :
मान लीजिए ∆ABC समकोण त्रिभुज हैं जिसके A पर समकोण है।
AB और AC का माप क्रमकर 3 cm और 4 cm है।

भुजा BC (कर्ण) की लंबाई = \(\sqrt{3^{2}+4^{2}}=\sqrt{9+16}\) = 5 cm
यहां, AO (या A’O ) प्राप्त द्विशंकु के साझें आधार की त्रिज्या समकोण त्रिभुज भुज BC के पास घूमकर बनती है।

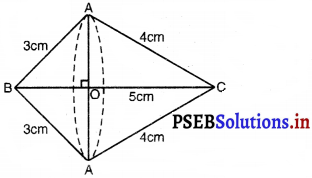
शंकु BAA’ की ऊँचाई BO और तिर्यक ऊँचाई 3 cm है।
शंकु CAA’ की ऊँचाई CO और तिर्यक ऊँचाई 4 cm है।
अब, ∆AOB ~ ∆CAB (AA समरुपता)
∴ \(\frac{\mathrm{AO}}{4}=\frac{3}{5}\)

⇒ AO = \(\frac{4 \times 3}{5}=\frac{12}{5}\) cm

साथ ही \(\frac{\mathrm{BO}}{3}=\frac{3}{5}\)

⇒ BO = \(\frac{3 \times 3}{5}=\frac{9}{5}\) cm
अत: CO = BC – OB
= 5 – \(\frac{9}{5}\)
= \(\frac{16}{5}\)
अब द्विशंकु का आयतन = शंकु ABA’ का आयतनन + शंकु ACA’ का आयतन

प्रश्न 3.
एक टंकी, जिसके आंतरिक मापन 150 cm × 120 cm × 110 cm हैं, में 129600 cm पानी है। इस पानी में कुछ छिद्र वाली ईंटें तब तक डाली जाती हैं, जब तक कि टंकी पूरी ऊपर तक भर न जाए। प्रत्येक ईंट अपने आयतन का, पानी सोख लेती है। यदि प्रत्येक ईंट का माप 22.5 cm x 7.5 cm x 6.5 cm हैं, तो टंकी में कुल कितनी ईंटें डाली जा सकती हैं, ताकि उसमें से पानी बाहर न बहे ?
हल :
ईंटों का आयतन = 22.5 × 7.5 × 6.5 cm³ = 1096.87 cm³
टंकी का आयतन = 150 × 120 × 110 cm³ = 1980000
मान लीजिए प्रयुक्त ईंटों की संख्या = n
n ईंटों का आयतन = n (एक ईंट का आयतन)
= n [1096.87] cm³
ईंटों के लिए उपलब्ध पानी का आयतन = 1980000 – 129600 = 1850400 cm³
प्रत्येक ईंट अपने आयतन का \(\frac{1}{17}\) वाँ आयतन पानी अवशोषित करती है।
ईंटों द्वारा अवशोषित पानी का आयतन = \(\frac{17}{10}\) × ईंटों के लिए उपलब्ध पानी का आयतन
= \(\frac{17}{10}\) × 1850400
ईंटों द्वारा अवशोषित पानी का आयतन = 1966050 cm³
n ईंटों का कुल आयतन = ईंटों द्वारा अवशोषित पानी की मात्रा
n[1096.87] cm³ = 1966050 cm³ .
n = \(\frac{1966050}{1096.87}\)
n = 1792.42
प्रयुक्त ईंटों की संख्या = 1792.

प्रश्न 4.
किसी महीने के 15 दिनों में, एक नदी की घाटी में 10 cm वर्षा हुई। यदि इस घाटी का क्षेत्रफल 97280 km है, तो दर्शाइए कि कुल वर्षा लगभग तीन नदियों के सामान्य पानी के योग के समतुल्य थी, जबकि प्रत्येक नदी 1072 km लंबी, 75 m चौड़ी और 3 m गहरी है।.
हल :
घाटी का क्षेत्रफल = 97280 km²
घाटी में वर्षा = 10 cm
∴ कुल वर्षा का आयतन = 97280 × \(\frac{10}{100} \times \frac{1}{1000}\) km³
= 9.728 km³

प्रश्न 5.
टीन की बनी हुई एक तेल की कुप्पी 10 cm लंबे एक बेलन में एक शंकु के छिन्नक को जोड़ने से बनी है। यदि इसकी कुल ऊँचाई 22 cm है, बेलनाकार भाग का व्यास 8 cm है और कुप्पी के ऊपरी सिरे का व्यास 18 cm है, तो इसके बनाने में लगी टीन की चादर का क्षेत्रफल ज्ञात कीजिए। ( देखिए आकृति)

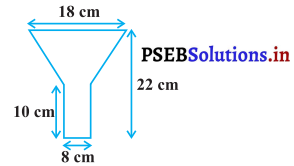
हल :
कुप्पी के ऊपरी सिरे का व्यास = 18 cm
∴ कुप्पी के ऊपरी सिरे की त्रिज्या (R) = \(\frac{18}{2}\) cm = 9 cm
कुप्पी के आधार का व्यास = 8 cm
कुप्पी के आधार की त्रिज्या (r) = 4 cm
बेलनाकार भाग की ऊँचाई (h) = 10 cm
छिन्नक की ऊँचाई (H) = (22 – 10) = 12 cm
छिन्नक की तिर्यक ऊँचाई (l) = \(\sqrt{\mathrm{H}^{2}+(\mathrm{R}-r)^{2}}\)
= \(\sqrt{(12)^{2}+(9-4)^{2}}\)
= \(\sqrt{144+(5)^{2}}\)
= \(\sqrt{144+25}=\sqrt{169}\)
छिन्नक की तिर्यक ऊँचाई (I) = 13 cm
टीन की चादर का क्षेत्रफल = बेलनाकार आधार का वक्र पृष्ठीय क्षेत्रफल + छिन्नक का वक्र पृष्ठीय क्षेत्रफल
= 2πrh + πL [R + r]
= 2 × \(\frac{22}{7}\) × 4 × 10 + \(\frac{212}{7}\) × 13 [9 + 4] cm²
= 251.42 + 531.14
= 782.56 cm²
प्रयुक्त की गई धातु की चादर का कुल क्षेत्रफल = 782.56 cm²

प्रश्न 6.
शंकु के छिन्नक के लिए, पूर्व स्पष्ट किए संकेतों का प्रयोग करते हुए, वक्र पृष्ठीय क्षेत्रफल और संपूर्ण पृष्ठीय क्षेत्रफल के उन सूत्रों को सिद्ध कीजिए, जो अनुच्छेद 13.5 में दिये गए हैं।
हल :
एक लंब वृत्तीय शंकु के छिन्नक दो असमान वृत्ताकार आधार और वक्र पृष्ठ होता है।
मान लीजिए भाग VCD को हटाकर प्राप्त छिन्नक ACDB है।
दोनों आधारों के केन्द्रों को मिलाने वाला रेखाखंड OP छिन्नक की ऊँचाई कहलाता है।
छिन्नक ACDB का प्रत्येक रेखाखंड AC और BD तिर्यक ऊँचाई है।

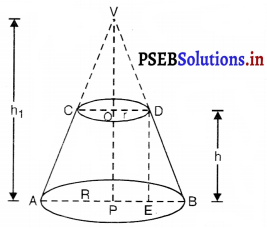
मान लीजिए R और r (R > r) शंकु (VAB) को छिन्नक ACDB के वृत्तीय सिरों की त्रिज्याएँ हैं ।
हम शंक्वाकार भाग VCD को पूरा करते हैं। मान लीजिए h और l क्रमश: ऊर्ध्वाधर ऊँचाई और तिर्यक ऊँचाई है।
तब OP = h और AC = BD = l.

लंब वृत्तीय शंकु के छिन्नक को दो लंबवृत्तीय शंकुओं के बराबर VAB और VCD के अंतर के रूप में देखा जा सकता है।
मान लीजिए शंकु VAB की ऊँचाई h, और तिर्यक ऊँचाई l है।
अर्थात् VP = h₁, और VA = VB = l₁.
अब समकोण त्रिभुज ∆ DEB में,
DB² = DE² + BE²
⇒ l² = h² + (R – r)²
l = \(\sqrt{h^{2}+(\mathrm{R}-r)^{2}}\)
पुनः ∆VOD ~ ∆VPB

शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल = πRl₁ – πr(l₁ – l)
[शंकु का वक्र पृष्ठीय क्षेत्रफल = π × r × l]
= πR . \(\frac{l \mathrm{R}}{\mathrm{R}-r}\) – πr . \(\frac{l r}{\mathrm{R}-r}\)
= πl \(\left(\frac{\mathrm{R}^{2}-r^{2}}{\mathrm{R}-r}\right)\)
= \(\frac{\pi l(\mathrm{R}-r)(\mathrm{R}+r)}{(\mathrm{R}-r)}\)
= πl (R + r) वर्ग मात्रक
∴ लंब वृत्तीय शंकु की छिन्नक का वक्र पृष्ठीय क्षेत्रफल = πl (R + r) वर्ग मात्रक
जहाँ l = \(\sqrt{h^{2}+(\mathrm{R}-r)^{2}}\)
और लंब वृत्तीय शंकु की छिन्नक का कुल पृष्ठीय क्षेत्रफल = वक्र पृष्ठीय क्षेत्रफल + आधार का क्षेत्रफल + ऊपरी सिरे का क्षेत्रफल
= πl (R + r) + πR² + πr²
= π [R² + r² + l (R + r)] वर्ग मात्रक।

प्रश्न 7.
शंकु के एक छिन्नक के लिए, पूर्व स्पष्ट किए संकेतों का प्रयोग करते हुए, आयतन का वह सूत्र सिद्ध कीजिए, जो अनुच्छेद 13.5 में दिया गया है।
हल :
एक लंब वृत्तीय शंकु के छिन्नक दो असमान वृत्ताकार आधार और वक्र पृष्ठ होता है।
मान लीजिए भाग VCD को हटाकर प्राप्त छिन्नक ACDB है।
दोनों आधारों के केन्द्रों को मिलाने वाला रेखाखंड OP छिन्नक की ऊँचाई कहलाता है।
छिन्नक ACDB का प्रत्येक रेखाखंड AC और BD तिर्यक ऊँचाई है।

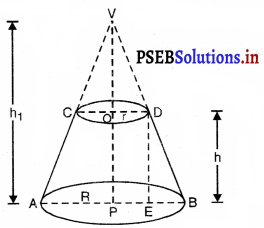
मान लीजिए R और r (R > r) शंकु (VAB) को छिन्नक ACDB के वृत्तीय सिरों की त्रिज्याएँ हैं।
हम शंक्वाकार भाग VCD को पूरा करते हैं। मान लीजिए h और l क्रमश: ऊर्ध्वाधर ऊँचाई और तिर्यक ऊँचाई है।
तब OP = h और AC = BD = l.

लंब वृत्तीय शंकु के छिन्नक को दो लंबवृत्तीय शंकुओं के बराबर VAB और VCD के अंतर के रूप में देखा जा सकता है।
मान लीजिए शंकु VAB की ऊँचाई h, और तिर्यक ऊँचाई है।
अर्थात् VP = h₁, और VA = VB = l₁.
∴ शंकु VCD की ऊँचाई = VP – OP
= h₁ – h
क्योंकि समकोण त्रिभुज VOD और VPB समरूप हैं
⇒ \(\frac{\mathrm{VO}}{\mathrm{VP}}=\frac{\mathrm{OD}}{\mathrm{PB}}=\frac{h_{1}-h}{h_{1}}=\frac{r}{\mathrm{R}}\)

⇒ 1 – \(\frac{h}{h_{1}}=\frac{r}{\mathrm{R}}\)

⇒ \(\frac{h}{h_{1}}=1-\frac{r}{\mathrm{R}}=\frac{\mathrm{R}-r}{\mathrm{R}}\)

⇒ h₁ = \(\frac{h \mathrm{R}}{\mathrm{R}-r}\)
शंकु की ऊँचाई VCD = h₁ – h
= \(\frac{h \mathrm{R}}{\mathrm{R}-r}\) – h
= \(\frac{h \mathrm{R}-h \mathrm{R}+h r}{\mathrm{R}-r}=\frac{h \mathrm{R}}{\mathrm{R}-r}\)
शंकु VAB के छिन्नक ACDB का आयतन = शंकु (V, AB) का आयतन – शंकु (V, CD) का आयतन

= \(\frac{1}{3}\) πh (R² + Rr + r²)
अतः शंकु के छिन्नक का आयतन = \(\frac{1}{3}\) πh (R² + Rr + r²)
पुनः यदि A₁ और A₂ (A₁ > A₂) दो वृत्ताकार आधारों के पृष्ठीय क्षेत्रफल हैं।
A₁ = πR² और A₂ = πr².
अब शंकु के छिन्नक का आयतन = \(\frac{1}{3}\) πh (R² + Rr + r²)
= \(\frac{h}{3}\left(\pi \mathrm{R}^{2}+\pi r^{2}+\sqrt{\pi \mathrm{R}^{2}} \sqrt{\pi r^{2}}\right)\)
= \(\frac{h}{3}\left(\mathrm{~A}_{1}+\mathrm{A}_{2}+\sqrt{\mathrm{A}_{1} \mathrm{~A}_{2}}\right)\)